1 Introduction

The calculation of load capacities in gears is essential in the designing process of a gearbox. The increasingly accurate predictions of pittings, micropittings, scuffing damages and root fractures have partially led to an optimization of gear designs. Those fatigue failures are prevented by varying the macro- and microgeometry, change in lubrication and surface hardening, mechanically or chemically by means of heat treatments. Consequently, the occurrence of the damage mechanism of tooth flank fractures has become more frequent. Flank fractures are categorized as interior tooth fractures that often take place with large-module gears and/or relatively low case-hardening depths [1]. Both the inhomogeneous depth profile of the material strength and the residual stresses have a major influence on the damage mechanism.

With today’s state of the art, residual stresses can be estimated analytically by different methods, such as by Lang [2] or the research project FVA 835, considering the distance from the surface. Some approaches include the local perpendicular tooth width, which can be easily determined for spur gears. Flank fractures, however, can also occur in bevel gears. Therefore, the methods often include the conversion to equivalent spur gears [3, 4]. In order to design the calculation process more efficiently, a new methodology is developed to calculate residual stresses of case-hardened gears independently from the geometry. The analytical approaches is transferred from spur gears to bevel gears in this paper. This allows to mirror the calculation approaches for bevel gears with experimental test results and to continue developing them further in the future on that basis.

2 Transfer of analytical approaches for the calculation of residual stresses to bevel gears

To calculate the load bearing capacity of bevel gears, the application BECAL (Bevel Gear Calculation) can be used, which is developed by the Institute of Machine Elements and Machine Design (IMM, TUD Dresden University of Technology). Since BECAL is a FEM-enhanced loaded tooth contact analysis (LTCA), three-dimensional meshes of surfaces, whole teeth and gears can be created based on the real geometry and are used fully automatically. Thanks to continuous further development over the past 30 years, BECAL is capable of calculating the load-bearing capacity against all classic gear damages very accurately. The work presented here on transferring the estimation methods for residual stresses from cylindrical gears is an important step towards implementing a true local, three-dimensional load bearing capacity estimation for the entire inner tooth volume. In the following, the state of the art as well as the newly developed transfer of approaches from cylindrical to bevel gears are described.

2.1 State of the art for residual stress calculations

Residual stresses are caused by heat treatment in case-hardened gears. With the purpose of designing gears without the risk of flank fractures, it is necessary to predict those residual stresses in order to be able to take them into account in the calculation process. Considering that, different methods have been developed. Lang [2] described one of the most common approaches ((1), (2)) that determines the residual stress σres based on the difference between the local hardness HV(y) and core hardness HVC. HV(y) can be calculated with [2, 5]. The method does not consider tensile stresses at higher material depth, which are necessary for the stress equilibrium. Hertter [6] modified the Eq. 1 by increasing the last constant from 400 to 460.

$$\sigma _{\mathrm{res}}\left(y\right)=\frac{2}{7}\left(HV\left(y\right)-HV_{C}\right)-400 \quad\text{ for } HV\left(y\right)-HV_{C}> 300$$
(1)
$$\sigma _{\mathrm{res}}\left(y\right)=-\frac{5}{4}\left(HV\left(y\right)-HV_{C}\right)\quad\text{ for } HV\left(y\right)-HV_{C}\leq 300$$
(2)

The report of FVA 835 [7] is one of the latest publications regarding the analytical calculation of residual stresses. The herein presented equations are based on a variety of heat treatment simulations and depend on the regarded material depth. Different significant residual stresses and their locations are needed for the application of this method, e.g. the maximum compressive and tensile stresses and the surface stress.

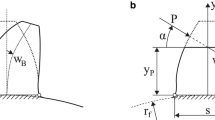
The described methods above are directly transferable onto bevel gears. Böhme [4] developed a method in which he extended the modified Lang equations by adding a 4th degree polynomial to represent tensile residual stresses in the core. The following equation is added:

$$\sigma _{\mathrm{res}}\left(y\right)=a\left(y-s_{\mathrm{n}\upalpha }\right)^{4}+b\left(y-s_{\mathrm{n}\upalpha }\right)^{2}+c \quad\text{ for } y\geq CHD$$
(3)

with

$$s_{\mathrm{n}\upalpha }=\frac{s_{n}}{2\cdot \cos \left(\alpha \right)}$$
$$a=\frac{-\sigma _{\mathrm{res}{,}\mathrm{CHD}}+\frac{{\sigma }_{\mathrm{res}{,}\mathrm{CHD}}^{'}}{2}\left(CHD-s_{\mathrm{n}\upalpha }\right)+c}{\left(CHD-s_{\mathrm{n}\upalpha }\right)^{4}}$$
$$b=\frac{{\sigma }_{\mathrm{res}{,}\mathrm{CHD}}^{'}-4a\cdot \left(CHD-s_{\mathrm{n}\upalpha }\right)^{3}}{2\cdot \left(CHD-s_{\mathrm{n}\upalpha }\right)}$$
sn:

Local chordal tooth width

snα:

perpendicular tooth width

α:

local pressure angle

CHD:

case-hardening depth

σres,CHD:

res. stress at CHD

\({\sigma }_{\mathrm{res}{,}\mathrm{CHD}}^{'}\):

res. stress gradient at CHD

Figure 1 shows the predicted residual stress of a spiral bevel gear [4]. Therefore, the mean normal section of a tooth is used to create an equivalent spur gear.

Fig. 1
figure 1

Residual stress model for a bevel gear calculated with Böhme’s approach [4, 8]

Full size image

2.2 Transfer of residual stress calculation methods for bevel gears in BECAL

Considering different mesh strategies that are already implemented in BECAL [9], it is not effective to calculate the residual stresses for one specific case or a substitute model. For this reason, a method was newly developed in order to determine the residual stresses of every node in the tooth volume independently of the mesh strategy. The method shown in the following can also be seen as a first step to initiate further research. Based on the functioning implementation of a mechanically reasonable and proven method in the area of spur gears, further development can follow to optimize the methodology on any gear geometry. The following steps are necessary to transfer Böhme’s method [4] according to Eq. 3 to spiral bevel gears.

To determine the necessary local tooth width snα,i of every internal node, the normal vectors of the surface nodes \(\vec{n}_{i}\) are needed. With that, the node’s snα,i can be derived by calculating the intersection of the normal vectors and the tooth’s centre (Fig. 2a). This step is followed by the process of creating a temporary element that is defined by four surface nodes and their corresponding intersections with the tooth’s middle face. At that every internal node is investigated to determine which temporary element it lies within. In view of the geometry of spiral bevel gears, it is possible that areas are created where internal nodes cannot be assigned to an element, for example in the tooth head or the end faces of spiral bevel gears.

Fig. 2
figure 2

Projection of a respective node towards the surface and tooth’s mid using a temporary element with four surface nodes (P2, P3, P6, P7) and their corresponding points of intersection (P1, P4, P5, P8)

Full size image

In order to determine if a node is positioned within an element, shape functions \(N_{i}\left(\xi {,}\eta {,}\zeta \right)\) can be used that typically are part of FEM-systems (Eq. 4). The irregular element is then transformed into a regular cube in a natural coordinate system as well as the respective node (Fig. 2b). If the coordinates of the investigated node are within a specific range, then it can be assigned to the respective element.

For any node i with the position \(\vec{x}_{i}\) in the tooth volume, a set of natural coordinates \(\vec{\xi }_{i}=\left[\xi _{i}\:\eta _{i}\:\zeta _{i}\right]^{T}\) can be found numerically, which describes its position inside the associated temporary element using the shape functions N of a linear hexahedral element:

$$N_{1}\left(\xi {,}\eta {,}\zeta \right)=(1-\xi )(1-\eta )(1-\zeta )/8$$
$$\vdots$$
(4)
$$N_{8}\left(\xi {,}\eta {,}\zeta \right)=(1-\xi )(1+\eta )(1+\zeta )/8$$
$$\vec{x}_{i}=\left[\vec{x}_{P1}\cdots \vec{x}_{P8}\right]\cdot \left[\begin{array}{c} N_{1}\left(\xi _{i}{,}\eta _{i}{,}\zeta _{i}\right)\\ \vdots \\ N_{8}\left(\xi _{i}{,}\eta _{i}{,}\zeta _{i}\right) \end{array}\right]$$
(5)

Knowing the natural coordinates \(\vec{\xi }_{i}\) of any node in its temporary element, the associated tooth depth snα,i can be determined by calculating the distance from the tooth flank to the tooth center using the same methodology. After the verification of the node’s position, the coordinate ξ can be set to 1 and −1 for its projection towards the front and back face of the unit cube. Those faces are equivalent to the tooth’s surface and the middle face, which can be provided by the operating LTCA-program, which in this case is BECAL. The projected nodes are then transformed back into the global coordinate system. In addition, the depth of the node beneath the surface yi can be found that way:

$$s_{\mathrm{n}\upalpha i}=\Bigg| \left[\vec{x}_{P1}\cdots \vec{x}_{P8}\right]\cdot \left(\left[\begin{array}{c} N_{1}\left(1{,}\eta _{i}{,}\zeta _{i}\right)\\ \vdots \\ N_{8}\left(1{,}\eta _{i}{,}\zeta _{i}\right) \end{array}\right]- \left[\begin{array}{c} N_{1}\left(-1{,}\eta _{i}{,}\zeta _{i}\right)\\ \vdots \\ N_{8}\left(-1{,}\eta _{i}{,}\zeta _{i}\right) \end{array}\right]\right)\Bigg|$$
(6)
$$y_{i}=\Bigg| \left[\vec{x}_{P1}\cdots \vec{x}_{P8}\right]\cdot \left(\left[\begin{array}{c} N_{1}\left(1{,}\eta _{i}{,}\zeta _{i}\right)\\ \vdots \\ N_{8}\left(1{,}\eta _{i}{,}\zeta _{i}\right) \end{array}\right]-\left[\begin{array}{c} N_{1}\left(\xi _{i}{,}\eta _{i}{,}\zeta _{i}\right)\\ \vdots \\ N_{8}\left(\xi _{i}{,}\eta _{i}{,}\zeta _{i}\right) \end{array}\right]\right) \Bigg|$$
(7)

2.3 Application of the developed method

Figure 3 displays the application of the described method on a spiral bevel gear. Therefore, the local tooth width snα,i was calculated in order to determine the residual stress as a function of the distance from the surface yi.

Fig. 3
figure 3

Residual stress in a cross section of a spiral bevel gear

Full size image

The grey areas are non-calculable due to the blind spot that is created by the curved flanks and thus does not provide snα,i. The section beneath the tooth roots is not considered in this analysis since it is not associated with the affected area of flank fractures. The plot shows an even distribution of residual stresses along the flanks. The tooth’s head displays higher tensile stresses, which can occur due to the comparably large surface that is exposed to the heat treatment’s effects. The principle of residual stress development during the case-hardening process is displayed in Fig. 3b. It shows a tooth that is exposed to gas containing carbon, marked as “C”. As a result of the size of the surrounding surface and the local tooth width, the residual stresses can vary in its value. The compressive stress transitions into tensile stresses. The figure shows that the inner tooth’s head is affected more by heat treatment and therefore leads to higher tensile stresses. The tensile stress at snα is limited for the newly implemented calculation model [4, 10] to avoid excessive stresses in the head.

It is apparent that the calculation methods that include the local tooth thickness can be problematic near the gear tooth’s head. This obstacle can be evaded by interpolating the values from the nearby nodes. However, due to the large affected area, this method might be unreliable. An alternative would be to build the stress equilibrium along a section orthogonal to the tooth’s head that crosses the whole gear. This, however, would imply a large-scale extension of the calculation model for an area that is unaffected by flank fracture failures. Therefore, the calculations should be reduced to the nodes that are relevant for this kind of gear failure.

The described methodology of interpolation based on shape functions can also be used for other applications, e.g. when the user has conducted a heat treatment simulation with a different mesh from which the residual stresses can be derived from. To map the simulated stresses onto the LTCA-mesh, the reference cube should not be the above-described temporary element defined by the surface nodes and their center-intersections. Moreover, it must be a single element originating from the heat treatment mesh since the residual stress is not linearly distributed along the tooth width snα. However, the stress value can be linearly interpolated within an element of a single layer (Fig. 4).

Fig. 4
figure 4

Applications for the interpolation method

Full size image

After the application of the new methodology, based on the nodes scalar residual stress values, tensors are obtained and transformed into the global coordinate system. This allows the addition of the residual stress tensor to the stress tensor σ caused by the local externally induced load, provided by BECAL.

3 Determination of amplitudes and mean stresses based on stress tensors

As a consequence of the geometry and the combined rolling and sliding of the contacting flanks, the stress tensor components show highly complex stress tensor-time curves. Integral equivalent stress hypotheses have proven themselves to be the most suitable method to calculate the flank fracture safety. It allows the consideration of every material plane [1, 6, 8, 11]. Therefore, the amplitudes and mean stresses of the normal and shear stress shall be calculated.

The principle of calculating the amplitudes and mean stresses can best be presented by using a unit sphere. Every single material plane can be defined with the angles φ and ϑ. The resulting vector

$$\vec{n}_{1}=\left[\begin{array}{ccc} \sin \vartheta \cdot \cos \varphi & \sin \vartheta \cdot \sin \varphi & \cos \vartheta \end{array}\right]^{T}$$

is perpendicular to the material plane. The stress tensor can then be transformed or converted into the respective plane. While the amplitude and mean stress of the normal stress \(\sigma _{\upvartheta \upvarphi }={\vec{n}_{1}}^{T}\cdot \boldsymbol{\sigma }\cdot \vec{n}_{1}\) can easily be calculated based on the maximum and minimum normal stress in the regarded plane, the determination of the shear stresses is more complicated. Using the vectors \(\vec{n}_{2}\) and \(\vec{n}_{3}\), the components \(\tau _{\upvartheta \upvarphi {,}\vartheta }\left(t\right)={\vec{n}_{3}}^{T}\cdot \boldsymbol{\sigma }\cdot \vec{n}_{1}\) as well as \(\tau _{\upvartheta \upvarphi {,}\varphi }\left(t\right)={\vec{n}_{2}}^{T}\cdot \boldsymbol{\sigma }\cdot \vec{n}_{1}\) can be determined. This leads to the shear stress τϑφ(t) that describes a closed path on the respective material plane displayed in Fig. 5. Various different approaches can be used to calculate the amplitudes and mean stresses, e.g. the minimum circumscribed circle (MCC) or maximum rectangular hull (MRH).

Fig. 5
figure 5

Definition of a material plane based on a unit sphere (a) and the determination of amplitude and mean shear stresses (b) [12]

Full size image

For each material plane, an amplitude or mean stress can be derived for each shear and normal stress. Consequently, every value can be assigned to a point on the unit sphere. Böhme used a reduced stress tensor [4], which has led to the τa-plot shown in Fig. 6a calculated by BECAL. For the purpose of simplification, four shear stress components were left out. For the most accurate calculation of flank fractures, however, the complete stress tensor should be considered. The result is shown in Fig. 6b.

Fig. 6
figure 6

Wrapped surface plot of τa for an arbitrary node with a reduced 2D (a) and a complete 3D stress tensor (b)

Full size image

To get a better overview of the values of amplitudes and mean stresses, the sphere plots were unwrapped into a 2D-plot (Fig. 7; [4]). The reduction of the stress tensor has resulted in amplitudes and mean stresses that are symmetrical in the two directions of the plane-defining-angles ϑ and φ. Consequently, the number of calculations could be reduced by three quarters.

Fig. 7
figure 7

Unwrapped surface plots of an arbitrary node in Böhme’s calculation example [4]

Full size image

Similar symmetric figures were generated by BECAL when the stress tensor was reduced accordingly (Fig. 8a). Figure 8b however, shows the influence of the completed tensor exemplary on τa for an arbitrary node. Instead of the double symmetry that is displayed in Fig. 7, the following plot shows a point symmetry. If a reduction of calculations is pursued, then the number can only be halved.

Fig. 8
figure 8

Unwrapped τa surface plot of the respective node in Fig. 6 with a reduced (a) and a complete stress tensor (b)

Full size image

4 Exemplary flank fracture calculation

The computed amplitudes and mean stresses can be utilized for an integral equivalent stress hypothesis to derive σeq. The material utilization A regarding flank fractures compares the equivalent stress with the respective fatigue strength and can be calculated with the following equation [4]:

$$A_{\mathrm{BO}}=\frac{ \sqrt{ \begin{array}{c} \frac{15}{8\pi }{\int }_{\vartheta =0}^{\pi }{\int }_{\varphi =0}^{2\pi }\big(\left(a{\tau }_{\upvartheta \upvarphi {,}a}^{2}+b{\sigma }_{\upvartheta \upvarphi {,}a}^{2}\right)\cdot \left(1+c\sigma _{\upvartheta \upvarphi {,}m}\right)^{2}\\ +d\tau _{\upvartheta \upvarphi {,}a}\tau _{\upvartheta \upvarphi {,}m}\big)d\phi d\vartheta \end{array} }}{\sigma _{W}}$$
(8)

The constants a and b are equivalent to the ones that are defined by Liu and Zenner in [13,14,15]. c and d however, are described in [4]. All four constants contain strength values such as uniaxial fatigue strength for alternating and oscillating loads, as well as their shear fatigue strength equivalents that can differ depending on the local hardness profile.

Figure 9 as well as Fig. 10 display the resulting material utilization of a gear in a middle cross-section that has failed due to flank fracture [16, 17]. The free-form surface or body that is plotted in the figure is a contour plot that depicts a requested value, which is in this case \(A=0.8\). The size of the contour created by the complete stress tensors (on the right) is larger than the one of the reduced stress tensors (left). The difference is even more apparent when the value of the material utilization is increased to \(A=1.2\) (Fig. 11). The highest value of A in the reduced model equals 1.27 while the complete one is 1.41. By increasing the material utilization that is supposed to be displayed in the contour plot, the position with the highest risk of crack initiation can be visualized.

Fig. 9
figure 9

Cross sections of the gear’s tooth as well as the internal position of the contour plot with the value \(A=0.8\)

Full size image
Fig. 10
figure 10

Material utilization A of a gear [16, 17] (\(m_{\mathrm{mn}}=3.02\,\mathrm{mm}\)) with a contour plot for the value 0.8 for a reduced (a) and complete stress tensor (b)

Full size image
Fig. 11
figure 11

Material utilization A of a gear [16, 17] (\(m_{\mathrm{mn}}=3.02\,\mathrm{mm}\)) with a contour plot for the value 1.2 for a reduced (a) and complete stress tensor (b)

Full size image

An additional calculation has been carried out in which the residual stresses were not taken into account. The plot can be seen in Fig. 12. The material utilization points that exceed the value of \(A=1.2\) without residual stresses are displayed in orange, whereas the blue contour plot represents the calculation with those stresses. It becomes clear that the residual stresses cause the area with the highest material utilization to be shifted towards the core.

Fig. 12
figure 12

Comparison of the material utilization models with and without the consideration of residual stresses

Full size image

5 Summary

In this paper, a new proposal to use residual stress calculation methods for spur gears on spiral bevel gears has been presented. It implies the usage of shape functions that are known from FEM-simulations. A disadvantage of transferring the approaches that include the local tooth thickness is, that blind spots can occur at the ends of the teeth on account of the flank’s geometry. However, if the bevel gear has been properly designed and was correctly adjusted in production, these areas are not relevant for flank fractures anyway. It was shown that the stress tensor-time curve and the multiaxial superposition with the residual stress state is essential for the flank fracture calculation and the computed location of the maximum material utilization. Therefore, the stress components are all needed, which is unproblematic since they are calculated for the entire meshing of the teeth anyway, both in FE models and in BECAL. Thus, with the available resources, every detail must be taken into account for the calculation model, especially for such a gear damage that cannot be safely predicted yet. Detailed examinations of the effect of specific simplifications can be done afterwards to reduce the model in order to save resources. It was shown that the automated application of arbitrarily complex failure hypotheses is therefore possible without any problems, which was exemplified using the integral approach according to Böhme.

The herein described method for the calculation of residual stresses in bevel gears should be compared to results of case-hardening heat treatment simulations and measured stresses.

In future work, the now available basis can be used to better understand and predict the causes and damage mechanisms of subsurface fatigue on gears. This includes optimizing the multiaxial residual stress estimation for arbitrary tooth geometries like spiral bevel gears and implementing different failure hypotheses, testing them in detail and mirroring them on experimental results.