Abstract
This paper presents a study on pitch bearing basic rating life affected by wind field characteristics at both onshore and offshore wind sites. The National Renewable Energy Laboratory 5 MW reference wind turbine is selected for the study. Wind field characteristics including reference hub height mean wind speed, wind speed distribution, wind shear, and vertical inflow are studied. A decoupled approach is employed where global analysis is performed first. Second, the load effects from the global analysis are applied on a reference pitch bearing designed based on best industrial practices. For the case study onshore site, it is found that the Kernel density estimation best fits the wind distribution, while the International Electrotechnical Commission proposed distribution appears to be not suitable. Moreover, it is shown that the seed number has high effect on the bearing life in turbulence wind and the wind speeds around rated have the highest contribution in both bearing fatigue damage and extreme load failure. The results contribute to better understanding of the wind field characteristics on the pitch bearing life.
Zusammenfassung
In diesem Beitrag wird eine Studie über den Einfluss von den Windfeldeigenschaften an Onshore- und Offshore-Windstandorten auf die Lebensdauer von Rotorblattlagern vorgestellt. Die 5‑MW-Referenz-Windkraftanlage des National Renewable Energy Laboratory wurde für die Studie ausgewählt. Die Windfeldcharakteristiken, einschließlich der mittleren Windgeschwindigkeit in Nabenhöhe, der Windgeschwindigkeitsverteilung, der Windscherung und der vertikalen Anströmung werden untersucht. Es wird ein entkoppelter Ansatz verwendet, bei dem zunächst eine globale Analyse durchgeführt wird. Anschließend werden die Lasten aus der globalen Analyse auf ein Referenz-Rotorblattlager aufgeprägt, welches auf der Grundlage bewährter industrieller Verfahren entwickelt wurde. Für den Onshore-Standort der Fallstudie wird festgestellt, dass die Kerndichteschätzung am besten zur Windverteilung passt, während die von der Internationalen Elektrotechnischen Kommission vorgeschlagene Verteilung nicht geeignet zu sein scheint. Darüber hinaus zeigt sich, dass die Anzahl der Simulationen einen großen Einfluss auf die Lagerlebensdauer bei turbulentem Wind hat und dass die Windgeschwindigkeiten nahe des Nennwerts den größten Beitrag sowohl zu Lagerermüdungsschäden als auch zu Extremlastbedingungen leisten. Die Ergebnisse tragen zu einem besseren Verständnis der Windfeldcharakteristiken auf die Lebensdauer von Rotorblattlagern bei.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Wind turbines as a whole, and multimegawatt offshore wind turbines specifically, are considered as a solution for the large-scale realization of renewable power generation. Practically, a higher failure rate along with repair and maintenance requirements leads to a higher cost of energy [1]. Experiences show that faults or damages in the drivetrain, bearing, and gearbox contribute significantly to the wind turbine’s downtime and nonavailability [2, 3]. The maintenance and repair are particularly too costly, especially for offshore wind turbines where a special vessel and crane barge are needed to replace a faulty drivetrain. In addition, the harsh offshore weather reduces the repair period to only a few months, often in summer [4]. Pitch systems are among the largest contributor to overall downtime, representing more than 15\(\%\) of wind turbine failures [5]. In another survey, 25\(\%\) of total failures occurred in the pitch system in offshore wind turbines, and its failure rate in onshore wind is 10\(\%\) [6].
From the wind field perspective, different characteristics are recorded during wind site measurement. The wind speed distribution is significant for the wind turbine design because it determines the frequency of occurrence of the individual load components. Different distributions are used in the wind industry. Carta et al. [7] reviewed different probability distribution functions (PDFs) with case studies in the Canary Islands. Even though Weibull distribution has advantages with respect to the PDFs analyzed, it cannot represent all the wind regimes encountered in nature such as, for example, those with high percentages of null wind speeds, and bimodal distributions. Many earlier works have focused on the distribution fitting, parameter estimations, and goodness of the fit metrics [8], but limited works are found on the effect of the wind speed on the pitch bearing load and life.
Each of the wind characteristics has its own importance. Wind site measurement sometimes does not include the vertical component, but its effect on the pitch bearing is valuable for the turbine designer. Seed number is a random number and different seeds affect bearing loads differently and due to the spatial coherence, different random seeds produce a Gaussian distribution of turbulence intensity in the longitudinal wind component [9]. Extreme and normal turbulence have a great role in the bearing’s safety factor and life. Consequently, a comprehensive study on the pitch bearing in different aspects of the wind field in extreme load and fatigue life was performed. In addition, the contribution of wind speed on the bearing life and loads in the long term and short term is analyzed and is described in the methodology section.
This paper is structured into five sections. In the next section, the reference wind turbine (RWT) is stated together with the nominated wind site. Additionally, the pitch bearing design process is presented. The methodology is described afterward, and the results and discussion present the findings with respect to the wind field, safety factors, and life. In the end, the conclusion is stated.
2 5 MW reference wind turbine and pitch bearing design
2.1 Reference wind turbine
The National Renewable Energy Laboratory’s (NREL’s) 5 MW reference wind turbine was considered as a case study [10]. The turbine was considered on two support structures: fixed-bottom and land-based. The turbine configuration is given in Table 1.
2.2 Wind sites
Two wind farms, onshore and offshore, have been studied. The offshore wind site is Anholt wind farm [11] located in the Kattegat, between Djursland and the island of Anholt in Denmark (56° \(35^{\prime}\) \(44.39^{\prime\prime}\) N, 11° \(09^{\prime}\) \(09.82^{\prime\prime}\) E). Wind data measurement was performed at different heights from 65.6 m to 250 m for two years from January 2013 to December 2014. The onshore wind site is Khaf wind farm [12], located in the northeast of Iran (34° \(29^{\prime}\) \(10.2^{\prime\prime}\) N, 60° \(18^{\prime}\) \(32.9^{\prime\prime}\) E). Wind data measurement was performed at heights from 10 to 40 m from June 2007 to March 2009.
The measurements taken at 65.6 and 85.6 m for the offshore site and 30 and 40 m for the onshore site are considered. These measurements are projected to the hub height using the power law [13]. The position of the onshore and offshore sites taken from Google Maps are depicted in Fig. 1.
2.3 Pitch bearing design
Because the NREL 5 MW reference wind turbine does not include a pitch bearing design, a design is specified as described in this section. The main restriction for the bearing design is the blade’s root dimensions. According to definition of 5 MW RWT [10], the blade root diameter is 3542 mm. It is assumed that the tension bolts in the blade side and hub side are M42 as a first guess. The bolt circle diameter of the blade root, \(D_{ \textit{b,bcd}}\), is derived in Eq. 1 from the geometrical design of the hole pattern, where \(e\) is the distance of the bolt axis from the edge of the clamped part which is equal to \(e=1.5D_{h}\), and \(D_{ \textit{b,out}}\) is the blade root’s outer diameter [14]. According to ISO 273, \(D_{h}\), the hole diameter, is equal to 45 mm for bolt M42 [15].
The distance between the bolts is assumed \(3D_{h}\) [14], which leads to the determination of the number of bolts. Other assumptions on the bolt design are as follows:
-
The friction of the surface of the bearing to the hub and blade is assumed to be 0.15.
-
Hexagon head screw with shank according to DIN EN ISO 4014 is assumed [16].
-
Bolt length assumed to be 300 mm. This parameter can be modified after the bearing design is completed.
The bolt dimensions of M36, M39, M42, M45, and M48 with safety factors against exceeding the yield point, the surface pressure, and slipping with minimal preload are evaluated. The bolt design and calculation for safety factors are performed based on VDI-2230 [14]. The results of safety factors are given in Table 2.
As shown in the table, all bolt arrangements have safety factors above one, but according to VDI 2230 [14] the recommended minimum safety factor SG is 1.2. By this criterion, the arrangement with the M42 bolt satisfied the condition and is considered as the arrangement of the blade and pitch bearing connection. The material of the bolts is grade 10.9 according to ISO 898 [17].
The bearing ball diameter and pitch circle diameter sizing are based on the following conditions:
-
It is assumed that around 80 percent of the raceway is filled with balls [18]. This assumption is consistent with DG03 [19].
-
It is considered that the distance between the raceway and bolt hole is 25\(\%\) of the ball diameter [18].
-
The raceway groove radius-to-diameter ratio is considered to be 0.52 [19].
-
The surface hardness is assumed to be 58 hardness on Rockwell scale C (HRC) [19, 20].
-
The Core hardness is assumed to be 250 Brinell hardness (HB) [19, 20].
The sizing of the pitch bearing is performed in a way that all parameters are related to the ball diameter. The ball diameters of 50, 60, 75, 90, and 100 mm were studied. The designed pitch bearing main dimensions are stated in Table 3 and Fig. 2. The figure is an adopted figure from Thyssenkrupp Rothe erde Catalogue [21]. The pitch bearing arrangement in a wind turbine is also illustrated in Fig. 2.
3 Methodology
Extraction of the wind characteristics is the first stage in the analysis. It is described in the first subsection. The turbine response simulation, a global analysis, in which the loads and motions are extracted, is described afterward. In the end, the calculations of the bearing life and safety factors are presented.
3.1 Wind field characteristics
Several characteristics in the wind fields such as mean wind speed, wind shear, turbulence intensity, and wind speed distribution, which are important for the wind turbine, are described in Germanischer Lloyd (GL) guidelines [23] and standards [13].
Mean wind speed is considered as an annual average of 10-min means of the wind speed at hub height.
The vertical inflow wind is caused in different ways. Hills in the wind stream in front of the turbine and stable atmosphere can cause the inflow wind. In addition, other turbines in the wind farm can produce inflow wind. The International Electrotechnical Commission (IEC) 61400‑1 recommends 8° for inclination of the mean flow with respect to a horizontal plane [13].
Generally, two mathematical models have been used to model the vertical profile of wind speed. The logarithmic profile (log law) and power law [24]. In this study, the power law that is recommended by IEC [13] is used. The power law is as follows:
where \(\alpha\) is the power law exponent and wind speed (\(U\)) at height (\(z\)) can be calculated from wind speed at reference height (\(z_{r}\)). The power law exponent according to GL 2010 guideline [23] and standard IEC 61400 [13] are 0.11 and 0.2, respectively, for extreme and normal onshore wind profile models, and it changes to 0.14 for the normal offshore wind profile model [25].
Turbulence intensity (TI) is defined as a fraction of the standard deviation (\(\sigma_{u}\)) to the mean of wind speed, according to Eq. 3.
The wind speed distribution at the site is significant for the wind turbine design because it determines the frequency of occurrence of the individual load components. Different distributions are used in the wind industry. In this study the following distributions are nominated:
-
Lognormal distribution
-
Weibull distribution
-
Rayleigh distribution
-
Nakagami distribution
-
Kernel density estimation
The pdf and cumulative density functions (CDFs) of the nominated distribution are described in Appendix 1.
To evaluate the accuracy of each distribution, three different methods of root-mean-squared error (RMSE), coefficient of determination (\(R^{2}\)), and coefficient of efficiency (CE) as criteria for goodness-of-fit are considered. The criteria are calculated by Eqs. 4–6 [26], respectively:
where \(x_{o,i}\) and \(x_{p,i}\) are the observed and predicted data of \(x_{i}\) and the ones with the (-) overbar are the mean of the parameter. Goodness levels for \(R^{2}\) and CE are, respectively, 0.85 and 0.9 [26].
3.2 Turbine response simulation
In this section the global model of the 5 MW reference wind turbine in the OpenFAST as well as the nominated design load cases (DLCs) and wind condition are described.
The wind turbine simulation is performed in OpenFAST [27]. OpenFAST is a multiphysics, multifidelity tool for nonlinear aero-hydro-servo-elastic simulation of wind turbines. The wind turbine model is considered from the reference model in GitHub/OpenFAST [28].
Two types of DLCs are considered in this paper. One set of DLCs is considered in the ultimate strength analysis. The other set is considered for both ultimate and fatigue strength analysis. In all DLCs wind shear is considered according to site or standard conditions. The load results are according to the blade coordinate system, which is described in the FAST user manual [29].The main load on the pitch bearing is the bending moment. According to Su et al. [30] and Technical University of Denmark (DTU) 10 MW RWT reports [31], DLCs 6.1 and 1.3 are the extreme value for the blade root bending moment. Subsequently, the mentioned DLCs are considered for ultimate strength analysis. According to IEC, DLCs 1.2, 2.4, 3.1, 4.1 and 6.4 are used for fatigue analysis. DLC 1.2 is considered in this study with higher resolution than proposed by IEC. DLC 2.4 is for fault condition does not cause an immediate shutdown of the turbine. In this study, it is considered that fault in electricity result in an immediate shutdown of the turbine. DLCs 3.1 and 4.1 are the start-up and shutdown conditions of the turbine and do not relate to wind characteristics and they are not considered. DLC 6.4 is in park condition. Because the turbine is not operating (the turbine is in idle mode), the pitch system is not moving, and it is not possible to calculate the life according to method based on oscillation of the bearing. The list of DLCs and their characteristics are presented in Table 4.
Generally, the definition of DLCs and the wind models are according to IEC 61400-1 [13] and DNV 437 [32].
Two different post-analyses are carried out in the paper; short term and long term. The short-term analysis is referred to as simulation with a short-term wind condition i.e. 10-min simulation at a given wind speed. In this case, the wind speed distribution is not considered and is assumed that all wind speeds occur with an equal probability. This is indeed not a real case, but when it is compared with the long term, the influence of the wind speed distribution – which is site specific – is better illustrated. In long-term analysis, the site specific wind speed distribution is considered for the loads and life calculation.
3.3 Pitch bearing life analysis
The radial, axial, and bending loads at each blade root obtained from the global analysis are applied on individual pitch bearings. To evaluate the design of oscillating pitch bearings, the classic Lundberg-Palmgren theory for estimating dynamic load capacity and fatigue life for continuously rotating rolling bearings [33] was extended and correlated to laboratory fatigue life data [34]. This included defining the critical amplitude of oscillation, the angle below which the raceway is stressed by only one roller and receives two stress repetitions per oscillation cycle because the pitch oscillation is relatively small. The calculation of the equivalent load and number of loading cycles for oscillatory applications was later presented [35]. These formulations were then simplified and applied on wind turbine pitch bearings [36]. A dither angle was defined for pitch motions even smaller than the critical amplitude, for which the stressed area is only partially uncovered and retraced. In this situation, fretting corrosion is often experienced and the developed fatigue life models are not applicable. A similar model was also applied to a four-point contact ball bearing in a wind turbine [37].
Based on these earlier works, in 2009 NREL published a pitch and yaw bearing design guide (DG03), which summarized the design criteria, calculation methods, and applicable standards recommended for use in performance and life analyses of these bearings [19]. However, other methods presented such as works done by Wöll et al. [38] or Breslau et al. [39], DG03 is very commonly used in the wind industry and guidelines for determining rating life of blade bearings [40]. The DG03 uses a comparison of the maximum contact stress, \(\sigma_{ \textit{max}}\), in the limit load condition to the maximum allowable stress of 4,200 MPa, to define the static safety factor as [41]
where the maximum contact stress, \(\sigma_{ \textit{max}}\), is also expressed in megapascals. It recommends that the safety factor in this condition be greater than 1.5, which is the same as the ISO 76 recommendation for applications subjected to shock loads [42].
The DG03 modifies the basic dynamic axial load rating, \(C_{a}\), and defines a basic dynamic axial load rating for oscillating conditions, \(C_{ \textit{a,osc}}\). The formulation depends on a prorated angle of oscillation, \(\theta\) , in comparison to the critical angle of oscillation, \(\theta_{ \textit{crit}}\).
where the life exponent \(p=3\) for ball bearings, Z is the number of ball and the prorated angle of oscillation, \(\theta\) is
where \(K\) is the number of load cases. Parameters \(t_{k}\) and \(N_{k}\) denote the decimal fraction of time and speed of oscillation, respectively, for the bearing operated under the condition yielding \(\theta_{k}\). A sample of pitch motion at 12 m/s in the normal turbulence model (NTM) and low turbulence model (LTM) in the IEC-onshore condition is depicted in Fig. 3.
The dynamic equivalent load, \(P_{ \textit{ea}}\), is formulated as
where \(F_{r}\), \(F_{a}\), and \(M\) denote the applied radial, axial, and moment loads, respectively. \(D_{ \textit{pw}}\) denotes the pitch diameter of the bearing. This formulation takes into account the moment loading on the pitch bearing. To include various duty cycle loading, a prorated dynamic equivalent load \(\bar{P_{ \textit{ea}}}\) is defined as
where the summation is performed over the discrete number of normal load cases and depends on the angle of oscillation, \(\theta\), relative to the critical angle, \(\theta_{ \textit{crit}}\). \(p\) denotes the life exponent and it equals 3 for ball bearings.
The rating life is the predicted value of life before the first evidence of fatigue occurs on a raceway. The basic rating life, \(L_{10}\), is the rating life associated with 90% reliability for bearings manufactured with commonly used high-quality material, of good manufacturing quality, and operating under conventional operating conditions.
where the resulting value of \(L_{10}\) is in millions of revolutions of the bearing rings relative to each other. The DG03 uses this basic dynamic axial load rating for oscillating conditions to estimate the basic rating life
More information on the procedure and definition of the parameter are presented in reference [41] and DG03 [19].
4 Results and discussion
Results are categorized in four main subsections: wind field characteristics, extreme load, safety factor, and life.
4.1 Wind speed distribution of onshore and offshore site
4.1.1 Offshore wind site
The results of wind speed at hub height are projected using the power law. The power law exponent is equal to 0.1173. This value is derived from averaging the calculated power law in every 10-min measurement step. The wind speed with different distribution functions are depicted in Fig. 4. Different distribution parameters defining the behavior of wind speed are presented in Table 5.
Summarized statistical errors of different criteria, goodness-of-fit, in different PDFs are presented in Table 6.
The Weibull distribution has the most favorable value in all three criteria, and the Nakagami and the Rayleigh positioned afterward. The result of the lognormal distribution fitting is the lowest. Other wind field features are presented in Table 7. The result shows the similarity and difference of the Anholt wind site with IEC class I offshore wind site.
4.1.2 Onshore wind site
The results of wind speed at hub height are projected by means of the power law. The power law exponent is equal to 0.0991. This value is derived from averaging the calculated power law in every 10-min measurement step. The wind speed distribution with different distribution functions are depicted in Fig. 5. Corresponding PDFs parameters at 90 m, are stated in Table 8.
The results of different criteria of goodness-of-fit in different PDFs are presented in Table 9.
The Kernel distribution has the most favorable value in all three criteria, followed by the Nakagami and Weibull distributions. The results of the lognormal and Rayleigh distribution fitting are below the other three; however, the later one is the proposed distribution according to the IEC 61400 standard [13], guideline GL 2010 [23], and DNV 437 [32]. Other wind field features are presented in Table 10.
Comparing the result of the onshore and offshore wind distributions, it can be seen that the proposed Rayleigh distribution could not be fitted to the measurement in the onshore as precisely as the offshore wind site. One of the reasons for the lack of accuracy in onshore wind sites is the bimodal pattern of wind, in which the wind speed density curve has an extra hump [7].
4.2 Extreme loads at the pitch bearing
Nominated DLCs are simulated, and extreme loads in the blade coordinate system [29] are extracted. There are eight load components in each extreme case. Six of them are forces and moments in the blade coordinate system and the latter two are the in-plane vector resultant force and moment. Each of these eight components has negative and positive extremes that make a matrix of 8\(\times\)16. The presented format of extreme loads is compatible with IEC 61400 [13]. The detailed results of the extreme loads in different sites are presented in Appendix 2. The equivalent load according to Eq. 9 is the indicator for the load on the pitch bearing. The results of \(P_{ \textit{ea}}\) in different wind sites are illustrated in Fig. 6.
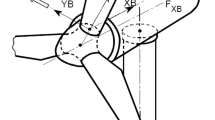
The results show that the load is dominant in the maximum of \(F_{x}\), \(M_{x}\), \(M_{y}\), \(F_{r}\), and \(M_{r}\), from which \(F_{x}\) and \(F_{r}\) are the radial load in the \(x\)-direction and the in-plane vector resultant force at the blade root plane, respectively; \(M_{x}\) and \(M_{y}\) are the bending moments in the \(x\)- and \(y\)-directions, respectively; and \(M_{r}\) is the in-plane vector resultant moment at the blade root plane. It should be noted that in the maximum of \(F_{x}\) and \(F_{r}\), the bending moment is the reason for increase in the equivalent loads. In addition, all of these extremes resulted from DLC 1.3, ETM wind condition. This is consistent with the results of the DTU 10 MW design [31]. The GL guideline [23] does not consider this DLC, so wind turbine design based on this guideline may result in an underestimation of extreme loads in the pitch bearing.
The short-term and long-term contributions of wind speed on the pitch bearing equivalent loads are illustrated in Fig. 7 at different sites.
From both short-term and long-term results, it can be seen that a wind speed of 10 m/s is dominant in both IEC standards for onshore and offshore, however, the peaks will change in Anholt and Khaf to 11 and 12 m/s, respectively. These two wind speeds bracket the wind turbine rated speed of 11.4 m/s. In addition, the peaks in IEC cases are much sharper than those for Khaf. Khaf has a broader curve with more wind speeds contributing to extreme loads. Moreover, the maximum contribution of IEC cases and Anholt are double compared to Khaf’s maximum contribution. Furthermore, the results also express that the peak of contribution increases from \(24\%\) to around \(28\%\) in the IEC onshore case in the long term while Khaf is still a little above \(10\%\). The wider distribution for Khaf could be the result of higher extreme turbulence intensity with respect to other wind sites.
4.3 Pitch bearing safety factor
The result of safety factors in different wind sites are presented in Fig. 8. The safety factor of the pitch bearing in Khaf is lowest, which is expected, due to the high equivalent load observed in Fig. 6. Normal turbulence in Khaf is lower than the IEC standard, but higher extreme turbulence results in higher load and lower safety factor. The normal turbulence in Anholt at 15 m/s is lower than the IEC standard, but the safety factors are comparatively the same. It should be noted that in this paper the safety factor is limited to the static load factor, and the safety factor of the fretting corrosion types of failure is not considered [19].
4.4 Pitch bearing life
The life of the bearing according to seed number in turbulence intensity, vertical inflow, and wind shear was studied and the results presented. Moreover, contribution of the wind speed at normal and low turbulence wind regimes in the life of the pitch bearing is stated.
The bearing life in the NTM condition at four different wind sites with six different seed numbers in long term and short term is depicted in Fig. 9. Different seeds in each wind site create different wind speed time series with the same turbulence intensity.
The results both in the long term and short term indicated that bearing life is not independent of the seed number but is affected by it. Anholt shows higher pitch bearing life compared to the other three cases. The calm wind regime in Anholt increases the life of the bearing. The IEC onshore case has the lowest overall and lowest short-term bearing life, while seed number 1 of Khaf has the lowest life in the long term. This change of lowest bearing life from short term to long term is the effect of wind speed distribution at Khaf. However, bearing life does not change considerably in the long term and short term, and the effect of seed numbers is dominant.
The effect of turbulence intensity is studied in all four sites in the short term and long term. The results based on NTM and LTM are depicted in Fig. 10. According to Fig. 10, the TI has a large effect on the life of the bearing; however, it does not happen at the Anholt wind site, especially in the long term. One of the reasons could be the lower TI of the Anholt site. Furthermore, the long-term condition decreases the life in LTM and does not considerably affect the life in NTM.
The results in the IEC offshore case are not comparable in LTM and NTM, because in LTM the wind shear power exponent intentionally changed to 0.01. The short-term bearing life of four wind sites in Fig. 10 have the same parameters in wind pattern in LTM, and the only difference is the power law exponent that changes from 0.2 in the IEC onshore case to 0.01 in the IEC offshore case. The lowest and highest life belong to Anholt and Khaf, which have a power law exponent of around 0.1, and the bearing life in the IEC onshore and offshore cases is in between. In this regard, wind shear does not have an upward or downward effect on the bearing life.
The effect of the vertical component of wind speed is studied in LTM conditions. The bearing life results are illustrated in Fig. 11. In bars with a legend (W Vinflow), vertical inflow is considered and in bars with a legend (W/O Vinflow), vertical inflow is not considered.
The Khaf wind site did not have vertical component measurements, so it was omitted from this analysis. It is observed that considering the vertical inflow in the total wind speed increases the life of the bearing. Furthermore, long-term bearing life results, which considered wind speed distribution, have lower life compared to short-term bearing life results. Consequently, considering the vertical inflow increases the bearing life while the wind speed distribution decreases it.
In order to investigate the effect of each wind speed in the life of the pitch bearing, the short-term and long-term contributions of wind speed on the bearing life are presented in Fig. 12. The figure shows that the overall pattern in all four wind sites is the same, and the peaks increased by decreasing the turbulence content of the wind. The peaks are in over-rated wind speed in all wind sites in short term and shifted to under-rated wind speed in long term except Khaf. The largest peaks both in the long term and short term belong to Anholt. Life reduction has a narrower peak at the Anholt site compared to the three others. The contribution of high wind speed, practically above 20 m/s, is decreased drastically. This change has less effect on Khaf because of the high content of high wind speed.
Fig. 13 shows the short-term and long-term contribution of LTM wind speed on the bearing life. In all cases, the wind model is LTM, therefore, the contribution of bearing life due to wind shear (short-term) and wind speed recurrence (long-term) are presented.
The short-term figure shows that the contributions in all wind conditions are to some extent the same; therefore, wind shear has a small effect on the contribution of life reduction in wind distribution. Life reduction has a narrower peak in the distribution in LTM compared to NTM. The Anholt NTM result has the same narrow peak as a result of a low TI value.
The result shows that wind speed contribution to bearing life reduction is increased by adding the effect of wind speed recurrence. In addition, compared to extreme cases, the contribution has a wider distribution in all four wind sites.
5 Conclusion
In this paper, the effect of wind field characteristics on the pitch bearing life was evaluated. The 5 MW reference turbine was employed in two onshore and offshore sites where different distributions were fitted to the wind measurements. While Rayleigh distribution is the proposed distribution by IEC, it was found that the Weibull is a better choice for offshore and Kernel performs best for onshore, at least for the case study sites.
It is also found that the bending moment has the highest contribution to the equivalent bearing load. The extreme turbulence model governs the extreme loads of the pitch bearing and it is crucial to consider it in pitch bearing design. The contribution of wind speeds in the extreme load in the short term and long term show that IEC sites have sharper peaks in wind speed contribution, and it is observed that wind sites similar to IEC can be designed on the extreme load conditions with around-rated wind speeds. For example, the offshore Anholt site pitch bearing can be designed based on extreme loads just by analyzing around-rated wind speeds. On the contrary, the onshore wind site has a wide distribution, and it is not reasonable to design a bearing just by around-rated wind speeds in extreme conditions. The safety factor of the Khaf onshore wind site is lower than the IEC case, and if the bearing is designed and selected according to IEC results, it will be underestimated.
The bearing life contribution to wind speeds shows the importance of around-rated wind speed analysis. It is also realized that the power exponent in wind shear does not have a definite effect on the bearing life. Additionally, in equal total wind speed, the vertical component of the wind speed increases the bearing life in both short-term and long-term analysis. It is noticed that the bearing life is largely affected by the turbulence intensity of the wind speed. This change is more noticeable in the short term than in the long term of the bearing life. The effect of random seed number of turbulence on bearing life is considerable for both the short term and long term, and further investigation is needed besides studying more wind sites with different topography.
References
Carroll J, McDonald A, McMillan D (2016) Failure rate, repair time and unscheduled o&m cost analysis of offshore wind turbines. Wind Energy 19(6):1107–1119. https://doi.org/10.1002/we.1887
Faulstich S, Hahn B, Tavner PJ (2011) Wind turbine downtime and its importance for offshore deployment. Wind Energy 14(3):327–337. https://doi.org/10.1002/we.421
Ossai CI, Boswell B, Davies IJ (2016) A Markovian approach for modelling the effects of maintenance on downtime and failure risk of wind turbine components. Renew Energy 96:775–783. https://doi.org/10.1016/j.renene.2016.05.022
Nejad AR, Odgaard PF, Moan T (2018) Conceptual study of a gearbox fault detection method applied on a 5-MW spar-type floating wind turbine. Wind Energy 21(11):1064–1075. https://doi.org/10.1002/we.2213
He L, Hao L, Qiao W (2021) Remote monitoring and diagnostics of pitch-bearing defects in an MW-scale wind turbine using pitch symmetrical-component analysis. IEEE Trans on Ind Applicat 57(4):3252–3261. https://doi.org/10.1109/TIA.2021.3079221
Dao C, Kazemtabrizi B, Crabtree C (2019) Wind turbine reliability data review and impacts on levelised cost of energy. Wind Energy 22(12):1848–1871. https://doi.org/10.1002/we.2404
Carta J, Ramırez P, Velazquez S (2009) A review of wind speed probability distributions used in wind energy analysis. Renew Sustain Energy Rev 13:933–955. https://doi.org/10.1016/j.rser.2008.05.005
Jung C, Schindler D (2019) Wind speed distribution selection – a review of recent development and progress. Renew Sustain Energy Rev 119:109–290. https://doi.org/10.1016/j.rser.2019.109290
Jonkman B (2009) Turbsim user’s guide: Version 1.50. Tech. rep., NREL/TP-500-46198. National Renewable Energy Lab.(NREL), Golden https://doi.org/10.2172/965520
Jonkman J, Butterfield S, Musial W, Scott G (2009) Definition of a 5-MW reference wind turbine for offshore system development. Tech. rep., National Renewable Energy Lab.(NREL), Golden https://doi.org/10.2172/947422
Ørsted (2022) Green solutions: Offshore wind data. https://orsted.com/en/our-business/offshore-wind/wind-data. Accessed 4 June 2022
Renewable Energy and Energy Efficiency Organization (SATBA) (2022) http://www.satba.gov.ir/en/. Accessed 24 May 2022
IEC (2019a) 61400-1: Wind energy generation system, part 1: Design requirements. https://webstore.iec.ch/publication/26423. Accessed 31 August 2022
VDI (2003) 2230: Systematic calculation of high duty bolted joints. VDI-Gesellschaft Entwicklung Konstruktion Vertrieb
ISO (1979) 273, fasteners — clearance holes for bolts and screws
DIN EN ISO (2022) 4014 fasteners – hexagon head bolts – product grades a and b
ISO (2013) 898‑1, mechanical properties of fasteners made of carbon steel and alloy steel–part 1: Bolts, screws and studs with specified property classes–coarse thread and fine pitch thread
Heras I, Aguirrebeitia J, Abasolo M, Coria I (2019) An engineering approach for the estimation of slewing bearing stiffness in wind turbine generators. Wind Energy 22(3):376–391. https://doi.org/10.1002/we.2292
Harris T, Rumbarger J et al (2009) Wind turbine design guideline dg03: Yaw and pitch rolling bearing life. Tech. rep., NREL/TP-500-42362. National Renewable Energy Lab.(NREL), Golden https://doi.org/10.2172/969722
He P, Hong R, Wang H, Ji X, Lu C (2018) Calculation analysis of yaw bearings with a hardened raceway. Int J Mech Sci 144:540–552. https://doi.org/10.1016/j.ijmecsci.2018.06.016
thyssenkrupp rothe erde (2021) Complete delivery range, rothe erde slewing bearings: Customer-specific solutions for individual requirements. https://www.thyssenkrupp-rotheerde.com/en/downloads/brochures-and-catalogues. Accessed 12 December 2021
Bayles CD (2019) Extending wind turbine life with pitch bearing upgrades. https://www.kaydonbearings.com/downloads/whitepapers/Kaydon-wind-pitch-bearing-upgrades-WP.pdf. Accessed 9‑December-2022
Germanischer Lloyd (2010) Guideline for the certification of wind turbines
Manwell JF, McGowan JG, Rogers AL (2009) Wind energy explained, theory, design and application, 2nd edn. John Wiley & Sons, Chippenham
IEC (2019b) 61400, wind energy generation systems-part 3‑1: Design requirements for fixed offshore wind turbines. International Electrotechnical Commission, Geneva, Switzerland
Dawson CW, Abrahart RJ, See LM (2007) Hydrotest: a web-based toolbox of evaluation metrics for the standardised assessment of hydrological forecasts. Environ Model Softw 22(7):1034–1052. https://doi.org/10.1016/j.envsoft.2006.06.008
NREL Openfast. https://github.com/OpenFAST/openfast. Accessed 2 August 2022
NREL (2022) Nrel 5mw reference turbine openfast model. https://github.com/OpenFAST/r-test/tree/main/glue-codes/openfast/5MW_Baseline. Accessed 25 August 2022
Jonkman JM, Buhl ML Jr et al (2005) Fast user’s guide. national renewable energy laboratory, golden. Technical Report No NREL/EL-500-38230. https://doi.org/10.2172/15020796
Su WN, Huang CC, Lin HJ (2015) Comparison of load calculation between IEC and gl offshore wind turbine design guideline using nrel 5 MW reference wind turbine. OnePetro, International Ocean and Polar Engineering Conference, vol All Days, iSOPE-I-15-216. https://onepetro.org/ISOPEIOPEC/proceedings-pdf/ISOPE15/All-ISOPE15/ISOPE-I-15-216/1342677/isope-i-15-216.pdf. Accessed 24 August 2022
Bak C, Zahle F, Bitsche R, Kim T, Yde A, Henriksen LC, Hansen M, Natarajan A (2013) Description of the DTU 10 MW reference wind turbine. Tech. rep., DTU Wind Energy Report-I-0092. https://rwt.windenergy.dtu.dk/dtu10mw/dtu-10mw-rwt/-/blob/master/docs/DTU_Wind_Energy_Report-I-0092.pdf. Accessed 24 November 2021
DNV (2016b) DNV-ST-0437, loads and site conditions for wind turbines
Lundberg G, Palmgren A (1949) Dynamic capacity of rolling bearings. J Appl Mech 16(2):165–172. https://doi.org/10.1115/1.4009930
Rumbarger JH, Jones AB (1968) Dynamic capacity of oscillating rolling element bearings. J Lubr Technol 90(1):130–138. https://doi.org/10.1115/1.3601528
Houpert L (1999) Bearing life calculation in oscillatory applications. Tribol Trans 42(1):136–143. https://doi.org/10.1080/10402009908982200
Rumbarger JH (2003) Simplification of dynamic capacity and fatigue life estimations for oscillating rolling bearings. J Tribol 125(4):868–870. https://doi.org/10.1115/1.1576424
González J, Echarte Casquero F, Vázquez MJ, González-Posada M (2008) Blade bearing friction and fatigue mathematical mode. Proceedings of the STLE/ASME 2008 International Joint Tribology Conference, pp 427–431 https://doi.org/10.1115/IJTC2008-71147
Wöll L, Jacobs G, Kramer A (2018) Lifetime calculation of irregularly oscillating bearings in offshore winches. Model Identif Control 39(2):61–72. https://doi.org/10.4173/mic.2018.2.2
Breslau G, Schlecht B (2020) A fatigue life model for roller bearings in oscillatory applications. Bear World J 5:65–80
DNV (2016a) DNV-ST-0361, machinery for wind turbines
Keller J, Guo Y (2022) Rating of a pitch bearing for a 1.5-MW wind turbine. Tech. rep., NREL/TP-5000-82462. National Renewable Energy Lab.(NREL), Golden https://doi.org/10.2172/1902646
ISO (2006) 76 rolling bearings — static load ratings
Ang AS, Tang WH (2007) Probability concept in engineering emphasis on applications in civil & environmental engineering, 2nd edn. John Wiley & Sons, Hoboken
McCOOL JI (2012) Using the Weibull Distribution Reliability, Modeling, and Inference. John Wiley & Sons, Hoboken
Bain LJ, Antle CE (1967) Estimation of parameters in the weibull distribution. Technometrics 9:621–627. https://doi.org/10.2307/1266200
Nakagami M (1960) The m‑distribution—a general formula of intensity distribution of rapid fading, statistical methods in radio wave propagation. In: Hoffman W (ed) Statistical methods in radio wave propagation. Pergamon, Oxford, pp 3–36 https://doi.org/10.1016/B978-0-08-009306-2.50005-4
Acknowledgements
The last author gratefully acknowledge the financial support of the Research Council of Norway through the InteDiag-WTCP project (Project Number 309205). This work was also authored in part by the National Renewable Energy Laboratory operated by the Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under contract no. DE-AC36-08GO28308. Funding was provided by the U.S. Department of Energy Office of Energy Efficiency and Renewable Energy Wind Energy Technologies Office. The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government. The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.
Funding
Open access funding provided by NTNU Norwegian University of Science and Technology (incl St. Olavs Hospital - Trondheim University Hospital)
Author information
Authors and Affiliations
Corresponding author
Additional information
Yi Guo, Jonathan Keller, and Amir R. Nejad contributed equally to this work.
Appendix
Appendix
1.1 Probability distributions
In this section, the definition and equations of the nominated distributions are presented. The following parts are extracted from references [43] and [44].
1.1.1 Lognormal distribution
The logarithmic normal or simply lognormal distribution is a probability that its PDF follows Eq. 14.
where \(\mu\) and \(\sigma\) are mean and standard deviation of \(\ln{x}\) respectively. The cumulative distribution function is stated in Eq. 15 where \(\Phi\) is CDF of standard normal distribution (N(0,1)).
1.1.2 Weibull distribution
The probability density function of the Weibull distribution is described in Eq. 16. The parameters \(k\) and \(C\) are the shape and scale parameters of the Weibull function.
The CDF of the Weibull distribution is presented in Eq. 17.
There are different ways to estimate the scale and shape parameters of the distribution function. In this study, the maximum likelihood estimation (MLE) is used. Shape and scale parameters are estimated by following Eqs. 18 and 19, respectively [45].
In this method, numerical iterations are required to determine the shape parameter of the Weibull function.
1.1.3 Rayleigh distribution
Rayleigh distribution is a special case of the Weibull distribution with a shape parameter equal to 2.0. Subsequently, the PDF and CDF follow the Eqs. 20 and 21, respectively.
1.1.4 Nakagami distribution
The Nakagami distribution is commonly used in communication theory. The PDF of the distribution follows the Eq. 22.
where \(\mu\) and \(\omega\) are the shape and speed parameters respectively and \(\Gamma(x)\) is \(\Gamma\) function as below Eq. 23.
The CDF of the Nakagami distribution is as Eq. 24 where \(P\) is the regularized (lower) incomplete gamma function.
The shape and speed parameters are calculated, respectively, as [46]:
where \(\overline{x^{2}}\) is mean of \(x^{2}\).
1.2 Extreme load results
In this section the extreme loads at the blade root in different wind sites are presented. Figs. 14–17 relate to IEC-onshore, IEC-offshore, Anholt, and Khaf wind sites, respectively.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rezaei, A., Guo, Y., Keller, J. et al. Effects of wind field characteristics on pitch bearing reliability: a case study of 5 MW reference wind turbine at onshore and offshore sites. Forsch Ingenieurwes 87, 321–338 (2023). https://doi.org/10.1007/s10010-023-00654-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10010-023-00654-x