1 Introduction

Wind energy is expected to make the greatest contribution to the expansion of renewable energies. To increase the efficiency of wind turbine drivetrains during the development process, a traceable and comparable method is required for determining the efficiency of wind turbine drivetrains on nacelle system test benches (NTBs).

As part of the EMPIR project 19ENG08 WindEFCY [1], such an efficiency determination method has been developed based on traceable mechanical and electrical power measurement. In this method, so-called transfer standards with known accuracy and measurement uncertainty are installed in the 4 MW NTB at the Center for Wind Power Drives (CWD) of RWTH Aachen University. The transfer standard for mechanical power measurement consists of a 5 MN · m torque transducer and the NTB’s own magnetic encoder for measuring rotational speed. The reference power measurement system (RPMS) consists of a power analyser, a high-precision voltage divider and several very precise current transformers.

A number of difficulties are associated with this methodology, particular with respect to the measurement of mechanical power. One crucial parameter for torque measurement is the torque offset, which needs to be determined at the beginning of each measurement day and eliminated from the torque step signals by subtraction. Because of dynamic disturbances such as ripples and oscillations, especially in the torque and speed signals on the low-speed shaft (LSS), the signals need to be averaged over six full revolutions of the drivetrain at each load step. On test benches for electrical machines, the measurement of electrical and mechanical power is performed simultaneously by power analysers. Due to the large number of measuring points and the spatial distance between them in the NTB, it was not possible to record all the data using a single power analyser. But since simultaneous data acquisition is important here, all data acquisition (DAQ) systems were synchronised via Network Time Protocol (NTP).

Another challenge in determining the efficiency of wind turbines in general is the large number of operating points (pairs of speed and torque values). In order to be able to determine the efficiency at as many load points as possible, so-called iso-efficiency maps were designed. This paper will examine the measurements done to produce these iso-efficiency maps, consider the possible influences involved, and show how the efficiency and the associated measurement uncertainty per operating point were calculated. A standardisation of this test procedure for determining the efficiency of wind turbine drivetrains prior to installation in the field could strengthen the competitiveness of the wind technology sector.

2 Specifications of the transfer standards

A transfer standard is used to calibrate the measurement system in situ in an NTB and enables traceable measurements with a well-defined uncertainty model.

The transfer standard for mechanical power measurement consists of a 5 MN · m torque transducer and the NTB’s own magnetic encoder for measuring the rotational speed. The RPMS used to calibrate the electrical power measurement in the NTB consists of three power analysers, a high-precision voltage divider and several very precise current transformers.

2.1 Mechanical power measurement

In order to be able to determine the efficiency of the device under test (DUT) on the NTB, the mechanical input power must be measured. This is done by measuring the torque directly at the rotor hub of the DUT nacelle. For this purpose, a 5 MN · m torque transfer standard was installed and integrated into the LSS. In addition, a torque transducer was mounted between the gearbox and the generator. This torque measurement on the high-speed shaft (HSS) enables the efficiency of the gearbox to be determined.

2.1.1 5 MN · m torque transfer standard on the LSS

The torque transfer standard (TTS) used on the LSS is a hollow-shaft transducer (Fig. 1) that can be installed in the drivetrain via flanges using screw connections. It measures torque by means of strain gauges and provides traceability up to 5 MN · m. Up to 1.1 MN · m it is calibrated against a reference standard at the Physikalisch-Technische Bundesanstalt (PTB). Above 1.1 MN · m, no such reference standard is available and the metrological characterisation uses an extrapolation method assuming a linear behaviour based on a linear calibration curve [2]:

$$M_{\mathrm{TTS}}=3850\mathrm{\,kN}\cdot \mathrm{m}\left(\frac{\mathrm{mV}}{\mathrm{V}}\right)^{-1}\cdot S_{\mathrm{TTS}}{,}$$
(1)

where STTS is the output signal in mV / V and MTTS is the corresponding calibrated torque output in kN · m. The expanded relative uncertainty interval (\(k=2\)) for the linear calibration curve up to 1.5 MN · m is 0.290%.

Fig. 1
figure 1

5 MN · m TTS including DAQ and telemetry system installed at the DUT’s rotor hub

Full size image

The torque signal is read out by a high-precision amplifier with a sampling frequency of 150 Hz and a 50 Hz Bessel filter. To synchronise the autonomous DAQ system of the 5 MN · m torque transducer to the DAQ system of the NTB, the test bench’s NTP signal is used for the time stamps of the torque signal. The measurement data is transmitted via WLAN using a rotating and a stationary access point.

2.1.2 80 kN · m torque transducer on the HSS

To measure the torque on the HSS between the gearbox and the generator, an 80 kN · m hollow-shaft torque transducer (Fig. 2) was installed in the drivetrain. The relationship between the measurement signal and the applied torque, which was defined with the help of a calibration, is described as

$$M_{T}=\frac{2.666\mathrm{\,kN}\cdot \mathrm{m}}{\mathrm{kHz}}\cdot S_{T}{,}$$
(2)

where again ST is the output signal of the transducer in kHz and MT is the corresponding calibrated torque output in kN · m. The relative expanded measurement uncertainty of the transducer is 0.1%. The data is transmitted via the transducer’s own telemetry system.

Fig. 2
figure 2

80 kN · m torque transducer installed in the drivetrain between the gearbox and the generator inside the DUT

Full size image

2.1.3 Rotational speed measurement

In previous work [3, 4], a calibrated inclinometer was centred on the inner side of the 5 MN · m torque transducer’s cover plate to establish the traceability of the rotational speed measurement in another NTB. Overall, the inclinometer can achieve 0.018% relative uncertainty at 4.5 rpm. Comparing the measurement results from the inclinometer and the NTB’s magnetic encoder, it was surprising to find that the encoder, due to its significant number of poles per rotation, provided a similar and even better accuracy than the inclinometer used as transfer standard. In this measurement campaign, the NTB’s encoder is therefore used directly for efficiency determination with a relative measurement uncertainty that is considered less than 0.02%.

2.2 Electrical power measurement

The RPMS used in this measurement campaign consists of two LMG 671 multi-channel power analysers and a HST 12‑3 high voltage divider from ZES Zimmer, as well as nine PCT2000/DL2000ID precision current transducers from Danisense.

Simultaneous measurement for all channels can be achieved with the power analyser. The accuracy of the power measurement is 0.015% of the measured value [5]. The Danisense precision current transducers are contact free, closed loop, flux gate-based current measuring sensors. The maximum current (RMS) is 2500 A under the practical operating conditions used here, and the transducers are well suited for use as a transfer standard in NTBs due to their very good linearity and wide temperature range. The voltage divider used for voltage measurement has a measuring range of 16.8 kV RMS with frequencies from DC to 300 kHz.

3 Measurement set-up

At the Center for Wind Power Drives (CWD) of RWTH Aachen University in Aachen, Germany, on-shore wind turbines and their components with a rated power of up to 4 MW can be tested.

3.1 Nacelle test bench

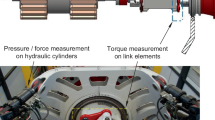
The NTB is operated by a low-speed permanent magnet synchronous machine (PMSM) direct drive prime mover. This allows high dynamic torque loads and rotational speeds of up to 30 rpm to be applied. The maximum torque applicable at the test bench is 3.4 MN · m. The non-torque-loading (NTL) unit is a servo hydraulic system that provides forces in three and bending moments in two directions. It is situated between the prime mover and the DUT. The NTB’s own torque transducer is installed on the LSS between the prime mover and the NTL unit. Since the frictions in the NTL unit bring losses in the torque measurement, this transducer was not used for efficiency determination in this measurement campaign (Fig. 3).

Fig. 3
figure 3

4 MW NTB at CWD of RWTH Aachen University

Full size image

3.2 Device under test

The DUT is a research nacelle provided by the FVA (Forschungsvereinigung Antriebstechnik) and operated by the CWD (Fig. 4). The wind turbine nacelle is designated NEG MICON NM80, and its performance data are shown in Table 1.

Fig. 4
figure 4

FVA Research Nacelle on the 4 MW NTB of CWD

Full size image
Table 1 Technical details of the DUT [Technical Description NM80/2750]
Full size table

The drivetrain of the FVA Research Nacelle contains a main bearing that carries the rotor, a gearbox that transforms the speed, a single fed induction generator with six poles that converts mechanical into electrical energy, and a full-size converter concept. The gearbox consists of a planetary gear stage and two helical gear stages, which enable generator speeds of up to 1100 rpm.

3.3 Additional measurement points

In addition to the overall system efficiency, the behaviour of each component is also important. To measure the efficiency of each component individually, multiple measurement points were implemented for the measurement campaign. The mechanical power was measured both on the LSS at the DUT’s rotor hub and on the HSS between the gearbox and the generator inside the DUT. Three additional electrical measurement points were placed between the generator, the frequency converter, the transformer and the middle voltage grid (Fig. 5).

Fig. 5
figure 5

Equivalent circuit diagram of the NTB, the DUT and the three additional measurement points (MP1–3)

Full size image

4 Measurement methodology

The efficiency of electrical machines η is defined as the ratio of useful output Pout to total input power Pin:

$$\eta =\frac{P_{\mathrm{out}}}{P_{\mathrm{in}}}.$$
(3)

For DUTs on NTBs, the energy efficiency is determined by measuring the electrical output power Pel, which is the sum of the electrical power Pel, phase in three phases, and the mechanical input power Pme, which is the product of torque M and rotational speed n:

$$\eta =\frac{P_{\mathrm{out}}}{P_{\mathrm{in}}}=\frac{P_{\mathrm{el}}}{P_{\mathrm{me}}}=\frac{P_{\mathrm{el}{,}\text{phase}1}+P_{\mathrm{el}{,}\text{phase}2}+P_{\mathrm{el}{,}\text{phase}3}}{2\uppi \cdot n\cdot M}.$$
(4)

In addition to the overall system efficiency, the efficiency of the individual components can also be determined by measuring the power flow between each component.

4.1 Mechanical power measurement

The mechanical input power is determined via transient torque M(t) and rotational speed n(t):

$$P_{\mathrm{me}}=\frac{1}{T}\cdot 2\uppi {\int }_{0}^{T}M\left(t\right)\cdot n\left(t\right)\mathrm{d}t.$$
(5)

To minimise periodically recurring oscillations, torque and speed are in practice separately averaged over the largest possible integer number of drivetrain revolutions. The actual number of revolutions should be as high as possible while maintaining acceptable measurement times per load step. The measurement time T depends on the rotational speed:

$$P_{\mathrm{me}}=\frac{1}{T}\cdot 2\uppi {\int }_{0}^{T}n\left(t\right)dt\cdot {\int }_{0}^{T}M\left(t\right)\mathrm{d}t.$$
(6)

In practice, the applicability of Eq. 6 is related to the torque quality and should be examined according to the method proposed in [6].

4.1.1 Static torque offset

Torque transducers are characterised by a signal offset caused by pre-stress in the strain gauges and in the transducer itself. This signal offset needs to be determined at the beginning of each measurement day. Since the torque measurement axis is installed horizontally, reading the value of a single signal is not sufficient. To take the rotation-dependent influence of the transducer’s deadweight and the non-torque load into account, the static offset M0 is averaged over one full revolution at twelve evenly distributed positions relative to the starting position of the drivetrain. This static offset is then used in a post-processing step to tare the torque signal Ms of all measurements:

$$M=M_{s}-M_{0}.$$

More information about determining the static offset of torque transducers in NTBs can be found in [7].

4.1.2 Ripples in raw torque and rotational speed signals

Ripples in the torque and rotational speed signals are dynamic effects caused by the excitation and the general construction of rotating electrical machines. Due to the air gap variance, the non-ideal sinusoidal magnetic field leads to these torque ripples. The LSS torque oscillation depicted in Fig. 6 results in a speed oscillation with a 90° delay. For better visualisation, the signals were smoothed with a moving mean of 150 points for one second. With the torque and speed ripples ratio being smaller than 1% and 90° shifted, the assumption in Eq. 6 is valid [6].

Fig. 6
figure 6

Torque and speed signal ripple over six full revolutions with a phase shift of 90° to each other

Full size image

4.1.3 Signal evaluation

The continuously acquired signals are analysed for each load step. Unlike in the static calibration of torque transducers, a single value per load step cannot be taken when measuring under rotation. The deadweight effect (due to the horizontal mounting of the transducers), misalignment errors (such as eccentricity, non-parallelism, and tilting in the drivetrain), and the aforementioned ripples will affect the torque output signal. These periodical effects can be minimised by performing measurements in a nearly stationary state and averaging the torque signal on the LSS over six full revolutions. On the HSS it is not so important to average over an exact number of revolutions since such a large number of rotations occur within a short time. Instead, averaging can be done over a fixed time interval of 20 s.

4.2 Electrical power measurement

The electrical output power is calculated as the sum of the power of the three phases determined by the transient current and voltage in the power analyser:

$$P_{\mathrm{el}}=\frac{1}{T}\left({\int }_{0}^{T}u_{1}\left(t\right)\cdot i_{1}\left(t\right)dt+{\int }_{0}^{T}u_{2}\left(t\right)\cdot i_{2}\left(t\right)dt+{\int }_{0}^{T}u_{3}\left(t\right)\cdot i_{3}\left(t\right)dt\right).$$
(7)

To eliminate measurement errors, the electrical signals are synchronously averaged over the same period as applied for mechanical power.

However, since the voltage and current measurements are calibrated for their RMS values at defined frequencies, the calibration results are not applicable in Eq. 7. Therefore, Eq. 8 is used instead for the uncertainty analysis. Since the power factor is a constant and close to 1 on the grid side, this approximation is valid for the measurement uncertainty analysis.

$$P_{\mathrm{el}}=U_{1}\cdot I_{1}\cdot \cos \varphi _{1}+U_{2}\cdot I_{2}\cdot \cos \varphi _{2}+U_{3}\cdot I_{3}\cdot \cos \varphi _{3}.$$
(8)

4.3 Iso-efficiency map

Unlike in Hardware-in-the-Loop (HiL) tests on NTBs, standardised measurement procedures such as IEC 60034-2‑1 [8] are designed to determine the efficiency at only one rotational speed. To determine the efficiency of rotating electrical machines at different load points, so-called iso-efficiency contours were introduced by [9,10,11]. In iso-efficiency maps, efficiency is a function of speed and torque, with speed plotted on the abscissa and torque on the ordinate. They allow efficiency to be visualised over a wide operating range. This approach is suitable for identifying the best possible interaction between individual components of a wind turbine drivetrain. To do this, a large number of speed and torque combinations must be measured. The arrangement of operating points is called an iso-efficiency map (Fig. 7a) while the sequence of load cycle combinations is referred to as the load sequence (Fig. 7b). For the load sequence, the rotational speed is periodically kept constant, with the torque gradually increasing and decreasing. The signal averaging as explained in Sect. 4.1.3 happens at stable working conditions after a dwelling time of 30 s [12].

Fig. 7
figure 7

Iso-efficiency map (a) and load sequences (b) divided into three separate measurements, iso1, cm1a and iso2, which were performed on three different days

Full size image

In the present measurement campaign, the iso-efficiency map was divided into several parts because some measurements were also used to calibrate the test bench’s own sensors for mechanical and electrical power measurement. For now, no additional loads (such as wind load simulations) are applied. The operating points approached were specially determined for the present measurement set-up depending on the given NTB and DUT.

5 Measurement results and analysis

To perform the iso-efficiency map measurements as described in Fig. 7, the mechanical or electrical power for the LSS, the HSS, the generator output, the converter output and the transformer output are measured synchronously. Thanks to these intermediate measuring points, the efficiencies of the components can be investigated individually.

5.1 Gearbox efficiency

The efficiency of the gearbox is determined by comparing the input mechanical power from the LSS and the output at the HSS. The measured efficiencies are presented in Fig. 8a and the contour of efficiency mapping is shown in Fig. 8b. The efficiency is related mainly to the torque loads, with transmission more efficient at higher torque loads. The reason is that the load related losses are dominant, so that speed related churning losses impact only the low torque steps.

Fig. 8
figure 8

Efficiency map for the gearbox (a) and the efficiency contour (b)

Full size image

It occurs that the efficiency variation is not consistent between the neighbouring load steps measured on different days. This inconsistency is more straightforwardly apparent in the torque loss plot given in Fig. 9. The load steps measured in the cold state at the beginning of a sequence produce higher losses than do the neighbouring load steps measured at the end of another sequence in the warm state. This results in distortions of the efficiency contour in Fig. 8b. The temperature influence is explained by the following simulation model.

Fig. 9
figure 9

Losses of LSS torque in the gearbox measured on three different days

Full size image

Temperature influences are simulated using an efficiency model consisting of load and speed related loss models for the components. In particular, bearing losses are considered according to [13], and for gearing losses, only the sliding friction losses of the gears are modelled with the relative sliding speed [14, 15]. The mean sliding coefficient and the simplified normal load distribution are acquired according to [16]. The temperature influence is depicted by adapting the viscosity accordingly. Figure 10 shows the result of efficiency simulations for different torques and temperatures.

Fig. 10
figure 10

Drivetrain efficiency for different temperatures and torques at 17.5 rpm

Full size image

The efficiency increases with increasing temperatures until it reaches its maximum asymptotically. The reason for this lies in the churning losses that decrease at lower viscosity due to higher temperatures.

5.2 Generator efficiency

Figure 11 shows the generator efficiency calculated from the HSS mechanical input and the generator output power. The most efficient load step was measured near 18 kN · m at 1050 rpm with 96% efficiency. Contour distortion due to temperature issues is observed as well.

Fig. 11
figure 11

Efficiency map for the generator (a) and the efficiency contour (b)

Full size image

5.3 Frequency converter and transformer efficiencies

The efficiencies of the frequency converter and the transformer are measured by their input and output power. The efficiency maps are presented in Figs. 12 and 13. Their efficiencies vary from 70% to over 95% and are directly related to the input power.

Fig. 12
figure 12

Efficiency map for the frequency converter (a) and the efficiency contour (b)

Full size image
Fig. 13
figure 13

Efficiency map for the transformer (a) and the efficiency contour (b)

Full size image

5.4 System efficiency

The efficiency map of the overall NTB system is presented in Fig. 14. The system can achieve an overall efficiency of up to 89% in the high torque and high speed range; for the extremely low torque and speed range, the efficiency may drop below 40%. Even for the same power, the efficiency varies at different torque and speed combinations. In the real world it is therefore important to operate the nacelle at the optimal load step selected on the basis of an accurately measured system efficiency map.

Fig. 14
figure 14

Overall efficiency map for the system (a) and the efficiency contour (b)

Full size image

6 Measurement uncertainty

A reliable and complete measurement includes not only the measured values but the corresponding measurement uncertainty as well. This section investigates the uncertainties for all measured parameters of the LSS and grid output, which in the end contribute to the total uncertainty associated with the determination of system efficiency.

6.1 Torque measurement uncertainty model

The calibration of the 5 MN · m torque transducer was performed statically with the torque load applied by hydraulic actuators (direct deadweight loading for smaller calibration machines). In NTBs the torque loads differ from those in static calibration as follows:

  • Torque is measured under rotation with ripples and a noisier signal.

  • Zero offset is difficult to achieve due to the remaining static friction of the bearings, and the transducer is tortionally tensed on the test bench even in standstill.

  • Torque loads are kept constant by the NTB controller. Disturbances such as torque ripples could result in instability within the measurement intervals.

These influences are taken into account in addition to the statically calibrated uncertainty.

6.1.1 Resolution

The static zero offset was measured in the morning on all three measurement days. By rotating the shaft in the operating direction in 30° increments, torque offset was averaged over 60 s at standstill in each of the 12 positions (Fig. 15a).

Fig. 15
figure 15

Static zero offset measured at 12 shaft angle positions (a) and the histogram (b)

Full size image

Within the 60 s averaging interval, the signal tends to distribute into two narrow sidebands separated by a distance of 0.5 kN · m (Fig. 15b). This distance r can be treated as the resolution of the torque sampling points. The corresponding absolute expanded uncertainty (\(k=2\)) is estimated according to [17] as:

$$U_{M{,}\mathrm{res}}=\frac{2}{\sqrt{N}}\sqrt{2\left(\frac{r}{2\sqrt{3}}\right)^{2}}=7.7\,\mathrm{N}\cdot \mathrm{m}{,}$$
(9)

where the resolution is considered twice for both zero offset and torque measurement, since every torque step needs taring by subtracting the zero offset (cf. Sect. 4.1).

Moreover, because the torque is averaged over six revolutions, the uncertainty is further divided by the square root of the minimum number of averaged sampling points \(N=2700\) at a maximum speed of 20 rpm.

The relative expanded uncertainty for the resolution is calculated as:

$$W_{M{,}\mathrm{res}}=\frac{U_{M{,}\mathrm{res}}}{M}.$$
(10)

6.1.2 Determination of zero offset

The averaged offsets for each angle position for the three measurement days are presented in Fig. 16. As the TTS is not sensitive to the applied non-torque loads, the signals are randomly distributed with no position-related tendency.

Fig. 16
figure 16

The averaged offset for each angle position for the three measurement days

Full size image

The remaining static friction in the bearing is related to the stopping process just before standstill is reached, when the direction of the remaining friction is counter to the direction of rotation. Therefore, the best way to estimate the static zero offset with compensated friction would be to repeat the 12 position measurements with the shaft rotated in the reverse direction and then average the offset over all 24 values.

In the practical implementation of the static zero measurements, however, rotation in the reverse direction is an irregular operation and not ideal for either the DUT or for other test bench components, even if done only briefly. In this measurement campaign, reverse rotation was not possible.

To compensate for the missing half of the measurement, the 12 measured values are fitted to a half normal distribution function, and the empty left-hand side for reverse rotation is symmetrically estimated in Fig. 17.

Fig. 17
figure 17

The histogram of the averaged zero offset and the fitted half normal distribution

Full size image

In this case, the expanded uncertainty (\(k=2\)) for static torque offset UM,zero can be acquired as:

$$U_{M{,}\text{zero}}=\frac{2\sigma _{\text{normal}}}{\sqrt{12}}=841.2\,\mathrm{N}\cdot \mathrm{m}.$$
(11)

The relative expanded uncertainty for zero offset is calculated as:

$$W_{M{,}\text{Zero}}=\frac{U_{M{,}\text{zero}}}{M}.$$
(12)

6.1.3 Load step instability

Compared to static torque calibration, torque in NTBs is measured under rotation with ripples and a noisier signal. Moreover, disturbances under rotation will result in instability in control, the effect of which was investigated from a metrological perspective in [18].

As described in Sect. 4.1, to correctly account for the periodic oscillations, torque signals are averaged over six full revolutions for each load step. To evaluate the uncertainty of this averaging process, the averaged torque values for each of the six revolutions are plotted in Figs. 18 and 19.

Fig. 18
figure 18

Variance of the averaged torque values for each of the six revolutions and the resulting variance in speed and generator power output at 1.5 MN · m and 12.5 rpm

Full size image
Fig. 19
figure 19

Variance of the averaged torque values for each of the six revolutions and the resulting variance in speed and generator power output at 150 kN · m and 17.5 rpm

Full size image

It can be observed that at higher torque steps (Fig. 18), the torque variation of each revolution is very small, and the resulting rotational speed and generator output power vary periodically as expected.

At lower torque steps (Fig. 19), the ratio of the torque oscillation increases. The load step instability due to the control system is more perceptible: At the 5th revolution, the control system increased the torque considerably to correct for the drop in rotational speed. As a result, the variation of both torque and generator output is greater than at higher torque steps.

For torque step instability, the relative expanded uncertainty is estimated for each load step based on the standard deviation σM of the six averaged torque values as:

$$W_{M{,}\mathrm{in}}=\frac{2\sigma _{M}}{M}.$$
(13)

The results are presented for each load step in Fig. 20. It can be observed that the torque instability is more significant at lower torque steps within a certain speed range.

Fig. 20
figure 20

Relative expanded torque uncertainty (%) due to load step instability

Full size image

The instability and oscillation of torque have an instant influence on the rotational speed and consequently lead to a change in the generated electrical power. As a result, similar instabilities are observed in these measurement quantities. As the oscillations among M, n, U and I are correlated, they can’t directly contribute to the relative expanded uncertainty of the efficiency measurement:

$$W_{\eta {,}\mathrm{in}}\neq \sqrt{{W}_{M{,}\mathrm{in}}^{2}+{W}_{n{,}\mathrm{in}}^{2}+{W}_{U{,}\mathrm{in}}^{2}+{W}_{i{,}\mathrm{in}}^{2}}.$$
(14)

Instead, Wη,in should be estimated by observing the oscillation of efficiency measurements over six revolutions, using the same method as in Eq. 13.

Figure 21 shows that the relative expanded uncertainty of the load step instability starts from 0.007% at higher torque steps and increases up to 0.33% at lower torque steps. Compared to other measurements, the 1.071% uncertainty measured at step 150 kN · m and 18.5 rpm is unusually high and therefore not included.

Fig. 21
figure 21

Relative expanded efficiency uncertainty (%) due to load step instability

Full size image

As the instability effect is considered later in the efficiency determination, the overall torque uncertainty is derived from the contributions of the static calibration, the zero offset and the resolution in Eq. 15, and these uncertainties are summarised in Table 2.

$$W_{M}=\sqrt{{W}_{M{,}\text{static}}^{2}+{W}_{M{,}\text{zero}}^{2}+{W}_{M{,}\mathrm{res}}^{2}}.$$
(15)
Table 2 Relative expanded uncertainty contributions for torque measurement
Full size table

6.2 Rotational speed measurement uncertainty model

As elaborated in Sect. 2.1, encoders with a high number of poles per rotation can provide a better uncertainty than the inclinometer used as a transfer standard. Therefore, in this measurement campaign, the rotational speed measurement is given a relative measurement uncertainty of 0.02%.

6.3 Electrical power uncertainty model

Compared to the mechanical quantities, current and voltage can be measured with higher accuracy. For the measurement of electrical power output to the grid (MP3), the current (120 A) and voltage (6 kV) signals are set above the limit of the power analyser’s direct input channels. Hence, the current transducers and the voltage divider mentioned in Sect. 2.2 are used to reduce the current and voltage values at the power analyser input by factors of 1:1500 and 1:4000, respectively. In this case, the measurement chain consists of the external sensors and the power analyser channels, and both parts contribute to the uncertainty of the power measurement. All components were calibrated at 50 Hz, and the corresponding uncertainties for amplitude deviation are listed in Table 3. As for the deviation on phase measurement, all components show very small uncertainties (smaller than 100 µrad). Since the power factor is always close to 1 at MP3, the influence of phase deviation can be neglected.

Table 3 Relative expanded uncertainty contributions for electrical power measurement
Full size table

The relative expanded uncertainty for each phase is calculated as:

$$W_{\mathrm{Pe}{,}\text{phase}}=\sqrt{{W}_{U{,}\mathrm{PA}}^{2}+{W}_{U{,}\mathrm{VD}}^{2}+{W}_{I{,}\mathrm{PA}}^{2}+{W}_{I{,}\mathrm{CT}}^{2}}.$$
(16)

Assuming that the power among all three phases is symmetrical, the relative expanded uncertainty for the total power measurement of the three phases can be determined by Eq. 17. A summary of the uncertainty contributions is provided in Table 3.

$$W_{\mathrm{Pe}}=\frac{\sqrt{3{U}_{\mathrm{Pe}{,}\text{phase}}^{2}}}{3P_{e{,}\text{phase}}}=\frac{W_{\mathrm{Pe}{,}\text{phase}}}{\sqrt{3}}.$$
(17)

6.4 System efficiency uncertainty model

The aforementioned measurement of torque, rotational speed and electrical power, as well as the load step instability, contribute to the total relative expanded uncertainty associated with the determination of system efficiency:

$$W_{\eta }=\sqrt{{W}_{M}^{2}+{W}_{n}^{2}+{W}_{\mathrm{Pe}}^{2}+{W}_{\eta {,}\mathrm{in}}^{2}}.$$
(18)

The contribution of each component from Eq. 18 is listed in Table 4, and the load step related uncertainty Wη is plotted in Fig. 22. Torque measurement represents the greatest source of uncertainty, with an overall uncertainty of 0.30% seen in the higher torque range and up to 0.72% in the lower torque range.

Table 4 Relative expanded uncertainty contributions for efficiency determination
Full size table
Fig. 22
figure 22

Overall relative expanded uncertainty (%) for system efficiency determination

Full size image

For the other three measurement points, the uncertainty models are similar to the model mentioned above. As the torque range on the HSS is significantly smaller, the uncertainty is smaller as well. The uncertainties for the generator output (MP1) and the converter output (MP2) are smaller compared to MP3, and the voltage is measured directly in the power analyser without external sensors. Since their uncertainties are smaller and not directly relevant for determining system efficiency, these uncertainties are not listed in this paper.

7 Conclusion and future work

In this paper, the efficiency of a 2.75 MW nacelle drivetrain on an NTB was determined traceably at various load points, which represent different torque/rotational speed combinations. For this purpose, so-called transfer standards for mechanical and electrical power measurement were additionally installed and integrated into the nacelle drivetrain. The overall system efficiency of the DUT amounts to 89% in the high torque and high speed range. The relative expanded measurement uncertainty for efficiency determination was between 0.30% and 0.72% over the entire operating range. Both the efficiency and the relative expanded measurement uncertainty were calculated for each operating point.

For the torque measurement, determining the offset is important. Unlike static measurements, a measurement under rotation cannot measure just a single value. A method for static offset determination was presented which takes into account the influence of both the rotation and installation position of the torque transducer in the NTB. In addition, the influence of dynamic disturbances, such as ripples and oscillations, was examined. For a reliable torque measurement, especially on the LSS, torque and speed signals must be averaged over six full revolutions per load step. Besides the 0.65% relative expanded measurement uncertainty of the torque measurement using the 5 MN · m torque transfer standard, the uncertainty of the load step instability is also significant with 0.33% at minimum torque. The uncertainty contribution of the electrical power measurement using calibrated high-precision measuring devices is negligible at 0.019%.

The influence of temperature on the efficiency is significantly high, particularly with respect to the gearbox and the generator. The efficiency variance due to temperature changes can be far above the given uncertainty range in each load step. The problem is that it takes several hours for the NTB-DUT set-up to reach a thermal static state. This makes it extremely time consuming and impractical to repeat the measurement for every load step. In real world applications, the nacelle likewise operates at varying temperatures due to changes in the wind speed and in the ambient environment. Therefore, a standardised test procedure for determining the efficiency of wind turbines should include temperature measurement and use torque, rotational speed and temperature to define the operating points and their respective efficiencies.