1 Introduction

Spheroidal graphite cast iron (EN-GJS) as a material for structural components in wind turbines boasts advantages due to its higher design flexibility and potential for lightweight design. Due to significantly higher cooling rates, caused by faster heat dissipation in the chill casting process, the finer structure of components offers additional potential for increased strength compared to components produced using the sand casting process. However, because of the lack of knowledge of the fatigue strength of chill-cast EN-GJS-400-18-LT, a reliable lightweight component design using this material and fabrication process is not yet feasible.

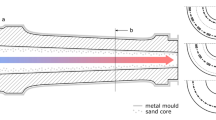
To address the above mentioned shortcoming, the publicly funded Gusswelle [1] project was carried out. Gusswelle is the German term for cast-iron shaft. The component at the heart of this project is a cast-iron hollow rotor shaft for wind turbines. Earlier project results on an optimized hollow rotor shaft design and the underlying design process, as well as the intended validation plan and test setup, have been previously published in [2]. The Fraunhofer Institute for Structural Durability and System Reliability LBF conducted extensive material tests on a comparable hollow rotor shaft of a wind turbine both to determine the cyclic behavior of the material and fabrication method previously discussed and to identify unused reserves in order to qualify a higher-strength casting material for application in the wind industry [3]. One principal aim of the project was to develop and verify the design concept for cyclically stressed large cast components made of EN-GJS-400-18-LT chill cast using material tests as an essential input. Subsequently, a sample full-scale fatigue test was performed at Fraunhofer Institute for Wind Energy Systems IWES to verify the predicted lifetime.

This contribution is structured chronologically: it starts in Sect. 2 with the final setup and plan for the full-scale experiment with a focus on the necessary adjustments compared to the originally intended test plan. In Sect. 3, the chosen sensor concept as well as the underlying operational concept including the automation of the test rig are explained. An adequate FEM model of the specimen and relevant neighboring components as well as the validation thereof to ensure that the loading and the resulting local strains representing the real test bench situation are described in Sect. 4. For that purpose, model sensitivities regarding certain model features (e.g., bolt connection, modeling of the main bearing and bearing seat) is investigated and only relevant model features are considered to reduce complexity and calculation time. To validate this application, an optimized FEM model of the specimen was tested on different load levels. Based on the validated model, among other things the required shear force from the hydraulic system could be determined accurately to achieve the desired local strain in the area of the critical hot spot. In Sect. 5 the usage of non-destructive testing to document the condition of the specimen from initial crack formation until integrity loss is explained. The component fatigue test results are then compared to the material based life-time forecast. To conclude in Sect. 6 the performance of simulation-based crack propagation studies are described to qualitatively verify the responsible loads for the observed cracks of the component test and to further develop the possible method for crack predictions.

2 Test setup and test plan

To validate the underlying design process explained in [2], a full-scale test campaign on the main shaft fatigue test bench of IWES (see Fig. 1) was carried out. This modular drivetrain test bench was developed, assembled and successfully operated by IWES as part of the Beben XXL [4] project. The lifetime achieved for the rotor shaft is later compared to the expected lifetime considering the used design process in the sense of a random sample. To provoke a technical crack in the trumpet section as a result of fatigue damage, a constant rotating bending moment is applied on the rotor shaft for a specific number of cycles. The test setup as shown in Fig. 1 and explained in more detail in [2] consists of the main shaft (specimen) supported with the original main bearing (2-row spherical roller bearing) also used in the wind turbine assembly. The gearbox dummy is designed in such a way that it allows the same degrees of freedom as the gearbox in the turbine assembly without being prone to fatigue failure while simultaneously reducing costs. At the far end of the load lever, a shear force is introduced with the help of hydraulic load application. This shear force translates via the load lever into the desired bending moment at the critical notch area near the shaft shoulder in the trumpet section. The drive is able to rotate the drivetrain with up to 60 rpm and leads to a rotating bending moment on the rotor shaft. The oil lubrication system ensures adequate lubrication and cooling of all involved bearings.

Fig. 1
figure 1

Main shaft test bench (© Fraunhofer IWES/Kyling)

Full size image

The magnitudes of the applied bending moments were refined prior to testing based on the results from material tests carried out at LBF and finally adjusted regarding the maximum principal stress in the critical notch area based on the validated FEM model as described in Sect. 4. The different load stages are as follows:

  1. 1.

    Load stage

    • Maximum principal stress in the critical notch: 131 MPa

    • Number of load cycles: 50,000

    • Bending moment at main bearing position: 5.254 MNm

  2. 2.

    Load stage

    • Maximum principal stress in the critical notch: 169 MPa

    • Number of load cycles: 1,600,000

    • Bending moment at main bearing position: 6.723 MNm

  3. 3.

    Load stage

    • Maximum principal stress in the critical notch: 208 MPa

    • Number of load cycles: 2,000,000

    • Bending moment at main bearing position: 8.237 MNm

The first load stage is dedicated to completing commissioning of the test setup. A focus lay on the identification of potential ring creeping on the connection of the inner ring of the main bearing to the main shaft. The bending moment was determined as a function of the specific load of the main bearing in such a way that it remained below the specific load at which fretting corrosion and bearing ring creep occurred in an earlier project with a similar setup [4]. The second load stage is characterized by a resulting local stress in the notch area (see Sect. 3.1) slightly above the kink point of the Wöhler line at 90% survival probability of the flat specimens for a stress ratio of \(R=-1\), which have a lower highly stressed volume than the test shaft. The third load stage was chosen in such a way that two million load cycles should result in a survival probability of less than 10% for the rotor shaft based on the information gained by LBF [5] for the flat specimens for a stress ratio of \(R=-1\). Thus, damage is highly probable for this load stage.

3 Sensor and operational concept

3.1 Sensors

There are sensors for the actual fatigue test and further ones to ensure controlled and safe test operation. Only the fatigue relevant strain gauge sensors (SGs) are explained here. The SGs are placed at three axial positions as shown in Fig. 2.

Fig. 2
figure 2

Strain gauge positions on rotating rotor shaft

Full size image

Strain gauge quarter bridges are used to acquire the local strains in the trumpet critical notch area with an angular spacing of \(9^{\circ}\). The strains in the conical and in the trumpet nominal area are acquired via opposing double SG, which are connected as full bridges. Thermal compensation ensures that only the strain due to the external load is measured.

3.2 Operational concept

The test bench runs 24/7 fully automatically. Relevant sensor readings as strains, deflections and temperatures are controlled. The test can be followed remotely using an internet browser. If certain thresholds are exceeded, the test bench stops automatically and the users responsible for testing are informed via e‑mail with the triggering event. An on-site inspection follows to check for the integrity of the setup and to clarify if the test should be continued.

4 FEM model development and validation

4.1 Model setup

The most relevant parts of the test setup to be modeled are the hollow rotor shaft, inner bearing ring, outer bearing ring, both distance rings along with shaft nut, adapter disc and load lever as shown in Figs. 3 and 4.

Fig. 3
figure 3

FEM model of relevant test components

Full size image
Fig. 4
figure 4

Detailed cross-sectional view of FEM model

Full size image

The principal boundary conditions of this model are as follows:

  1. 1.

    At position A (gearbox dummy, non-locating bearing), only the translational degrees of freedom in the y and z directions are locked. Since a static state is considered, locking of the rotation around the x and z axis is possible for better convergence behavior.

  2. 2.

    At position B (main bearing, locating bearing), translational degrees of freedom in the x, y and z directions are locked. Since a static state is considered, locking of the rotation around the x and z axis is possible for better convergence behavior.

  3. 3.

    At position C (vertical shear/lateral load introduction on the load lever), a load from 0 to 1500 kN is applied in the y direction.

  4. 4.

    Fixed support on the outer ring of the main bearing

  5. 5.

    Main bearing inner to outer ring: all translational degrees of freedom are fixed, all rotational degrees of freedom are given.

Flange connections are modeled as bonded contacts (e.g. shaft and adapter disc). The shaft nut is bonded to the rotor shaft. The inner ring of the bearing is assembled onto the shaft as a press fit. This press fit can be implemented by either modifying the dimensions in the CAD model or by a positive offset which increases interference. Both methods require a contact type where penetration can be considered. The inner surface of the inner bearing ring is defined as the contact body and the bearing seat on the shaft as the target body. The inner bearing ring, the distance rings on both sides of the inner ring as well as the shaft nut are axially in frictional contact. The inner bearing ring as well as the distance rings are circumferentially in a frictional contact to the rotor shaft.

The simulation requires the following steps:

  1. 1.

    The press fit of the main bearing inner ring with the shaft is created. For this step, the friction is temporarily set to zero so that no shear stresses arise due to the formation of the press fit

  2. 2.

    The friction in the main bearing seat is activated and the hold constraints for convergence enhancement are disabled

  3. 3.

    Gravity force is activated

  4. 4.

    The external vertical shear/lateral load is applied

Mesh refinement, the process of resolving the different components of the model with the necessary mesh sizes, so that a further refinement does not lead to changed strain results, is done. Fine meshing is used in areas of interest and high-stress gradients.

A sensitivity study was carried out to identify the impact of more detailed modelling of, for example, the bolt connections in the flanges and the rolling elements. The small changes in the acquired strain results did not justify the significant additional modeling and calculation effort. Consequently, in the final FEM model only the above mentioned fidelity was implemented.

4.2 Validation runs

After the test setup was successfully commissioned, step runs with different bending load levels were carried out. Fig. 5 shows exemplary strain plots from such a step test run. First a load profile with a smaller maximum bending moment load was run to check for functionality of the whole system. This was followed by the relevant step tests with load steps of 500 kNm and a duration of 5 minutes each to reach a maximum bending moment of 8 MNm. These step runs were carried out twice to gather a robust data set. To exclude any influences from the operational side, these step runs were run automatically with a predefined test profile. The acquired measurement data was post processed and statistically evaluated as shown in Fig. 6. The blue bottom line correlates the applied external vertical shear/lateral force in kN to the measured strain amplitudes in the conical area of the rotor shaft. The orange center and grey top lines correlate analogously the strain in the nominal strain area respectively the critical notch area of the trumpet (also compare with Sect. 3.1) to the external loading. As expected a linear correlation is given for all three of them.

Fig. 5
figure 5

Obtained strain plots over time for step test runs

Full size image
Fig. 6
figure 6

Post-processed measured strain amplitudes in the critical notch area

Full size image

4.3 Model validation

Fig. 6 shows the post-processed measured strain amplitudes. The strain amplitude results from the FEM model simulation and the validation runs were compared as shown on the example of the local strain in the trumpet notch area in Fig. 7. A relative difference in the strain amplitudes in the range of 0.31 to 2.98% is achieved. Consequently, it can be stated that the FEM model is validated and can be used e.g. to correlate external load to local strain and vice versa.

Fig. 7
figure 7

Comparison of simulated and measured strain in the critical notch area

Full size image

5 Test conduction, non-destructive testing and component fatigue results

5.1 Test execution

The test ran 24/7 whenever it was not it was not stopped manually due to a planned inspection or automatically due to a certain trigger, e.g. if the maximum strain value was exceeded. The inspections were carried out according to an inspection protocol and documented in a logbook.

Over the entire test setup, more than 50 SGs were installed in different bridge configurations. Given such a large number of SGs, isolated malfunctions are anticipated during installation, commissioning, the first regular days of operation and finally over the entire test period. In order to be able to check or repair defective SGs, testing must be stopped. During the first two load stages, priority was given to the availability of the SGs in order not to lose any relevant measurement data. A persistently high failure frequency of the rotating SGs mounted to the specimen, especially those in the critical notch area of the trumpet, was witnessed during regular test operation. The resulting stops to repair these SGs combined with the difficulties of having trained people on site due to the corona pandemic delayed the execution of the test considerably. This led in the course of the third load stage to the decision that only some of these SGs should be maintained. Unfortunately, a dominant cause for the high failure rate of the SGs could not be identified despite extensive efforts. The following list provides an overview of causes identified in an arbitrary order, some of which could be solved sustainably:

  1. 1.

    Interference from a defective SG channel on the neighboring three channels on a common Beckhoff terminal (ELM3504)

  2. 2.

    Insufficient earthing of the metrological installation

  3. 3.

    Insufficient shielding of the sensor lines

  4. 4.

    Insufficient line clearance in loaded condition

  5. 5.

    Usage of solder contact SG to cable

  6. 6.

    Quality of the surface preparation prior to sensor application

5.2 Non-destructive testing

The runs on load stages 1 and 2 could be carried out without identifying any crack initiation. During the later course of the fatigue test on load stage 3 non-destructive testing (NDT) methods were used to quantify and document crack propagation progress. Due to the aforementioned problems with the SG measurements and the automated monitoring of the measured strain amplitudes as an indicator for a possible crack, test operation had to be adapted in this respect. It was decided no longer to identify and document a possible crack or its progress based on strain measurement, but with the help of the non-destructive dye penetrant testing method (PT) in accordance with [6]. The first cracks were identified during an inspection after 1.723 mio. load cycles with the naked eye and confirmed by PT testing as shown in Fig. 8.

Fig. 8
figure 8

Exemplary results from the dye penetrant testing method applied to angular section 18–\(27^{\circ}\) at various load cycles on load stage 3

Full size image

Due to the high density of SGs in the critical notch area and the limited accessability, the PT method could not be used regularly. From the PT testing it can be derived that already after 1.5 mio. load cycles a crack initiation could be assumed. This crack initiation was not identified as such earlier due to the inclined crack front. The load situation with a very dominant bending load compared to the driving torque necessary to achieve the desired rotational speed (approximately factor of 1,000 between bending and torque load) led to an assumed vertical crack front, i.e. a crack front parallel to the shaft shoulder.

After the first cracks were identified the majority of the SGs were disassembled to allow for better application of PT testing. Additionally the crack depths were determined using a device based on the potential probe method as shown in Fig. 9 left and center. Finally, the rotor shaft suffered a total fracture after \(N=1,792,779\) load cycles as shown in Fig. 9 on the right.

Fig. 9
figure 9

Left: applied PT testing, center: crack depth measurement, right: critical notch trumpet area of entirely fractured specimen

Full size image

5.3 Component fatigue test results

Fig. 10 summarizes the documented crack depths and lengths until the components’ lifetime was reached. The crack depths determined with the crack depth measuring device on the still intact component could be largely confirmed by the measurement on the fracture surface.

Fig. 10
figure 10

Measured crack depths and lengths at different load cycle numbers on load stage 3

Full size image

A long-term evaluation of the measured strain readings in the notch base led to the same conclusion as the visual inspections: The initial crack formation occured at about 1.5 mio. load cylces.

Fig. 11 summarizes the results of the fatigue tests at material and component level. The evaluation of the material test results in the form of Wöhler lines was carried out using the maximum likelihood method according to [7,8,9]. As expected, no component failure (crack initiation) was observed at load stages 1 and 2. At load stage 3 and the determined number of cycles until crack initiation of about 1.5 million, component failure was to be expected with a probability of nearly 97.7% based on the material tests carried out by LBF on the flat specimens (rectangular symbols) with a more comparable highly stressed volume (HSV) for the critical notch area than given for the round specimens (round symbols). The fatigue life prediction for the rotor shaft based on material level testing and the full-scale test are thus in accordance. The design process conceived in the Gusswelle project could therefore be confirmed via the sample of the component test. No other failure mechanisms were witnessed during the full-scale test. The assumed strength increase for chill-cast large components could be demonstrated on the example of the rotor shaft. A direct comparison of the resulting bearable nominal stress for 10 million load cycles based on round specimen M32 trials between sand (136 MPa) and chill (212 MPa) cast components indicates a strength improvement of 56%.

Fig. 11
figure 11

Results of material tests vs. component test (© Fraunhofer LBF & IWES)

Full size image

The resulting fatigue crack front under a very dominant bending load is theoretically expected to be parallel to the shaft shoulder. However, as documented in Fig. 9 (right side) and Fig. 10, the test resulted in an average inclination relative to the shaft shoulder of \(8.5^{\circ}\). In the following Sect. 6 the question whether the low driving torque in relation to the bending moment can cause the inclined crack front is addressed.

6 Simulation of crack propagation

A simulation-based investigation is performed to analyse the crack propagation in the trumpet section that was witnessed during the fatigue testing of the rotor shaft. Two load cases have been considered to analyze the crack propagation:

  1. 1.

    with applied bending moment

  2. 2.

    with applied bending moment and torque on drive side

Cracks initiate in regions of high stress concentration usually caused by structural discontinuities. The detailed crack simulation in the high stresses area is performed using the sub-modeling approach. This involves an initial evaluation of the global FEM model described in Sect. 4 using a coarser mesh, followed by a detailed analysis of a sub-model containing the regions of interest with a much more refined mesh (see Fig. 12). The sub-model contains the trumpet section of the rotor shaft.

Fig. 12
figure 12

FEM modeling for crack propagation simulation

Full size image

For crack initiation, the maximum principal stress criteria was used to identify the critical crack location. In the identified critical location, a crack was modeled in the trumpet section in the sub-model. The modeled crack is semi-elliptic with geometric parameters to define the crack shape and crack front in three dimensional analyses. Separating Morphing and Adaptive Re-meshing Technology (SMART) [10] was used to simulate the crack propagation trajectory. This feature is based on the unstructured mesh method that allows automatic generation of mesh for crack fronts.

As described in the theory of linear-elastic fracture mechanics [11], any fracture mode in a cracked body may be described by one of the following three fundamental fracture modes, or their combinations:

  • Mode I for tensile mode

  • Mode II for in-plane shearing

  • Mode III for out-of-plane tearing

These fracture modes of crack deformation can be defined by the stress intensity factors (SIF) corresponding to stress fields of opening mode (\(K_{{I}}\)), in-plane shearing mode (\(K_{{II}}\)) and out-of-plane tearing mode (\(K_{{III}}\)) [12]. The developed FEM model calculates the SIF and simulates the crack propagation according to the Paris Law [13] which relates the stress-intensity-factor range to the crack-growth rate for the region under fatigue-stress regime as follows:

$$\frac{da}{dN}=C\Updelta K^{m}$$
(1)

where \(a\) is the crack extension, \(N\) is the fatigue cycle count, \(C\) and \(m\) are the Paris Law constants dependent on the material characteristics and stress ratio, and \(\Updelta K\) is the stress-intensity-factor range during the fatigue cycle. An equivalent stress-intensity-factor range (\(\Updelta K_{\text{eqv}}\)) can be used:

$$\Updelta K_{\text{eqv}}=\frac{1}{2}\cos\left(\frac{\Theta}{2}\right)\left[\Updelta K_{{I}}\left(1+\cos\Theta\right)-3\Updelta K_{{II}}\sin\Theta\right]$$
(2)

where \(\theta\) defines the direction of crack propagation as follows:

$$\Theta=\cos^{-1}\left(\frac{3K^{2}_{{II}}+K_{{I}}\sqrt{K^{2}_{{I}}+8K^{2}_{{II}}}}{K^{2}_{{I}}+9K^{2}_{{II}}}\right)$$
(3)

SMART updates the mesh for geometry changes due to crack growth at each solution step and uses the crack-extension increment to calculate the load-cycle increment. The associated instantaneous value of SIF follows the changes in crack geometry and stresses during crack growth. The simulation stops when the maximum crack length (which is user defined) is reached.

The crack propagation simulation results for the two load cases are presented in Fig. 13. The model subject only to bending loads showed a clear opening crack mode. However, the model subject to both bending and torsional loads showed crack propagation with a tilt of approximately \(9^{\circ}\).

Fig. 13
figure 13

Crack propagation for bending load (left) and for bending load with additional torque (right)

Full size image

A comparison of the resulting SIF around the crack region is plotted in Fig. 14. The SIF corresponding to the first crack mode (\(K_{{I}}\)) are high in both load cases. However, the SIF of second and third crack modes (\(K_{{II}}\) and \(K_{{III}}\) respectively) remain significantly low for both load cases. The bending causes loads to act perpendicular to the crack surface resulting in crack opening. An additional torque can result in shear loads parallel to the crack plane leading to tearing mode. The strength of the corresponding SIFs for these individual modes determine the resulting direction of crack propagation. The simulation results suggest that the SIF corresponding to the tearing fracture mode is not sufficent to cause a tilt in the crack propagation as observed in the experimental findings.

Fig. 14
figure 14

Comparison of stress intensity factors of the crack modes for the considered two load cases

Full size image

7 Conclusion

The top three lessons learnt from the Gusswelle project confirm in part common engineering knowledge, nonetheless, it is worth mentioning them explicitly here:

  1. 1.

    The FEM modeling approach should be from simple to complex. Higher complexity is only justified by significantly improved simulation results.

  2. 2.

    Fewer rotating SGs would have simplified the test preparation as well as conduction and allowed for better NDT during the inspections combined with no little loss of the acquired measurement data.

  3. 3.

    A second method to identify a potential crack initiation should be applied from the start.

A good degree of consensus was achieved between the fatigue life prediction of the rotor shaft based on material-level testing and the full-scale test. The conceived design process in the Gusswelle project was confirmed by means of the sample of the component full-scale test. The expected strength increase for chill-cast large components could be demonstrated on the example of the rotor shaft and is in the range of 50%. It can be assumed that it is sufficient to carry out material tests with adequate sampling in order to estimate the service life of very large chill-cast components. Nevertheless a large-scale test can supplement this prognosis in the sense of minimizing risk, especially with regard to other influencing variables and damage modes.

The rotor shaft test has shown an inclined crack front in experimental findings, but not in high-fidelity crack simulation results. This leads to the conclusion that the experimentally observed crack inclination may not be caused by the driving torque. Further investigation is required to determine the true reason for the experimentally identified crack inclination under the applied loads. Nevertheless, the experimental findings are relevant for future inspection instructions for cast shafts, thus offering field technicians more specific guidance on what potential cracks may look like. This more precise indication of the shape of possible cracks reduces the risk of overlooking them. As under field operational conditions the torque is way higher the assumptions to the conducted simulation have to reconsidered.