1 Introduction

Gear drives of various power classes are used in the drive trains of machines and vehicles. Depending on the torque to be transmitted and the gear geometry, large tooth forces can occur. Since the stiffness of the teeth is not constant during meshing, these forces are subject to strong dynamics. Therefore, gears and their forces have a major influence on the shafts and their bearings. The tooth forces expose the shafts to bending and misalignment. This leads to a shifted position and orientation of the gears relative to each other, which in turn influences the tooth contact and finally the resulting forces. In contrast to spur gears, bevel and hypoid gears are sensitive to a change of the relative axis position. This can worsen the running characteristics and considerably reduce the load capacity.

Since meshing forces, axial position, shaft deflection and bearing deflection influence each other, it is difficult to analytically determine the axial position under load and therefore the load capacity of a hypoid gear set. This led to the development of several software solutions to account this problem [1, 6]. These provide a loaded tooth contact analysis (LTCA) with respect to the deflections under load. To acquire results with those tools, the loads must be known. This might be a maximum projected load or a load spectrum. With the absence of measurement data, multi-body simulations (MBS) can be used to acquire the load spectrum of a gear stage. However, commercial solutions reveal some severe deficits in the calculation of tooth forces regarding the treatment of hypoid stages in MBS simulations. Thereby, an incorrect axial position can lead to errors in the load capacity calculation of bearings, gears and shafts. Furthermore, inaccurately calculated tooth forces lead to inaccurate excitations of the complete system.

To benefit from the features of the bevel gear calculation software BECAL [4, 5], an MBS-co-simulation module is being developed. In a former article [7] the functionality has been described in general. During the ongoing development, several details of the loaded tooth contact analysis are examined with the aim to improve the result quality or accelerate the computation. One crucial component is the calculation of the load distribution between contact points. While BECAL provides an established and trusted procedure, their application in context with MBS simulations has shown discrepancies.

2 The co-simulation module

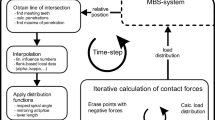
The purpose of the developed serial MBS-co-simulation of a bevel gear stage is to calculate the local load distribution on the contact flank based on the relative position of pinion and gear as well as their rotational position. Due to the complex geometry of bevel gears [3], a previous determination of the flank topography must be performed. During the simulation, the penetration of the flank surfaces must be figured out. This penetration is used to calculate the load distribution. As those computations take place during the time integration of the MBS-solver, they must be performed as efficiently and quickly as possible. For this reason, the influence number method is used. The deformations of the tooth flank caused by point loads are therefore saved as compliances (the influence numbers) prior to the simulation. These compliances describe the deformation of each point of the contact line caused by each single point load, acting on this contact line. Combined with additionally computed non-linear contact compliances the load distribution can be calculated.

The method provides the possibility to investigate various influences on the load distribution. For example, the measured flank topography of each tooth or pitch deviations might be included in the tooth contact analysis. The influence numbers describing the tooth stiffness, can be calculated previously by utilizing FEA enabling the possibility to take not rotationally symmetric gear bodies with non-constant rotational stiffnesses into account. The details of this procedure were described in [2].

Since the publication of the article “Co-simulation of the tooth contact of bevel gears within a multibody simulation” [7] the co-simulation module has been improved so that hypoid and beveloid gears can be included.

3 Calculation of the load distribution

As described in a previous article [7], the load distribution calculation in BECAL is performed using a variable number of n discrete contact points. Due to the continuously changing relative position of the gears, these contact points must be recalculated for each meshing position, which implies a recalculation in every time step of the MBS simulation. This results in a varying number of contact points in every time step. The contact points are determined on spherical sections. The origin of those spherical sections is the pitch cone apex of one of the gears. For each section, the point of greatest penetration with the opposing tooth flank is considered as the contact point. Due to the geometry of bevel gears and the changing relative positions, there is not a penetration for every section. Therefore, the number of contact points fluctuates. In Fig. 1 a pinion is shown with the remaining contact points on two teeth. The contact forces are shown as arrows.

Fig. 1
figure 1

Contact line split on two teeth

Full size image

3.1 The current method of load distribution calculation

To calculate the load distribution \(\boldsymbol{f}=(f_{i})_{i=1\cdots n}\) Fig. 2c) from the local penetrations \(\boldsymbol{d}=(d_{i})_{i=1\cdots n}\) Fig. 2a, b), the \((n\times n)\) compliance matrix \(\boldsymbol{C}=(c_{ij})_{i=1\cdots n, \, j=1\cdots n}\) is required. This matrix describes the displacement of contact point j for a force acting on point i. As also described in [7], these compliances are divided into a linear bending component B and a non-linear contact component K(f):

$$\begin{array}{l} \boldsymbol{B}=\left(\begin{array}{ccc} b_{11} & \cdots & b_{1n}\\ \vdots & \ddots & \vdots \\ b_{n1} & \cdots & b_{nn} \end{array}\right) \\ \boldsymbol{K}\left(\boldsymbol{f}\right)=\left(\begin{array}{ccc} k_{11}\left(f_{11}\right) & 0 & 0\\ 0 & \ddots & 0\\ 0 & 0 & k_{nn}\left(f_{nn}\right) \end{array}\right) \end{array}$$
(1)
Fig. 2
figure 2

a intersecting bodies b penetrations c forces 1st iteration d deformed shape

Full size image

The linear component is calculated in the pre-process step for both flanks of the two meshing gears. The contact compliances depend on the local geometry and the current loading condition. They must be determined iteratively for each meshing position. The employed model assumes that the contact compliances Kij have no effect on the neighbouring points. This simplification can be applied, as the compliances are computed for infinitely long cylinders. This results in a small error, that has been found to be negligible in former studies [4]. The matrix of contact compliances K(f) is therefore a diagonal matrix.

In the established method for iterative load distribution calculation in BECAL, a uniform load distribution is used to start with and thus the contact stiffness of all points is roughly estimated. More elaborate methods to estimate the starting load distribution have been tested. Those where discarded due to the risk of prematurely eradicating contact points. Furthermore, the potential reduction in the number of iteration steps was found to be minimal. These estimated contact compliances K0 are added to the diagonal elements of the immutable bending compliance matrix. Afterwards the linearized system of equations for the load distribution is solved for f:

$$\left(\boldsymbol{B}+K^{\mathbf{0}}\right)\cdot \boldsymbol{f}=\mathbf{C}\cdot \boldsymbol{f}=\boldsymbol{d}$$
(2)

This usually results in a negative load for the contact points with the smallest penetration. Since no negative forces can be transmitted via the tooth contact (adhesion is neglected), those contact points are removed from the system of equations. If the ith force becomes negative, the ith row and column are deleted from the compliance matrices. Likewise, the ith value is removed from the penetration vector. For a negative force f1 the resulting matrix \(B\boldsymbol{'}\) and vector \(d\boldsymbol{'}\) are reduced as followed:

$$\begin{array}{ccc} \boldsymbol{f}=\left(\begin{array}{c} \begin{array}{c} -f_{1}\\ +f_{2} \end{array}\\ \begin{array}{c} \vdots \\ +f_{n} \end{array} \end{array}\right) & B\boldsymbol{'}=\left(\begin{array}{ccc} b_{22} & \cdots & b_{2n}\\ \vdots & \ddots & \vdots \\ b_{n2} & \cdots & b_{nn} \end{array}\right) & d\boldsymbol{'}=\left(\begin{array}{c} d_{2}\\ \vdots \\ d_{n} \end{array}\right) \end{array}$$
(3)

For the remaining points, the contact compliances \(K\boldsymbol{'}\) are now calculated with regard to the new contact forces \(\boldsymbol{f}'\). A new system of equations can then be formed for the next iteration step:

$$\left(\boldsymbol{B'}+\boldsymbol{K'}\right)\cdot \boldsymbol{f'}=\mathbf{C'}\cdot \boldsymbol{f'}=\boldsymbol{d'}$$
(4)

This iterative process reduces the number of active contact points until all resulting forces are positive. The iteration continues until the chosen target threshold for the relative deviation of forces per step is reached. The iteration steps of the load distribution calculation are shown in Fig. 3.

Fig. 3
figure 3

Flowchart of the load distribution calculation

Full size image

3.2 Shortcomings of the currently used method

The described method has the disadvantage that a single contact point is either involved in the load transfer or not. If there is a small change in the position of the flanks, a single point at the end of the contact line may completely disappear. This effectively means that its stiffness also vanishes. This results in a stiffness discontinuity for the entire system of the tooth contact. The transmission error under load thus experiences bumps. In a conventional BECAL calculation with about 40 meshing positions over one pitch (Fig. 4, left, blue graph), this effect is neither visible nor of importance. Only with a significantly increased number of 181 meshing positions the effect is observable in BECAL (Fig. 4, right, blue graph). The absence of the bumps for the load free transmission error (black graph) confirms, that the calculated stiffnesses cause this problem. Within an MBS calculation, such a stiffness difference can lead to a worse convergence behaviour of the MBS solver and could result in phantom vibrations.

Fig. 4
figure 4

BECAL transition error with 40 (a) and 181 (b) meshing positions

Full size image

To understand the root cause of those bumps the computation method must be investigated a bit further. The stiffness of a single contact point results from the linear bending stiffness of the corresponding section and the contact stiffness. The curvature and the distance to the tip edge as well as the angle of the tip edge are also required for the calculation of the contact compliance. Since each contact point represents a piece of the contact line, these parameters are implicitly assumed to be constant for a contact line section. The length li of a contact line section depends on the discretization of the contact area.

In Fig. 5 two contacting bodies (light grey) are shown in their undeformed state. The bodies are separated into contact sections with the length li. The forces fi are plotted for the second iteration step and with relation to body 1. Due to coupling stiffnesses point 1 receives a negative force f1. For each contact section the penetration di is calculated as the distance of the contact points of the bodies. Nevertheless, not only the geometric properties are constant along the contact section, but also those penetrations di. This results in a penetration deviation along the section. The true penetration is only met at the contact point.

Fig. 5
figure 5

Contact sections of two contacting bodies

Full size image

This fact does not have a decisive effect on the results at points that are fully in contact (Fig. 5, points 2 and 3). For those points the negative and positive penetration deviations almost cancel each other out, despite the nonlinearity of the problem. This can be assumed, as the curvature along the contact line is small in general.

If the calculated force at a contact point is exactly 0 like in Fig. 6a, it means that this contact section should still carry with about half its length. Along the section negative and positive forces are cancelling out each other (Fig. 6b). As negative forces should not be transmitted by the contact, those should be eradicated (Fig. 6c). This implies that points coming into contact are first underrepresented, as they get deleted due to negative forces. When they finally remain with a positive force, they are overrepresented until that section is fully in contact.

Fig. 6
figure 6

partially contacting section with calculated point load (a), theoretical line load (b), effective line load (c) and true effective point load (d)

Full size image

3.3 Introduction of a modified method

One obvious solution to the stated problem is to increase the number of contact points. This reduces the length of the contact line sections represented by each point. The deviation of the penetration per section is lowered and thus the jumps in the stiffness are reduced. While the effect can be decreased, the calculation times are growing as the square of the number of contact points. This leads to the requirement to find a better and faster solution. In Fig. 7, section l1 from Fig. 5 is shown again in detail. The light grey areas are body 1 (bottom) and body 2 (top). The dark grey area represents the penetration of the undeformed bodies. In Subfigure a) a constant deviation for a contact section is shown in blue. It is assumed, that this section receives a negative force in orange and would be deleted with the old method. In Fig. 7b the theoretical variant with higher discretisation is shown.

Fig. 7
figure 7

Penetration along contact section

Full size image

The base idea is that only for the boundary sections a higher discretization is necessary. Adding more points to a section requires the new positions to be calculated. The curvature, the penetration and other parameters would have to be computed as well. To avoid this trouble, virtual contact points are introduced for this section. All of them share the same parameter values, except the penetration. To circumvent the costly exact calculation of the penetration along the section, the slope is approximated as linear. By linearizing the penetration (Fig. 7c), the sum of the stiffnesses of the virtual elements can be represented by a simple factor, the relative contact proportion w.

$$\boldsymbol{w}=\left(w_{i}\right)_{i=1\cdots n} \quad \text{with} \; 0\leq w_{i}\leq 1$$
(5)

Actually, the combination of the virtual points would lead to a shift of the centroid of the line load and thus of the contact point position, as shown in Fig. 7d by the grey arrow. However, this influence is again neglected to avoid a costly recalculation of the point positions.

To better represent the gradual load-bearing of a section, the relative contact proportion was introduced for each contact point. For a contact point fully in contact the value is 1, while points completely out of contact receive a factor of 0. Values between 0 and 1 are allotted to represent the percentage of effective contact length of the section. The factor w must be applied to the compliance matrix. It is assumed that the deformation caused by other contact points is independent of the width of the influenced element. At the same time, a force applied at the point will still have the same effect on distant points, no matter how large the section is. Therefore, the off-diagonal elements of the compliance matrix \(\boldsymbol{C}=\boldsymbol{B}+\boldsymbol{K}(\boldsymbol{f})\) remain unchanged. The diagonal elements are element wise multiplicated with the inverse of the relative contact proportion w:

$$C_{ij}^{*}=\begin{cases} \begin{array}{l} C_{ij}\cdot w_{i}^{-1}\\ C_{ij} \end{array} & \begin{array}{l} \quad \forall i=j\\ \quad \forall i\neq j \end{array} \end{cases}$$
(6)

This leads to a problem when \(w_{ij}=0\), as there would occur a division by zero. Furthermore, the diagonal elements tend to infinity for small wi. To avoid this and to improve the condition of the system of equations, w is used as a preconditioner.

$$C_{ij}^{\# }=C_{ij}^{*}\cdot w_{i}=\begin{cases} \begin{array}{l} C_{ij}\\ C_{ij}\cdot w_{i} \end{array} & \begin{array}{l} \quad \forall i=j\\ \quad \forall i\neq j \end{array} \end{cases}$$
(7)
$$d_{i}^{\# }=d_{i}^{\$ }\cdot w_{i}$$
(8)
$$C^{\# }\cdot \boldsymbol{f}=d^{\# }$$
(9)

Thus, the problem of an overestimation of the stiffness in the range of small positive forces can be reduced. For points with small negative resulting forces, further modifications are necessary, as the computation of the contact compliances requires positive forces. To achieve positive resulting forces for points with a relative contact proportion \(w_{i}< 0.5\) the penetration is adjusted. This will be called adjusted penetration \(d^{\$ }\). It is assumed that the remaining contacting portion of the section has a greater penetration than the nominal value for the representing contact point. This difference shall also be determined by the factor w. For a contact proportion \(w_{i}=1\) the penetration remains unchanged, for \(w_{i}=0\) the penetration is raised by half the sections penetration difference vi. The modified penetration \(d^{\$ }\) for the shortened section is shown in Fig. 7d as blue area—slightly bigger than the original penetration in Fig. 7a.

$$d_{i}^{\$ }=d_{i}+\frac{v_{i}}{2}\cdot \left(1-w_{i}\right)$$
(10)

Choosing the right penetration tolerance is crucial for a useful result. A global value for all points would be simple but would result in some points being in contact too early. This particularly affects single contact points as they occur when a new flank comes into contact. Ideally, the penetration tolerance is determined individually for all contact points. Since the influence of the partial contact due to the different penetration along a contact section is to be captured via the contact proportion w, the penetration tolerance should therefore be determined just by using this. The simplest thing would be to calculate the penetration at the beginning and end of the contact section. However, this would require additional contact points to be determined (approximately twice as many). Thus, a method must be used that only uses properties that are available at a single contact point.

To determine the difference in penetration over a section, the angle γ that the flanks have with respect to each other at the contact point is used. Normally, the normals of the two flanks lie in the meshing plane. Thus, the angle between the normals of the flanks can be used to determine the penetration deviation. The angle cannot be used for contact points that are located at the tooth tip edge of the wheels. Therefore, the normal from the pinion NP,i and the tangent on the gear TG,i in the contact line direction is used instead to calculate the angle (Fig. 8):

$$\gamma _{i}=90^{\circ}-\mathrm{\sphericalangle }\left(N_{P,i},T_{G,i}\right)$$
(11)
Fig. 8
figure 8

Determination of the contact angle. Orange: normal of pinion NP,i; blue: tangent of wheel in direction of contact line TG,i; green: angle between flanks γi in °

Full size image

Changes in the normal and tangent directions due to the deformation are neglected. The angle γ is then used to find the approximated penetration difference vi along each section with the section length li:

$$v_{i}=\tan (\gamma _{i})\cdot l_{i}$$
(12)

Since this is an iterative process, it is necessary to be able to determine the contact proportion w from the intermediate result f. Since f is a force, it makes sense to set it in relation to a reference force fref. The local reference force fref,i should be the one that is needed to approximately cause a full contact in one section i. With contact compliances \(k_{i}^{+}\), calculated for a pressure of 0.1 MPa, the reference force is obtained as:

$$f_{\mathrm{ref},i}=\frac{v_{i}}{k_{i}^{+}}$$
(13)

This now enables the computation of the contact proportion w. It is limited to the range of 0 to 1 for forces in the range of \(-f_{\mathrm{ref},i}\) to \(+f_{\mathrm{ref},i}\):

$$w_{i}=\begin{cases} \begin{array}{c} \begin{array}{c} 0\\ \frac{1}{2}+\frac{1}{2}\cdot \frac{f_{i}}{f_{\mathrm{ref},i}}\\ 1 \end{array} \end{array} & \begin{array}{l} \quad\quad f_{i}< -f_{\mathrm{ref},i}\\ \quad\quad -f_{\mathrm{ref},i}< f_{i}< +f_{\mathrm{ref},i}\\ \quad\quad f_{i}> +f_{\mathrm{ref},i} \end{array} \end{cases}$$
(14)

In each iteration step, factor w must be determined anew and thus the target penetration. In addition, the contact stiffnesses must be determined for each step and the system of equations must be adjusted with factor w. The penetration difference v and the reference load are constant and must be determined only once for each engagement position. (Fig. 9).

Fig. 9
figure 9

Flowchart of the adjusted load distribution calculation

Full size image

3.4 Application of the new method

To demonstrate the effect of the presented modification of the load distribution calculation, a simple model is used. For a bevel gear pair with 12 and 37 teeth a model with zero degree of freedom is implemented (Fig. 10). The gears are able to rotate, but with a forced speed and the exact theoretical transmission ratio. This simplistic model without transmission error was used, to ensure that the different methods are computed with the same relative gear positions in each time step. The starting position introduces a torque of about 323 Nm. The gears are rotated by exactly one pitch in 1000 steps.

Fig. 10
figure 10

Simpack model with pinion and gear

Full size image

To show the extent of the stated problem the model has been processed with two different contact discretisations. First, a reference was created by using a quite high number of at most 200 points per flank. That results in the smooth black curve in Fig. 11. The second variant with 40 points per flank is shown in Fig. 11 as orange graph. This obviously results in a much more angular graph, while the general course remains the same. To ease the comparison of the variants, Fig. 12 allows a more detailed view on the graphs. Furthermore, in Fig. 12 the step wise determined derivatives are shown, aiding in spotting the discrepancies of the old method of load distribution calculation. It exposes critical leaps in the derivatives for the low discretisation variant, which are prone to stressing an MBS solver.

Fig. 11
figure 11

Torque of pinion over one pitch

Full size image
Fig. 12
figure 12

Detail of Fig. 11

Full size image

The modified approach to calculate the load distribution has been applied for the model with 40 points per flank. In Fig. 11 through Fig. 13 the result is shown in blue (“new/40”). This graph is nearly as smooth as the one with 200 contact points per flank. This can also be seen when looking at the derivatives in Fig. 13.

Fig. 13
figure 13

Derivates of the torque over one pitch

Full size image

Of special interest is the comparison of the old method with 200 points and the new method. While the general course is largely identical, a small offset can be observed. The mean values of the transmitted torque differ by about \(0.1\% .\) This appears to be a systematic error. This offset most likely origins in the fact that the contact compliances are calculated for infinitely long cylinders. However, the error is acceptable as it is in the same order of magnitude as the deviations of the old method, but the direction and variation of the deviation are much smaller.

The improved results at the same point count in combination with the computation times from Table 1 expose the advantage of the introduced procedure.

Table 1 Computation times
Full size table

4 Summary

During further development of the BECAL co-simulation module the load distribution calculation has been investigated specifically. It was shown that the implemented method of BECAL has shortcomings regarding the continuity of calculated reaction moments and forces. An alternative approach was presented. It reduces the effect of single contact points joining or leaving the contact line due to small changes in the meshing position. The method was applied on a bevel gear set within a simplistic MBS model to demonstrate the impact on the result quality. A significant decrease in deviations of the torque has been achieved while the computation times were not impaired in a negative manner.

The presented modified load distribution calculation improves the usability of the BECAL co-simulation as it aids the MBS solver in convergence.