Abstract
When the simulation of a system, or the verification of its model, needs to be resumed in an online context, we face the problem that a particular starting state needs to be reached or constructed, from which the process is then continued. For timed automata, especially the construction of a desired clock state, represented as a difference bound matrix (DBM), can be problematic, as only a limited set of DBM operations is available, which often does not include the ability to set DBM entries individually to the desired value. In online applications, we furthermore face strict timing requirements imposed on the generation process. In this paper, we present an approach to construct a target clock state in a model via sequences of DBM operations (as supported by the model checker Uppaal), for which we can guarantee bounded lengths, solving the present problem of ever-growing sequences over time. The approach forges new intermediate states and transitions based on an overapproximation of the target state, followed by a constraining phase, until the target state is reached. We prove that the construction sequence lengths are independent of the original trace lengths and are determined by the number of system clocks only, allowing for state construction in bounded time. Furthermore, we implement the (re-)construction routines and an extended Uppaal model simulator which provides the original operation sequences. Applying the approach to a test model suite as well as randomly generated DBM operation sequences, we empirically validate the theoretical result and the implementation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
State (re-)construction, i.e., setting a system to a desired state, is a common task. Ranging from physical systems to programs and executable models, a system may need to be in some specific state to execute particular routines and test or verify a certain system behavior. The general task of constructing a state is as follows: Starting from a particular known (and usually static) state \(s_{\mathrm{init}}\), find a sequence of state transformations \(S = (tr_{1}, \ldots , tr_{n})\) (imposed by, e.g., actions in a physical system or transitions in an automaton), such that the sequence leads to a known target state \(s_{\mathrm{target}}\), i.e., find an S with \(S(s_{\mathrm{init}}) = s_{\mathrm{target}}\). In the easiest case, the system is static, a valid “reference” transformation sequence \(S_{\mathrm{ref}}\) to the target state is known from observing a previous system execution, and the construction process is unconstrained in time. Then, we can simply replay the given sequence \(S_{\mathrm{ref}}\) to reach the target state. However, systems are usually more complex and impose constraints that render the trivial approach inapplicable in many cases:
- C1:
-
The system may change dynamically over time (e.g., as some actions become inapplicable in a changed environment); a previously valid sequence that correctly reached the target state may become invalid or lead to a wrong state due to changed actions.
- C2:
-
The reference transformation sequence may be unknown (e.g., as the system actions are unobservable, or as we want to construct a state not reached by a previous execution); such a sequence needs to be manually constructed.
- C3:
-
The feasible time frame may be constrained (e.g., if the construction is embedded in an online setting for ongoing monitoring and thus frequently repeated); the restoring sequence needs to be limited both in terms of its length and the complexity of its transformations.
As the trivial approach requires access to the observed reference sequence, which grows linearly with system progress, and further assumes an unchanged system to apply the formerly valid sequence to, a conflict with all three constraints becomes clear, and alternative construction approaches are needed.
A prominent example of executable models that are frequently initialized to updated states—and the motivation of our work—is the field of online model checking. Model checking in general proves that specific system properties hold and provides guarantees on the correct behavior of a system, and for checking timed systems in particular, the modeling formalism of timed automata (TA) is commonly used, which represents time as (zones of) real-valued clocks. For online model checking, a technique that incrementally verifies or falsifies properties of a model under simulation for limited time scopes, a starting model state that reflects the state of the real system is required, so that one can continue model checking from that state on. In this article, we approach the state construction problem for TAs regarding the initially described system constraints, i.e., for potentially dynamic models in an online setting.
Adding online constraints to the overall construction task, one can distinguish two scenarios based on the availability of a reference sequence:
- S1:
-
If the reference sequence \(S_{\mathrm{ref}}\) is given, we need to find a transformation \(red = (red_{1}, \ldots , red_{m})\) that reduces \(S_{\mathrm{ref}}\) to a bounded sequence S, but still reaches the target state when applied to the initial state, i.e., find a red with \(S {\mathop {=}\limits ^{\mathrm {def}}}red(S_{\mathrm{ref}})\), \(|S| \le bound\) and \(S(s_{\mathrm{init}}) = S_{\mathrm{ref}}(s_{\mathrm{init}}) = s_{\mathrm{target}}\).
- S2:
-
If \(S_{\mathrm{ref}}\) is not given, we need to determine a bounded state transformation sequence S that leads to the target state, based on the characteristics of the initial and target state and the supported actions A, i.e., find an \(S = f(s_{\mathrm{init}}, s_{\mathrm{target}}, A)\) with \(|S| \le bound\) and \(S(s_{\mathrm{init}}) = s_{\mathrm{target}}\).
Regardless of the concrete construction approach, one is usually tied to a limited set of operations and actions supported by a system to lead from its initial state to the target state. However, depending on the concrete field of application, the requirements and restrictions for intermediate states and transitions between the initial and target state differ: In case of physical systems, we can only use given actions applied in the scope of the system semantics, e.g., move an entity in defined directions. Consequently, the visited states have to lie in the original system state space, and the executed transitions need to correspond to the supported actions. For executable models such as those used in model checking, these strict requirements may be relaxed. Compared to a physical system, we may not be bound to existing states and transitions to reach the target state; in fact, the strict requirement is only imposed on a model if its system description cannot be altered, or if a physical system is already executed alongside the model during construction of the starting state. Otherwise, we can adapt the model by introducing new states and transitions which allow reaching the target state faster, or—in case of adaptive models—enable state construction in the first place. Instead of requiring original actions exclusively, we are only bound to a set of atomic, model-checker specific operations then.
A general problem is that a model checker may not allow us to set the concrete clock state of a TA directly by assignment. Our work uses the model checker Uppaal, a modeling and verification tool developed in a collaboration of the Uppsala and Aalborg universities. Here, the set of possible operations is limited to the reset of individual model clocks, constraining of clock differences, and time delays. Furthermore, all its simulations start at a well-defined clock state, where all clocks are initially set to 0. On the one hand, the assignment restriction guarantees that any clock state which the model takes is indeed valid and reachable in terms of the underlying semantics. On the other hand, the restriction raises the need for another strategy to set the system to a desired clock state. For an online model checking interface, which relies on a repeated manual manipulation of the clock state in bounded time to iteratively restore the most current state for the next verification run, such a strategy is mandatory.
We already discovered in the beginning that the trivial approach neither meets time constraints due to growing sequence lengths over time, nor can it be used if the model changes and the prior observed transformation sequence thus becomes inapplicable. For the case of a changeable model, Rinast [31] introduced a graph-based approach that keeps track of visited states and traversed transitions and forges new transitions as shortcut between existing states on the fly. Thus, the states belong to the original state space, while the intermediate transitions are potentially composed of segments of existing transitions. Even though the approach improves on the trivial result, the dependency on original states and transition segments still leads to ever-growing state construction sequences if no suitable shortcuts are found.
To tackle the sequence growth problem, we propose a new approach that utilizes both forged intermediate states and transitions to reach a desired starting state via DBM operation sequences of guaranteed bounded length. This article makes the following contributions:
-
1.
We propose and prove a clock state construction approach for timed automata based on DBM overapproximation and constraining (which we call OC approach), which guarantees bounded lengths of DBM operation sequences S that depend quadratically on the number of system clocks T only (i.e., \(0 \le |S| \le 1 + 2*|T| + |T|*(|T|+1)\)), and covers both the scenarios of known (S1) and unknown (S2) reference sequences.
-
2.
We provide an implementation of all OC approach variants as well as the trivial and graph-based Rinast approach for comparison, alongside an extended simulator for Uppaal timed automata which exposes the applied DBM operation sequences required by our approach on the fly.
-
3.
We perform a comparison of the new approach with existing alternatives, i.e., the trivial and graph-based approaches.
The proposed overapproximation and constraint strategy derives a DBM operation sequence that first generates a superzone of the target state, and then constrains it until that state is reached.
An example of a model representing a simple process illustrates the state construction problem. The example model as shown in Fig. 1) has three locations (On, Off, and Execute) and two clocks (t_active and t_exec). The model, which is initially in On, can either perform an execution if the system state is not critical, with a duration \(d \in [2,5]\) given by the guard t_exec >= 2 and the invariant t_exec <= 5, or else restart the system via Off. Consider a path starting in On, which traverses the Execute location ten times, turns Off once, and then visits Execute another ten times. An execution of this path, assuming all clocks are initially set to 0, leads to the following difference bound matrix (cf. Sect. 3.3 for the definition of DBM):

Different reasons may require us to restore the concrete model state, assuming the system was already running for some time: We may want to verify that the system remains uncritical for another amount of time steps; then, we do not want to perform verification from the original initial model state on, as what lies in the past was verified already, but from the most current model state. Or we may want to set the upper bound for an execution step to a lower value (e.g., 4) according to real observations. As the system was previously running with time value 5, and the (verified) current state might not lie in the reachable state space for the adapted system anymore, we need to reach that state in another way.
Setting the location and variable state is straight-forward; we can directly select Init locations which are active on model initialization, and set variables via direct assignments. The challenge though, as stated before, lies in the recovery of the clock state. If we had access to a trivial operation SetValue that sets a specific entry of a DBM with system clocks T to any particular value and is directly callable in a model, we could simply set all clock state values on a single transition via at most \((|T|+1)^{2}\) applications of SetValue, and would be done. Unfortunately, such an operation is not supported by common TA model checkers due to their underlying semantics, and furthermore, the operations supported by a checker cannot be called directly and individually, as they are called in groups bound to the state and transition semantics of a TA. Thus, we have to compose or derive a supported sequence of DBM operations (and based on that, a corresponding sequence of automaton locations and edges)—which leads to this exact clock state DBM and does not require replaying the full execution path.
The article is structured as follows: We describe the related work in Sect. 2, followed by prerequisite knowledge of timed automata and DBMs in Sect. 3. Afterward, we introduce our approach in Sect. 4, where we refer back to the initial example, and describe the overapproximation and constraining phases of our approach in Sect. 5 and Sect. 6. Then, we transfer the approach to concrete Uppaal models in Sect. 7 and cover the tool implementation in Sect. 8, followed by the conducted experiments in Sect. 9. Finally, we provide a conclusion in Sect. 10.
2 Related work
In general terms, our work aims at the optimization of system state constructions, allowing model checkers like Uppaal to restore a given state more efficiently while relying on semantically supported operations only. Our work shares the motivation with fault tolerance and trace replay techniques commonly used to restore (past) system states, and draws technically on DBM operation sequences, their transformations, and DBM-based constraint solving.
In broad terms, our work contributes to research in state (re-)construction. Typically, research on this field can be found in debugging, testing, optimization, and in particular in fault tolerance since the 1960s. In fault tolerance, one prominent technique is checkpoint-recovery, during which a system on failure is reinitialized to a complete snapshot and optionally updated along several incremental checkpoints. Over the past decades, it was used for state recovery both in software (e.g., for databases [28] and shared memory multiprocessor systems [38]) and cyber-physical hardware applications [22]. Compared to our approach, while often targeting entirely different domains unrelated to model checking (even though variants of checkpoint recovery are also used in model checking, e.g., for non-explicit storage of states in colored Petri nets [14]), such a technique is used to reduce the memory and runtime overhead to reach a certain state. For instance, using context-aware [25] and online [40] variants of checkpoint derivation, or optimized techniques such as two-state checkpointing in hard real-time systems [33], one tries to reduce the number and extent of checkpoints during recovery. For all these techniques, the initial state is the snapshot of the full state, which the system can be directly assigned to, while the target state is the one before the failure occurred, reachable via a sequence of incremental checkpoints and additional instructions after the final checkpoint. In our approach, the initial state is the starting state specified by the concrete model checker, and the target state is the most recently simulated state which we want to recover.
Other techniques, such as full-system-restart applied in cyber-physical systems [18] or software rejuvenation [17], rely on a restart of the affected system. The initial state then becomes the system state directly after the restart, and the goal remains getting back to the latest error-free state within limited time. The differences to our work are the application domain (these techniques are usually applied to concrete programs and actuator systems rather than abstract system models), the requirements (e.g., full restarts are only feasible in applications with non-exponential state spaces to keep the recovery time bounded), and the absence of clock state abstractions (i.e., clock zones) as used in timed automata.
A major challenge to make the aforementioned techniques feasible in practice is to find suitable reduction strategies for the involved instructions, so that not all original actions need to be replayed on recovery. Therefore, aside from fault tolerance, different forms of state reconstruction are used in software optimization, debugging, and testing. The aspect of instruction sequence reduction can be found, among others, in the field of source code analysis and optimization [9]. A common aspect of such an optimization is the identification of shorter instruction sequences to a specific state by omitting redundant instructions, or those leading to unread intermediate states. Likewise, in testing applications, traces of instructions observed during simulation are optimized for the purpose of reduced replay times or memory space usage, e.g., during virtual memory simulations [21].
For the problem of clock state (re-)construction in particular, only few works can be found. Closely related, in the domain of timed automata, Rinast approaches the recovery problem under the term state space reconstruction [31]. In his work, he constructs “shortcut” transitions to states observed during simulation, i.e., transitions from which DBM operations are removed that were overwritten by subsequent operations and thus were rendered redundant. As main use case of his work, applied in multiple medical case studies [30], he used the approach to reconstruct a target state via such shortcut transitions, visiting only a reduced (and preferably bounded) number of intermediate states. The approach requires that resets of all clocks in all model cycles exist to guarantee bounded (re-)construction lengths. Our approach omits this requirement and allows the construction of a specific state via a finite amount of transitions linearly proportional to the number of system clocks (cf. Sect. 7).
Several model checking techniques either rely on, or may benefit from, clock state (re-)construction techniques: Incremental model checking [27] verifies multiple iterations of a system design, and aims for reusing portions of previous checking results. Restoring a state, which is visited in one system, in another candidate system directly before reaching a differing component (compared to the former system), may reduce the time required to check incrementally designed system candidates. As the candidates are individual systems, a trivial transfer of one system state to another system is not generally possible, and thus, the state needs to be reconstructed. Bounded model checking [10] reduces the general model checking approach to limited scopes of k steps, and was applied to timed systems [4], including timed automata [37], in the past. Building on this boundedness, online model checking [39] verifies a system iteratively for limited future time scopes and derives temporarily valid guarantees. With optimized state (re-)construction techniques, we can faster restore the most recently verified state that fits new observations, from which another verification iteration is then started; otherwise, the recovery of such a state would require growing amounts of time.
Technically, we draw on DBM operation sequences, sequence transformations, and constraint solving. The concept of difference bound matrices (DBMs), the data structure which is used, e.g., for timed automata to represent the clock state, was covered in detail by Bengtsson et al. [8]. Our approach works on such a representation of clocks to restore the overall clock state. For that, it applies algebraic transformations to DBM operation sequences to reach DBM overapproximations and eliminate redundant constraints. Different DBM overapproximation techniques were already used in the literature, e.g., for the convex hull calculation of state unions [32] or zone extrapolation [6] in Uppaal, or for compact graph construction of real-time preemptive Petri net systems [1]. Compared to these techniques, tightness is not required by our approach, as the constraint phase reaches a target DBM independent of the concrete overapproximation; however, more efficient constraint sequences may result from tightness requirements.
Our \(DBM_{\mathrm{target}}\)-based overapproximation approach relies on constraint solving, and, more precisely, the selective discarding of constraints. In model checking, various data structures such as difference bound matrices (DBMs) [8], clock difference diagrams (CDDs) [24], or the more recent constraint matrix diagrams (CMDs) [13] are used to span the clock state by a set of constraints. Constraint solving can then, among others, be applied to such structures to manipulate the state space symbolically [29] and obtain valid clock value assignments, or to temporal logic formulae [15] to verify system properties. Furthermore, constraints need to be relaxed in certain cases to deal with inconsistencies of constraint systems, e.g., for constraint networks [16] or during model repair [3], often with the goal of minimal relaxations or consideration of constraint priorities or uncertainties in real world systems [12]. In our case, the relaxed constraints do not necessarily need to be minimal, but the constraints cannot be relaxed independent of each other, as they are bound to certain DBM operations (e.g., the future delay) semantically.
The constraint phase of our approach derives suitable sets of constraints that reduce the former overapproximated zone to the zone of the target DBM. An efficient approach is the use of minimal constraint systems (MCS), a technique introduced by Larsen et al. [23] for timed automata that is based on the transitive reduction in directed graphs [2] and commonly used as a compact representation of DBM data. Our approach builds upon the idea of MCS and extends it to regard constraints that are already fulfilled by the overapproximating DBM, which eliminates redundancy and results in shorter operation sequences.
In regard to tool dependencies and support, our work uses models for the model checking tool Uppaal [7]. Its implementation and formalisms impose specific requirements for our work, i.e., an operation-based construction of DBMs and a defined clock space initialization (all clocks set to 0 initially), respectively. The applicability of our approach is not limited to that particular model checker, though.
3 Automata and DBM prerequisites
In this section, we provide preliminary details on the definitions of the syntax and semantics of timed automata (Sect. 3.1), the model state (Sect. 3.2), DBMs and their operations (Sect. 3.3), the graph representation of DBMs (Sect. 3.4), sequences of DBM operations (Sect. 3.5), and a method for flow dependency analysis on DBM data (Sect. 3.6).
3.1 Timed automata
Our work uses timed automata as underlying modeling formalism. We define the syntax of timed automata as follows:
Definition 1
(TA-Syntax) A timed automaton (TA) is a tuple \(\langle L,l_{0},C,E,g,r,I \rangle \), where L is a finite set of locations, \(l_{0}\) is the initial location, C is a finite set of (real-valued) clocks, \(E \subseteq L \times L\) is a set of edges between locations, \(g: E \rightarrow \Phi (C)\) is a mapping from edges to guards, \(r: E \rightarrow R(C)\) is a mapping from edges to partial resets, and \(I: L \rightarrow \Phi (C)\) is a mapping from locations to invariants. The set \(\Phi (C)\) contains all possible conjunctions over constraints \(t_{a}<> c\) and \(t_{a}-t_{b} <> c\), with \(t_{a},t_{b} \in C\), \(c \in {\mathbb {N}}\), and \(<> \in \{<, \le , =, \ge , >\}\). \(R(C) = [C \rightharpoonup {\mathbb {N}}_{0}]\) denotes the set of all partial functions \(\rho : C \rightharpoonup {\mathbb {N}}_{0}\), where each \(\rho \) represents a right-unique mapping from a subset of clocks to reset values (i.e., any natural number including 0, where the latter is the usual reset value).
Both edge guards and location invariants express constraints on the valuations of clocks C, which control when an edge can eventually be triggered, and for how long a location may remain active, respectively. Extending the TA formalism, an extended timed automaton (ETA) is a tuple \(\langle L,l_{0},C,V,E,g,r,I,a,L_{U},L_{C},Ch_{Bi},\) \(Ch_{Br} \rangle \), where V is a set of variable, \(a: E \rightarrow A(V)\) is a mapping from edges to variable assignments, \(L_{U}\) and \(L_{C}\) are urgent and committed locations, and \(Ch_{Bi}\) and \(Ch_{Br}\) are binary and broadcast channels. We define \(A(V) = [V \rightharpoonup {\mathbb {B}} + {\mathbb {Z}}]\) as the set of all partial assignment functions \(\alpha : V \rightharpoonup {\mathbb {B}} + {\mathbb {Z}}\), where each \(\alpha \) represents a right-unique mapping from a subset of variables to boolean or integer values.
Commonly, the semantics of TAs is defined via real-valued delays on transitions in a labeled transition system, which results in an uncountable state space. Using a zone-based abstraction (via convex polyhedra of clock constraints), one can reduce the state space to a finite set. We use the latter for our work and thus define the symbolic TA semantics similar to the definition of Behrmann et al. [5] and adapted for \({\mathbb {N}}_{0}\)-resets, zero-initialized zones, and included variable states as follows:
Definition 2
(TA-Symbolic Semantics) Let \(Z_{0} = \bigwedge _{x \in C} x = 0\) be the initial zone, and \(\forall x \in V: u_{v,0}(x) = 0\) be the initial variable valuation. The symbolic semantics of a timed automaton \(\langle L,l_{0},C,V,E,g,r,I,a \rangle \) is defined as a transition system \((S, s_{0}, \Rightarrow )\), called the simulation graph, where \(S = L \times \Phi (C) \times U_{v}\) is the set of symbolic states, \(s_{0} = (l_{0}, Z_{0} \wedge I(l_{0}), u_{v,0})\) is the initial state,  is the transition relation, with:
is the transition relation, with:
-
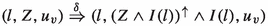
-
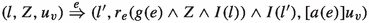 if \(e = (l,l') \in E\),
if \(e = (l,l') \in E\),
where \(Z^{\uparrow } = \{u + d\ |\ u \in Z \wedge d \in {\mathbb {R}}_{\ge 0}\}\) (the future operation), and \(r_{e}(Z) = \{[r(e)]u\ |\ u \in Z\}\) (the reset operation). \(u: C \rightarrow {\mathbb {R}}_{\ge 0}\) is a clock valuation function (note that the definitions consider guards and invariants as sets of clock valuations by abuse of notation), \(u + d\) maps each clock \(x \in C\) to the value \(u(x) + d, d \in {\mathbb {R}}_{\ge 0}\), and [r(e)]u denotes the clock valuation which maps a subset \(C_{r}\) of clocks C to natural numbers as defined by r(e), and agrees with u over \(C {\setminus } C_{r}\). Likewise, \(u_{v}: V \rightarrow {\mathbb {B}} + {\mathbb {Z}}\) is a variable valuation function (where \(U_{v}\) is the set of all variable valuations), and \([a(e)]u_{v}\) denotes the variable valuation which maps a subset \(V_{a}\) of variables V to boolean or integer numbers as defined by a(e), and agrees with \(u_{v}\) over \(V {\setminus } V_{a}\).
For a definition of the semantics of networks of timed automata and channel synchronization, see [7].
3.2 Model state
An execution trace of a model is a sequence of transitions. During such an execution, each transition leads to a concrete model state. A state of an ETA consists of three components: (a) The location state covering the currently active location of each sub-automaton, (b) the variable state spanning all global and local integer, bool, etc. valuations that are used by components of the ETA, and (c) the clock state including all clock differences (e.g., for our work, represented as a DBM). The construction of a location and variable state is easily done: The targeted location can be set as initial location (\(l_\mathrm{init}\)), and will be active on model initialization. The variables are set directly to their targeted values by assignment. The clock state, in contrast, needs to be constructed via a sequence of invariants, guards, resets, and other operations defined in the following sub-section and is the focus of this paper.
3.3 DBM and operations
Clocks can take values from a given interval, which is defined by the previous invariants, guards, and resets along a path through the model. In case of TAs, the concrete value intervals of these clocks are represented as DBMs [8], which have the following structure:

In a DBM, the matrix entry in the row of clock \(t_{i}\) and column of clock \(t_{j}\) represents the upper bound of their clock value difference, i.e., \(t_{i} - t_{j} \le c_{ij}\), and the diagonal entries are naturally 0 (as \(t_{i} - t_{i} = 0\)). Note that a reference clock t(0) is added, which has a constant value of 0, to turn any single clock constraint into a two-clock constraint \(t_{i} - t(0) \le c\) or \(t(0) - t_{i} \le c\). We denote the set of clocks of a DBM as \(T_{0}(DBM)\) if the reference clock is included, and as T(DBM) otherwise. Altogether, such a DBM represents the complete clock state.
The symbolic definition of TA semantics provides three types of operations that are applied to clock zones over transitions in the simulation graph: The \(\uparrow \) operation delays the clock arbitrarily to include all futures, the logical \(\wedge \) operation adds constraints to the clock zone, and the \(r_{e}\) operation resets selected clocks to natural numbers. In the context of DBMs in the scope of our work, we call these operations DelayFuture, Constraint, and Reset, respectively. A fourth operation is Close, which determines the tightest constraints representing the original zone, i.e., the transitive closure of constraints. While not required by the base semantics, that operation is commonly applied by model checkers after adding constraints to the zone, enabling a more efficient application of subsequent operations. The full set of operations applied during transitions through a model [5] is thus
which we will abbreviate as DF, R, C, and Cl, respectively, where appropriate. On the level of DBM transformations, the operations are formally defined as follows for a DBM with n clocks (\(\forall i,j \in {\mathbb {N}} \cap [0,n]\)):
A graphical overview of the operations in OP (Eq. 3.2) is shown in Fig. 2. All clocks are infinitely delayed into the future whenever a new (neither urgent nor committed) set of locations is reached, before the new invariant constraints of the target locations can be applied. The \(\mathbf {DelayFuture}\) operation removes the upper bound of all DBM clocks by setting their DBM entries in the first column to \(\infty \) (see Fig. 2(1)).
The \(\mathbf {Reset(t_{a},v)}\) operation resets a single clock \(t_{a}\) to the value v. The operation adapts all DBM entries in the row and column of \(t_{a}\) (see Fig. 2(2)), i.e., the difference between that clock and all other clocks, according to the reset value.
The \(\mathbf {Constraint(t_{a},t_{b},v)}\) operation constrains the DBM zone by updating a single DBM entry \(DBM[t_{a},t_{b}]\) to the minimum of its value and v (see Fig. 2(3)). As Constraint is the only operation in OP which does not preserve the closedness of the input DBM zone, a following \(Close(t_{a},t_{b})\) call is required.
The \(\mathbf {Close(t_{a},t_{b})}\) operation transforms the DBM to its closed form (see Fig. 2(4)) in case that only one single constraint operation \(Constraint(t_{a},t_{b},v)\) was applied beforehand (cf. [11]). A general form, Close(), exists, which recalculates all shortest paths between pairs of clocks from scratch. For a more compact presentation of the construction sequences, we will use a single \(\mathbf {Close}\) operation after sequences of constraints instead of selective \(\mathbf {Close(t_{a},t_{b})}\) operations after each constraint.
3.4 DBMs and graphs
A DBM can be represented as weighted complete digraph [8] as shown in Fig. 3. In such a graph, each edge \((t_{i},t_{j})\) represents the clock difference \(t_{j} - t_{i}\), and the edge weight represents the value of DBM[j, i]. Self-edges, which represent the diagonal DBM entries with 0 weight, are usually omitted. The weight of a path is the sum of weights of edges included in the path. Three facts become important in the graph-based version of our DBM overapproximation approach:
Fact 1
(Emptyness and weights) A DBM represents a non-empty zone iff its graph G has no negative-weight cycles [8].
Fact 2
(Minimum edge costs) Given a DBM, each edge \(e = (t_{i},t_{j})\) in its graph G has minimum edge costs [23], i.e., given a weight function w, \(w(e) \le w(p)\) holds for each longer path \(p=((t_{i},t_{k}), \ldots , (t_{l},t_{j}))\) from \(t_{i}\) to \(t_{j}\), iff that DBM is in closed form (i.e., represents the transitive closure for a set of constraints).
Fact 3
(Cycles with \(\infty \)-weight edges) The total path cost of a cycle with at least one \(\infty \)-weight edge is \(\infty \).
Finally, we point out the following path types:
-
A simple cycle in a digraph is a cycle where no vertex except for the start vertex is repeated (as the cycle starts and ends in the same vertex).
-
A Hamiltonian path is a path that visits each vertex of a graph exactly once.
-
A Hamiltonian cycle is a simple cycle over all vertices of a graph.
-
A cycle chord of a cycle in a digraph is an edge between two (non-immediately) consecutive vertices of the cycle, i.e., a “short-cut” between two cycle vertices, such as \((t_{1},t_{3})\) for the cycle \((t_{1},t_{2}), (t_{2},t_{3}), (t_{3},t_{1})\).
-
A path prefix of a path p is a subpath starting with the same vertex as p.
-
A prefix cycle of a cycle c is a subcycle over a path prefix of c followed by an edge to the start vertex of c.
-
An all-positive-prefix path p in a weighted digraph is path in which all path prefixes (including p itself) have positive weights.
3.5 DBM operation sequences
We denote the sets of all possible R, C, and Cl operations as follows:
Multiple operations form a sequence, which we denote as \(S = (op_{1},op_{2},\ldots ,op_{n})\), with \(op_{i} \in \mathcal{OP}\mathcal{}(DBM)\), and for which we define its application to a DBM based on function composition as:
We define the merging of two operation sequences \(S_{1} = (op_{1},\ldots ,op_{m})\) and \(S_{2}=(op_{m+1},\ldots ,op_{n})\) as
Furthermore, we define the set of all merged sequences over the cartesian product of two sequence sets \({\mathcal {S}}_{a} = \{S_{a,1}, \ldots , S_{a,n}\}\) and \({\mathcal {S}}_{b} = \{S_{b,1}, \ldots , S_{b,m}\}\) as
and, based on \(\otimes \) (written as \(\otimes _{i}\) indicating the i-th occurrence of the operator), define for a single sequence set \({\mathcal {S}}\)
Finally, we denote the subsequence relation between a sequence \(S = (x_{1},..., x_{n})\) and a subsequence \(S' = (x_{i_{k}})_{k \in [1,n]}, i_{1}< i_{2} < \ldots \) as \(S'|S\).
For a single operation op, we define
for sets of sequences where op is applied once (\(op^{1}\)), zero or more times (\(op^{*}\)), zero or one time (op?), or one or more times (\(op^{+}\)), and for a set OP of operations, we define
to denote the sets of sequences S with length \(|S| = 1\) (\(OP^{1}\)), \(|S| \ge 0\) (\(OP^{*}\)), \(|S| \ge 1\) (\(OP^{+}\)), or \(|S| \in [0,1]\) (OP?).
Finally, we define the following particular types of sequences which become relevant in our approach:
-
A reset-all sequence for a DBM is a sequence \(S \in {\mathcal {R}}(DBM)^{*}\) in which each clock \(t \in T(DBM)\) is reset exactly once.
-
A reset-df-all sequence for a DBM is a sequence \(S \in ({\mathcal {R}}(DBM)^{1} \otimes DF^{1})^{*}\) in which each clock \(t \in T(DBM)\) is reset exactly once, and each reset is followed by a DF.
-
A reset-(df)-all sequence for a DBM is a sequence \(S \in ({\mathcal {R}}(DBM)^{1} \otimes DF?)^{*}\) in which each clock \(t \in T(DBM)\) is reset exactly once, and each reset may be followed by a DF; note that the sets of reset-all and reset-df-all sequences are subsets of the set of all reset(-df)-all sequences.
In our O(DBM) approach (cf. Sect. 5.2), a major focus lies on the order of resets in operation sequences. In general, the two DBM entries DBM[i, j] (representing \(t_{i} - t_{j} \le DBM[i,j]\)) and DBM[j, i] (representing \(t_{j} - t_{i} \le DBM[j,i]\), i.e., \(t_{i} - t_{j} \ge -DBM[j,i]\)), span the interval of possible difference values \(t_{i} - t_{j} \in [-DBM[j,i], DBM[i,j]]\). For such an interval, the following fact holds:
Fact 4
(Order of clock difference intervals) Given a DBM reached via an operation sequence \(S \in \mathcal{OP}\mathcal{}(DBM)^{*}\), for each pair of clocks \(t_{i},t_{j} \in T(DBM)\), with \(t_{i} - t_{j} \in [l,u]\), lower bound \(l = -DBM[j,i]\), and upper bound \(u = DBM[i,j]\), we can distinguish between four cases:
where “reset before” and “reset after” imply that a potential delay happened between both resets, while “simultaneously” means without intermediate delay.
Note that the fourth case can only occur if we reset to values other than 0, as only then, a reset may set a clock to a value greater than another clock which was actually reset before, so that the reset order is “not explicitly known” from the interval bounds alone.
For DBMs reached via reset-df-all sequences (as shown in Fig. 4), we note that each entry DBM[i, j] becomes either \(v_{i} - v_{j}\) or \(\infty \) based on the reset order, and the following fact holds:
Fact 5
(DBM value after reset-df-all sequence) Given a DBM with n clocks (\(\forall i,j \in {\mathbb {N}} \cap [0,n]\)), a reset-df-all sequence S sets each entry DBM[i, j] to \(v_{i} - v_{j}\) for which \(t_{i}\) is reset after \(t_{j}\), and to \(\infty \) otherwise:
Proof
Fact 5 can be proven with the sets wr(DF) and \(wr(R(t_{a},v))\) (see Eqs. 3.16 and 3.17 in Sect. 3.6). An entry DBM[i, j], \(i,j \ne 0\) is overwritten twice by a reset-df-all sequence; once by \(R(t_{i},v_{i})\), for which the entry DBM[i, j] lies in the row of \(t_{i}\) and is overwritten with the value \(DBM[0,j]+v_{i}\), and once by \(R(t_{j},v_{j})\), for which DBM[i, j] lies in the column of \(t_{j}\) and is overwritten with the value \(DBM[i,0]-v_{j}\). We also notice that the DF operations set the values \(DBM[i,0], i \ne 0\), to \(\infty \) between the resets. It follows that if \(t_{i}\) is reset after \(t_{j}\), DBM[i, j] becomes \(DBM[0,j]+v_{i}\) by \(R(t_{i},v_{i})\), with \(DBM[0,j] = -v_{j}\) due to the previous reset \(R(t_{j},v_{j})\), resulting in \(DBM[i,j]=v_{i}-v_{j}\). Conversely, if \(t_{i}\) is reset before \(t_{j}\), DBM[i, j] becomes \(DBM[i,0]-v_{j}\) by \(R(t_{j},v_{j})\), with \(DBM[i,0] = \infty \) due to the previous DF, resulting in \(DBM[i,j]=\infty \). \(\square \)
For the relation between reset orders in a reset-df-all sequence and paths in a graph G of a DBM, we note the following facts:
Fact 6
(Hamiltonian cycles and reset order) For a DBM and its graph G, a \(one\hbox {-}to\hbox {-}one\) relation exists between Hamiltonian cycles \(p_{H}\) in G and total reset orders of clocks T(DBM).
Fact 7
(\(\infty \)-edges after reset-df-all sequence) Given a DBM and its graph G, a reset-df-all sequence sets all edges \((t_{i},t_{j}) \in E(G)\) to \(\infty \) for which the clocks \(t_{i}\) and \(t_{j}\) are not in reset order.
Fact 8
(Hamiltonian path over non-\(\infty \) edges) Given a DBM and its graph G resulting from a reset-df-all sequence, only the Hamiltonian path \(p_{H}\) over all vertices \(t_{i} \in V(G)\) in reset order and all its sub-paths via cycle chords traverse no edges with \(\infty \) costs.
Proof
Fact 6 holds as in a complete digraph with exactly one edge per ordered vertex pair, only one unique cycle exists that traverses all vertices in a particular order. \(\square \)
Proof
Fact 7 directly follows from Fact 5. \(\square \)
Proof
Fact 8 holds as all other paths contain at least one edge in reverse reset order, for which Fact 7 holds. \(\square \)
3.6 Flow dependency of DBM operations
To prove that particular operations in a sequence can be omitted without changing the resulting DBM, we need to analyze at which points individual DBM entries are read or written. For that, we define the function \(rd: \mathcal{OP}\mathcal{}(DBM) \rightarrow {\mathbb {N}} \rightarrow {\mathbb {N}} \rightarrow 2^{{\mathbb {N}} \times {\mathbb {N}}}\), which returns the read set of an operation op for a particular entry DBM[i, j], i.e., the set of index pairs (a, b) of all entries DBM[a, b] read by op for the calculation of DBM[i, j]. Furthermore, we define the function \(wr: \mathcal{OP}\mathcal{}(DBM) \rightarrow 2^{{\mathbb {N}} \times {\mathbb {N}}}\), which returns the write set of the operation op, i.e., the set of index pairs (a, b) of all entries DBM[a, b] written to by op. For the supported set of operations \(OP = \{DF, R(t_{a},v), C(t_{a},t_{b},v), Cl(t_{a},t_{b})\}\), rd and wr are defined as follows:
Based on the rd and wr functions, we define the flow dependency function \(fd: \mathcal{OP}\mathcal{}(DBM) \rightarrow 2^{{\mathbb {N}} \times {\mathbb {N}}} \rightarrow 2^{{\mathbb {N}} \times {\mathbb {N}}}\), which determines how the dependencies from previous operations are forwarded by an operation op:
In other words, to determine how the dependency on a set I of marked index pairs is maintained by an operation op, the function fd removes all index pairs from I whose DBM values are overwritten by op (i.e., \(I {\setminus } w(op)\)), and (re-)adds all those index pairs (i.e., the set \(I_{op}\)) whose new DBM values calculated by op depend on marked entries of the original I. That way, we get a new set of marked index pairs based on the original marked indices and the dependencies from these indices forwarded by op. To determine if an operation \(op_{1}\) can be omitted from a sequence S, we initialize I with the write set of \(op_{1}\), and recursively apply fd to I for each following operation until the resulting index set becomes \(\emptyset \).
To prove flow independency on infinite sets of operation sequences composed from a finite set of operations as required in Sect. 5.1.2, we use the following properties:
from which follows that if a set of marked indices becomes \(\emptyset \) after applying some sequence S, a subset of that index set will certainly become \(\emptyset \) as well after applying S. Thus, it is sufficient to check the superset only.
4 DBM-based clock state construction
The main task of this work is to determine a sequence of operations that allows reaching an originally observed model clock state. In this section, we describe the general idea of our approach (Sect. 4.1), allowing state construction in limited time, and revisit the example from the introduction to compare concrete state construction approaches (4.2).
4.1 Approach description
In Sect. 1, we introduced the general state construction task, i.e., finding a sequence S that transform a starting state \(s_{\mathrm{init}}\) into a target state \(s_{\mathrm{target}}\), as well as the boundedness requirement \(|S| \le bound\) for some strict bound imposed by online settings. Our approach splits that state construction task into two phases, the O-phase and the C-phase, where the former constructs an overapproximation of the target state, and the latter constraints that overapproximation until it equals the target state:
-
O-Phase: Given a starting state \(s_{\mathrm{init}}\) and a target state \(s_{\mathrm{target}}\), determine a bounded sequence \(S_{\mathrm{approx}}\) that transforms \(s_{\mathrm{init}}\) into an overapproximation of \(s_{\mathrm{target}}\), i.e., find an \(S_{\mathrm{approx}}\) with \(S_{\mathrm{approx}}(s_{\mathrm{init}}) \supseteq s_{\mathrm{target}}\).
-
C-Phase: Given a target state \(s_{\mathrm{target}}\) and an overapproximating state \(s_{\mathrm{approx}} \supseteq s_{\mathrm{target}}\), determine a bounded sequence \(S_{\mathrm{constr}}\) that transforms \(s_{\mathrm{approx}}\) into \(s_{\mathrm{target}}\), i.e., find an \(S_{\mathrm{constr}}\) with \(S_{\mathrm{constr}}(s_{\mathrm{approx}})\) \(= s_{\mathrm{target}}\).
The main advantage of this constructive approach is, as we will show later, that it is possible to generate operation sequences with bounded lengths for both phases, which do not grow throughout a simulation, but keep a constant length depending only on the number of clocks involved.
Combining both phases leads to a formulation of the overall state construction task for our approach:
-
Bounded state construction via OC-approach: Given a starting state \(s_{\mathrm{init}}\) and a target state \(s_{\mathrm{target}}\), determine a bounded sequence \(S=S_{\mathrm{approx}} \oplus S_{\mathrm{constr}}\) that transforms \(s_{\mathrm{init}}\) into \(s_{\mathrm{target}}\), where \(S_{\mathrm{approx}}\) leads to an overapproximation of \(s_{\mathrm{target}}\) which is then constrained by \(S_{\mathrm{constr}}\) to \(s_{\mathrm{target}}\), i.e., find an \(S=S_{\mathrm{approx}} \oplus S_{\mathrm{constr}}\) with \(|S| \le bound\), \(S_{\mathrm{approx}}(s_{\mathrm{init}}) {\mathop {=}\limits ^{\mathrm {def}}}s_{\mathrm{approx}} \supseteq s_{\mathrm{target}}\), \(S_{\mathrm{constr}}(s_{\mathrm{approx}}) = s_{\mathrm{target}}\), and thus, \(S(s_{\mathrm{init}}) = s_{\mathrm{target}}\).
We mentioned in Sect. 3 that setting the variable and location state is trivially solved for Uppaal TAs, and thus, our approach is focused on the construction of the clock state. Thus, in our concrete case of state construction for clock states in TAs, each state s represents a DBM clock state, and the sequences S are composed from a limited set of operations OP supported by the TA formalism, i.e., we apply \(s = DBM\) and require \(S \in \mathcal{OP}\mathcal{}(DBM)^{*}\).
4.2 Introductory example
Recall the example model of a simple process in Fig. 1, as well as the sample trace and reached DBM (i.e., the target clock state) described in Sect. 1. In this sub-section, we show the differences between possible clock-state construction approaches, i.e., the trivial approach, the graph-based approach [30], and our OC approach.
For the example, applying the trivial approach leads to unbound sequences along all model paths on the long run. The construction sequence is equal to the executed model path and thus grows linearly with the amount of transitions taken. The graph-based approach by Rinast keeps track of all model states that were reached, and finds shortcuts between these states, which can be taken as replacement for longer paths leading to the exact same state during construction. The approach limits the size of the construction path as long as at some point, re-reaching a previous state is guaranteed along all paths, which requires a recurrent reset of all clocks along such a path. In the example, the resulting states of all paths that periodically also take the transitions over Off, which leads to a reset of the clock t_active, can be constructed by a path shorter than the original. Otherwise, if only transitions over Execute are taken consecutively, the clock t_active increases, and thus, no model states are repeated.
Using our approach, we can either refer to the example trace and reduce it to a bounded-length sequence, or construct one independent from the actual execution path, considering only the target state. In both cases, the size depends only on the number of clocks involved, instead of the actual, growing execution path length; this boundedness is the major theoretical contribution of our work.
Using the three approaches, we get the construction sequences shown in Fig. 5. Applying the trivial approach (Fig. 5a), we get a sequence of 43 locations, which have to be traversed before we reach the targeted state. This sequence will keep growing over time, without an upper bound in length. Using the approach by Rinast, the first sequence of 10 Execute steps can be discarded, as the clock state after the Off section is identical to the one at the initial model state. This identified shortcut is used to perform the construction only via the second round of Execute steps. Nevertheless, the Off location is not necessarily reached frequently, and therefore, paths exist for which this approach does not return a length-bounded construction sequence. Finally, the approach introduced in this work leads to a construction sequence which requires 10 DBM operations, which are transformed into a sequence of 5 locations. In general, we can guarantee that our approach always requires at most \(1 + 2*|T| + |T|*(|T|+1) = 1 + 2*2 + 2*3 = 11\) operations for the clock state construction of this model, based on the number of \(|T| = 2\) clocks.
5 Overapproximation phase (O-phase)
In the first phase, the O-phase, we determine a sequence \(S_\mathrm{approx}\), which, when applied to \(\text {DBM}_\mathrm{init}\), results in an approximation \(\text {DBM}_\mathrm{approx} \in \mathcal {DBM}_{\mathrm{approx}}\), where \(\mathcal {DBM}_{\mathrm{approx}}\) is the set of all overapproximations of \(\text {DBM}_{target}\):
This overapproximation is required, so that we can constrain \(DBM_{\mathrm{approx}}\) selectively in a second step to finally obtain \(DBM_{\mathrm{target}}\). Generally, a \(DBM_{a}\) overapproximates another \(DBM_{b}\) if the first forms a superzone of the other. A DBM forms such a superzone if the following condition holds:
Similarly, \(DBM_{a}\) is called a subzone of \(DBM_{b}\) (denoted as \(DBM_{a} \subseteq DBM_{b}\)) iff \(DBM_{a}[i,j] \le DBM_{b}[i,j]\) for all DBM entries.
In the simplest case, \(DBM_{\mathrm{init}}\) is already an overapproximation of \(DBM_{\mathrm{target}}\) (\(DBM_{\mathrm{init}} \in \mathcal {DBM}_{\mathrm{approx}}\)), and the O-phase returns an empty transformation sequence \(S = ()\). In that case, we can directly continue with the C-phase procedure. Otherwise, if \(DBM_{\mathrm{init}}\) does not overapproximate \(DBM_{\mathrm{target}}\), there exist entries in \(DBM_{\mathrm{init}}\) which, following from Eq. (5.2), are smaller than the corresponding entries of \(DBM_{\mathrm{target}}\). To obtain an overapproximation, those entries need to be overwritten by values which are equal or greater than the ones in \(DBM_{\mathrm{target}}\). As mentioned before in Sect. 1, a SetValue operation which would set the DBM entry in the row of \(t_{i}\) and column of \(t_{j}\) to c (with \(c \ge DBM_{\mathrm{target}} [i,j]\)) is not defined in OP, nor is it supported by model checkers such as Uppaal. Therefore, we have to determine a suitable sequence of supported non-constraining operations (i.e., Reset and DF) that leads to \(DBM_{\mathrm{approx}}\). In the next two sub-sections, we introduce two approaches to find such a sequence \(S_{\mathrm{approx}}\): If a reference sequence that leads from \(DBM_{\mathrm{init}}\) to \(DBM_{\mathrm{target}}\) is given, we show how to reduce the sequence to obtain \(S_{\mathrm{approx}}\). If such a sequence is not known beforehand, we derive an overapproximating sequence from \(DBM_{\mathrm{target}}\) only.
5.1 O(SEQ): overapproximation based on given sequence S
If an original sequence from \(DBM_{\mathrm{init}}\) to \(DBM_{\mathrm{target}}\) is already given, e.g., because \(DBM_{\mathrm{target}}\) was reached via an observable simulation, the sequence construction task is the following: For an operation sequence \(S_{\mathrm{ref}}\) that transforms \(DBM_{\mathrm{init}}\) into \(DBM_{\mathrm{target}}\), construct a bounded sequence \(S_{\mathrm{approx}}\) which overapproximates \(DBM_{\mathrm{target}}\).
In particular, considering the set of all possible overapproximation sequences \({\mathcal {S}}_{\mathrm{approx}}\), we obtain an \(S_{\mathrm{approx}}\) \( \in {\mathcal {S}}_{\mathrm{approx}}\) by repeated elimination of selected operations from \(S_{\mathrm{ref}}\). As result, we get a sequence which has, independent of the original sequence size, a bounded length. In fact, we show that it is always possible to reach an overapproximation by at most |T| Reset and \(|T|+1\) DF operations, where T is the set of clocks of the particular model.
We split the argumentation for the individual sequence reductions into two steps, recalling the operations OP described in Sect. 3.3: First, we show that we can eliminate all Constraint and Close operations from \(S_{\mathrm{ref}}\), where each elimination results in a shorter sequence that leads from \(DBM_{\mathrm{init}}\) to an overapproximation of \(DBM_{\mathrm{target}}\). Second, we show that we can furthermore eliminate Reset and DF operations that are redundant or already overwritten, which leads to a length-bounded \(S_{\mathrm{approx}}\).
5.1.1 Constraint and close elimination
In this step, we consecutively remove Constraint and Close operations from \(S_{\mathrm{ref}}\). For the proof that all such operations can be removed while obtaining an overapproximation of \(DBM_{\mathrm{target}}\), we have to prove the following three lemmas (cf. Fig. 6):
Lemma 5.1
(Subzone via Constraint and Close) For a given DBM, applying a C or Cl operation to the DBM leads to a subzone of that DBM:
Lemma 5.2
(Chaining of Constraint and Close Eliminations) Given a DBM and a sequence \(S = ({\mathcal {C}}(DBM) \cup \mathcal{CL}\mathcal{}(DBM))^{*}\), the subsequence \(S_{el}\), (i.e., \(S_{el}|S\)), obtained by repeated elimination of operations from S results in \(S_{el}(DBM) \supseteq S(DBM)\).
Lemma 5.3
(Preserved superzone relation) The superzone relation is preserved by the operations DelayFuture and \(Reset(t_{a},v)\), i.e., for \(op \in (\{DF\} \cup {\mathcal {R}}(DBM))\):
Proof
Lemma 5.1 is easily shown based on the definition of a superzone (Eq. 5.2) and the min operation applied by C and Cl (Fig. 2). For both operations, entries DBM[a, b] are only changed by min operations, which take the original entry value \(c_{ab}\) as argument (e.g., \(min(c_{ab},v)\) for the Constraint operation). Therefore, each affected entry can only be decreased or remains equal, resulting in a subzone of the original DBM. \(\square \)
Proof
For Lemma 5.2, we need to show that a zone that is obtained via a reduced sequence with multiple C and Cl operations eliminated, is a superzone of the DBM obtained via the original sequence, i.e., show monotonicity of the “greater-than” relation for C and Cl operations. This is the case if a superzone \(DBM_{S2}\) obtained for a superzone \(DBM_{S1}\) of a DBM is also a superzone of DBM, i.e., for any \(DBM_{a}\), \(DBM_{b}\), \(DBM_{c}\), the transitivity property holds:
It is straightforward to show that this implication holds, based on the definition of a superzone in Eq. (5.2): From \(DBM_{a} \supseteq DBM_{b}\) follows for all DBM entries that \(DBM_{a}[i,j] \ge DBM_{b}[i,j]\). Correspondingly, \(DBM_{b} \supseteq DBM_{c}\) implies that \(DBM_{b}[i,j] \ge DBM_{c}[i,j]\) for all DBM entries. As a result, \(DBM_{a}[i,j] \ge DBM_{b}[i,j] \ge DBM_{c}[i,j]\), and thus, via the transitivity property of “greater-than,” \(DBM_{a}[i,j] \ge DBM_{c}[i,j]\). In conclusion, following the reverse implication of Eq. (5.2), we get \(DBM_{a} \supseteq DBM_{c}\). \(\square \)
Proof
For Lemma 5.3, we need to show monotonicity of DF and R, that is, the “greater-than” relation between the entries of two DBMs does not change when applied to both of them. This property ensures that when we obtain a superzone by C and Cl elimination, following operations keep the superzone property intact. Again, that property is easily shown: DF sets all the entries of the first column to \(\infty \), so that for two DBMs (\(DBM_{a}\), \(DBM_{b}\)), with \(DBM_{a} \supseteq DBM_{b}\), the corresponding entries either remain unchanged or are both set to \(\infty \) when \(DF(DBM_{a})\) and \(DF(DBM_{b})\) are applied. The \(Reset(t_{a},v)\) operation sets all row values DBM[a, j] to \(DBM[0,j]+v\), and all column values DBM[i, a] to \(DBM[i,0]-v\). So again, if \(DBM_{a} \supseteq DBM_{b}\), those corresponding entries are set to values for which the “greater-than” relation holds (DBM[0, j] or DBM[i, 0]), shifted by a constant value v. Therefore, for both DF and \(Reset(t_{a},v)\), the superzone relation is preserved. \(\square \)
Following from the three lemmas, we can derive two sequence transformation rules that preserve the subzone relation:
We can thus conclude for the resulting DBMs of both sequences:
Proposition 5.1
(Overapproximation by elimination of C/CL) For any sequence \(S \in \mathcal{OP}\mathcal{}(DBM)^{*}\) and its subsequence \(S_{\mathrm{sub}}|S\) obtained by elimination of all C and Cl operations, \(S_{\mathrm{sub}}(DBM) \supseteq S(DBM)\) holds.
At this point, the reduced operation sequence \(S_{\mathrm{sub}}\) has the following form:
Example 5.1
(Example of C and Cl elimination) Given a zero-initialized \(DBM_{\mathrm{init}}\), i.e., all entries are initially 0, and the following reference sequence:
which leads to the target DBM

After elimination of C and Cl operations, which are \(C(t_{1}, t(0),5)\), \(C(t(0),t_{2},-3)\), and their corresponding Close operations, the approximating sequence becomes:
which leads to the overapproximating DBM

5.1.2 Reset and delay-future elimination
Now that we derived a reduced operation sequence by removing all Constraint and Close operations, which results in a superzone of \(DBM_{\mathrm{target}}\), we show that we can further reduce the sequence \(S_{\mathrm{approx}}\) by removing specific Reset and DelayFuture operations while retaining the relation \(DBM_{\mathrm{approx}} \supseteq DBM_{\mathrm{target}}\). For that, we use the reduction rules formulated in the following two lemmas:
Lemma 5.4
(DF sequence reduction) A sequence of DF operations \(S = DF^{+}\) can be reduced to a single DF operation without affecting the outcome of applying S to a DBM:
Lemma 5.5
(Reset elimination in reset-df sequences) Given a DBM and an operation sequence \((R(t_{a},v_{a,1})) \oplus S_{RD,\mathrm{sub}} \oplus (R(t_{a},v_{a,2}))\) with \(S_{RD,\mathrm{sub}} \in ({\mathcal {R}}(DBM)_{{\setminus } \{a\}} \cup \{DF\})^{*}\), i.e., a sequence that starts and ends with a reset of the same clock \(t_{a}\) (to arbitrary values), and between both resets, only contains DF operations and resets of clocks \(t_{i}\), with \(i \ne a\), we can omit the first reset of \(t_{a}\) without affecting the outcome of applying S to a DBM:
Proof
Lemma 5.4 is easily proven; as a DF operation only assigns the first-column entries \(DBM[i,0], i \ne 0\) to \(\infty \), subsequent DF operations keep the DBM unchanged. \(\square \)
Proof
We prove Lemma 5.5 based on the flow dependency function in Eq. (3.20). Given a DBM with \(n = |T(DBM)|\), we first initialize \(I_{0}\):
Then, we either apply a first DF (resulting in \(I_{1,1}\)) or \(R(t_{i},v_{i}), i \ne a\) (resulting in \(I_{1,2}\)):
As \(I_{1,1} \subseteq I_{0}\) and \(I_{1,2} = I_{0}\) hold, we can make use of Eq. (3.23) and consider \(I_{0}\) the “worst-case” dependency after any sequence \(S_{RD,sub} \in ({\mathcal {R}}(DBM)_{{\setminus } \{a\}} \cup \{DF\})^{*}\). In other words, using \(I_{0}\) means that in the most dependent case resulting from any sequence \(S_{RD,sub}\), still only the entries in the row and column of \(t_{a}\) depend on values written by \(R(t_{a},v_{a,1})\). Finally, we apply \(R(t_{a},v_{a,2})\) and get:
From \(I_{2} = \emptyset \), we can conclude that no DBM entry is affected by the operation \(R(t_{a},v_{a,1})\) anymore after we applied \(R(t_{a},v_{a,2})\), and thus, \(R(t_{a},v_{a,1})\) can be omitted from the sequence. \(\square \)
We can now apply rule (5.8) repeatedly, followed by rule (5.7) where applicable, which leads to the following lemma:
Lemma 5.6
(Reset-df sequence reduction) Any sequence \(S \in ({\mathcal {R}}(DBM) \cup \{DF\})^{*}\), can be reduced to a sequence \(S_{red} \in (DF? \otimes (R_{1}) \otimes DF? \otimes \ldots \otimes (R_{m}) \otimes DF?), R_{i} \in {\mathcal {R}}(DBM)\), with \(\forall R(t_{a},v_{a}), R(t_{b},v_{b}) \in S_{red}: t_{a} \ne t_{b}\) by eliminating each but the last reset of every clock which is reset in S, and removing all but one DF operation in each subsequence of DF operations.
Example 5.2
(Example of R and DF elimination) Based on the intermediate overapproximation sequence \(S_{\mathrm{approx}}\) obtained in Example 5.1, eliminating the overwritten operations, i.e., the operation \(R(t_{1},0)\), results in the final overapproximation sequence
which leads to the overapproximation of \(DBM_{\mathrm{target}}\):

5.1.3 Operation sequence reduction: summary
In summary, for the O(SEQ) approach based on a given sequence S, we proved that all Constraint and Close operations can be removed from a sequence of operations, if we aim for a \(DBM_{\mathrm{approx}}\) which overapproximates \(DBM_{\mathrm{target}}\) (cf. Sect. 5.1.1). Furthermore, we can reduce the resulting sequence by eliminating subsequent occurrences of DF operations and resets of clocks which are reset again later in the sequence (cf. Sect. 5.1.2). Therefore, we have proved the following for the overapproximation of DBM states:
Proposition 5.2
(Overapproximation sequences) Given a DBM, any sequence \(S \in \mathcal{OP}\mathcal{}(DBM)^{*}\), i.e., any arbitrary sequence of DF, R, C, and Cl operations, can be reduced to a sequence \(S_{appr} \in (DF? \otimes (R_{1}) \otimes DF? \otimes \ldots \otimes (R_{m}) \otimes DF?), R_{i} \in {\mathcal {R}}(DBM)\), with \(\forall R(t_{a},v_{a}), R(t_{b},v_{b}) \in S_{appr}: t_{a} \ne t_{b}\), i.e., a sequence of DF and R operations in which each clock is reset at most once, and DF operations occur at most once between resets, such that \(S_{appr}(DBM) \supseteq S(DBM)\) holds.
Overall, we can conclude that for each sequence of operations in OP for any DBM, there exists a reduced sequence with at most |T(DBM)| Reset and \(|T(DBM)|+1\) DelayFuture operations.
5.2 O(DBM): overapproximation sequence based on \(DBM_{\mathrm{target}}\)
In this section, we approach the second scenario S2 from Sect. 1, i.e., the case that \(S_{\mathrm{ref}}\) is not given and an overapproximation sequence \(S_{\mathrm{approx}}\) (for which the relation \(S_{\mathrm{approx}}(DBM_{\mathrm{init}}) \supseteq DBM_{\mathrm{target}}\) holds) must be derived from characteristics of \(DBM_{\mathrm{init}}\), \(DBM_{\mathrm{target}}\), and the operation set OP alone.
The following two lemmas provide the base for our approach:
Lemma 5.7
(Approximation sequence existence) Given a zero-initialized \(DBM_{\mathrm{init}}\), for each \(DBM_{\mathrm{target}} = S(DBM_{\mathrm{init}})\) reached by a sequence \(S = \mathcal{OP}\mathcal{}(DBM_{\mathrm{init}})^{*}\), there exists a sequence \(S_{\mathrm{approx}}=(DF,R_{1},DF,R_{2},\ldots ,\) \(R_{n},DF), R_{i} \in {\mathcal {R}}(DBM_{\mathrm{init}})\), with \(S_{\mathrm{approx}}(DBM_{\mathrm{init}}) \supseteq DBM_{\mathrm{target}}\).
Lemma 5.8
(reset-(df)-all to reset-df-all) If a reset-(df)-all sequence overapproximates a DBM, the reset-df-all sequences obtained by enforcing a DF after each reset overapproximates the DBM as well.
Proof
Lemma 5.7 holds as zero-initialization implies a prefix sequence \(S_{R}=(R(t_{1},0), \ldots , R(t_{n},0))\), with \(n=|T(DBM)|\), which turns each sequence S into \(S_{ext}=S_{R} \oplus S\). It follows that each clock is reset at least once, and due to Proposition 5.2, we can reduce \(S_{ext}\) to \(S_{\mathrm{approx}}\), with \(S_{\mathrm{approx}}(DBM_{\mathrm{init}}) \supseteq DBM_{\mathrm{target}}\). \(\square \)
Proof
Lemma 5.8 holds as DF operations only set particular entries to \(\infty \) (cf. Eq. (3.3)) and thus always lead to superzones of the original DBM. \(\square \)
The challenge is to determine a reset-(df)-all sequence without access to an \(S_{\mathrm{ref}}\) to reduce. The potentially suitable reset-(df)-all sequences differ in three characteristics: The order of resets (C1), the reset values (C2), and the occurrence of DF operations between the resets (C3); the set of such sequences is infinite. Due to Lemma 5.8, we can remove C3 by limiting the search space to reset-df-all sequences. The search space becomes finite for classes of automata that restrict C2, including the formalism of TAs as defined in [5], which supports resets to 0 (i.e., 0-resets) only; the Uppaal tool allows arbitrary positive reset values (i.e., \({\mathbb {N}}_{0}\)-resets) during simulation, but limits support to 0-resets during verification. In the remainder of this section, we approach DBM overapproximation for both the case of 0-resets (Sect. 5.2.1) and \({\mathbb {N}}_{0}\)-resets (Sect. 5.2.2).
5.2.1 O(DBM) approach for 0-resets
The approach for 0-resets is straightforward, as we can directly infer reset orders from the two-clock constraints \(DBM[i,j], i \ne j \ne 0\) (cf. Fact 4). From Fact 4, we know that DBM[i, j] is strictly positive iff \(t_{i}\) is reset before \(t_{j}\). Thus, a possible algorithmic approach to determine a valid reset order is to sum the amount of positive values for each column j, and order the clocks \(t_{j}\) accordingly in ascending order of the sums. This approach builds on the fact that the higher the amount of positive values in a column j, the more clocks were reset before \(t_{j}\), so that the clock with the lowest column sum was reset first, while the clock with the highest sum was reset last. If clocks are reset simultaneously (i.e., without intermediate delay), the same number of clocks must be reset before them, and thus, their sums of positive column values are equal; the order of these clocks can be chosen arbitrarily.
The order is formally expressed as follows: Given a DBM with \(n = |T(DBM)|\), the set \(PSUM = \{(c_{1},t_{1}), \) \(\ldots , (c_{n},t_{n})\}, t_{j} \in T(DBM), c_{j} = |\{i\ |\ i \in {\mathbb {N}} \cap [1,n],\) \(DBM[i,j] > 0\}|\) and any valid order \(\le _{C}: PSUM \times PSUM\), with \((c_{i}, t_{i}) \le _{C} (c_{j}, t_{j}) \iff c_{i} \le c_{j}\), we can derive a corresponding reset order \(Ord_{R}: T(DBM) \times T(DBM)\), with
The resulting orderings \(Ord_{R}\) only differ in the order of their “simultaneously” reset clocks. Each reset-df-all sequence that follows such order is guaranteed to lead to an overapproximation of \(DBM_{\mathrm{target}}\).
5.2.2 O(DBM) approach for \({\mathbb {N}}_{0}\)-resets
While the reset order is the only variable for the case of 0-resets, neither the reset order nor the reset values are known for the case of \({\mathbb {N}}_{0}\)-resets. In the following, we provide a method to derive overapproximating reset-df-all sequences with \({\mathbb {N}}_{0}\)-resets, and split the argumentation into two parts:
- P1:
-
We show how reset values are obtained if the reset order is given.
- P2:
-
We show how reset orders are obtained for which valid reset valuations exist.
Determine reset values (P1) The process for the determination of reset values is shown in Fig. 7. Given a reset-df-all sequence S with unknown reset values (Fig. 7-(1)), we derive a constraint system on reset values from the relation between the entries of the overapproximating and target DBM (Fig. 7-(2)). Following from Fact 5, the constraints are either \(v_{i}- v_{j} \ge DBM_{\mathrm{target}}[i,j]\) or \(\infty \ge DBM_{\mathrm{target}}[i,j]\) (Fig. 7-(3a–c)). As the constraints \(DBM_{\mathrm{target}}[i,j] \le \infty \) trivially hold, they can be omitted from the constraint system. Furthermore, \({\mathbb {N}}_{0}\)-resets impose constraints \(v_{i} \ge 0\) for each \(i \in {\mathbb {N}} \cap [1,|T(DBM)|]\) (Fig. 7-(4)). The adapted constraint system, which solely consists of constraints on some particular (pairs of) reset values now, can be extended to a constraint system over all reset value pairs by adding the trivially satisfied \(v_{i} - v_{j} \le \infty \) for the remaining value pairs, and introducing an artificial reset value \(v(0) = 0\) (Fig. 7-(5)) similar to t(0) for clock differences. We can represent this new constraint system as DBM, which we denote as \(DBM_{v}\) (Fig. 7-(6)), as it expresses constraints on reset values v, unlike the usual DBM that expresses constraints on clock values. For the system \(DBM_{v}\), the following lemma holds:
Lemma 5.9
(Reset values from \(DBM_{v}\)) Given a reset-df-all sequence S with unknown reset values, each valid reset valuation of \(DBM_{v}\) provides reset values such that S leads to an overapproximation of \(DBM_{\mathrm{target}}\).
Proof
Lemma 5.9 holds as \(DBM_{v}\) is composed of all reset value constraints that need to be satisfied to overapproximate \(DBM_{\mathrm{target}}\). \(\square \)
Finally, the \(DBM_{v}\) can be transformed to a graph \(G_{v}\) (Fig. 7-(7), cf. Sect. 3.4).
Valid reset valuations only exist if \(DBM_{v}\) is non-empty, and thus, if \(G_{v}\) has only non-negative weight cycles (cf. Fact 1). Only a subset of cycles needs to be checked; in fact, we can reduce the check as follows:
Lemma 5.10
(Non-emptyness of \(\textit{DBM}_{v}\) by \(p_{H}\)) Given a \(\textit{DBM}_{\mathrm{target}}\) and a reset-df-all sequence S leading to \(\textit{DBM}_{\mathrm{approx}}\), the \(\textit{DBM}_{v}\) derived from \(\textit{DBM}_{\mathrm{approx}}\) \( \supseteq \textit{DBM}_{\mathrm{target}}\) is non-empty iff the unique Hamiltonian cycle \(p_{H}\) over non-\(\infty \) edges, i.e., the cycle over all vertices in inverse reset order, is an all-positive-prefix path in its graph \(G_{v}\).
Proof
Fact 8 transfers to \(G_{v}\) if we consider the Hamiltonian path \(p_{H}\) over all vertices \(v_{i} \in V(G_{v})\) in inverse reset order instead (evident from Fig. 7-(7)), and due to Fact 3, we can then ignore all paths that are neither \(p_{H}\) nor its sub-paths via cycle chords. The remaining cycles traverse only edges with \(-DBM_{\mathrm{target}}[i,j]\) and 0 weights; recall that the 0 weights were artificially introduced by \(v_{i} \ge 0\) for edges \(e = (v_{i}, v_{0})\). Given a closed \(DBM_{\mathrm{target}}\) with minimum edge costs (cf. Fact 2), we can infer that a maximum edge costs property holds for all paths that only traverse edges with \(-DBM_{\mathrm{target}}[i,j]\) weights, and in consequence, we can ignore shorter paths derived via cycle chords from paths with known positive costs. Based on the maximum edge costs property, we can ignore all sub-cycles of \(p_{H}\) (via cycle chords) that do not traverse the artificial 0 weights, i.e., we only have to check \(p_{H}\) and its prefix cycles. As the final edge of such prefix cycles has 0 weight and thus does not affect the accumulated path cost, it suffices to check the prefix paths of \(p_{H}\) instead, and thus, the final set of paths to check are \(p_{H}\) and all its prefix paths, i.e., we check if \(p_{H}\) is an all-positive-prefix path. Thus, Lemma 5.10 holds. \(\square \)
Determine reset order (P2) In the general case, however, the reset-df-all sequence is unknown, so we first need to find a suitable reset order that leads to a non-empty \(DBM_{v}\) before we can derive suitable reset values from that \(DBM_{v}\) as described in P1. We denote the sets of all potential \(DBM_{v}\) and their graphs \(G_{v}\) as \(\mathcal {DBM}_{v}\) and \({\mathcal {G}}_{v}\), respectively. Recall that \(DBM_{\mathrm{approx}} \supseteq DBM_{\mathrm{target}}\) yields constraints \(v_{i} - v_{j} \ge DBM_{\mathrm{target}}[i,j]\) only for a subset of value pairs \((v_{i},v_{j})\) depending on the reset order, and if we chose another reset order, we would obtain constraints on a different subset of value pairs. The concept to determine a suitable reset order is shown in Fig. 8. We first assume the reset-all sequence (Fig. 8-(1)), whose resulting clock zone of \(DBM_{\mathrm{approx}}\) (Fig. 8-(2)) represents a single point, and which thus results in the most restrictive \(DBM_{v,R}\) (Fig. 8-(3)) with constraints \(DBM_{\mathrm{target}}[i,j] \le v_{i} - v_{j}\) on all pairs \((v_{i}, v_{j})\). For this most restrictive constraint set (whose solution set is usually empty unless \(DBM_{\mathrm{target}}\) was constructed by exactly such reset-all sequence), we determine which constraints have to be removed to transform \(DBM_{v,R}\) into a valid and non-empty \(DBM_{v}\) (Fig. 8-(5)), which corresponds to turning the reset-all sequence into a reset-df-all sequence with a suitable reset order (Fig. 8-(4)). The task is now to derive a reset order from the data in \(DBM_{v,R}\), which we approach on the level of the corresponding graphs \(G_{v,R}\) and \(G_{v}\). In terms of Hamiltonian paths (cf. Lemma 5.10), the relation between \(G_{v,R}\) and \(G_{v}\) is expressed as follows:
Lemma 5.11
(Relation between \(G_{v,R}\) and \(G_{v}\)) If \(p_{H}\) is an all-positive-prefix Hamiltonian path over edges with non-\(\infty \) weights in \(G_{v,R}\), then there exists a graph \(G_{v} \in {\mathcal {G}}_{v}\), such that \(p_{H}\) is an all-positive-prefix Hamiltonian path over edges with non-\(\infty \) weights in \(G_{v}\).
Proof
Lemma 5.11 holds as we can obtain such a \(G_{v}\) by setting all edges \(e = (v_{i},v_{j}), e \not \in p_{H}, v_{j} \ne v_{0}\) in \(G_{v,R}\) to \(\infty \), which is equivalent to removing all constraints not implied by the reset order that corresponds to the order of vertices in \(p_{H}\). \(\square \)
We can use such a path \(p_{H}\) in \(G_{v,R}\) to derive a valid graph \(G_{v}\) and thus a suitable reset order:
Proposition 5.3
(Reset order from \(p_{H}\)) Given a \(DBM_{\mathrm{target}}\) reached by an (unknown) sequence \(S \in \mathcal{OP}\mathcal{}(DBM_{\mathrm{init}})^{*}\) from a zero-initialized \(DBM_{\mathrm{init}}\), if a cycle \(p_{H}=((v_{0},v_{a}),(v_{a},v_{b}),\) \(\ldots \) \(,(v_{k},v_{l}),(v_{l},v_{0}))\) is an all-positive-prefix Hamiltonian cycle in the graph \(G_{v,R}\), the corresponding reset order \(Ord = \{(t_{l},t_{k}), \ldots , \) \((t_{b},t_{a})\}\) leads to a zone \(DBM_{v}\), and thus, to reset-df-all sequences \(S_{\mathrm{approx}} = (DF, R(t_{l},x_{l}), DF, R(t_{k},x_{k}), DF, \) \(\ldots , R(t_{a},x_{a}), DF\)) that result in valid overapproximations of \(DBM_{\mathrm{target}}\) for some reset values \(x_{i}\).
Proof
Proposition 5.3 directly follows from Lemma 5.11. \(\square \)
A concrete reset valuation for the reset-df-all sequence can then be picked arbitrarily from the zone \(DBM_{v}\) as described in P1 (cf. Lemma 5.9).
Algorithm Based on Lemma 5.9, Proposition 5.3, and the steps shown in Fig. 8, we propose the algorithm shown in Fig. 9 for the overapproximation task. In ll.\(1-4\), we derive the graph \(G_{v,R}\) via \(DBM_{v,R}\), which we calculate as \(DBM_{v,R} = -DBM_{\mathrm{target}}^{T}\), and apply the artificial constraints \(v_{i} \ge 0\) for non-negative reset values. As optimization, we already derive a partial clock reset order \(Ord_{P}\) at this point, based on the fact that constraints \(v_{i} - v_{j} \le -\infty \) (which result from \(\infty \) values in \(DBM_{\mathrm{target}}\)) are never satisfiable and thus certainly need to be removed (i.e., replaced by \(v_{i} - v_{j} \le \infty \)) by choosing the reset order in the reset-df-all sequence accordingly (ll.\(5-6\)). Based on that ordering, we apply the sub-algorithm AllPosPrefixPath (Fig. 10), which determines an all-positive-prefix path in \(G_{v,R}\) and its corresponding total clock reset order \(Ord_{T}\) (l.8, cf. Proposition 5.3). Afterward, we obtain the graph \(G_{v}\) for our particular reset order by setting all weights of edges in \(G_{v,R}\) that correspond to clock pairs in reset order to \(\infty \) (ll.\(9-12\)), and transform \(G_{v}\) back to a (non-empty) \(DBM_{v}\) (l.13), for which we restore the closed form (l.14). Finally, we derive an arbitrary valuation of reset values from \(DBM_{v}\) (ll.15-16, cf. Lemma 5.9), and based on both the reset order and reset values, derive and return the overapproximation sequence \(S_{\mathrm{approx}}\) (ll.\(17-18\)).
Example 5.3
(Overapproximation via O(DBM)) Given \(DBM_{\mathrm{target}}\) introduced in Example 5.1. We determine \(DBM_{v,R} = -DBM_{\mathrm{target}}^{T}\) and its corresponding DBM graph \(G_{v,R}\), and search for an all-positive-prefix path in \(G_{v,R}\), which is \(p_{H} = (v_{0},v_{3}),\) \((v_{3},v_{1}),(v_{1},v_{2}),(v_{2},v_{0}))\), from which we can derive the overapproximation sequence
leading to the overapproximation of \(DBM_{\mathrm{target}}\):

5.3 Time and size complexity
To conclude the discussion of the O-phase, we analyze the resulting length and generation time of \(S_{\mathrm{approx}}\). Given a DBM with clocks T, for the sequence length, we have shown that any given sequence \(S_{\mathrm{ref}}\) of operations \(op \in \mathcal{OP}\mathcal{}(DBM)\) can be reduced to a reset-df sequence \(S_{\mathrm{approx}}\) (Proposition 5.2), where each clock is reset at most once (i.e., |T| resets at most), and as multiple consecutive DF operations can be reduced to one single DF, \(S_{\mathrm{approx}}\) has \(|T|+1\) DF operations at most. Therefore, the number of required operations during the O-phase, considering a minimum bound of 0 operations for the case \(DBM_{\mathrm{init}} == DBM_{\mathrm{approx}}\), is:
Regarding the generation time, we notice that the reduction in a given \(S_{\mathrm{ref}}\) depends on its length and the number of clocks. Algorithmically, we start with the last element of \(S_{\mathrm{ref}}\), and check for each element, if it is a Reset not encountered yet, or a DF; if neither is true, we remove the element. As each element is compared against the set of already encountered resets, the upper bound of steps required is therefore \(|S| * (|T|-1)\). For the second approach, the derivation of \({S_\mathrm{approx}}\) from \(DBM_{\mathrm{target}}\), the transformation steps to \(DBM_{v}\) and then to \(G_{v}\), have a complexity of \(O(|T|^2)\). Then, for the determination of an all positive prefix path, in the worst case, no \(-\infty \) weights are given, and thus, no a priori information of a partial ordering exists. In that case, a possibly full search through the graph is required by AllPosPrefixPath (Fig. 10). There again, in the worst case, only the last searched path yields positive weight sums on all its prefixes, and all other paths turn negative on the last edge, which leads to a complexity of \(O((|T|-1)!)\). In the general case though, a path can turn negative earlier, and is discarded then (together with all paths of which that path is a prefix); also, an all positive prefix path can potentially be discovered earlier. Furthermore, the graph size depends only on the number of clocks, which is usually small (between 3 and 10 clocks per model in our experiment model suite). Among all remaining steps, the Close operation on \(DBM_{v}\) has the highest complexity \(O(|T|^3)\). In conclusion, the complexity of the O(SEQ) approach grows linearly with the sequence length, and is therefore suitable for shorter sequences, e.g., for the processing of incoming sequence sections in an on-the-fly application, while the O(DBM) approach guarantees upper construction time bounds for DBMs resulting from sequences of arbitrary length.
6 Constraint phase (C-phase)
At this point, we have derived an overapproximating sequence \(S_{\mathrm{approx}}\), which, when applied to \(DBM_{\mathrm{init}}\), results in \(DBM_{\mathrm{approx}}\), overapproximating \(DBM_{\mathrm{target}}\). In the second phase, the C-phase, we now determine a sequence \(S_{\mathrm{constr}}\), which transforms \(DBM_{\mathrm{approx}}\) to the final \(DBM_{\mathrm{target}}\):
All entries of \(DBM_{\mathrm{approx}}\) fulfill the superzone property of Eq. (5.2) compared to \(DBM_{\mathrm{target}}\) at this point. Therefore, the main task is now to decrease each entry of \(DBM_{\mathrm{approx}}\) so that it becomes equal to those of \(DBM_{\mathrm{target}}\). While OP does not contain an operation to increase individual DBM entries for the O-phase, it provides such an operation for decreasing individual entries: \(Constraint(t_{a},t_{b},v)\). Therefore, the goal of the C-phase is to obtain a sequence of constraint operations:
We describe three approaches to derive such a constraining sequence \(S_{\mathrm{constr}}\) with different trade-offs between generation time and sequence length: A trivial approach using the full constraint system (FCS) in Sect. 6.1, a reduced approach using a minimal constraint system (MCS) (introduced by Larsen et al. [23]) in Sect. 6.2 as well as a minimal approach using a newly introduced relative constraint system (RCS) in Sect. 6.3. Among these approaches, the former already solves the problem of constraining \(DBM_{\mathrm{approx}}\) to \(DBM_{\mathrm{target}}\) in general, and the latter two optimize the resulting sequence lengths.
6.1 C(FCS): full constraint system approach
The first approach uses the FCS, i.e., a system of all constraints contained in a DBM, so we perform an individual constraint operation \(C(t_{i},t_{j},DBM_{\mathrm{target}}[i,j])\) on \(DBM_{\mathrm{approx}}\) for each entry of \(DBM_{\mathrm{target}}\). This is the simplest form, and in fact, for its construction we only turn every entry of \(DBM_{\mathrm{target}}\) into a Constraint operation:
While the simplicity of generation is a clear advantage of this approach, the downsides are manifold, even if we remove the constraints on diagonal DBM entries, representing the differences \(t_{i} - t_{i}\) for clocks \(t_{i} \in T(DBM)\), which are constantly 0 and thus do not need an explicit constraint operation. Certain constraints are already implied by others, and thus, setting a constraint may—via a Close operation—already set multiple DBM entries to their targeted values; applying their Constraint operations from \(S_{\mathrm{constr}}\) is then redundant. Furthermore, several entries may already equal those of \(DBM_{\mathrm{target}}\) after the O-phase, so that a constraint for these entries is not required either. Still, this approach allows us to determine a worst case upper bound of required Constraint operations during the C-phase as \((|T|+1)^2\), i.e., every entry of \(DBM_{\mathrm{target}}\), which has \(T+1\) clocks (the model clocks plus the reference clock t(0)).
Example 6.1
(Full constraint system) Given the reference sequence \(S_{\mathrm{ref}}\) and target DBM \(DBM_{\mathrm{target}}\) introduced in Example 5.1. Applying the C(FCS) approach to \(DBM_{\mathrm{target}}\) results in the constraining sequence
6.2 C(MCS): minimal constraint system approach
The second sequence generation strategy uses the data of an MCS, i.e., a minimal system of constraints that implies all remaining constraints. The idea is to perform a constraint operation on \(DBM_{\mathrm{approx}}\) for each entry of the MCS of \(DBM_{\mathrm{target}}\). An algorithm for the reduction in an FCS to an MCS was introduced by Larsen et al. [23].
The algorithm performs the following steps: For a graph G representing a given DBM, it determines vertex equivalence classes \(E_{i}\) regarding zero-equivalence, which means that a cycle with a weight of 0 (zero-cycle) containing those vertices exists. In each equivalence class \(E_{i}\), it determines a cycle over all its vertices (in index ordering), where each weight between two vertices is the shortest path weight between them. The edges of those cycles are added to the MCS. Furthermore, between equivalence classes \(E_{i}\) and \(E_{j}\), it takes the vertex with smallest index from each of the two classes, and includes two edges between them with shortest path weight.
As only a single cycle instead of the complete graph is considered inside each equivalence class, and only two edges are needed between each pair of equivalence classes, it is obvious that the total number of constraints in an MCS can be much smaller compared to the FCS. On average, the MCS contains a number of constraints reduced by 70–86% [23]. The trade-off lies in the time complexity, as the complexity of determining the equivalence classes is \(O(n^2)\), getting the edges between equivalence classes is O(n), and finding the cycles within \(E_{i}\) is O(n), leading to an overall complexity of \(O(n^2)\) (or \(O(n^3)\), if the DBM is not in closed form). Additionally, when applied in our approach, the MCS may still include constraints whose corresponding DBM entries already had the targeted values.
Example 6.2
(Minimal constraint system) Given the reference sequence \(S_{\mathrm{ref}}\) and target DBM \(DBM_{\mathrm{target}}\) introduced in Example 5.1. Applying the C(MCS) approach to \(DBM_{\mathrm{target}}\) results in the constraining sequence
6.3 C(RCS): relative constraint system approach
To minimize the required amount of constraints, we introduce the RCS, a system which contains only those constraints that are not already correctly set (i.e., entries \(DBM_{\mathrm{approx}}[i,j] \ne DBM_{\mathrm{target}}[i,j]\)) or implied by other constraints in the DBM. This approach can be based on the concepts of either FCS or MCS. In the following, we will refer to edges of constraints that are already correctly set as fixed edges, and all remaining ones as non-fixed edges.
Using the FCS, the procedure is straight-forward: While transforming each entry of \(DBM_{\mathrm{target}}\) into a Constraint operation, we check if the corresponding \(DBM_{\mathrm{approx}}\) entry has the same value as the \(DBM_{\mathrm{target}}\) entry. In that case, the Constraint operation is not added to the final sequence of constraints.
Deriving an RCS with the properties of an MCS requires additional steps. The overall idea is to obtain a minimal set of constraints not already included in \(DBM_{\mathrm{approx}}\), which, together with the constraints included in \(DBM_{\mathrm{approx}}\), implies all remaining constraints of \(DBM_{\mathrm{target}}\). Recall that for the construction of an MCS [23], we determine a) two opposing edges between each pair of equivalence classes \(E_{i}\) and \(E_{j}\) and b) a cycle over all vertices within each equivalence class \(E_{i}\). In steps where vertices are selected, the original MCS construction algorithm uses the index order of vertices to eliminate non-determinism, which could occur as usually multiple minimal sets of constraints exist for a given constraint system. Our RCS approach introduces an additional step which picks fixed edges first, and only then—if still multiple ambiguous choices exist—relies on the vertex order for the remaining edges like the original MCS algorithm. That way, we refine the selection of vertices in favor of constraints that are already correctly set, and thus, reduce the amount of constraints required additionally.
Figure 11 shows the adapted procedure, where l.11, l.17 and ll.\(19-20\) (with \(E_{f} = \emptyset \), i.e., no fixed edges) match the original MCS algorithm, and ll.\(7-9\), ll.\(13-15\) and ll.\(19 - 21\) (with \(E_{f} \ne \emptyset \)) implement our adaptions for the case that fixed edges are involved. For the determination of edge pairs in a), we will first search for edges of already correctly set DBM entries (l.\(7-9\)), and only revert to edges of index ordered vertices (l.11)—as in the original algorithm—if none can be found. For the equivalence classes \(E_{i}\) and \(E_{j}\) (with \(t_{a} \in E_{i}, t_{b} \in E_{j}\), and \(minE_{i}\) the vertex with smallest index among vertices in \(E_{i}\)), we proceed as follows: Among fixed edges \((t_{a},t_{b})\), we choose the one with the smallest index a (l.7), and if multiple such edges exist, the one with smallest index b (l.8) among them. If no such fixed edge exists, we choose the edge \((minE_{i},minE_{j})\) (l.11) as defined in the reference algorithm. Similarly, we determine the second, opposing edge \((t_{b},t_{a})\) (ll.\(13-15\)), but with swapped indices, i.e., first the smallest b (l.13) and then the smallest a (l.14), and \((minE_{j},minE_{i})\) (l.17) otherwise.
For (b), in each equivalence class \(E_{i}\), we want to determine a cycle over all its vertices, which additionally contains the maximal possible number of fixed edges. This problem is NP-complete and can be transformed to the traveling salesman problem by assigning weight 0 to fixed edges and weight 1 to non-fixed edges. Then, the task is to find the lowest-cost Hamiltonian cycle in that graph, i.e., one that contains as few non-fixed edges that impose additional constraints, and as many fixed edges as possible. Fortunately, the problem complexity grows non-polynomially only in the number of clocks in the DBM, which is rather low in the general case (e.g., between 3 and 10 clocks in our experiment suite, cf. Sect. 9). Therefore, it is viable to determine a solution by both brute force and heuristic methods.
Proof
The correctness argument for Fig. 11 is as follows: In the original MCS algorithm, the choice of both the concrete edge pairs between equivalence classes and the edges on a Hamiltonian cycle within each equivalence class could be arbitrary, and each solution would be a correct minimal constraint system (cf. [23] for justification). While the MCS algorithm uses the index order of vertices to choose one of these correct solutions deterministically, our approach just adds another objective (i.e., favoring of fixed edges) to that choice in ll.\(7-8\), ll.\(13-14\), and l.19. That way, the resulting constraint system is still necessarily correct, and as we pick fixed edges first whenever possible, the resulting RCS is also minimal with respect to \(DBM_{\mathrm{approx}}\). \(\square \)
Example 6.3
(Relative constraint system) Given the reference sequence \(S_{\mathrm{ref}}\) and target DBM \(DBM_{\mathrm{target}}\) introduced in Example 5.1, and the resulting overapproximation DBM \(DBM_{\mathrm{approx}}\) of Example 5.2. Applying the C(MCS) approach to \(DBM_{\mathrm{target}}\) starting from \(DBM_{\mathrm{approx}}\) results in the constraining sequence
6.4 Time and size complexity
Again, we analyze the resulting length and generation time of \(S_{\mathrm{constr}}\) and further consider the application times of sequences based on FCS, MCS, and RCS. Given a DBM with clocks T, in the worst case (FCS), one C operation is required for every entry of \(DBM_{\mathrm{approx}}\), which has \(|T|+1\) columns and \(|T|+1\) rows. Considering 0 operations as the lower bound for the case \(DBM_{\mathrm{approx}}\) \( == DBM_{\mathrm{target}}\), this leads to the following estimate of required operations:
The actual maximal number of required operations lies below that bound, as the main diagonal entries are always 0, leading to \(|S_{\mathrm{constr}}| \le |T| * (|T|+1)\). As certain DBM entries may already be implied by other entries (MCS), or are already set correctly in \(DBM_{\mathrm{approx}}\) (RCS), we can further reduce the bound by \(\sim 80\%\) or \(\sim 90\%\), respectively (see Sect. 9).
Combining the sequence length bounds of the O-phase and C-phase, we obtain the total size of our sequence S—the major theoretical result of this work:
Theorem 1
(CSC sequence complexity bound) Any valid and closed DBM can be reached by a clock state construction sequence S of
operations.
Regarding generation times, deriving the FCS has a time complexity of \(O(|T|^2)\), as we directly transform each DBM entry into a Constraint operation. For the MCS, the complexity is \(O(|T|^3)\), which follows from the complexity of deriving the shortest-path reduction \(G^R\) (cf. [23]). Finally, the RCS approach has a complexity of \(O(|T|^2)\) for the edges between equivalence classes, and \(O((|T|-1)!)\) to obtain a Hamiltonian cycle with most fixed edges within an equivalence class. However, as for the factorial-time step of the O-phase, the actual costs depend only on the number of clocks, which is comparatively small in the common case.
Finally, we consider the complexity of applying the derived constraint sequence for the C-phase. On the one hand, the FCS approach has the greatest sequence length, but does not require a final Close operation, as all constraints are explicitly contained in the sequence and do not need to be inferred. On the other hand, the MCS and RCS approaches result in shorter sequences, but require a closing step with \(O(|T|^3)\) complexity which infers the left out constraints. In the end, the most suitable approach in practice depends on the concrete aim, i.e., whether we require a comparatively short sequence, a shorter execution time, or faster generation times; this question cannot be answered universally though.
7 State construction for Uppaal extended timed automata
At this point, we are given the targeted system state, which—as a reminder—contains the information of the variable values, active locations, and clock state that we want to set, and a clock state construction sequence derived in Sect. 5 and Sect. 6. In this section, we explain how this information extends a concrete (network of) Uppaal automata to restore the desired starting state from which the model simulation will then continue. Note that this section focuses on the (more complex) case of state construction in ETAs (see Sect. 3.1 for the definition of ETAs); however, for a simple TA without synchronization, urgency, and variables, one would proceed similarly, but add the construction sequences directly into the given TA, and implement urgency via explicit invariants \(t_{u} \le 0\) on a helper clock \(t_{u}\) that was reset before. For state construction in ETAs, we transform the clock state construction sequence and variable data into an additional automaton whose execution restores the clock and variable state before the original system is re-entered at the targeted starting locations. An example of the adapted form of the introduction model (Fig. 1) is shown in Fig. 12, and we will explain the changes in the following.
To integrate the derived DBM operation sequence leading to \(DBM_{\mathrm{target}}\) into an Uppaal automaton system, we need to translate the operations into a sequence of artificially added locations and edges, each labeled with invariants, or guards and resets, respectively. Transferring the symbolic semantics (cf. Definition 2), i.e., the execution of transitions and validity checks of active locations, to corresponding DBM operations, we obtain the following types of operation sequences:
-
Initialization: \(S_{\mathrm{init}} = (R(t_{1},0), \ldots , R(t_{n},0))\)
Initially, all clocks are reset to 0.
-
Location: \(S_{\mathrm{loc}} \in DF? \otimes {\mathcal {C}}(DBM)^{*} \otimes Cl^{1}\)
In a location l, a DF is applied if no urgent or committed next transition is enabled, and all invariants \(C_{l}\) (represented as constraint operations) are applied to the DBM. Afterward, a Cl operation is performed to restore DBM closedness.
-
Edge: \(S_{\mathrm{edge}} \in {\mathcal {C}}(DBM)^{*} \otimes Cl^{1} \otimes {\mathcal {R}}(DBM)^{*} \otimes {\mathcal {C}}(DBM)^{*}\) On an edge \(e_{ab}\) from \(l_{a}\) to \(l_{b}\), the atomic guard constraints in \(g(e_{ab})\) (again represented as C operations) are applied to the clock state DBM, followed by a Cl operation to turn the DBM into closed form again. Then, all clock resets in \(r(e_{ab})\) (represented as R operations) are applied to the DBM, and finally, the invariants \(I(l_{b})\) of the target location are checked.
Recall that our construction sequence S consists of a subsequence of (alternating) R and DF operations (O-phase), followed by a sequence of C operations (C-phase), which, when based on the MCS or RCS approach, require a final Cl operation to adapt the remaining DBM entries:
The individual elements of this sequence need to be mapped to components of the NTA, i.e., locations and edges, based on the operation sequences applied during simulation identified above. For the subsequence \(S_{\mathrm{approx}} \in ({\mathcal {R}}(DBM)^{1} \otimes DF?)^{*}\), we can use edges with corresponding resets but without guards to new (non-urgent and non-committed) locations without invariants, which results in the sequences \(S_{\mathrm{edge}} \in {\mathcal {R}}(DBM)^{*}\) and \(S_{\mathrm{loc}} = (DF)\). That way, we can express each subsequence \({\mathcal {R}}(DBM)^{*} \otimes DF^{1}\) by an edge–location pair; a sequence of those pairs will cover the complete O-phase. In Fig. 7a, these are the locations Init, Rec1, and Rec2, and their corresponding edges. To enforce all constraints of the C-phase, i.e., the subsequence \(S_{\mathrm{constr}} \in ({\mathcal {C}}(DBM)^{*} \otimes Cl^{1})\), we can use an edge without resets to an unconstrained location, which results in \(S_{\mathrm{edge}} \in ({\mathcal {C}}(DBM)^{*} \otimes Cl^{1})\). Note for all these sequences that in Uppaal, a partial \(Close(t_{a},t_{b})\) operation is applied after each \(Constraint(t_{a},t_{b},v)\) instead of a single Close over all clocks after a sequence of Constraint operations.
The construction of the variable state, which is introduced by the ETA formalism, can be performed via a single transition. We can set the individual variable values, in contrast with the DBM state, directly via variable assignments (cf. Definition 2). In Fig. 7a, we added these assignments to a new edge from Rec3 to End for a separation of concerns; however, a separate edge is not needed for these assignments, as we could add them to the last edge of the clock state construction sequence (i.e., the edge with the constraining guards of the C-phase).
Furthermore, we need to reach the original active locations in the adapted model after the variable and DBM state construction. Normally, we would simply define those locations as initial in Uppaal, so that they become active on model initialization. To traverse our artificially added construction sequence though, the first location of that sequence needs to be defined as initial, and the final edge of the construction section should lead to the targeted initial location of the original model section. Once the construction sequence is fully traversed (and only then), the original model sections of all automata are re-entered (which is achieved in ETAs by broadcast synchronization via DBM_init_end).
8 Implementation
We provide a Python implementation of the introduced OC approach, as well as the required interface and interpreter code needed to apply the approaches to Uppaal models. The project implementation is open source [34] [35] under MIT license, and mainly consists of:
-
An Uppaal model and Uppaal C code parser (via EBNF grammars building up on the BNF grammar provided with Uppaal),
-
An Uppaal model simulator, which allows tracking the simulated operation sequences (= \(S_{\mathrm{ref}}\)) [34],
-
The DBM data structure and operations,
-
The state constructor implementations for the trivial approach, Rinast approach (port from Java [20]), and the variants of our OC approach,
-
The experiments performed in this paper, including a random sequence generator as alternative input data source.
Compared to the concepts introduced in Sect. 5 and 6, the concrete implementation differs in the following aspects:
-
The O(DBM) implementation uses \(DBM_{v}\) directly instead of its graph representation \(G_{v}\); the result is identical.
-
The C(RCS) implementation checks only up to a fixed amount of cycle permutations; while this limitation may not preserve minimality of the resulting sequences, the boundedness is not affected, and it allows a time-efficient application to models with higher amounts of clocks as well.
-
Where suitable for sequence-based algorithms (i.e., trivial, Rinast, O(SEQ)), on-the-fly versions are implemented, which process only the newly tracked operations instead of the complete \(S_{\mathrm{ref}}\) on each call.
After installation, executing run in the experiments CLI will run all clock state construction experiments and store the corresponding analysis data. The experiments are available online [36], and the experiment setup and results are explained in Sect. 9.
8.1 Random operation sequence generation
The experiments in Sect. 9 use operation sequences that are either obtained from simulation of TA models, or generated (semi-)randomly based on the subsequences for location states and transitions described in Sect. 7. In general, the sequence generator generates operation sequences via a simulating approach, which keeps track of the current DBM to which each generated operation is applied; based on that current DBM, the next invariant, guard, or reset values are selected from intervals that keep the DBM non-empty, and thus, keep the sequences feasible. The generation process starts with specifying if non-zero resets should be allowed, and if the sequence should start with an initialization sequence (i.e., a sequence of resets of all clocks to 0). Then, the generator randomly chooses whether a DF is added, followed by a sequence of single-clock invariants on a random subset of clocks with (valid) values (i.e., constraints \(C(t_{i}, t(0), v_{i})\), with \(t_{i} \in T_{\mathrm{sub}} \subseteq T(DBM), v_{i} \in [a,b], a = -DBM[0,i], b = DBM[i,0]\)) that are random within bounds, and a Cl operation; this part reflects the sequence imposed by the initially active locations. Afterward, until the targeted sequence length is reached, we repeatedly add an operation sequence reflecting a transition, followed by another sequence for the newly active location state. Each transition sequence is composed of a sequence of single-clock guards on a random subset of clocks with random (valid) values (i.e., constraints \(C(t(0), t_{i}, -v_{i})\), with \(t_{i} \in T_{\mathrm{sub}} \subseteq T(DBM), v_{i} \in [a,b], a = -DBM[0,i], b = DBM[i,0]\)), followed by a Cl and a sequence of resets of a random subset of clocks to values that are either random (within bounds) if non-zero resets are allowed, or 0 otherwise. The generation of sequences of the newly active location state is identical to the process described for the initial location state. Note that we restrict infinite intervals (i.e., constraint intervals \([a,\infty )\) or the reset value interval \([0, \infty )\)) to finite ones during value choice (i.e., \([a,a+c_{1}]\) and \([0, c_{2}]\), respectively, for some constants \(c_{1}, c_{2} \in {\mathbb {N}}_{0}\)).
9 Empirical evaluation
Using the described implementation, we evaluate the presented approaches for the O-phase and C-phase. All experiments were executed on an Ubuntu 18.04 LTS system with AMD Ryzen 7 2700X eight-core CPU and 16GB RAM. Overall, we perform three types of experiments, by which we compare:
-
1.
The overall state construction sequence lengths of the trivial, Rinast, and our OC approach, which confirms that in contrast with the former two, our approach generates bounded sequences over time in all tested cases.
-
2.
The constraint sequence lengths of the C-phase approaches C(FCS), C(MCS), and C(RCS), showing that the C(MCS) and C(RCS) approaches reduce the sequence lengths compared to the C(FCS) approach.
-
3.
The construction times of the O-phase and C-phase approaches.
We apply these experiments to two types of data:
-
1.
A test suite composed of 6 Uppaal demo models and 2 case study models, from which we derive DBM operation sequences during ongoing execution.
-
2.
1000 randomly generated operation sequences (per experiment), reflecting the general sequence structure of execution traces in a TA (see Sect. 7 and Sect. 8.1), as a stress test for validation of the model experiment insights.
The main parameters of the experiments are the model size, the number of clocks, and the observed sequence length.
Our experiment model suite consists of 8 models in total, among which the 6 models 2doors, bridge, fischer, fischer-symmetry, train-gate, and train-gate-orig are the complete set of cyclic, deadlock-free models of the demo model suite of standard Uppaal (i.e., without extensions such as Uppaal SMC), and csmacd2 [19] and tdma [26] were developed in case studies. Figure 13 gives an overview of their characteristics. The suite contains models with different amounts of locations (10–100), edges (21–217), and clocks (3–10). For each model, we execute 1000 simulation runs over 100 transitions, and calculate the minimum, average, and maximum of sequence lengths and construction times over all runs at each individual simulation step.
Applying the approaches to the test suite gives the results shown in Figs. 14 and 15, as well as the data table as shown in Fig. 20 provided in appendix 1, which shows the construction sequence lengths after 1, 10, 50, and 100 executed transitions during model simulation for all Uppaal models. For 3 selected models of the test suite (2doors, bridge, and csmacd2), the graphs in Fig. 14 show the state construction sequence lengths of the trivial, Rinast, and OC approach for a simulation up to 50 steps, together with the calculated bounds of the OC approach. Finally, Fig. 15 shows the total construction sequence generation and application time required for all 8 Uppaal models on each step during simulation.
Applying the approaches to random DBM operation sequences based on a range of different numbers of clocks and sequence lengths gives the results shown in Figs. 16, 17, 18, and 19. For a fixed number of 5 clocks, Figs. 16 and 18 show the ranges of reduced lengths and construction times, respectively, for different O-phase and C-phase approaches applied to different lengths of random input sequences (50–500 operations). Figures 17 and 19 show the lengths of state construction sequences derived by the OC approach variants and construction times, respectively, from fixed-length random sequences (100 operations) based on different numbers of clocks (1–10 clocks).
9.1 Evaluation
The model-based experiments show that, as expected for all models, the sequences of the trivial approach are not bounded, and grow linearly over time (cf. Figure 20). The approach by Rinast produces bounded sequences for all models except for bridge, which has a global clock that is never reset, and thus, never re-visits any reached state during simulation. Our approach generates bounded sequences in all cases, with lengths that are generally shorter than the other two approaches in the long run (e.g., 26 operations for O(DBM) + C(FCS) for bridge, compared to 212 operations of trivial).
Figure 14 underlines these results. It shows that at an (early) point during simulation (for the three models between 8 and 28 steps), the sequence lengths of the trivial approach outgrow the lengths of our OC approach. For csmacd2, we observe that the Rinast approach performs best, as Reset operations overwrite the clock values on almost every edge in the model. Furthermore, we see that the actual sequence lengths of our approach lie well below the theoretically calculated bounds (dashed lines) for the most part. These properties also hold for the remaining models.
As last experiment applied to the test suite, Fig. 15 shows that the construction times lie in a real-time feasible range; during the experiments, below 50 milliseconds were required for most constructions. Only for very few outliers, especially in the first steps of fischer-symmetry (outside of the plotted range), the construction time exceeds 1 second, with averages still below 1 second. In the regular case, it is possible to restore a model state 2–20 times within a second.
The experiments on generated DBM operation sequences validate the results of the test suite in a systematic manner, and yield the following results: The construction sequence lengths lie in constant ranges for growing input sequence lengths (Fig. 16). With increasing numbers of clocks (Fig. 17), the construction sequence lengths grow linearly for the O-phase and quadratically for the C-phase, both as expected from Theorem 1. Furthermore, we see that the MCS and RCS sequence lengths always lie below the FCS sequence length, and the C(RCS) approach leads to sequences that are \(\sim 25\%\) shorter compared to the C(MCS) approach. In terms of construction times for growing input sequences (Fig. 18), the random sequence experiments confirm that for both O-phase and C-phase the required times stay constant, except for O(SEQ); the latter is expected as O(SEQ) gets the complete sequence as a whole in this experiment, in contrast with the step-wise data increments of the model experiments, so that in the worst case, the full input sequence needs to be searched. From Fig. 19, we see that increasing the number of clocks results in constant times for O(DBM) and non-polynomial times for O(SEQ) (cf. Sect. 5.3) in the O-phase, and in the C-phase, the times grow quadratically for C(FCS), cubically for C(MCS), and non-polynomial for C(RCS) (cf. Sect. 6.4). C(RCS), however, switches to cubic growth similar to C(MCS) once the number of clocks leads to permutation counts that exceed the predefined limit (cf. Sect. 8).
Overall, we can conclude that the new approach allows generating length-bounded sequences throughout the complete model simulation, and does so within real-time capable time frames.
10 Conclusion and future work
In this article, we introduced and implemented multiple approaches to derive bounded-length operation sequences to restore given DBM states in timed automata. We found out that the complexity of the individual approach variants either only depends on the (fixed) amount of clocks in a system (i.e., for O(DBM), C(FCS), C(MCS), and C(RCS)) or allows the formulation of alternative versions (i.e., for O(SEQ)) which process operations on the fly, making them suitable for use in online model checking contexts. The experiments revealed that early during simulation (between 8 and 28 steps for the test model suite), the sequence lengths of the OC approaches become (and remain) shorter than the lengths of the trivial approach and—except for one model—of the Rinast approach as well.
In future versions, the sequence lengths could be further shortened by an extension of our approach that handles short sections in which not all clocks have been reset already, or by a hybrid approach that selects the minimum sequence of the trivial and our OC approach. Furthermore, more efficient algorithms may be used for the graph-based search problems of O(DBM) and C(RCS), so that the approach becomes applicable for systems with high amounts of clocks. The insights on overapproximating and constraining sequences may be used for model checking routines, e.g., for time efficient falsification of safety properties, and deserve further investigation.
Availability of data and material
The models 2doors, bridge, train-gate, train-gate-orig, fischer, and fischer-symmetry are part of the demo model suite of Uppaal available at https://www.uppaal.org/. The models csmacd2 [19] and tdma [26] were developed in case studies. All other experimental data were programmatically generated by the authors via the experiments linked under Code availability.
Code availability
The project implementation is open source under MIT license. The base Uppyyl simulator is available at https://github.com/S-Lehmann/uppyyl-simulator, the Uppyyl state constructor is available at https://github.com/S-Lehmann/uppyyl-state-constructor, and the examples and experiments covered in this article are altogether available at https://github.com/S-Lehmann/uppyyl-state-constructor-experiments.
References
Abdelli, A.: Improving the construction of the DBM over approximation of the state space of real-time preemptive systems. Acta Cybern. 20, 347–384 (2012)
Aho, A.V., Garey, M.R., Ullman, J.D.: The transitive reduction of a directed graph. SIAM J. Comput. 1(2), 131–137 (1972)
André, É., Arcaini, P., Gargantini, A., Radavelli, M.: Repairing timed automata clock guards through abstraction and testing. In: Tests and Proofs, pp. 129–146 (2019)
Audemard, G., Cimatti, A., Kornilowicz, A., Sebastiani, R.: Bounded model checking for timed systems. In: Formal Techniques for Networked and Distributed Sytems—FORTE 2002, pp. 243–259 (2002)
Behrmann, G., Bengtsson, J., David, A., Larsen, K.G., Pettersson, P., Yi, W.: Uppaal implementation secrets. In: Formal Techniques in Real-Time and Fault-Tolerant Systems, pp. 3–22 (2002)
Behrmann, G., Bouyer, P., Larsen, K.G., Pelánek, R.: Lower and upper bounds in zone based abstractions of timed automata. In: Tools and Algorithms for the Construction and Analysis of Systems, pp. 312–326 (2004)
Behrmann, G., David, A., Larsen, K.G.: A tutorial on Uppaal 4.0 (2006)
Bengtsson, J.: Clocks, dbms and states in timed systems. Ph.D. thesis, Uppsala University (2002)
Bücker, H.M., Petera, M., Vehreschild, A.: Code optimization techniques in source transformations for interpreted languages. In: Advances in Automatic Differentiation, pp. 223–233 (2008)
Clarke, E., Biere, A., Raimi, R., Zhu, Y.: Bounded model checking using satisfiability solving. Formal Methods Syst. Des. 19, 7–34 (2001)
David, A.: Uppaal DBM library programmer’s reference (2006)
Dubois, D., Fargier, H., Prade, H.: Possibility theory in constraint satisfaction problems: Handling priority, preference and uncertainty. Appl. Intell. 6, 287–309 (1996)
Ehlers, R., Fass, D., Gerke, M., Peter, H.: Fully symbolic timed model checking using constraint matrix diagrams. In: 2010 31st IEEE Real-Time Systems Symposium, pp. 360–371 (2010)
Evangelista, S., Pradat-Peyre, J.F.: Memory efficient state space storage in explicit software model checking. In: Model Checking Software, pp. 43–57 (2005)
Fages, F., Rizk, A.: From model-checking to temporal logic constraint solving. In: Principles and Practice of Constraint Programming—CP 2009, pp. 319–334 (2009)
Hertzberg, J., Güsgen, H.W., Vo\(\beta \), A., Fidelak, M., Vo\(\beta \), H.: Relaxing constraint networks to resolve inconsistencies. In: Künstliche Intelligenz, pp. 61–65 (1988)
Huang, Y., Kintala, C., Kolettis, N., Fulton, N.D.: Software rejuvenation: analysis, module and applications. In: Twenty-Fifth International Symposium on Fault-Tolerant Computing. Digest of Papers, pp. 381–390 (1995)
Jagtap, P., Abdi, F., Rungger, M., Zamani, M., Caccamo, M.: Software fault tolerance for cyber-physical systems via full system restart. ACM Trans. Cyber-Phys. Syst. 4(4), 1–20 (2020)
Jensen, H., Larsen, K., Skou, A.: Modelling and analysis of a collision avoidance protocol using SPIN and UPPAAL. BRICS Rep. Ser. 3(24), 1–20 (1996)
Jonas Rinast: OMC framework. https://www.tuhh.de/sts/research/model-checking-abstract-interpretation/online-model-checking.html
Kaplan, S.F., Smaragdakis, Y., Wilson, P.R.: Trace reduction for virtual memory simulations. Tech. rep. (1998)
Kong, F., Xu, M., Weimer, J., Sokolsky, O., Lee, I.: Cyber-physical system checkpointing and recovery. In: 2018 ACM/IEEE 9th International Conference on Cyber-Physical Systems (ICCPS), pp. 22–31 (2018)
Larsen, K.G., Larsson, F., Pettersson, P., Yi, W.: Efficient verification of real-time systems: compact data structure and state-space reduction. In: Proceedings Real-Time Systems Symposium, pp. 14–24 (1997)
Larsen, K.G., Pearson, J., Weise, C., Yi, W.: Clock difference diagrams. Nordic J. Comput. 6(3), 271–298 (1999)
Liu, Y., Leangsuksun, C., Song, H., Scott, S.L.: Reliability-aware checkpoint/restart scheme: a performability trade-off. In: 2005 IEEE International Conference on Cluster Computing, pp. 1–8 (2005)
Lonn, H., Pettersson, P.: Formal verification of a TDMA protocol start-up mechanism. In: Proceedings Pacific Rim International Symposium on Fault-Tolerant Systems, pp. 235–242 (1997)
Makowsky, J.A., Ravve, E.V.: Incremental model checking for decomposable structures. In: Mathematical Foundations of Computer Science 1995, pp. 540–551 (1995)
Mohan, C.: A cost-effective method for providing improved data availability during DBMS restart recovery after a failure. In: Proceedings of the 19th International Conference on Very Large Data Bases, VLDB ’93, pp. 368–379 (1993)
Pettersson, P.: Modelling and verification of real-time systems using timed automata: Theory and practice. Ph.D. thesis, Department of Computer Systems, Uppsala University (1999)
Rinast, J.: An online model-checking framework for timed automata. Ph.D. thesis, Hamburg University of Technology (2015)
Rinast, J., Schupp, S., Gollmann, D.: State space reconstruction in UPPAAL: an algorithm and its proof. Int. J. Adv. Syst. Meas. 7(1–2), 91–102 (2014)
Salah, R.B., Bozga, M., Maler, O.: On interleaving in timed automata. In: CONCUR 2006—Concurrency Theory, pp. 465–476 (2006)
Salehi, M., Khavari Tavana, M., Rehman, S., Shafique, M., Ejlali, A., Henkel, J.: Two-state checkpointing for energy-efficient fault tolerance in hard real-time systems. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 24(7), 2426–2437 (2016)
Sascha Lehmann: Uppyyl simulator. https://github.com/S-Lehmann/uppyyl-simulator
Sascha Lehmann: Uppyyl state constructor. https://github.com/S-Lehmann/uppyyl-state-constructor
Sascha Lehmann: Uppyyl state constructor experiments. https://github.com/S-Lehmann/uppyyl-state-constructor-experiments
Sorea, M.: Bounded model checking for timed automata. Electron. Notes Theor. Comput. Sci. 68(5), 116–134 (2003)
Sorin, D.J., Martin, M.M.K., Hill, M.D., Wood, D.A.: Safetynet: improving the availability of shared memory multiprocessors with global checkpoint/recovery. In: Proceedings 29th Annual International Symposium on Computer Architecture, pp. 123–134 (2002)
Zhao, Y., Rammig, F.: Online model checking for dependable real-time systems. In: 2012 IEEE 15th International Symposium on Object/Component/Service-Oriented Real-Time Distributed Computing, pp. 154–161 (2012)
Ziv, A., Bruck, J.: An on-line algorithm for checkpoint placement. IEEE Trans. Comput. 46(9), 976–985 (1997)
Acknowledgements
We thank the anonymous reviewers who spotted a serious flaw in our argumentation on the removal of operations and who provided numerous helpful hints that improved the readability and accessibility of the article.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Model-based experiments: detailed data table
Model-based experiments: detailed data table
See Fig. 20.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lehmann, S., Schupp, S. Bounded DBM-based clock state construction for timed automata in Uppaal. Int J Softw Tools Technol Transfer 25, 19–47 (2023). https://doi.org/10.1007/s10009-022-00667-x
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10009-022-00667-x






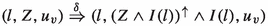
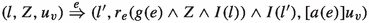 if
if 

















