The review of advances in interfacial electrochemistry in Estonia: electrochemical double layer and adsorption studies for the development of electrochemical devices

Abstract

The electrochemistry nowadays has many faces and challenges. Although the focus has shifted from fundamental electrochemistry to applied electrochemistry, one needs to acknowledge that it is impossible to develop and design novel green energy transition devices without a comprehensive understanding of the electrochemical processes at the electrode and electrolyte interface that define the performance mechanisms. The review gives an overview of the systematic research in the field of electrochemistry in Estonia which reflects on the excellent collaboration between fundamental and applied electrochemistry.

Introduction

The chemical composition and crystallographic structure of electrodes, as well as the chemical composition and dielectric characteristics of electrolytes, have a remarkable influence on the electrical double layer (EDL) characteristics, adsorption kinetics of organic compounds and ions, faradaic processes of electroreduction of oxygen, complex cations and anions, and on the fuel oxidation kinetics. The latter has been systematically studied at the University of Tartu since 1990 [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. Detailed theoretical analyses and experimental results have been discussed based on previously published models [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34].

The current results of the Tartu electrochemistry working group are based on the fundamental studies at solid drop bismuth electrodes (started in 1965) [35] and at single-crystal Bi(hkl) facets (started in 1974) [36, 37]. Therefore, the pioneering ideas of Grahame, Frumking, and Trasatti have been all applied for the development of fundamental electrochemistry at the University of Tartu [1,2,3,4,5,6,7,8,9,10,11,12, 20,21,22,23,24,25,26,27,28, 36, 37]. The role of the potential drop in the electrode surface layer, obtained by the electronic characteristics of metal or carbon electrodes, has been discussed in [11, 12, 33, 38,39,40,41,42,43]. Systematic analysis of experimental data indicates that the electronic characteristics of the sp-metals and carbon electrodes (effective mass and concentration of effective charge carriers, dielectric constant, Fermi energy levels work function dependence of crystallographic structure and orientation, etc.) [1, 2, 9, 11, 38,39,40,41,42,43] can have a more significant role on the EDL structure (including interfacial capacitance values) and Gibbs adsorption and Gibbs free energy values than the solvent (dielectric constant, dipole moment, etc.) or anion solvation/adsorption characteristics [5,6,7,8, 13]. Additionally, the EDL structure has been simulated by density functional theory (DFT) and molecular dynamics (MD) methods [44,45,46,47,48,49,50,51,52].

The influence of surface roughness on the EDL characteristics [53, 54] has been analysed based on models developed by Daikin et al. [55,56,57]. It was demonstrated that the surface roughness values established from electrochemical impedance spectroscopy (EIS) data depend on the electrode potential (surface charge density), electrolyte concentration (Debye screening length), and temperature. In addition, the surface roughness depends on the electrode’s crystallographic and electronic structure (Fermi energy differences), and the difference in work function values for different crystallographic planes exposed on the rough polycrystalline surface [1, 2, 53,54,55,56,57].

EDL and adsorption studies have been conducted on Bi(hkl), Sb(hkl), Cd(hklf), and C(0001) single-crystal electrodes [2, 9,10,11,12, 44, 45, 53, 54, 58,59,60,61,62,63,64,65,66], as well as on porous carbon electrodes [7, 44, 45, 53, 54, 67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85]. Gibbs adsorption and Frumkin molecular interaction coefficient values depend remarkably on the crystallographic structure of the electrode, the chemical nature of electrode metal and electronic parameters, solvent chemical composition, and organic molecule characteristics. This was explained by the different solvation energies of the metal surface, organic molecules and solvent polarisability, and electrode potential, i.e., surface charge density applied. Therefore, the electrode metallic characteristics and crystallographic structure play a critical role in the density and geometrical structure of the adsorbed molecular layers formed, i.e., calculated Gibbs adsorption values.

A detailed comparison of specific adsorption at metal Bi(hkl), Sb(hkl), and Cd(0001) electrodes, glassy carbon, highly oriented pyrolytic graphite basal plane C(0001), graphene electrodes, and micro-mesoporous (MMP) carbons with high surface area will be given [25,26,27,28,29,30,31,32]. It was found that the influence of the solvent properties on the adsorption kinetics of iodide, bromide, and chloride and Gibbs energy of adsorption can most clearly be established using simple single-crystal plane | surface-active electrolyte systems, including 1-ethyl-3-methylimidazolium tetrafluoroborate (EMImBF₄) with additions of 1-ethyl-3-methylimidazolium chloride (EMImCl), 1-ethyl-3-methylimidazolium bromide (EMImBr), and 1-ethyl-3-methylimidazolium iodide (EMImI). It should be noted that surface pre-treatment processes hugely influence the EDL, adsorption kinetics, and faradaic reaction kinetics.

The fundamental knowledge collected has been applied for the development of very high energy and power density electrical double layer capacitors (EDLCs) [7, 68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89] prepared by applying the sol–gel method for syntheses of very mesoporous carbons [81, 90, 91], hybrid superacpacitors (HSCs), and Li⁺- and Na⁺-ion batteries (LIBs and SIBs) [92,93,94,95,96,97,98]. It should be stressed that the porous structure (hierarchical porosity) of metal and complex oxide electrodes, but especially of the carbon electrodes, has a large influence on the limiting series capacitance (C_s), characteristic adsorption time constant (t_char), Gibbs adsorption and adsorption free energy, and on the power density (P) values. In order to widen the ideal polarisability region, ionic liquids (ILs) with variable chemical compositions have been studied [60,61,62,63,64,65, 99,100,101,102,103,104,105,106,107,108,109,110]. Systematic EIS studies of electrodes in aqueous and non-aqueous electrolytes, ILs and IL mixtures containing surface-inactive ions and surface-active anions and cations, and some additions of organic solvents [60, 62,63,64,65, 99,100,101,102,103,104,105,106,107,108,109] demonstrate a high correlation with electrolytes based on non-aqueous solvents with additions of specifically adsorbing, so-called surface-active, anions and physically adsorbing organic compounds. The role of electrode potential on the region of ideal polarisability has been demonstrated by in situ Fourier transform infrared (FTIR), Raman, EIS, and synchrotron beam–based X-ray photoelectron spectroscopy (XPS) studies [5, 65, 101, 107,108,109,110,111,112,113,114,115]. Electrochemical blocking of electrodes under high overpotentials due to the electropolymerisation of active organic compounds has been demonstrated, and patents have been received [116]. This effect is significant in avoiding overcharging EDLC, HSC, LIBs, and SIBs.

The influence of the polymer membrane characteristics on EDLCs, HSCs, LIBs, and SIBs has been studied by Tõnurist (Liivand) et al. [99, 117, 118]. It was demonstrated that the power density, as well as energy density of EDLCs completed with various self-made polyvinylidene membranes using the electrospinning method [119,120,121,122,123], depends very strongly on the electrolyte membrane characteristics (on the meso-macroporosity, thickness, pore size distribution, etc.), especially in solvents with high viscosity (including ILs).

The carbide-derived carbons (CDCs), such as Mo₂C-derived hierarchically porous carbon with an optimal ratio of micro- and mesopore volumes, have been used for the fabrication of artificial switches/muscles [124,125,126]. The quickest relaxation times have been established for highly mesoporous carbon–based switches [124,125,126,127]. The carbon materials synthesised have been studied by novel in situ methods, including small angle neutron scattering (SANS), quasielastic (QENS), and inelastic (INS) neutron scattering methods, wide-angle X-ray diffraction, and other synchrotron beam based and traditional gas adsorption methods [8, 128,129,130,131,132,133,134]. It was found that for hydrogen storage, very microporous carbon materials can be applied. The same tendency is valid for CH₄ storage [133,134,135,136].

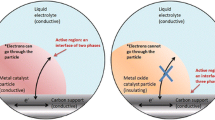
The Faradaic processes at MMP carbon electrodes activated with Pt, Pt-Ru, Pt-Ir, Pt-CeO₂, Pt-Pr₆O₁₁, and d-metal = nitrogen nanoclusters (Fe = N₂, Co = N₂, FeCo = N₂) activated catalysts depend exceptionally strongly on the carbon support specific surface area, mesopore volume ratio to micropore volume, and pore size distribution function of carbon support and to surprisingly large extent on the electrical conductivity of powder under application [4, 5, 137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170].

Solid oxide materials for solid oxide fuel cells (SOFC) and electrolysers [66, 171,172,173,174,175,176,177,178,179,180], including complex perovskite oxides, Ni–cermet anodes, and fluoride-type electrolytes, have been synthesised and tested for solid oxide fuel cells and electrolysers by Nurk, Kivi, Lillmaa, Korjus, Maide, and Heinsaar since 2001 [181,182,183,184,185,186,187,188,189,190,191,192,193,194,195,196,197,198,199,200,201,202,203,204,205,206,207,208,209,210,211,212,213]. Different complex oxide electrode synthesis methods have been applied, starting from the solid oxide high-temperature sintering method.

Electrical double layer structure at single-crystal metal and carbon electrodes

The electrical double layer structure at different electrodes has been studied in various electrolytes such as H₂O, acetonitrile (ACN), ethanol, methanol, propylene carbonate (PC), gamma butyrolactone (GBL), ethylene carbonate (EC), and dimethyl carbonate (DMC) [36, 59, 214,215,216,217,218,219,220]. For that purpose, various methods such as cyclic voltammetry (CV), EIS, in situ scanning tunnelling microscopy (STM) and atomic force microscopy (AFM), in situ FTIR and Raman as well as operando synchrotron radiation beam–based photoelectron (SR-XPS), and SANS have been applied. Typically, the CV method is employed first when studying the systems mentioned above to determine their ideal polarisability range. It was found that the region of ideal polarisability is narrow for Cd(hklf) and very wide for C(0001) and graphene electrodes. The series capacitance, electrode potential curves (C vs E curves) calculated from Nyquist complex plane (− Z”, Z′) plots, given in Fig. 1, show that the interfacial properties of electrode | H₂O and electrode | non-aqueous electrolyte solution depend on the metal electronic characteristics and used solvent chemical composition. The series capacitance can be divided into the inner layer (C_i) and outer layer (C_d) capacitances, connected in series:

Fig. 1

a Series capacitance, electrode potential curves (C vs E curves); b inner capacitance, electrode potential curves (C_i vs E curves) for Bi(111) electrode in 0.1 M LiClO₄ solution in different solvents (given in the figure) [5, 215,216,217,218, 221]

$$\begin{array}{c}\frac{1}{C}=\frac{1}{{C}_{\mathrm{i}}}+\frac{1}{{C}_{\mathrm{d}}}.\end{array}$$

(1)

In 1980–1990s [1, 2, 11, 12, 21, 38,39,40,41,42,43, 58, 59], it was demonstrated that C_i can be represented as:

$$\begin{array}{c}\frac{1}{{C}_{\mathrm{i}}}=\frac{1}{{C}_{\mathrm{m}}}+\frac{1}{{C}_{\mathrm{dip}}}+\frac{1}{{C}_{\mathrm{H}}},\end{array}$$

(2)

where C_m is the capacitance of the metal or thin surface film, C_dip is the solvent layer capacitance, and C_H is the Helmholtz capacitance.

The influence of electrode material on the interfacial capacitance has been demonstrated by Oll et al. [62]. In the given study, very low C_s values have been measured for ionic liquid–based systems (Fig. 2), increasing from C(0001) (non-metallic electrode) towards Au, known as an ideal electronic conductor. For a semi-metallic Bi, the moderate C_s values, similar to Pb, have been calculated. It should be stressed that for Bi, Pb, Pt, and Au, the high-vacuum electromagnetic deposition method of electrode materials has been used to avoid any chemical contamination of surfaces during the chemical or electrochemical polishing steps. Furthermore, it can be seen how the crystallographic structure of the carbon electrode influences the C_s values. A very sharp capacitance minimum can be seen for a very high-quality graphene electrode and C(0001). This capacitance minimum is mainly caused by the potential drop inside the graphene and C(0001) surface layer due to the very low concentration of charge carriers in the electrode surface layer [2, 58, 222], which results in low C_m. Oll et al. also showed that there is no hysteresis of C_s vs E curves that is visible in the case of amorphous carbon electrodes. It is very interesting that the potential of capacitance minimum somewhat depends on the carbon electrode under study, but overlapping E_min values can be seen for graphene and partially graphitised porous carbon synthesised from TiC using chlorination method and further cleaned during high-temperature (800 °C for 4 h) hydrogen reduction step. Surprisingly, there is no capacitance minimum in the C_s vs E curve for amorphous carbon electrode, explained by the non-ideal metal phase structure and slow kinetics of formation of EDL at the micro-mesoporous surface.

Fig. 2

C vs E dependences for different electrode materials measured in EMImBF₄ [62]

In addition to experimental investigations, numerous computational studies have been conducted to study the electrode | ionic liquid EDL structure and its properties [46,47,48,49,50,51,52, 223,224,225,226]. Followingly, these studies have allowed investigation of the adsorption of ionic liquid ions on the electrode’s surface, which is experimentally challenging, as well as the influence of the electrode’s potential on the EDL structure. For instance, in the case of Bi(111) | ionic liquid interface, the DFT calculations allowed to reason the difference between the measured capacitance of EMImBF₄ and 1-butyl-4-methylpyridinium tetrafluoroborate (BMPyBF₄) by estimating the optimal distance between the electrode’s surface and ionic liquid ions, which are related to the C_H [227]. Under intensive scrutiny has been the computational estimation of C vs E dependence, as it can be determined both experimentally using EIS and computationally. Numerous aspects of C vs E dependence and capacitance-structure dependence at the metal | ionic liquid interface have been investigated by Ivaništšev et al. [46, 47, 223,224,225,226]. Using constant field MD simulations, the occurrence of aforementioned capacitance hysteresis has been reasoned with the formation of different ionic liquids interfacial structures, which need overpotential to transition from one structure to another [50]. The impact of the surface charge plane position at Au(hkl) | ionic liquid interfaces has been highlighted by Voroshylova et al. by showing that a simple correction of computational data significantly improves the agreement with the experimental results [48]. Furthermore, a recent study showed that the peaks in a C vs E curve arise due to the restructuring of the ionic liquid near the electrode’s surface [51]. The effect of temperature and quantum capacitance (i.e., C_m) on the C vs E dependence of graphene | ionic liquid interface has been studied by Ers et al. [49, 52], showing that the quantum capacitance has a significant impact on the overall interfacial capacitance. In contrast, the temperature has a minor effect on the interfacial capacitance near the potential of zero charge (pzc) when the quantum capacitance is very low, as shown in Fig. 3b.

Fig. 3

a The structures of EMImBF₄ ionic pair on Bi(111) surface together with measured distances [227]. b The C vs E curves for graphene | EMImBF₄ obtained from experimental measurements [62] and using molecular dynamics simulations at temperatures 27 °C and 177 °C [52]

Adsorption of organic compounds from H₂O and IL electrolytes

The adsorption of organic compounds at Bi(hkl), Sb(hkl), Cd(hklf), and C(0001) electrodes has been studied mainly by EIS and in situ STM and AFM methods [228,229,230,231,232,233,234,235,236,237,238,239,240,241,242]. The data collected for the adsorption of aliphatic alcohols, cyclohexanol, cyclohexanone, and cyclohexane carboxylic acid at Bi(hkl), Sb(111), and Cd(0001) facets have been discussed in detail in Lust et al. [13]. It was concluded that the Gibbs adsorption energy increases from Bi(111) to Bi(011) facet and from Bi(111) to Sb(111). The small positive calculated formal charge transfer coefficient values (from 0 to 0.09) characterise the substitution of water clusters, consisting of two or three molecules and a small dipole contribution of the functional group of adsorbate, which is directed towards the solution. Additionally, it was found that the organic compound adsorption activity is lowest at Cd(0001) and highest at Sb(111) facet [13, 228,229,230,231,232, 240,241,242]. Thus, the H₂O adsorption activity decreases from Cd(0001) to Sb(111) [1, 2].

The adsorption behaviour of 2,2′-bipyridine (2,2′-BP) and 4,4′-bipyridine (4,4′-BP) molecules has been investigated by in situ STM method [237,238,239,240,241]. For 2,2′-BP and 4,4′-BP, the compact adsorption layer forms, which has been visualised. The in situ STM data, given in Fig. 4, show the highly organised molecular rows of 4,4′-BP at various electrodes together with the models of formed layers. Interestingly, these rows’ configurations depend on the electrode’s crystal structure and metallic properties.

Fig. 4

In situ STM images of 4,4′-bipyridine monolayers together with proposed packing models on a Bi(111), b Sb(111), and c Cd(0001) single-crystal electrode [239, 240, 242]

It should be stressed that the atomic level adsorption layer structure of 4,4′-BP depends on the concentration of surface-inactive electrolyte [239]. With the increase of ionic strength, the Gibbs adsorption of 4,4′-BP increases in agreement with data for other organic molecules’ adsorption at metal electrodes [13]. Interestingly, recently, Pikma et al. showed that in an ionic liquid environment, the adsorption of 4,4′-BP takes place in two distinctive self-assembled layers, one on top of the other, not just in a monolayer [241].

Additionally, the adsorption of camphor and thiourea was investigated on the Bi(111) surface. Similarly to 4,4′-BP, camphor forms a highly regular adsorbed layer at Bi(111) (Gibbs adsorption 2.3·10⁻¹⁰ mol·cm⁻²) [238]. It is fascinating that, in contrast, the thiourea, exhibiting weak specific chemisorption behaviour at Bi(111), does not form a regular adsorption layer. Surprisingly, there are no adsorbed thiourea molecules at ideally flat monocrystal areas. Instead, the adsorbed molecules can be observed at defect surface areas, i.e., on the step edges of the characteristic triangular steps [234], illustrated in Fig. 5.

Fig. 5

In situ STM image and model highlighting the adsorption of thiourea at the defect surface areas of Bi(111) surface [234]

EIS, Raman, and infrared spectroscopy methods have been used to study the chemical interaction between Bi(hkl) and other sulphur-containing organic compounds [243]. It was identified that the interaction is very strong, and due to chemisorption, a bismuth-thiolate layer forms at the Bi(111) surface.

Adsorption of halide anions at single-crystal Bi(hkl), Sb(111), and Cd(0001)

Specific adsorption of ions from H₂O, non-aqueous, and IL mixture electrolytes at metal and carbon electrodes has been a focus of intensive studies and discussions since the 1960s [1, 2, 5, 20, 22, 24, 25, 33, 60, 62,63,64,65, 99,100,101, 112,113,114, 215,216,217,218, 220, 221, 244,245,246,247,248,249,250,251,252,253,254,255]. Various models (Hurwitz-Parsons [244,245,246], Kolotyrkin et al. [256], Damaskin [257], Palm and Damaskin [258], etc.) and modified isotherms and models [38, 259,260,261,262,263,264,265], including the conception of partial charge transfer, have been developed and tested. It was found that the Frumkin adsorption isotherm can be used for the interpretation of specific adsorption data calculated at fixed potentials [215,216,217,218, 220, 221, 247,248,249,250,251,252,253, 255, 257, 258]. The specific adsorption of halides has been studied by CV, EIS, SR-XPS, and subtractively normalised interfacial Fourier transform infrared spectroscopy (SNIFTIRS), in situ Raman, and in situ STM/AFM methods. It was found that the adsorption of halide anions depends on the single-crystal plane structure, solvent characteristics, and on the anion or cation chemical composition. The anion surface activity increases from Cd(0001) to Sb(hkl) and from F⁻ to I⁻. The halide adsorption is nearly reversible up to C vs E curves peak potentials in agreement with in situ STM data. As for the Bi(111) interface, very stable adsorption superstructures have been observed for I⁻ and Br⁻ containing electrolytes. The contact adsorption of Cl⁻ is more questionable at the Bi(111) interface as only a weak Moire structure of an adlayer has been observed. It is interesting that within a very wide potential region (even over 1 V), the Br⁻ and I⁻ superstructure is stable and drastic reorganisation processes of the electrode surface structure have been observed only at very high negative (desorption of anions) and at very positive potentials, where dissolution/oxidation of Bi(hkl) surface started [5].

The adsorption of halide anion starts at a very negatively charged electrode surface, in agreement with in situ STM and SR-XPS data, and this phenomenon is known as the specific adsorption of anions as it takes place against the electrostatic repulsion forces. Data in Fig. 6 and in Table 1 indicate that the Gibbs adsorption energy is influenced by the solvent chemical composition, and the strongest adsorption of I⁻ takes place from ACN (where the solvation energy of anions is lowest).

Fig. 6

C_s vs E curves for Bi(111) electrode in 0.1 M LiI in different solvents [5]

Table 1 The Gibbs adsorption energy values for I⁻ ions at the Bi and Cd electrodes from different solvents

Surprisingly, it was found that the simple virial isotherm can be applied for the analysis of specific adsorption data from ACN, ethanol (EtOH), methanol (MeOH), PC, and ethyl methyl carbonate (EMC) mixed binary electrolyte solutions with moderate constant ionic strength [12, 59, 215,216,217,218, 220, 221, 247,248,249,250,251,252,253, 255, 258]. According to the Hurwitz–Dutkiewicz-Parsons method [244, 245], charges for specifically adsorbed ions σ₁° can be calculated at constant surface charge density σ or at constant electrode potentials E, according to formulas:

$${\sigma }_{1}=(\frac{F}{RT}){(\frac{\Delta \xi }{ln x})}_{\sigma =const}$$

(3)

$${\sigma }_{1}=(\frac{F}{RT}){(\frac{\Delta \gamma }{ln x})}_{E=const}$$

(4)

where ζ is the Parsons’ function ζ = γ + σE and Δζ = ζ₀ − ζ at constant σ, γ is the specific surface work value, Δγ = γ₀ − γ at constant E, and the parameters with index 0 corresponding to these values in the supporting electrolyte. The most important adsorption characteristic, the Gibbs energy of adsorption − ΔG_A, was obtained by fitting the σ₁ values to the semi-empirical simple virial isotherm [12, 20,21,22, 33, 59, 215,216,217,218, 220, 221, 244,245,246,247,248,249,250,251,252,253, 255].

$$ln (\frac{{\sigma }_{1}}{zxc}) =-\frac{\Delta {G}_{A}}{RT}-\frac{2{{B}_{\mathrm{eff}}\sigma }_{1}}{z}$$

(5)

or to the corrected virial isotherm

$$ln (\frac{{\sigma }_{1}}{zxc}) =-\frac{\Delta {G}_{A}}{RT}-\frac{2{{B}_{\mathrm{eff}}\sigma }_{1}}{z}$$

(6)

with

$${\psi }_{0}=\frac{2RT}{\left|z\right|F}arcsh\left(\frac{\sigma +{\sigma }_{1}}{2A\sqrt{c}}\right)$$

(7)

where z is the charge number of the adsorbed anion (− 1 in the case of I⁻, Br⁻, and Cl⁻ anions), c is the total concentration of electrolyte solution (0.1 M), and B_eff is the second virial coefficient, characterising the mutual repulsion (and size) of the adsorbed ions. Using a simple virial isotherm, the B_eff is an effective parameter because we have neglected the dependence of the diffuse layer potential drop (ψ₀ from σ₁) in isotherm (3) and calculations. However, the B_eff values can be used for very preliminary analysis of the mutual interaction of adsorbed ions from various solvent systems [12, 59, 215,216,217,218, 220, 221, 247,248,249,250,251,252,253, 255, 258], especially at E_min potential (pzc), where the ψ₀ potential drop value is zero and B_eff can have some (comparative) physical meaning. The coinciding σ₁ value, calculated both ways, gives evidence of the self-consistency and correctness of the obtained data. Similar to non-aqueous mixed electrolytes, Damaskin and Palm introduced additional corrections for isotherms [257, 258], but surprisingly deviation of the corrected experimental isotherm from linear correlation increases further. This approximation has been criticised by Vorotyntsev [266], but no final theory has not been developed yet.

The slope of a virial isotherm depends on the electrode metal studied, and for Bi(hkl), not shown for shortness, the slope values are higher if compared with Cd(0001) plane. Thus, B_eff values calculated using uncorrected isotherm can be used only for qualitative analysis of data, assuming that in the same solvent, the ψ₀ effects are comparable for different Bi(hkl) planes.

Systematic analysis of experimental data for Bi and Sb electrodes demonstrates that the ψ₀ potential drop corrections in diffuse layer applied for corrected isotherm (4) are usually strongly overestimated [12, 26, 27, 30, 59, 215,216,217,218, 220, 221, 247,248,249,250,251,252,253, 255, 258]. Only for water-based binary electrolyte systems with constant ionic strength electrolyte systems the diffuse layer potential drop (ψ₀ potential drop) corrections for quantitative analysis of data at Bi(hkl) electrodes can be used [12, 59, 247, 258]. The same effect, i.e., overestimated ψ₀ value, has been observed for analyses of faradic charge transfer processes at Bi(hkl) and Cd(0001) electrodes [267,268,269,270,271,272,273,274,275,276] if the Frumkin slow charge transfer theory [21, 26,27,28, 30, 66, 277,278,279,280,281,282,283], including ψ₀ potential correction, has been applied. Thus, the role of diffuse layer seems to be insignificant for specifically adsorbing anions from non-aqueous electrolytes and nearly contact adsorption of Cl⁻, Br⁻, I⁻, and SCN⁻ anions at single-crystal planes from non-aqueous electrolytes [12, 59, 215,216,217,218, 220, 221, 247,248,249,250,251,252,253, 255, 258], including from ILs and IL mixtures as well as IL with addition of solvent [5, 63,64,65, 101, 107,108,109, 112,113,114], demonstrated using in situ STM [5, 100, 114, 284], infrared spectroscopy [60], and in situ synchrotron beam–based XPS measurements data [109, 110].

This is in agreement with the very weak influence of solvent characteristics (dipole moment, dielectric permittivity, donor–acceptor number, etc.) on the Gibbs adsorption energy, but specifically on the values of formal charge transfer coefficient (so-called electrosorption valency) and effective dipole moment [38, 216,217,218, 220, 247,248,249,250,251,252,253, 259, 262,263,264,265], created at metal | electrolyte interface, being 10 times lower for Bi, Sb, and Cd electrodes, than the dipole moment values calculated for ideal conductor | anion at vacuum interface [12, 26, 27, 30, 59, 215,216,217,218, 220, 221, 247,248,249,250,251,252,253, 255, 258]. Due to the partial charge transfer process being reversible within the moderate potential region at non-ideal metals (Bi, Sb), the adsorption of halide ions is a complicated process, and new systematic studies and detailed comparison of experimental data from various aprotic and technologically important solvents (ACN, EC, PC, EMC, DMC, diethyl carbonate (DEC), GBL) and IL mixtures, potentially applicable in modern energy storage and conversion devices like batteries and EDLCs [215,216,217,218, 250], have a more straightforward direction of studies.

The Gibbs adsorption energy values, given in Table 1, indicate that there are noticeable differences between Cd, Bi(hkl), and Sb(hkl) electrodes with the increasing adsorption activity in the presented order of metals. The most active adsorption for Bi(hkl) has been observed for most reticular density plane Bi(011) plane and very lyophilic C(0001). Adsorption of I⁻ anions (like Br⁻ and Cl⁻ anions) increases in the order of solvents; H₂O < MeOH < EtOH < EC < PC < GBL < ACN, demonstrating that with the decrease of solvation energy of anions, the Gibbs adsorption energy increases.

Data in Fig. 7a show that the C_s depends extremely strongly on the chemical composition of IL under study. Very low capacitance values have been calculated for big anions with high molar volume. The surface structure of Bi(111) and Bi(01 $\overline{1 }$) has shown to be very stable within a wide potential region [114, 285]. Only at moderately negatively charged electrode surface (E =  − 1.6 V vs Fc/Fc⁺ reference electrode) the Moire superstructure has been observed, dependent on the electrode crystallographic structure, surface electrochemical activity, and electrode potential.

Fig. 7

a C_s vs E curves for Bi(111) | IL systems [5]; b C_s vs E curves for Bi(hkl) | EMImOTf systems with specified water content [114]

The capacitance values are very sensitive for water additions in IL. For extremely well-dried 1-ethyl-3-methylimidazolium trifluoromethanesulfonate (EMImOtf), very low capacitance values have been calculated, demonstrated in Fig. 7b. In very well-dried IL, the capacitance values are higher for the Bi(01 $\overline{1 }$) plane and lower for Bi(001), like for H₂O electrolytes. The capacitance values increase noticeably when the H₂O concentration increases. Detailed analysis of EIS data demonstrates that the adsorption of anions is quicker than cations (nearly 1.5 orders), but the series capacitance values are very low for big fluorinated anions (OTf⁻) within all adsorption regions demonstrating slow adsorption kinetics similar for big cations. Nearly ideal capacitive behaviour has been observed from − 1.7 to − 0.6 V vs Fc/Fc⁺.

The specific adsorption of Cl⁻, Br⁻, and I⁻ anions from surface-inactive IL EMImBF₄ mixture has been analysed (Fig. 8). Very similar behaviour as already discussed for H₂O [12, 59], non-aqueous surface-active electrolytes [218, 220, 221, 247,248,249,250,251,252,253, 255] has been established for halide ions + IL electrolytes for Bi(hkl), Sb(111), Cd(0001), and C(0001) planes by Siinor and Siimenson et al. [63, 65, 286, 287]. STM images in Fig. 8 show the well-organised adsorbed layers of I⁻, Br⁻ from EMImBF₄. With the increase of halide anion concentration in surface-inactive electrolyte, the differential capacitance curve shifts towards more negative potentials, but the maximal capacitance values (C_s(max) = 58 μF·cm⁻²) are independent of Br⁻ (or I⁻) additions in surface-inactive IL. The back-integration method of C_s vs E curves has been used to calculate surface charge density values in [5]. Using the given method, very high surface charge densities have been calculated, indicating the high surface activity of halide anions at Bi(hkl) and Sb(111) surface from IL. Therefore, the higher charges for non-aqueous solutions containing specifically adsorbed I⁻ ions have been calculated.

Fig. 8

C_s vs E curves for Bi(111) | IL systems containing specifically adsorbing halide anions, together with in situ STM images of systems containing Br⁻ and I⁻ ions [5, 65, 100]

At very negative potentials, there is no halide adsorption and only with the increase of electrode potential does the specific adsorption start. It is surprising that the I⁻ and Br⁻ adsorption is very intensive, and it takes place already at a highly negatively charged (− 12 or − 10 μC·cm⁻², respectively) surface. It is to be stressed that the adsorption of halides is nearly reversible up to capacitance maximum potentials for Sb(hkl) and Bi(hkl) electrodes. Thus, halide specific adsorption–based pseudocapacitors can be developed for enhanced energy density storage. The in situ STM data show that there are ions at the Bi(111) electrode surface with a regular distance of 0.42 nm between the Br⁻-anion centres. The Cl⁻ adsorption is weak, and only after long-lasting polarisation of Bi(111) at fixed potentials the Moier’s superstructure is formed at the electrode with constant ionic strength.

There is a significant influence of the single-crystal planes and carbon electrode surface crystallographic structure (C(0001), graphene, porous carbon) on the shape of complex plane EIS plots (− Z” vs Z′) and C vs E [7, 63, 65, 68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87, 89, 286,287,288,289,290]. Thus, the surface charge density vs potential curves (σ vs E), established using the back-integration method of C vs E curves, depend very remarkably on the electrode studied. For comprehensive analysis and development of supercapacitors, HSC, LIBs, and SIBs, systematic analysis of data, including analysis of the influence of solvent polarisability, dielectric constant, and viscosity, is inevitable. Specific adsorption of iodide and bromide from non-aqueous surface-inactive electrolyte (E₄NBF₄, E₃MNBF₄, and EM₃NBF₄ in ACN) and from IL systems (EMImBF₄ + EMImI, EMImBF₄ + EMImBr, and EMImBF₄ + EMImCl) at carbon electrodes [63, 65, 284, 286, 287] has been applied for the enhancement of specific energy and power densities of HSC based on MMP carbon or carbon microsphere electrodes.

Electrochemical kinetics at single-crystal electrodes

Thomberg, Jäger, and Härk have studied the electroreduction of [H₃O]⁺ [14, 273] and [S₂O₈]²⁻ at Bi(111) [271] and Cd(0001) [268, 270, 274], as well as (Co[NH₃]₆)³⁺ [269, 272] and Eu³⁺ [275] at Bi(hkl) and Cd(0001) by CV, EIS, and chronoamperometry methods. [Fe(CN)₆]³⁻ anions at Cd(0001) electrode have been studied by Nerut et al. [276]. It was found that the reduction rate depends on the crystallographic structure of the electrode used, as well as on the chemical composition and electronic characteristics of the electrode material (Bi or Cd) studied.

The overvoltage of [H₃O]⁺ electroreduction increases from Bi(111) to Bi(01 $\overline{1 }$) [14, 268,269,270,271, 273,274,275] in the same order as established for the increase of adsorption activity of anions and organic compounds, explained by weaker adsorption of water molecules at Bi(111) and Bi(hkl) as well as weaker chemical adsorption of [H₃O]⁺ on Bi(111) plane compared with Bi(01 $\overline{1 }$). For more chemically active planes, i.e., Bi(01 $\overline{1 }$) and Bi(001), some deviation from Frumkin’s slow discharge theory [26, 277] has been observed. This deviation has been explained by the weak adsorption of reacting compounds at the electrode surface. The given knowledge collected has been used for the development of electrochemical waste water purification systems [291].

The same order of activities has been recognised for [S₂O₈]²⁻ and [Co(NH₃)₆]³⁺ reduction at Bi(hkl). For more hydrophilic Cd(0001), a weaker deviation from Frumkin classical model has been observed. A more pronounced deviation of Bi(hkl) from the classical model [26, 277,278,279,280, 283, 291] can be explained by the semi-metallic character of Bi(hkl) compared with Cd(0001) and Au(hkl) surface planes [278,279,280, 283]. The electroreduction of Eu₂(SO₄)₃ has been studied at Bi(01 $\overline{1 }$) electrode in acidic HClO₄ and H₂SO₄ solutions (at similar pH = 3.0) with additions of LiClO₄ and Na₂SO₄ electrolytes as surface-inactive electrolyte solutions. The kinetics of Eu³⁺ cations depends on the electrode potential applied and on the concentration of the supporting electrolyte.

The systematic analysis of the electroreduction data for Bi(hkl) indicates that similar to the specific adsorption of anions, the diffuse layer potential drop values are overestimated. Therefore, it seems that the centre for charge transfer for real systems is closer to the electrode than that assumed by the classical Frumkin slow discharge model, i.e., ψ₀ potential values are overestimated [14, 268,269,270,271, 273,274,275,276]. The new model developed by Damaskin et al. [30] is in better agreement than the classical ψ₀ correction model. Detailed analysis of EIS data indicates that within the moderate ac frequency region, the system is controlled by an adsorption step. Only mixed kinetic processes occur at very low ac frequencies, i.e., the adsorption and mass-transfer step processes are the rate-limiting steps at Bi(hkl) and Cd(0001) surfaces.

Development of electrical double layer and hybrid supercapacitors

Syntheses and characterisation of micro-mesoporous carbon powders from metal carbides

Carbon electrodes have been systematically studied since 1991 in order to establish the electrical double layer characteristics and pzc values for geometrically rough carbon and glassy carbon electrodes in ACN + (C₂H₅)₄NBF₄ solutions [1, 2]. Experimental EIS data measured at different ac frequencies demonstrated that the surface is geometrically rough, and the capacitance values depend on the glassy carbon and graphite electrode surface treatment methods, i.e., on the surface roughness values of electrodes. Also, the role of half-metal (semi-metallic) surface film properties of glassy carbon and graphite electrodes were analysed [86].

Since 1997, the binary (α-SiC, TiC, VC, B₄C, WC, Mo₂C, Al₄C₃, Cr₃C₂, etc.) [7, 67, 68, 70, 72,73,74,75,76,77,78,79,80,81,82,83, 85, 87] and ternary carbides (Ta₄HfC₅, WTiC₂) [82] have been used for the preparation of MMP carbon electrode powders with hierarchical porous structure. The so-called high-temperature chlorination method has been used for the synthesis of corresponding MMP carbon powders, respectively. The carbon powders were purified by the high-temperature hydrogen treatment step (by applying 750–850 °C for 2–6 h). HCl, CO₂, KOH, and ZnCl₂ or a combined ZnCl₂ + KOH mixture of activators were used for additional activation of C(α-SiC) and other carbon powders [83,84,85].

The carbon materials were analysed using X-ray diffraction spectroscopy (XRD), focused ion beam time-of-flight secondary ion mass spectrometry (FIB-TOF–SIMS), Raman spectroscopy, scanning electron microscopy with energy dispersive X-ray analysis (SEM–EDX), and high-resolution transmission electron microscopy (HR-TEM) combined with electron energy loss spectroscopy (EELS) and selected area electron diffraction spectroscopy (SAED) analysis methods [7, 67, 68, 70, 72,73,74,75,76,77,78,79,80,81,82,83, 85, 87]. The SEM–EDX data show that prepared carbon particles have complicated and variable shapes, containing wrinkled, blocked, and amorphous regions [84]. It is interesting that, for different CDCs, nearly graphitised blocks form between amorphous particles at sintering temperatures lower than 1200 °C. The HR-TEM-SAED-EELS data confirm this conclusion, demonstrating that the ordering of carbon takes place even at T ≥ 900 °C [78,79,80,81,82]. The Raman spectra (l = 514 nm) were fitted with a combination of two Lorentzian and two Gaussian functions for both first-order and second-order Raman scattering regions [8, 70, 72,73,74,75,76,77,78,79,80,81,82,83, 85, 128,129,130,131,132,133,134, 288, 289, 292]. Detailed analysis of spectra indicates that with the increase of the final treatment temperature, the 2D peak and other second-order excitation peaks increased, demonstrating that the graphitisation processes have already started at 900 °C.

The Brunauer–Emmett–Teller (BET) gas adsorption method and Hg intrusion porosimetry methods have been used for detailed porosity analysis [7, 8, 67, 68, 70,71,72,73,74,75,76,77,78,79,80,81,82,83, 85, 87, 128,129,130,131,132,133,134,135,136, 169, 293,294,295]. For BET analyses, N₂, Ar, Kr, CO₂, and H₂ were used as test gases; various fitting methods (non-local density functional theory (NLDFT) and Saieus program integrating different fitting models); different pore models (cylindrical pore, heterogeneous surface, standard slit, and aspect ratio 6) have been used [8, 71, 128,129,130,131,132,133,134,135,136, 169, 293,294,295].

Based on the BET gas adsorption method, the carbon powder micro-mesoporosity characteristics (ratio of micropore (V_micro) to mesopore volume (V_meso), the ratio of micropore surface area (S_micro) to mesopore surface area (S_meso)) are influenced by binary and ternary carbide chemical composition, raw carbide crystallographic structure, and synthesis temperature (Table 2). The X-ray scattering and SANS data show that the nanostructure of C(Mo₂C) prepared at different chlorination temperatures depends on applied T [130, 132]. The specific inner surface area for C(Mo₂C), together with the volume fraction of the pores, increases with the chlorination temperature up to 900 °C, but at higher temperature values (T > 1000 °C), a significant decrease of both parameters takes place. Materials prepared at T = 600 °C or 700 °C are ultramicroporous, having a slit-like or cylindrical pore shape with an average size in the order of 0.6 nm. C(Mo₂C) synthesised at T > 900 °C have pore widths around 1 to 3 nm. Using the wide-angle X-ray scattering (WAXS), it was demonstrated that the pore shape of different CDCs varies, C(α-SiC) (1000 °C) has sphere-like pores (d = 1 nm), C(TiC) (950 °C) has cylinder-like pores, and C(Mo₂C) (1000 °C) has slit-like pores [129]. Thus, the raw CDC chemical composition and crystallographic structure have a significant influence on the geometrical shape of micropores formed. The pore surface roughness decreases with the chlorination temperature as well as with the increase of activation temperature used, established by SANS method results [8, 71, 128,129,130,131,132,133,134].

Table 2 Results of the sorption measurements for the different micro- and mesoporous carbide–derived carbon materials

A more detailed study was conducted using the SANS method, where C(Mo₂C) were synthesised at fixed Cl₂ reaction temperatures of 700, 800, 900, and 1000 °C [130]. Results demonstrated that the shape of prevailing pores depends on the chlorination temperature applied, and there are structural geometry changes at the surface of the porous structure of materials studied. With increasing temperatures (from 700 to 1000 °C), microporous structures of materials change from mixed cylindrical/slit-like to purely slit-like. The observed changes in the geometries, expressed by the increase of the dimensionality parameter from 1.3 to 1.8, empirically correlate with the decrease of disorder between graphitic layers. Thus, the formation of the cylindrical pores can be explained by the curvature of graphitic carbon layers formed at T < 800 °C [130].

A combination of Raman spectroscopy and WAXS methods have been applied for detailed analysis of different CDC carbons synthesised from 6 different carbides at different temperatures (given after carbon powder in brackets) by chlorination and hydrogen cleaning methods from: Mo₂C (600 °C, 700 °C, 800 °C, 900 °C, 1000 °C, 1100 °C), Ta₄HfC₅ (800 °C, 900 °C, 1000 °C, 1100 °C), WTiC₂ (800 °C, 900 °C, 1000 °C, 1100 °C), WC (800 °C, 900 °C, 1000 °C, 1100 °C), TiC (800 °C, 900 °C, 1000 °C, 1100 °C), and VC (500 °C, 600 °C, 700 °C, 800 °C, 900 °C, 1000 °C, 1100 °C) [129]. The 5-peak fit of the Raman spectrum first-order scattering region, suggested by Sadezky et al. [297], obtained the most coherent results. Thus, the influence of the T_syn on the peak shape, i.e., on the structural parameters of the collected results, showed the influence of the precursor carbide structural and chemical composition on the stage of graphitisation at equivalent temperatures at T = 1000 °C [129]. The graphitisation of C(Mo₂C) and C(VC), both synthesised at 1000 °C, was evident from the considerable narrowing of the G-band and from the increase in average graphitic areas stacking size, L_C, values obtained from WAXS data. The use of the ratio of Ad/Ag for the determination of the coherent domain length from Raman spectra based on the Ribeiro-Soares et al. method [298] yielded the most reliable results when compared to the L_a values calculated from WAXS data. The coherent domain length obtained from the Raman spectra was large (4.4 nm) than the average graphene layer extent value, L_a, obtained from WAXS. This discrepancy has been attributed to the number of defects and curvature in the graphene domains in the CDC-derived particles. Thus, this relates to the non-ideal structure of graphitic domains synthesised and formed into C(Mo₂C) and C(VC) at T = 1000 °C. Detailed Raman and WAXS analysis data demonstrated that these methods are complementary to each other, and the simultaneous application of the mentioned methods is of high importance for the characterisation of disordered partially graphitic/non-graphitic carbon materials.

For the development of materials with more advanced mesoporous structures, the sol–gel method was used for the preparation of mesoporous TiC raw powders [90]. After the chlorination and hydrogen cleaning steps, the XRD, Raman, SEM–EDX, XPS, X-ray fluorescence (XRF), HR-TEM, combined SAED and EELS, and BET measurements were conducted. It was established that the mesoporosity of sol–gel prepared carbons is noticeably higher than the corresponding values for C(TiC) derived from industrial carbon powders (Fig. 9). Also, the experimental Nyquist plots show that the EDLCs based on the carbon materials prepared using the sol–gel method have a very wide region of ideal polarisability up to 3.4–3.6 V [41].

Fig. 9

Pore size distribution for commercially available (C(TiC)) and sol–gel prepared TiC derived (C(SgTiC)) carbon electrodes, calculated from combined N₂ and CO₂ adsorption isotherms [90]

Micro-mesoporous carbon materials prepared from glucose, white sugar, and Estonian well-decomposed peat

Fascinating nanospherical carbon materials have been synthesised from glucose, white sugar solutions, and Estonian well-decomposed peat powder [97, 137, 149, 150, 157, 299,300,301,302,303,304], shown in Fig. 10. Highly homogeneous carbon material consisting of nano- and microspheres with diameters nearly 0.9–1.0 μm has been prepared from glucose (C(Glc)), with particle size and shape practically independent of synthesis T (800–1400 °C) [97, 149, 150, 299,300,301,302], different from white sugar–derived carbon (C(WS)) [301], where the diameter of carbon spheres varies from 1 to 4 μm. HR-TEM data show that the surface of C(Glc) is nicely graphitised. It is interesting that the diameter of these C(Glc) nanospheres is independent from the applied activation temperature. Only at very harsh activation conditions with KOH have the nanospheres been destroyed for open meso- and macropores.

Fig. 10

Surface images measured using HR-SEM for various samples (noted in the figure) [97, 137, 149, 150, 157, 299,300,301,302,303,304]

Estonian well-decomposed peat has been used for the preparation of carbon powders (C(EP)) using high-temperature decomposition as well as hydrothermal carbonisation methods [137, 157]. Very well-oriented carbon graphitic areas can be seen in C(EP) material from with Raman spectroscopy, SEM–EDX, and HR-TEM data. For application in EDLCs, proton-exchange membrane fuel cells (PEMFCs), and gas adsorbing devices (mainly H₂ and CH₄), an additional carbon material treatment process at high activation temperatures using KOH or ZnCl₂ has been conducted [305]. Depending on the activation temperature and activation reactant applied, the micro-mesoporous structure has been developed with a specific surface area from 540 up to 2150 m²·g⁻¹. The Raman spectra indicate that some graphitisation (or crystallographic ordering) has started already at 900 °C, 1100 °C, and 1400 °C [3].

Electrochemical results for EDLC and hybrid supercapacitors based on non-aqueous electrolyte solutions

For electrochemical studies, both three-electrode and two-electrode electrochemical setups were applied. The electrodes have been assembled using carbon materials described earlier and the Teflon suspension in H₂O as the binder [7, 67, 68, 70, 72,73,74,75,76,77,78,79,80,81,82,83, 85, 87, 90,91,92,93,94,95,96,97, 137, 149, 150, 157, 299, 300, 302,303,304, 306, 307]. The pastes of electrode materials were roll-pressed into thin carbon films with thicknesses from 60 to 400 μm. Generally, the Al current collectors were deposited onto one side of the roll-pressed film electrodes using the electromagnetic deposition method (in a high vacuum (10⁻⁸ bar)) for good electrical contact. Other times the electrospinning method of carbon layer deposition and followed by isostatic compression has been used for comparison. It should be noted that the influence of the electrode thickness on the energy and power densities is substantial [67]. This phenomenon will be discussed in more detail later, but in the referred works, electrodes with a thickness of 100 μm have been mainly used. The other aspect is that the electrolyte concentration has a significant influence on the electrochemical results. The complex impedance plane plot shape changes with the decrease of electrolyte concentration and the high-frequency series resistance R_s(hf) somewhat increases [86, 87]. Furthermore, the high-frequency polarisation charge transfer (R_ch) resistance (i.e., the wideness of small high-frequency semicircle) and the mass-transfer limited processes resistance (R_D) (wideness of linear area with 45° slope) increases, and the limiting capacitive (at very low ac frequencies) behaviour has been established only at very high series resistance values.

Various non-aqueous solvents (ACN, GBL, PC, DMC, EC, etc.) and mixtures of organic carbonates (EC:DMC; PC:EC; DMC:EC:PC, etc.), as well as ethylacetate, acetone (AC), solutions of Et₄NBF₄, but mainly TEMABF₄ as electrolytes have been used, and the results are displayed in Fig. 11 [69]. It was found that the region of ideal polarisability is very wide for well-dried ACN + TEMABF₄ solution (up to 3.2–3.4 V) for example C(VC) 900 °C [7, 67, 68, 70, 72,73,74,75,76,77,78,79,80,81,82,83, 85, 87, 89,90,91,92]. The electrolyte composition influence of fluorinated organic compounds addition to PC + 1 M Et₃MeNBF₄ mixture has been tested. It was found that the influence of fluoroethylene carbonate on the PC-based solution was weak in the system containing microporous titanium carbide–derived carbon (TiC-CDC) electrodes [307]. The EDLC cell characteristics based on TiC-CDC electrode and 1 M Et₃MeNBF₄ solutions in PC within a very wide temperature region from − 45 to 100 °C have been tested [308]. The results showed that the region of ideal polarisability decreases if T > 80 °C.

Fig. 11

C vs E curves at a cell potential scan rate of 50 mV·s.⁻¹ for the EDLCs in 1.0 M TEMABF₄ in ACN, GBL, AC, and PC [69]

Almost simultaneously with the first publications from the Tartu University [67,68,69,70,71], Gogotsi et al. published a paper where CDC characteristics of micro-mesoporous carbon prepared from Ti₃SiC₂ were discussed [309]. Followingly, numerous papers were published, which investigated the parameters of CDCs, which were pepared from boron carbide [310] and ZrC [311, 312]. One of the first papers by Gogotsi et al. in cooperation with P. Simon was published in 2008 [313] that was pursued by a Nature Materials paper in the same year [314], which focused on the influence of carbon micro-mesoporosity onto gas adsorption characteristics. In 2016, Huang et al. [315] demonstrated that the CDC-based EDLCs can be integrated with silicon-based microelectronic devices. In papers [316, 317], more information analysing CDC characteristics in various conditions have been published. One of the shortcomings in the analysis of numerous papers is that the capacitance values have been calculated from the CVs, which are not corrected by ohmic drop. This results in overestimated capacitance and power density values.

The coworkes (A. Jänes, G. Nurk, P. Möller, E. Lust) and Ph.D students (M. Arulepp, L. Permann, M. Lätt) of the Univesrsity of Tartu were also engaged in Tartu Tehnoloogiad AS from 1997 to 2005. In this company, they established a laboratory and participated in the development of electrochemical background of EDLC studies, characterised the CDC materials in non-aqueous electrolytes, and measured the energy/power density characteristics of assembled supercapacitors. Based on the fundamental knowledge and technical information collected, common papers have been published [67,68,69,70,71,72,73,74,75] and many World and US patent applications have been completed and accepted. Unfortunately at these times, the supercapacitors were too expensive for wide areas technological application. Following the bankruptcy of Tartu Technologies AS at 2009, the supercapacitor development for commercial applications has carried on in Estonia. For example, one of the leading supercapacitor producers in EU, Skeleton Technologies OY has won 2018 SET Awards in “innovative mobility category.”

LiClO₄, NaClO₄, LiBF₄, NaBF₄, LiPF₆, NaPF₆, KBF₄, KPF₆, etc., were used to study the influence of electrolyte chemical composition on the electrical double layer parameters in non-aqueous solutions by analysing cation and anion chemical composition and geometric structure [7, 67, 68, 70, 72,73,74,75,76,77,78,79,80,81,82,83, 86, 87, 92,93,94,95,96,97, 307, 308]. Very noticeable specific adsorption of Cs⁺ cations, as well as weak adsorption of K⁺ and Na⁺ ions, was observed from non-aqueous solutions using the constant current charging–discharging method [94,95,96,97, 307, 308].

For comparison, H₂O-based supercapacitors containing Na₂SO₄, Li₂SO₄, Rb₂SO₄, and LiClO₄, NaClO₄, etc., have been studied [89]. Due to high hydrogen evolution overvoltage at carbon electrodes, the region of ideal polarisability in H₂O is nearly up to 1.6 V for Na₂SO₄ + H₂O. The ideal polarisation region is noticeably narrower for Rb₂SO₄ + H₂O electrolyte due to weak solvation of Rb⁺ cations and specific adsorption of Rb⁺ at carbon electrodes. Some faradic processes started at higher cell potentials E > 1.6 V [89].

For analysis of experimental results, the complex plane plots have been measured and used for the calculation of series capacitance (C_s) and parallel capacitance (C_p) values. If the system is ideally polarisable, then the C_s and C_p are overlapping at low ac frequencies, where there is no dependence of C_p or C_s on f [29, 31]. Only these values have been used as the accurate capacitance values [7, 60,61,62,63,64,65, 67, 68, 70, 72,73,74,75,76,77,78,79,80,81,82,83, 85,86,87, 90,91,92,93,94,95,96,97, 105, 300, 306,307,308] corresponding to limiting Gibbs adsorption values. Collected data show that the C_s values highly depend on the electrode total and meso-microporosity, i.e., on the specific surface area (S_BET) and on the DFT total pore volume values, calculated using the 2D-NLDFT-HS model [3]. The C_s values increase with the gas phase activation using CO₂ up to 10 h, but at longer activations, the noticeable decrease of microporous surface area initiates the decrease of C_s and C_p values. The same tendency is valid for materials that were chemically activated with ZnCl₂ and KOH. However, it should be noted that only optimal activation times for electrode materials increase the energy densities of EDLCs [305].

The characteristic relaxation times have been calculated using the complex power values ($S\left(\omega \right)=P\left(\omega \right)+jQ(\omega )$), where active and reactive power are equal to $P\left(\omega \right)=\frac{\omega {C}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\left(\omega \right)\Delta {E}_{max}^{2}}{2}$ and $Q\left(\omega \right)=-\frac{\omega {C}^{\mathrm{^{\prime}}}\left(\omega \right)\Delta {E}_{max}^{2}}{2}$, respectively [29, 31]. Data in Table 3 show that characteristic relaxation time depends on the electrolyte viscosity increasing from ACN to PC and further to IL. Very short relaxation times have been calculated for mesoporous carbon EDLCs prepared by the sol–gel syntheses method [90, 91, 306].

Table 3 Calculated characteristic relaxation time constants (τ_R) for the different electrolyte-based supercapacitors. MPCC denotes microporous carbon cloth

The energy density vs power density plots (Ragone plots) have been measured using the constant power method [7, 67, 68, 70, 72,73,74,75,76,77,78,79,80,81,82,83, 85, 87, 89,90,91, 306]. The energy density increases in a row of solvents PC < GBL < EC + PC < ACN (Fig. 12), from microporous materials to mesoporous and future to sol–gel derived very mesoporous carbon. The energy and power density depend on the cation’s chemical composition, and it increases in a row of cations: Li⁺  < Na⁺  < K⁺  < Rb⁺  < Cs⁺ [92,93,94,95, 97, 307, 308]. The dependence of energy density on anion composition is more complicated, and with the decrease of cation solvation energy, adsorption activity increases, but for Cs⁺, very slow specific adsorption started decreasing the physical adsorption of electrolyte cations due to the blocking effect of the electrode surface with the chemically bonded cations. This effect is heavily dependent on the solvent used.

Fig. 12

Ragone plots for the EDLCs in 1.0 M TEMABF₄ in ACN, GBL, AN, and PC, highlighting that higher energy and power density can be achieved with other organic solvents than commercially used PC [69]

EDLC in ionic liquids

For the analysis of the influence of IL composition on the region of ideal polarisability, the two-electrode systems have been completed based on various ILs (EMImBF₄, 1-ethyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide (EMImTFSI), 1-ethyl-3-methylimidazolium tetracyanoborate (EMImTCB), 1-ethyl-3-methylimidazolium tris(pentafluoroethyl)trifluorophosphate (EMImFAP), 1-ethyl-3-methylimidazolium thiocyanate (EMImSCN), 1-ethyl-3-methylimidazolium bis(fluorosulfonyl)imide (EMImFSI), etc.), as well as for ILs with the addition of ACN and other solvents [105, 318, 319]. Based on CV and EIS data, the widest region of ideal polarisability was measured for EMImTCB [254] (Fig. 13). It was found that the addition of ACN very slightly decreases (100–200 mV) the region of ideal polarisability compared to pure IL, especially for EMImTCB. EIS data show that in EMImBF₄, nearly ideal capacitive behaviour was established up to 3.2 V and only at higher cell potentials a deviation of the ideal capacitive behaviour (phase angles higher than − 88°) takes place. However, the addition of ACN significantly decreases the characteristic time constant values (more than one order), thus increasing the power densities of EDLC remarkably.

Fig. 13

Cyclic voltammograms for various microporous carbon cloth | IL-based EDLCs (noted in the figure) measured with scan rate 1 mV·s.⁻¹ up to 3.2 V [254]

To analyse the effect of the carbon electrode, EDLCs based on hierarchical micro-mesoporous sol–gel TiC–derived carbon (SgTiC-CDC) electrodes and EMImBF₄ and 1 M TEMABF₄ + ACN as the electrolytes were tested to establish the electrochemical characteristics and region of ideal polarisability. A very wide region of ideal polarisability (up to 3.8 V) can be achieved if the cell potential limit has been shifted by small potential steps (∆E = 0.1 V) from 3.4 to 3.6 V and further to 3.8 V (Fig. 14) [91]. This effect has been explained by the dissolution of most active defect amorphous areas of carbon electrodes during the so-called surface passivation (defect and active surface area dissolution) step. Very high capacitance (energy values) values have been calculated for IL-based cells.

Fig. 14

C vs E curves calculated from cyclic voltammograms at various potentials at a scan rate of 100 mV·s.⁻¹ in EMImBF₄ and TEMABF₄ + ACN electrolytes (noted in the figure) [91]

The EIS revealed that the high-frequency series resistance depends on the electrolyte applied, and the R(hf) values are nearly one order higher for the EMImBF₄-based systems. Additionally, for EMImBF₄, the so-called micro-mesoporous mass-transfer area in the Nyquist plot is three times wider than that for TEMABF₄ + ACN electrolyte-based EDLCs [91]. The Bode phase angle vs log f plots show (Fig. 15a) that the characteristic relaxation frequency is one order longer for IL-based EDLCs. The calculated series resistance values are higher than for ACN-based systems (Fig. 15b). Interestingly, the C_s values for ACN are practically independent of the electrode potential applied if the cell potential is around 3 V, indicating that the limiting Gibbs adsorption values have been established. EMImBF₄-based EDLCs show that only at very high cell potentials (3.8 V) the limiting Gibbs adsorption (C_s independent of ac frequency) has been established.

Fig. 15

a Phase angle (θ) vs ac frequency and b specific series capacitance (C_s) vs ac frequency dependencies for EDLCs completed with C(SgTiC) electrodes in EMImBF₄ and TEMABF₄ + ACN electrolytes (noted in the figure) [91]

Additionally, it has been shown that the micro-mesoporous structure, i.e., the ratio of S_micro/S_meso and V_micro/V_meso, has a remarkable influence on the limiting capacitance values, characteristic time constants, and real power and imaginary power values if the same electrolyte has been tested [91]. Very short characteristic time constant values have been established for two-electrode cells consisting of mainly mesoporous sol–gel method–derived carbon as a working electrode and TEMABF₄ + ACN as an electrolyte. Very long characteristic charging/discharging times were calculated mainly for very microporous α-SiC-derived carbon-based systems. However, the latter systems exhibit high limiting capacitance values and very long characteristic relaxation times, especially in EMImBF₄ [91].

It has been shown that the limiting series and parallel capacitance values are higher for ionic-liquid-based EDLC. Nevertheless, the characteristic time constant values are longer than that for ACN-based EDLCs. Thus, the solvent molecules adsorbed at the carbon surface decrease the Gibbs adsorption of ions from ACN-based electrolytes compared with IL data [91].

The constant power discharged method has been applied to analyse energy densities at fixed power density. Data in Fig. 16 show that the highest energy densities have been calculated with optimal porous structure, i.e., for systems with high microporosity and mesoporosity, prepared using the sol–gel method for syntheses of TiC compared to microporous carbon derived from commercially available TiC, D-glucose-derived carbon (C(Glc)-12 h), micro-mesoporous D-glucose-derived carbon (MMP C(Glc)), steam activated carbon derived from SiC (C(SteamSiC)), and carbon derived from granulated white sugar (C(WS)) [3, 91, 112, 300]. EDLCs with very high microporosity demonstrated moderate or even low power densities and cannot be used as peak power generating devices.

Fig. 16

Gravimetric Ragone plots for different carbon materials (noted in the figure) measured within cell potential range 3.0 to 1.5 V in EMImBF₄ electrolyte [91]

Electropolymerisation of ILs at carbon electrode surface

In order to identify the ideal polarisability region and processes limiting the ideal capacitive behaviour, the EMImBF₄-based two-electrode system has been overpolarised [60, 109]. At negative potentials (E =  − 2.4 V), the electroreduction of [EMIm]⁺ cations takes place, and a cyclic compound is formed, demonstrated in Fig. 17a, experimentally established by FTIR [60] as well as by synchrotron XPS studies [109]. At very positive potentials (E = 2.0 V) (three-electrode data), the oxidation (decomposition) of EMImBF₄ to MImBF₃, CH₃CH₂F, and B₂F₇ takes place, established by XPS studies [108, 320]. For ideal blocking of the carbon electrode surface, the oxidation of butyl methyl propyldicyanamide (BMPDA) to polydicyanamide (polyDCA) has been conducted and demonstrated at the carbon electrode (Fig. 17b) [106]. Very high energy density supercapacitors have been prepared if compared with ceramic, aluminium oxide, and tantalum oxide–based capacitors [106, 107], and this method has been patented in USA and UK [116, 321].

Fig. 17

a Proposed reaction scheme for the electroreduction of [EMIm]⁺ cations [60]. b The formation of the carbon–nitrogen polymer from [DCA]⁻ anion [106]

Influence of specifically adsorbing anions onto the EDLC characteristics

For the future increase of the capacitance and energy density of EDLCs, the mixtures of salt and ILs with the addition of surface-active anions (Cl⁻, Br⁻, and I⁻) have been investigated by Thomberg, Siinor, Siimenson, and Oll [60, 63,64,65, 100, 112, 113, 304]. Figure 18 demonstrates that the carbon surface is chemically stable and nearly ideally polarisable within cell potential region ΔE > 2.0 V. The given CVs show that the capacitance increases with the cycle number applied up to 1000 cycles, and the future increase of the cycle number does not improve the capacitance values. It is interesting that the charging and discharging cycle capacitance values are nearly the same, indicating the nearly reversible adsorption of I⁻ at the MMP carbon electrode. However, cycling within a wide potential region indicates that at ΔE > 2.4 V, partial charge transfer takes place (in agreement with synchrotron XPS data at positively charged electrode), and the I₃⁻ or Br₃⁻ complex anion formation occurs (discussed by Rogers et al. [115]). In the discharging curve, the reduction current peak is formed; thus, the reduction of the surface compound takes place. It is important to mention that E_peak(red) is independent of the potential scanning rate indicating that the limiting step for the reoxidation process (I₃⁻ to I⁻) is the desorption/adsorption rate determined step from the electrode surface [112, 113, 115]. Impedance data indicate that with the increase of the specific adsorption of anions, the characteristic time constant increases, but only nearly 10%. Also, higher E_max values have been calculated for electrolytes with the addition of I⁻ in IL mixture than the values calculated for surface-inactive EMImBF₄.

Fig. 18

Cycling voltammetry curves expressed as specific capacitance vs cell potential dependencies of electrical double layer capacitors based on microporous–mesoporous carbon electrodes in EMImBF₄ + 5% EMImI mixture within different cell potential ranges at potential scan rate 10 mV·s⁻¹ [112]

A noticeable increase in energy densities accumulated by the adsorption of halide anions has been demonstrated for two-electrode single cells at moderate power densities. Very high E_max values have been established at lower power density Ragone plot region, where the E_max is 20% higher than that for EMImBF₄-based EDLC. However, a quicker decrease of E_max takes place at very high power densities compared with EDLCs based on surface-inactive electrolyte solutions [112, 113]. The energetic efficiency of supercapacitors containing specifically adsorbing anions is lower than for surface-inactive IL–based EDLCs due to the partial charge transfer between carbon surface and adsorbed anions.

Influence of membrane parameters on EDLC characteristics

The influence of separator characteristics on the two-electrode supercapacitor cells has been studied using standard (TF-4425 from Nippon Kodoshi, Japan; Cellgard Japan) and self-made polyvinylidene difluoride (PVDF) separators [99, 117, 118, 120,121,122,123]. PVDF was dissolved in dimethyl formamide, and used in the electrospinning method at different electric field strengths (10–40 kV·m⁻¹), spinning rates, polymer pressing out rates, etc., have been used for the preparation of membranes with different thicknesses, densities, total porosity, etc. [99, 117, 118, 122, 123].

The influence of polymer membranes’ geometrical structure, thickness, and porosity values on EDLC parameters has been analysed by Thomberg et al. [99, 117, 118, 122, 123] using the EIS method for cells with various membranes. The characteristics of membranes have been established using the Hg intrusion porosimetry measurement method and BET gas adsorption methods [99, 117, 118, 122, 123]. The EIS data show that the very high-frequency series resistance value depends on the micro- and mesoporosity (hierarchical porosity parameters) of the membrane used. The characteristic relaxation frequency values, given in Table 4, noticeably depend on the membrane thickness selected for the completion of two-electrode cells. Therefore, the power density of a two-electrode supercapacitor cell depends strongly on the micro-meso-macroporosity of the membrane separating the positively and negatively charged electrodes. The low-frequency parameters are also influenced by high-frequency resistance R_s values, but this influence is moderate compared with that observed within the high-frequency (high power density) region. However, for extremely high power density supercapacitors, the optimisation of membrane porosity (ion–ion transfer resistance within the membrane) is extremely important. A more detailed discussion is given in [99, 117, 118, 122, 123].

Table 4 The parameters of different poly(vinylidene fluoride) separator materials prepared using electrospinning, as discussed in [118], and measured in a system consisting of C(TiC) electrodes and 1 M TEMABF₄ + ACN solution. The specific surface area and total porosity were determined using mercury intrusion porosimetry. The characteristic time constant is noted with τ_R

For comparison, the same electrode systems have been completed using the EMImBF₄ as an electrolyte and serial-produced membranes TF4425, etc. A comparison of data with standard separator TF4425 based cells shows that even higher power densities have been achieved for well-optimised membranes made in University of Tartu. Therefore, similarly to organic electrolyte–based systems, optimisation of membrane characteristics is very important for IL-based EDLCs, and as for EDLCs containing thick membranes (TUX 5), very low power densities were measured [99, 117, 118, 120,121,122,123].

Hydrogen and methane adsorption at carbon materials and thin-film complex metal hydrides

Hydrogen and methane adsorption in different CDCs: C(TiC) 950 °C, C(SiC) 1000 °C, C(Mo₂C) 900 °C, with well-defined pores and different sizes and shapes, volumetric adsorption has been studied using in situ quasi-elastic neutron scattering methods by Härmas et al. [133], Koppel et al. [134], Palm et al. [135]. The predominant shape of pores for three of these carbons (spherical-C(SiC) 1000 °C, cylindrical C(TiC) 1000 °C, and slit-like C(Mo₂C) 900 °C) has been established using the small angle neutron scattering method [128]. In addition to the strong effect of the presence of sub-nanometre pores, as in the case of C(TiC) 950 °C and C(SiC) 1000 °C, the effect of the pore shape on the diffusion coefficient of hydrogen has been observed and discussed. While the C(TiC) 950 °C and C(SiC) 1000 °C have the same, nearly similar pore size distributions, the prevalently shaped pores in C(SiC) 1000 °C restrict the diffusion of H₂ to a large degree in comparison with C(TiC) 950 °C. In the case of low H₂ loading pressure, no mobile H₂ was detected in C(SiC) 1000 °C, but the H₂ mobility has been demonstrated for C(TiC) 950 °C. It was found that the prevalently slit-shape and large pores for C(Mo₂C) with flatter pore potential enabled a higher mass-transfer processes rate for confined hydrogen molecules and therefore exhibited weaker interaction between hydrogen molecule and adsorbing carbon surface. The observed molecular behaviour of hydrogen confined into micropores of C(SiC) 1000 °C, C(TiC) 950 °C, and in C(Mo₂C) 900 °C allowed the explanation of differences in gas adsorption isotherms, given in Fig. 19, where it is visible that C(TiC) has a microporous structure and C(Mo₂C) has a micro-mesoporous structure with well-expressed hysteresis in BET gas sorption curves [3]. The best fit of the experimental data for C(TiC) and C(Mo₂C) has been established using the Aspect ratio 6 model or heterogeneous surface model [293,294,295].

Fig. 19

a N₂ adsorption isotherms of carbons derived from Mo₂C at different temperatures (noted in the figure) and b N₂ adsorption isotherms of different carbide-derived carbons (noted in the figure) [132, 135]

The localisation and low mobility of H₂ in sub-nanometre pores lead to higher gas adsorption (intake) at lower pressures. Higher pressure needs to be applied to confine H₂ in pores with flatter surface potential and weaker interactions between adsorbate and adsorbent, i.e., mainly the influence of H₂ pressure and the interaction of H₂ with C(Mo₂C) have been analysed. It is shown that the increase in H₂ pressure and the amount of confined H₂ molecules leads to the increase in cooperative molecular interactions. A similar effect has been observed for H₂ adsorbing in zeolites, and the establishment of this effect for very weakly adsorbing H₂ molecules suggests the universal character of the phenomenon discussed [136, 322].

A detailed analysis of the porosity and solid base geometrical structure of different CDCs (α-SiC, TiC, Mo₂C) (Fig. 19b) and peat-derived carbons has been conducted for moderate temperature and pressure. It was found that the hydrogen adsorption in non-modified CDC carbons decreases in order: α-SiC, TiC, Mo₂C and thus with the decrease of microporosity. For fixed Mo₂C carbons as well as for α-SiC-derived materials, H₂ adsorption decreases with the increase of carbon syntheses temperature, thus with the increase of mesoporosity, and decrease of microporosity.

SANS, QENS, and INS data indicate that the carbon surface roughness influences the specific interaction of hydrogen, porous structure, tortuosity, etc., which has been discussed in [129, 130, 132, 134]. The decisive influence of CDC crystallographic structure (cubic, tetrahedral, rhombic, and hexagonal) on the CDC carbon structure synthesised has been investigated.

It was demonstrated by SEM, HR-TEM, AFM, and FIB-TOF–SIMS methods that the ball-like shape of pores prevails on/in CDC prepared from α-SiC, cylindric from TiC, and slit-shape pores in carbon prepared from Mo₂C. Additionally, they have very different characteristic relaxation times and power densities increasing from C(α-SIC) to C(Mo₂C). The QENS and INS studies of molecular hydrogen adsorption verified complicated adsorption/desorption kinetics of materials with different porous structures of hydrogen at very low temperatures (− 253 °C) [133, 134, 136].

The adsorption of methane also depends on the structure of the porous carbon, increasing with the increase of microporosity from C(α-SiC) to C(TiC) and lastly to C(Mo₂C). The effect of pore size and surface morphology of carbon materials on the adsorption of methane was studied using C(TiC) 950 °C and 1100 °C, and C(Mo₂C) 1000 °C materials. Nitrogen adsorption, Raman spectroscopy, and XRD have been used for the characterisation of methane adsorption. All materials have a high specific surface area: C(TiC) 950 °C, 1450 m²·g⁻¹; C(TiC) 1100 °C, 870 m²·g⁻¹; and C(Mo₂C) 1000 °C, 820 m²·g⁻¹, but the pore size distribution depends strongly on the synthesis temperature and the applied activation method. C(TiC) 950 °C contains mainly micropores, C(TiC) 1100 °C, activated with HCl, contains micro- and mesopores with a pore size distribution maximum from 1.5 to 5 nm, and C(Mo₂C) 1000 °C is mainly mesoporous from 2.4 to 10 nm. The methane adsorption increases from C(Mo₂C) to C(TiC) 950 °C, being 165 cm³·g⁻¹ and 295 cm³·g⁻¹, respectively. Excess isotherms of methane adsorption were measured at different temperatures from − 100 to 40 °C and pressures from 0.35 to 1.35 MPa and modelled enthalpies and entropies of CH₄ adsorption. It was found that the changes in entropy are the key factor determining the amount of CH₄ adsorbed per unit surface area of CDC. It was established that up to 55% more methane can be adsorbed in C(TiC) 950 °C, compared with C(Mo₂C) 1000 °C if the carbon structure is optimised [135].

For higher hydrogen adsorption values, the MMP carbon electrodes have been modified with thin films of NaAlH₄ [323]. Differently from homogenous NaAlH₄ solid particles (7.5 wt% of H₂ per 1 g NaAlH₄), the release of hydrogen started at moderate temperatures (60–80 °C) differently from monolithic materials where H₂ evolution started only at 240–280 °C. It means that the thin-film hydrogen storage materials can be used for the release of hydrogen using the heat generated by the PEMFC stack when it generates electricity for ac motors. It is great to point out that the hydrogen adsorption capacity in thin-film NaAlH₄ is nearly 3–3.5 times bigger than that for MMP carbons (up to 2.5–3.0 wt%). In addition, the gravimetric hydrogen capacity is 4–5 times bigger than that for compressed hydrogen up to 700 bar, as well as nearly two times larger than for liquefied hydrogen. It should be stressed that the adsorption/desorption of hydrogen into nanostructural NaAlH₄ is an energy-efficient process compared with the liquefaction of hydrogen.

Development of carbon materials for Li⁺-ion and Na⁺-ion batteries

The carbon materials synthesised from different raw materials (from carbides (CDC), glucose (glucose-derived hard carbon, HC(Glc)), and Estonian well-decomposed peat (peat-derived hard carbon, HC(EP)) at different syntheses temperatures from 1200 to 1700 °C have been used as negatively charged electrodes for LIBs and SIBs, where Li metal and Na metal have been used as positively charged electrodes, respectively. Very open porous 3D structures (S_BET up to 1100 m²·g⁻¹ for HC(Glc) and 1050 m²·g⁻¹ for HC(EP)) with a partially graphitised curved graphitic surface, established by Raman spectroscopy, have been prepared. The partial graphitisation of HC(Glc) and HC(EP) is very important, giving materials under study good electrical conductivity compared with amorphous non-graphitised carbons [92,93,94, 96, 97, 299,300,301,302,303].

Due to the low graphitisation level of CDC and not partially graphitised carbons like HC(Glc), white sugar–derived hard carbon (HC(WS)), or HC(EP) carbons, the adsorption capacity values for Li⁺ are only moderate and mentioned CDC could not be used for high energy density LIBs. Surprisingly high capacities have been observed for glucose, and peat-derived carbons, even up to 320–360 mAh·g⁻¹, thus showing very promising high capacity values (Fig. 20). The limiting capacity values depend on the electrolyte (salt and solvent) used. The highest capacity values have been calculated for NaPF₆ electrolyte solutions dissolved in EC + PC 1:1 mol/mol mixed solvent system at a 50 mAh·g⁻¹ charging rate. An increase in the PC molar ratio in the mixed solvent system also decreases the limiting capacity of negatively charged electrodes. The exchange of NaClO₄ to NaPF₆ increases the capacity values notably [303]. It should be noted that for C(EP), there is no noticeable dependence of limiting capacity values on the chemical nature of the cation tested, i.e., for LiBF₄ and NaBF₄, as well as for LiClO₄ and NaClO₄; nearly comparable high capacity values (320–360 mAh·g⁻¹) have been established.

Fig. 20

Galvanostatic charge/discharge profiles measured at 50 mA·g⁻¹ current density for half-cells based on Li⁺- and Na.⁺-ions in different electrolytes, marked in the figure [97]

These systems have been studied using different operando testing methods, including XPS, XRD, AFM, and FIB-TOF–SIMS. It is interesting that the 20% larger Na atoms compared with Li atoms adsorption onto HC(Glc) surface causes a 60% increase in in-plane bond lengths values, established by operando X-ray total scattering study of HC(Glc) in Li⁺-ions and Na⁺-ions containing solutions [8, 131]. Thus, the Na adsorption to the surface or intercalation between the HC(Glc) graphitic layers could affect the neighbouring π-electron graphitic electron systems. Sodiation causes an increase in interlayer distances in the charging curve sloping region, characterising the different intercalation/charge collection mechanisms for Li⁺- and Na⁺-based systems [131]. FIB-TOF–SIMS data show that the surface chemistry for Li⁺-ions containing electrolytes is more complicated than that for Na⁺-ions containing systems. Therefore, at the carbon electrode surface in Na⁺-ions containing electrolytes, there is no dense blocking SEI differently from Li⁺-ions containing solutions. It was observed that the Na adsorption capacity depends very strongly on the hard carbon syntheses temperature, and the highest capacity values have been established for HC(Glc) and HC(EP), synthesised at 1400–1500 °C.

The accumulation of Li⁺-ions (formation of Li) and Na⁺-ions (Na) into hard carbon materials is very slow, and maximal capacity (maximal faradic current density) values have been calculated only at a very slow potential scanning rate (0.1 mV·s⁻¹). The cyclic stability (so-called cyclability) of HC(Glc) is good, and after 80 cycles, the capacity stabilises at 160 mAh·g⁻¹ level (at a high charging rate of 50 mA·g⁻¹ applied). The charging Coulombic efficiency after the preliminary 10 cycles increases up to 98%.

Thus, based on the results collected for the three-electrode cell, it was decided to complete the two-electrode cells with real positively charged electrodes. The two-electrode cell capacity, containing HC(Glc) or HC(EP) and Li⁺-ions or Na⁺-ions electrolytes, is limited by the capacity of positively charged electrodes, and future studies are inevitable for completing high power density SIBs. At the moment, Na⁺-ions–based electrolyte systems can be used for stationary electricity storage only, where the capacity values (stored energy per g of device) of devices are not critical, and the cheap prize of SIBs is more important than the high volumetric or gravimetric density of devices.

The development of Pt-metal-nanoclusters activated and d-metal-nitrogen active centres based electrocatalysts for PEMFC electrodes and PEM single cells

Preparation and physical characterisation of Pt and Ru modified catalysts

Various micro-mesoporous carbons have been used as carbon supports for oxygen electroreduction and PEMFC single-cell studies. These carbon materials have been prepared from carbides [4, 138,139,140,141,142,143,144,145,146,147,148, 151,152,153, 155, 162,163,164,165,166,167,168,169,170, 324,325,326], glucose solution [149, 150], and from Estonian well-decomposed peat [137, 154, 156, 157]. The materials were activated using different methods, e.g., with CO₂ gas (at different temperatures and for different durations of 1–12 h), ZnCl₂, or KOH powders. Most of the carbons were post-treated with molecular hydrogen (at T = 800 °C for 2–6 h). Pt and Ru, Pt-Ru, Pt-Ir alloys [148, 169] nanoclusters were deposited on the supports using mainly the NaBH₄ reduction method. H₂PtCl₆·xH₂O, RuCl₃·xH₂O, and IrCl₃·xH₂O have been used as metal donors for the deposition of metal nanoclusters onto various MMP carbon supports, i.e., C(Mo₂C) (600–1200 °C), C(VC) (900–1200 °C), C(WC) (900–1100 °C), C(TiC) (800–1200 °C), C(SiC) (900–1100 °C), and C(Cr₃C₂). In addition to the self-made carbons, the traditional Vulcan XC72R and Ketjenblack carbon powders have been used to see how the carbon support structure, specific surface area, hierarchical porosity, graphitisation level, the ratio of microporous surface area to mesoporous surface area, and the ratio of mesopore volume to micropore volume influence the oxygen electroreduction rate in acidic and alkaline aqueous electrolyte solutions. Thus, the same carbon supports, tested in EDLCs and hybrid capacitors, have been used.

The catalyst suspension consisting of catalyst, Nafion solution, MilliQ⁺ water, and isopropanol was used for preparing thin-film electrodes. For some electrodes, ultrasonic spraying has been used.

For the analysis of materials, the HR-TEM, FIB-TOF–SIMS, FIB-SEM–EDX, XRF, XPS, and XRD studies have been conducted. The results indicate that a nearly homogeneous distribution of Pt and Pt-Ru nanoclusters has been achieved (Fig. 21).

Fig. 21

HR-TEM images for a Pt–C(Mo₂C) 800 °C and b Pt–Ru–C(Mo₂C) 600 °C catalysts; c SAED image of Pt–Ru–C(Mo₂C) 600 °C catalyst [165, 168]

Very well-oriented single-crystal Pt areas have been deposited onto well-treated C(Mo₂C) supports. The systematic analysis of materials indicates that depending on the deposition conditions, Pt nanoparticles with different ratios of facets ((111), (100), (011), (321), and (331)) have been deposited (Fig. 21a). The single-crystal areas are nearly 4–14 nm wide. The porosity characteristics have been measured by the nitrogen gas adsorption method (discussed above). It should be mentioned that after the deposition of Pt, the Pt-C(Mo₂C) has a hierarchical structure like that of the carbon support with well-expressed mesopores and micropores at the surface (Fig. 22a). The same is valid for glucose solution derived carbon materials activated with Pt clusters, noted as Pt-C(Glc) (Fig. 22b).

Fig. 22

a Dependence of the differential pore volume on the pore width for various catalysts: 1 — C(Mo₂C) 750 °C; 2 — 3.5 wt% Pt-C(Mo₂C) 750 °C; 3 — 8.3 wt% Pt-C(Mo₂C) 750 °C; 4 — 12.4 wt% Pt-C(Mo₂C) 750 °C and b low-temperature nitrogen adsorption/desorption isotherms for the catalyst powders: 1 — 60 w% Pt-C(Mo₂C) 800 °C and 2 — 60 wt% Pt-C(Glc) [325]

Oxygen reduction data on platinum-based catalysts in acidic and alkaline electrolyte solutions

The cyclic voltammetry and rotating disc electrode methods were used to characterise the oxygen reduction reaction (ORR) kinetics. There are very well-developed surface oxygen compounds’ reduction peak at 0.8 V and hydrogen evolution peaks at 0.25 and 0.1 V (vs SHE) for Pt-C(Mo₂C) electrodes in cyclic voltammograms (Fig. 23a) in 0.5 M H₂SO₄ saturated with Ar at electrode potential rate 10 mV·s⁻¹. It should be stressed that the carbon structure, specific surface area, the ratio of micro/mesopores surface area and volume, and the existence of the graphitised surface structure of catalysts have a great impact on the deposition of the Pt nanoparticles. It is interesting that the hydrogen adsorption/desorption peak potentials are nearly independent of the micro-mesoporous structure of the carbon support material used, indicating that the reaction rate is mainly controlled by the Pt nanoclusters activity deposited onto carbon C(Mo₂C) support. The intensity of cyclic voltammetry peaks corresponding to the adsorption/desorption of O₂ (oxygen-containing surface compounds) and H₃O⁺ ions (kinetics) depends on the micro/mesoporosity ratio and graphitisation level of supporting carbon structure. Data in Fig. 23a show that the hydrogen adsorption/desorption rate has maximum values for Pt-C(Mo₂C) 850 °C. Thus, for moderately microporous carbon supports [139, 141, 142, 162, 163, 170], the rate of mass transport in micropores seems to be quite slow. There is only a very weak dependence of adsorption/desorption peak potentials as well as peak current densities on the potential scanning rate, indicating that the adsorption/desorption step rate limited processes prevail at Pt-C(Mo₂C) electrode surfaces in a solution saturated with argon. Very high electrochemical surface area values have been calculated (from 14 to 30 m²·g⁻¹ for Pt-C(Mo₂C) 700, 750, 800, and 850 °C) [4], indicating that optimal micro/mesoporous structure is important for high O₂ reduction kinetics in order to avoid the accumulation of H₂O₂ (including other intermediates) and H₂O into micropores, observed for Pt-C(Mo₂C) 600 °C catalyst with high microporosity, but with low mesoporosity.

Fig. 23

a Calculated capacitance C_CV, E plots for Pt-C(Mo₂C) electrodes (noted in the figure); b RDE data for Pt-C(Mo₂C) electrodes at 3000 rev·min.⁻¹ in 0.5 M H₂SO₄ solution saturated with O₂; c corrected Tafel plots calculated from RDE data (noted in the figure) [4]

The ORR for Pt-C(Mo₂C) catalysts is demonstrated in Fig. 23b. The O₂ reduction kinetics is highest at Pt-C(Mo₂C), where Pt was deposited onto carbon synthesised at 750–850 °C. These materials also demonstrate the best supercapacitors’ energy density vs power density characteristics [3]. It is interesting that for the Pt catalysts synthesised using other CDC supports, i.e., C(VC), C(WC), C(TiC), and C(SiC), there is a very weak dependency of ORR rate on the carbon support micro-mesoporosity characteristics under study explained by the catalytic role of the structure of Pt nanoclusters deposited.

Taleb et al. studied ORR kinetics at Pt catalysts deposited onto HC(Glc) in acidic and alkaline media and came to the same conclusion [149]. The electroreduction of oxygen is quite a complicated process, and it depends on the nanocrystal surface structure of the Pt particles [140]. Based on the HR-TEM data, all basal planes (111, 001, 011) and catalytically more active high-index Pt planes (311, 211, 331, etc.) have been observed at Pt-C(Mo₂C) surface in agreement with XRD and HR-TEM-SAED data [138, 143, 145]. It should be noted that for some mainly microporous CDC (no hysteresis in BET adsorption data), there is only a very weak dependence of oxygen reduction rate on the surface structure (like for C(WC), C(VC), C(Cr₂C₃)). Thus, it can be concluded that the Pt-carbon electrodes with macro-heterogeneous porous structure, combined with hierarchical micro-mesoporous structure, have demonstrated the quickest catalysis of O₂. The rotating disk electrode (RDE) data show that nearly Levich and Koutecky–Levich models [327] can be applied for the mathematical analysis of experimental data in spite of crystallographic inhomogeneous and surface roughness of Pt-nanoclusters activated electrodes. It seems that the catalytically active Pt centres can be found only at the open surface regions, where the oxygen reduction takes place [142, 163]. Therefore, for more active catalysts, the mesoporous and microporous carbon supports with high mesopore volume, giving more attainable catalytic centres per flat-gross section surface area, could be created for more high energy and power density PEMFCs.

The kinetic current densities (Fig. 23c) have been calculated using a modified Koutecky–Levich method [327, 328]:

$$\begin{array}{c}\frac{1}{j}=\frac{1}{{j}_{k}}+\frac{1}{{j}_{d}}+\frac{1}{{j}_{f}}=\frac{1}{{j}_{k}}+\frac{1}{0.62nF{D}^\frac{2}{3}{v}^{-\frac{1}{6}}{c}_{0}{\omega }^\frac{1}{2}}+\frac{L}{nF{c}_{f}{D}_{f}},\end{array}$$

(8)

where ${j}_{k}$, ${j}_{d}$, and ${j}_{f}$ are kinetically limited, diffusion-limited, and Nafion film diffusion-limited current densities, respectively. In addition, the remaining variables are B — Levich constant, ${c}_{0}$ — the O₂ concentration in the solution, L — the film thickness, ${c}_{f}$ — the O₂ concentration in Nafion film, D — the O₂ diffusion coefficient in the electrolyte, and ${D}_{f}$ — the O₂ diffusion coefficient in the Nafion film.

The role of the third component, i.e., processes in the Nafion layer, is unimportant as the ${j}_{f}$ values are very high in comparison with kinetic current values j_k for the electrodes studied in our works [170, 324] (like it was established by Paulus et al. [328]). For well-optimised electrodes, the number of electrons transferred is nearly 4 [4, 137, 139, 140, 145,146,147, 149, 152, 154, 155, 165, 167,168,169,170], indicating that the formed H₂O₂ reduces to the final product in acidic electrolyte solutions. However, for less meso-macroporous electrodes, the number of electrons transferred is lower than 3.5 (or even lower than 2.9), and the reaction is not going to the end and some intermediate products (H₂O₂) form, blocking the active electrode surface and lowering the diffusion-limited currents, observed experimentally at very many microporous electrodes at very high negative potentials, where the oxygen reduction faradic charge transfer step is not limiting process any more, but ORR is controlled by adsorption/desorption kinetics inside of the limiting diffusion (mass-transfer) layer.

The influence of Pt loading on the ORR has been studied using C(Mo₂C) 750 °C (Pt-C(Mo₂C)) and C(Vulcan) as supports (noted as Pt-C(V)) [140, 141, 143]. Electroreduction of oxygen has been studied at catalysts with very low Pt loading [141, 143, 324, 325] 3.5–20 wt% and small Pt nanoparticles (linear dimension from 2 to 5 nm) deposited onto C(Mo₂C) support. Pt has been deposited by the NaBH₄ method, and the well-crystallised Pt nanoparticles with increasing reflex intensity with the increased amount of Pt have been prepared and confirmed by XRD. The Pt particle size increases from 2.6 to 3.4 nm with the increase of Pt wt% in the catalyst, according to HR-TEM histograms in Fig. 24.

Fig. 24

a X-ray diffraction data and b HR-TEM histograms for various Pt catalysts: 1 — 3.5 wt% Pt-C(Mo₂C) 750 °C; 2 — 8.3 wt% Pt-C(Mo₂C) 750 °C; 3 — 12.4 wt% Pt-C(Mo₂C) 750 °C; and c HR-TEM images (noted in the figure) [325]

The gas adsorption data analyses indicate that with the increase of Pt wt%, the S_BET (multipoint analyses method) noticeably decreases from 1942 to 1672 m²·g⁻¹ with a well-expressed mesoporous and microporous structure. The ORR polarisation curves for Pt-modified C(Mo₂C) catalysts demonstrate that the 8 ± 1 wt% Pt loading is optimal. Somewhat higher ORR activity has been measured for 0.1 M HClO₄ solutions compared with the 0.05 M H₂SO₄ solution, and the lowest activity was observed for 0.1 M KOH solution (Fig. 25). The Pt mass corrected current |j_Pt| decreases with the increase of Pt wt% in the catalyst [143].

Fig. 25

a Polarisation curves for Pt catalysts: 1 — 3.5 wt% Pt-C(Mo₂C) 750 °C; 2 — 8.3 wt% Pt-C(Mo₂C) 750 °C; 3 — 12.4 wt% Pt-C(Mo₂C) 750 °C in 0.1 M HClO₄ electrolyte solutions saturated with O₂ at v = 10 mV·s⁻¹ and at electrode rotation rate 3000 rev·min⁻¹ [325]; b dependence of the Pt mass corrected current (j_Pt) on the Pt loading in a catalyst in various electrolyte solutions: 1 — 0.1 M KOH; 2 — 0.05 M H₂SO₄; 3 — 0.1 M HClO₄ (j_Pt values were obtained from cyclic voltammogram at onset potential at v = 5 mV·s⁻¹)

The calculated Tafel-like plots were linear within a narrow potential region with the Tafel slope values somewhat decreasing (independent of the chemical composition of acid) with the increase of Pt wt% deposited onto carbon support. However, for KOH solutions, the lower Tafel plot slope values have been established. The change in the Tafel slope value can be attributed to a change from the Langmuir ORR mechanism at low current densities to a more complicated mechanism in the high current density region [329, 330].

In addition to Pt wt% in the catalyst, the effect of catalyst loading on the ORR activity was investigated [326]. The 20 wt% Pt-C(Mo₂C) 750 °C and commercially available modified carbon 20 wt% Pt-Vulcan XC72R (with different catalyst loadings from 0.1 to 1.0 mg·cm⁻²) have been studied in 0.1 M KOH solution (Fig. 26a). The Pt-C(Mo₂C) has higher current densities |j| than commercial Pt catalyst within the mixed kinetic region demonstrating higher O₂ reduction kinetics. For both catalysts, the half-wave potential value increases with the Pt loading; however, for Pt-C(Mo₂C), the change is more pronounced. According to the CV analysis (Fig. 26b), the threefold increase of the ORR electroreduction peak current density |j_peak| has been observed for Pt-C(Mo₂C) if the catalyst loading increases tenfold. Thus, the same current densities can be achieved for Pt-C(Mo₂C) at the three times lower catalyst loading compared with the commercial catalyst, explained by the influence of C(Mo₂C) supporting effect for O₂ reduction. Therefore, the enhanced O₂ reduction activity has been explained by the meso-macroporous structure and the existence of well-conducting graphitic areas with some catalytically active defects expressed on partially graphitised C(Mo₂C) surface near the Pt clusters [331].

Fig. 26

a RDE data for 20 wt% Pt-Vulcan XC72R (1,2) and 20 wt% Pt-C(Mo₂C) 750 °C (3,4) with catalyst loading of 0.4 mg·cm⁻² (1,3) and 1.0 mg·cm⁻². b Reduction peak current density (j_peak) from CV data (at electrode potential scan rate 5 mV·s.⁻¹) as a function of catalyst loading for 20 wt% Pt-Vulcan XC72R (1) and 20 wt% Pt-C(Mo₂C) 750 °C (2) [141]

The time stability of Pt catalysts deposited onto different C(Mo₂C) is very good, determined by the results of 30 000 current cycles using the RDE method and accelerated stability tests [145, 146, 151, 163]. The ORR studies of Pt-C(Mo₂C) 750 °C have been performed over a wide temperature range (from 10 to 80 °C), and good thermal stability of the electrode materials has been demonstrated [144]. Also, the influence of chemical composition and amount of intermixed ionomer (polyvinyl alcohol or Nafion) in the catalyst layer on the oxygen reduction reaction characteristics have been investigated [324]. It was demonstrated that the highest electrochemical activity towards ORR was achieved by adding 30 wt% Nafion to the catalyst layer.

For a detailed analysis of the reaction mechanism, the EIS method has been used [4, 168, 169]. In good agreement with CV and RDE data, the complex plane impedance plots indicate that the adsorption/desorption step-limited processes are very slow at Pt-C(Mo₂C) catalysts as the nearly ideal limiting capacitive behaviour has been observed at very low ac frequencies, demonstrated in Fig. 27. Only at ac frequencies higher than 100 Hz, the faradic charge transfer processes control the O₂ electroreduction. At 0.1 Hz < f < 100 Hz, the mixed kinetics (mass transfer and adsorption step kinetics) determines the total process rate and at f < 0.1 Hz, the adsorption/desorption processes are rate-limiting. This is the main reason why some hysteresis in rotating disk electrode data has been observed, as well as why the diffusion-limited currents depend on the micro/mesoporosity ratio of the catalysts applied. It should be stressed that the EIS data fitted indicate that at low ac frequency, totally blocking behaviour for systems has been observed. The limiting series capacitance C_s and parallel capacitance C_p values overlap at ac f = 1 Hz, indicating that the developed catalysts can be applied as capacitive electrodes for supercapacitors.

Fig. 27

For Pt-C(Mo₂C) 800 °C system [168], a Nyquist plots at different potentials (E vs SHE, noted in the figure) and b Bode phase angle θ, log f- and log |Z|, log f-plots in O₂ saturated 0.5 M H₂SO₄ solution at different fixed electrode potentials (noted in the figure)

Oxygen reduction data on catalyst supports in acidic and alkaline electrolyte solutions

The ORR kinetics on the catalyst support and observed capacitive behaviour is also important in the PEMFC applications as catalyst structure has an enormous impact on the rate of ORR. Therefore, the ORR has been studies on various MMP carbons like CDC, C(Glc), and C(EP) [4, 137,138,139, 143, 149, 150, 152, 153, 155, 156, 164,165,166,167,168,169,170]. In order to characterise the influence of the support material structure on the ORR, the dependence of the ORR kinetic current (at a constant potential) on the specific surface area of the material was constructed (Fig. 28). There is some systematic dependence of log j_k on S_BET. In general, the ORR activity increases with increasing the specific surface area of the carbon support. Most importantly, the role of the carbon source (different CDCs, D-glucose, white sugar, Estonian well-decomposed peat) is clearly visible.

Fig. 28

Dependence of the ORR kinetic current (at a constant potential) on the specific surface area of the carbon material in a acidic and b alkaline solutions [4, 137, 149, 150, 155, 164, 166, 167, 332,333,334,335]

In acidic solution (0.1 M HClO₄ or 0.5 M H₂SO₄), the most active materials are based on ZnCl₂-activated C(EP) at 700 °C (S_BET = 1270 m²·g⁻¹) and C(Mo₂C) 750 °C (S_BET = 2020 m²·g⁻¹) with optimal micro/mesoporosity ratio [4, 137, 154, 156, 157]. It should be noted that the ORR reduction rate may depend somewhat on the chemical nature of the electrolyte anions (SO₄²⁻ or ClO₄⁻). Certainly, the least active is commercial carbon black Vulcan XC72R due to quite low specific surface area and non-defective structure. If Mo₂C is used as a carbon source, the CDCs with different specific surface areas are synthesised, and the ORR rate increases from C(Mo₂C) 600 °C to C(Mo₂C) 750 °C, and thereafter, the activity starts to decrease, being the slowest at C(Mo₂C) 1000 °C [4, 139, 164, 165, 168, 170]. Interestingly, the mesoporous CDCs with low micropore volume (C(Mo₂C) 1000 °C, fewer defects at the surface) have lower ORR kinetics compared with other CDCs [139, 141].

In a 0.1 M KOH aqueous solution, very high catalytic activity has also been established for C(Mo₂C) 750 °C and for peat-derived carbon activated by ZnCl₂ at 700 °C for 6 h [156, 164]. Surprisingly, C(Glc) prepared by hydrothermal carbonisation method (S_BET = 1190 m²·g⁻¹) is most active compared to activity in acidic solution [150]. It should be noted that only C(Mo₂C) 750 °C has a measurable amount of mesopores. But the macroscopic structures of C(Glc) and C(EP) are totally different as the nanospheres form the very highly macroscopic structure of C(Glc) and C(EP). According to the physical and electrochemical characterisation methods of the C(EP) synthesised using various carbonisation protocols, it could be concluded that depending on the carbonisation method used, carbons with very different surface morphologies, elemental compositions, porosities, and graphitisation levels and the ORR activities were obtained, influencing the ORR rate strongly [136].

Generally, for unmodified carbons, the number of electrons transferred per one oxygen molecule varies from two to three in acidic and alkaline media. This indicates that ORR is mainly a two-electron H₂O₂ forming process. However, for most active carbons, it could be above three, indicating that further reduction of peroxide is possible, i.e., the 2 + 2 reaction mechanism seems to be applicable.

The calculated Tafel plots are linear within a narrow potential range in acidic media, and the calculated Tafel-like plot slope values in acidic solutions range from 120 to 155 mV, depending on the micro/mesoporosity ratio and graphitisation level of carbon (support materials) used. In 0.1 M KOH solution, the Tafel-like plot slope values are lower (around 70–90 mV), indicating the change of reaction mechanism in alkaline media [152, 164, 166].

Oxygen reduction at d-metal-nitrogen nanoclusters activated carbon electrodes

Nowadays, it is increasingly important to find a substitute for precious metal catalysts for electrochemical oxygen electroreduction. Therefore, different d-metal compounds (FeSO₄·7H₂O or Co(NO₃)₂·6H₂O) together with nitrogen-containing compounds as nitrogen donors (e.g., urea, ethylenediaminetetraacetic acid (EDTA), 1,3-di(1H-imidazol-1-yl)-2-propanol (DIPO), 1,10-phenanthroline (Phen), and 2,2′-BP) and carbon source (CDC, C(EP) and Vulcan XC72R) have been used to synthesise non-noble metal catalysts. Catalysts prepared have been characterised by novel informative methods such as HR-TEM, XPS, XRD, SEM–EDX, FIB-TOF–SIMS, XPS, and physical adsorption of gases (N₂, Ar) [151,152,153, 155]. RDE data in 0.1 M KOH (Fig. 29a) show that very active Fe–N catalysts have been prepared with nearly the same activity as for Pt-Vulcan. The catalytic activity decreases in the order Fe–N-2,2′-BP ≥ DIPO ≥ Phen > EDTA > urea, thus depending on the chemistry of nitrogen donors [152, 153, 155]. For the most active three Fe–N catalysts, the number of electrons transferred per one oxygen molecule is nearly 4. For some less active materials, the number of electrons transferred is lower than 4, and the H₂O₂ (or other intermediates) production cannot be discarded. The ORR kinetics in 0.1 M HClO₄ has also been studied, and the activity is higher in 0.1 M KOH solution compared to the acidic solution. The same tendency has been achieved for Co–N/C type catalysts (Fig. 29b).

Fig. 29

RDE data for ORR a for Fe–N/C catalysts using various nitrogen sources (noted in the figure) in O₂ saturated 0.1 M KOH solution (3000 rev·min⁻¹, 10 mV·s⁻¹) and b for Co–N/C catalysts synthesised by varying synthesis conditions (noted in the figure) in O₂ saturated 0.1 M HClO₄ solution (1500 rev·min⁻¹, 10 mV·s.⁻¹). c Activity decrease rates for the Co–N/C catalysts (noted in the figure) [152, 154]

The results of this work indicate that tuning the synthesis conditions, such as the mixing environment, pyrolysis gas, and post-treatment, does not have a substantial effect on the ORR activity of the Fe–N/C and Co–N/C catalysts. This presents an opportunity to choose the synthesis parameters so that the catalyst manufacturing process is as cost-effective and environmentally friendly as possible. Co-doping the C(EP) with both cobalt and nitrogen shows significantly high ORR activity, and a more active ORR catalyst can be synthesised from carbon support which shows better ORR activity [137]. The more serious problem is that the time stability and the cyclability of these catalysts depend somewhat on the used nitrogen donor and synthesis method applied [154, 155]. In addition, the number of cycles that can be applied decreases with the same row of materials as the catalytic activity given above. Therefore probably, the mentioned best-developed catalysts currently can be applied only for devices where long-lasting catalytic activity is not needed (for some rescue devices and military applications because they are less expensive than the Pt-catalysts-based devices).

Methanol oxidation reaction catalysts

Various carbon supports have been used for the preparation of Pt/CeO₂/C and Pt/Pr₆O₁₁/C complex catalysts for the electrooxidation of methanol as a fuel [158,159,160,161]. It was found that the Pt/Pr₆O₁₁/C complex catalyst demonstrated higher current densities than the Pt/CeO₂/C complex catalyst (Fig. 30). The measured catalytic activity has been compared with the standard Pt-Vulcan XC72R catalysts for methanol reduction, and higher current densities have been established for self-made Pt/CeO₂/C and Pt/Pr₆O₁₁/C complex catalysts. The chronopotentiometry measurements demonstrated very good time stability of catalysts prepared onto CDC carbon support.

Fig. 30

Methanol oxidation on the C/Pr₆O₁₁/Pt catalysts and commercial catalyst (noted in the figure) in 0.5 M H₂SO₄ + 1 M CH₃OH solution saturated with argon. a Cyclic voltammograms at the potential sweep rate 10 mV·s.⁻¹; b chronoamperometry results measured at E =  − 0.2 V vs MSE; and c the final current densities after 1800s [158,159,160,161]

Development of solid oxide materials, fuel cells, and electrolysis cells

Development of complex oxide materials

Solid oxide fuel cells are very high energy–density power-generation devices that have been developed for more than 100 years, with the main progress achieved during the last 40–50 years [171,172,173,174,175,176,177,178,179,180]. However, there are many unsolved problems still up to the present day. The scientists at the University of Tartu have prepared solid oxide complex materials with perovskite structure since 2001 [181,182,183,184,185, 208, 209, 336]. The gained insight has been used for the development of fuel cell-powered self-driving car and solid oxide fuel cells for Elcogen OÜ/OY and H2Electro OÜ.

Cubic structured La_(1−x)Sr_xCoO_3−δ (LSC) and Gd_(1−x)Sr_xCoO_3−δ or hexagonally structured Pr_(1−x)Sr_xCoO_3−δ perovskites, showing mixed ionic electronic conductivity at T > 600 °C, were among the first synthesised materials, which were prepared from corresponding oxides (so-called solid-state reaction method) [181, 182, 336] or nitrate solutions (La(NO₃)₃·6H₂O; Pr(NO₃)₃·xH₂O; Gd(NO₃)₃·6H₂O, Sr(NO₃)₂ and Co(NO₃)₂·6H₂O) via the so-called nitrate solution thermal decomposition method in Pt beaker at 302–402 °C [184, 185, 209]. The fluorite structured electrolytes Ce_(1−x)Gd_xO_2−δ, Ce_(1−x)Sm_xO_2−δ (S_BET = 19.9 m²·g⁻¹) were synthesised by the dry pressing of commercial oxides at different pressures and, thereafter, sintered at 1300–1427 °C. Good quality compact complex oxygen anions conducting electrolytes with 99.99% theoretical density were produced [181, 182, 184, 185, 208, 209, 336].

The anodes were prepared in two or three layers. The anode functional layer was prepared from a mixture of commercial NiO and Ce_0.9Gd_0.1O_2−δ with S_BET = 70.8 m²·g⁻¹. A more porous anode diffusion layer was prepared from commercial NiO/Ce_0.9Gd_0.1O_2−δ (S_BET = 6.5 m²·g⁻¹ with 1% of carbon powder removed at T = 1200 °C). The anode layers were screen printed and sintered at 1200–1350 °C (or sometimes at lower or higher T). The anodes have been studied using SEM–EDX, XRD, and FIB-TOF–SIMS methods. Thereafter, the cathodes were deposited onto a half-cell consisting of bi- or single layer electrolyte at different sintering temperatures [181, 182, 184, 185, 209, 336]. The supporting electrolyte half-cells, used for electrochemical studies, were prepared from oxides using the solid-state reaction method [184, 185].

The prepared materials were analysed by XRD, SEM, gas adsorption, and electrochemical characterisation methods. XRD data show that good structural ordering of cathode, anode, and electrolyte has been achieved. Furthermore, the SEM–EDX measurements show that the cathodes and anodes have a very porous and rough structure. Mixed ionic and electronic conductors (MIEC) are widely studied as SOFC cathode and anode materials. Chemical composition and the position of atoms determine the perovskite structured (ABO₃) LSC electrode characteristics. The trivalent A-site (La³⁺, Gd³⁺, Pr³⁺) is doped with bivalent cation (Sr²⁺) to generate crystallographic defects/oxygen vacancies with the aim of improving the ionic conductivity of the electrode. Heterovalent atoms (Co, Fe, Mn), also responsible for the charge balance in the lattice because of the ability to hold several different valence (redox) states, are usually incorporated in the B-site [171,172,173,174,175,176,177,178,179,180,181,182,183,184,185, 208, 209, 336]. It has been established that oxide ion conductivity in ABO₃ structured materials takes place by oxide ion hopping through a triangular plane made up of two A-site cations and a B-site cation. The oxygen ion mobility is, therefore, influenced by the radii of these cations. The transfer of electron density from oxygen to cations decreases the radius of oxide ions, increasing the capability of passing oxygen anions through the triangle. Oxide ion mobility tends to decrease as the oxide ion vacancies are associated with other defects, influencing both the ionic and electronic conductivities [173,174,175,176,177,178,179,180,181,182,183,184,185, 208, 209, 336].

The LSC electrodes have very poor tolerance against certain contaminants due to the high surface energy of the material [173,174,175,176,177,178, 213]. The rearrangement of cations leads to the segregation of Sr to the surface, being more available to various contaminants, inducing the formation of secondary phases, like SrCO₃ or Sr(OH)₂. The formation of SrCO₃ accelerates the Sr segregation process even further in CO₂-rich environments. The Sr segregation rate increases with the temperature. Sr-rich SrCO₃ and SrO are electrical insulators and, therefore, will lower the surface electrocatalytic activity for oxygen electroreduction reaction. The variation of A-site dopant and concentration, respectively, can have a contrary influence on the segregation mechanics. For example, doping LSC or La_1−xSr_xMnO_3−δ (LSM) with Ba²⁺ in the A-site increases the Sr²⁺ segregation because of the large mismatch between the dopant and the host cation as when the A-site of LaMnO₃ is doped with the smaller cation, like Ca²⁺, with smaller size mismatch between the dopant and the host cations has been found to reduce the segregation level of dopant [172,173,174,175,176,177,178,179,180,181,182,183,184,185, 208, 209, 336].

Electrochemical and physical characteristics of complex oxide materials at moderate temperatures

The University of Tartu has focused the research of intermediate temperature SOFC cathode materials on three main areas: the optimisation of materials porosity, the use of nanoscale raw powders, and the search for novel electrochemically active materials. Regardless of many published papers, there were only a few examples of statistically correct systematic optimisation studies published before Küngas et al. [185] paper, where the performance of electrolyte–supported Ni | Ce_0.9Gd_0.1O_2−d | Ce_0.9Gd₀₋₁O_2−d | Ln_0.6Sr_0.4Co_3−δ (Ln = La, Gd, or Pr) symmetric single cells were optimised for anode diffusion layer porosity, anode functional layer starting powder specific surface area (S_{BET, powder}), and cobaltite-based cathode material chemical composition in a single designed experiment according to the so-called response surface methodology method (RSM) [185]. The optimal cell was found to have either La_0.6Sr_0.4CoO_3−δ or Pr_0.6Sr_0.4CoO_3−δ (PSC) cathode, whereas the Ln metal cations (La³⁺ or Pr³⁺) had a minor effect on the total polarisation resistance values confirmed by the analysed experimental results. For the best cell, an anode active layer prepared of a starting powder with the smallest particle sizes, i.e., with maximal specific surface area S_BET = 135 m²·g⁻¹ and a maximal pore former content of 2% in raw anode material, used for the preparation of single cells. Obtained data are in good agreement with Zhao and Virkar’s results [210]. In addition, it should be stressed that the final electrode preparation conditions, i.e., the temperature and duration of the sintering, the exact weight and thickness of the screen-printed layer, the density of the screen-printed layer, exact reduction conditions of the anode and amount of binder, and acting as an additional pore former in a raw unsintered anode layer, all had a very big influence on the anode porosity and final activity.

The increasing porosity of cathodes was achieved with various carbon powders, which were added as pore formers into the raw powders of SOFC cathodes [181, 182, 184,185,186, 209, 336, 338]. It was established that very porous La_0.6Sr_0.4CoO_3−δ can be prepared at optimal carbon powder additions and carbon particle diameters [208]. Very highly porous materials were synthesised, as demonstrated in Figs. 31 and 32.

Fig. 31

SEM images and corresponding FIB-SEM 3D reconstructions of the SOFC cathode structures [337]

Fig. 32

Influence of cathode porosity on SOFC performance. Different amounts of carbon acetylene black powder were used as pore-forming agents [339]

Cathode porosity had a considerable influence on the oxygen reduction rate, with optimal porosity of 63–66% established for La_0.6 Sr_0.4CoO_3−δ and was achieved with 0.5 wt% pore-former addition into the raw cathode paste. It should be stressed that the cathode porosity depends on the sintering temperature and duration, cathode raw layer thickness and particles size distribution of pore former, binder addition wt% in raw cathode layer, and particle size distribution of raw oxide powder [181, 182, 184, 185, 209, 336].

The FIB-SEM–based 3D tomography has been used to create a 3D model of porous cathode microstructure [21], and it was found that the optimal total porosity is 54%. It was demonstrated that the surface area of the electrode is a very important parameter in addition to the microporosity of the materials under study.

Very high current and power densities have been established for Pr_0.6Sr_0.4CoO_3–δ | Ce_O.9Gd_0.1O_2–δ | Zr_0.86Y_0.15O_2–δ | Ni/Zr_0.92Y_0.08O_2–δ (Fig. 33) [339]. The bilayered electrolyte was deposited to avoid the formation of isolating bilayer of SrZrO_2–δ or other Sr-containing compounds at the cathode surface. The chrono-potentiometry measurements data show that after the quick decrease of current density at the beginning of polarisation, the currents stabilised at high values for very long times.

Fig. 33

Power density vs current density plots for PSCO|GDC|YSZ|Ni-/YSZ single cell at working temperatures (noted in the figure) [339]

The supporting anode microstructure can be a dominating factor in determining the overpotential of the electrooxidation reaction of the fuel at the so-called three-phase boundaries (TPB) and long-term stability of the anode in the fuel cell operating conditions. The anode must have sufficient porosity to allow gas transport to the reaction sites and product species away from the reaction centres. At the time, most of the papers approached the optimisation of Ni-GDC anodes (gadolinium-doped ceria based electrolytes) similarly to Ni-YSZ anodes (yttria-stabilised zirconia based electrolytes) [340, 341]. Tamm et al. [202, 204] optimised the microstructure of supporting Ni-GDC anodes for intermediate SOFC by changing the amount of pore former in the anode raw material. In addition, the influence of pore former particle size distribution on the anode microstructure was studied. The gas adsorption and FIB-SEM were used for the meso-macroporosity analysis of the prepared anodes and cathodes. Assembled single cells were analysed using CV, EIS, and chronopotentiometry or chronoamperometry methods. For the identification of the characteristic frequencies and corresponding process parameters of cathode and anodic processes, the single-cell impedance spectra were recorded and compared analytically as a function of applied potential, partial pressure of hydrogen in the fuel compartment, and partial pressure of oxygen in the cathode compartment. The measured EIS data were analysed in detail using the non-linear regression analysis fitting method and differential derivate of impedance modulus vs frequency dependence methods [177, 185, 187].

MIEC ceramic electrodes like Sr₂Fe_1.5Mo_0.5O_6−δ (SFM) with double perovskite-type structure (A₂BB′O₆) or La_1−xSr_xCr_0.5Mn_0.5O_3−δ (LSCM) or La_1−xSr_xTiO_3−δ (LST) with perovskite structure (ABO₃) can be used instead of metal-cermet hydrogen electrodes [197,198,199,200,201]. SFM has been demonstrated to be a relatively good conductor. The conductivity of LSCM increases at high oxygen partial pressures (high water concentrations) at operating temperatures, which makes it very attractive for electrolysis systems. The main disadvantage of these materials is relatively low electrocatalytic activity. To improve the catalytic activity and stability of the ceramic electrode materials, it is possible to manipulate the bulk stoichiometries and dopant concentrations. Possible dopants for the A-site of SFM are La and Ca and Ni or Cu in the B-site, as well as Ni to the B-site of LSCM. Doping of crystal structure influences the stability of MIEC material, and because of that, better stability could be obtained in some cases by impregnation (creating catalytic centres onto the MIEC surface by using treatment with a solution of catalytically active metal ions) of porous stoichiometrically balanced (no deficiency between A and B sites) non-doped material [197,198,199,200,201, 213].

Infiltration method for SOFC electrode synthesis and its electrochemical characteristics

Tamm et al. employed the aqueous salt solution infiltration method [203] for the preparation of Ni-free low-temperature solid oxide fuel cell anodes, including ceramic 20 vol% La_0.7Sr_0.3VO_3−δ (LSV) composite electrode, infiltrated into 38 μm thick Ce_0.85Sm_0.15O_2−δ electrolyte scaffold with 0.019 S·cm⁻¹ ionic conductivity at 600 °C [186, 187, 202,203,204,205, 210]. The cells, without CeO₂ and Pd promoters, exhibited very low catalytic activity towards H₂ oxidation, with a total high polarisation resistance of 2.0 Ω·cm² and a maximal power density of 17 mW·cm⁻² at 600 °C, comparable to the results established for (La_0.7Sr_0.3)VO_3−δ + YSZ published by Park et al. [342]. The cell, activated with 2.1 vol% CeO₂ catalyst, was only slightly more active with a total polarisation resistance of 1.4 Ω·cm² and maximum power density of 25 mW·cm⁻² at 600 °C. Activation of LSV with 0.3 vol% of Pd increased the performance of LSV to 59 mW·cm⁻². The maximum power density of the cell infiltrated with 2.1 vol% CeO₂ and 0.3 vol% Pd (i.e., complex activated) increased up to 139 mW·cm⁻² at low T = 600 °C. The CeO₂ and Pd activated cells with mentioned anode composition and porous La_0.8Sr_0.2CoO_3−δ cathodes demonstrated low total electrode polarisation resistances 0.3 Ω·cm² and 0.6 Ω·cm² in humified H₂ and CH₄, respectively. Improved anode performance was also achieved by modifying the surface of the porous scaffold through etching with an aqueous HF solution, decreasing the total cell resistance down to 0.1 Ω·cm² and 0.4 Ω·cm² at 600 °C in humidified H₂ and CH₄, respectively. A power density of up to 238 mW·cm⁻² was achieved for the H₂-fuel-feeded cell. The anodes based on LSV-SDC (samaria-doped ceria) composites exhibited stable performance for at least 40 h under load. However, the industrial use of infiltration technology is still hindered by the multistep nature of the method, making it very time and space consuming [202,203,204,205].

Further enhancement of cells was achieved by the optimisation of the scaffold porosity and thickness. After etching the SDC with 10% HF aqueous solution at T = 22 °C, the specific surface area increased from 0.32 to 0.53 m²·g⁻¹. Compared to the YSZ scaffold, where the surface area increased from 0.48 to 2.1 m²·g⁻¹, the complete restructuring of the electrode took place as the entire pore network changed to a sheet and pillar-like structure. The surface roughness increased for the SDC scaffold, explained by the different solubility of Ce⁴⁺ and Zr⁴⁺ in H₂O [186, 187, 202,203,204,205, 210].

Development of novel operando methods for analyses of processes at different interfaces

The FIB-TOF–SIMS method, introduced by Kilner et al. [178], has been used for analyses of Sr segregation processes at cathode | electrolyte interfaces [192, 195, 343]. It was found that the segregation of Sr takes place already during the sintering of LnSrCoO_3-δ cathodes onto the barrier Ce_1−xGd_xO_2−δ layer deposited onto YSZ dense electrolyte to avoid contact of electrolyte with the electrode (Fig. 34). It is mainly caused by the problem that the deposited chemical barrier layer is not dense and defect-free.

Fig. 34

a FIB-TOF–SIMS and b SEM images for YSZ | GDC electrolyte system with PSC cathode showing unwanted Sr mobility and forming of SrZrO₃ phase between GDC chemical barrier layer and electrolyte layers [343]

Therefore, the pulsed laser deposition (PLD) has been applied, and due to the nearly defect-free barrier layer, the Sr segregation effect has been minimised [192, 195, 343]. The main problem is that the PLD is a very time-consuming method and also not usable for large electrodes. Magnetron sputtering (MS) deposited barrier layer has been tested as well. More expressed Sr mobility through the barrier layer has been observed compared with the PLD layer. For some systems, ultrasonic spray (hot) pyrolysis (deposition onto a hot cathode or hot anode) has been successfully used to develop a chemical barrier layer. However, the mobility of Sr through these layers was slightly higher compared to PLD layers because of the very small grain size and a significant amount of grain boundary interfaces.

The operando XRD diffraction method under reactant feeding conditions and electrode polarisation has been used by Kivi et al. [188, 189]. Kinetics of crystallographic changes caused oxide ion flux through the membrane to the porous electrode was studied. This is valuable information for the interpretation of impedance data and for separation for interfacial reorganisation processes and crystallographic changes if electrode polarisation is varied. Differences in crystallographic response for polarisation changes were analysed in the case of (La_1−xSr_x)_yCoO_3−δ and La_0.6Sr_0.4Co_0.2Fe_0.8O_3−δ.

Nurk et al. developed the methods for the analyses of processes at SOFC anodes [193] and the influence of contaminants [194] on SOFC Ni-cermet anode surface composition, i.e., the oxidation state of Ni and Ce_0.9Gd_0.1O_2−δ electrolyte characteristics (Ce oxidation state).

Kooser et al. [195] improved the ambient pressure XPS method discussed by Nenning et al. [196] and applied it in the operando high-temperature near-ambient pressure conditions (HT-NAP-XPS) in conjunction with EIS. A pulsed laser-deposited Ni-Ce_0.9Gd_0.1O_2−δ anode thin film was studied in a novel three-electrode dual-chamber cell at different H₂ pressures and electrode potentials at around 650 °C. The simultaneous use of HT-NAP-XPS and EIS methods made it possible to describe possible redox reactions on the surface of Ni-Ce_0.1Gd_0.1O_2−δ (Ni²⁺ to Ni(O) and Ce⁴⁺ to Ce³⁺). Depth probing of the anode showed remarkable variations in the valence band of XPS spectra with H₂ concentration change at the electrode. The formation of a metal-like structure at the valence edge indicates an electrical conductivity gradient directly beneath the anode surface at lower hydrogen pressure values (around 1 mbar). At higher H₂ pressure (5 mbar), the metal-like valence edge was dominant at all probed anode materials. Changes in the electronic structure of the Ce 3d and Ni 2p photoelectron spectra caused by the electrode potential and hydrogen pressure variations were observed, and corresponding fitting of curves was conducted. The O 1 s and valence band photoelectron data were used for the calculation of the chemical composition and redox changes in/at the Ni-Ce_0.9Gd_0.1O_2−δ electrode. Curve fitting of the Ce 3d photoelectron spectra gave a quantitative estimation of the Ce³⁺ to Ce⁴⁺ ratio at the anode surface (Ce³⁺/Ce⁴⁺ dependence on H₂ pressure and electrode potential/polarisation). At open circuit voltage (OCV) (− 1.263 V) and low H₂ pressure (p_H2 = 1.17 mbar), the concentration of Ce³⁺ at the electrode surface was 53.7%, but at 5 mbar of H₂ (OCV =  − 1.263 V), the concentration of Ce³⁺ was 67.2%. At electrode potential E =  − 0.9 V, at 5 mbar H₂ pressure, the concentration of Ce³⁺ was 60.2%. Thus, the influence of the electrode potential on the chemical (redox) state of anode components was demonstrated. The HT-NAP-XPS data were compared with the EIS data, depending strongly on the electrode potential and hydrogen pressure applied and indicating that the resistance of mass-transfer processes correlates positively with Ce⁴⁺ reduction to Ce³⁺ [193, 195, 196].

Influence of A-site deficiency and chemical composition of B-site including the concentration of Ni, Co, and Cr on electrochemical characteristics of hydrogen electrode in (La_(1−x)Sr_x)_yCr_0.5−zMn_0.5−wNi_z+wO_3−δ | (Sc₂O₃)_0.1(CeO₂)_0.01ZrO₂)_0.89 | La_0.8Sr_0.2FeO_3−δ reversible solid oxide fuel cell has been studied by Maide et al. [197], Lillmaa et al. [206]. The infiltration method has been used for the preparation of cathode and anode electrodes. The dense (Sc₂O₃)_0.1(CeO₂)_0.01(ZrO₂)_0.89 electrolyte layer was sandwiched and co-sintered between two porous ScCeSZ layers. Thereafter, the anode and cathode were impregnated into the porous ScCeSZ matrixes. The wafers were fabricated by laminating three green tapes (porous–tense–porous) using isostatic compression, followed by the high-temperature sintering at 1400 °C for 5 h. Electrochemical characterisation using EIS and CV has been conducted in fuel cell and electrolysis modes. It was established that in the fuel cell mode, the most notable limiting steps were detected around 0.5 Hz and were attributed to a gas-porous solid adsorption–desorption slow rate process. Oxygen partial pressure variations led to small variations in the total impedance of single cells. In electrolysis mode, the dissociative adsorption process was established as an important limiting stage, and the kinetic limitations of the charge transfer step were remarkable. The increase of A-site deficiency caused a significant increase in high-frequency resistance values as well as some increase in total polarisation resistance. Variations in B-site composition had a significant influence on the electrochemical performance with very different frequency dependence of impedance. At 850 °C, the highest current density values of 0.27 A·cm⁻² (fuel cell mode, p_H2 = 0.97 atm and p_H2O = 0.03 atm) and 0.66 A·cm⁻² (electrolysis mode) at unit cell potentials of 0.9 and 1.5 V, respectively, were measured for La_0.75Sr_0.25Cr_0.3Mn_0.5Ni_0.2O_3−d (fuel cell mode) and for (La_0.8Sr_0.2)_xCr_0.49Mn_0.49Ni_0.02O_3−δ (electrolysis mode) in hydrogen fuel gas with p_H2 = 0.70 atm and p_H2O = 0.3 atm, respectively. It should be noted that the electrode compositions and porosities should be different for optimal current densities established for FC mode and EL mode. This was explained by the different rate-limiting processes observed for fuel cell mode and electrolysis mode.

Co-electrolysis of CO₂ and H₂O has been investigated by Maide et al. [197], Lillmaa et al. [206] using the A-site deficient La_1−xSr_xCr_1−xMnO_3−δ electrodes grown via the impregnation method. The thickness of the dense electrolyte and the porous scaffold was approximately 75 μm and 40 μm, respectively. Ceramic perovskite-structured (La_0.8Sr_0.2)_x(Cr_0.5Mn_0.5)_yNi_zO_3−δ (x = 1, 0.9, 0.8; y = 1.0, 0.94; z = 0.0, 0.06) with various A-site deficiencies and 6 mol% of Ni in B-site were used as hydrogen electrodes and La_0.8Sr_0.2FeO_3−δ as O₂ electrode. Moderate reaction activity and stability have been observed.

Conclusions

This review summarises the major achievements in interfacial electrochemistry in Estonia since 1990. Electrical double layer characteristics, adsorption of organic compounds and specific adsorption of anions at sp-metal single-crystal planes and micro-mesoporous carbons from aprotic and other non-aqueous electrolytes, and ionic liquids and ionic liquid mixtures have been studied and discussed. Electrochemical characteristics of supercapacitors, including hybrid capacitors and Li⁺-ion and Na⁺-ion batteries, have been established and analysed. The influence of carbon support materials characteristics (micro-, meso-, and macroporosity, pore size distribution and hierarchical porous structure, graphitisation level, and electric conductivity) on the Pt-metal nanoclusters, and Pt-metals free polymer membrane fuel cells parameters have been analysed. The influence of rare earth metal oxide nanoclusters deposited onto Pt nanoparticles activated carbon particles on direct methanol fuel cell characteristics has been demonstrated. The electrochemical properties of high-temperature solid oxide fuel cells and high-temperature electrolysis cells have been established, and the influence of the electrode (negatively and positively charged, compositions, porous structure, etc.) on the electrochemical characteristics has been discussed.

Different in situ and operando methods like operando electrochemical high-temperature X-ray diffraction spectroscopy for solid oxide electrode analyses, synchrotron beam near ambient pressure dual chamber XPS for anode and cathode processes in solid oxide fuel cells, in situ XPS for the study of the influence of electrode potential on the electrochemical processes at carbon electrodes in ionic liquids, neutron beam small angle scattering studies at porous carbon, and complex metal hydride materials characteristics have been conducted and results have been analysed.

The strong influence of sp-metals (Bi, Sb, Cd) and single-crystal carbon (C(0001)) electronic characteristics (concentration of charge carriers, effective mass of electrons) on the potential of zero charge, differential capacitance, Gibbs adsorption, and Gibbs free energies of adsorption values have been demonstrated. The effect of solvent chemical composition and dielectric characteristics on the surface activity and Gibbs adsorption energy values of anions at sp-metal single-crystal and carbon electrodes has been demonstrated. The influence of ionic liquid anion composition on the specific adsorption characteristic, including time constant, at Bi(hkl), Sb(hkl), Cd(hklf), and C(0001) single-crystal electrodes have been demonstrated. The applicability limits of various ionic liquids in electrical double layer capacitors, hybrid supercapacitors, secondary-ion batteries, and other electrochemical devices determining the energy and power density parameters have been verified. Appreciable increase of specific energy and power densities for supercapacitors, hybrid capacitors, and Na⁺-ion batteries with ionic liquid and ionic liquid mixture electrolytes containing surface-active iodide and bromide anions has been demonstrated.

The solid fundamental basis and continuous emphasis on the development of a comprehensive understanding of electrochemical processes at the electrode | electrolyte interface in collaboration with the drive to design and enhance the performance of novel energy storage devices has led to the publication of numerous scientific papers with exciting discoveries, e.g., 4–10 V capacitors with graphene-based electrodes, the visualisation of adsorbed layers at single-crystal electrodes, and synthesis of carbide-derived carbon materials with outstanding properties. Furthermore, the group has set their focus on supporting the Estonian transition to green energy through supporting science-based policy-making and industrial processes.