Introduction

A wide variety of materials ranging from fundamental materials in modern society such as Al [1], Ti [2], and Si [3] to functional materials [4] can be produced using molten salt electrolysis. Such large-scale production of these materials through continuous electrolysis requires to the inert anode as one of the key technologies and solves resource and energy problems. Conventional electrolysis using a consumable graphite anode emits various greenhouse gases in a melt containing oxide ions [1, 4], thereby adding to the global warming problem. Driven largely by the demand for reduced greenhouse gas emissions, various types of oxides, including SnO2 (rutile), NiFe2O4 (ferrite), and CaRuO3 (perovskite) [4,5,6], have been investigated as potential candidates for inert anodes. Although these oxides have limited solubility in melts, their conductivity and long-term stability are inadequate [7]; therefore, Fe–Ni [8] and Fe–Cr [9] alloys have been investigated as potential inert anode materials. However, impurity deposition on the cathode cannot be avoided in metal/alloy anode. Against this background, as shown in Fig. 1, an inert anode system using an yttria-stabilized zirconia (YSZ) membrane was proposed [10]. The YSZ membrane is a key component of inert anode systems and performs important functions. For example, it acts as a physical block to avoid the direct mixing of cathode products and the anode. Moreover, it acts as a selective conduction path for oxide ions while blocking solvent anions and ensuring high chemical stability [11, 12]. Liquid Ag anodes are thermodynamically stable in oxygen and electrically conductive to evolve oxygen [10]. The La0.8Sr0.2MnO3-δ (LSM82) current collector exhibits mixed ionic-electronic conductivity and low diffusivity of oxide ions at high temperatures [13,14,15,16,17] and works as an ion-blocking inert anode. During electrolysis, as the oxide ion in the melt penetrates the YSZ membrane and is oxidized at the liquid Ag and LSM82 anode, the anode should exhibit high conductivity and low polarization pertaining to oxygen evolution. However, LSM82 typically exhibits low electronic conductivity [18]. A high electronic conductivity is required for anode for large-scale material production through molten salt electrolysis [4]. As shown in Table 1 [18,19,20,21,22], La1-xSrxCoO3-δ (LSC) is considered an attractive anode candidate because of its high electronic conductivity; moreover, to produce functional nanomaterials, the electrolysis is performed below intermediate temperatures, that is, at ~ 800 K, while curtailing the particle growth [4]. Therefore, La1-xBaxCoO3-δ (BLC) is also interesting owing to its high electronic conductivity at intermediate temperatures (La0.5Ba0.5CoO3-δ (BLC55): 760 S‧cm-1 and La0.4Ba0.6 CoO3-δ(BLC64): 365 S‧cm-1 [23]). Furthermore, Co ion substitution in perovskites lowers the anode polarization for oxygen evolution [20, 23].

Fig. 1
figure 1

Schematic illustration of molten salt electrolysis using an inert anode system with YSZ membrane [10]

Full size image
Table 1 Conductive properties of Sr-doped perovskite oxides [18,19,20,21,22]
Full size table

The lifetime of this inert anode system was determined by the oxide ion diffusivity of LSM82. During long-term electrolysis, some oxide ions penetrating from the melt through the YSZ membrane and liquid Ag transport through LSM82 to arrive at the metal/alloy current collector. The progress of this oxide ion transportation inside LSM82 oxidizes the metal/alloy current collector and degrades the anode system; therefore, the oxide ion transportation must be curtailed. The oxide ion diffusivities in La1-xAxCoO3-δ (A = Sr, Ba) depend on the doped ion content (Table 1 [21,22,23]). Additionally, by nanostructure fabricating an inert anode while considering the diffusion pathway of the oxide ions in La1-xAxCoO3-δ nanoparticles, the oxide ion transportation can be reduced while maintaining the high electronic conductivity.

In this study, La1-xAxCoO3-δ was characterized by lattice dynamics using X-ray diffractometry (XRD) measurements, and the relationships between oxide ion diffusivities and crystallographic structures were investigated. The oxide ion diffusivities of these perovskites were conventionally measured isotropically using isotope exchange depth profiling [21] and conductivity relaxation techniques [22]. In contrast, the Debye temperature (\({\Theta }_{D}\)) characterization using XRD measurements, which can be applied to compare the oxide ion diffusivity of a material [24, 25], requires a powdered sample instead of a sintered pellet. The \({\Theta }_{D}\) is a specific parameter used to characterize the atomic vibrational behavior of a crystal lattice (phonon) and is defined as follows [26]:

$$\hslash {\omega }_{D}={k}_{B}{\Theta }_{D}$$
(1)

where ℏ is the Dirac constant, \({\omega }_{D}\) is the Debye frequency that denotes the phonon maximum frequency, and kB is the Boltzmann constant. The Debye temperature (\({\Theta }_{D}\)) was determined from the temperature dependence of the specific atomic displacement parameter (U) of the material using high-temperature XRD measurements as follows:

$$U=\frac{{3\mathrm{\hslash }}^{2}T}{{m\;k}_{B}{\Theta }_{D}^{2}}$$
(2)

where T is the absolute temperature and m is the molar weight of the material or specific ion. Owing to its simplicity, XRD can be used for a wide range of material characterizations, including environmental dependency evaluations and/or operando measurements. In perovskite oxides, \({\Theta }_{D}\) is correlated with carrier diffusivity, and anisotropic diffusivity corresponding to the crystallographic face has been observed [25]. Therefore, this study focuses on the compositions and morphologies of La1-xAxCoO3-δ nanoparticles.

Experimental

A solid-state method was used to synthesize the LSC nanoparticles [27]. The carbonates and oxides used in the mixture were La2O3 (99.9%, Furuuchi Chemical Co., Japan), SrCO3 (99.99%, Honjo Chemical Co., Japan), and 2CoCO3 \(\cdot\) 3Co(OH)2 \(\cdot\) 4H2O (99.9%, Kanto Chemical Co. Inc., Japan). The starting materials were homogenously mixed in appropriate stoichiometric amounts using planetary zirconia ball milling for 12 h. The slurry was then dried at 393 K in a vacuum oven; the obtained LSC nanoparticles were characterized using XRD (RINT2200V, Rigaku Corp., Japan). XRD data were obtained for the 2θ range of 10–120° with a step interval of 0.02° using Cu-Kα radiation.

The synthesized LSC and commercially available BLC nanoparticles (Kusaka Rare Metal Products Co. Ltd., Japan) were characterized using high-temperature synchrotron radiation XRD (SR-XRD) measurements. A large Debye–Scherrer camera installed at beamline BL19B2 at the SPring-8 synchrotron radiation facility (Hyogo, Japan) and a photographic plate [28,29,30] were used for the measurements. To evaluate the temperature dependence of U in a crystal lattice, high-temperature SR-XRD patterns were measured at the temperature range of 300-900 K. The perovskite nanoparticles were sealed in a quartz capillary tube (inner diameter of 0.3 mm) in air. The sample capillary temperature was stabilized to values within ± 0.5 K using N2 gas flow. SR-XRD data were obtained for the 2θ range of 5–70° with a step interval of 0.01° and an X-ray wavelength of 0.5 Å, which was determined by calibrating a CeO2 standard sample from the National Institute of Standards and Technology. The obtained diffraction patterns were analyzed using Rietveld refinement, which was performed using RIETAN-FP [31] with a modified split pseudo-Voigt function. The corresponding crystal structures were visualized using VESTA [32]. The valence of Co ions in the perovskites was estimated using the bond valence sum (BVS) method [33, 34].

Results and discussion

La1-xSrxCoO3-δ nanoparticles

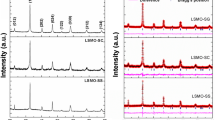
Figure 2a shows the XRD patterns of the LSC nanoparticles with different Sr ion contents measured at room temperature. The observed diffraction patterns were ascribed to a typical LSC with a trigonal R-3c structure [35]. The XRD patterns in the 2θ range of 32–34° are shown in Fig. 3a, exhibiting the structural change of the LSC nanoparticles with increasing Sr ion content. The diffraction peak corresponding to the LSC (110) face shifted to a lower angle due to Sr ion doping in LaCoO3, and subsequently the peak shifted to a higher angle with higher Sr ion content, corresponding to the change in the lattice constant, a-axis (b-axis). In contrast, the diffraction peak of the LSC (104) face shifted to a lower angle, indicating that the LSC crystal lattice was enlarged in the c-axis direction. The LSC crystal lattice expanded due to Sr ion doping at x < 0.15. It is known that the phase for x < 0.15 shows semiconductive behavior and that for x ≥ 0.15 exhibits metallic behavior in electron conduction [36,37,38,39,40,41,42,43]. Oxygen defects were introduced in the LSC crystal lattice at x ≥ 0.15, as follows [44, 45]:

Fig. 2
figure 2

(a) XRD patterns of La1-xSrxCoO3-δ nanoparticles with different Sr ion contents (x) at room temperature. (b) Schematic diagram of the La1-xSrxCoO3-δ crystal lattice

Full size image
Fig. 3
figure 3

(a) XRD patterns enlarged at 2θ = 32–34° and (b) lattice parameters of a and c-axes of La1-xSrxCoO3-δ nanoparticles

Full size image
$$LaCo\left(III\right){O}_{3}+xSr\left(II\right)\to {La}_{1-x}{Sr}_{x}{Co}_{1-y}\left(III\right){Co}_{y}\left(IV\right){O}_{3-\delta }+xLa\left(III\right)+\delta /{20}_{2}$$
(3)

Some Co(III) ions in the B-site of LSC were oxidized to Co(IV) to compensate for the oxygen defects introduced at the A-site of LSC by Sr ion doping. Furthermore, structural inflections of the LSC crystal lattice were observed at LSC82 (x = 0.2) and LSC64 (x = 0.4), and these compositions of LSC were considered as the singularity points of the crystal structure. Figure 4 shows the dependency of Co ion valency on the Sr ion content, which was evaluated using the BVS method. Inflections were observed at LSC82 and LSC64, and these compositions of LSC were singularity points even in the electronic state. The valencies of Co ions in the LSC nanoparticles were 3.2 (y = 0.25) and 3.3 (y = 0.29) for LSC82 and LSC64, respectively. Using potentiometric–titration measurements, Itoh et al. [27] found that the Co ion valencies in the LSC nanoparticles were 3.19 and 3.30 for LSC82 and LSC64, respectively. These results show that the BVS method can roughly estimate the valency values even in the singularity points of the crystal structure. Using X-ray absorption spectrometry, Itoh et al. [27] confirmed that increasing in the Co–O bond length of the phase x < 0.15 corresponds to the change in spin configuration from the low-spin state to intermediate-spin and/or high-spin state. As the Sr ion content of LSC increased, the O–Co–O angle approached 90°, indicating that the symmetry of CoO6 in LSC increases with increasing Sr ion content. The Co–O–Co bond angle between the CoO6 hexahedrons in LSC approached 180° with an increase in the Sr ion content, and discontinuous changes in the Co–O–Co bond angles at LSC82 and LSC64 were observed. The composition x = 0.15 and the discontinuous changes were in good agreement with the changing tendency of the Co–O bond length and the metal–insulator transition. Therefore, Itoh et al. [27] concluded that the Co–O–Co bond angle also exhibits the spin state.

Fig. 4
figure 4

(a) Results of the BVS calculations and (b) bond angles of La1-xSrxCoO3-δ nanoparticles

Full size image

Figures S1 and S2 show the SR-XRD patterns of the LSC82 and LSC64 nanoparticles measured at 300 and 800 K, respectively. Although no crystal structural changes were observed at 800 K, the growth of LSC nanoparticles was observed at 800 K in LSC82 and 600 K in LSC64 as shown in Fig. 5a. These grain growths were caused by the structural phase transition from trigonal to cubic of LSC and are consistent with the results of Mastin et al. [45]. The transition temperature decreased as Sr ion content in LSC increased [45]. The temperature dependences of the isotropic atomic displacement parameters (Uiso) of each consistent ion in LSC82 and LSC64 are shown in Fig. 6. According to the Debye model [26], the atomic vibrational amplitude (atomic displacement parameter, U) is classified into two disordered states, that is, the static state and dynamic state. U does not depend on the temperature in the static state at low temperatures and linearly increases with temperature in the dynamic state at high temperatures [26]. The slope of U in a dynamic state is the dynamic Debye temperature (\({\Theta }_{D}\), Dynamic). The carrier diffusivity is accelerated in this dynamic state, and the material properties are evaluated using \({\Theta }_{D}\), Dynamic. Herein, \({\Theta }_{D}\), Dynamic (defined in Eq. (2) [26]) is used as \({\Theta }_{D}\).

Fig. 5
figure 5

Temperature dependences of the full width half maximum (FWHM) of the diffraction peak corresponding to the (110) face in La1-xAxCoO3-δ (A = Sr, Ba) nanoparticles: (a) La1-xSrxCoO3-δ and (b) La1-xBaxCoO3-δ

Full size image
Fig. 6
figure 6

Temperature dependences of the atomic displacement parameter (Uiso) for La1-xSrxCoO3-δ nanoparticles: (a) La0.8Sr0.2CoO3-δ and (b) La0.6Sr0.4CoO3-δ

Full size image
$${U}_{Dynamic}=\frac{{3\mathrm{\hslash }}^{2}T}{{m\;k}_{B}{\Theta }_{D,\; Dynamic}^{2} }$$
(4)

The Uiso parameter of each consistent ion in LSC82 depended only slightly on temperatures below 900 K (Fig. 6a). Therefore, the \({\Theta }_{D}\) value for LSC82 was not calculated. This tendency was also observed in LSM82 [25]. Although the value of \({\Theta }_{D}\) for LSM82 was 348 K, the transition from a static state to a dynamic state was not observed until 800 K [25]. In LSC64, the Uiso values of each constituent ion increased linearly with the temperature (Fig. 6b). Furthermore, \({\Theta }_{D}\) was obtained from the slope of plot in Fig. 6b in the dynamic state. The value of \({\Theta }_{D}\) in the LSC64 nanoparticle was estimated to be 400 ± 8 K, and those of the constituent ions of the LSC64 nanoparticles are listed in Table 2. The total \({\Theta }_{D}\) was calculated as the sum of the \({\Theta }_{D}\) of each constituent ion, while considering the composition of LSC64.

Table 2 Debye temperatures (\({\Theta }_{D}\)) of La0.6Sr0.4CoO3-δ nanoparticles
Full size table

La1-xBaxCoO3-δ nanoparticles

Figure S3 shows the SR-XRD patterns of the BLC nanoparticles measured at 300 K. The observed diffraction patterns were ascribed to a typical BLC with a cubic Pm-3 m structure [46]. The calculated valencies of Co ion in BLC nanoparticles using the BVS method were 3.1 (Co–O bond length = 1.94714 Å) and 3.0 (Co–O length: 1.95872 Å) for BLC55 and BLC64, respectively. These results indicate that oxygen defects were slightly introduced by Ba ion doping in BLC nanoparticles, because few Co(III) ions were oxidized for the charge compensation of the oxygen defects. Figure S4 shows the SR-XRD patterns of the BLC nanoparticles measured at 800 K. Although crystal structural changes were not observed at 800 K, the grains grew at higher temperatures as shown in Fig. 5b. The temperature dependences of the Uiso of each consistent ion in BLC nanoparticles are shown in Fig. 7. The temperature dependence of the Uiso of each ion in BLC64 significantly fluctuated, which was mainly caused by the grain growth (Fig. 5b). The Uiso values of each constituent ion increased at temperatures higher than 500 K. The \({\Theta }_{D}\) is obtained from the slope of the temperature dependence of Uiso, and the \({\Theta }_{D}\) values in the BLC55 and BLC64 nanoparticles were estimated to be 382 K and 361 K, respectively. The \({\Theta }_{D}\) values of the constituent ions in the BLC nanoparticles are listed in Table 3. A higher oxide ion diffusivity was observed for higher \({\Theta }_{D}\) perovskites (Fig. S5) [25]. Therefore, Table 3 suggests that the oxide ion diffusivity in BLC55 is higher than that in BLC64. Furthermore, in comparison with the diffusivity of other perovskite oxides [25], the \({\Theta }_{D}\) value in BLC is lower than that in LSC, and BLC is expected to show superior oxide ion blocking characteristics.

Fig. 7
figure 7

Temperature dependences of the atomic displacement parameter (Uiso) for La1-xBaxCoO3-δ nanoparticles: (a) La0.5Ba0.5CoO3-δ and (b) La0.4Ba0.6CoO3-δ

Full size image
Table 3 Debye temperatures (\({\Theta }_{D}\)) of La1-xBaxCoO3-δ nanoparticles
Full size table

Diffusion anisotropy of oxide ion in La1-xAxCoO3-δ (A = Sr, Ba) nanoparticles

This section presents a detailed evaluation of the diffusion pathway in the crystal structures of these materials. The lifetime of an inert anode system is determined by the oxide ion diffusivity of the La1-xAxCoO3-δ (A = Sr, Ba). Oxide ion transportation inside La1-xAxCoO3-δ oxidizes the metal/alloy current collector and degrades the anode system. Therefore, the oxide ion transportation must be curtailed. By fabricating an inert anode while considering the diffusion pathway of oxide ion in La1-xAxCoO3-δ nanoparticles, the oxide ion transportation can be curtailed while maintaining high electronic conductivity. In the XRD pattern, the diffraction peak (In, hkl) is attributed to the crystallographic face (hkl) as [26]

$$I_{\mathrm n,\;hkl}\propto\exp{(-\frac{8\pi^2\mathrm \;U_{\mathrm n,\;hkl}}{{(\sin\theta/\lambda)}^2})}^2$$
(5)

where θ and λ are the diffraction angle and wavelength, respectively. Un, hkl is the atomic displacement parameter of the material or ion on the crystallographic face (hkl) at temperature (Tn). By taking the natural logarithm of Eq. (5) and considering Eq. (2), we obtain

$$\ln\frac{I_{1,\;hkl}}{I_{2,\;hkl}}=\frac{48\pi^2\hslash^2\;}{mk_B}\frac{T_2-T_1}{\triangle\Theta_{{\mathrm D},hkl}^2}{(\sin\;\theta/\lambda)}^2$$
(6)

where I1, hkl and I2, hkl are the diffraction peaks corresponding to the crystallographic face (hkl) at temperatures T1 and T2, respectively, and \({\Delta\Theta }_{D, hkl }\) is the anisotropic Debye temperature at the crystallographic face (hkl). As shown in Eq. (6), \({\Delta\Theta }_{D, hkl }\) can be calculated using the temperature differences between the diffraction peaks, and its orientation depends on the crystallographic face. Perovskites show that a higher diffusivity is observed with a higher \({\Theta }_{D}\) material (Fig. S5) [25]. Therefore, \({\Delta\Theta }_{D, hkl }\) accounted for the diffusional anisotropy at each crystal face.

The \({\Delta\Theta }_{D, hkl }\) values were determined using Eq. (6) with the XRD patterns obtained at temperature above 600 K (T > \({\Theta }_{D }\)). The \({\Delta\Theta }_{D, hkl }\) values for LSC revealed that \({\Delta\Theta }_{D}\) values at the (300) and (330) faces increased (Table 4), suggesting high diffusivity at these faces. These results indicate that oxide ions preferentially diffused along the (a, b) plane in the LSC crystal lattice, as shown in Fig. 8. This tendency is consistent with that of other Sr-doped perovskite oxides [25]. In contrast, the \({\Delta\Theta }_{D, hkl }\), values for the BLC showed that the (444) face yielded increased \({\Delta\Theta }_{\mathrm{D}}\) values (Table 5), thus suggesting high diffusivity in c-axis direction in the BLC crystal lattice. Consequently, it was suggested that the oxide ion transportation of the anode was curtailed using layered La1-xAxCoO3-δ particles.

Table 4 Anisotropic Debye temperatures (\({\Delta\Theta }_{\mathrm{D}}\)) at each crystallographic face of La1-xSrxCoO3-δ nanoparticles
Full size table
Fig. 8
figure 8

Schematic illustration of the diffusion pathway of oxide ions in the La1-xAxCoO3-δ (A = Sr, Ba) crystal lattice: (a) La1-xSrxCoO3-δ and (b) La1-xBaxCoO3-δ

Full size image
Table 5 Anisotropic Debye temperatures (\({\Delta\Theta }_{\mathrm{D}}\)) at each crystallographic face of La1-xBaxCoO3-δ nanoparticles
Full size table

Conclusions

This study characterized the La1-xAxCoO3-δ (A = Sr, Ba) nanoparticles as inert anodes in molten salts using phonon vibrations and investigated the compositions and morphologies of La1-xAxCoO3-δ nanoparticles used for fabricating an inert anode to curtail the oxide ion transportation. The O–Co–O angle approached 90°, and the Co–O–Co angle between the CoO6 hexahedrons in the LSC approached 180° with an increase in the Sr ion content, suggesting an increase in the symmetry of the CoO6 hexahedrons in LSC. The singularity structure changed with increasing Sr ion content in the LSC nanoparticles, showing transient spin state change from a low-spin state to intermediate-spin state and/or high-spin state. The valencies of Co ion in the LSC nanoparticles were calculated to be 3.2 and 3.3 for LSC82 and LSC64, respectively, which suggested that oxygen defects were introduced by Sr ion doping in the LSC nanoparticles. Some Co(III) ions in the B-site of LSC crystal lattice were oxidized to Co(IV) to compensate for the oxygen defects introduced at the A-site of LSC by Sr ion doping. The ratios of Co (IV) ions in the LSC crystal lattice were 25% in LSC82 and 29% in LSC64. The valencies of Co ion in the BLC nanoparticles were calculated to be 3.1 and 3.0 for BLC55 and BLC64, respectively, which suggested that oxygen defects were introduced slightly by Ba ion doping in the BLC nanoparticles. The isotropic phonon vibrations of the La1-xAxCoO3-δ nanoparticles were estimated using high-temperature SR-XRD measurements. First, considering the temperature dependence of the isotropic atomic displacement parameters, the isotropic Debye temperatures were estimated to be 400 ± 8 K, 382 K, and 361 K in air for LSC64, BLC55, and BLC64, respectively. Crystal anisotropy measurements of phonon vibrations revealed that oxide ions diffused preferentially along the (a, b) plane in the LSC crystal lattice and toward the c-axis direction in the BLC crystal lattice. These results suggest that oxide ion transportation was curtailed using layered La1-xAxCoO3-δ particles to fabricate an inert anode.