Introduction

Properties and applications of electroactive ion-exchange membranes are attributed to ion fluxes within the membrane and ion transfer across the membrane–solution interface. These effects are particularly important in the field of ion-selective electrodes (ISEs). These sensors are established tools of routine potentiometric analysis in different fields: industrial, medical, environment protection, etc. A significant progress in the improvement of analytical parameters of these sensors, concerning lower detection limit, higher sensitivity and selectivity, is owing to new constructions and membrane compositions as well as precise tailoring of ion fluxes in the membrane and at the membrane–sample solution interface [1–3]. Theoretical studies, based initially on simplified models taking into account a steady state diffusion [4–6] and then on more advanced models [7–10] as well as those based on Nernst–Planck–Poisson equations [11, 12], are related to this issue.

However, because ISEs typically work under potentiometric/open circuit conditions, it is not easy to study experimentally these fluxes; to achieve quantitative data on ion transport, external polarization or spectroscopic studies of the membrane were usually necessary. Gyurcsanyi et al. [13] have applied scanning electrochemical microscopy supplemented with potentiometric measurements to follow up a time-dependent buildup of steady state diffusion layers. Ion fluxes and obtained concentration profiles under zero-current conditions have been also studied by mass spectrometry with laser ablation of the membrane material [14].

In this work, we proposed a simple protocol enabling the determination of ion fluxes under open circuit conditions, based on potential measurements and their changes in time, in the absence and presence of solution stirring. The role of solution stirring for affecting ion fluxes to decrease the detection limit and to optimize the sensor performance has been already shown earlier [15, 16]. Measurements under open circuit conditions are obviously advantageous due to a lack of external polarization which can bias the spontaneously occurring phenomena; moreover, the experimental conditions are similar or the same as in a routine analysis.

In typical applications, ISEs with membranes saturated by primary ions are used; however, this is not always the optimal option. Due to a relatively high concentration of primary ions in the membrane, leakage to the adjacent solution layer is possible, resulting in elevated detection limit [5]. Therefore, extended linear response range and lowered detection limit are observed for precisely and partially saturated membranes [1, 5]. Since such optimal saturation is hardly available in the course of typical open circuit conditioning, some methods of controllable preparation of such membranes have been proposed, e.g. application of two ion exchangers with primary and interferent cations [17], galvanostatic tailoring of primary ion contents in the membrane [18]. Comparison of potentiometric characteristics with membrane composition confirmed that the saturation degree of a membrane with primary ions significantly below 100 % offered the best potentiometric performance with lowered detection limit [17, 18].

In this work, we concentrated on fluxes observed for non-saturated membranes, since knowing parameters characterizing ion fluxes in this case enables a more precise control of the membrane saturation, what is important for obtaining optimal potentiometric characteristics. These data would be also useful for modelling and ultimately optimizing potentiometric responses what is of high interest, e.g. from the point of view of sensors application. As a model example, silver-selective ISEs with poly(vinyl chloride)-based membrane were chosen, with polypyrrole used as a solid contact, to study silver ions fluxes.

To show a more general significance of the proposed method, analogous studies were carried out for electrodes coated by another kind of ion-exchange membrane-conducting polymer (polypyrrole) where ion transport is of significance. Diffusion and migration phenomena in such polymers have been described e.g. by Lyons et al. [19, 20].

In the present work, a layer of polypyrrole doped by poly(4-styrenesulfonate) ions (without added ion-selective membrane) was studied. In this case, the ion flux results from a spontaneous reduction of silver ions by polypyrrole. This conducting polymer, in the presence of oxygen, is typically in a semi-oxidized state. Therefore, polypyrrole can be further oxidized by metal ions of relatively high oxidation potential. This process can be useful for metallisation on polymer pads [21], recovery of noble metals [22] as well as development of heavy metal ions sensors (e.g. [23]). Silver electroless deposition on/in polypyrrole layers has been studied in detail by Song and Shiu [24], who discussed the role of silver ion concentration, film thickness, conditioning time, solution pH, etc. This system and, particularly, kinetics of silver deposition in polypyrrole films have been also studied in our laboratory [25], using rotating disc electrode voltammetry. Thus, comparison of results collected using this method with those using the procedure described in the present paper was shown.

Experimental

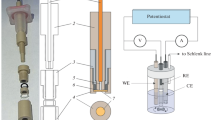
Apparatus and electrodes

In the potentiometric experiments, a multi-channel data acquisition set-up and software obtained from Lawson Labs, Inc. (3217 Phoenixville Pike, Malvern, PA 19355, USA) was used. The pump systems 700 Dosino and 711 Liquino (Metrohm, Herisau, Switzerland) were applied to obtain sequential dilutions of calibrating solutions and to stir the solution in the course of its pumping in/out.

For chronopotentiometric measurements, galvanostat–potentiostat CH Instruments Model 660A (Austin, TX, USA) was used.

In potentiometric experiments, a double-junction Ag/AgCl reference electrode with 1 M lithium acetate in outer sleeve (Möller Glasbläserei, Zürich, Switzerland) was used. In chronopotentiometric experiments, the same reference electrodes were used; moreover, platinum plate of surface area 2 cm2 served as a counterelectrode. Glassy carbon (GC) disc electrodes used as working electrodes (area 0.07 cm2) were polished with Al2O3, 0.3 μm.

Reagents

Tetrahydrofuran (THF), poly(vinyl chloride) (PVC), bis(2-ethylhexyl sebacate) (DOS), sodium tetrakis[3,5-bis(trifluoromethyl)phenyl]borate (NaTFPB), silver ionophore IV (O,O″-bis[2-(methylthio)ethyl]-tert-butylcalix[4]arene), pyrrole and sodium poly(4-styrenesulfonate) (NaPSS) were from Sigma-Aldrich (Germany).

Doubly distilled and freshly deionised water (resistivity 18.2 MΩ cm, Milli-Q Plus, Millipore, Austria) was used throughout this work. All used salts were of analytical grade and were obtained from POCh (Gliwice, Poland).

Electrodes with polypyrrole/silver-selective membranes

GC electrodes were coated by polypyrrole layers, obtained by potentiostatic polymerization (E = 0.9 V) carried out from aqueous solution of 0.1 M NaPSS and 0.05 M pyrrole; polymerization charge was 100 mC. After polymerization, the electrodes with polypyrrole film were conditioned in 0.1 M NaNO3 solution for 1 h.

PVC-based membranes contained (in wt%) 2.3 % of silver ionophore, 1.1 % of NaTFPB, 67.4 % of DOS and 29.2 % of PVC; total 100 mg of membrane components were dissolved in 1.5 mL of THF.

The PVC-based ion-selective membranes used were applied on the glassy carbon electrode with polypyrrole layer placed in upside down position. For poly(vinyl chloride)-based membranes, 20 μL of PVC cocktail in THF (two 10 μL portions) was applied per electrode (unless otherwise stated) and left to dry in laboratory atmosphere for 20 h.

The membrane thickness was determined after the experiment using a micrometre caliper, and it was around 200 ± 20 μm (unless otherwise stated). The prepared sensors before tests were conditioned overnight in 0.1 M NaNO3 solution.

Procedure

If a cation-sensitive ion-selective electrode with a membrane, not containing primary cations, is immersed in a sample solution, spontaneous extraction of primary cations into the membrane occurs. At the same time, a counterflux of cations introduced primarily to the membrane with cation exchanger, typically Na+ or K+, is released from the membrane, resulting in zero-current conditions. However, these phenomena change not only the membrane composition but also the composition of the adjacent phases and result in concentration polarization. Particularly, the concentration of primary ions close to the membrane surface is lower than that in the solution bulk. Within a short period of time, the flux, J, of primary ions can be assumed constant, and in this case, the following relation between the bulk concentration of primary ions, c 0, and the concentration at the membrane–solution interface (solution side), c(0,t), holds [26]

$$ c\left(0,t\right)={c}^0-2J\sqrt{\frac{t}{ D\pi}} $$
(1)

where D is the diffusion coefficient of primary ions in solution, and t is the time.

The electrode potential is sensitive to primary ion concentration at the surface, c(0,t), and if this concentration differs significantly from c 0, the potentiometric calibration plot—potential vs. logarithm of ion concentration in the bulk—deviates from Nernstian behaviour. Since the concentration polarization effect is significant for rather low concentrations c 0, the above mentioned deviation is seen as a super-Nernstian behaviour for low analyte concentrations.

The procedure of J value determination, proposed here, was based on recording potential in diluted solution, for which a significant super-Nernstian deviation on calibration plots was visible. The potential recorded in diluted solution is dependent on several factors such as physical state of the membrane, saturation degree of the membrane with primary ions, oxidation state of the conducting polymer solid contact as well as primary ion concentration at the membrane–solution interface. In order to observe only the effect of concentration polarization, stirring of the solution can be switched on for a short time (Scheme 1). At this moment, the existing diffusion layer in the aqueous solution disappears, and c(0,t) can be assumed to be equal to c 0. After the stirring is switched off, a new diffusion layer builds up, and recorded potential changes result from a decreasing surface concentration, c(0,t). Due to rather short time of the measurement after switching off, other parameters affecting the potential can be assumed constant, similarly as the flux, J. Then, using the recorded potentials just after switching off the stirring and basing on Nernst equation (assuming also that at the moment of switching off the stirring, the surface concentration is c 0), the concentration c(0,t) can be calculated as a function of time. Then, the obtained c(0,t) values can be inserted into Eq. 1, and the value of J can be calculated. Since the value of J recorded in the solution is equal to the flux in the membrane, information about ion transfer rate within the membrane material can be obtained as well. The short stirring step can be introduced at several times, leading to destroying the old and building a new diffusion layer. For each case, the above calculations can be repeated, and in this way, the value of flux as a function of time (e.g. of conditioning) can be obtained.

Scheme 1
scheme 1

Changes of open circuit potential in stirring on/off procedure

Full size image

On the other hand, lack of stirring influence on recorded potential can denote the absence of primary ions flux [10] or its low value, resulting in negligible concentration polarization effects for the existing bulk concentration.

The above procedure described for the ISE case can be also applied to other kinds of membranes, where spontaneous ion extraction occurs and the membrane potential is sensitive to activity of ions undergoing incorporation.

Results and discussion

PVC-based silver-selective membranes

Figure 1 presents calibration plots recorded in AgNO3 solutions for silver-selective ISE with non-saturated membrane, conditioned overnight in 0.1 M NaNO3 solution. A linear dependence of potential on logarithm of AgNO3 concentration was observed with slope close to Nernstian in the concentration range above 10−4 M. In our measurements, AgNO3 concentrations higher than 10−3 M were not used in order to avoid advanced accumulation of silver ions in the membrane in the course of measurement in concentrated AgNO3 solution [27]. For the electrode tested just after conditioning in NaNO3 solution, for AgNO3 concentration lower than 10−4 M, a significant decrease of potential was observed (a super-Nernstian behaviour). This effect results from both spontaneous extraction of silver ions into the membrane and, as a consequence, concentration polarization comparable with concentration in solution bulk. For consecutive calibrations, the super-Nernstian effect became weaker due to slower incorporation of silver ions to the membrane. The most exposed effect of potential changes in separate calibrations was observed for various concentration ranges. During the first hours of contact with AgNO3 solutions, the most significant potential changes were observed at AgNO3 concentration 10−5 M, pointing to a high influence of concentration polarization. Therefore, this concentration was chosen for further studies on silver ion fluxes to non-saturated membranes, based on tracing potential transients in stirred or non-stirred solutions.

Fig. 1
figure 1

Potentiometric calibration plots in AgNO3 solutions recorded for Ag+-selective ISE conditioned overnight in 0.1 M NaNO3 solution: directly after conditioning (squares), directly after the first calibration (triangles), after following 1 h conditioning in 10−3 M AgNO3 (circles) and after following 24 h conditioning in 10−3 M AgNO3 (inverse triangles)

Full size image

Figure 2 presents the dependence of open circuit potential on time recorded for silver-selective ISE with two different membrane thicknesses, recorded in 10−5 M AgNO3 solution. The potential increased monotonously in time as an effect of membrane saturation with silver ions. During these measurements, a procedure of exchanging and stirring of AgNO3 solution was applied, by pumping out and in of a part of 10−5 M AgNO3 solutions. This resulted in an instantaneous potential increase during solution exchange (the electrode was still immersed in the solution) and then in a slower and continuous potential decrease after switching off the pumping/stirring. Analogous application of this procedure to 10−3 M AgNO3 solution did not result in significant potential changes when stirring was switched on/off.

Fig. 2
figure 2

Potential vs. time dependences during stirring on/off procedure recorded in 10−5 M AgNO3 solution for Ag+-selective ISE for membrane of different thicknesses (see text). Inset indicates dependence of the calculated flux on time for two values of membrane thickness [SL single layer (typical thickness close to 200 μm), DL double layer (two times greater thickness)]

Full size image

The potential decrease, observed in 10−5 M AgNO3 solution, results from lowering the concentration of silver ions at the membrane–solution interface, compared to solution bulk. Then, the procedure described above, with application of Eq. 1, was used to calculate the J values, and the calculations were carried out for a number of points at the decreasing part of potential vs. time plot, assuming the Nernstian slope of potential vs. logarithm of Ag+ surface concentration, c(0,t), dependence. The obtained J data were consistent within each stirring on/off step, and the calculated fluxes are shown as inset in Fig. 2. The results show that a flux in an order of 0.5–2 pmol cm−2 s−1 was obtained, and it was only slightly dependent on time (in the applied time interval) and on membrane thickness (Fig. 2). These values are equal to the fluxes within the ion-selective membrane and are consistent with our earlier results concerning PVC-based membranes [18]. Under these conditions (concentration and measurement time up to 104 s), based on the obtained J values, the amount of incorporated silver ions was around 10−9 mol, denoting a saturation degree (in relation to the amount of ion exchanger in the membrane) below 10 %.

The rate of incorporation of silver ions can be interpreted by taking into account processes occurring in the membrane: interaction of silver ions with ionophore molecules, diffusion of ionophore from the membrane bulk, diffusion of the silver ion–ionophore complex in the membrane, diffusion of sodium ions in the membrane in the opposite direction, dissociation of the complex and incorporation of silver ions into the conducting polymer (polypyrrole) solid contact, coupled with possible reduction to metallic silver [22]. Taking into account the time of conditioning in AgNO3 solution and approximate diffusion coefficient of silver(I) ionophore in the membrane, D mem, around 10−8 cm2 s−1, the expected penetration depth of the membrane as (2D mem t)1 / 2 was around 0.1 mm, i.e. lower than the membrane thickness (~0.2 mm for the thinner membrane). Thus, the influence of incorporation of silver ions into the conducting polymer solid contact could be excluded as the diffusing ions practically did not reach the conducting polymer–membrane interface in the applied time interval; therefore, only a slight influence of membrane thickness on the resulting flux was observed.

Assuming now that the diffusion of silver(I)–ionophore complex is the rate-determining step and that the thickness of diffusion layer in the membrane is (πD mem c mem)1 / 2, the flux of diffusing ions could be estimated as [26]

$$ J={c}_{\mathrm{mem}}\sqrt{\frac{D_{\mathrm{mem}}}{\pi t}} $$
(2)

where c mem is the concentration of silver(I) ionophore in the membrane, close to the membrane–solution interface. It could be assumed to be equal to the concentration of ion exchanger in the membrane, i.e. 0.01 M. Thus, assuming t close to 5,000 s, the flux of the order of 1 pmol cm−2 s−1 was obtained. This value is close to the experimental results (Fig. 2), confirming that the diffusion of silver ions in the membrane determines the rate of ion flow.

The possible role of free ionophore diffusion to the membrane–solution interface could be also estimated using Eq. 1. Taking c 0 as free ionophore concentration in the membrane bulk (~0.03 M), the diffusion coefficient close to 10−8 cm2 s−1, total conditioning time of 104 s and experimental J around 1 pmol/cm2 s−1, the estimated decrease of surface concentration of ionophore (related to membrane bulk concentration) was below 5 %. This denotes that ionophore at the interface was still in sufficiently high concentration to form complexes with silver ions. This confirms that the diffusion of the silver(I)–ionophore complex is the factor determining the observed flux in the studied time interval.

A verification method for the above results can be an application of anodic galvanostatic polarization to the electrode, performed in 10−5 M AgNO3 solution (with a membrane previously conditioned in a silver ion-free solution). In this case, cations are forced to be released from the membrane into the solution, i.e. the flux is in opposite direction to the spontaneous saturation process. Therefore, for anodic polarization, the current can counterbalance the flux of spontaneously incorporated silver ions, and the net flux of Ag(I) ions should be reduced or even blocked. Under these conditions, switching on/off the stirring of AgNO3 solution should not result in significant potential changes, due to only limited concentration polarization effect. A similar method of checking galvanostatic compensation of spontaneous fluxes has been proposed by Pretsch et al. [28].

The ion flux value can be recalculated to current, I, based on relation (for +1 cations)

$$ I= JFA $$
(3)

where A is the electrode surface area.

Figure 3 presents potential–time curves recorded in 10−5 M AgNO3 solution in the presence of anodic galvanostatic polarization. These results show that the lowest potential changes accompanying stirring were observed for the current 20 nA. According to Eq. 3, this current corresponded to the flux J = 2 pmol/cm2 s−1, i.e. consistent with the flux value obtained from open circuit potential measurements.

Fig. 3
figure 3

Potential vs. time dependences during stirring on/off procedure recorded in 10−5 M AgNO3 solution for Ag+-selective ISE under chronopotentiometric conditions

Full size image

Accumulation of silver in polypyrrole layers

Similar studies were carried out for a GC electrode coated by another kind of membrane, by polypyrrole layer doped by PSS ions (without ion-selective membrane) and immersed in AgNO3 solution. For this system, spontaneous deposition of silver in the polypyrrole film occurs [22], due to accompanying oxidation of the conducting polymers and release of Na+ from the polymer layer

$$ {\mathrm{PPy}\mathrm{PSS}}^{-}{\mathrm{Na}}^{+}+{\mathrm{Ag}}^{+}\to {\mathrm{PPy}}^{+}{\mathrm{PSS}}^{-}+\mathrm{Ag}+{\mathrm{Na}}^{+} $$
(4)

This system was chosen as a model example to test the proposed method, as it was previously characterized by us in detail, and kinetics of polypyrrole oxidation by silver ions was studied by rotating disc electrode voltammetry [25]. Thus, it would be possible to compare these earlier data with results achieved using the present method.

Figure 4 presents potential vs. time dependence for polypyrrole electrode in 10−5 M AgNO3 solution. A monotonous increase of the potential in quiescent solution was observed, resulting from polymer oxidation, and then, an almost constant value was reached. The potential increase recorded in non-stirred solution resulted from polypyrrole oxidation. While stirring was switched on, instantaneous potential increase was seen, accompanied by decrease after stirring was switched off. Similarly, as in previous case, this change resulted from silver ion concentration polarization due to Ag(I) extraction to the membrane. Based on these data, the surface concentration of Ag(I) could be calculated, and then, flux of Ag(I) ions, using Eq. 1, could be calculated. The obtained flux was close to 1.5 pmol cm−2 s−1.

Fig. 4
figure 4

Potential vs. time dependences during stirring on/off procedure recorded in 10−5 M AgNO3 solution for electrode coated with polypyrrole layer (polymerization charge, 100 mC)

Full size image

Assuming that incorporated silver ions take part in reaction (Eq. 4), the flux value can be related to the rate of silver ion reduction/polypyrrole oxidation with a rate constant, k

$$ J=k{\displaystyle {\int}_0^d}c\left(x,t\right) dx $$
(5)

where d is the polymer layer thickness, and c(x,t) is the silver ion concentration in the polymer, for the distance x from the polymer–solution interface. Assuming then that the reaction occurs in a thin surface layer [25] of thickness μ, with Ag+ ions concentration c(0,t), Eq. 5 can be simplified to

$$ J= k\mu \cdot c\left(0,t\right)={k}_{\mathrm{h}}\cdot c\left(0,t\right) $$
(6)

where k h is the heterogeneous rate constant of silver ion reduction.

Using Eq. 6 with J = 1.5 pmol cm−2 s−1 and c(0,t) around 2 × 10−6 M (lower than 10−5 M due to concentration polarization), the obtained rate constant, k h, was 7 × 10−4 cm s−1. This rate constant is slightly lower than that reported earlier (around 10−3 cm s−1 at potential corresponding to open circuit potential) [25]. In our opinion, the observed difference can result from the influence of real surface area of the polymer layer. In the paper [25], the data obtained from rotating disc electrode voltammetry were used. Recalculation of current to rate constant requires information about electrode surface area; in that case, the geometrical surface was used. However, due to a porous structure of the polymer and rough surface, the physical surface area could be higher than the geometrical one; thus, the real rate constant most probably is lower than that reported in [25]. Due to this effect of surface area, a significant advantage of the proposed method in the present work seems evident, because information on electrode surface area was not required to calculate the flux from changes of the open circuit potential and thus to calculate the rate constant.

The penetration depth by silver ions, μ, is achieved after time period, t μ , when fluxes corresponding to charge transfer reaction (Eq. 6) and silver ion diffusion in the film (analogous to Eq. 2) become equal

$$ {k}_{\mathrm{h}}\cdot c\left(0,t\right)=c\left(0,t\right)\sqrt{\frac{D_{\mathrm{Ag}}}{\pi {t}_{\mu }}} $$
(7)

and after rearrangement

$$ {t}_{\mu }=\frac{D_{\mathrm{Ag}}}{{k_{\mathrm{h}}}^2\pi } $$
(8)

where D Ag is the diffusion coefficient of silver ions in the polypyrrole film.

Using Eq. 8, with D Ag ~10−7 cm2 s−1 [25] and obtained k h = 7 × 10−4 cm s−1, the time needed to obtain penetration depth, μ, was 0.06 s. This corresponds to μ = (2D Ag t μ )1 / 2 around 1 μm.

The determined flux value can be also applied to calculate the charge, q, exchanged between the polypyrrole and silver ions to oxidize the conducting polymer

$$ q= JAtF $$
(9)

where t is the measurement time (8,000 s). The obtained estimated charge for electrode with polypyrrole was close to 0.1 mC.

This charge value could be compared with that calculated from open circuit potential vs. time dependence in quiescent solution. In this case, it could be assumed that potential changes corresponding to polypyrrole oxidation were coupled with exchanged charge by equation

$$ q= C\varDelta E $$
(10)

where C is the polymer film low-frequency capacitance. The capacitance value was obtained from the slope of linear part of a chronopotentiometric curve recorded for oxidation/reduction of this polymer layer, using the Bobacka method [29] (data not shown). After applying Eq. 10, q value only slightly higher than 0.1 mC was obtained, i.e. consistent with that calculated from flux value (Eq. 9).

Conclusions

A simple straightforward method of determination of ion fluxes to ion-exchange membranes coated on electrodes, based on potential–time dependences in the absence/presence of solution stirring, was presented. This approach needs no sophisticated apparatus. Results obtained for a model example of silver-selective electrode with poly(vinyl chloride)-based membrane in silver ion solution showed that the flux to non-saturated membrane was governed by diffusion and ion concentration gradient in the membrane. On the other hand, fluxes observed for a polypyrrole layer in silver ion solution resulted from silver deposition accompanied by conducting polymer oxidation, and the determined rate of this process was consistent with that derived from rotating disc electrode voltammetry.

The obtained results confirmed the applicability of the proposed method to various kinds of ion-exchange membranes.