Abstract
DFT calculations were performed to shed light on the molecular mechanism of [3 + 2] cycloadditions of simple conjugated nitroalkenes to benzonitrile N-oxides. In particular, it was found that these processes proceed by a one-step mechanism through asynchronous transition states. According to the latest terminology, they should be considered polar but not stepwise processes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
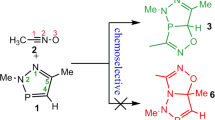
The most versatile method of synthesizing ∆2-isoxazolines (3,4-dihydroisoxazoles) is through [3 + 2] cycloaddition reactions between nitrile N-oxides (which are allenyl-type three-atom components: TACs [1]) and alkenes [2–6]. The use of nitroalkenes as dipolarophiles in these reactions permits the synthesis of nitro-substituted isoxazolines under mild conditions [5, 7]. These can easily be further functionalized because of their unique tendency to convert the NO2 group into other functional groups [7–9]. It is worth mentioning that [3 + 2] cycloadditions of nitrile N-oxides to conjugated nitroalkenes proceed in a highly selective manner. For example, the reaction of benzonitrile N-oxide (1) (or its aryl-substituted analogs) with nitroethene (2) can theoretically proceed along two competing paths, leading to regioisomeric 4- and 5-nitro nitroisoxazolines (3 and 4, respectively) (Scheme 1).
In practice, these reactions are realized in a fully regioselective manner, giving high yields of 3-aryl-5-nitroisoxazolines (4) [6, 10].
It should be noted at this point that the molecular mechanism of these reactions is not well understood. On the one hand, the literature is often plagued by a belief in a one-step (“pericyclic” [11]) mechanism of [3 + 2] cycloaddition, regardless of the composition of the addent. On the other hand, a number of works challenging this view have been published recently [12–19]. A broad range of mechanisms are now known to occur, proceeding through transition states (TSs) with a range of synchronicities and polarities [1]. Stepwise [3 + 2] cycloaddition is a unique case that can involve zwitterion or diradical formation. Some examples of stepwise [3 + 2] cycloadditions involving conjugated nitroethenes were recently described, including reactions of nitroethene with thiocarbonyl ylides [12] and 1-substituted nitroethenes with diarylnitrones [13, 14]. Additionally, several examples of stepwise cycloadditions involving components other than conjugated nitroalkenes were described; for example, reactions between fluorinated alkenes [15] or phenylisocyanate [16] and N-alkylnitrones, dialkyl 2,3-dicyanobut-2-enedioates and azomethine ylides [17], dimethyl 2,3-dicyanofumarate and di(tert-butyl)diazomethane [18], as well as methyl nitrile N-oxide and tetraaminoethene [19].
With this in mind, we have found that the molecular mechanism of [3 + 2] cycloadditions of nitrile N-oxides to conjugated nitroalkenes requires comprehensive theoretical study using DFT methods. It should be emphasized that the aforementioned reactions have not yet been investigated in this manner, even though such work is important from theoretical and practical points of view. Due to the strong electrophilicity (ω) of the conjugated nitroalkenes (ω > 1.5 eV [20–22]), it is in fact very likely that these reactions proceed through a zwitterionic intermediate (paths A and B in Scheme 2). At the same time, it is possible that zwitterionic structures with “extended” conformations are created along the competing paths of the cycloaddition reaction (paths C and D in Scheme 2). Such a path for addition has recently been analyzed for the reactions of nitroacetylene with a series of allenyl-type TACs [23]. All of the above options deserve detailed consideration.
Recently, we performed theoretical studies of a number of different cycloaddition processes involving conjugated nitroalkenes [24–30], and subsequently carried out experiments examining the reaction selectivity [27, 28, 30–32], activation parameters [33], and kinetic effects of the solvent and substituents [29, 34] for these processes. This comprehensive approach provided good insight into the key properties of the transition states involved. We concluded that DFT calculations should be capable of determining the molecular mechanism of these [3 + 2] cycloadditions. Therefore, in the work reported in the present paper, in order to allow general conclusions to be drawn, benzonitrile N-oxide as well as analogs of it containing substituents with different electronic properties were tested as model TACs. In particular, we decided to (a) probe the nature of the interaction between the addents in an elementary cycloaddition step and (b) run simulations of theoretically possible reaction paths of nitroethene with various nitrile N-oxides. As an extension of those studies, we also present theoretical studies of similar reactions involving the extremely electrophilic [13] 1,1-dinitroethene molecule here.
Computational methods
Global reactivity indices (electronic chemical potential μ, chemical hardness η, global electrophilicity ω, global nucleophilicity N) were estimated according to the equations recommended by Parr [33] and Domingo [35–37]. In particular, the electronic chemical potentials and chemical hardnesses of the reactants studied here were evaluated in terms of the one-electron energies of the frontier molecular orbitals using the following equations [35, 36]:
The values of μ and η were then used to calculate ω according to the formula
N can be expressed [37] as
The local electrophilicity (ω k ) [38] concentrated on atom k was calculated by projecting the index ω onto any reaction center k in the molecule using the Parr function P+ k :
The local nucleophilicity (N k ) [38] concentrated on atom k was calculated using the global nucleophilicity N and the Parr function P− k according to the formula
The global and local electronic properties of the reactants considered in this work are collected in Tables 1 and 2.
To localize the transition states (TSs), the hybrid B3LYP functional and the 6-31G(d) basis set included in the GAUSSIAN 09 software package were applied. We subsequently also performed analogous computation at the more advanced B3LYP/6-31 + G(d) and B3LYP/6-311G(d) levels of theory.
The structures corresponding to critical points on the PES along the reaction paths were localized in an analogous manner to that used in a previous analysis of [3 + 2] cycloadditions of (Z)-C,N-diphenylnitrone with 1,1-dinitroethene [13]. First-order saddle points were localized using the QST2 and Berny procedures. The transition states were verified by diagonalizing the Hessian matrix and analyzing the intrinsic reaction coordinates (IRC). The polarizable continuum model (PCM) [39], in which the cavity is created as a series of overlapping spheres, was used to calculate solvent effects. Calculations of all critical structures were performed for a temperature T = 298 K and pressure p = 1 atm. The global electron density transfer (GEDT) [40] was calculated according to the formula
where q A is the net Mulliken charge, and the sum is performed over all the atoms of nitroalkene.
Indices of σ-bond development (l) were calculated according to the formula [14]
where r TS A–B is the distance between the reaction centers A and B at the TS and r P A–B is the corresponding distance at the product.
The kinetic parameters as well as important properties of the critical structures are displayed in Tables 3, 4, 5, and 6.
Results and discussion
Analysis of interactions between addents
First, we decided to shed some light on the nature of the interactions between the addents. To do this, we used the electronic properties of the reactants, which were estimated using equations defined based on conceptual density functional theory [41]. A similar approach was successfully used recently to explain the paths followed by a number of different biomolecular processes (see for example [42–45]). In this theory, nitroethene is classified as a strong electrophile (ω > 1.5 eV) [36]. Its electrophilicity can be enhanced by introducing a second electron-withdrawing group (EWG) at position 1 of the nitrovinyl fragment. Accordingly, the presence of a Cl substituent increases the value of ω for nitroalkene to 2.88 eV, and that of the nitro group to 3.56 eV.
The electronic properties of N-oxides of aromatic nitriles vary widely. The global electrophilicity of benzonitrile N-oxide 2d is 1.46 eV, which makes it a moderate electrophile. However, gradually increasing the electron-donating power of a substituent at the 4-position on the N-oxide phenyl ring causes a gradual change in its electronic properties. In particular, for the 4-dimethylamino-substituted N-oxide 2a, ω is below 1 eV. This means that 2a will exhibit only marginally electrophilic properties, but will show strong nucleophilic power, as indicated by the value of N (>3.8 eV). Replacing the dimethylamino group with a strongly electron-withdrawing nitro group results in a dramatic change in the properties of the N-oxide. In particular, the 4-nitro-substituted N-oxide 2h is characterized by strong electrophilic properties (ω > 3 eV)—stronger than nitroethene (!).
We then analyzed the local reactivity for different pairs of reactants. We found that the oxygen atom on the CNO fragment is a strongly nucleophilic reaction center in all of the N-oxides. In turn, the strongest electrophilic reaction center is always the β atom of the nitrovinyl fragment in the nitroalkenes. If we assume that these centers govern the reaction path, then the products of the cycloadditions should be 4-nitroisoxazolines. However, this conclusion conflicts with the experimental data, because only the corresponding 5-nitroisoxazolines are formed in this process.
It should be noted at this point that only extremely electrophilic addents were considered for further detailed study of the mechanistic aspects of the corresponding cycloadditions. This allowed us to get a good idea of the mechanism associated with the [3 + 2] cycloaddition processes without having to calculate the full reaction paths for all such processes.
Kinetic aspects
DFT calculations show that the [3 + 2] cycloaddition of nitroethene (1) to N-oxide 2d in weakly polar toluene proceeds by a one-step mechanism (Fig. 1, Table 3). In the first step of the process, the enthalpy of the reacting system decreases due to the formation of a pre-reaction complex (MC). Depending on the reaction path, this complex can be converted to regioisomeric isoxazoline 3d or 4d. Each of these conversions entails overcoming an activation barrier. The kinetically favored conversion is that associated with path B, leading to the formation of a 5-nitro-substituted adduct, which—as shown by experimental studies—does indeed form during this reaction [6, 10]. So, contrary to expectations arising from regioselectivity, based on the analysis of the stationary states of the addends (see the preceding paragraph), a DFT-based exploration of the reaction pathways can accurately determine the regiochemistry of cycloaddition. However, all attempts to find a reaction path that leads to the adduct through an acyclic intermediate were unsuccessful. We also failed to obtain any stable structures of hypothetical zwitterions in an “extended” conformation.
Similar studies were also performed for reactions involving representative N-substituted analogs of benzonitrile N-oxide. In the calculations of the reaction paths for the parent reaction system involving nitroethene and unsubstituted benzonitrile N-oxide, several basis sets were applied (Table 3). It was found that calculations using the simple 6-31G(d) basis set gave practically identical (from a mechanistic point of view) results to calculations using higher levels of theory. In particular, in each instance, DFT calculations indicated a one-step reaction mechanism in which the favored path leads to a product with the nitro group at the 5-position on the heterocyclic ring. Thus, only the B3LYP/6-31G(d) level of theory was applied in subsequent investigations.
We found that, in quantitative terms, the energy profiles for the cycloadditions 1 + 2a and 1 + 2h are the same as that for 2d + 1 cycloaddition, although they would be somewhat different quantitatively. In particular, introducing the (electron-donating) dimethylamino substituent at the 4-position of the phenyl ring of the N-oxide reduces the activation barrier, whereas the introduction of the (electron-withdrawing) nitro group increases the aforementioned barrier. However, reaction path B is always kinetically favored.
We then decided to investigate the effect of solvent polarity on the course of the reaction. We found that replacing toluene with a more polar medium (water) prompts an increase in the activation barrier along both regioisomeric paths.
As an extension of our studies, we performed a similar analysis of the energy profile of a similar cycloaddition involving 1,1-dinitroethene 7 and N-oxide 2d (Scheme 3), which has not yet been studied experimentally. Our previous work [13] indicated that nitroalkene 7 will react with C,N-diphenylnitrone via a stepwise zwitterionic mechanism. As in the case of 1 + 2 cycloaddition, we considered both of the theoretically possible regioisomeric reaction routes (A and B; see Scheme 3).
The results indicated that, in toluene, the energy profile of 7 + 2d cycloaddition is qualitatively the same as that of 2d + 1 cycloaddition. However, due to the strongly electrophilic character of nitroalkene 7, these processes take place much more quickly than in the reaction involving nitroethene 1 (Table 4). The regioselectivity of this cycloaddition is different from that of 1 + 2d cycloaddition. In particular, from a kinetic point of view, the path leading to the 4-nitro-substituted adduct is favored. All attempts to find paths leading to cycloadducts through an acyclic intermediate step were unsuccesful, as were efforts to find paths leading to hypothetical zwitterions with an “extended” conformation. Very similar results were seen for calculations of 7 + 2d cycloaddition in the presence of a more polar medium (water).
The studies described above indicate that there is an important difference between the paths of the reactions of model nitriles and imine N-oxides with nitroethene 1 and dinitroethene 7. The former TAC reacts with both of those nitroalkenes (despite their rather different global electrophilicities) by a one-step mechanism, while the latter reacts with nitroethene 1 according to a single-step mechanism but with 1,1-dinitroethene 7 by a two-step zwitterionic mechanism [13].
Key structures
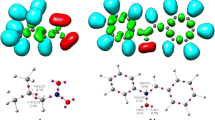
B3LYP/6-31G (d) calculations showed that two new σ-bonds always form in both TSs of the 1 + 2d reaction (Fig. 2). These bonds are formed between the atoms O1 and C5 and between C3 and C4, although the bond with the β carbon of the nitroalkene substructure forms faster. Thus, the structures of the TSs correlate well with the data obtained upon analyzing the local electrophilicity in nitroalkenes. The energetically favored TS along path B is even more asynchronous (see the ∆l values in Table 5). Both of the TSs considered are polar, as demonstrated by their dipole moments and GEDT values (Table 5).
The synchronicity of TS A can be controlled to some extent by altering the substituent on the phenyl ring of TAC. In particular, introducing an electron-donating group increases the asynchronicity of the TS, while adding an electron-withdrawing group reduces its asynchronicity. The type of substituent present does not appear to influence the asynchronicity of TS B .
Next, we analyzed the effect of the polarity of the reaction medium on the characteristics of the TSs. We found that replacing the weakly polar solvent toluene with a strongly polar medium (nitromethane or water) increases the asynchronicity of the TSs. At the same time, they increase in polarity. However, these changes are not significant enough to induce a stepwise zwitterionic mechanism.
A similar analysis was performed for the TSs in the reaction between dinitroethene 7 and TAC 2d. In accordance with our expectations, these structures were found to be far more asynchronous and strongly polar (Fig. 3, Table 6) than the corresponding TSs in the 1 + 2d reaction. Our attempts to optimize stable zwitterionic structures that could hypothetically form in the 7 + 2d reaction failed.
Conclusions
Regardless of the basis set applied, our B3LYP results clearly indicate that [3 + 2] cycloadditions of simple nitroalkenes to arylonitrile N-oxides proceed via a one-step mechanism. According to Domingo’s terminology [43], this mechanism should be interpreted as polar. DFT calculations also showed that the favored reaction path leads to an adduct with a nitro group on C5, which agrees well with experimental observations. The transition-state synchronicity can be controlled to a certain degree by changing the polarity of the reaction medium and the nature of the substituent on the N-oxide phenyl ring. However, this is not enough to induce a switch to a two-step reaction mechanism with a zwitterionic intermediate. Nor was such a mechanism found to be possible in an analogous cycloaddition with a much stronger electrophilic component (1,1-dinitroethene).
References
Domingo LR, Ríos-Gutiérrez M, Pérez P (2016) A new model for C–C bond formation processes derived from the molecular electron density theory in the study of the mechanism of 3 + 2 cycloaddition reactions of carbenoid nitrile ylides with electron-deficient ethylenes. Tetrahedron 72:1524–1532
Kaur K, Kumar V, Sharma AK, Gupta GK (2014) Isoxazoline containing natural products as anticancer agents: a review. Eur J Med Chem 77:121–133
Elkanzi N (2013) Review on synthesis of isoxazolines, pyrazolines, compounds. LAP Lambert, Saarbrücken
Namboothiri INN, Rastori N (2008) Isoxazolines from nitro compounds: synthesis and applications. Top Heterocycl Chem 12:1–44
Belenkii LI (2007) Nitrile oxides, nitrone and nitronates in orgnanic synthesis. Wiley, New York
Jasiński R (2015) 1,3-Dipolar cycloaddition reactions: mechanistic aspects and applications in organic synthesis. RTN, Radom
Boyer JH (1986) Nitroazoles: the C-nitro derivatives of five-membered N- and N,O-heterocycles. VCH, Weinheim
Ono N (2001) The nitro group in organic synthesis. Wiley, Weinheim
Nielsen A (1995) Hydrocarbons. Wiley-VCH, Weinheim
Koroleva EV, Bondar NF, Katok YM, Chekanov NA, Chernikhova TV (2007) 2-Isoxazolines with an electron-acceptor substituent at C(5) in reactions with nucleophilic reagents. Chem Heterocycl Compd 43:362–369
Huisgen R (1984) 1,3-Dipolar cycloaddition chemistry. Wiley, New York
Jasiński R (2015) In the searching for zwitterionic intermediates on reaction paths of 3 + 2 cycloaddition reactions between 2,2,4,4-tetramethyl-3-thiocyclobutanone S-methylide and polymerizable olefins. RSC Adv 5:101045–101048
Jasiński R (2013) Competition between the one-step and two-step, zwitterionic mechanisms in the 2 + 3 cycloaddition of gem-dinitroethene with (Z)-C,N-diphenylnitrone: a DFT computational study. Tetrahedron 69:927–932
Jasiński R (2015) A stepwise, zwitterionic mechanism for the 1,3-dipolar cycloaddition between (Z)-C-4-methoxyphenyl-N-phenylnitrone and gem-chloronitroethene catalysed by 1-butyl-3-methylimidazolium ionic liquid cations. Tetrahedron Lett 56:532–535
Wójtowicz-Rajchel H, Koroniak H (2012) Synthesis of 5-fluorovinyl derivatives of pyrimidines via Suzuki–Miyaura coupling and their 1,3-dipolar cycloaddition reactions with nitrones. J Fluor Chem 135:225–230
Darù A, Roca-López D, Tejero T, Merino P (2016) Revealing stepwise mechanisms in dipolar cycloaddition reactions: computational study of the reaction between nitrones and isocyanates. J Am Chem Soc 81:673–680
Khlebnikov AF, Koneva AS, Virtseva AA, Yufit DS, Mlostoń G, Heimgartner H (2014) Concerted vs. non-concerted 1,3-dipolar cycloadditions of azomethine ylides to electron-deficient dialkyl 2,3-dicyanobut-2-enedioates. Helv Chim Acta 97:453–470
Huisgen R, Pöchlauer P, Młostoń G, Polsborn K (2007) Reactions of di(tert-butyl) diazomethane with acceptor-substituted ethylenes. Helv Chim Acta 90:983–998
Siadati SA (2015) An example of a stepwise mechanism for the catalyst-free 1,3-dipolar cycloaddition between a nitrile oxide and an electron rich alkene. Tetrahedron Lett 56:4857–4863
Jasiński R, Koifman O, Barański A (2011) A DFT study on the regioselectivity and molecular mechanism of nitroethene 2 + 3 cycloaddition to (Z)-C,N-diphenylnitrone and C,C,N-triphenylnitrone. Mendeleev Commun 21:262–263
Domingo LR, Aurell MJ, Pérez P, Contreras R (2002) Quantitative characterization of the global electrophilicity power of common diene/dienophile pairs in Diels–Alder reactions. Tetrahedron 58:4417–4423
Jasiński R, Mróz K, Kącka A (2016) Experimental and theoretical DFT study on synthesis of sterically crowded 2,3,3,(4)5-tetrasubstituted-4-nitroisoxazolidines via 1,3-dipolar cycloaddition reactions between ketonitrones and conjugated nitroalkenes. J Heterocycl Chem 53:1424–1429
Jasiński R (2015) Nitroacetylene as dipolarophile in 2 + 3 cycloaddition reactions with allenyl-type three-atom components: DFT computational study. Monatsh Chem 146:591–599
Jasiński R, Barański A (2010) Reactivity of (E)-2-aryl-1-cyano-1-nitroethenes in carbo and hetero Diels–Alder reactions with cyclopentadiene: a DFT study. J Mol Struct (THEOCHEM) 949:8–13
Jasiński R, Kwiatkowska M, Barański A (2009) A competition between carbo and hetero Diels–Alder reactions of E-2-phenyl-1-cyano-1-nitroethene to cyclopentadiene in the light of B3LYP/6-31G(d) computational study. J Mol Struct (THEOCHEM) 910:80–87
Jasiński R, Kwiatkowska M, Barański A (2011) Stereoselectivity and kinetics of 4 + 2 cycloaddition reaction of cyclopentadiene to para‐substituted E‐2‐arylnitroethenes. J Phys Org Chem 24:843–853
Jasiński R, Kwiatkowska M, Sharnin V, Barański A (2013) Experimental and theoretical studies of Diels–Alder reaction between methyl (Z)-2-nitro-3-(4-nitrophenyl)-2-propenoate and cyclopentadiene. Monatsh Chem 144:327–335
Jasiński R, Ziółkowska M, Demchuk OM, Maziarka A (2014) Regio-and stereoselectivity of polar 2 + 3 cycloaddition reactions between (Z)-C-(3,4,5-trimethoxyphenyl)-N-methylnitrone and selected (E)-2-substituted nitroethenes. Cent Eur J Chem 12:586–593
Jasiński R, Kubik M, Łapczuk-Krygier A, Kącka A, Dresler E, Boguszewska-Czubara A (2014) An experimental and theoretical study of the hetero Diels–Alder reactions between (E)-2-aryl-1-cyano-1-nitroethenes and ethyl vinyl ether: one-step or zwitterionic, two-step mechanism? React Kinet Mech Cat 113:333–345
Jasiński R (2015) Synthesis and properties of azoles and their derivatives. Part 70. Nitroallylic systems in 2 + 3 cycloaddition reactions with nitrones: a DFT computational study. J Heterocyc Chem 52:185–192
Jasiński R (2009) Regio-and stereoselectivity of 2 + 3 cycloaddition of nitroethene to (Z)-N-aryl-C-phenylnitrones. Coll Czech Chem Commun 74:1341–1349
Łapczuk-Krygier A, Ponikiewski Ł, Jasiński R (2014) The crystal structure of (1RS,4RS,5RS,6SR)-5-cyano-5-nitro-6-phenyl-bicyclo[2.2.1]hept-2-ene. Crystallogr Rep 59:961–963
Parr, RG, Yang W (1989) Density-functional theory of atoms and molecules. Oxford University Press, Oxford, 4:70–86
Jasiński R, Mróz K (2015) Kinetic aspects of 3 + 2 cycloaddition reactions between (E)-3,3,3-trichloro-1-nitroprop-1-ene and ketonitrones. React Kinet Mech Cat 116:35–41
Pérez P, Domingo LR, Aizman A (2007) The electrophilicity index in organic chemistry. In: Toro-Labbe A (ed) Theoretical aspects of chemical reactivity. Elsevier, Amsterdam, 9:139–201
Perez P, Domingo LR, Aurell MJ, Contreras R (2003) Quantitative characterization of the global electrophilicity patternof some reagents involved in 1,3-dipolar cycloaddition reactions. Tetrahedron 59:3117–3125
Pérez P, Domingo LR, Duque-Noreña M, Chamorro E (2009) A condensed-to-atom nucleophilicity index an application to the director effects on the electrophilic aromatic substitutions. J Mol Struct (THEOCHEM) 895:86–91
Domingo LR, Perez P, Saez JA (2013) Understanding the local reactivity in polar organic reactions through electrophilic and nucleophilic Parr functions. RSC Adv 3:1486–1494
Cossi M, Rega N, Scalmani G, Barone V (2003) Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J Comp Chem 24:669–681
Domingo LR (2014) A new C–C bond formation model based on the quantum chemical topology of electron density. RSC Adv 4:32415–32428
Domingo LR, Ríos-Gutiérrez M, Pérez P (2016) Applications of the conceptual density functional theory indices to organic chemistry reactivity. Molecules 21:784
Chattaraj PK, Giri S, Duley S (2011) Electrophilicity index. Chem Rev 111:PR43–PR75
Domingo LR, Saez JA (2009) Understanding the mechanism of polar Diels–Alder reactions. Org Biomol Chem 7:3576–3583
Kapłon K, Demchuk OM, Wieczorek M, Pietrusiewicz KM (2014) Brönsted acid catalyzed direct oxidative arylation of 1,4-naphthoquinone. Curr Chem Lett 3:23–36
Emamian S (2016) How the mechanism of a 3 + 2 cycloaddition reaction involving a stabilized N-lithiated azomethine ylide toward a π-deficient alkene is changed to stepwise by solvent polarity? What is the origin of its regio- and endo stereospecificity? A DFT study using NBO, QTAIM, and NCI analyses. RSC Adv 6:75299–75314
Acknowledgments
The quantum-chemical calculations were performed on the SGI-Altix-3700 computer at the Cracow Computing Center “CYFRONET” (grant no. MNiSW/Zeus_lokalnie/PK/009/2013). The authors also thank the Polish State Committee for financial support (grant no. C-2/88/2016/DS).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Jasiński, R., Jasińska, E. & Dresler, E. A DFT computational study of the molecular mechanism of [3 + 2] cycloaddition reactions between nitroethene and benzonitrile N-oxides. J Mol Model 23, 13 (2017). https://doi.org/10.1007/s00894-016-3185-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00894-016-3185-8