Introduction

Chlorine atoms are important stratospheric species taking an active part in ozone destruction cycles [1, 2]. The main sources of the atmospheric chlorine atoms are the photochemically labile chlorine compounds such as Cl2 and ClNO2 produced in some aqueous-phase reactions in the airborne seawater droplets. The gas-phase reactions of chlorine atoms with the hydrogen-containing atmospheric halocarbons lead to the facile generation of the corresponding free radicals via hydrogen atom abstraction [1, 3].

Monofluoromethane is the simplest of hydrofluorocarbons (HFCs), which are man-made organics predominantly used as safe replacements for ozone-depleting substances [1]. HFCs are chemically low reactive and have an ozone depleting potential of zero as they contain no chlorine. HFCs have long lifetimes in the atmosphere, and are only slowly removed by solar photolysis [4–6]. The main impact of HFCs on the environment is related with global warming.

Chloromethane (CH3Cl) is the most abundant halocarbon in the atmosphere with an atmospheric lifetime of 17 months [7–9]. Major natural sources of CH3Cl are biomass burning, oceanic emissions and vegetative emissions. The products of the atmospheric destruction of CH3Cl may be involved in various catalytic atmospheric reaction cycles responsible for the depletion of the ozone layer [1]. The reaction with hydroxyl radicals is considered as the dominant sink for atmospheric CH3Cl.

The most important carrier of bromine to the stratosphere is bromomethane (CH3Br) which is produced by both anthropogenic and natural processes. CH3Br is a very efficient catalyst for ozone destruction. The atmospheric lifetime of CH3Br is estimated to be approximately two years [10]. The fate of atmospheric methyl bromide is primarily determined by degradation processes in the troposphere, especially by its reaction with OH radicals [1, 11].

The hydrogen abstraction reactions of chlorine atoms with halomethanes, CH3X (where X = F, Cl, Br) have been the subjects of many kinetic studies [12–14]. The primary tropospheric sink for halogenated methanes including these three of interest in this study (CH3F, CH3Cl and CH3Br) is their reaction with OH radicals. The recent investigations suggest that concentrations of chlorine atoms in the marine boundary layer may be as much as one-tenth as high as the hydroxyl radical levels [1]. Since reactions of Cl atoms with many organics proceed considerably faster than the corresponding OH reactions [12–14], it is possible that reactions with atomic chlorine could be a non-negligible sink for many hydrogen-containing atmospheric halomethanes.

In this study we present a theoretical analysis of the mechanism and kinetics of the reactions of monosubstituted halogenated methanes CH3X with atomic chlorine:

$$ \mathrm{C}{{\mathrm{H}}_3}\mathrm{X}+\mathrm{Cl}\to \mathrm{C}{{\mathrm{H}}_2}\mathrm{X}+\mathrm{HCl}, $$
(1)

where X = F, Cl and Br. One expects that the mechanism of the reaction (1) is complex and H-abstraction proceeds through the formation of intermediate complexes. The possible competitive reaction channels related with the abstraction of halogen X from the CH3X molecule, and the formation of XCl products are probably related with high activation energies and proceed very slowly. Any trace of XCl products was not found in the experimental studies, which was the grounds to omit the halogen abstraction in the mechanism of the reactions CH3X + Cl.

Our theoretical analysis of the reaction systems concerns ab initio calculations using molecular orbital theory in order to locate and characterize the characteristic points of the potential energy surface. The main attention of our study is focused on the possible influence of the formed molecular complexes on the reaction mechanism. The theoretical method used for the description of the reaction kinetics enables the rate constant calculations for a bimolecular reaction proceeding through the formation of intermediate complexes. Results of these calculations provide structural and energetic information on the reaction pathways, which enable us to evaluate the rate constants and their temperature dependence using computational methods of reaction rate theory. The calculated properties of the molecular structures taking part in the reaction mechanism should be useful for a better understanding and correct interpretation of experimental findings.

The kinetics of the reactions CH3F/CH3Cl/CH3Br + Cl has been the subject of many experimental [15–38] and theoretical [20, 39–44] studies. The available experimental kinetic data show, however, substantial scattering in the values of the rate constants. The most credible and preferable for the kinetic analysis are then the results of measurements obtained by the same research group and using the same experimental method. Kinetics of the reactions CH3F + Cl, CH3Cl + Cl and CH3Br + Cl was recently studied experimentally in our laboratory using the same experimental technique, the same reference reaction and performed in the same temperature range [22, 32, 38]. Besides that, the reactions of entirely deuterated reactants

$$ \mathrm{C}{{\mathrm{D}}_3}\mathrm{X}+\mathrm{Cl}\to \mathrm{C}{{\mathrm{D}}_2}\mathrm{X}+\mathrm{DCl}, $$
(2)

were simultaneously studied under the same experimental conditions. The obtained results are then valuable reference data for the theoretical comparative kinetic analysis.

Computational details

The halogenated alkanes were studied theoretically using quantum mechanical ab initio methods at various levels of theory. Results of these calculations performed for a wide class of organic compounds show that the G2 method [45] reproduces well the structural parameters and molecular properties of a wide group of organic compounds. The reliable values of the thermochemical properties and vibrational frequencies have been obtained using G2 methodology for perhalogenated methanols, methyl hypohalites, halogenated alkyl and alkoxy radicals [46–56]. The G2 method was also successfully used in the theoretical description of the kinetics and mechanism of the hydrogen abstraction from methanol by halogen atoms [57–59]. Therefore, we decided to use this level of theory in our investigations.

All quantum mechanical ab initio calculations were carried out using the Gaussian 09 program [60] package. The geometries of all stationary point structures of the potential energy surface were fully optimized at both the SCF and MP2 levels with the 6-31G(d) basis set. Relative total energies were examined using G2 methodology [45]. This approach requires some additional calculations at the MP4/6-311G(d,p), MP4/6-311+G(d,p), MP4/6-311G(2df,p), MP2/6-311+G(3df,2p), and QCISD(T)/6-311G(d,p) levels using the MP2/6-31G(d) optimized geometry as a reference to obtain improved energy values.

The rate constants of the reactions studied were analyzed in terms of conventional transition-state theory (TST) [61, 62]. The thermochemical formulation of TST leads to the rate constant, kTST, given by

$$ {k_{\mathrm{TST}}}=\sigma \frac{{{{\mathrm{k}}_{\mathrm{B}}}\mathrm{T}}}{\mathrm{h}}\exp \left( {\frac{{\varDelta {S^{\ne }}}}{R}} \right)\exp \left( {-\frac{{\varDelta {H^{\ne }}}}{RT }} \right), $$
(3)

where σ denotes a symmetry factor related to reaction path degeneracy, kB and h are the Boltzmann and Planck constants, respectively, ΔS≠ is the activation entropy, and ΔH≠ the activation enthalpy for the reaction under investigation. The vibrational and rotational contributions to the thermodynamic functions were derived by the classical harmonic-oscillator rigid-rotor approximation (no free or internal rotation was considered).

Results and discussion

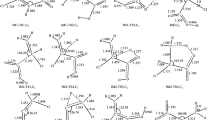
The molecular arrangements and definitions of the structural parameters of the CH3X and CH2X (X = F, Cl, and Br) structures are shown in Fig. 1. The geometries of all molecular structures taking part in the reactions under investigation were fully and independently optimized using analytical gradients at the SCF and MP2 levels with the 6-31G(d) basis set. At each level of theory the potential energy surface was explored independently for the possible existence of transition states and intermediate complexes. The results of calculations including the optimized geometrical parameters at the MP2/6-31G(d) level, the harmonic vibrational frequencies, the rotational constants and the total G2(0 K) energies for the reactants CH3X, products CH2X, molecular complexes CH3X…Cl (denoted by MC1X) and CH2X…HCl (MC2X) as well as transition states CH2X…H…Cl (TS1X) are given in Tables 1 and 2. The structural parameters of the hydrogen halides, HX were published elsewhere [57–59].

Fig. 1
figure 1

Definition of the geometrical parameters of the molecular structures taking part in the mechanism of the reactions CH3X + Cl, where X = F, Cl and Br

Full size image
Table 1 Molecular properties of the reactants and products of the reactions under investigation calculated at the G2 levela)
Full size table
Table 2 Molecular properties of the structures taking part in the mechanism of the H/D-abstraction reactions CH3X/CD3X + C1 (X=F, C1 and Br) calculated at the G2 level a)
Full size table

Optimized molecular structures

The most stable structures of monohalogenated methanes CH3X appears to have molecular symmetry of the C3v point group. Except for the C-X bond lengths, the structural parameters of CH3F, CH3Cl and CH3Br obtained in the geometry optimization performed at the MP2(full)/6-31G(d) level are very close one to another. The halogenated methyl radicals CH2F, CH2Cl and CH2Br are the molecular structures with the Cs symmetry. Either C-X or C-H bonds in these radicals are considerably shorter than their counterparts in molecules of the parent halogenated methanes. In contrast to that the values of angular parameters in CH2X radicals, X-C-H and H-C-H are distinctly greater than those in the corresponding reactants.

Except for fluoromethane, the attack of chlorine atom on molecule of halomethane leads to formation of the pre-reaction adducts, CH3Cl…Cl (denoted by MC1Cl) and CH3Br…Cl. (MC1Br). These intermediate complexes possess the Cs symmetry, because the attacking chlorine atom is moving across the symmetry plane of the halomethane. The pre-reaction adducts MC1X are loose molecular structures with long contact distances between the attacking chlorine and CH3X. The geometrical parameters of these molecular complexes retain the values which appear in the isolated reactants, CH3Cl and CH3Br.

The transition states (CH2X…H…Cl)≠, denoted by TS1X, describe the hydrogen abstraction from halomethane CH3X by Cl atom. Of all these saddle points, TS1X have Cs symmetry, with the C-H1 and H1-Cl bond located in the symmetry plane XCH1Cl. The transition states, TS1X are reactant-like structures, and the attack of chlorine atom at TS1X structure is nearly collinear. The calculated lengths of the breaking bond C-H1 are of 1.40 Å (TS1F, TS1Br) and 1.38 Å (TS1Cl), which corresponds to a relative elongation of 30% with respect to the C-H in isolated reactants. On the other hand, the formed H1-Cl bonds of 1.45–1.46 Å are about 15% longer than in HCl molecule. Values of the other structural parameters of the transition states TS1X are close to their counterparts in the reactants, CH3X.

The post-reaction adducts, CH2X…HCl designated by MC2X are intermediates which distinctly consist of two subunits, radical CH2X and molecule of hydrogen chloride, HCl bonded in a molecular complex. The geometrical parameters of these subunits are close to those of the isolated molecules. The contact distances C…H1, are over twice as long as those in isolated reactants, CH3X. All MC2X complexes retain symmetry of the Cs point group.

Reaction energetics

It is well known that using the G2 method leads to a realistic estimate of the total energy of a wide group of molecular structures. The accuracy of these estimations based on the G2-energies is usually considered to be better than 6 kJ mol−1, as was established for a set of about 150 compounds [45, 63, 64]. The enthalpy of formation, \( \varDelta H{{_f^0}_{,298 }} \), can be directly evaluated as the G2 enthalpy at room temperature for the reaction in which the relevant molecule is formed from the gas-phase elements, such as C(g), H2(g), F2(g), Cl2(g), and Br2(g), and by using the well-established values of enthalpy of formation at 298 K of gaseous carbon atom C(g) and molecule of Br2(g) of 715.0 kJ mol−1 and 30.9 kJ mol−1 [12, 14], respectively.

The calculated values, given in Table 3, of the enthalpy of formation \( \varDelta H{{_f^0}_{,298 }} \) for reactants and products of the reactions under investigation are in very good agreement with those found experimentally [12, 14]. The greatest divergence between theoretical and experimental estimates of \( \varDelta H{{_f^0}_{,298 }} \) occurred for the bromine compounds, CH3Br and CH2Br does not exceed 6 kJ mol−1. The reaction enthalpy \( \varDelta H{{_r^0}_{,298 }} \) calculated for reaction CH3Br +Cl ↔ CH2Br + HCl of −6.0 kJ mol−1 at room temperature is in excellent agreement with experimental one of −6.5 ± 5.5 kJ mol−1 [12]. The theoretical value of \( \varDelta H{{_r^0}_{,298 }} \) of −11.1 kJ mol−1 for CH3Cl +Cl ↔ CH2Cl + HCl is also very close to that of −14.4 ± 3.7 kJ mol−1 derived from the experimentally estimated values of \( \varDelta H{{_f^0}_{,298 }} \) of the reaction reagents. The theoretical description of the reaction thermochemistry seems to be the worst for CH3F +Cl ↔ CH2F + HCl. The calculated heat of reaction of −3.1 kJ mol−1 at 298 K is distinctly higher than the experimental values of \( \varDelta H_{r,298}^0 \) of −12.0 kJ mol [12] and −7.6 kJ mol [12]. However, one should take into account that the experimental values of \( \varDelta H{{_f^0}_{,298 }} \) of CH3F and CH2F were estimated with low precision, which may result in a final error of the reaction enthalpy of 16 kJ mol−1 or even more. Therefore, the theoretical description of the thermochemistry of the reactions under investigation based on the G2-energies should be considered as reliable.

Table 3 Comparison of the experimental \( \varDelta H_{f,298}^0 \) (exp.) and theoretical \( \varDelta H_{f,298}^0 \) (calc.) values of the enthalpy of formation of the reactants CH3X and products CH2X, (X = F, Cl and Br) obtained at the G2 level
Full size table

Reaction mechanism

The hydrogen abstraction from CH3F by Cl proceeds in accordance with the two-step reaction mechanism

$$ \mathrm{C}{{\mathrm{H}}_3}\mathrm{F} + \mathrm{C}\mathrm{l}\ \leftrightarrows \mathrm{C}{{\mathrm{H}}_2}\mathrm{F}\ldots \mathrm{HCl}\to \mathrm{C}{{\mathrm{H}}_2}\mathrm{F}+\mathrm{HCl}. $$
(4)

The intermediate complex, MC2F formed in the first elementary step dissociates into the final reaction products, radical CH2F and HCl. Profile of the potential energy surface for the CH3F + Cl reaction system is shown in Fig. 2a. The H-abstraction reaction CH3F + Cl is a weakly exothermic process. The calculated reaction enthalpy is of −5.9 kJ mol−1 at 0 K. The post-reaction adduct, CH2F…HCl (MC2F) is the lowest energy molecular structure formed during the reaction. The potential energy of MC2F at 0 K calculated at the G2 level is by 9.8 kJ mol−1 lower than the reactants’ energy. The thermal stability of MC2F with respect to the reaction products, CH2F + HCl is estimated of 4.8 kJ mol−1 at 0 K. The first elementary step is related to an energy barrier determined by the energy of the transition state, CH2F…H…Cl (TS1F). The height of the energy barrier is relatively small of 9.9 kJ mol−1, which indicates that the decay of the reactants should be a fast process, with the rate constant of 10−13 cm3molecule−1s−1 at room temperature.

Fig. 2
figure 2

Schematic profiles of the potential energy surfaces for the reactions: a) CH3X + Cl, and b) CD3X + Cl where X = F, Cl and Br. The energies are calculated at the G2 level including zero-point energy corrections

Full size image

In the case of the reactions CH3Cl/CH3Br + Cl, the H-abstraction process requires three elementary steps:

$$ \mathrm{C}{{\mathrm{H}}_3}\mathrm{X} + \mathrm{C}\mathrm{l}\ \leftrightarrows \mathrm{C}{{\mathrm{H}}_3}\mathrm{X}\ldots \mathrm{C}\mathrm{l}\ \leftrightarrows \mathrm{C}{{\mathrm{H}}_2}\mathrm{X}\ldots \mathrm{HCl}\to \mathrm{C}{{\mathrm{H}}_2}\mathrm{X} + \mathrm{HCl}, $$
(5)

where X = Cl, Br. The hydrogen abstraction from CH3Cl and CH3Br by chlorine atom is more exothermic compared with the reaction of CH3F + Cl. The profiles of the potential energy surface for these reaction systems are also shown in Fig. 2a. The first and third elementary processes are recombination and unimolecular dissociation, while the second is related to an energy barrier. In the first elementary step, a chlorine atom approaching a CH3X molecule is oriented in such a manner that enables the formation of a loose molecular complex, MC1X with the long and almost equal contact distances, Cl…X, Cl…H2 and Cl…H3. The pre-reaction adduct, MC1Br is the lowest energy structure in the CH3Br + Cl reaction system. The next elementary step leads, via TS1X to the molecular complex MC2X, which dissociates to the final channel products, CH2X + HCl. The heights of the energy barrier for the second step calculated for CH3Cl + Cl and CH3Br + Cl are slightly lower than that for CH3F + Cl. This implies either high values of the rate constants or their weak dependence on temperature.

The substitution of a hydrogen atom by deuterium changes physical properties of the molecule. The most distinct differences occur in the C-H and C-D stretching modes. This results in a decrease of the zero-point vibrational energy (ZPE) of the deuterated reactant compared with the unsubstituted one. The profiles of the potential energy surface for the reactions of the entirely deuterated reactants, CD3X with Cl atom are presented in Fig. 2b. The reactions of deuterated reactants, CD3X + Cl are by 5 kJ mol−1 less exothermic compared with those of CH3X + Cl. On the other hand, the changes in the relative energy of the pre-reaction adducts related to the D-substitution are only small, around 0.5 kJ mol−1. The considerably higher differences appear in the energy of the deuterated (DMC2X) and non-deuterated (MC2X) post-reaction adducts. A decrease of ZPE of the deuterated reactant compared with the unsubstituted one is obviously reflected in the relative energy of the transition states. Consequently, the D-abstraction reaction is thus related to an energy barrier distinctly higher compared with the analogous H-abstraction.

Rate constant calculations

A method for the rate constant calculation for a bimolecular reaction which proceeds through the formation of two weakly bound intermediate complexes (MC1X and MC2X) has been successfully applied to describe the kinetics of the H-abstraction from methanol [57–59]. The general equation, which takes into account the rotational energy, is derived from RRKM theory. Accordingly to this formalism, the rate coefficient k for the three-step reaction mechanism, such as for reaction (5) with formation of the pre-reaction (MC1X) and post-reaction (MC2X) adducts, can be expressed as:

$$ k=\frac{z}{{h{Q_{RX }}{Q_{Cl }}}}\int\limits_{{{V_{TS1X}}}}^{\infty } {\sum\limits_J {{W_{MC1X }}\left( {E,J} \right)\times \frac{{{W_{TS1X }}\left( {E,J} \right)}}{{{W_{MC1X }}\left( {E,J} \right)+{W_{TS1X }}\left( {E,J} \right)}}} } \times \frac{{{W_{MC2X }}\left( {E,J} \right)}}{{{W_{MC2X }}\left( {E,J} \right)+{W_{TS1X }}\left( {E,J} \right)}}\times \exp \left( {-E/RT} \right)dE, $$
(6)

where Q RX and Q Cl are the partition functions of CH3X and atomic chlorine, respectively, with the center of mass partition function factored out of the product Q RX Q Cl and included in z together with the partition functions of those inactive degrees of freedom which are not considered by the sums of the states under the integral. V TS1X is the height of the energy barrier toward the reactants CH3X + Cl whereas W TS1X (E,J), W MC1X (E,J), and W MC2X (E,J) denote the sum of the states at energy less than or equal to E and with angular momentum J for the transition state TS1X and the activated complexes for the unimolecular dissociations of MC1X and MC2X, respectively. All computational effort is then related to calculating the sum of the states, W(E,J). This calculation depends on the level at which the conservation of angular momentum is considered and is discussed in detail in refs. [57–59].

Equation (6) can be directly used in the description of kinetics of the reactions CH3Cl + Cl and CH3Br + Cl. In the case of the two-step mechanism such as for reaction CH3F + Cl one should replace W MC1X (E,J) by W TS1X (E,J) and omit the first fraction under the integral in Eq. 6. Analysis of the results of the direct calculations of Brudnik et al. [49, 56] shows that the dominant contribution to the rate constant is given by the states with energy E not higher than V TS1X + 3RT. In the case of a sizable (compared with RT) energy barrier V TS1X , the value of the product of the microcanonical branching fractions at an energy slightly higher than V TS1X becomes close to unity. Therefore, if the adducts are not stabilized by collisions and can rapidly undergo subsequent processes, the TST rate constant k TST seems to be a very good approximation of the exact rate coefficient, especially at ambient temperatures [49, 56, 59].

Reaction CH3F + Cl

The values of the calculated rate constants are given in Table 4. The height of the energy barrier is clearly the major factor determining the magnitude of the rate constant and its dependence on temperature. As is shown in Fig. 2a, the minimum energy path for CH3F + Cl reaction system that leads to the formation of CH2F + HCl is characterized by the relatively small height of the energy barrier of 9.9 kJ mol−1. The calculated value of the rate constant for the hydrogen abstraction reaction CH3F + Cl of 3.3×10−13 cm3molecule−1s−1 at 298 K is very close to that of 3.5×10−13 cm3molecule−1s−1 unamimously recommended by the IUPAC and NASA [12–14] evaluations of the kinetic data. Our calculated value of k(CH3F+Cl) at room temperature is very close to the reported results of 2.7×10−13 derived by Hitsuda et al. [19], 3.2×10−13 of Wallington et al. [18], 3.4×10−13 of Tuazon et al. [17], 3.5×10−13 of Sarzyński et al. [22], (3.5–3.9) ×10−13 of Marinkovic et al. [21], 3.6×10−13 of Manning and Kurylo [15], and that of 3.8×10−13 cm3molecule−1s−1 of Tschuikow-Roux et al. [16] after correction taking into account the current value of the rate constant for the reference reaction CH4 + Cl [65]. Figure 3 shows a comparison of calculated values of k(CH3F+Cl) with the available results of experimental measurements in a wide temperature range. The calculated rate constant k(CH3F+Cl) can be expressed in the temperature range 200–3000 K as:

Table 4 The rate constants calculated for the H/D-abstraction reactions CH3F + Cl, CD3F + Cl and their reverse processes
Full size table
Fig. 3
figure 3

Arrhenius plot for the CH3F + Cl reaction comparing the available results of kinetic measurements with obtained theoretically in this study

Full size image
$$ \begin{array}{*{20}c} {k\left( {\mathrm{C}{{\mathrm{H}}_3}\mathrm{F}+\mathrm{Cl}} \right)=6.75\times {10^{-12 }}\times {{{\left( {\mathrm{T}/300} \right)}}^{2.12 }}\times\exp \left( {-900/\mathrm{T}} \right)}{\mathrm{c}{{\mathrm{m}}^3}\mathrm{molecul}{{\mathrm{e}}^{-1 }}{{\mathrm{s}}^{-1 }}} \\ \end{array}. $$
(7)

The calculated values of k(CH3F+Cl) are, in the temperature range of 300–400 K, in satisfactory agreement with those estimated using the various experimental techniques. At the higher temperatures, our calculated values of k(CH3F+Cl) seem to be overestimated. However, the temperature dependence of the rate constant k(CH3F+Cl) derived experimentally shows substantial differences in values of either the pre-exponential factor or the activation energy. This is reflected in the form of the recommended Arrhenius’ expression for k(CH3F+Cl)/cm3molecule−1s−1 of 4.0×10−12exp(−730/T) preferred by IUPAC [13] and that of 1.96×10−11exp(−1200/T) favored by NASA [12]. On the other hand, the results of the kinetic investigations performed recently by Marinkovic et al. [21], in the widest temperature range of 200–700 K suggest a non-Arrhenius behavior of the kinetics of CH3F+Cl, which is described by k(CH3F+Cl)/cm3molecule−1s−1 in the form of the 1.14×10−12×(T/298)2.26×exp(−313/T). Unfortunately, there are no other studies on the kinetics CH3F+Cl conducted at sufficiently high temperatures, which could confirm this conclusion of Marinkovic et al. [21].

Reaction CH3Cl + Cl

The minimum energy path for the reaction CH3Cl + Cl is also shown in Fig. 2a. The mechanism of the H-abstraction from CH3Cl by Cl atoms is complex and consists of three elementary steps including the formation of the pre- and post-reaction adducts, MC1Cl and MC2Cl. The energy barrier for reaction CH3Cl + Cl of 8.1 kJ mol−1 is 1.8 kJ mol−1 lower than that for CH3F + Cl. The values of the calculated rate constants, k(CH3Cl+Cl) and k TST (CH3Cl+Cl) are collected in Table 5. Our calculated value of k(CH3Cl+Cl) of 4.5×10−13 cm3molecule−1s−1 at room temperature is very close to those of (4.8±0.5)×10−13 cm3molecule−1s−1 [14] and (4.9±0.5)×10−13 cm3molecule−1s−1 [12] recommended by IUPAC and NASA evaluations, respectively. The calculated value of the rate constant at 298 K can be compared with the reported results of experimental studies [12–14]. Our value of 4.5×10−13 cm3molecule−1s−1 is in line with the estimate of (4.4±0.6)×10−13 obtained by Beichert et al. [27], (4.7±0.6)×10−13 of Orlando [28], (4.8±0.4)×10−13 of Wallington et al. [26], (5.1±1.3)×10−13 of Pritchard et al. [23], (5.2±0.4)×10−13 of Sarzyński et al. [32], (5.2±0.3)×10−13 of Bryukov et al. [29], and (5.4±0.2)×10−13 cm3molecule−1s−1 of Manning and Kurylo [15]. A similar value of (5.1±0.7)×10−13 cm3molecule−1s−1 at 298 K can be derived from the expression describing the temperature dependence of the rate constant found by Tschuikow-Roux et al. [16]. A comparison between the values of the rate constant for the reaction CH3Cl + Cl calculated in this study and available experimental results are shown in Fig. 4. The values of k(CH3Cl+Cl) can be, in the temperature range of 200–3000 K, expressed as:

Table 5 The rate constants calculated for the H/D-abstraction reactions CH3Cl + Cl, CD3Cl + Cl and their reverse processes
Full size table
Fig. 4
figure 4

Arrhenius plot for the CH3Cl + Cl reaction comparing the available results of kinetic measurements with obtained theoretically in this study

Full size image
$$ \begin{array}{*{20}c} {k\left( {\mathrm{C}{{\mathrm{H}}_3}\mathrm{Cl}+\mathrm{Cl}} \right)=6.97\times {10^{-12 }}\times {{{\left( {\mathrm{T}/300} \right)}}^{1.73 }}\times\exp \left( {-795/\mathrm{T}} \right)}{\mathrm{c}{{\mathrm{m}}^3}\mathrm{molecul}{{\mathrm{e}}^{-1 }}{{\mathrm{s}}^{-1 }}} \\ \end{array}. $$
(8)

Except for the high temperature range, i.e., above 500 K, the reported values of the rate constant k(CH3Cl+Cl) estimated by different experimental techniques are very similar from one to another. The discrepancy of the experimental results is only small. The values calculated from Eq. 8 of k(CH3Cl+Cl) reproduce well the observed trend in experimental results in a wide temperature range. At temperatures above 500 K, the experimental values of k(CH3Cl+Cl) are limited by the results of Bryukov et al. [29] and Clyne and Walker [25]. The theoretically derived temperature dependence of k(CH3Cl+Cl) described by Eq. 8 can be considered the best compromise for all experimental points.

Reaction CH3Br + Cl

The profile of the potential energy surface for CH3Br + Cl reaction system shows that two molecular complexes, MC1Br and MC2Br are formed during reaction as intermediate products. The pre-reaction adduct, MC1Br is the lowest energy molecular structure in CH3Br + Cl reaction system. The calculated energy barrier corresponding to the relative potential energy of the transition state TS1Br toward the reactants of 8.3 kJ mol−1, is only slightly higher than that of 8.1 kJ mol−1 found for CH3Cl + Cl. This implies very similar values of the rate constants for both CH3Cl + Cl and CH3Br + Cl reactions. The results of the rate constant calculations for CH3Br + Cl are given in Table 6. The calculated values of k(CH3Br+Cl) are compared with experimental ones in Fig. 5. The results of kinetic measurements performed over a wide temperature range and using different experimental techniques are in very good agreement. Especially similar are values of the rate constant derived at room temperature [33–38]. Our calculated value of k(CH3Br+Cl) of 4.1×10−13 cm3molecule−1s−1 at 298 K is close to that of (4.4±0.6)×10−13 obtained by Sarzyński et al. [38], (4.5±0.4)×10−13 of Gierczak et al. [34], (4.6±0.3)×10−13 of Piety et al. [37], and (4.8±0.2)×10−13 obtained at 303 K by Kambanis et al. [36], and value of (4.4±0.6)×10−13 cm3molecule−1s−1 derived at 295 K by Orlando et al. [35]. In addition our value of k(CH3Br+Cl) is in good agreement with that of (4.4±0.2)×10−13 cm3molecule−1s−1 recommended by NASA data evaluation [12] at room temperature. Our k(CH3Br+Cl)-value is also included in the error limits of the estimate of (5.5±1.7)×10−13 cm3molecule−1s−1 obtained by Tschuikow-Roux et al. [33]. The temperature dependence of k(CH3Br+Cl) can be described as:

Table 6 The rate constants calculated for the H/D-abstraction reactions CH3Br + Cl, CD3Br + Cl and their reverse processes
Full size table
Fig. 5
figure 5

Arrhenius plot for the CH3Br + Cl reaction comparing the available results of kinetic measurements with obtained theoretically in this study

Full size image
$$ \begin{array}{*{20}c} {k\left( {\mathrm{C}{{\mathrm{H}}_3}\mathrm{Br}+\mathrm{Cl}} \right)=6.26\times {10^{-12 }}\times {{{\left( {\mathrm{T}/300} \right)}}^{1.82 }}\times\exp \left( {-795/\mathrm{T}} \right)}{\mathrm{c}{{\mathrm{m}}^3}\mathrm{molecul}{{\mathrm{e}}^{-1 }}{{\mathrm{s}}^{-1 }}} \\ \end{array}. $$
(9)

Results of the theoretical investigations indicate a non-Arrhenius behavior of the reaction kinetics, especially at high temperatures. This is in line with conclusion of Piety et al. [37], however results of the other experimental investigations do not confirm a curvature of the Arrhenius plot. The temperature dependence of the rate constant predicted by Eq. 9 is steeper than that derived by Piety et al. [37] and probably overestimates reaction rate at high temperatures.

Reactions CH2F/CH2Cl/CH2Br + HCl

The values of the enthalpy of formation and vibrational levels of the reactants and products calculated at the G2 level are in reasonable agreement with those obtained experimentally. One can expect that the calculated values of the thermodynamic functions and equilibrium constants for the reactions under investigation are realistic. The values of the rate constants for the reverse reactions of CH2X + HCl can be derived via the respective equilibrium constants. The hydrogen chloride, HCl is considered as a one of the most abundant natural chlorine containing compounds in the atmosphere. A great part of the chlorine released from chlorofluorocarbons is stored in the HCl reservoir at high altitudes, over 50 km [1]. The tropospheric concentrations of HCl reach especially high values either near the surface of remote ocean regions or in the coastal urban areas. Therefore, the kinetics of the reactions of HCl with such reactive species as the halogenated methyl radicals is of some importance for modeling and kinetic description of the complex processes occurring in the polluted atmosphere. In addition, to the best of our knowledge there is no experimental information on the kinetic investigations of the reactions CH2X + HCl (X = F, Cl and Br) conducted under typical atmospheric conditions. The rate constants, for the reverse reactions derived on the basis of the calculated equilibrium constants can be expressed in the following form:

$$ \begin{array}{*{20}c} {k\left( {\mathrm{C}{{\mathrm{H}}_2}\mathrm{F}+\mathrm{HCl}} \right)=2.88\times {10^{-13 }}\times {{{\left( {\mathrm{T}/300} \right)}}^{2.02 }}\times\exp \left( {-1255/\mathrm{T}} \right)}{\mathrm{c}{{\mathrm{m}}^3}\mathrm{molecul}{{\mathrm{e}}^{-1 }}{{\mathrm{s}}^{-1 }}} \\ \end{array} $$
(10)
$$ \begin{array}{*{20}c} {k\left( {\mathrm{C}{{\mathrm{H}}_2}\mathrm{Cl}+\mathrm{HCl}} \right)=2.42\times {10^{-13 }}\times {{{\left( {\mathrm{T}/300} \right)}}^{1.57 }}\times\exp \left( {-2100/\mathrm{T}} \right)}{\mathrm{c}{{\mathrm{m}}^3}\mathrm{molecul}{{\mathrm{e}}^{-1 }}{{\mathrm{s}}^{-1 }}} \\ \end{array} $$
(11)
$$ \begin{array}{*{20}c} {k\left( {\mathrm{C}{{\mathrm{H}}_2}\mathrm{Br}+\mathrm{HCl}} \right)=2.21\times {10^{-13 }}\times {{{\left( {\mathrm{T}/300} \right)}}^{1.69 }}\times\exp \left( {-1485/\mathrm{T}} \right)}{\mathrm{c}{{\mathrm{m}}^3}\mathrm{molecul}{{\mathrm{e}}^{-1 }}{{\mathrm{s}}^{-1 }}} \\ \end{array}. $$
(12)

The calculated rate constants for the forward processes, CH3F + Cl and CH3Br + Cl well describe the reaction kinetics in the temperature range of 250–400 K. In the case of CH3Cl + Cl, the derived kinetic expression (10) describes very well the reaction kinetics in a whole temperature range. Therefore, the equations (10–12) should reliably describe the values and temperature dependence of k(CH2X+HCl) in the temperature ranges given above. The kinetics of the hydrodehalogenation of CF2ClBr with hydrogen has been experimentally studied by Yu et al. [66] at the high temperatures of 673 – 973 K. In their kinetic computational model, the temperature dependence of the rate constant for reaction CH2F + HCl was described by the Arrhenius equation of 9.56×10−13×exp(−1225/T) cm3molecule−1s−1 estimated by referring to the analogous reactions of the halogenated methyl radicals with hydrogen bromide [66]. This leads to values of the rate constant k(CH2F+HCl) of 1.66×10−13, 2.06×10−13 and 2.45×10−13 cm3molecule−1s−1 at 700, 800 and 900 K, respectively. These values are about two times lower than those obtained in this study.

Kinetic isotope effect

The substitution of a hydrogen atom by deuterium changes the physical properties of the molecule. In consequence, the deuterated reactants react with a different rate compared to the reaction of non-deuterated molecules. The knowledge of the rate constants, k(CH3X+Cl) and k(CD3X+Cl) enables a determination of the kinetic isotope effect (KIE), defined by the ratio of k(CH3X+Cl)/k(CD3X+Cl). Values of KIE and its dependence on temperature can provide useful information for interpreting the stable isotope composition of the organic compounds in the atmosphere.

The calculated values of the rate constants k(CD3X+Cl) for the D-abstraction processes can be analytically written in the form:

$$ \begin{array}{*{20}c} {k\left( {\mathrm{C}{{\mathrm{D}}_3}\mathrm{F}+\mathrm{Cl}} \right)=9.18\times {10^{-12 }}\times {{{\left( {\mathrm{T}/300} \right)}}^{1.97 }}\times\exp \left( {-1675/\mathrm{T}} \right)}{\mathrm{c}{{\mathrm{m}}^3}\mathrm{molecul}{{\mathrm{e}}^{-1 }}{{\mathrm{s}}^{-1 }}} \\ \end{array} $$
(13)
$$ \begin{array}{*{20}c} {k\left( {\mathrm{C}{{\mathrm{D}}_3}\mathrm{Cl}+\mathrm{Cl}} \right)=8.63\times {10^{-12 }}\times {{{\left( {\mathrm{T}/300} \right)}}^{1.63 }}\times\exp \left( {-1490/\mathrm{T}} \right)}{\mathrm{c}{{\mathrm{m}}^3}\mathrm{molecul}{{\mathrm{e}}^{-1 }}{{\mathrm{s}}^{-1 }}} \\ \end{array} $$
(14)
$$ \begin{array}{*{20}c} {k\left( {\mathrm{C}{{\mathrm{D}}_3}\mathrm{Br}+\mathrm{Cl}} \right)=8.73\times {10^{-12 }}\times {{{\left( {\mathrm{T}/300} \right)}}^{1.70 }}\times\exp \left( {-1560/\mathrm{T}} \right)}{\mathrm{c}{{\mathrm{m}}^3}\mathrm{molecul}{{\mathrm{e}}^{-1 }}{{\mathrm{s}}^{-1 }}} \\ \end{array}. $$
(15)

The profiles of the potential energy surface show that D-abstraction process is related with the energy barrier of 5 kJ mol−1 higher than the H-abstraction from the corresponding non-deuterated molecule. These differences in the height of the energy barrier are reflected in values of the rate constants. The abstraction of deuterium from CD3X by Cl atom proceeds slower compared with the analogous H-abstraction from CH3X. The values of the rate constants, k(CD3X+Cl) are distinctly lower than values of their counterparts, k(CH3X+Cl), especially at low temperatures. The calculated values of KIE at room temperature are of 10.1, 8.6 and 9.6 for the CH3F/CD3F, CH3Cl/CD3Cl and CH3Br/CD3Br reaction systems, respectively. These calculated values of KIE at 298 K are distinctly higher than those obtained experimentally of 5.1–6.2 [21, 22], 4.9–5.4 [30–32] and 6.5 ± 0.3 [38] for the reaction systems ordered analogously as above. The significance of the kinetic isotope effect diminishes with rising temperature and the values of KIE at 500 K are over twice as low as those at room temperature. The values of KIE of 3.8, 3.5 and 3.6 calculated at 500 K are comparable with those of 3.3, 2.9 and 2.9 derived experimentally in our laboratory [22, 32, 38] at 527 K for CH3F/CD3F, CH3Cl/CD3Cl and CH3Br/CD3Br reaction systems, respectively. This suggests that values of the calculated rate constants, k(CD3X+Cl) gain in reliability with a rise in temperature.

There are several possible reasons for the observed disagreement between the theoretical and experimental estimations of KIE. One of them is related to the mechanism of the studied reactions. The stabilization by collisions of the molecular complexes formed during the reactions may need a more detailed approach. The influence of the formed adducts on the reaction kinetics is directly observed in the reactions of atomic chlorine with methyl and ethyl iodides [67, 68], which at room and lower temperatures proceed mainly via reversible adduct formation with the distinct pressure dependence of the kinetics of these reactions. At temperatures above 350 K, the rate constants become pressure independent.

It is worth noting that the recent kinetic experimental studies [22, 38] proposed a very simple interpretation of the KIE values for the CH3X/CD3X + Cl reaction systems, based on the assumption that the transition states for the investigated H/D-abstraction reactions are reactant-like structures. In consequence, the vibrational frequencies of the reactant (CH3X or CD3X) are very close to those of their counterparts in the respective transition state. The increase in the energy barrier ΔE for the reaction of the deuterated reactant compared to the non-deuterated one is then given by the change in ZPE during H/D-abstraction. The value of ΔE is approximately equal to half the difference between the vibrational frequencies of the C-H and C-D stretching modes because one of the C-H/D bonds is broken in the reaction. With the average C-H/D frequencies calculated from those of 2930 cm−1 and 3006(2) cm−1 for CH3F [69], 2110 cm−1 and 2258(2) cm−1 for CD3F [69], 2937 cm−1 and 3039(2) cm−1 for CH3Cl [69], 2160 cm−1 and 2283(2) cm−1 for CD3Cl[69], 2935 and 3056(2) cm−1 for CH3Br [69], and 2160 and 2297(2) cm−1 for CD3Br [69], one can obtain a value for ΔE of 386, 382 and 382 cm−1, for CH3F/CD3F + Cl, CH3Cl/CD3Cl + Cl and CH3Br/CD3Br + Cl reaction systems, respectively. Assuming no influence of tunneling correction on the KIE, the value of the KIE can be approximately described by exp(ΔE/RT). These values of ΔE lead to very similar values of KIE, which is confirmed by results of the measurements using the same experimental techniques and methodology. The derived from exp(ΔE/RT) values of KIE are of 6.3, 4.2 and 2.8 for the all investigated systems at the 298, 385 and 527 K, respectively. These values are in line with results of measurements of KIE at the same temperatures of 6.2 ± 0.4, 4.2 ± 0.3 and 3.3 ± 0.2 for CH3F/CD3F + Cl [22], of 5.4 ± 0.3, 4.2 ± 0.2 and 2.9 ± 0.2 for CH3Cl/CD3Cl + Cl [32], and 6.5 ± 0.4, 4.8 ± 0.3 and 2.9 ± 0.2 for CH3Br/CD3Br + Cl [38]. In spite of simplicity of the computational procedure the calculated KIE values are in better agreement with results of experiments than those obtained using the advanced theoretical kinetic models. This agreement supports the conclusion that changes in ZPE during the CH3X/CD3X+Cl reactions seem to make a predominant contribution to the KIE. It also suggests that the molecular structure of the transition states for reactions CH3X + Cl should be a more reactant-like structure than those derived by quantum chemistry methods so far.

The derived values of the rate constants, k(CD3X+Cl) enable also a determination of the rate constants for the backward processes, CD2X + DCl via the calculated equilibrium constants. The obtained values of k(CD2X+HCl) can be expressed as:

$$ \begin{array}{*{20}c} {k\left( {\mathrm{C}{{\mathrm{D}}_2}\mathrm{F}+\mathrm{DCl}} \right)=1.57\times {10^{-13 }}\times {{{\left( {\mathrm{T}/300} \right)}}^{2.18 }}\times\exp \left( {-1340/\mathrm{T}} \right)}{\mathrm{c}{{\mathrm{m}}^3}\mathrm{molecul}{{\mathrm{e}}^{-1 }}{{\mathrm{s}}^{-1 }}} \\ \end{array} $$
(16)
$$ \begin{array}{*{20}c} {k\left( {\mathrm{C}{{\mathrm{D}}_2}\mathrm{Cl}+\mathrm{DCl}} \right)=1.11\times {10^{-13 }}\times {{{\left( {\mathrm{T}/300} \right)}}^{1.82 }}\times\exp \left( {-2070/\mathrm{T}} \right)}{\mathrm{c}{{\mathrm{m}}^3}\mathrm{molecul}{{\mathrm{e}}^{-1 }}{{\mathrm{s}}^{-1 }}} \\ \end{array} $$
(17)
$$ \begin{array}{*{20}c} {k\left( {\mathrm{C}{{\mathrm{D}}_2}\mathrm{Br}+\mathrm{DCl}} \right)=1.17\times {10^{-12 }}\times {{{\left( {\mathrm{T}/300} \right)}}^{1.90 }}\times\exp \left( {-1535/\mathrm{T}} \right)}{\mathrm{c}{{\mathrm{m}}^3}\mathrm{molecul}{{\mathrm{e}}^{-1 }}{{\mathrm{s}}^{-1 }}} \\ \end{array}. $$
(18)

There is no experimental data on kinetics of this class of reactions. One can expect that the most credible values of k(CD2X+DCl) are those describing the reaction kinetics at high temperatures.

Conclusions

The main aim of the present study is related to a theoretical analysis of the kinetics of the hydrogen abstraction from monohalogenated methanes by chlorine atoms. Theoretical investigations based on ab initio calculations of the CH3X + Cl (X = F, Cl and Br) reaction systems at the G2 level were performed to gain insight into the reaction mechanism. The results of the calculations also allow an estimation of the reaction energetics and the molecular properties of the structures taking part in the reaction mechanism.

The calculated values of the enthalpy of formation of the reactants and products are in very good agreement with the reported values estimated experimentally. All the reactions studied are exothermic processes, with the calculated values of the reaction enthalpy at 298 K of −5.9, -9.0 and −14.2 kJ mol−1 for CH3F + Cl, CH3Br + Cl and CH3Cl + Cl, respectively.

The calculated profiles of the potential energy surface of the reaction systems show that the mechanism of the reactions studied is complex and the H-abstraction proceeds via the formation of intermediate complexes. The multi-step reaction mechanism consists of two - in the case of CH3F + Cl - and of three for CH3Cl+Cl and CH3Br + Cl elementary steps. The heights of the energy barrier related to the H-abstraction are of 8–10 kJ mol−1, the lowest value corresponds to CH3Cl + Cl and the highest one to CH3F + Cl. These low energy barriers result in the high values of the rate constants, of 10−13 cm3molecule−1s−1 at room temperature. The rate constants were calculated using the theoretical method based on the RRKM theory and the simplified version of the statistical adiabatic channel model [57]. However, the values of the rate constant calculated at the low temperatures (i.e., below 1000 K) using the conventional transition state theory are very close to those derived in the exact calculations.

The calculated values of the rate constants well describe the kinetics of CH3X + Cl reactions systems. An especially good agreement between the calculated and reported values of the rate constant has been reached for the reaction CH3Cl + Cl. The calculated values of the rate constant for this reaction indeed form the trend line in the experimentally estimated results. The derived kinetic expression describes very well the kinetics of CH3Cl + Cl in the whole range of the experimental measurements of 250–1000 K, with an accuracy at least no worse than the one given by various kinetic data evaluations. In the temperature range of 250–400 K, the kinetic parameters derived theoretically also allow a quantitative description of the reaction kinetics of CH3F + Cl and CH3Br + Cl. At the higher temperatures, the agreement between the calculated and experimental values of the rate constants for these reactions deteriorates because the calculated values of k(CH3F+Cl) and k(CH3Br+Cl) slightly exceed the experimental findings. This may be an effect of the treatment of the lowest degrees of freedom of TS1F and TS1Br as the harmonic vibrations.

The substitution of a hydrogen atom by deuterium changes the physical properties of the reactant molecules, which may essentially have an influence on the kinetics of the reactions studied. The results of the reaction path calculations show that the D-abstraction is related with the energy barrier of 5 kJ mol−1 higher than the H-abstraction from the corresponding non-deuterated reactant molecule. The calculated values of the rate constants k(CD3X+Cl) are distinctly lower compared with the values of their counterparts, k(CH3X+Cl), especially at low temperatures. On the other hand, the values derived in this study and the reported values of KIE [21] calculated at the different levels of theory are higher than those estimated experimentally. It may suggest that the stabilization by collisions of the molecular complexes formed during the reaction should be explicitly considered in the description of the reaction kinetics. The formation of the molecular complexes is experimentally observed in the case of reactions of iodomethane and iodoethane with chlorine atoms [67, 68]. This is probably a reason for the serious discrepancy in the reported values of KIE for CH3I/CD3I + Cl and C2H5I/C2D5I + Cl reaction systems at temperatures below 350 K. There are also some arguments in support of the conclusion that changes in ZPE during the CH3X/CD3X + Cl reactions seem to make a predominant contribution to KIE. If it is assumed that the transition states for the investigated H/D-abstraction reactions are very reactant-like structures then the increase in the energy barrier for D-abstraction, ΔE should be approximately equal to half the difference of the vibrational frequencies of the C-H and C-D stretching modes because one of the C-H/D bonds is broken in the reaction. The values of KIE for the reactions derived in this simple way as calculated from the expression exp(ΔE/RT) are in good agreement with experimental estimates. This may suggest that the molecular structures of the transition states, TS1X obtained in the geometry optimization by quantum chemistry should be more reactant-like structures, which is an incentive to further theoretical studies.

The rate constants, for the reverse reactions CH2X + Cl and CD2Cl + DCl were derived based on the calculated equilibrium constants. There is no experimental information on the kinetics of this class of reactions. Therefore, the derived values of the rate constants, k(CH2X+HCl) and k(CD2Cl+DCl) are a substantial supplement of the kinetic data necessary for description and modeling of the processes of importance in atmospheric chemistry.