Investigation of the potential of asymptotic homogenization for elastic composites via a three-dimensional computational study

Abstract

Asymptotic homogenization is employed assuming a sharp length scale separation between the periodic structure (fine scale) and the whole composite (coarse scale). A classical approach yields the linear elastic-type coarse scale model, where the effective elastic coefficients are computed solving fine scale periodic cell problems. We generalize the existing results by considering an arbitrary number of subphases and general periodic cell shapes. We focus on the stress jump conditions arising in the cell problems and explicitly compute the corresponding interface loads. The latter represent a key driving force to obtain nontrivial cell problems solutions whenever discontinuities of the coefficients between the host medium (matrix) and the subphases occur. The numerical simulations illustrate the geometrically induced anisotropy and foster the comparison between asymptotic homogenization and well established Eshelby based techniques. We show that the method can be routinely implemented in three dimensions and should be applied to hierarchical hard tissues whenever the precise shape and arrangement of the subphases cannot be ignored. Our numerical results are benchmarked exploiting the semi-analytical solution which holds for cylindrical aligned fibers.

Appendix: The asymptotic model for aligned fibers

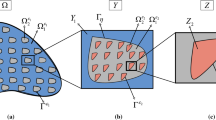
In order to compare our results to those found in [24], we specialize our model by matching any assumption enforced by the authors of that paper. We identify our domain $\varOmega$ with a periodic composite reinforced by aligned fibers, where each subphase $\varOmega _{\alpha }$ is a fiber which extends up to the domain boundary, whereas $\varOmega _c$ represents the host medium. Once periodicity is exploited, the periodic cell then comprises a number N of aligned fibers which extend from bottom to top of it. They are, without loss of generality, aligned with the $\varvec{e}_3$ axis. See Fig. 9, where the geometrical setting related to the particular case of a single cylindrical fiber in a regular prismatic lattice is depicted.

Material properties $\mathbb {C}^c$ and $\mathbb {C}^{\alpha }$ are assumed constant with respect to both the fine scale $\varvec{y}$ and the coarse scale $\varvec{x}$. According to this scenario, the cell problem (51–54) reads

$$\begin{aligned} \displaystyle&C_{ijpq}^c \frac{\partial ^2 \chi _{pkl}^c}{\partial y_j \partial y_q} =0\,\, \text {in}\,\, \varOmega _c, \end{aligned}$$

(90)

$$\begin{aligned}&C_{ijpq}^{r} \frac{\partial ^2 \chi _{pkl}^{r}}{\partial y_j \partial y_q} =0\,\, \text {in}\,\, \varOmega _{r}, \end{aligned}$$

(91)

$$\begin{aligned}&C_{ijpq}^c \frac{\partial \chi _{pkl}^c}{\partial y_q} n_j^{r}+C_{ijkl}^cn^{r}_j \nonumber \\&\quad =C_{ijpq}^{r} \frac{\partial \chi _{pkl}^{r}}{\partial y_q} n_j^{r}+C_{ijkl}^{r}n^{r}_j \,\, \text {on} \,\, \varGamma ^{r}, \end{aligned}$$

(92)

$$\begin{aligned}&\chi ^c_{ikl}=\chi ^{r}_{ikl} \,\, \text {on} \,\, \varGamma ^{r}, \end{aligned}$$

(93)

$r=1,\ldots N$ and summation over repeated indices $j,p,q=1,2,3$ is understood. In the above problem, we slightly rearranged terms, we replaced the dummy index $\alpha$ with r, cf. [24], and exploited property (10). We then recognize that the unknowns $\chi ^c$, $\chi ^{r}$ do not depend on $y_3$ for reasons of symmetry. In particular, since

$$\begin{aligned} n^r_1=n^r_1(y_1,y_2);\quad n^r_2=n^r_2(y_1,y_2);\quad n_3^r=0, \end{aligned}$$

(94)

and the elasticity tensors $\mathbb {C}^c$ and $\mathbb {C}^r$ are $\varvec{y}$-constant, the solution ansatz

$$\begin{aligned} \chi ^c (y_1,y_2);\quad \chi ^{r}(y_1,y_2) \end{aligned}$$

(95)

satisfies the cell problems (90–93). Hence, the cell problems (90–93) are now to be solved in two dimensions only and they can be rewritten, setting $\mathbb {C}^c=\mathbb {C}^0$, as

$$\begin{aligned}&C_{i\alpha s \beta }^{r} \frac{\partial ^2 \chi _{skl}^{r}}{\partial y_{\alpha } \partial y_{\beta }} =0\,\, \text {in}\,\, D_{r}, \end{aligned}$$

(96)

$$\begin{aligned}&C_{i\alpha s\beta }^0 \frac{\partial \chi _{skl}^0}{\partial y_\beta } n_{\alpha }^{r}+C_{i\alpha k l}^0n^{r}_{\alpha }\nonumber \\&\quad =C_{i\alpha s\beta }^{r} \frac{\partial \chi _{skl}^{ r}}{\partial y_{\beta }} n_{\alpha }^{r}+C_{i\alpha kl}^{r}n^{r}_{\alpha } \,\,\, \text {on} \,\, \partial D^{r}, \end{aligned}$$

(97)

$$\begin{aligned}&\chi ^0_{ikl}=\chi ^{r}_{ikl} \,\,\, \text {on} \,\, \partial D^{r}, \end{aligned}$$

(98)

$r=0,1,\ldots N$, and summation over repeated indices $s=1,2,3$, $\alpha , \beta =1,2$ is understood. Here, the domain $D \subset \mathbb {R}^2$ represents the two-dimensional cross section of the periodic cell $\varOmega$. We set $\varOmega _0=\varOmega _c$ and introduce the following notation for the sake of convenience:

$$\begin{aligned}&\varOmega =D\times (0,1); \quad \varOmega _{r}=D_{r} \times (0,1);\nonumber \\&\bar{D}=\bigcup ^{N}_{r=0} \bar{D}_{r}; \quad \varGamma ^{r}=\partial D_{r}\times (0,1). \end{aligned}$$

(99)

Accounting for notation (99), the componentwise definition of the effective elasticity tensor (60), and continuity (98), we finally have:

$$\begin{aligned}&\tilde{C}_{ijkl}=\sum _{r=0}^N \phi _r C_{ijkl}^r+\sum ^{N}_{r=1} \left( C_{ijs\beta }^{r}-C^{0}_{ijs \beta } \right) \left\langle M^r_{s \beta k l}\right\rangle _r,\nonumber \\&\phi _r=\frac{|\varOmega _r|}{|\varOmega |}=\frac{|D_r|}{|D|}, \end{aligned}$$

(100)

$$\begin{aligned}&\left\langle M^r_{s\beta k l}\right\rangle _r= \left\langle \frac{\partial \chi _{skl}^r}{\partial y_{\beta }} \right\rangle _r=\frac{1}{|D|} \int _{\partial D_r} \chi _{skl}^r n_{\beta }^{r}\,\,\text {dl}. \end{aligned}$$

(101)

The functional form of the effective elasticity tensor (100), as well as the corresponding cell problems (96–98) and auxiliary tensor (101), exactly coincide¹ with those found in [24], which were derived accounting for a periodic fiber reinforced composite and applying asymptotic homogenization to the domain cross section only.