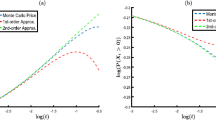Extreme ATM skew in a local volatility model with discontinuity: joint density approach

Abstract

This paper concerns a local volatility model in which the volatility takes two possible values, and the specific value depends on whether the underlying price is above or below a given threshold. The model is known, and a number of results have been obtained for it. In particular, option pricing formulas and a power-law behaviour of the implied volatility skew have been established in the case when the threshold is taken at the money. In this paper, we derive an alternative representation of option pricing formulas. In addition, we obtain an approximation of option prices by the corresponding Black–Scholes prices. Using this approximation streamlines obtaining the aforementioned behaviour of the skew. Our approach is based on the natural relationship of the model with skew Brownian motion and consists of the systematic use of the joint distribution of this stochastic process and some of its functionals.

1 Introduction

This paper concerns a local volatility model (LVM) in which the volatility takes only two possible values. If the underlying price is larger than or equal to some threshold $R$, the volatility is equal to $\sigma _{+}$, and if the underlying price is less than $R$, the volatility is equal to $\sigma _{-}$, where $\sigma _{+}$ and $\sigma _{-}$ are given positive constants. In what follows, we refer to this model as the two-valued LVM. If $\sigma _{+}=\sigma _{-}=\sigma$, this is just the classic lognormal model with constant volatility $\sigma$, under which the celebrated Black–Scholes (BS) formula for the price of a European option has been obtained.

The two-valued LVM is well known, and a number of results for the model are available (see e.g. Gairat and Shcherbakov [4], Lipton [8], Lipton and Sepp [9], Pigato [10] and the references therein). Pricing formulas for European options have been obtained in [4] for arbitrary spot $S_{0}$ and strike $K$. In [10], option pricing formulas have been obtained in the case when $S_{0}=R$ or $K=R$. The other results in [10] concern the analysis of the implied volatility surface in the case when $S_{0}=R$. In particular, it was shown that if strike $K$ and maturity $T$ are related by the equation $K=e^{\gamma \sqrt{T}}$ (“the central-limit regime”), the implied volatility $\sigma _{{\mathrm { BS}}}(T,K)=\sigma _{{\mathrm { BS}}}(T,e^{\gamma \sqrt{T}})$ converges to a smooth function $\sigma _{{\mathrm { BS}}}(\gamma )$ of $\gamma$ as $T\to 0$, and a Taylor expansion of the second order for this limit function was explicitly computed. Moreover, an exact formula for the at-the-money (ATM) implied volatility skew was obtained. These results were then used to show that the ATM skew behaves like $T^{-1/2}$ as $T\to 0$.

The result concerning the short term behaviour of the ATM skew is of particular interest for the following reasons. On the one hand, this reproduces the well-known power-law behaviour of the skew for short-term maturities observed in some data (see [10] and the references therein for more details). On the other hand, in Guyon and El Amrani [6], the authors claim that “our study suggests that the term structure of the equity ATM skew has a power-law shape for maturities above 1 month, but has a different behaviour, and in particular may not blow up, for shorter maturities”. This difference in results and opinions should be taken into account when using the two-valued LVM. In addition, note that in foreign exchange option markets, the standard practice is to quote implied volatility in terms of delta moneyness $\frac{\log (K/F)}{\sigma \sqrt{T}}$, where $F$ is the forward price (see e.g. Clark [1, Chap. 3] and the references therein). As a result, the skew asymptotically behaves as $T^{-1/2}$ when the implied volatility is quoted in terms of the moneyness $\log (K/F)$.

The research approach in [10] was based on using the Laplace transform and related techniques. In the present paper, we demonstrate another approach to the study of the two-valued LVM. This alternative method is based on the natural relationship of the two-valued LVM with a skew Brownian motion (SBM). The latter is a continuous-time Markov process obtained from a standard Brownian motion (BM) by independently choosing with certain fixed probabilities the signs of the excursions away from the origin. If these probabilities are equal to $1/2$, the process is a standard BM. It turns out that if the underlying price follows the two-valued LVM, the natural logarithm of the price divided by the volatility is a special case of SBM with a two-valued drift (to be explained). Our approach consists of using the joint distribution of this process and its functionals, such as the local time at the origin, the last visit to the origin and the occupation time. The distribution was obtained in [4], where it was applied to option valuation under the two-valued LVM. Using this distribution allowed to streamline some computations in a special case of SBM in Gairat and Shcherbakov [5]. In the present paper, we give another example of the application of the joint distribution.

First of all, we use the distribution to obtain option pricing formulas in the case $S_{0}=R=1$ (the assumption $R=1$ is just a technical one, as the case of general $R$ can be readily reduced to this one by dividing the underlying price by $R$). As mentioned above, option pricing for a general initial underlying price was considered in [4] (see Sect. 3 below for details). However, the case $S_{0}=R=1$ was not explicitly mentioned in that paper. Although pricing formulas in this case can be obtained by passing to the limit $S_{0}\to 1$ in more general formulas in [4], we derive them here directly by using the aforementioned joint distribution (as we did in [4] in the general case). This allows us to once again demonstrate the proposed method. Besides, the corresponding computations are simplified in the case when the discontinuity threshold is taken at the money. We also obtain a new representation of the option prices in this case by combining the joint distribution with the well-known Dupire forward equation. These new option pricing formulas take the form of a convolution of ATM prices with the density of the first passage time to zero of a standard Brownian motion, which is easy to interpret in probabilistic terms. Furthermore, we use our distributional results to obtain an approximation of option prices in the two-valued LVM by the corresponding BS prices (BS approximation). Briefly, the BS approximation is as follows. Consider a European option with maturity $T$ and strike $K\geq 1$. Let $C_{\mathrm {lvm}}(K, T)$ be the option price under the two-valued LVM and $C_{\mathrm { BS}}(\sigma ,K, T)$ the BS price of the same option, when the volatility is equal to $\sigma$. Then $|C_{\mathrm {lvm}}(K,T)-2pC_{\mathrm { BS}}(\sigma _{+}, K, T)|\leq cT$ for all sufficiently small $T$, where $p=\frac{\sigma _{-}}{\sigma _{-}+\sigma _{+}}$. A similar approximation holds for prices of European put options. The BS approximation was already briefly noted in [4], although it was not sufficiently appreciated there. In the present paper, we discuss the approximation in more detail and apply it to obtain some key results concerning the short-term behaviour of the implied volatility. In addition, we obtain a new form of the approximation and apply it to estimate the implied volatility.

The rest of the paper is organised as follows. In Sect. 2, we formally define the two-valued LVM and state the key result concerning the aforementioned joint distribution. Option pricing formulas and the BS approximation are stated in Sect. 3. Section 4 concerns the analysis of the implied volatility surface. Proofs of most of the results are given in Sect. 5. In Sect. 6, a modification of the BS approximation is discussed.

2 The model

We start with some notations. Let $(\Omega , {\mathcal{F}}, \mathbb{P})$ be a probability space on which all random variables under consideration are defined. The expectation with respect to ℙ is denoted by $\mathbb{E}$. Throughout, $W = (W_{t})_{ t\geq 0}$ denotes a standard Brownian motion (BM), and ${\mathbf{1}}_{A}$ denotes the indicator function of a set or an event $A$.

Without loss of generality, we assume throughout that the threshold $R$ of the underlying price where the volatility changes its value is $R=1$.

In the two-valued LVM that was briefly described in the introduction, the underlying price $S=(S_{t})_{t\geq 0}$ follows the equation

$$ dS_{t}= S_{t} \sigma (\log S_{t}) dW_{t}, $$

where the function $\sigma$ is given by

$$ \sigma (x)=\sigma _{+}{\mathbf{1}}_{\{x\geq 0\}}+\sigma _{-}{\mathbf{1}}_{\{x< 0\}} $$

for some constants $\sigma _{+}>0$ and $\sigma _{-}>0$. Further, consider the process $X=(X_{t})_{t\geq 0}$ defined by

$$ X_{t}= \textstyle\begin{cases} \frac{\log S_{t}}{\sigma _{+}}&\quad \text{for } S_{t}\geq 1, \\ \frac{\log S_{t}}{\sigma _{-}}&\quad \text{for } S_{t}< 1. \end{cases} $$

(2.1)

By [4, Lemma 1], the process $X$ follows the equation

$$ dX_{t}=m(X_{t})dt+(p-q)dL_{t}+dW_{t}, $$

(2.2)

where

$$\begin{aligned} m(x)&=-\frac{\sigma _{+}}{2}{\mathbf{1}}_{\{x\geq 0\}}-\frac{\sigma _{-}}{2}{\mathbf{1}}_{\{x< 0 \}}, \end{aligned}$$

(2.3)

$$\begin{aligned} p&=\frac{\sigma _{-}}{\sigma _{-}+\sigma _{+}}, \end{aligned}$$

(2.4)

$$\begin{aligned} q&=1-p=\frac{\sigma _{+}}{\sigma _{-}+\sigma _{+}} \end{aligned}$$

(2.5)

and

$$ L_{T}=L^{(X)}_{T}=\lim \limits _{\varepsilon \to 0}\frac{1}{2\varepsilon }\int \limits _{0}^{T} {\mathbf{1}} _{\{-\varepsilon \leq X_{u}\leq \varepsilon \}}du $$

(2.6)

is the local time of the process at the origin.

The process $X$ is a special case of a skew Brownian motion (SBM) with a two-valued drift. Recall that SBM (without drift) is obtained from a standard BM by independently choosing with certain probabilities the signs of the excursions away from the origin. An excursion is chosen to be positive with a fixed probability $p$ and negative with probability $q=1-p$ (if these probabilities are equal to $\frac{1}{2}$, the process is a standard BM). The process $X$ is SBM with probabilities $p$ and $q$ given by (2.4) and (2.5), respectively, and the two-valued drift (2.3) (see the Appendix).

As already mentioned in the introduction, a key ingredient in our analysis of the two-valued LVM is the use of the joint distribution of the process $X$ and some of its functionals. These functionals include the local time of the process and the following quantities. Namely, given $T>0$, let

$$\begin{aligned} \tau _{0}&= \min \{t\in [0,T]: X_{t}=0 \}, \\ \tau &=\max \{t\in (0,T]: X_{t}=0\} \end{aligned}$$

(2.7)

be the first and last visits to the origin, respectively, (on the interval $[0,T]$) and let

$$\begin{aligned} V&=\int \limits _{\tau _{0}}^{\tau}{\mathbf{1}}_{\{X_{t}\geq 0\}}dt \end{aligned}$$

(2.8)

be the occupation time of the nonnegative half line on the interval $[\tau _{0}, \tau ]$.

The distribution of interest is given in Theorem 2.1 below. Note that the theorem is a special case of a more general result for SBM obtained in Gairat and Shcherbakov [4] (see Theorem A.1 in the Appendix).

Theorem 2.1

Let $X$ be the process defined in (2.1). Let $L_{T}$, $\tau$ and $V$ be the quantities of this process defined by (2.6)–(2.8) and let $X_{0}=0$. Then the joint density of the random variables $\tau , V, X_{T}$ and $L_{T}$ is given by

$$\begin{aligned} f_{T}(t, v, x, \ell ) &=2\alpha (x) h(v, \ell p)h(t-v, \ell q)h(T-t, x) \\ & \hphantom{=:} \times e^{-\frac{\sigma _{+}^{2}v+\sigma _{-}^{2}(t-v)+\sigma ^{2}(x)(T-t)}{8}- \frac{\sigma (x)}{2}x} \end{aligned}$$

(2.9)

for $0\leq v\leq t\leq T$ and $\ell \geq 0$, where

$$ \alpha (x)=p{\mathbf{1}}_{\{x\geq 0\}}+q{\mathbf{1}}_{\{x< 0\}}, $$

(2.10)

the probabilities $p$ and $q$ are defined in (2.4) and (2.5), respectively, and

$$ h(s, y)=\frac{|y|}{\sqrt{2\pi s^{3}}}e^{-\frac{y^{2}}{2s}}, \qquad y \in {\mathbb{R}}, s\in {\mathbb{R}}_{+}, $$

is the density of the first passage time to zero of a standard BM starting at $y$.

Remark 2.2

Note that it is convenient to rewrite the density in terms of the variables $u=t-v$ and $s=T-t$ for $t\in [0,T]$. It is easy to see that if $X_{0}=0$ and $x\geq 0$, the variable $u$ is the occupation time of the negative half-line and the variable $v+s$ is the total occupation time of the positive half-line, and if $X_{0}=0$ and $x<0$, the occupation time of the negative half-line is $u+s$ and the total occupation time of the positive half-line is $v$. In these terms, we have that

$$\begin{aligned} f_{T}(t, v, x, \ell )&=\widetilde{f}_{T}(v, u, s, x, \ell ) \\ &=2\alpha (x) h(v, \ell p)h(u, \ell q)h(s, x) e^{- \frac{\sigma _{+}^{2}v+\sigma _{-}^{2}u+\sigma ^{2}(x)s}{2}-\frac{\sigma (x)}{2}x} \end{aligned}$$

(2.11)

for $\ell \geq 0$ and $v, u, s\geq 0$ with $s=T-t$ and $u = t-v$ (so that $v+u+s=T$).

Theorem 2.3

Let $X$ be the process defined in (2.1). Let $p(0,x,T)$ be the density function of $X_{T}$ given that $X_{0}=0$. Then

$$\begin{aligned} p(0,x,T)&= 2\alpha (x)e^{-\frac{\sigma (x)}{2}x}\int _{0}^{T}\phi (T-s)h(s,x)e^{- \frac{\sigma ^{2}(x)}{8}s}ds \\ &= \textstyle\begin{cases} 2pe^{-\frac{\sigma _{+}}{2}x}\int _{0}^{T}\phi (T-s)h(s,x)e^{- \frac{\sigma _{+}^{2}}{8}s}ds& \quad \textit{for } x\geq 0, \\ 2qe^{-\frac{\sigma _{-}}{2}x}\int _{0}^{T}\phi (T-s)h(s,x)e^{- \frac{\sigma _{-}^{2}}{8}s}ds& \quad \textit{for } x< 0, \end{cases}\displaystyle \end{aligned}$$

where

$$\begin{aligned} \phi (t)&= \frac{1}{\sqrt{2\pi t}\,(\sigma _{+}-\sigma _{-})} (\sigma _{+}e^{- \frac{\sigma _{-}^{2}}{8}t}-\sigma _{-}e^{-\frac{\sigma _{+}^{2}}{8}t} ) \\ & \hphantom{=:} + \frac{1}{2}\frac{\sigma _{+}\sigma _{-}}{(\sigma _{+}-\sigma _{-})} \bigg({\mathrm {N}}\Big( \frac{\sqrt{t} \sigma _{-}}{2}\Big)-{\mathrm {N}}\Big(\frac{\sqrt{t} \sigma _{+}}{2}\Big) \bigg) \end{aligned}$$

(2.12)

and

$$ {\mathrm {N}}(z)=\int _{-\infty}^{z}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^{2}}{2}}dx $$

for $z\in {\mathbb{R}}$.

Theorem 2.3 is proved in Sect. 5.1.

Remark 2.4

The function $\phi$ defined in (2.12) has a natural probabilistic meaning. Recall that the function $h(s,x)$ is the density of the first passage time to 0 of a standard BM starting at $x$. The distribution of the first passage time converges, as $x\to 0$, to the point mass at 0. It follows from this fact and Theorem 2.3 that

$$ \phi (T)=\frac{1}{2p}\lim \limits _{x\downarrow 0}p(0,x,T)= \frac{1}{2q}\lim \limits _{x\uparrow 0}p(0,x,T). $$

3 Option valuation

Let us briefly recall some results of Gairat and Shcherbakov [4] concerning option valuation under the two-valued LVM. Pricing formulas were obtained in that paper for knock-in call options in the cases $R=1, S_{0}\geq 1, K>1$ and $R=1, S_{0}<1, K>1$. By combining these results with the Black–Scholes prices for knock-out call options, one can obtain prices of European call options for other values of $S_{0}$ and $K$. The pricing formula in the case $R=1, S_{0}\geq 1, K>1$ in [4] is given in terms of a single integral, where an integrand is analytically expressed in terms of the cumulative distribution function (cdf) ${\mathrm {N}}$ of the standard normal distribution ${\mathcal{N}}(0,1)$. In the special case $R=S_{0}=1, K>1$, one gets the price of the European option call option. This case is considered in Theorem 3.1 below. The pricing formula in the case $R=1, S_{0}<1, K>1$ in [4] is also given in terms of a single integral with an integrand analytically expressed in terms of the standard normal distribution and a bivariate normal distribution.

3.1 Pricing formulas

Let

$$\begin{aligned} &\psi (a, s, k) \\ &= \textstyle\begin{cases} \int \limits _{k}^{\infty}e^{ax}h(s,x)dx =\frac{1}{\sqrt{2\pi s}}e^{ak- \frac{k^{2}}{2s}}+a\,e^{\frac{a^{2}}{2}s} {\mathrm {N}}(\frac{as-k}{\sqrt{s}})& \quad \text{for } k\geq 0, \\ \int \limits _{-\infty}^{k}e^{ax}h(s,x)dx =\frac{1}{\sqrt{2\pi s}}e^{ak- \frac{k^{2}}{2s}}-a\,e^{\frac{a^{2}}{2}s} {\mathrm {N}}(\frac{k-as}{\sqrt{s}})& \quad \text{for } k< 0. \end{cases}\displaystyle \end{aligned}$$

(3.1)

Note that the equation for the function $\psi$ can be rewritten as

$$ \psi (a,s,k)=\frac{1}{\sqrt{2\pi s}}e^{ak-\frac{k^{2}}{2s}} +a\, {\mathrm { sgn}}(k) e^{\frac{a^{2}}{2}s} {\mathrm {N}}\bigg({\mathrm { sgn}}(k) \frac{as-k}{\sqrt{s}}\bigg) \qquad \text{for } k\in {\mathbb{R}}, $$

where

$$ {\mathrm { sgn}}(k)= \textstyle\begin{cases} 1& \quad \text{for } k\geq 0, \\ -1& \quad \text{for } k< 0. \end{cases} $$

Define

$$ F\left (T, a, k\right )=\int \limits _{0}^{T}\phi (T-s)\psi (a,s,k)e^{- \frac{a^{2}}{2}s}ds, $$

(3.2)

where $\phi$ is the function defined in (2.12).

Consider European options with strike $K$ and time to expiry $T$. Let $C_{\mathrm {lvm}}(S_{0}, K, T)$ and $P_{\mathrm {lvm}}(S_{0}, K, T)$ be the price of the call and put option, respectively, when the initial value of the underlying price is $S_{0}$.

Theorem 3.1

If $S_{0}=1$ and $K>1$, then

$$ C_{\mathrm {lvm}}(1, K, T)=2p\bigg(F\Big(T,\frac{\sigma _{+}}{2}, k\Big)-e^{\sigma _{+}k} F \Big(T, -\frac{\sigma _{+}}{2},k\Big)\bigg), $$

where $k=(\log K)/\sigma _{+}$. If $S_{0}=1$ and $K<1$, then

$$ P_{\mathrm {lvm}}(1, K, T)=2q\bigg(e^{\sigma _{-}k}F\Big(T,-\frac{\sigma _{-}}{2}, k\Big)- F \Big(T, \frac{\sigma _{-}}{2},k\Big)\bigg), $$

where $k=(\log K)/\sigma _{-}$.

By Theorem 3.1, we immediately get for the ATM price the equation

$$\begin{aligned} V_{\mathrm { atm}}(T)&=C_{\mathrm {lvm}}(1,1,T)=2p\bigg(F\Big(T,\frac{\sigma _{+}}{2}, 0\Big)- F \Big(T, -\frac{\sigma _{+}}{2},0\Big)\bigg) \\ &=P_{\mathrm {lvm}}(1,1,T) =2q\bigg(F\Big(T,-\frac{\sigma _{-}}{2}, 0\Big)-F\Big(T, \frac{\sigma _{-}}{2},0\Big)\bigg), \end{aligned}$$

(3.3)

which still involves the function $F$. Corollary 3.2 below shows that (3.3) can be simplified in such a way that the ATM price is analytically expressed in terms of the error function

$$ {\mathrm{Erf}}(x)=\frac{2}{\sqrt{\pi}}\int \limits _{0}^{x}e^{-t^{2}}dt. $$

Corollary 3.2

If $S_{0}=K=1$, then

$$ \begin{aligned} V_{\mathrm { atm}}(T) &= \frac{\sigma _{-}^{2}\sigma _{+}^{2}}{4(\sigma _{-}^{2}-\sigma _{+}^{2})}\bigg( \frac{\sqrt{8T}}{\sigma _{+}\sqrt{\pi}}e^{-\frac{\sigma _{+}^{2}}{8}T}- \frac{\sqrt{8T}}{\sigma _{-}\sqrt{\pi}}e^{-\frac{\sigma _{-}^{2}}{8}T}\bigg. \\ & \hphantom{=:\frac{\sigma _{-}^{2}\sigma _{+}^{2}}{4(\sigma _{-}^{2}-\sigma _{+}^{2})}\bigg(} +\Big(\frac{4}{\sigma _{+}^{2}}+T\Big){\mathrm{Erf}}\Big( \frac{\sigma _{+}\sqrt{T}}{\sqrt{8}}\Big) -\Big(\frac{4}{\sigma _{-}^{2}}+T\Big){ \mathrm{Erf}}\Big(\frac{\sigma _{-}\sqrt{T}}{\sqrt{8}}\Big)\bigg). \end{aligned} $$

The proofs of Theorem 3.1 and Corollary 3.2 are given in Sects. 5.2 and 5.3.

Remark 3.3

It should be noted that the option pricing formulas in Theorem 3.1 differ from those given in Pigato [10]. In both papers, the option price is given by a single integral, but the corresponding integrands look different. The reason is that the formulas for option prices are obtained here by a method that is different from the one used in [10]. We are unable to derive these formulas from each other, and it is of interest to investigate the relationship between them. However, the ATM price in Corollary 3.2 is exactly the same as in [10]. In addition, note that the ATM price can be rewritten as

$$ V_{\mathrm { atm}}(T)=\frac{\sigma _{-}^{2}\sigma _{+}^{2}}{4(\sigma _{-}^{2}-\sigma _{+}^{2})} \big(I( \sigma _{+}, T)-I(\sigma _{-}, T)\big), $$

where

$$ I(x, T)=\frac{\sqrt{8T}}{x\sqrt{\pi}}e^{-\frac{x^{2}}{8}T} +\bigg( \frac{4}{x^{2}}+T\bigg){\mathrm{Erf}}\bigg(\frac{x\sqrt{T}}{\sqrt{8}} \bigg). $$

3.2 Option prices and Dupire’s forward equation

In this section, we provide (in Theorem 3.4 below) another representation of option prices. This gives the price of an in-the-money option in terms of a weighted integral of the corresponding ATM price over the time until maturity. It is based on the well-known Dupire forward equation (see Dupire [2, 3]), which we recall below.

If the underlying price follows the local volatility model

$$ dS_{t}=S_{t} \sigma (t, S_{t})dW_{t}, $$

then the price $C_{\mathrm {lvm}}(K,T)$ of a European call option with strike $K$ and time to expiry $T$ satisfies the forward equation

$$ \frac{\partial C_{\mathrm {lvm}}(K, T)}{\partial T}=\frac{1}{2}K^{2}\sigma ^{2}(T,K) \frac{\partial ^{2} C_{\mathrm {lvm}}(K,T)}{\partial K^{2}}. $$

It follows from the forward equation that

$$\begin{aligned} C_{\mathrm {lvm}}(K,T )- (S_{0}-K )^{+} &=\int \limits _{0}^{T} \frac{\partial}{\partial t}C_{\mathrm {lvm}}(K,t )dt \\ &=\frac{K^{2}}{2}\int \limits _{0}^{T}\sigma ^{2}(t,K) \frac{\partial ^{2}}{\partial K^{2}}C_{\mathrm {lvm}}(K,t )dt \\ &=\frac{K^{2}}{2}\int \limits _{0}^{T}\sigma ^{2}(t,K) \frac{\partial ^{2}}{\partial K^{2}} \mathbb{E}[\max (S_{t}-K,0)|S_{0}]dt \\ &=\frac{K^{2}}{2}\int \limits _{0}^{T}\sigma ^{2} (t,K)\mathbb{E}[ \delta (S_{t}-K)|S_{0}]dt, \end{aligned}$$

where $\delta (\,\cdot \,)$ is the delta function. Noting that $\mathbb{E}[\delta (S_{t}-K)|S_{0}]=p_{S}(S_{0},K,t)$, where $p_{S}(S_{0},\,\cdot \,,t)$, is the density function of $S_{t}$ given $S_{0}$, we arrive to the equation

$$ C_{\mathrm {lvm}}(K,T)-(S_{0}-K)^{+}=\frac{K^{2}}{2}\int \limits _{0}^{T}\sigma ^{2}(t,K)p_{S}(S_{0},K, t)dt, $$

(3.4)

which we are going to use in the proof of Theorem 3.4 below.

Theorem 3.4

If $S_{0}=1$ and $K>1$, then

$$ C_{\mathrm {lvm}}(1,K,T)=\sqrt{K}\int \limits _{0}^{T}V_{\mathrm { atm}}(T-s)h\big(s,(\log K)/ \sigma _{+}\big) e^{-\frac{1}{8} \sigma _{+}^{2} s}ds. $$

If $S_{0}=1$ and $K<1$, then

$$ P_{\mathrm {lvm}}(1,K,T)=\frac{1}{\sqrt{K}}\int \limits _{0}^{T}V_{\mathrm { atm}}(T-s)h \big(s,-(\log K)/\sigma _{-}\big) e^{-\frac{1}{8} \sigma _{-}^{2} s}ds, $$

where in both cases $V_{\mathrm { atm}}$ is the ATM price.

The proof of Theorem 3.4 is given in Sect. 5.4.

3.3 Black–Scholes approximation

In this section, we discuss the approximation of option prices in the two-valued LVM model (i.e., $C_{\mathrm {lvm}}(1, K, T)$ and $P_{\mathrm {lvm}}(1, K, T)$) by the corresponding BS prices.

Denote by $C_{\mathrm { BS}}(\sigma , S_{0}, K, T)$ and $P_{\mathrm { BS}}(\sigma , S_{0}, K, T)$ the BS prices of a European call and put option, respectively, with strike $K$ and time to maturity $T$, when the volatility of the underlying asset is equal to $\sigma$.

Theorem 3.5

If $K>1$, then

$$ |C_{\mathrm {lvm}}(1, K, T)-2pC_{\mathrm { BS}}(\sigma _{+}, 1, K, T)|\leq cT, $$

and if $K<1$, then

$$ |P_{\mathrm {lvm}}(1, K, T)-2qP_{\mathrm { BS}}(\sigma _{-}, 1, K, T)|\leq cT, $$

for some constant $c$ and all sufficiently small $T$.

The proof of Theorem 3.5 is given in Sect. 5.5.

Remark 3.6

The BS approximation of option prices in Theorem 3.5 is an important tool in our analysis of the implied volatility in Sect. 4. Another application of the approximation is given in Sect. 6, where it is used for estimating the implied volatility.

It should also be noted that the BS approximation is not immediately visible from the final pricing formulas. However, it is readily obtained if the option price is written in terms of an integral of the joint density of the underlying price process and its functionals.

4 Implied volatility

In this section, we use the BS approximation to obtain some results from Pigato [10] concerning the implied volatility. Recall that the implied volatility $\sigma _{{\mathrm { BS}}}(T, k)$ is considered as a function of maturity $T$ and log-moneyness $k=\log (K/S_{0})$. Note that we have $k=\log K$ in the case when $S_{0}=1$.

We start with a remark that is almost verbatim to [10, Remark 3.4] concerning the ATM implied volatility $\sigma _{\mathrm { atm}}(T):=\sigma _{{\mathrm { BS}}}(T,0)$. By definition, $\sigma _{\mathrm { atm}}(T)$ is the solution of the equation

$$ C_{\mathrm { BS}}\big(\sigma _{\mathrm { atm}}(T), 1, 1, T\big)=V_{\mathrm { atm}}(T). $$

Recall that given a volatility $\sigma$, we have that

$$\begin{aligned} \mathrm {BS}_{\mathrm { atm}}(\sigma , T)&:= C_{\mathrm { BS}}(\sigma , 1, 1, T) \\ & \hphantom{:} ={\mathrm {N}}\bigg(\frac{\sigma \sqrt{T}}{2}\bigg)-{\mathrm {N}}\bigg(- \frac{\sigma \sqrt{T}}{2}\bigg) \\ & \hphantom{:} ={\mathrm{Erf}}\bigg(\frac{\sigma \sqrt{T}}{\sqrt{8}}\bigg). \end{aligned}$$

(4.1)

Therefore,

$$ \sigma _{\mathrm { atm}}(T)=\frac{\sqrt{8}}{\sqrt{T}}{\mathrm{Erf}}^{-1}\big(V_{\mathrm { atm}}(T) \big). $$

Further, using that

$$ {\mathrm{Erf}}^{-1}(x)= \frac{\sqrt{\pi}}{2}\bigg(x+\frac{\pi}{12}x^{3} \bigg)+o(x^{3}) \qquad \text{as } x\to 0, $$

we obtain for the ATM implied volatility the short-term expansion

$$ \sigma _{\mathrm { atm}}\left (T\right )=2 \frac{\sigma _{-}\sigma _{+}}{ \left (\sigma _{-}+\sigma _{+}\right )}- \frac{\left (\sigma _{-}\sigma _{+}\right )^{2} \left (\sigma _{-}-\sigma _{+}\right )^{2}}{12 \left (\sigma _{-}+\sigma _{+}\right )^{3}}T+o(T) \qquad \text{as } T\to 0. $$

In addition, note that

$$ \sigma _{\mathrm { atm}}:=\sigma _{\mathrm { atm}}\left (0\right )=2 \frac{\sigma _{-}\sigma _{+}}{ \left (\sigma _{-}+\sigma _{+}\right )} =2p\sigma _{+}=2q\sigma _{-}. $$

4.1 Implied volatility in the central-limit regime

In this section, we consider the short-term behaviour of the implied volatility in the case when strike and maturity are related by the equation $K=e^{\gamma \sqrt{T}}$. This case was considered in [10, Theorem 3.1], where it was called the central-limit regime (and we use the same terminology).

One of the results of [10, Theorem 3.1] is the equation

$$\begin{aligned} &\lim _{T\to 0}\sigma _{{\mathrm { BS}}}(T, \gamma \sqrt{T}) \\ &=\frac{2 \sigma _{-}\sigma _{+}}{\sigma _{-}+\sigma _{+}}+ \frac{\sqrt{\pi}}{\sqrt{2}} \frac{ \sigma _{+}-\sigma _{-}}{\sigma _{-}+\sigma _{+}}\gamma \\ & \hphantom{=:} + \frac{\sigma _{+}-\sigma _{-}}{ \sigma _{+}\sigma _{-}}\bigg( \frac{\sigma _{+}-\sigma _{-}}{ 2 (\sigma _{-}+\sigma _{+})}- {\mathrm { sgn}}(\gamma )\bigg)\gamma ^{2} + o(\gamma ^{2}) \qquad \text{as }\gamma \to 0. \end{aligned}$$

(4.2)

In other words, the implied volatility $\sigma _{{\mathrm { BS}}}(T, \gamma \sqrt{T})$ can be approximated for short-term maturities $T$ by a quadratic function of $\gamma$, which can be computed explicitly. Below, we compute this quadratic function by using the BS approximation derived in Theorem 3.5.

For definiteness, assume that $\gamma >0$ (i.e., $K=e^{\gamma \sqrt{T}}>1$) and use our results for prices of call options. Let $C_{\mathrm {lvm}}(1,e^{\gamma \sqrt{T}},T)$ be the call price in the two-valued LVM (Theorem 3.1). The equation for the implied volatility $\sigma _{{\mathrm { BS}}}$ is

$$ C_{\mathrm { BS}}(\sigma _{{\mathrm { BS}}}, 1, e^{\gamma \sqrt{T}}, T )=C_{\mathrm {lvm}}(1,e^{\gamma \sqrt{T}},T ), $$

(4.3)

where the left-hand side is the BS price of the call option with maturity $T$ and strike $K=e^{\gamma \sqrt{T}}$. Then

$$ C_{\mathrm { BS}}(\sigma , 1, e^{\gamma \sqrt{T}}, T )={\mathrm {N}}(d_{1})- e^{\gamma \sqrt{T}} {\mathrm {N}}(d_{0}), $$

where $d_{1}=-\frac{\gamma}{\sigma}+\frac{\sigma \sqrt{T}}{2}$ and $d_{0}=-\frac{\gamma}{\sigma}-\frac{\sigma \sqrt{T}}{2}$. By Taylor’s theorem, we have that

$$\begin{aligned} &C_{\mathrm { BS}}(\sigma , 1, e^{\gamma \sqrt{T}}, T) = \bigg( \frac{\sigma}{\sqrt{2\pi}}-\frac{\gamma}{2}+ \frac{\gamma ^{2}}{\sigma \sqrt{2\pi}}\bigg) \sqrt{T}+o (\sqrt{T} ) \\ &\qquad \text{as } T\to 0. \end{aligned}$$

(4.4)

Further, combining the BS approximation (Theorem 3.5) for the right-hand side of (4.3) with (4.4) gives that

$$ \begin{aligned} C_{\mathrm {lvm}}(1,e^{\gamma \sqrt{T}},T )&=2pC_{\mathrm { BS}}(\sigma _{+}, 1, e^{ \gamma \sqrt{T}}, T ) \\ &=2p\bigg(\frac{\sigma _{+}}{\sqrt{2\pi}}-\frac{\gamma}{2}+ \frac{\gamma ^{2}}{\sigma _{+}\sqrt{2\pi}}\bigg)\sqrt{T}+o (\sqrt{T} ). \end{aligned} $$

(4.5)

Replacing both the left-hand and the right-hand sides of (4.3) by their approximations (provided by (4.4) and (4.5), respectively), we obtain the equation

$$ \bigg(\frac{\sigma}{\sqrt{2\pi}}-\frac{\gamma}{2}+ \frac{\gamma ^{2}}{\sigma \sqrt{2\pi}}\bigg) \sqrt{T}=2p\bigg( \frac{\sigma _{+}}{\sqrt{2\pi}}-\frac{\gamma}{2}+ \frac{\gamma ^{2}}{\sigma _{+}\sqrt{2\pi}}\bigg)\sqrt{T}+o (\sqrt{T} ), $$

which means that under the assumptions made, the implied volatility $\sigma _{{\mathrm { BS}}}(\gamma , e^{\gamma \sqrt{T}})$ converges to a limit as $T\to 0$, and moreover, this limit can be estimated by the solution of the equation

$$ \frac{\sigma}{\sqrt{2\pi}}-\frac{\gamma}{2}+ \frac{\gamma ^{2}}{\sigma \sqrt{2\pi}} =p\sigma _{+}\sqrt{\frac{2}{\pi}}-p \gamma +\frac{p}{\sigma _{+}}\sqrt{\frac{2}{\pi}}\gamma ^{2}. $$

(4.6)

It is easy to see that (4.6) is basically a quadratic equation for the unknown $\sigma$ with coefficients analytically depending on $\gamma$. This implies that the solution is an analytic function $\sigma (\gamma )$ of $\gamma$. Consider Taylor’s expansion of the second order for this function at $\gamma =0$, that is,

$$ \sigma (\gamma )= \bigg(c_{0}+c_{1}\gamma +\frac{1}{2}c_{2}\gamma ^{2} \bigg)+o (\gamma ^{2} ) \qquad \text{as } \gamma \to 0, $$

where $c_{0}$, $c_{1}$ and $c_{2}$ denote the values at 0 of the function itself and its first and second derivatives, respectively. Using this expansion for approximating the left-hand side of (4.6) gives the equation

$$\begin{aligned} &\frac{c_{0}+c_{1}\gamma +\frac{1}{2}c_{2}\gamma ^{2}}{\sqrt{2\pi}}- \frac{\gamma}{2}+\frac{\gamma ^{2}}{\sqrt{2\pi}} \frac{1}{(c_{0}+c_{1}\gamma +\frac{1}{2}c_{2}\gamma ^{2})} \\ &=\frac{c_{0}}{\sqrt{2\pi}}+\left (\frac{c_{1}}{\sqrt{2\pi}}- \frac{1}{2}\right )\gamma + \frac{1}{\sqrt{2\pi}}\left ( \frac{c_{2}}{2}+\frac{1}{c_{0}}\right )\gamma ^{2}+o(\gamma ^{2}), \end{aligned}$$

which in turn implies that

$$\begin{aligned} &\frac{c_{0}}{\sqrt{2\pi}}+\bigg(\frac{c_{1}}{\sqrt{2\pi}}- \frac{1}{2}\bigg)\gamma + \frac{1}{\sqrt{2\pi}}\bigg( \frac{\sigma _{2}}{2}+\frac{1}{c_{0}}\bigg)\gamma ^{2} \\ & =p\sigma _{+}\frac{\sqrt{2}}{\sqrt{\pi}}-p\gamma +\frac{p}{\sigma _{+}} \frac{\sqrt{2}}{\sqrt{\pi}}\gamma ^{2}+o (\gamma ^{2} ). \end{aligned}$$

(4.7)

Equating the coefficients of $\gamma ^{i}$ for $i=0,1,2$ in (4.7), we obtain that

$$ c_{0}=2p\sigma _{+}, \qquad c_{1}=\frac{\sqrt{2}}{\sqrt{\pi}}(1-2p) , \qquad c_{2}=\frac{4p^{2}-1}{p\sigma _{+}} $$

and hence

$$\begin{aligned} \sigma (\gamma )&=2p\sigma _{+}+\frac{\sqrt{2}}{\sqrt{\pi}}(1-2p)\gamma + \frac{1}{2}\frac{4p^{2}-1}{p\sigma _{+}}\gamma ^{2} +o(\gamma ^{2}) \\ &= \frac{2 \sigma _{-}\sigma _{+}}{\sigma _{-}+\sigma _{+}}+ \frac{\sqrt{\pi}}{\sqrt{2}} \frac{ \sigma _{+}-\sigma _{-}}{\sigma _{-}+\sigma _{+}}\gamma + \frac{\sigma _{+}-\sigma _{-}}{ \sigma _{+}\sigma _{-}} \bigg(\frac{\sigma _{+}-\sigma _{-}}{ 2(\sigma _{-}+\sigma _{+})}- 1\bigg)\gamma ^{2} \\ & \hphantom{=:} +o (\gamma ^{2} ). \end{aligned}$$

(4.8)

Alternatively, one can use the put price and repeat the above argument in the case when $\gamma <0$, i.e., $K=e^{\gamma \sqrt{T}}<1$, to obtain that

$$\begin{aligned} \sigma (\gamma )&= 2q\sigma _{-}+\frac{\sqrt{2}}{\sqrt{\pi}}(2q-1)\gamma + \frac{1}{2}\frac{4q^{2}-1}{q\sigma _{-}}\gamma ^{2} +o\big(\gamma ^{2}\big) \\ &= \frac{2 \sigma _{-}\sigma _{+}}{\sigma _{-}+\sigma _{+}}+ \frac{\sqrt{\pi}}{\sqrt{2}} \frac{ \sigma _{+}-\sigma _{-}}{\sigma _{-}+\sigma _{+}}\gamma + \frac{\sigma _{+}-\sigma _{-}}{ \sigma _{+}\sigma _{-}} \bigg(\frac{\sigma _{+}-\sigma _{-}}{ 2(\sigma _{-}+\sigma _{+})}+ 1\bigg)\gamma ^{2} \\ & \hphantom{=:} +o (\gamma ^{2} ). \end{aligned}$$

(4.9)

Finally, note that (4.8) and (4.9) are special cases of (4.2) depending on the sign of $\gamma$.

4.2 ATM implied volatility skew

Recall that $C_{\mathrm { BS}}(\sigma ,1,e^{k},T)$ is the BS price (with volatility $\sigma$) of the call option with log-strike $k=\log K$ and maturity $T$. As before, let $C_{\mathrm {lvm}}(1, e^{k}, T)$ be the call price of the same option in the two-valued LVM. Given the log-strike $k$ and maturity $T$, the corresponding implied volatility $\sigma _{{\mathrm { BS}}}(T,k)$ is defined as the solution of the equation $C_{\mathrm { BS}}(\sigma , 1, e^{k}, T)=C_{\mathrm {lvm}}(1, e^{k}, T)$ for $\sigma$.

Denote $\partial _{k}=\frac{\partial }{\partial k}$.

Theorem 4.1

The ATM skew is given by

$$\begin{aligned} &\partial _{k}\sigma _{{\mathrm { BS}}}(T,0) \\ &=\frac{\sqrt{\pi}}{\sqrt{2T}}e^{\frac{1}{8}\sigma _{{\mathrm { BS}}}^{2}(T,0)T} \bigg(1-\frac{2\sigma _{-}}{\sigma _{-}+\sigma _{+}}\big( F (T,-\sigma _{+}/2,0 )+F (T,\sigma _{+}/2,0 )\big)\bigg) \end{aligned}$$

(4.10)

and

$$ \partial _{k} \sigma _{{\mathrm { BS}}}(T,0) =\frac{\sqrt{\pi}}{\sqrt{2T}} \frac{\sigma _{+}-\sigma _{-}}{\sigma _{-}+\sigma _{+}}+o (\sqrt{T} ) \qquad \textit{as } T\to 0. $$

(4.11)

Remark 4.2

Equation (4.10) is similar to the equation for the ATM skew obtained in Pigato [10, Theorem 3.5]. In particular, the factor $\frac{\sqrt{\pi}}{\sqrt{2T}}e^{\frac{1}{8}\sigma _{{\mathrm { BS}}}^{2}(T,0)T}$ is exactly the same as in that theorem. However, the term $F(T,-\sigma _{+}/2,0)+F(T,\sigma _{+}/2,0)$ differs from the similar term in [10]. This is due to the difference between option pricing formulas used here and in [10] (see Remark 3.3). Note that the short-term asymptotic behaviour of the ATM skew given by (4.11) is exactly the same as in [10] (see e.g. [10, Remark 3.2]).

Before proceeding to the proof of Theorem 4.1, we prove below two auxiliary statements. The first is Proposition 4.3 that provides an asymptotic result for the function $F$ defined in (3.2). The second auxiliary statement is Proposition 4.4 that concerns the derivative of the call price with respect to the log-strike.

Proposition 4.3

For any fixed $a\in {\mathbb{R}}$, we have

$$ F(T,a,0)=\frac{a}{\sqrt{2\pi}}\sqrt{T}+\frac{1}{2}+o (\sqrt{T} ) \qquad \textit{as } T\to 0. $$

Proof

Observe that

$$\begin{aligned} \psi (a,t,0)&=\frac{1}{\sqrt{2\pi t}}+\frac{a}{2}+O\big(\sqrt{t}\big) \qquad \text{as } t\to 0, \\ \phi (t)&=\frac{1}{\sqrt{2\pi t}}+\bigg( \frac{\sigma _{+}+\sigma _{-}}{8\sqrt{2\pi}}-\frac{\sigma _{+}\sigma _{-}}{4}\bigg)\sqrt{t} +o ( \sqrt{t} ) \qquad \text{as } t\to 0. \end{aligned}$$

Therefore

$$\begin{aligned} F\left (T,a,0\right )&= \frac{1}{\sqrt{2\pi}}\int _{0}^{T} \frac{e^{-\frac{a^{2}}{2}s}}{\sqrt{T-s}} \bigg(\frac{a}{2} + \frac{1}{\sqrt{2\pi s}}\bigg)ds+o (\sqrt{T} ) \\ &=\frac{a}{2\sqrt{2\pi}}\int _{0}^{T}\frac{1}{\sqrt{T-s}}ds+ \frac{1}{2\pi}\int _{0}^{T} \frac{1}{\sqrt{s(T-s)}}ds+o (\sqrt{T} ) \\ & =\frac{a}{\sqrt{2\pi}}\sqrt{T}+\frac{1}{2}+o (\sqrt{T} ) \qquad \text{as } T\to 0. \end{aligned}$$

 □

Proposition 4.4

We have

$$ \partial _{k}C_{\mathrm {lvm}}(1,e^{k},T)= -2\frac{\sigma _{-}}{\sigma _{-}+\sigma _{+}}F (T,-\sigma _{+}/2,k/ \sigma _{+})e^{k} $$

(4.12)

and

$$\begin{aligned} &\partial _{k}C_{\mathrm {lvm}}(1,1,T) \\ &:=\partial _{k}C_{\mathrm {lvm}}(1,e^{k},T )|_{k=0} \\ & \hphantom{:} =-2\frac{\sigma _{-}}{\sigma _{-}+\sigma _{+}} F (T,-\sigma _{+}/2,0 ) \end{aligned}$$

(4.13)

$$\begin{aligned} & \hphantom{:} =-\frac{\sigma _{-}}{\sigma _{-}+\sigma _{+}} + \frac{1}{\sqrt{2\pi}} \frac{\sigma _{-}\sigma _{+}}{\sigma _{-}+\sigma _{+}}\sqrt{T}+o (\sqrt{T} ) \qquad \textit{as } T\to 0. \end{aligned}$$

(4.14)

Proof

By Theorem 3.1, we have

$$ C_{\mathrm {lvm}}(1, e^{k}, T )=2p\big(F (T,\sigma _{+}/2, k/\sigma _{+})-e^{k} F (T, -\sigma _{+}/2, k/\sigma _{+})\big), $$

where

$$ F (T, a, k/\sigma _{+})=\int _{0}^{T}\phi (T-s)\psi (a,s, k/\sigma _{+}) e^{- \frac{a^{2}}{2}s}ds $$

and the functions $\phi$ and $\psi$ are given by (2.12) and (3.1), respectively. Further, observe that $\partial _{k}\psi (a,s,k)=0$ for all $a, s$ and $k$. Therefore

$$\begin{aligned} \partial _{k}C_{\mathrm {lvm}}(1,e^{k},T ) &=-2p e^{k}\int _{0}^{T}\phi (T-s) \psi (-\sigma _{+}/2,s, k/\sigma _{+})e^{-\frac{\sigma _{+}^{2}}{8}s}ds \\ &= -2\frac{\sigma _{-}}{\sigma _{-}+\sigma _{+}}F (T,-\sigma _{+}/2,k/\sigma _{+})e^{k}, \end{aligned}$$

as claimed in (4.12), and hence we get that

$$ \partial _{k}C_{\mathrm {lvm}}(1,1,T)=-2\frac{\sigma _{-}}{\sigma _{-}+\sigma _{+}}F (T,-\sigma _{+}/2,0 ) $$

as claimed in (4.13). Applying Proposition 4.3 with $a=-\frac{\sigma _{+}}{2}$ gives the claimed short term asymptotics of $\partial _{k}C_{\mathrm {lvm}}(1,1,T)$ in (4.14).  □ □

Proof of Theorem 4.1

Similarly to $\partial _{k}=\frac{\partial }{\partial k}$, denote $\partial _{\sigma}=\frac{\partial }{\partial \sigma}$. By the chain rule, we have

$$ \partial _{k}\sigma _{{\mathrm { BS}}}(T,k)= \frac{\partial _{k}C_{\mathrm {lvm}}(1,e^{k},T )-\partial _{k}C_{\mathrm { BS}}(\sigma _{{\mathrm { BS}}}(T,k), 1, e^{k},T )}{\partial _{\sigma} C_{\mathrm { BS}}(\sigma _{{\mathrm { BS}}}(T,k),1, e^{k},T )}. $$

(4.15)

Further, observe that

$$\begin{aligned} \partial _{\sigma} C_{\mathrm { BS}}\big(\sigma _{{\mathrm { BS}}}(T,0),1,1,T\big)&= \frac{\sqrt{T}}{\sqrt{2\pi}} e^{-\frac{1}{8}\sigma _{{\mathrm { BS}}}^{2}(T,0)T}, \end{aligned}$$

(4.16)

$$\begin{aligned} \partial _{k}C_{\mathrm { BS}}\big(\sigma _{{\mathrm { BS}}}(T,0),1,1,T\big)&= \frac{1}{2}\bigg(-1+{ \mathrm{Erf}}\Big(\frac{\sqrt{T} \sigma _{{\mathrm { BS}}}(T,0)}{2 \sqrt{2}}\Big)\bigg) \end{aligned}$$

(4.17)

and

$$ {\mathrm{Erf}}\bigg(\frac{\sqrt{T} \sigma _{{\mathrm { BS}}}(T,0)}{2 \sqrt{2}}\bigg)= C_{\mathrm { BS}}\big(\sigma _{{\mathrm { BS}}}(T,0),T\big)=V_{\mathrm { atm}}(T). $$

(4.18)

Using (4.16)–(4.18), we can rewrite (4.15) in the case $k=0$ as

$$ \partial _{k}\sigma _{{\mathrm { BS}}}(T,0)=\frac{\sqrt{2 \pi} }{\sqrt{T}} e^{ \frac{1}{8}\sigma _{{\mathrm { BS}}}^{2}(0,T)T} \bigg(\partial _{k}C_{\mathrm {lvm}}(1,1,T)+ \frac{1}{2}-\frac{V_{\mathrm { atm}}(T)}{2}\bigg). $$

(4.19)

Next, by (3.3),

$$ V_{\mathrm { atm}}(T)= \frac{2\sigma _{-}}{\sigma _{-}+\sigma _{+}} \big(F (T,\sigma _{+}/2,0 )-F (T,-\sigma _{+}/2,0 )\big) $$

and by Proposition 4.4,

$$ \partial _{k}C_{\mathrm {lvm}}(1,1,T)=-\frac{2\sigma _{-}}{\sigma _{-}+\sigma _{+}}F (T,-\sigma _{+}/2,0 ). $$

Therefore

$$\begin{aligned} &\partial _{k}C_{\mathrm {lvm}}(1,1,T)+\frac{1}{2}-\frac{V_{\mathrm { atm}}(T)}{2}\\ &\quad = \frac{1}{2}-\frac{\sigma _{-}}{\sigma _{-}+\sigma _{+}}\big( F (T,-\sigma _{+}/2,0 )+F (T,\sigma _{+}/2,0 )\big) \end{aligned}$$

and, getting back to (4.19), we obtain after simple algebra that $\sigma _{{\mathrm { BS}}}(T,0)$ is equal to (4.10), as claimed. Finally, (4.11) follows from (4.10) and Proposition 4.3; we skip the details.  □ □

5 Proofs

5.1 Proof of Theorem 2.3

By (2.11), we have that

$$ p(0,x,T) =2\alpha (x)e^{-\frac{\sigma (x)x}{2}}Q(x,T), $$

(5.1)

where

$$\begin{aligned} Q(x,T) =\int ^{T}_{0} \int ^{T-s}_{0} \bigg(\int _{0}^{\infty}h(v, \ell p)h(u, \ell q)d\ell \bigg)h(s, x) e^{- \frac{\sigma _{+}^{2}v+\sigma _{-}^{2}u+\sigma ^{2}(x)s}{8}}dv ds, \end{aligned}$$

where $u=T-s-v$. Recall two equations that were used in the proof of [4, Theorem 3, Part 1)], namely

$$ \int \limits _{0}^{\infty }h(v,\ell p)h(u,\ell q)d\ell = \frac{pq}{2\sqrt{2 \pi } (p^{2}u+q^{2}v )^{3/2}} $$

and

$$ \int \limits _{0}^{w} \frac{pq}{\sqrt{2 \pi } (p^{2}(w-v)+q^{2}v )^{3/2}}e^{- \frac{\sigma _{\mathrm{p}}^{2}v+\sigma ^{2}_{\mathrm{m}}(w-v)}{8}}dv =\phi (w) \qquad \text{for } w>0, $$

where the function $\phi$ is defined in (2.12). Using these equations in (5.1) gives the claimed equation for the density of $X_{T}$. □

5.2 Proof of Theorem 3.1

Since $S_{0}=1$ and $K>1$, we have $X_{0}=(\log S_{0})/\sigma _{+}=0$ and $k=(\log K)/\sigma _{+}> 0$. By Theorem 2.3, we have

$$\begin{aligned} C_{\mathrm {lvm}}(1, K, T)&=\int _{k}^{\infty} (e^{\sigma _{+}x}-e^{\sigma _{+}k} )p(0,x,T)dx \\ &=2p\int _{k}^{\infty} (e^{\sigma _{+}x}-e^{\sigma _{+}k} ) e^{-\frac{\sigma _{+}}{2}x} \bigg(\int _{0}^{T}\phi (T-s)h(s,x)e^{-\frac{\sigma _{+}^{2}}{8}s}ds\bigg)dx \\ &=2p\int _{0}^{T}\phi (T-s)e^{-\frac{\sigma _{+}^{2}}{2}s}\bigg(\int _{k}^{ \infty} (e^{\frac{\sigma _{+}}{2}x} - e^{\sigma _{+}k}e^{-\frac{\sigma _{+}}{2}x} ) h(s,x)dx \bigg)ds \\ &=2p\int _{0}^{T}\phi (T-s)e^{-\frac{\sigma _{+}^{2}}{8}s}\big( \psi (\sigma _{+}/2,s,k ) -e^{\sigma _{+}k}\psi (-\sigma _{+}/2,s,k )\big)ds \\ &=2p\big(F (T, \sigma _{+}/2, k )-e^{\sigma _{+}k} F (T, -\sigma _{+}/2, k )\big), \end{aligned}$$

as claimed. The equation for the put price $P_{\mathrm {lvm}}(1, K, T)$ is obtained similarly. □

5.3 Proof of Corollary 3.2

Note first that

$$\begin{aligned} \psi (a,s,0)-\psi (-a,s,0)&=ae^{\frac{a^{2}}{2}s} \qquad \text{for all } a. \end{aligned}$$

(5.2)

Combining (5.2) with (3.3), we obtain that

$$\begin{aligned} V_{\mathrm { atm}}(T)&=C_{\mathrm {lvm}}(1,1,T) \\ &=2p\int \limits _{0}^{T}\phi (T-s)e^{-\frac{\sigma _{+}^{2}}{8}s} \big( \psi (\sigma _{+}/2,s,0 )- \psi (-\sigma _{+}/2,s,0 )\big)ds \\ &=p\sigma _{+}\int \limits _{0}^{T}\phi (T-s)ds \\ &=\frac{\sigma _{-}\sigma _{+}}{\sigma _{-}+\sigma _{+}}\int \limits _{0}^{T}\phi (s)ds. \end{aligned}$$

Further, a direct computation gives that

$$ \begin{aligned} \int _{0}^{T}\phi (s)ds={}& \frac{\sqrt{T}}{\sqrt{2\pi}} \frac{1}{(\sigma _{-}-\sigma _{+})} (\sigma _{-}e^{-\frac{\sigma _{+}^{2}}{8}T}- \sigma _{+}e^{- \frac{\sigma _{-}^{2}}{8}T} ) \\ &{}+\frac{\sigma _{-}(4+\sigma _{+}^{2}T)}{4\sigma _{+}(\sigma _{-}-\sigma _{+})}{\mathrm{Erf}} \bigg( \sigma _{+}\frac{\sqrt{T}}{\sqrt{8}}\bigg) - \frac{\sigma _{+}(4+\sigma _{-}^{2}T)}{4\sigma _{-}(\sigma _{-}-\sigma _{+})}{\mathrm{Erf}} \bigg(\sigma _{-}\frac{\sqrt{T}}{\sqrt{8}}\bigg). \end{aligned} $$

Combining the above and simplifying gives the ATM price, as claimed.  □

5.4 Proof of Theorem 3.4

Recall that in the two-valued LVM, we have $\sigma (t, K)=\sigma _{+}{\mathbf{1}}_{\{K\geq 1\}}+\sigma _{-}{\mathbf{1}}_{\{K<1\}}$. If $S_{0}=1$, then (3.4) becomes

$$\begin{aligned} C_{\mathrm {lvm}}(1,K,T ) &=\frac{K^{2}\sigma _{+}^{2}}{2}\int \limits _{0}^{T}p_{S} (S_{0},K,t )dt \qquad \text{for } K>1. \end{aligned}$$

Noting that

$$ p_{S} (1,K,t )=\frac{p(0,(\log K)/\sigma _{+},t)}{K\sigma _{+}} $$

for $K>1$, where $p(0,\,\cdot \,,t)$ is the density of $X_{t}$ given that $X_{0}=0$ (see Lemma 2.3), we get that

$$\begin{aligned} C_{\mathrm {lvm}}(1,K, T)&=\frac{K\sigma _{+}}{2}\int \limits _{0}^{T} p\big(0,(\log K)/ \sigma _{+},t\big)dt \\ &=\sqrt{K}p \sigma _{+}\int \limits _{0}^{T}\int \limits _{0}^{t}\phi (t-s)h \big(s,(\log K)/\sigma _{+}\big) e^{-\frac{\sigma _{+}^{2}}{8}s}dsdt \\ &=\sqrt{K} \int \limits _{0}^{T}h \big(s,(\log K)/\sigma _{+}\big)e^{- \frac{\sigma _{+}^{2}}{8}s} \bigg(p\sigma _{+}\int _{0}^{T-s}\phi (t)dt\bigg)ds \\ &=\sqrt{K}\int \limits _{0}^{T}h \big(s,(\log K)/\sigma _{+}\big)e^{- \frac{\sigma _{+}^{2}}{8}s}V_{\mathrm { atm}}(T-s)ds \qquad \text{for } K>1, \end{aligned}$$

where $V_{\mathrm { atm}}(T-s)$ is the ATM price (Theorem 3.2) for maturity $T-s$.  □

5.5 Proof of Theorem 3.5

We derive the BS approximation only for the call option price $C_{\mathrm {lvm}}(1, K, T)$, as the case of the put option is similar. Using (5.1) for the density of $X_{T}$ gives

$$ C_{\mathrm {lvm}}(1, K, T)=2p\int \limits _{k}^{\infty} (e^{\sigma _{+}x}-e^{\sigma _{+}k} )e^{- \frac{\sigma _{+}}{2}x} A(x,\sigma _{+},\sigma _{-})dx, $$

where

$$\begin{aligned} &A(x,\sigma _{+},\sigma _{-}) \\ &= \int \limits _{0}^{\infty}\int \limits _{0}^{T}\int \limits _{0}^{T-s}h(v, \ell p) h(T-v-s,\ell q)h(s,x) e^{- \frac{\sigma _{+}^{2}v+\sigma _{-}^{2}(T-v-s)+\sigma _{+}^{2} s}{8}}dvdsd\ell . \end{aligned}$$

For the BS price of the same call option when the volatility is equal to $\sigma _{+}$, we have

$$ C_{\mathrm { BS}}(\sigma _{+}, 1, K, T)=\int \limits _{k}^{\infty} (e^{\sigma _{+}x}-e^{\sigma _{+}k} )e^{- \frac{\sigma _{+}}{2}x} A(x,\sigma _{+},\sigma _{+})dx. $$

Set $u=T-v-s$ and observe that

$$\begin{aligned} |e^{-\frac{\sigma _{+}^{2}v+\sigma _{-}^{2} u+\sigma _{+}^{2} s}{8}} - e^{- \frac{\sigma _{+}^{2}T}{8}} |&= |1-e^{-\frac{1}{8}(\sigma _{-}^{2}-\sigma _{+}^{2})u} |e^{- \frac{\sigma _{+}^{2}T}{8}}. \end{aligned}$$

Therefore,

$$\begin{aligned} |e^{-\frac{\sigma _{+}^{2}v+\sigma _{-}^{2} u+\sigma _{+}^{2} s}{8}} - e^{- \frac{\sigma _{+}^{2}T}{8}} | & \leq \frac{|\sigma _{-}^{2}-\sigma _{+}^{2}|T}{8}e^{- \frac{\sigma _{+}^{2}}{8}T}+o(T) \qquad \text{as }T\to 0. \end{aligned}$$

This gives that

$$ \bigg|\int \limits _{k}^{\infty} (e^{\sigma _{+}x}-e^{\sigma _{+}k} ) e^{- \frac{\sigma _{+}}{2}x} \big(A(x,\sigma _{+},\sigma _{-})-A(x,\sigma _{+}, \sigma _{+})\big)dx\bigg| \leq C_{1}T $$

for some constant $C_{1}$ and all sufficiently small $T$, which in turn implies that

$$ |C_{\mathrm {lvm}}(1,K,T)-2pC_{\mathrm { BS}}(\sigma _{+}, 1, K, T)|\leq cT $$

for some constant $c$ and all sufficiently small $T$.  □

6 BS approximation revisited

In this section, we revisit the BS approximation. In particular, we obtain another form of the approximation. The new approximation corrects a certain drawback of the original one (to be explained). Then we apply the modified BS approximation for the estimation of the implied volatility in the two-valued LVM.

We start by noting that

$$\begin{aligned} C_{\mathrm {lvm}}(1,K,T)&\approx 2pC_{\mathrm { BS}}(\sigma _{+},1,K,T) \qquad \text{for } K>1, \end{aligned}$$

(6.1)

$$\begin{aligned} P_{\mathrm {lvm}}(1,K,T)&\approx 2qP_{\mathrm { BS}}(\sigma _{-},1,K,T) \qquad \text{for } K< 1. \end{aligned}$$

(6.2)

In the ATM case $K=1$, the equation (6.1) gives $V_{\mathrm { atm}}(T)\approx 2p\mathrm {BS}_{\mathrm { atm}}(\sigma _{+}, T)$, while (6.2) gives $V_{\mathrm { atm}}(T)\approx 2q\mathrm {BS}_{\mathrm { atm}}(\sigma _{-}, T)$. Below, we obtain another form of the BS approximation in which this discrepancy is eliminated.

Using Theorem 3.4, we obtain that

$$\begin{aligned} &C_{\mathrm {lvm}}(1,K,T) \\ &=\sqrt{K}\int \limits _{0}^{T}V_{\mathrm { atm}}(T-s)h\big(s,(\log K)/\sigma _{+}\big) e^{- \frac{1}{8} \sigma _{+}^{2} s}ds \\ &=\sqrt{K} \int \limits _{0}^{T}\frac{V_{\mathrm { atm}}(T-s)}{\mathrm {BS}_{\mathrm { atm}}(\sigma _{+}, T-s)} \mathrm {BS}_{\mathrm { atm}}(\sigma _{+}, T-s)h \big(s,(\log K)/\sigma _{+}\big) e^{-\frac{1}{8} \sigma _{+}^{2} s}ds, \end{aligned}$$

where $\mathrm {BS}_{\mathrm { atm}}(\sigma _{+}, \,\cdot \,)$ is the BS ATM price defined in (4.1). Approximating the time-dependent ratio $\frac{V_{\mathrm { atm}}(T-s)}{\mathrm {BS}_{\mathrm { atm}}(\sigma _{+}, T-s)}$ by $\frac{V_{\mathrm { atm}}(T)}{\mathrm {BS}_{\mathrm { atm}}(\sigma _{+},T)}$, i.e., by its value at a single instant $T$, gives the new BS approximation for the price of the call option as

$$\begin{aligned} C_{\mathrm {lvm}}(1,K,T)&\approx \frac{V_{\mathrm { atm}}(T)\sqrt{K}}{ \mathrm {BS}_{\mathrm { atm}}(\sigma _{+},T)} \int \limits _{0}^{T}\mathrm {BS}_{\mathrm { atm}}( \sigma _{+}, T-s)h\big(s,(\log K)/\sigma _{+}\big) e^{-\frac{1}{8} \sigma _{+}^{2} s}ds \\ &=\frac{V_{\mathrm { atm}}(T)}{\mathrm {BS}_{\mathrm { atm}}(\sigma _{+},T)}C_{\mathrm { BS}}(\sigma _{+},1,K,T) \qquad \text{for } K>1. \end{aligned}$$

(6.3)

Similarly, we obtain the new approximation for the price of the put option, namely

$$\begin{aligned} P_{\mathrm {lvm}}(1,K,T)&\approx \frac{V_{\mathrm { atm}}(T)}{\mathrm {BS}_{\mathrm { atm}}(\sigma _{-},T)}P_{\mathrm { BS}}(\sigma _{-}, 1,K,T) \qquad \text{for } K< 1. \end{aligned}$$

In addition, note that the new BS approximation implies the approximation given by (6.1) and (6.2). For example, in the case of the call option, we have

$$ \mathrm {BS}_{\mathrm { atm}}(\sigma _{+}, T)\approx \frac{\sigma _{+}\sqrt{T}}{\sqrt{2\pi}} \qquad \text{and}\qquad V_{\mathrm { atm}}(T)\approx \frac{\sigma _{\mathrm { atm}}\sqrt{T}}{\sqrt{2\pi}}= 2p \frac{\sigma _{+}\sqrt{T}}{\sqrt{2\pi}}, $$

so that $\frac{V_{\mathrm { atm}}(T)}{\mathrm {BS}_{\mathrm { atm}}(\sigma _{+},T)}\approx 2p$, which gives (6.1) as claimed.

Below we provide results of a numerical experiment in which the new BS approximation was used to estimate the implied volatility. In the experiment, the implied volatility (considered as a function of moneyness $\frac{\log \left (K/S\right )}{\sigma (K,T)\sqrt{T}}$) is estimated in a two-valued LVM with parameters $\sigma _{+}=0.2$ and $\sigma _{-}=0.9$. Figure 1 shows the implied volatility smile for maturity $T=5$ years (Y) obtained by numerical integration of the option pricing formulas in Theorem 3.1 and its approximation obtained by using (6.3).

Fig. 1

Implied volatility smile and its approximation for maturity $5{\mathrm { Y}}$

Figure 2 shows the difference between the implied volatility and its approximation for maturities $0.1{\mathrm { Y}}$, $0.5{\mathrm { Y}}$ and $5{\mathrm { Y}}$.

Fig. 2

Plots of differences between the implied volatility and its approximation for maturities $0.1{\mathrm { Y}}$, $0.5{\mathrm { Y}}$ and $5{\mathrm { Y}}$

In addition, it should be noted that the new form of the BS approximation can be used for the arbitrage-free parametrisation of the implied volatility with given skew and constrained volatilities on wings (we do not discuss this here).

7 Conclusion

In this paper, we consider the local volatility model in which the volatility takes two possible values. The value depends on the position of the underlying price with respect to a given threshold. The model is well known, and a number of results have been obtained for it in recent years. In particular, explicit pricing formulas for European options have been given in Pigato [10] in the case when the threshold is taken at the money. These formulas have then been used to establish that the skew explodes as $T^{-1/2}$ as maturity $T\to 0$, which reproduces the power-law behaviour of the skew observed in some real data. The research method in [10] is based on the Laplace transform and related techniques.

In the present paper, we propose another approach to the study of the two-valued LVM. Our approach is based on the natural relationship of the two-valued LVM with skew Brownian motion and consists of using the joint distribution of SBM and some of its functionals; see Gairat and Shcherbakov [4]. We use our distributional results for obtaining new option pricing formulas and approximations of option prices in terms of the corresponding BS prices. The BS approximation is a key ingredient of our analysis of the implied volatility and the skew. Using this approximation allows obtaining the aforementioned behaviour of the implied volatility surface by rather elementary methods (e.g. Taylor expansion of the second order). In addition, we show that the BS approximation can be improved and used to estimate the implied volatility.

Appendix:  Skew Brownian motion with a two-valued drift

The process $X$ defined in (2.1) is a special case of the process $Z=(Z_{t})_{t\geq 0}$ defined as a strong solution of the equation

$$ dZ_{t}=m(Z_{t})dt+(p-q)dL^{(Z)}_{t}+dW_{t}, $$

(A.1)

where $m(z)=m_{1}{\mathbf{1}}_{\{z\geq 0\}}+m_{2}{\mathbf{1}}_{\{z<0\}}$, $p\geq 0$ and $q\geq 0$ are given constants such that $p+q=1$ and $L^{(Z)}$ is the local time of the process $Z$ at the origin (defined similarly to (2.6)). The existence and uniqueness of the strong solution of (A.1) is well known (see e.g. Lejay [7] and the references therein). In the special case $m_{1}=m_{2}=0$, the process $Z$ is SBM with parameter $p\in [0,1]$ (see e.g. [7] and the references therein). By analogy, the process $Z$ can be called an SBM with the two-valued drift $m$. Theorem 2.1 is a special case of the theorem below.

Theorem A.1

[4, Theorem 2]

Let $\tau ^{(Z)}, V^{(Z)}$ and $L^{(Z)}$ be the last visit to the origin, the occupation time and the local time at the origin of the process $Z$. If $Z_{0}=0$, then the joint density of the random variables $\tau ^{(Z)}, V^{(Z)}, Z_{T}$ and $L^{(Z)}_{T}$ is given by

$$ f_{T}(t, v, x, \ell ) =2\alpha (x)h(v, \ell p)h(t-v, \ell q)h(T-t, x) \beta (t,v,x,\ell ) $$

(A.2)

for $0\leq v\leq t\leq T$ and $\ell \geq 0$, where the function $\alpha$ is defined in (2.10) and

$$ \beta (t,v,x,\ell )= e^{-\frac{1}{2}(m_{1}^{2}v+m^{2}_{2}(t-v)+m^{2}(x)(T-t))- \ell (pm_{1}-qm_{2})+m(x)x}. $$

Example A.2

In the special case $m_{1}=m_{2}=m$ and $p=1/2$, (2.9) becomes

$$ f_{T}(t, v, x, \ell ) =h(v, \ell /2)h(t-v, \ell /2)h(T-t, x) e^{- \frac{m^{2}T}{2}+mx} $$

for $0\leq v\leq t\leq T$ and $\ell \geq 0$, which is the joint density of the quantities $\tau ^{(Z)}, V^{(Z)}, Z_{T}$ and $L^{(Z)}_{T}$ corresponding to the process $Z_{t}=mt+W_{t}$, $t \geq 0$, in the case when $Z_{0}=0$.

Remark A.3

The SDE (2.2) is a special case of (A.1) with the drift specified by the values $m_{1}=-\frac{\sigma _{+}}{2}$ and $m_{2}=-\frac{\sigma _{-}}{2}$ and the probabilities $p$ and $q$ given by (2.4) and (2.5), respectively. In this case, we have $pm_{1}-qm_{2}= -\frac{\sigma _{-}\sigma _{+}}{2(\sigma _{-}+\sigma _{+})}+ \frac{\sigma _{+}\sigma _{-}}{2(\sigma _{-}+\sigma _{+})}=0$, which reduces the density (A.2) to (2.9).