Abstract
We perform a detailed theoretical study of the value of a class of participating policies with four key features: (i) the policyholder is guaranteed a minimum interest rate on the policy reserve; (ii) the contract can be terminated by the holder at any time until maturity (surrender option); (iii) at the maturity (or upon surrender), a bonus is credited to the holder if the portfolio backing the policy outperforms the current policy reserve; (iv) due to solvency requirements, the contract ends if the value of the underlying portfolio of assets falls below the policy reserve.
Our analysis is probabilistic and relies on optimal stopping and free boundary theory. We find a structure of the optimal surrender strategy which was undetected by previous (mostly numerical) studies on the topic. Optimal surrender of the contract is triggered by two ‘stop-loss’ boundaries and by a ‘too-good-to-persist’ boundary (in the language of Ekström and Vaicenavicius in Stoch. Process. Appl. 130: 806–823, 2020). Financial implications of this strategy are discussed in detail and supported by extensive numerical experiments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Participating policies with minimum rate guarantee are insurance contracts appealing predominantly to individuals during their work periods as a form of low-risk financial investment. The subscriber of a participating policy (policyholder) pays a premium (either single or periodic) which is used by the insurance company to set up a so-called policy reserve for the policyholder. The policy reserve is linked to a portfolio of assets held by the insurance company and accrues interest tracking the performance of that portfolio (the details of the contract are illustrated in Sect. 2). The minimum rate guarantee is in the form of a minimum interest rate (usually lower than the risk-free rate) paid by the insurance company towards the policy reserve irrespective of the performance of the portfolio backing the policy. In the absence of any further contract specifications, the policy terminates at a given maturity, at which the policyholder receives an amount equal to the value of the reserve, plus a bonus if the current value of the portfolio is sufficiently high relative to the reserve.
The contract may incur early termination. That happens if the value of the portfolio backing the policy is not sufficient to cover the policy reserve. In that case, we say that the insurance company fails to meet the solvency requirements on the participating policy and the policyholder receives the value of the policy reserve at that time. More interestingly, early termination of the contract may be an embedded option in the policy specification. Indeed, along with the standard contract, the policyholder can buy the right to an early cancellation of the policy, the so-called surrender option (SO). If the policyholder exercises the surrender option prior to the maturity of the contract, she receives at that time the value of the policy reserve, plus the above-mentioned bonus.
While surrender options share similarities with financial options of American type due to their early exercise feature, they are actually rather different in nature. Indeed, the presence of a surrender option embedded in a participating policy changes the structure of the whole contract. As a consequence, the price of embedded options is normally defined as the difference between the value of a policy which includes the option and the value of a policy which does not include the option (see (2.8) for a mathematical expression).
Participating policies with surrender option (PPSOs) have been studied extensively in the academic literature. This paper contributes to that strand of the literature which assumes that the policyholder is fully rational and the surrender option is exercised optimally from a financial perspective. Other papers analyse PPSOs in which surrender occurs as a randomised event (see Cheng and Li [9]) or without assuming rational behaviour of the policyholder (see Nolte and Schneider [27]). Several papers adopt a numerical approach to analyse PPSOs without solvency requirements for the insurance company (see Andreatta and Corradin [1], Bacinello [2], Bacinello et al. [3] and Grosen and Jørgensen [22], among others). Chu and Kwok [10] provide an analytical approximation for the price of a participating policy without taking into account the surrender option. Finally, Siu [32] considers the fair valuation of a PPSO when the market value of the portfolio backing the policy is modelled by a Markov-modulated geometric Brownian motion. In [32], the author approximates the solution of a free boundary problem by a system of second-order piecewise-linear ordinary differential equations.
In this paper, we develop a fully theoretical analysis of participating policies with minimum rate guarantee, embedded surrender option and early termination due to solvency requirements. Following the example of other papers on this topic (see e.g. Chu and Kwok [10], Fard and Siu [18], Grosen and Jørgensen [22], Siu [32]), we focus purely on the financial aspects of the policy and ignore the demographic risk, in the sense that the contract does not account for a possible demise of the policyholder. From the point of view of applications, we may imagine that there are multiple beneficiaries of the policy, so that the demographic risk is negligible. Moreover, it is well known (see e.g. Cheng and Li [9], Stabile [33]) that the assumption of a constant force of mortality independent of the financial market results in a shift in the discount rate adopted for pricing; this does not affect the methods we employ and the qualitative outcomes of our work. The study becomes substantially more involved if one considers a time-dependent mortality force (as in e.g. De Angelis and Stabile [15]) or, even worse, a stochastic mortality. We leave these extensions for future work.
Our main contributions are (i) an analytical study of the pricing formula for the PPSO, (ii) a characterisation of the optimal exercise strategy for the surrender option, in terms of an optimal exercise boundary, and (iii) an extensive numerical analysis of the option value and the surrender boundary. The price of the policy is obtained as the value function of a suitable finite-horizon optimal stopping problem for a two-dimensional degenerate diffusion which lives in an orthant of the plane and is absorbed upon leaving the orthant. The diffusive coordinate of that process models the dynamics of the portfolio backing the policy, while the other coordinate represents the dynamics of the policy reserve. After a suitable transformation, the dynamics is reduced to a one-dimensional diffusion in the form of a stochastic differential equation (SDE) with absorption upon hitting zero. This process corresponds to the so-called bonus distribution rate of the contract, which is introduced in more detail in the next section. We are then led to consider a state process \((t,X_{t})\) in \([0,T]\times \mathbb{R}_{+}\) which is absorbed if \(X_{t}\) reaches zero, so that our state space is the \((t,x)\)-strip with \(t\in [0,T]\) and \(x\ge 0\).
The optimal stopping problem poses a number of challenges. It has a finite horizon, hence is not amenable to explicit solutions using the associated free boundary problem (which is indeed parabolic); the SDE that describes the stochastic process does not admit an explicit solution so that numerous tricks often used in optimal stopping problems, relying on an explicit dependence of the process on its initial value, are not applicable (see e.g. the American put problem in Peskir and Shiryaev [28, Sect. VII.25.2]); the stopping payoff is independent of time, but as a function of \(x\), it is convex with discontinuous first derivative.
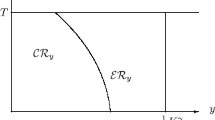
The combination of the above ingredients produces a very peculiar shape of the optimal stopping region, which we derive from a detailed analysis of the value function. We observe that the stopping region \(\mathcal{S}\), i.e., the points \((t,x)\) at which the policyholder should instantly surrender the contract, is not connected in the \(x\)-variable for fixed \(t\). Instead, \(\mathcal{S}\) may have two connected components for each \(t\in [0,T]\) (see Fig. 1), corresponding to two distinct ‘stop-loss’ boundaries and a ‘too-good-to-persist’ boundary (following Ekström and Vaicenavicius [17], we say that a boundary is ‘stop-loss’ or ‘too-good-to-persist’ if \(\mathcal{S}\) can be locally represented as a set \(\{(t,x):x\le b(t)\}\) or \(\{(t,x):x\ge b(t)\}\), respectively, for some \(b\)). This result was not observed in prior work on the same model, where a numerical approach to the problem could not detect this unusual feature (see e.g. Siu [32]). As it turns out, the shape of the stopping set is closely related to the bonus mechanism included in the PPSO, and it has fine implications on the optimal exercise of the surrender option. We elaborate further on this point in Sect. 3.3, once the mathematical details have been laid out more clearly.
The optimal surrender region and its boundaries in the case \(x_{1}=b_{1}(0)>0\) and \(b_{2}(\hat{c})=b_{3}(\hat{c})\) with \(\hat{c}>0\) (see Theorem 3.2, (b))
The stopping set is connected in the \(t\)-variable for each given \(x\ge 0\). This leads us naturally to consider an optimal stopping boundary \(c(\, \cdot \,)\) as a function of \(x\) (rather than as a function of \(t\), as in the vast majority of papers in the area). We obtain a wealth of fine properties of the map \(x\mapsto c(x)\) on \([0,\infty )\) which are of independent mathematical interest for the probabilistic theory of free boundary problems. Indeed, we show that \(c(\, \cdot \,)\) is continuous on \((0,\infty )\) and piecewise monotonic, with two strictly increasing portions and a strictly decreasing one. It is important to remark that questions of continuity of the optimal boundary \(x\mapsto c(x)\) are much harder to address than in the more canonical setting of time-dependent boundaries \(t\mapsto b(t)\). Here we resolve the issue in Theorem 5.11, by providing a probabilistic proof which is new in the literature and makes use of suitably constructed reflecting diffusions. Our proof provides a conceptually simple way to show (in more general examples) that time-dependent optimal boundaries \(t\mapsto b(t)\) cannot exhibit flat stretches unless the smooth-fit property fails.
The rest of the paper is organised as follows. In Sect. 2, we set up the model in a rigorous mathematical framework, and then we state our main results (Theorems 3.1 and 3.2) in Sect. 3. In particular, in Sect. 3.3, we obtain numerical illustrations of the value function, the stopping set and the related sensitivity analysis, accompanied by a financial interpretation. Section 4 contains preliminary technical results on the continuity and monotonicity of the value function. In Sect. 5, we analyse in detail the free boundary problem associated with the PPSO and prove Theorems 3.1 and 3.2. Section 6 extends our framework to include management fees in the valuation of the PPSO. The paper is completed by a short technical appendix.
2 Actuarial model and problem formulation
In this section, we provide a mathematical description of the price of a PPSO. We align our setup and part of our notations to those already used in other papers on this topic as e.g. Chu and Kwok [10], Grosen and Jørgensen [22] and Siu [32].
Given \(T>0\), we consider a market on a finite time interval \([0,T]\) on a complete probability space \((\Omega , \mathcal{F}, (\mathcal{F}_{t})_{t\in [0,T]}, \mathbb{Q})\) that carries a one-dimensional Brownian motion \(\widetilde{W}:=(\widetilde{W}_{t})_{t\in [0,T]}\). We assume that the filtration \((\mathcal{F}_{t})_{t\in [0,T]}\) is generated by the Brownian motion and completed with ℚ-nullsets. The measure ℚ is our pricing measure. It can be interpreted as the classical risk-neutral measure in a Black–Scholes market where the process \(A\), introduced in (2.1) below, is the only risky asset.
An investor can purchase a PPSO at time zero by making a lump payment \(V_{0}\) to an insurance company. In return, the insurer invests an amount \(R_{0}\) into a financial portfolio and commits the company to credit interests to the policyholder’s policy reserve according to a mechanism that is described below. Thanks to the surrender option embedded in the contract, the policyholder has the right to withdraw her investment at any time prior to the policy’s maturity \(T\). In this case, she receives the so-called intrinsic value of the policy.
2.1 The policy reserve
First we describe the rate at which the amount \(R_{0}\) invested by the insurer accrues interest, based on the performance of the portfolio backing the policy (the reference portfolio). We let \(A:=(A_{t})_{t\in [0,T]}\) be the process denoting the value of that portfolio and assume that \(A\) evolves as a geometric Brownian motion under ℚ; that is,
where \(r\), \(\sigma \) and \(a_{0}\) are positive constants and \(r\) is the risk-free rate.
During the lifetime of the policy, the policy reserve is denoted by \(R:=(R_{t})_{t\in [0,T]}\) and accrues interest based on a two-layer mechanism. First, the insurance company guarantees a minimum fixed interest rate which we denote by \(r^{G}\), and in line with financial practice, we assume
Second, at times when the portfolio performs particularly well, the policyholder participates in the returns. In particular, we define the so-called bonus reserve \(B_{t}:=A_{t}-R_{t}\) and as in Chu and Kwok [10], Siu [32], Shanahan et al. [31] and Fard and Siu [18], we consider a bonus distribution rate (BDR) of the form
The BDR measures the performance of the portfolio against the performance of the policy reserve. The insurance company compares the BDR to a constant, long-term target \(\beta >0\), known as target buffer ratio. If the BDR exceeds the target buffer ratio, a proportion \(\delta >0\) of the excess is shared with the policyholder.
Combining the minimum guaranteed interest rate with the bonus rate gives the instantaneous rate of interest on the policy reserve, that is,
It follows that the policy reserve \(R\) evolves under ℚ according to the dynamics
where \(\alpha \in (0,1)\) is fixed by the insurer. Hence the initial reserve \(R_{0}\) covers \(\alpha \) shares of the reference portfolio.
Remark 2.1
Notice that in the specification of the bonus mechanism in (2.3), we may alternatively consider \(\ln (\alpha A_{t}/R_{t})\) instead of \(\ln (A_{t}/R_{t})\). This would emphasise that the policyholder only receives a bonus proportional to her share of the portfolio backing the policy. From the mathematical point of view, there is no difference since \(\ln (\alpha A_{t}/R_{t})=\ln \alpha +\ln (A_{t}/R_{t})\) and the additional term \(\ln \alpha \) can be absorbed in the specification of the target buffer ratio \(\beta >0\).
2.2 Intrinsic value of the policy and pricing formula
Next we describe the so-called intrinsic value of the policy, which is the value that the policyholder receives either at the maturity of the policy or at an earlier time, should she decide to exercise the surrender option. The intrinsic value is equal to the policy reserve plus a bonus component. The latter is activated when the value of the policyholder’s shares in the portfolio \(A\) exceeds the current value of the policy reserve, that is, when \({\alpha A_{t}}>R_{t}\). In this case, the policyholder receives a bonus fraction \(\gamma \) of the surplus of her \(\alpha \)-share. In mathematical terms, the intrinsic value of the policy may be written as
where \(x^{+}:=\max \{x,0\}\) and \(\gamma \in (0,1)\) is the so-called participation coefficient.
The model also takes into account that the company may fail to meet the solvency requirement at any time before \(T\). In fact, denoting by \(\tau ^{\dagger }\) the stopping time (insolvency time)
the company’s solvency requirement is satisfied for \(t<\tau ^{\dagger }\). In the event of \(\tau ^{\dagger }< T\), the policy is liquidated and the policyholder receives (cf. (2.5))
i.e., the policy reserve value.
We denote by \(V_{0}\) the price of the PPSO at time zero. Notice that \(V_{0}=V_{0}(\alpha )\), in the sense that the contract is specified by indicating the portion \(\alpha \) of the portfolio which backs the policy. Recalling (2.1) and (2.4)–(2.6), we have
where \(\mathbb{E}^{\mathbb{Q}}\) is the expectation under the measure ℚ and the supremum is taken over all stopping times \(\tau \in [0,T]\) with respect to \((\mathcal{F}_{t})_{t\in [0,T]}\). In what follows, we refer to (2.7) as the PPSO problem.
The value of the surrender option embedded in the contract (usually referred to as early exercise premium in the mathematical finance literature) can be obtained as
where \(V^{E}_{0}\) is the price of the contract without the possibility of an early surrender, that is,
It is worth noticing that in practice, the use of surrender options may be disincentivised by insurance companies, which agree to pay out only a fraction of the policy reserve in case of early surrender. In our case, that would correspond to take \(\lambda g(A_{\tau },R_{\tau })\) in (2.7) on the event \(\{\tau <\tau ^{\dagger }\wedge T\}\), with \(\lambda \in [0,1)\). Here we focus on the model set out in (2.7), i.e., \(\lambda =1\), which is consistent with the existing literature (see e.g. Grosen and Jørgensen [22] and Siu [32]) and provides an upper bound for the prices of contracts with \(\lambda \in [0,1)\). As we shall see below, the model with \(\lambda =1\) is also the source of interesting mathematical findings.
2.3 Dimension reduction and bonus distribution rate
As noticed in Chu and Kwok [10] and [32], the PPSO problem can be made more tractable by considering the bonus distribution rate (2.2) (i.e., the logarithm of the ratio \(A/R\)) as the observable process in the optimal stopping formulation of (2.7). Indeed, set \(X:=(X_{t})_{t\in [0,T]}\) with
Then by (2.1) and (2.4), one gets
with initial condition
In terms of \(X\), the insolvency time becomes
Next we write the intrinsic value of the policy \(g(A_{t},R_{t})\) (see (2.4)) in terms of \(X_{t}\). Define the gain function
for \(x\in \mathbb{R}_{+}:=[0,\infty )\) and notice that
since \(\gamma \in (0,1)\). Then
From (2.14), we notice that for \(X_{t}>x_{\alpha }\), the participation bonus in the intrinsic value of the policy is strictly positive. So we can think of \(x_{\alpha }\) as the activation threshold for the participation bonus.
Now the key to the dimension reduction is a change of measure. Define the martingale process \(M:=(M_{t})_{t\in [0,T]}\) by
and the probability measure ℙ equivalent to ℚ on \(\mathcal{F}_{T}\) by \(\textrm{d}\mathbb{P}=M_{T} \,\textrm{d}\mathbb{Q}\). By Girsanov’s theorem, the process \(W:=(W_{t})_{t\in [0,T]}\) with
is a ℙ-Brownian motion. Then, under the new measure ℙ, the dynamics of \(X\) reads
where
For future reference, it is worth defining
Then \(x_{G}<\bar{x}_{0}\) since \(r^{G}< r\). When the BDR process exceeds \(x_{G}\) (i.e., \(X_{t}>x_{G}\)), the policyholder receives the bonus interest rate on the reserve, above the minimum guaranteed rate \(r^{G}\) (see (2.3)). Again by (2.3), the interest rate paid on the reserve is higher than the risk-free rate \(r\) when the BDR process exceeds \(\bar{x}_{0}\) (i.e., \(X_{t}>\bar{x}_{0}\)).
Using (2.14), (2.15) and the optional sampling theorem, one easily obtains for any stopping time \(\tau \in [0,T]\) that
with \(\mathbb{E}[\,\cdot \,]\) denoting ℙ-expectation. Hence (2.7) may be rewritten as \(V_{0}=a_{0}v_{0}\), where
Life-insurance contracts often charge management fees to the holder. The methods developed in this paper can be used to deal with fees charged at a rate proportional to the value of the portfolio \(A\) and to the policy reserve \(R\). If we add proportional fees to our model, the price of the PPSO changes from its expression in (2.7) to
for some \(p,q\ge 0\) (notice in particular that \(p=p(\alpha )\) should depend on the fraction \(\alpha \) of the portfolio backing the policy purchased by the policyholder). Also in this case, we can perform the change of measure displayed above and arrive at \(V_{0}=a_{0}v_{0}\), where now
It is important to emphasise that given a participation level \(\alpha >0\), the value \(V_{0}\) of the PPSO is specific to that value of \(\alpha \). Indeed, both the initial value \(R_{0}\) of the reserve and the participation bonus on the intrinsic value of the policy depend on \(\alpha \). So we should think of the PPSO’s value as \(V_{0}=V_{0}(\alpha )\) (and equivalently \(v_{0}=v_{0}(\alpha )\)).
3 Summary of main results
Thanks to the Markovian nature of the process \(X\), the value \(v_{0}\) only depends on the initial value of the process \(X_{0}=x_{\alpha }\) (see (2.10)) and on the maturity \(T\) of the contract. However, to be able to characterise \(v_{0}\) and the associated optimal stopping rule, we must embed our problem into a larger state-space by considering all possible initial values of the time-space dynamics \((t,X)\). For that, we denote by \(X^{x}\) the process \(X\) starting at time 0 from an arbitrary point \(x\ge 0\) and evolving according to (2.16). Similarly, we denote by \(X^{t,x}\) the process \(X\) starting at time \(t\) from \(x\ge 0\) and evolving according to (2.16). From now on, when notationally convenient, we write \(\mathbb{E}_{x}[\,\cdot \,]:=\mathbb{E}[\,\cdot \,|X_{0}=x]\). Since \(X\) is time-homogeneous, we have
Thus we can identify the dynamics \((s,X^{t,x}_{s})_{s\in [t,T]}\) and \((t+s,X^{x}_{s})_{s\in [0,T-t]}\) and use the latter in the problem formulation below. Thanks to time-homogeneity, we also have that \(\tau ^{\dagger }\) defined in (2.11) is independent of time. Sometimes, we write \(\tau ^{\dagger }(x)\) to emphasise that \(\tau ^{\dagger }\) depends on \(X_{0}=x\).
From now on, we study the finite-horizon optimal stopping problem given by
which embeds the PPSO problem (2.19). It is clear that we can go back to our original problem in two steps: first \(v_{0}=v(0,x_{\alpha })\), and then \(V_{0}=a_{0}v_{0}\). In the presence of management fees, we obtain by the same procedure the analogue of (3.1) as
Studying (3.1) and (3.2) is equivalent from the methodological point of view (see Sect. 6 for a detailed discussion), and so we focus on (3.1) for notational simplicity. We show in Sect. 6 (Fig. 4) how the addition of management fees affects the qualitative properties of the surrender policy.
3.1 Theoretical results: value function and optimal exercise boundary
In this section, we provide the main theoretical results of the paper. Their proofs are given at the end of Sect. 5 and build upon technical results obtained in Sects. 4 and 5. Let ℒ be the second-order differential operator associated to the diffusion (2.16), i.e.,
with \(\partial _{x}\) and \(\partial _{xx}\) denoting the first- and second-order partial derivatives with respect to \(x\). We also denote the partial derivative with respect to time by \(\partial _{t}\). As usual in optimal stopping theory, let us introduce the so-called continuation and stopping regions
respectively. For future reference, let \(\partial \mathcal{C}\) be the boundary of the set \(\mathcal{C}\) (notice that \(\{T\}\times \mathbb{R}_{+}\subseteq \partial \mathcal{C}\)) and introduce the first entry time of \((t+s,X_{s})\) into \(\mathcal{S}\), i.e.,
For the value function \(v\) of (3.1), we have the following result.
Theorem 3.1
On the set \([0,T]\times \mathbb{R}_{+}\), the function \(v\) is nonnegative, continuous and bounded by 1, with \(v\ge h\). The mappings \(t\mapsto v(t,x)\) and \(x\mapsto v(t,x)\) are both non-increasing. Moreover, \(v\in C^{1} ([0,T)\times (0,\infty ) )\), the second derivative \(\partial _{xx}v\) is continuous on \(\overline{\mathcal{C}}\cap ([0,T)\times (0,\infty ) )\), and \(v\) solves (uniquely) the free boundary problem
In the PDE literature, the above result is often presented in terms of a variational inequality. That is, \(v\) is the unique solution of the obstacle problem
with boundary conditions \(v(T,x)=h(x)\) for \(x\in \mathbb{R}_{+}\) and \(v(t,0)=h(0)\) for \(t\in [0,T)\). Uniqueness in Theorem 3.1 refers to the class of continuous functions \(w\) such that \(w\in C^{1}([0,T)\times (0,\infty ))\) with \(w_{xx}\in L^{\infty }_{{\mathrm{loc}}}([0,T)\times (0,\infty ))\).
From continuity of \(v\), we deduce that \(\mathcal{C}\) is open and \(\mathcal{S}\) is closed. Hence in particular \(\partial \mathcal{C}\subseteq \mathcal{S}\). Moreover, standard optimal stopping results (see Peskir and Shiryaev [28, Corollary I.2.9]) guarantee that the entry time \(\tau _{*}\) to the stopping set \(\mathcal{S}\) from (3.6) is optimal for \(v(t,x)\). It is then of interest to determine the geometry of \(\mathcal{S}\).
We first notice that since \(t\mapsto v(t,x)-h(x)\) is non-increasing, we can define
for \(x\in \mathbb{R}_{+}\). This gives a parametrisation of the stopping set as
In optimal stopping theory and its financial applications, it is often preferable to describe the set \(\mathcal{S}\) in terms of time-dependent boundaries. So in our analysis in Sects. 4 and 5, we use the boundary \(c(\, \cdot \,)\) as a useful technical tool, but we are also able to prove that it can be inverted locally and we present our results here in terms of time-dependent boundaries \(b_{1}\), \(b_{2}\) and \(b_{3}\).
It turns out that there are two different shapes of \(\mathcal{S}\) depending on the model parameters. Recalling \(\bar{x}_{0}=\beta +\frac{r}{\delta }\) and \(x_{\alpha }=\ln (1/\alpha )\), we address separately the cases \(x_{\alpha }<\bar{x}_{0}\) and \(x_{\alpha }\ge \bar{x}_{0}\). Our second main result is summarised below, where we denote by \(f(t-)\) the left limit of a function \(f\) at a point \(t\) and adopt the convention \([t,t)=\emptyset \) for any \(t\in \mathbb{R}\). The theorem states properties of the optimal surrender region \(\mathcal{S}\).
Theorem 3.2
The following hold:
(a) If \(x_{\alpha }\ge \bar{x}_{0}\), then there exist a function \(b_{1}:[0,T)\to [0,\bar{x}_{0}]\) and a constant \(t_{0}\in [0,T)\) such that \(b_{1}(t)=0\) for \(t\in [0,t_{0})\), \(b_{1}\) is strictly increasing and continuous on \([t_{0},T)\) with \(b_{1}(T-)=\bar{x}_{0}\), and the stopping region is of the form
Thus the optimal stopping time \(\tau _{*}\) reads
(b) If \(x_{\alpha }<\bar{x}_{0}\), then there exist constants \(t_{0}\in [0,T)\), \(\hat{c}\in [0,T]\) and functions \(b_{1}:[0,T) \to [0, x_{\alpha }]\) and \(b_{2},b_{3}:[\hat{c},T)\to [x_{\alpha },\bar{x}_{0}]\) such that
i) \(b_{1}(t)=0\) for \(t\in [0,t_{0})\) and \(b_{1}\) is strictly increasing and continuous on \([t_{0},T)\);
ii) \(b_{2}\) is strictly decreasing and continuous, while \(b_{3}\) is strictly increasing and continuous on \([\hat{c},T)\);
iii) \(b_{1}(t)\le b_{2}(t)\le b_{3}(t)\) for \(t\in [\hat{c},T)\) with \(b_{2}(\hat{c})=b_{3}(\hat{c})\) if \(\hat{c}>0\), and \(\hat{c}=0\) if \(b_{2}(\hat{c})< b_{3}(\hat{c})\);
iv) \(b_{1}(T-)=b_{2}(T-)=x_{\alpha }\) and \(b_{3}(T-)=\bar{x}_{0}\);
v) the stopping region is of the form
Thus the optimal stopping time \(\tau _{*}\) reads
Remark 3.3
A close inspection of Theorem 3.2 shows that \([0,T)\times \{x_{\alpha }\}\subseteq \mathcal{C}\) in all cases (see Proposition 5.2 for the proof).
As anticipated in the introduction, in case (b), we have two ‘stop-loss’ boundaries \(b_{1}\) and \(b_{3}\) which trigger the surrender option when the BDR process crosses them downwards, and a ‘too-good-to-persist’ boundary \(b_{2}\) which triggers the surrender option when the BDR process crosses it upwards. In case (a), we observe instead only a single stop-loss boundary. These results will be interpreted in Sect. 3.3 below.
At the technical level, the strict monotonicity and continuity of the time-dependent boundaries in (a) and (b) of Theorem 3.2 are derived from analogous properties for the \(x\)-dependent boundary in (3.8). In particular, in case (a), we prove that the function \(x\mapsto c(x)\) is continuous on \((0,\infty )\), there exists \(x_{1}\in [0,\bar{x}_{0})\) such that \(c(x)=0\) for \(x\in [0,x_{1})\), and it is strictly increasing on \((x_{1},\bar{x}_{0})\). So
In case (b), the geometry is more involved. We prove that there exist \(x_{1}\in [0,x_{\alpha })\) and \(x_{\alpha }< x_{2}\le x_{3}<\bar{x}_{0}\) such that
(i) \(x\mapsto c(x)\) is continuous on \((0,\infty )\), \(c(x)=0\) for \(x\in [0,x_{1})\), and it is strictly increasing on \((x_{1},x_{\alpha })\);
(ii) the set of minimisers of \(x\mapsto c(x)\) in \((x_{\alpha },\bar{x}_{0})\) is given by the closed interval \([x_{2},x_{3}] \subseteq (x_{\alpha },\bar{x}_{0})\) where \(c(\, \cdot \,)\) takes the value \(\hat{c}\), and if \(x_{2}< x_{3}\), then \(\hat{c}=0\);
(iii) \(c(\, \cdot \,)\) is strictly decreasing on \((x_{\alpha },x_{2})\) and strictly increasing on \((x_{3},\bar{x}_{0})\). Then the boundaries \(b_{1}\), \(b_{2}\) and \(b_{3}\) are obtained as
See Figs. 2, 3 and 4 for various illustrations with both \(\hat{c}=0\) and \(\hat{c}>0\) and with \(t_{0}=0\) and \(t_{0}>0\) (notice that \(t_{0}:=\lim _{x\to 0}c(x)\)).
Sensitivity of the optimal surrender boundary \(c(\, \cdot \,)\) with respect to \(\gamma \) (left plot) and to \(r^{G}\) (right plot). For \(\gamma =0.15\) (left plot), we omit the rightmost portion of the boundary which is never reached when \(X_{0}=x_{\alpha }\) and the policyholder stops optimally
The optimal surrender region and boundary in Case (ii) of management fees (see Proposition 6.1)
3.2 Some technical remarks
The choice to work with the boundary \(x\mapsto c(x)\) in our theoretical analysis is dictated by the fact that a priori, it seems too difficult to establish existence of the three boundaries \(b_{1}\), \(b_{2}\) and \(b_{3}\). Indeed, this would normally require proving piecewise monotonicity of the mapping \(x\mapsto v(t,x)-h(x)\) and/or convexity of the mapping \(x\mapsto v(t,x)\), plus developing arguments that guarantee non-emptyness of the set \(\{x\in \mathbb{R}_{+}:v(t,x)=h(x)\}\) depending on the choice of \(t\in [0,T)\). Neither of these tasks follows by standard arguments because of the lack of an explicit solution for the SDE (2.16) and due to the absorption of \(X\) at \(x=0\).
The probabilistic proof of the strict monotonicity of the optimal exercise boundaries in Theorem 3.2 is an interesting technical result in its own right, and so far it was missing from the optimal stopping literature. In the PDE literature, strict monotonicity of free boundaries (and even their smoothness) are well-known results. Classical references are Ladyzenskaja et al. [24, Chap. V.9] and Friedman [21, Chap. 8] for a general treatment, while for parabolic problems with one spatial dimension (i.e., closer to our setup), one can also refer to Cannon [7, Chaps. 17 and 18] and Friedman [20]. The techniques developed in those seminal contributions were then employed and tailored for optimal stopping problems in mathematical finance, for example in Bayraktar and Xing [5] and Chen and Chadam [8] for American option pricing, and in Dai and Yi [11] for optimal investment with transaction costs.
For the smoothness of the boundary (understood as its continuous differentiability or higher), PDE arguments often require smoothness of the obstacle (i.e., the option’s payoff) and in all cases continuous differentiability of the coefficients of the SDE underlying the stochastic optimisation. When the obstacle is not smooth (as in the American put problem), one often takes advantage of the explicit transition density of the underlying stochastic process (typically a geometric Brownian motion). In our case, we have neither a smooth payoff (see (2.12)) nor continuously differentiable coefficients (see (2.17)). Moreover, the transition density of our process \(X\) is not known. So we cannot apply classical results from the PDE literature to derive continuous differentiability of the optimal boundary, and we set this question aside.
For the strict monotonicity of free boundaries, the PDE literature relies on an application of Hopf’s lemma and an argument by contradiction. Our probabilistic proof complements those PDE techniques by employing methods more familiar to probabilists working on optimal stopping.
The shape of the stopping region in (b) of Theorem 3.2 is somewhat remarkable and was never observed in the context of participating policies with surrender options. Not only is the stopping region disconnected, but when \(\hat{c}>0\), there is a point in the stopping region at which one of the stop-loss boundaries meets the too-good-to-persist boundary (see Fig. 1). Similar geometries of optimal stopping regions in the time-space plane have been observed numerically (see e.g. Ekström and Vaicenavicius [17, Fig. 4]), but a complete theoretical analysis is usually not available. An instance of such a study, revealing a similar geometry in a finite-horizon optimal stopping problem, is Du Toit and Peskir [16]. However, the problem studied in [16] concerns the optimal prediction of the maximum of a Brownian motion with drift, whereas that studied in [17] concerns stopping of a partially observable Brownian bridge. Hence the similarities with the stopping rule in our setup appear to be a mere coincidence.
Before we present the full proofs of Theorems 3.1 and 3.2, the next section discusses in detail the financial interpretation of our results with the aid of extensive numerical tests. The complete theoretical analysis that leads to Theorems 3.1 and 3.2 is performed in Sects. 4 and 5.
3.3 Numerical results and financial interpretation
In order to investigate the shape of the continuation and stopping regions, we implement a binomial-tree algorithm based on the diffusion approximation scheme proposed in Nelson and Ramaswamy [26]. We take a partition of \([0,T]\) with \(N+1\) equally spaced time points. To each node in the tree, we associate a value of the underlying process \(X\) and of the corresponding time: in the \((n,j)\)-node, we have the pair \((n,x^{j}_{n})\); here \(j = 0, 1, \dots , n\) and \(n=0,1, \dots , N+1\). In the subsequent time-step, the process can move to one of the two nodes \((n+1,x^{j}_{n}\pm \sigma \sqrt{\Delta })\) with \(\Delta :=T/N\), so that the tree is recombining. If \(x^{j}_{n}>0\), the probability \(p^{j}_{n}\) of moving upwards from the \(n\)th node is calculated as in Nelson and Ramaswamy [26] as \({p^{j}_{n}=0\vee (1\wedge (\frac{1}{2}+\sqrt{\Delta } \pi (x^{j}_{n})/2 \sigma ))}\), where \(\pi \) is given by (2.17). If instead \(x^{j}_{n}\le 0\), the process can only move to \((n+1,0)\) with probability one. We compute the numerical approximation of the value function \(\tilde{v}_{n}(x^{j}_{n})\) of the PPSO with the usual backward recursion, starting from \(\tilde{v}_{N}(x^{j}_{N})=h(x^{j}_{N})\) for \(x^{j}_{N}\ge 0\). For any \(n< N\), if \(x^{j}_{n}\le 0\), then \(\tilde{v}_{n}(x^{j}_{n})=h(0)=1\); if instead \(x^{j}_{n}> 0\), then \({\tilde{v}_{n}(x^{j}_{n})=\max \{h(x^{j}_{n}),\mathbb{E}[\tilde{v}_{n+1}(X_{n+1})|X_{n}=x^{j}_{n}] \}}\). Since the binomial tree has recombining nodes, the evaluation of the continuation value \(\mathbb{E}[\tilde{v}_{n+1}(X_{n+1})|X_{n}=x^{j}_{n}]\) reduces to the weighted average of the payoff at the next two nodes.
Remark 3.4
Notice that the regularity we have obtained for the value function \(v\) allows us to obtain in principle an integral equation for the optimal boundary (see Peskir and Shiryaev [28, Chaps. VII and VIII] for some examples). However, as the explicit form of the transition density of the process \(X\) is not known, solving that integral equation numerically would not be possible. This motivates our use of binomial trees.
Unless otherwise specified, we choose in the rest of the section for the parameters (time is expressed in years, while \(r\), \(r^{G}\) and \(\sigma \) are annual rates) the values
For these parameter values, we get \(x_{\alpha }=2.3\), \(\bar{x}_{0}=3.15\) and \(x_{G}=3.1\) (see (2.10) and (2.18), respectively); so we are in the setting of \(x_{\alpha }<\bar{x}_{0}\) (see (b) in Theorem 3.2).
3.3.1 Financial interpretation of the surrender region
We recall that the structural properties of the intrinsic value of the policy (i.e., the function \(h\) in (2.19)) and the initial value of the reserve \(R_{0}\) are determined by the choice of \(\alpha \). From the financial perspective, the PPSO is priced for each fixed value of the parameter \(\alpha \), that is, \(V_{0}(\alpha )=a_{0}v_{0}(\alpha )\) (recall (2.7) and (2.19)), and the policyholder’s initial BDR process at time zero is \(X_{0}=x_{\alpha }\). Figure 1 shows the optimal surrender region \(\mathcal{S}\) and the boundary \(c(\, \cdot \,)\) as in (3.9) in the \((x,t)\)-plane.
Optimal surrender and default
Notice that in Fig. 1, the solvency requirement is always fulfilled if the policyholder exercises the surrender option optimally (i.e., \(\tau ^{*}<\tau ^{\dagger }\)). This corresponds to \(t_{0}=0\) in (i) of Theorem 3.2, (b) and in particular \(x_{1}:=b_{1}(0)>0\) (compare also with \(x_{1}\) in Proposition 5.3, (i)). Hence the optimal termination of the contract can only occur due to surrender or at maturity. A different situation appears in Fig. 2, (i), where \(t_{0}=c(0+)>0\) and early termination due to solvency requirements may occur if \(X\) hits zero prior to time \(t_{0}\).
Minimum rate guarantee, bonus rate and a stop-loss boundary
There is a natural interpretation for the shape of the surrender region for \(X\) close to zero and for \(X\ge \bar{x}_{0}\). On the one hand, when \(X\) is close to 0, we have \(c(A,R) =r^{G}\) and \(g(A,R) =R\) (see (2.3) and (2.5), respectively); thus the policy reserve grows at the rate \(r^{G}\) which is lower than the discount rate \(r\) used in (2.7). So the policyholder has an incentive to surrender in order to avoid an erosion of the present value of the reserve (which is due to the gap \(r^{G}-r<0\)). Hence it is natural to interpret the boundary \(b_{1}\) as a stop-loss boundary. On the other hand, for values of \(X\) larger than \(\bar{x}_{0}\), the policy reserve grows at a rate greater than \(r\) due to the bonus mechanism in (2.3). In this case, the policyholder has no incentive to surrender the contract and the stopping region disappears.
Stop-loss and too-good-to-persist boundaries for \(\boldsymbol{X}\boldsymbol{\in} \boldsymbol{(x_{\alpha },\bar{x}_{0})}\)
The peculiar shape of the surrender region between \(x_{\alpha }\) and \(\bar{x}_{0}\) can be explained as follows. The value \(x_{\alpha }\) is the critical value at which the participation bonus in the intrinsic value of the policy becomes active (see (2.5)). Then, if \(X=x_{\alpha }\), the investor delays the surrender with a view to possibly receiving the bonus. Moreover, in a neighbourhood of \(x_{\alpha }\) the drift in the dynamics (2.16) is positive (pulling the BDR process towards the bonus), so that the policyholder has an incentive to wait also if \(X\) is less than \(x_{\alpha }\), but not too small. When \(X>x_{\alpha }\), the participation bonus in the policy’s intrinsic value is active and can be collected by the policyholder upon immediate surrender. This gives rise to the too-good-to-persist boundary \(b_{2}\). When \(X>x_{G}\), the bonus on the policy reserve’s growth rate is also active (see (2.3)) and creates an incentive to wait. If the BDR process is close to \(\bar{x}_{0}\), surrendering is not appealing. In fact, the policyholder stays in the contract hoping that \(X\) will exceed \(\bar{x}_{0}\) and the reserve will grow at a higher rate than the risk-free rate. However, if \(X\) decreases, the participation bonus in the intrinsic value of the policy decreases, too. At the same time, for \(X\le \bar{x}_{0}\), the growth rate of the reserve is still smaller than the risk-free rate. So as the maturity approaches, the combined effect of these two mechanisms creates the stop-loss boundary \(b_{3}\).
3.3.2 Sensitivity analysis
Here we discuss the impact of various parameters on the shape of the surrender region and on the value of both the policy and the surrender option. In what follows, the parametrisations of the boundary \(\partial \mathcal{C}\) both in terms of \(c\) and of \(b_{1}\), \(b_{2}\), \(b_{3}\) are used.
The \(\boldsymbol{\alpha} \) -fraction of the initial portfolio
Figure 2 shows possible shapes of the optimal surrender boundary \(c(\, \cdot \,)\) that complement the one presented in Fig. 1. The plots are obtained for several values of the parameter \(\alpha \), or equivalently \(x_{\alpha }\) (see (2.10)). The possible presence of a portion of the continuation region below the local minimum of \(c(\, \cdot \,)\) (as in Fig. 1) and the value \(\hat{c}\) of the minimum itself depend on several factors, including the value of \(\alpha \). Large values of \(\alpha \) push the initial BDR \(X_{0}=x_{\alpha }\) towards zero so that the chances of benefiting from the bonus on the policy reserve’s growth rate (2.3) are slim and the policyholder will prioritise the participation bonus in the intrinsic value of the policy (2.5). That widens the area above the local minimum of \(c(\, \cdot \,)\) until the continuation region (3.4) becomes completely disconnected (see Fig. 2, (i)). It should be emphasised that since \(X_{0}=x_{\alpha }\), a completely disconnected surrender region means that the policyholder will surrender the contract as soon as the BDR process leaves the continuation region between the lower stop-loss boundary \(b_{1}\) and the too-good-to-persist boundary \(b_{2}\). As \(\alpha \) increases, this mechanism is reversed: the activation thresholds \(x_{\alpha }\) of the participating bonus and \(x_{G}\) of the bonus on the reserve’s growth rate become closer. Then the portion of stopping region above the local minimum of \(c(\, \cdot \,)\) shrinks as \(x_{\alpha }\) approaches \(\bar{x}_{0}\) from the left (see Fig. 2, (ii) and Fig. 1 where \(x_{\alpha }=2.3\)). In the limit, we arrive to the case of \(x_{\alpha }\ge \bar{x}_{0}\) (cf. (5.4)), which is also illustrated in Fig. 2, (iii). There the situation is less involved because the participating bonus kicks in after the process \(X\) has already exceeded \(\bar{x}_{0}\), so that the reserve is already growing at a rate higher than the discount rate. In that case, the policyholder’s waiting strategy is aimed at collecting both a large reserve and the participating bonus. The exercise of the SO in this setting is only optimal when \(X\) is sufficiently small, and it is purely triggered by the stop-loss mechanism due to discounting.
Participation coefficient and minimum rate guarantee
In Fig. 3, we study the sensitivity of the optimal surrender boundary \(c(\, \cdot \,)\) with respect to \(\gamma \) (left plot) and to \(r^{G}\) (right plot). We remark that \(\gamma \) only affects the intrinsic value of the policy (see (2.5)), but does not affect the reference portfolio \(A\) or the policy reserve \(R\). As \(\gamma \) increases, the participating bonus increases and counters the effect of discounting. So the policyholder is inclined to stay in the contract longer to see if the bonus mechanism on the reserve will also be activated. Likewise, as \(r^{G}\) increases, the policyholder has progressively more benefits from staying in the contract; then the SO becomes less appealing and the area between the boundaries \(b_{2}\) and \(b_{3}\) shrinks. In particular, as \(r^{G}\) approaches the risk-free rate \(r\), the stop-loss boundary \(b_{3}\) and the too-good-to-persist boundary \(b_{2}\) do not disappear, but become less extended (theoretically, this is expected because the interval \((x_{\alpha },\bar{x}_{0})\) does not depend on \(r^{G}\) and it is shown in Lemma 5.4 that \(\mathcal{S}\cap ([0,T)\times (x_{\alpha },\bar{x}_{0}))\neq \emptyset \)). In both situations, the incentive to surrender the contract decreases and the continuation region expands. As a result, the optimal boundary \(c(\, \cdot \,)\) is pushed upwards in our plots.
Values of the policy and of the surrender option
We conclude the section by analysing how the bonus distribution mechanism and the minimum interest rate guarantee in the policy reserve impact the value of the policy and the value of the embedded SO. The value of the SO is obtained, as in (2.8), by comparing the value of the PPSO to the value of its European counterpart (i.e., with no SO). Now we fix the initial portfolio value \(\text{$A_{0}=$ 1'000}\) so that \(R_{0}=100\). We collect in Table 1 the value \(V_{0}\) of the PPSO (see (2.7)), the value \(V_{0}^{E}\) of the contract without SO (see (2.9)) and the value \(V^{\text{opt}}\) of the SO. As in Grosen and Jørgensen [22], we consider the following three scenarios depending on the level of participation in the returns generated by the reference portfolio: low (\(\delta =0.1\) and \(\beta =3.4\)), medium (\(\delta =0.25\) and \(\beta =2.7\)), and high (\(\delta =0.6\) and \(\beta =2\)). The lower the value of \(\delta \), the less the policyholder participates in the reserve via (2.3). Moreover, the higher the value of the target buffer ratio \(\beta \), the smaller the surplus that the policyholder receives. The value of \(V_{0}^{E}\) is evaluated by using the same binomial-tree method as above, without the complication of the optimisation at each node in the PPSO. As expected, \(V_{0}\) is always greater than \(V_{0}^{E}\). Their difference gives the option value \(V^{\text{opt}}\).
In the low scenario, the value of the European contract \(V_{0}^{E}\) is below par for all values of the spread \(r-r^{G}\), i.e., \(V^{E}_{0}< R_{0}\). If the spread is relatively large, i.e., \(0.8\%\) or \(1.5\%\), the European contract trades below par also in the medium scenario. When the minimum interest rate guaranteed \(r^{G}\) is much smaller than the market risk-free rate and the level of participation in the returns is also relatively small, the policy is not financially appealing to an investor if compared, for example, to bond investments. However, since \(R_{0}>V^{E}_{0}\) (see Table 1), an investor who purchases the European contract incurs an initial outlay which is smaller than the initial amount credited to the reserve. This makes the policy potentially appealing as a form of secure savings.
The value \(V_{0}\) of the PPSO is always at or above par, i.e., \(V_{0}\ge R_{0}\), due to the American-type option embedded in the contract (at par, the SO is immediately exercised). The contract values \(V_{0}\) and \(V_{0}^{E}\) increase when we move from the low towards the high scenario, whereas the value of \(V^{\text{opt}}\) decreases. This shows that the incentive to exercise the SO is reduced by higher participation of the investor in the returns. In contrast, as \(r-r^{G}\) increases, the contract values decrease whereas \(V^{\text{opt}}\) increases. This is in line with the intuition that the higher the spread, the less the contract is profitable for the policyholder, hence creating a big incentive to exercise the SO.
4 Properties of the value function
In this section, we collect some facts about the underlying stochastic process \(X\), defined in (2.16), which are then used to infer regularity of the value function (3.1).
4.1 Path properties of the underlying process
Since the drift function \(\pi (\, \cdot \,)\) in (2.17) is Lipschitz-continuous and the diffusion coefficient is constant, there exists a modification \(\widetilde{X}\) of \(X\) such that the stochastic flow \((t,x) \mapsto \widetilde{X}^{x}_{t}(\omega )\) is continuous for a.e. \(\omega \in \Omega \) (see e.g. Protter [29, Chap. V.7]). As usual, throughout the paper, we work with a continuous modification which we still denote by \(X\) for simplicity.
Lemma 4.1
For any ℙ-a.s. finite stopping time \(\tau \ge 0\), we have
Proof
From the integral form of (2.16) (with \(X^{x}_{0}=x\) and \(X^{y}_{0}=y\)) and noticing that \(\pi (\, \cdot \,)\) is Lipschitz with constant \(\delta >0\), it is immediate to see that
Then an application of Gronwall’s inequality gives (4.1).
The argument for (4.2) is similar. Using that \(y>x\) and \(\pi (\, \cdot \,)\) is Lipschitz gives
where the second inequality uses (4.1). □
The next estimate on the local time of the process \(X\) is particularly useful to establish that the value function is Lipschitz in the time variable. In the rest of the paper, we denote by \(L^{z} =(L^{z}_{t})_{t\in [0,T]}\) the local time of the process \(X\) in the point \(z\ge 0\), which is defined (see e.g. Peskir and Shiryaev [28, Eq. (3.3.29)]) as

Recall that \(\mathbb{E}_{x}[\,\cdot \,]=\mathbb{E}[\,\cdot \,|X_{0}=x]\).
Lemma 4.2
Let \(0< t_{1}\le t_{2}\le T\), fix \(N> 0\) and recall \(x_{\alpha }\) from (2.10). Then there exists a positive constant \(\kappa :=\kappa (t_{1},N;x_{\alpha })\) such that
Proof
Thanks to (4.3), we can select a sequence \((\varepsilon _{n})_{n\ge 1}\) with \(\varepsilon _{n}\downarrow 0\) as \(n\to \infty \) and

Then using Fatou’s lemma, we get
It is well known that \(X\) admits a transition density with respect to its speed measure (see e.g. [30, Theorem V.50.11]). That is, we have
where \(S'\) is the derivative of the scale function and reads
Moreover, the map \((s,x,y)\mapsto p(s,x,y)\) is continuous on \((0,\infty )\times \mathbb{R}^{2}\) and clearly \(S'\) is continuous, too. Hence letting \(\varepsilon _{n}\le \varepsilon _{0}\) for all \(n\ge 1\) and some \(\varepsilon _{0}>0\) and setting
with the supremum taken over \((s,x,y)\in [t_{1},T]\times [0,N]\times [x_{\alpha }-\varepsilon _{0},x_{\alpha }+\varepsilon _{0}]\), it is immediate to obtain (4.4) from (4.5). □
Remark 4.3
Notice that in Lemma 4.2, \(t_{1}\) must be taken strictly positive as the constant \(\kappa (t_{1},N;x_{\alpha })\) might (and will) diverge as \(t_{1}\to 0\).
4.2 Continuity and monotonicity of the value function
Some parts of the analysis in our paper are more conveniently performed by considering a different formulation of problem (3.1). Recall the infinitesimal generator ℒ of \(X\) (see (3.3)) and define the function
with \(x_{\alpha }\) from (2.10). For future reference, it is worth noticing that since \(r^{G}< r\),
Clearly, \(H\) is discontinuous at \(x_{\alpha }\), and it is easy to check that \(H(x)=(\mathcal{L}h)(x)\) for \(x\neq x_{\alpha }\) (recall that \(h\) depends on \(\alpha \)). Since \(x\mapsto h(x)\) (see (2.12)) is a convex function and its first derivative has a single jump
we can apply the Itô–Tanaka formula to \(h(X_{\tau \wedge \tau ^{\dagger }})\) in (3.1) to obtain for problem (3.1) the equivalent formulation

Notice that \(u\) is nonnegative since \(v(t,x) \geq h(x)\) for all \((t,x)\in [0,T]\times \mathbb{R}_{+}\) by (3.1). We show in Proposition 5.2 below that the presence of the local time \(L^{x_{\alpha }}\) in (4.8) implies that it is never optimal to stop when the process \(X\) is equal to \(x_{\alpha }\).
Proposition 4.4
The following properties hold for the value function of the optimal stopping problem (3.1):
i) The map \(t\mapsto v(t,x)\) is decreasing and \(v(T,x)=h(x)\) for any fixed \(x\ge 0\).
ii) The map \(x\mapsto v(t,x)\) is decreasing and \(v(t,0)=h(0)=1\) for any fixed \(t\in [0,T]\). Moreover, for any \(0\le x_{1}\le x_{2}<+\infty \) and any \(t\in [0,T]\), we have
with \(\kappa _{0}:=e^{\delta T}\). The map \(t\mapsto v(t,x)\) is continuous on \([0,T]\) for any \(x\in \mathbb{R}_{+}\), and finally, for any \(0\le t_{1}\le t_{2}< T\) and any \(x\in [0,N]\) with fixed \(N>0\), there is a constant \(\kappa _{1}=\kappa _{1}(t_{2},N;x_{\alpha })>0\) such that
Proof
The monotonicity in i) follows from time-independence of \(h\) and \(\tau ^{\dagger }\), and the value of \(v\) at \(T\) follows from (3.1). As for ii), \(v(t,0)=h(0)\) since \(\tau ^{\dagger }(0)=0\) ℙ-a.s. To show monotonicity of \(v\) in \(x\), fix \(x_{1}< x_{2}\) and note that uniqueness of the solution to (2.16) implies \(X^{x_{1}}_{s\wedge \tau ^{\dagger }(x_{1})}\le X^{x_{2}}_{s\wedge \tau ^{\dagger }(x_{2})}\) ℙ-a.s. for all \(s\in [0,T]\). Since the inequality also holds if we replace \(s\) by a stopping time and the gain function \(h\) is decreasing, we obtain
Next we prove (4.9). Fix \(t\in [0,T]\), consider \(0\le x_{1}< x_{2}\) and denote by \(\tau ^{\dagger }_{i} := \tau ^{ \dagger }(x_{i})\) the first hitting time at zero of \(X^{x_{i}}\) for \(i= 1,2\). From pathwise uniqueness of the solution to (2.16), we have \(\tau ^{\dagger }_{1}\leq \tau ^{\dagger }_{2}\). Then \(\tau \wedge \tau ^{\dagger }_{1}\wedge \tau ^{\dagger }_{2}=\tau \wedge \tau ^{\dagger }_{1}\) ℙ-a.s. for every admissible stopping time \(\tau \). Recalling that \(v(t,\,\cdot \,)\) is decreasing and \(h\) is strictly decreasing and 1-Lipschitz (see (2.13)), we get
where the first inequality is obtained by taking \(\tau \wedge \tau ^{\dagger }_{1}\) in \(v(t,x_{2})\) and the last inequality follows by (4.1).
It remains to prove (4.10). We use (4.8) and notice that for \(0\le t_{1}\le t_{2}< T\) and \(x\in \mathbb{R}_{+}\), we have
where the inequality is due to i). For any stopping time \(\tau \) valued in \([0,T-t_{1}]\), we have that \(\tau \wedge (T-t_{2})\) is admissible for the problem with value \(u(t_{2},x)\). Then by direct comparison (recall that \(\tau ^{\dagger }\) only depends on \(x\in \mathbb{R}_{+}\)) and with \(x\in [0,N]\), we get

where the final inequality uses (4.7) and the fact that the local time \(t\mapsto L^{x_{\alpha }}_{t}\) is non-decreasing. Continuity of \(t\mapsto u(t,x)\) (hence of \(t\mapsto v(t,x)\)) is now clear by continuity of the sample paths of local time. Setting
and recalling Lemma 4.2, we also obtain (4.10). □
An immediate consequence of Proposition 4.4 and the fact that \(h\) is bounded and nonnegative is given in the next corollary.
Corollary 4.5
The value function \(v\) of the optimal stopping problem (3.1) is nonnegative, continuous on \([0,T]\times \mathbb{R}_{+}\) and bounded by 1.
Recalling the sets \(\mathcal{C}\) and \(\mathcal{S}\) defined in (3.4) and (3.5), we can express them in terms of the function \(u\) from (4.8) as
Continuity of \(v\) and \(h\) imply that the sets \(\mathcal{C}\) and \(\mathcal{S}\) are open and closed, respectively. Moreover, Peskir and Shiryaev [28, Corollary I.2.9] guarantees that \(\tau _{*}\) defined in (3.6) is optimal for the value function \(v(t,x)\) for any \((t,x)\in [0,T]\times \mathbb{R}_{+}\). Finally, [28, Theorem I.2.4] ensures that the process \(V^{t,x}=(V^{t,x}_{s})_{s\in [0,T-t]}\) given by \(V^{t,x}_{s}= v(t+s,X^{x}_{s})\) is a supermartingale, while \((V^{t,x}_{s\wedge \tau ^{*}})_{s\in [0,T-t]}\) is a martingale, for any \((t,x)\in [0,T]\times \mathbb{R}_{+}\). Using the martingale property and continuity of the value function, we obtain the next well-known result (see e.g. [28, Sect. III.7.1] for a proof).
Proposition 4.6
The value function \(v\) lies in \(C^{1,2}(\mathcal{C})\) and solves the boundary value problem
with \(v=h\) on \(\partial \mathcal{C}\).
The next simple technical lemma is a consequence of the maximum principle and used later to prove continuity and strict monotonicity of the stopping boundary.
Lemma 4.7
For all \((t,x)\in \mathcal{C}\), we have \(\partial _{t} v(t,x)<0\).
Proof
By way of contradiction, assume there is \((t_{0},x_{0})\in \mathcal{C}\) with \(\partial _{t} v(t_{0},x_{0})=0\). Since \(v(t_{0},x_{0})>h(x_{0})\) and \(v(T,x_{0})=h(x_{0})\), by continuity, there must exist \(t_{1}\in (t_{0},T)\) such that \((t_{1},x_{0})\in \mathcal{C}\) and \(\partial _{t} v(t_{1},x_{0})<-\varepsilon \) for some \(\varepsilon >0\). By continuity of \(\partial _{t} v\) inside \(\mathcal{C}\) and the fact that \(\mathcal{C}\) is open, there exists \(\delta >0\) such that \(\partial _{t} v(t_{1},x)<-\varepsilon /2\) for \(x\in (x_{0}-\delta ,x_{0}+\delta )\) and \(\{t_{1}\}\times (x_{0}-\delta ,x_{0}+\delta )\subseteq \mathcal{C}\).
Now letting \(\mathcal{O}:=(t_{0},t_{1})\times (x_{0}-\delta ,x_{0}+\delta )\), we have \(\mathcal{O}\subseteq \mathcal{C}\) and \(\partial _{t} v\in C^{1,2}(\mathcal{O})\) thanks to internal regularity results for solutions of partial differential equations applied to (4.11) (see e.g. Friedman [19, Theorem 3.5.10]). Moreover, differentiating (4.11) with respect to time and using Proposition 4.4, (i) with the observations above, we obtain that \(\hat{v}:= \partial _{t} v\) solves
Setting \(\tau _{\mathcal{O}}:=\inf \{s\ge 0:(t_{0}+s,X^{x_{0}}_{s})\notin \mathcal{O}\}\) and applying Dynkin’s formula gives
which leads to a contradiction as the process \((t_{0}+s,X^{x_{0}}_{s})\) exits \(\mathcal{O}\) by crossing the segment \(\{t_{1}\}\times (x_{0}-\delta ,x_{0}+\delta )\) with positive probability. □
It is clear by (4.8) that \(u\) inherits the continuity and boundedness properties of \(v\) (see (4.10), (4.9) and Corollary 4.5). Moreover, we have \(\partial _{t} u<0\) in \(\mathcal{C}\) with \(u\in C^{1,2}\) in \(\mathcal{C}\setminus \left ([0,T]\times \{x_{\alpha }\}\right )\) due to (2.12) and (4.6). Finally, in \(\mathcal{C}\setminus \left ([0,T]\times \{x_{\alpha }\}\right )\), the function \(u\) solves
with \(u=0\) on \(\partial \mathcal{C}\).
5 The free boundary problem
In this section, we study the free boundary problem associated with the stopping problem (4.8). We derive geometric properties of the continuation region \(\mathcal{C}\) and regularity of its boundary \(\partial \mathcal{C}\). These have a close interplay with the smoothness of the value function \(v\) on the whole space.
5.1 Analysis of the stopping region
We start the study of the stopping region by noting that for any \((t,x)\in [0,T]\times \mathbb{R}_{+}\), we have
since \(t\mapsto u(t,x)\) is non-increasing (see (i) in Proposition 4.4).
Some of the arguments we need to characterise the stopping region require the next lemma. Its proof is standard, but provided in the appendix for completeness.
Lemma 5.1
For \(\varepsilon >0\), define
Then for any \(\ell >0\), there exists \(t_{\varepsilon ,\ell }>0\) such that
Now we can show that it is never optimal to stop at \(x_{\alpha }\).
Proposition 5.2
We have \([0,T)\times \{x_{\alpha }\} \subseteq \mathcal{C}\).
Proof
Fix \(\varepsilon >0\) and let \(\rho _{\varepsilon }\) be as in Lemma 5.1. Take \(t\in [0,T)\) and \(s\in [0,T-t)\). Since stopping at \(s\wedge \rho _{\varepsilon }\) is admissible for the problem with value function \(u(t,x_{\alpha })\) and
for some \(c_{\varepsilon }>0\) only depending on \(\varepsilon \), one obtains

Applying Lemma 5.1 with \(\ell =2c_{\varepsilon }/(\gamma \alpha )\) and picking \(s>0\) sufficiently small gives \(u(t,x_{\alpha })>0\). Hence \((t,x_{\alpha })\in \mathcal{C}\). Since \(t\in [0,T)\) was arbitrary, the claim follows. □
For any initial point \((t,x)\) with \(t\in [0,T)\) and \(x\in \mathbb{R}_{+}\setminus \{x_{\alpha }\}\) such that \(H(x)>0\), we can choose to stop at the first exit time from a small interval centred at \(x\). Since \(H>0\) in such an interval and the stopping time is strictly positive ℙ-a.s., this well-known argument gives \(u(t,x)>0\). Then it follows that \(\mathcal{R}\subseteq \mathcal{C}\), where
Combining this observation with Proposition 5.2, we get
It is clear that the shape of the set ℛ varies depending on the parameters of the problem. Interestingly, this gives rise to two possible shapes of the stopping region, as we shall see in the rest of the section. Let us start by noticing that
where we used (2.17) and \(r>r_{G}\). Then based on the fact that
where \(\mathcal{R}^{c}\) is the complement of ℛ, we distinguish two cases:
Case 1: If \(x_{\alpha }<\bar{x}_{0}\), then
Case 2: If \(x_{\alpha }\ge \bar{x}_{0}\), then
We now focus on the study of the optimal stopping region in Case 1. Case 2 is easier and can be handled with simpler methods. Thanks to (5.1), we may write (recall (3.8))
Notice that
due to (5.2). The next proposition is the main result in this subsection. It provides piecewise monotonicity and right-/left-continuity of \(c(\, \cdot \,)\).
Proposition 5.3
Assume \(x_{\alpha }<\bar{x}_{0}\). The map \(x\mapsto c(x)\) attains a global minimum \(0\le \hat{c}\le T\) on \([x_{\alpha },\bar{x}_{0}]\). Moreover, there exist \(x_{1}\in [0,x_{\alpha })\), \(x_{2}\in (x_{\alpha },\bar{x}_{0})\) and \(x_{3}\in [x_{2},\bar{x}_{0})\) such that \(c(\, \cdot \,)\) is
(i) equal to zero on \([0,x_{1}]\), strictly increasing on \((x_{1},x_{\alpha }]\) and left-continuous on \([0,x_{\alpha })\);
(ii) strictly decreasing on \([x_{\alpha },x_{2})\) and right-continuous on \([x_{\alpha },x_{3})\);
(iii) strictly increasing on \([x_{3},\bar{x}_{0})\) and left-continuous on \([x_{2},\bar{x}_{0})\). (Notice that in (ii) and (iii), we might have \(x_{2}=x_{3}\).)
In all cases, \(\hat{c}= c(x_{2})=c(x_{3})\), and if \(x_{2}< x_{3}\), then \(\hat{c}=0\). Finally,
The proof relies on two technical lemmas which we are going to present first.
Lemma 5.4
Assume \(x_{\alpha }<\bar{x}_{0}\). Then:
(i) For \(z< x_{\alpha }\) and \(t\in (0,T]\), we have
(ii) For \(z_{1},z_{2}\in (x_{\alpha },\bar{x}_{0})\) with \(z_{1}< z_{2}\) and \(t\in (0,T]\), we have
The map \(x\mapsto c(x)\) is never strictly positive and constant (simultaneously) on intervals \((z_{1},z_{2})\) contained in \([0,x_{\alpha })\cup (x_{\alpha },\bar{x}_{0})\). Finally, for every interval \((z_{1},z_{2})\) contained in \([0,x_{\alpha })\cup (x_{\alpha },\bar{x}_{0})\), we have
Proof
First we prove (i) and (ii). The two claims are similar since \((t,0)\in \mathcal{S}\) for all \(t\in [0,T]\) (see Proposition 4.4, (ii)). Then it is enough to show (ii) as the proof of (i) is analogous up to obvious changes.
Let \((t,z_{1})\) and \((t,z_{2})\) belong to \(\mathcal{S}\) and \(x_{\alpha }< z_{1}< z_{2}\le \bar{x}_{0}\). If \(t=T\), the result is trivial due to (5.6). So let \(t< T\) and recall that \(H(x)<0\) for \(x\in (x_{\alpha },\bar{x}_{0})\). By (5.1), we know that \([t,T]\times \{z_{i}\}\subseteq \mathcal{S}\) for \(i=1,2\). Thus it suffices to show that also \(\{t\}\times (z_{1},z_{2})\subseteq \mathcal{S}\). By way of contradiction, assume there exists \(z_{3}\in (z_{1},z_{2})\) such that \((t,z_{3})\in \mathcal{C}\). Let \(\tau ^{*}_{3}=\tau ^{*}(t,z_{3})\) be optimal for the problem with value \(u(t,z_{3})\). Then

Since \([t,T]\times \{z_{i}\} \subseteq \mathcal{S}\) for \(i=1,2\), we get
Hence \(u(t,z_{3})< 0\) because for all \(s\ge 0\), we have \(L^{x_{\alpha }}_{s\wedge \zeta }=0\) and \(H(X_{s\wedge \zeta })<0\) \(\mathbb{P}_{z_{3}}\)-a.s. and \(\mathbb{P}_{z_{3}}[\tau ^{*}_{3}>0]=1\) by assumption. Thus we have reached a contradiction.
Next we show that \(c\) cannot be strictly positive and constant. We borrow some ideas from De Angelis [12]. Arguing by way of contradiction, assume there exists an interval \((z_{1},z_{2})\subseteq [0,x_{\alpha })\cup (x_{\alpha },\bar{x}_{0})\) where \(c(x)\) takes the constant value \(\bar{c}>0\). Then the open set \(\mathcal{O}:=(0,\bar{c})\times (z_{1},z_{2})\) is contained in \(\mathcal{C}\) and \(u\in C^{1,2}(\mathcal{O})\) since so are \(v\), by Proposition 4.6, and \(h\) (away from \(x_{\alpha }\)). It follows that \(u\) satisfies
Pick \(\varphi \in C^{\infty }_{c}(z_{1},z_{2})\), with \(\varphi \ge 0\). Thanks to (5.9), for \(s \in [0,\bar{c})\),
where we used integration by parts and \(\mathcal{L^{*}}\) is the adjoint operator of ℒ. Recalling that \(\partial _{t} u \leq 0\) (see Proposition 4.4, (i)), we use dominated convergence to obtain
where the last equality is due to \(u(\bar{c},y)=0\) and the strict inequality follows from the facts that \(H<0\) on \((0,\bar{x}_{0})\) and \(\varphi \) is arbitrary. Hence we get a contradiction.
Finally, we can prove (5.8) by an analogous argument. Indeed, if we have that \(\mathcal{O}:=(0,T)\times (z_{1},z_{2}) \subseteq \mathcal{C}\) for some interval \((z_{1},z_{2})\subseteq [0,x_{\alpha })\cup (x_{\alpha },\bar{x}_{0})\), then \(c(x)=T\) on \((z_{1},z_{2})\), contradicting that \(c\) cannot be strictly positive and constant. □
Lemma 5.5
Assume \(x_{\alpha }<\bar{x}_{0}\). The map \(x\mapsto c(x)\) is lower semi-continuous on \(\mathbb{R}_{+}\) and continuous at \(x_{\alpha }\) with \(c(x_{\alpha })=T\). Moreover,
Proof
Recall that \(c(x)=T\) for \(x\in (\bar{x}_{0},\infty )\) by (5.6). Thus \(c(\, \cdot \,)\) is continuous on \((\bar{x}_{0},\infty )\). Now fix \(z\in (0,\bar{x}_{0}]\) and take a sequence \((z_{n})_{n\ge 1}\subseteq (0,\infty )\) with \(z_{n}\to z\) as \(n\to \infty \). Then
and since \((c(z_{n}),z_{n})_{n\ge 1}\subseteq \mathcal{S}\) and \(\mathcal{S}\) is closed, we must have
The latter implies that \(\liminf _{n\to \infty }c(z_{n})\ge c(z)\) by the definition of \(c(z)\), and lower semi-continuity follows.
If \(z=0\), then \(c(0)=0\) by Proposition 4.4, (ii). Obviously \(\liminf _{n\to \infty }c(z_{n})\ge 0\) for \(z_{n}\to 0\); hence lower semi-continuity holds at \(z=0\), too. To prove continuity at \(x_{\alpha }\), recall that \(c(x_{\alpha })=T\) by Proposition 5.2. Then \(\liminf _{n\to \infty } c(z_{n})\ge c(x_{\alpha })=T\) together with \(c(\, \cdot \,)\le T\) implies for any \(z_{n}\to x_{\alpha }\) that
It remains to prove (5.10). Because \(c(0)=0\), it suffices to assume that there is some \(x\in (0,\bar{x}_{0})\setminus \{x_{\alpha }\}\) with \(c(x)=T\) and then argue by way of contradiction. Without loss of generality, assume \(x\in (x_{\alpha },\bar{x}_{0})\) since the case of \(x\in (0,x_{\alpha })\) can be treated analogously. Then we can pick \(z_{1},z_{2}\in (x_{\alpha },\bar{x}_{0})\) such that \(z_{1}< x< z_{2}\) and \(\bar{t}:=c(z_{1})\vee c(z_{2})< T\) by (5.8). Hence (ii) in Lemma 5.4 implies \((\bar{t}, x)\in \mathcal{S}\), i.e., \(c(x)\le \bar{t}\), which is a contradiction. □
Proof of Proposition 5.3
From Lemma 5.4, (i), we immediately deduce that \(x\mapsto c(x)\) is non-decreasing on \([0,x_{\alpha })\). Moreover, (5.10) and the fact that \(c(\, \cdot \,)\) cannot be strictly positive and constant (Lemma 5.4) also guarantee that there exists \(x_{1}\in [0,x_{\alpha })\) such that \(c(x)=0\) on \([0,x_{1}]\) and \(c(\, \cdot \,)\) is strictly increasing on \((x_{1},x_{\alpha }]\) (notice that it could be that \(x_{1}=0\) and \(c(\, \cdot \,)>0\) on \((0,x_{\alpha })\)). Left-continuity of \(c\) on \([0,x_{\alpha })\) follows by its monotonicity and lower semi-continuity.
By lower semi-continuity on \(\mathbb{R}_{+}\) and (5.10), there must be a minimum of \(c(\, \cdot \,)\) on \([x_{\alpha },\bar{x}_{0}]\), denoted by \(\hat{c}\in [0,T)\). We have two possible cases: either \(\hat{c}=0\) or \(\hat{c}>0\).
(a) If \(\hat{c}=0\), the minimum may occur at most on an interval \([x_{2},x_{3}] \subseteq (x_{\alpha },\bar{x}_{0}]\). Indeed, the set \(\mathrm{argmin}\{c(x) : x \in [x_{\alpha },\bar{x}_{0}]\}\) is closed by lower semi-continuity of \(c(\, \cdot \,)\) and must be connected by (ii) in Lemma 5.4. However, the interval \([x_{2},x_{3}]\) may collapse into a single point \(x_{2}=x_{3}\) (in which case \(c(\, \cdot \,)>0\) on \([x_{\alpha },x_{2})\cup (x_{2},\bar{x}_{0}]\)).
(b) If \(\hat{c}>0\), it may only occur at a single point \(x_{2}( \,=x_{3})\in (x_{\alpha },\bar{x}_{0}]\), again by (ii) in Lemma 5.4 and since \(c(\, \cdot \,)\) cannot be strictly positive and constant.
Strict monotonicity on \([x_{\alpha },x_{2})\) and \((x_{3},\bar{x}_{0}]\) now follows from (ii) in Lemma 5.4 and the fact that \(c(\, \cdot \,)\) cannot be strictly positive and constant. Left-/right-continuity are then obtained by monotonicity and lower semi-continuity. Finally, the first limit in (5.7) follows by Lemma 5.5, whereas the second one is trivial. □
By arguments as above, we obtain analogous results for the case of \(x_{\alpha }\ge \bar{x}_{0}\). Therefore we omit the proof of the next proposition.
Proposition 5.6
Assume \(x_{\alpha }\ge \bar{x}_{0}\). Then on the interval \([0,\bar{x}_{0})\), the map \(x\mapsto c(x)\) is non-decreasing and left-continuous with \(c(x)< T\). On the interval \([\bar{x}_{0},+\infty )\), we have \(c(x)=T\), and
Moreover, there exists at most a point \(x_{1}\le \bar{x}_{0}\) such that \(c(x)=0\) for \(x\in [0,x_{1}]\) and \(c(\, \cdot \,)\) is strictly increasing on \((x_{1},\bar{x}_{0}]\).
5.2 Higher regularity of the value function and of the optimal boundary
Thanks to the geometry of the optimal boundary, we obtain a lemma that will be used to establish global \(C^{1}\)-regularity of the value function (jointly in \((t,x)\)).
As shown in De Angelis and Peskir [14], the key to \(C^{1}\)-regularity of the value function is the probabilistic regularity of the stopping boundary. Since the two-dimensional process \((t,X_{t})_{t\ge 0}\) is not of strong Feller type, we actually use probabilistic regularity for the interior \(\mathcal{S}^{\circ }\) of the stopping region. For completeness, we recall that a process \(Z\) valued in \(\mathbb{R}^{d}\) is said to be of strong Feller type if \(z\mapsto \mathbb{E}_{z}[f(Z_{t})]\) is continuous for any \(t>0\) and any bounded measurable function \(f:\mathbb{R}^{d}\to \mathbb{R}\).
More precisely, letting
we say that a boundary point \((t,x)\in \partial \mathcal{C}\) is (probabilistically) regular for \(\mathcal{S}\) (or \(\mathcal{S}^{\circ }\)) if
Clearly, probabilistic regularity for \(\mathcal{S}^{\circ }\) implies the one for \(\mathcal{S}\). However, regularity for \(\mathcal{S}^{\circ }\) is not well defined at points \((t_{0},z_{0})\in \partial \mathcal{C}\) such that \(\mathcal{S}\) has empty interior in a neighbourhood of \((t_{0},z_{0})\). Therefore in what follows, we need both.
Lemma 5.7
The boundary \(\partial \mathcal{C}\) is probabilistically regular for \(\mathcal{S}\). Moreover, for any \((t_{0},z_{0})\in \partial \mathcal{C}\) and any sequence \((t_{n},x_{n}) \to (t_{0},z_{0})\) as \(n\to \infty \), we have
where \(\tau ^{*}\) is defined in (3.6).
Proof
Starting from a point \((t,z)\in \partial \mathcal{C}\) with \(t< T\), the process \((t+s,X^{z}_{s})_{s\ge 0}\) moves instantaneously towards the stopping region, due to the geometry of \(\mathcal{S}\). Notice that the drift \(\pi \) of the process \(X\) is locally bounded. Then by the law of the iterated logarithm for Brownian motion, almost every path of the process \(X^{z}\) oscillates above and below its initial point \(z\) for any arbitrarily small interval of time. These two observations imply that
for all \((t,z)\in \partial \mathcal{C}\) except at most along vertical stretches of the boundary corresponding to \(x_{1}=0\) and \(x_{2}=x_{3}\), as defined in Proposition 5.3. Indeed, at such points, a spike may occur so that \(\mathcal{S}^{\circ }\) may be (locally) empty. For simplicity, let us denote
By definition, \(\tau ^{*}(t,z)=0\) ℙ-a.s. for all \((t,z)\in \partial \mathcal{C}\). Then by (5.14), we have regularity of \(\partial \mathcal{C}\setminus \mathcal{E}\) for \(\mathcal{S}^{\circ }\) in the sense of (5.12). Hence (5.13) holds for any \((t,z)\in \partial \mathcal{C}\setminus \mathcal{E}\) (see e.g. [14, Corollary 6]).
Thanks to lower semi-continuity of \(c\), it only remains to consider regularity at ℰ in the cases (a) \(x_{2}=x_{3}\) but \(\hat{c}< c(x_{2}\pm )\), and (b) \(x_{1}=0\) but \(c(x_{1}+)>0\). We give a full argument for case (a); case (b) can be handled analogously.
Let us assume \(x_{2}=x_{3}\) but \(\hat{c}< c(x_{2}\pm )\). Then \(\sigma _{*}(t,x_{2})=\tau ^{*}(t, x_{2})\) ℙ-a.s. continues to hold for all \(t\in [0,T)\) such that \((t,x_{2})\in \partial \mathcal{C}\), by the law of the iterated logarithm. Hence the first assertion in (5.12) holds. Since the hitting time \(\sigma ^{\circ }_{*}(t,x_{2})\) is no longer zero for \(\hat{c} \le t < c(x_{2}+)\wedge c(x_{2}-)\) because there is no interior part to the stopping region in a neighbourhood of \((t,x_{2})\), the argument provided in [14] to prove the analogue of (5.13) needs a small tweak.
Fix \((t_{0},x_{2})\in \partial \mathcal{C}\) with \(\hat{c} \le t_{0} < c(x_{2}+)\wedge c(x_{2}-)\) and a sequence \((t_{n},x_{n})_{n \ge 1}\subseteq \mathcal{C}\) that converges to \((t_{0},x_{2})\) as \(n\to \infty \). Recall that we work with a continuous modification of the stochastic flow and let us pick \(\omega \in \Omega \) outside a nullset such that \((t,x)\mapsto X^{x}_{t}(\omega )\) is continuous. Then for any \(\delta >0\), there exist \(0< s_{1,\omega }< s_{2,\omega }<\delta \) such that \(X^{x_{2}}_{s_{1,\omega }}(\omega )< x_{2}< X^{x_{2}}_{s_{2,\omega }}( \omega )\) by the law of the iterated logarithm. By continuity of \(x\mapsto X^{x}\), for some \(N_{\delta ,\omega }\ge 1\) and all \(n\ge N_{\delta ,\omega }\), we have \(X^{x_{n}}_{s_{1,\omega }}( \omega )< x_{2}< X^{x_{n}}_{s_{2,\omega }}(\omega )\). Without loss of generality, we may assume \(N_{\delta ,\omega }\) is large enough so that \(t_{n} \ge t_{0}-s_{1,\omega }\) for \(n\ge N_{\delta ,\omega }\). Hence the points \((t_{n}+s_{1,\omega },X^{x_{n}}_{s_{1,\omega }}(\omega ))\) and \((t_{n}+s_{2,\omega },X^{x_{n}}_{s_{2,\omega }}(\omega ))\) lie in the two opposite half-planes that are adjacent to the segment \([t_{0},T]\times \{x_{2}\}\). This implies that for each \(n\ge N_{\delta ,\omega }\), there is \(s_{n,\omega }\in (s_{1,\omega },s_{2,\omega })\) such that \(X^{x_{n}}_{s_{n,\omega }}(\omega )=x_{2}\) and therefore \((t_{n}+s_{n,\omega }, X^{x_{n}}_{s_{n,\omega }}(\omega ))\in \mathcal{S}\). The latter implies \(\tau ^{*}(t_{n},x_{n})(\omega )\le \delta \) for all \(n\ge N_{\delta ,\omega }\), hence
Since \(\delta >0\) and \(\omega \) were arbitrary, we obtain (5.13). □
We now provide some useful estimates for \(\partial _{x} v\) in \(\mathcal{C}\). Below we use that \((t_{0},z_{0})\in \partial \mathcal{C}\) with \(t_{0}< T\) guarantees \(z_{0} \neq x_{\alpha }\) by Proposition 5.2, so that \(\partial _{x} h\) is continuous at \(z_{0}\). In particular, \(\partial _{x} h ( X^{x}_{\tau ^{*}} )\) is well defined on the event \(\{\tau ^{*}< T-t\}\) for any \((t,x)\in [0,T)\times \mathbb{R}_{+}\).
Lemma 5.8
For all \((t,x)\in \mathcal{C}\) and \(0< s<(\delta ^{-1}\ln 2)\wedge (T-t)\), we have

with \(\tau ^{*}=\tau ^{*}(t,x)\) and \(\tau ^{\dagger }=\tau ^{\dagger }(x)\).
Proof
Recall that for any initial condition \((t,x)\in [0,T]\times \mathbb{R}_{+}\), the process \(V^{t,x}\) given by \(V^{t,x}_{s}= v(t+s,X^{x}_{s})\) is a continuous supermartingale and \(s\mapsto V^{t,x}_{s\wedge \tau ^{*}}\) is a continuous martingale for \(s\in [0,T-t]\). Fix \((t,x)\in \mathcal{C}\) and \(\varepsilon >0\) such that \((t,x+\varepsilon )\in \mathcal{C}\) and \((t,x-\varepsilon )\in \mathcal{C}\). Notice that
and by (ii) in Proposition 4.4 that \(\tau ^{\dagger }(x)\ge \tau ^{*}(t,x)\) a.s., because \([0,T]\times \{0 \} \subseteq \mathcal{S}\). To simplify notation, set \(\tau ^{*}:=\tau ^{*}(t,x)\). Then for all \(s< T-t\), using the (super)martingale property gives
Thus with \(\kappa _{0}>0\) as in (4.9), we get

On \(\{\tau ^{*}\le s\}\), the decreasing property of \(h\) and \(|X^{x+\varepsilon }_{s}-X^{x}_{s} | \le \varepsilon e^{\delta s}\) (see (4.1)) give the inequality \(h(X^{x+\varepsilon }_{\tau ^{*}})\ge h(X^{x}_{\tau ^{*}}+\varepsilon e^{ \delta s})\). Hence we obtain

since \(h\) is absolutely continuous on \(\mathbb{R}_{+}\). Then

where the final equality follows by dominated convergence since \(|\partial _{x} h |\le 1\).
Now for each \(\omega \in \{\tau ^{*}\le s\}\), we have \(X^{x}_{\tau ^{*}}(\omega )\neq x_{\alpha }\) by Proposition 5.2 since \(s< T-t\). Hence there exists \(\bar{\varepsilon }_{\omega }>0\) such that the mapping \(z \mapsto \partial _{x} h ( X^{x}_{\tau ^{*}}(\omega )+z )\) is continuous on \([0,\bar{\varepsilon }_{\omega }e^{\delta s}]\), and an application of the fundamental theorem of calculus gives
Hence

Next we want to bound the difference \(v(t,x)-v(t,x-\varepsilon )\) from above. This requires a slight modification of the previous argument in order to account for the fact that \(\tau ^{\dagger }(x-\varepsilon )\le \tau ^{\dagger }(x)\) a.s. In particular, without loss of generality, we assume that \(\varepsilon \in (0,\varepsilon _{0}]\) for some fixed \(\varepsilon _{0}>0\). Letting \(\tau ^{\dagger }_{0}:=\tau ^{\dagger }(x-\varepsilon _{0})\) for simplicity, we have \(\tau ^{\dagger }_{0}\le \tau ^{\dagger }(x-\varepsilon )\). Then arguing as in (5.16) gives

Notice that the second term in the last expression is negative thanks to Proposition 4.4, (ii). Moreover, on the event \(\{\tau ^{*}\le s\wedge \tau ^{\dagger }_{0}\}\), we have
where the last step follows from the convexity of \(h(\, \cdot \,)\). Also on the event \(\{\tau ^{*}\!\le\! s \!\wedge\! \tau ^{\dagger }_{0}\}\), using (4.2) gives
by assuming \(s < \delta ^{-1}\ln 2\) without loss of generality. Since \(\partial _{x} h\le 0\), we then get
on \(\{\tau ^{*}\le s\wedge \tau ^{\dagger }_{0}\}\). Thus

and by arguments as in (5.17), we obtain

To conclude, we let \(\varepsilon _{0}\downarrow 0\) so that \(\tau ^{\dagger }_{0}=\tau ^{\dagger }(x-\varepsilon _{0})\uparrow \tau ^{\dagger }(x)\), and the upper bound in (5.15) follows by monotone convergence. □
Proposition 5.9
For any \((t_{0},z_{0})\!\in \!\partial \mathcal{C}\) with \(t_{0}< T\) and \(z_{0}>0\) and for any sequence \((t_{n},x_{n})_{n\ge 1}\subseteq \mathcal{C}\) with \((t_{n},x_{n})\rightarrow (t_{0},z_{0})\) as \(n\to \infty \), we have
Proof
We first prove (5.18). Notice that (5.15) holds for any point \((t_{n},x_{n})\!\in \! \mathcal{C}\) from a sequence that converges to \((t_{0},z_{0})\) as \(n\to \infty \), where \((t_{0},z_{0})\in \partial \mathcal{C}\) with \(t_{0}< T\) and \(z_{0}>0\). By Lemma 5.7, \(\tau ^{*}_{n}:=\tau ^{*}(t_{n},x_{n}) \rightarrow 0\) as \(n\to \infty \), and therefore \(\partial _{x} h( X^{x_{n}}_{\tau ^{*}_{n}}) \rightarrow \partial _{x} h(z_{0})\) (recall that \(z_{0}\neq x_{\alpha }\)). Then for \(0< s<(\delta ^{-1}\ln 2)\wedge (T-t_{0})\), dominated convergence and (5.15) give
Letting \(s \rightarrow 0\) yields (5.18).
To prove (5.19), fix \((t,x)\in \mathcal{C}\) with \(t< T\) and \(\varepsilon >0\) such that \((t+\varepsilon ,x)\in \mathcal{C}\). Let
and pick \(s< T-(t+\varepsilon )\). Then proceeding as in the proof of Lemma 5.8 with \(\tau ^{*}=\tau ^{*}(t,x)\), we get
Combining the above with (4.10) gives

Without loss of generality, we may assume that \(\varepsilon \in (0,\varepsilon _{0}]\) for some \(\varepsilon _{0}>0\) such that \(s< T-(t+\varepsilon _{0})\) and \(\kappa _{1}(t+\varepsilon +s,N)\le \hat{\kappa }_{1}(\varepsilon _{0},N)\) for some constant \(\hat{\kappa }_{1}(\varepsilon _{0},N)>0\). Hence we obtain
The result in the equation above holds for any \((t_{n},x_{n})\in \mathcal{C}\) from a sequence converging to \((t_{0},x_{0})\). Moreover, without loss of generality, we can assume that \(x_{n}\le x_{0}+1< N\) for all \(n\ge 1\) so that \(\tau _{N}(x_{n})\ge \tau _{N}(x_{0}+1)>0\) ℙ-a.s. and
Then thanks to Lemma 5.7, we get
Hence (5.19) holds. □
Propositions 5.9 and 4.6 imply continuous differentiability of \(v\).
Corollary 5.10
The value function \(v\) from (3.1) is continuously differentiable on the set \([0,T)\times (0,+\infty )\). Moreover, \(v\in C^{1,2}\) on the set \(\overline{\mathcal{C}}\cap ([0,T)\times (0,+\infty ))\) with
for \(t_{0}< T\) and \(z_{0}>0\).
Proof
We only need to prove (5.20). For that, it is sufficient to take limits in (4.11) and use Proposition 5.9. □
The next result shows that the optimal boundary is continuous as a function of \(x\). Notice that this type of continuity is not a standard result in optimal stopping problems for time-space processes \((t,X)\). Indeed, in the probabilistic literature, one normally proves continuity of the boundary as a function of time. Our proof relies on the use of a suitably constructed reflecting diffusion.
Theorem 5.11
The mapping \(x\mapsto c(x)\) is continuous on \((0,\infty )\). If \(c(0+)=0\), then continuity holds on \(\mathbb{R}_{+} =[0,\infty )\).
Proof
We give a full proof in the case \(x_{\alpha }<\bar{x}_{0}\) and consider the interval \([x_{3},\infty )\), with \(x_{3}\) as in Proposition 5.3, where the boundary is increasing. It will be clear that the intervals \([x_{1},x_{\alpha }]\) and \([x_{\alpha }, x_{2}]\) and the case \(x_{\alpha }\ge \bar{x}_{0}\) can be treated analogously.
Arguing by way of contradiction, assume that there exists a point \(z_{0}\in [x_{3},\infty )\) with \(c(z_{0})< c(z_{0}+)\) and let \(\mathcal{I}_{0}:=(c(z_{0}),c(z_{0}+))\). Then \(\mathcal{I}_{0}\times \{z_{0}\}\subseteq \partial \mathcal{C}\) and there exists \(z_{1}>z_{0}\) such that \(\partial _{t} u(t,z_{1})<-\varepsilon _{1}\) for some \(\varepsilon _{1}>0\) and for all \(t\in \mathcal{I}_{1}:=(t_{0},t_{1})\subseteq \mathcal{I}_{0}\), for some \(t_{1}>t_{0}\) (see Lemma 4.7). Since \(u\in C^{1}([0,T) \times \mathbb{R}_{+})\) by Corollary 5.10 and \(\mathcal{I}_{1}\times \{z_{0}\}\subseteq \partial \mathcal{C}\), we have
So for any \(\varepsilon >0\), there exists \(\delta _{\varepsilon }>0\) such that \(z_{0}+\delta _{\varepsilon }< z_{1}\) and
by uniform continuity on any compact set.
Now we consider a process that equals \((X_{t})_{t \ge 0}\) away from \(z_{0}+\delta _{\varepsilon }\) and is reflected (upwards) at \(z_{0}+\delta _{\varepsilon }\). It is well known (see e.g. Lions and Sznitman [25] or Bass [4, Sect. I.12]) that there exists a unique strong solution of the stochastic differential equation
where \(A^{\delta _{\varepsilon }}\) is a continuous, non-decreasing process that guarantees that ℙ-a.s.,

As in Lemma 4.7, we appeal to classical results on interior regularity for solutions of PDEs that guarantee \(\partial _{t} u\in C^{1,2}(\mathcal{I}_{1}\times (z_{0},z_{1}))\) and \((\partial _{t}+\mathcal{L})\partial _{t} u=0\) on \(\mathcal{I}_{1}\times (z_{0},z_{1})\). Then setting \(\tau ^{\varepsilon }_{1}:=\inf \{s\ge 0 : \widetilde{X}^{\varepsilon }_{s} =z_{1}\}\) and \(\hat{u}:= \partial _{t} u\), an application of Itô’s formula for semimartingales gives for any \(t\in \mathcal{I}_{1}\) that
where the inequality follows from (5.21) and the second condition in (5.22) implies

For the expression on the left-hand side of (5.23), we have

Hence (5.23) yields
The next step is to let \(\varepsilon \to 0\). However, the regularity of \(\partial _{tx}u\) as \(\delta _{\varepsilon }\downarrow 0\) might be problematic. We therefore use a trick with test functions to overcome this difficulty. Pick \(\varphi \in C^{\infty }_{c}(\mathcal{I}_{1})\), \(\varphi \ge 0\), such that \(\int _{\mathcal{I}_{1}}\varphi (t) \ dt = 1\). Multiplying both sides of (5.24) by \(\varphi \), integrating over \(\mathcal{I}_{1}\) and using Fubini’s theorem, we then obtain

where the penultimate inequality uses the bounds on \(\partial _{x} u\) in (5.21), and the final inequality that \(\varphi (t_{1}-s)=0\) for \(s\ge t_{1}\). Here \(\|\cdot \|_{\infty }\) is the supremum norm on \([0,T]\).
For the increasing process \(A^{\delta _{\varepsilon }}\), we have an upper bound which is independent of \(\varepsilon \). This can be deduced from the integral form of the SDE. Indeed, taking expectations in
gives
Using that \(\widetilde{X}_{s}^{\varepsilon }\in [z_{0}+\delta _{\varepsilon },z_{1}]\) and \(\pi (\widetilde{X}_{s}^{\varepsilon })\ge \pi (z_{1})\) for \(s \leq \tau ^{\varepsilon }_{1}\), we obtain
Hence
and letting \(\varepsilon \to 0\) gives
If we can show that the left-hand side above is strictly positive, we have reached a contradiction and there cannot be a discontinuity of \(c\).
For our final task, we introduce the change of measure
Under \(\widehat{\mathbb{P}}^{\varepsilon }\), the process \(\widetilde{X}^{\varepsilon }\) evolves according to
where \(\widehat{W}^{\varepsilon }:=(\widehat{W}^{\varepsilon }_{t})_{t\in [0,T]}\) is a Brownian motion defined as
For future reference, we also introduce the Dóleans-Dade exponential
Since the measures are equivalent on \(\mathcal{F}_{T}\), the process \(\widetilde{X}^{\varepsilon }\) is under \(\widehat{\mathbb{P}}^{\varepsilon }\) a Brownian motion reflected at \(z_{0}+\delta _{\varepsilon }\). Hence we have an explicit formula for the increasing process \(A^{\delta _{\varepsilon }}\) (see Karatzas and Shreve [23, Lemma 3.6.14]), namely
It remains to remove the dependence of the measure on \(\varepsilon \). For that, we take a filtered probability space \((\widehat{\Omega }, \widehat{\mathcal{F}},(\widehat{\mathcal{F}}_{t})_{t \in [0,T]}, \widehat{\mathbb{P}})\) equipped with a standard Brownian motion \(B =(B_{t})_{t\in [0,T]}\). On that space, we construct a Brownian motion \(Y\) starting from \(z_{0}+\delta _{\varepsilon }\) and reflected at its starting point. In other words,
where \(L\) has the same expression as (5.27), but with \(B\) instead of \(\widehat{W}^{\varepsilon }\). For future reference, we also define
By construction,
Setting \(\rho ^{\varepsilon }_{1}:=\inf \{t\ge 0:Y^{\varepsilon }_{t}=z_{1}\}\), denoting by \(\widehat{\mathbb{E}}^{\varepsilon }\) the expectation under \(\widehat{\mathbb{P}}^{\varepsilon }\) and letting \(\xi ^{\varepsilon }_{T}\) be defined as the Dóleans-Dade exponential in (5.26), but with \((Y^{\varepsilon },B)\) instead of \((\widetilde{X}^{\varepsilon },\widehat{W}^{\varepsilon })\), we then obtain

Using the explicit form of \(Y^{\varepsilon }\) gives that under \(\widehat{\mathbb{P}}\),
where the convergence is monotonic from above and therefore also

Hence Fatou’s lemma and (5.28) give

where \(\xi ^{0}_{T}\) is the Dóleans-Dade exponential associated to \((Y^{0},B)\) and the final inequality follows from well-known distributional properties of reflected Brownian motion (see e.g. [23, Sect. 2.8.B]). Finally, using Fatou’s lemma in (5.25) and the discussion above, we conclude that

where the final inequality uses that \(\varphi \) is nonnegative and arbitrary. This is a contradiction, and so continuity of \(x\mapsto c(x)\) is proved. □
If \(c(0+)>0\), the smooth-fit property may break down on \(\{0\}\times [0,c(0+))\), i.e., we may have \(\partial _{x} u(t,0+)\neq 0\) for some \(t\in [0,c(0+))\). That is why continuity of \(c( \cdot )\) only holds on \((0,\infty )\) in that case. Combining the continuity result with (5.7) and (5.11) also gives the next result.
Corollary 5.12
We have
We conclude this section by giving the proofs of the main results stated in Sect. 3.
5.3 Proofs of Theorems 3.1 and 3.2
Proof of Theorem 3.1
The first claim is a consequence of Corollary 4.5, and \(v\ge h\) follows by taking \(\tau =0\) in (3.1). Monotonicity of the mappings \(t\mapsto v(t,x)\) and \(x\mapsto v(t,x)\) is proved in Proposition 4.4. Continuous differentiability of \(v\) and continuity of \(\partial _{xx}v\) on \(\overline{\mathcal{C}}\cap ([0,T)\times (0,\infty ))\) are obtained in Corollary 5.10. Proposition 4.6 guarantees that \(v\) solves (3.7) in \(\mathcal{C}\). Moreover, \(v=h\) in \(\mathcal{S}\) and \(\mathcal{L}h(x) \le 0\) in \(\mathcal{S}\) by (5.2). Hence (3.7) holds.
As for uniqueness, if we can find another function \(w\) that solves (3.7) with \(\mathcal{C}=\{w>h\}\) and with the same regularity as \(v\), then a standard verification argument based on a well-known generalisation of Itô’s formula shows that \(w\) coincides with the value function of the optimal stopping problem (3.1). Further details in this direction are omitted as they are standard and can be found in Bensoussan and Lions [6, Theorem IV.4.2]. □
Proof of Theorem 3.2
We only provide the full argument for (b), which builds on the results of Proposition 5.3. The proof of (a) is easier and follows from analogous arguments and Proposition 5.6.
If \(x_{\alpha }< \bar{x}_{0}\), our boundary \(c\) is strictly monotonic and continuous on the intervals \([x_{1},x_{\alpha })\), \((x_{\alpha },x_{2})\) and \((x_{3},\bar{x}_{0})\) (with \(x_{1}\), \(x_{2}\) and \(x_{3}\) as in Proposition 5.3) and \(c(x)=T\) for \(x\ge \bar{x}_{0}\). Hence the map \(x\mapsto c(x)\) can be inverted separately on the intervals \([x_{1},x_{\alpha })\), \((x_{\alpha },x_{2})\) and \((x_{3},\bar{x}_{0}]\) to obtain three continuous and strictly monotonic functions of time that describe the boundary \(\partial \mathcal{C}\).
Recalling \(\hat{c}\) from Proposition 5.3, we can locally define the inverse functions
Clearly, \(0\le b_{1}(t)\le b_{2}(t)\le b_{3}(t)\) for \(t\in [\hat{c},T)\). Setting \(t_{0}:=c(0+)\), we have \(b_{1}(t)=0\) on \([0,t_{0})\) if \(t_{0}>0\); otherwise \(b(0+)=x_{1}\). Recalling that \(x\mapsto c(x)\) is strictly increasing and continuous on \([x_{1},x_{\alpha }]\) and \([x_{3},\bar{x}_{0}]\), we obtain that \(t \mapsto b_{1}(t)\) and \(t\mapsto b_{3}(t)\) are strictly increasing and continuous on \([t_{0},T)\) and \([\hat{c}, T)\), respectively. Analogously, since \(x\mapsto c(x)\) is strictly decreasing and continuous on \([x_{\alpha },x_{2}]\), we obtain that \(t\mapsto b_{2}(t)\) is strictly decreasing and continuous on \([\hat{c},T)\). Moreover, \(b_{1}(T-)=b_{2}(T-)=x_{\alpha }\) by the first limit in (5.7), and \(b_{3}(T-)=\bar{x}_{0}\) by Corollary 5.12. By construction, if \(\hat{c}>0\), we have \(b_{2}(\hat{c})= b_{3}(\hat{c})\) because \(\hat{c}\) is the unique point in the set \(\mathrm{argmin}\{c(x) : x \in [x_{\alpha },\bar{x}_{0}]\} \). If instead \(\hat{c}=0\), we have \(b_{2}(0)=x_{2}\) and \(b_{3}(0)=x_{3}\) by Proposition 5.3. This concludes the proof of i)–iv). The claims in v) are now straightforward. □
6 Some comments about management fees
In a model with proportional management fees as in (3.2), the only change in our analysis is due to the fact that the function \(H\) appearing in \(u\) (see (4.6) and (4.8)) is replaced by
where \(p,q\ge 0\) are as in (3.2).
The key features in our analysis from the previous sections are the presence of the local time at \(x_{\alpha }\) in the problem formulation (4.8), and the sign of the function \(H\) via (5.2) (whose interplay leads to the two separate cases \(x_{\alpha }<\bar{x}_{0}\) and \(x_{\alpha }\ge \bar{x}_{0}\)). In the setup with management fees, the local time produces the same effects so that Proposition 5.2 continues to hold and \([0,T)\times \{x_{\alpha }\}\subseteq \mathcal{C}\). However, we now need to look at the sign of the function \(H^{p,q}\) rather than that of \(H\).
It is immediate to check that for \(x\le x_{\alpha }\),
and if \(x_{\alpha }<\bar{x}_{q}\), then \(H^{p,q}(x)<0\). Similarly, for \(x>x_{\alpha }\),
where \(\bar{x}_{q,\gamma }>\bar{x}_{q}>x_{G}\) since \(\gamma \in (0,1)\) (recall \(x_{G}=\beta +r^{G}/\delta \)). Hence if \(x_{\alpha }<\bar{x}_{q}\), we get \(H^{p,q}(x)<0\) for \(x_{\alpha }< x<\bar{x}_{q,\gamma }\). So also in the presence of management fees, we must consider various cases depending on the position of \(x_{\alpha }\) relative to \(\bar{x}_{q}\) and \(\bar{x}_{q,\gamma }\). In keeping with the rest of the paper and in the interest of brevity, we briefly illustrate here only the case \(x_{\alpha }<\bar{x}_{q}\) and draw a parallel with the case \(x_{\alpha }<\bar{x}_{0}\) from the previous sections. The remaining cases can be studied analogously with the methods developed above.
From now on, let us assume \(x_{\alpha }<\bar{x}_{q}\). Then
In the special case \(p=0\), we have the exact analogue of (b) in Theorem 3.2, but with \(\bar{x}_{0}\) therein replaced by \(\bar{x}_{q,\gamma }\). If instead \(p>0\), only two sub-cases may arise and we must consider them separately:
Case (i) \(x-\bar{x}_{q,\gamma }\le \frac{p}{\delta }(1-\gamma )^{-1}e^{x}\) for all \(x\in \mathbb{R}_{+}\) (i.e., \(\ln (\frac{\delta }{p}(1-\gamma ))\le 1+\bar{x}_{q,\gamma }\)). Then
Case (ii) There exist \(\hat{x}_{2}>\hat{x}_{1}>\bar{x}_{q,\gamma }\) such that \(x-\bar{x}_{q,\gamma }> \frac{p}{\delta }(1-\gamma )^{-1}e^{x}\) for all \(x\in (\hat{x}_{1},\hat{x}_{2})\), and \(x-\bar{x}_{q,\gamma }\le \frac{p}{\delta }(1-\gamma )^{-1}e^{x}\) otherwise (i.e., \(\ln (\frac{\delta }{p}(1-\gamma ))> 1+\bar{x}_{q,\gamma }\)). Then
In Case (ii), the situation is similar to (5.3), with \(\bar{x}_{0}\) therein replaced by \(\hat{x}_{1}\) and noting the additional strip \([0,T]\times [\hat{x}_{2},\infty )\) intersecting the stopping set. In particular, repeating the same arguments as in Proposition 5.3, one can prove that the map \(x\mapsto c(x)\) (defined as in (5.5)) satisfies all claims in the proposition with \(\bar{x}_{0}\) replaced by \(\hat{x}_{1}\) throughout. In addition to that and by the same methods, one can also prove that \(c(x)< T\) for all \(x>\hat{x}_{2}\) and there exists \(\hat{x}_{3}>\hat{x}_{2}\) such that \(x\mapsto c(x)\) is strictly decreasing on \((\hat{x}_{2},\hat{x}_{3})\) with \(c(\hat{x}_{2}+)=T\) and \(c(x)=0\) for \(x\in [\hat{x}_{3},\infty )\). Thanks to piecewise monotonicity of the boundary, we can prove its continuity also in this setting as in Theorem 5.11.
While the strict monotonicity follows by the exact same arguments as in the proof of Proposition 5.3, we prove for completeness the existence of \(\hat{x}_{3}\) which did not appear in the previous analysis.
Proposition 6.1
In the setting of Case (ii), there exists \(\hat{x}_{3}>\hat{x}_{2}\) such that \(c(x)=0\) for \(x\in [\hat{x}_{3},\infty )\).
Proof
We argue by way of contradiction and assume \(c(x)>0\) for all \(x\ge \hat{x}_{2}\). In particular, let us first assume the stronger requirement that there exists \(\theta >0\) such that \(c(x)\ge \theta \) for all \(x\ge \hat{x}_{2}\). Consider the value function \(v(0,x)\) for \(x>m>\hat{x}_{2}\) and a fixed \(m\). For \(\tau _{m}=\inf \{t\ge 0:X^{x}_{t}\le m\}\) and letting \(\tau ^{*}\) be optimal for \(v(0,x)\), we have \(\tau ^{*}\ge \theta \wedge \tau _{m}\) ℙ-a.s. Using this observation, we get

On the event \(\{\tau ^{*}<\tau _{m}\}\), we have \(\tau ^{*}<\tau ^{\dagger }\) and \(\tau ^{*}\ge \theta \). Moreover, on that event, \(h(X^{x}_{\tau ^{*}\wedge \tau ^{\dagger }})\le h(m)\) since \(h\) is decreasing (see (2.13)) and \(X^{x}_{\tau ^{*}\wedge \tau ^{\dagger }}\ge m\). Recalling that \(h\) is positive and bounded by 1, we obtain the upper bound

Letting \(x\uparrow \infty \), we have \(\mathbb{P}_{x}[\tau _{m}\le T]\downarrow 0\). Then letting \(m\to \infty \), we also have \(h(m)\downarrow \alpha \gamma \) so that
The latter contradicts \(v(0,x)\ge h(x)\ge \alpha \gamma \) for all \(x\in \mathbb{R}_{+}\) (recall (2.12)). Hence we cannot have \(c(x)\ge \theta \) on \([\hat{x}_{2},\infty )\).
Now we prove that indeed it cannot happen that \(c(x)>0\) on \([\hat{x}_{2},\infty )\). By way of contradiction, assume the latter holds. For \(\theta >0\), let us introduce the auxiliary problem with value function
As \(h\) and the process \(X\) are time-homogeneous, we have \(v_{\theta }(t,x)=v(t-\theta ,x)\) for all \(t\in [\theta ,T]\) and \(x\in \mathbb{R}_{+}\). In particular, since we are assuming \(c(x)>0\) for \(x\ge \hat{x}_{2}\), the optimal stopping boundary for the auxiliary problem is \(c_{\theta }(x)=\theta +c(x)\) for \(x\ge \hat{x}_{2}\). Hence \(c_{\theta }(x)\ge \theta \) for all \(x\ge \hat{x}_{2}\). Then by the same argument as above with \(v_{\theta }(0,x)\) instead of \(v(0,x)\), we reach again a contradiction. □
Case (i) can be formally interpreted as the limiting situation of Case (ii) with \(\hat{x}_{1}=\infty \). By the same arguments as above, we obtain the analogue of (i) and (ii) in Proposition 5.3, but with \(c(x)=0\) for \(x\ge x_{2}\) therein and \(c(x_{2}-)=0\). Once again, continuity of the boundary follows from Theorem 5.11.
The presence of management fees paid at a constant (proportional) rate reduces the incentive created by the bonus mechanisms in the policy. That is why we observe an upper exercise boundary at which the policyholder surrenders the contract when the expected gains from staying in the contract (and collecting the bonus rate) are outweighed by the expected cost of future management fees (see Fig. 4).
References
Andreatta, G., Corradin, S.: Valuing the surrender options embedded in a portfolio of Italian life guaranteed participating policies: a least squares Monte Carlo approach. In: Real Option Theory Meets Practice, 8th Annual International Conference, Montréal Canada, June 17–19 (2004). Available online at www.realoptions.org/papers2004/Corradin031015.pdf
Bacinello, A.R.: Fair valuation of a guaranteed life insurance participating contract embedding a surrender option. J. Risk Insur. 70, 461–487 (2003)
Bacinello, A.R., Biffis, E., Millossovich, P.: Pricing life insurance contracts with early exercise features. J. Comput. Appl. Math. 233, 27–35 (2009)
Bass, R.F.: Diffusions and Elliptic Operators. Springer, New York (1998)
Bayraktar, E., Xing, H.: Analysis of the optimal exercise boundary of American options for jump diffusions. SIAM J. Math. Anal. 41, 825–860 (2009)
Bensoussan, A., Lions, J.L.: Applications of Variational Inequalities in Stochastic Control. North-Holland, Amsterdam (1982)
Cannon, J.R.: The One-Dimensional Heat Equation. Cambridge University Press, Cambridge (1984)
Chen, X., Chadam, J.: A mathematical analysis of the optimal exercise boundary for American put options. SIAM J. Math. Anal. 38, 1613–1641 (2007)
Cheng, C., Li, J.: Early default risk and surrender risk: impacts on participating life insurance policies. Insur. Math. Econ. 78, 30–43 (2018)
Chu, C.C., Kwok, Y.K.: Pricing participating policies with rate guarantees. Int. J. Theor. Appl. Finance 9, 517–532 (2006)
Dai, M., Yi, F.: Finite-horizon optimal investment with transaction costs: a parabolic double obstacle problem. J. Differ. Equ. 246, 1445–1469 (2009)
De Angelis, T.: A note on the continuity of free-boundaries in finite-horizon optimal stopping problems for one-dimensional diffusions. SIAM J. Control Optim. 53, 167–184 (2015)
De Angelis, T., Kitapbayev, Y.: On the optimal exercise boundaries of swing put options. Math. Oper. Res. 43, 252–274 (2018)
De Angelis, T., Peskir, G.: Global \(C^{1}\) regularity of the value function in optimal stopping problems. Ann. Appl. Probab. 30, 1007–1031 (2020)
De Angelis, T., Stabile, G.: On the free boundary of an annuity purchase. Finance Stoch. 23, 97–137 (2019)
Du Toit, J., Peskir, G.: The trap of complacency in predicting the maximum. Ann. Appl. Probab. 35, 340–365 (2007)
Ekström, E., Vaicenavicius, J.: Optimal stopping of a Brownian bridge with an unknown pinning point. Stoch. Process. Appl. 130, 806–823 (2020)
Fard, F.A., Siu, T.K.: Pricing participating products with Markov-modulated jump-diffusion process: an efficient numerical PIDE approach. Insur. Math. Econ. 53, 712–721 (2013)
Friedman, A.: Partial Differential Equations of Parabolic Type. Prentice Hall, Englewood Cliffs (1964)
Friedman, A.: Parabolic variational inequalities in one space dimension and smoothness of the free boundary. J. Funct. Anal. 18, 151–176 (1975)
Friedman, A.: Variational Principles and Free-Boundary Problems. Wiley, New York (1982)
Grosen, A., Jørgensen, P.L.: Fair valuation of life insurance liabilities. The impact of interest rate guarantees, surrender options and bonus policies. Insur. Math. Econ. 26, 37–57 (2000)
Karatzas, I., Shreve, S.: Brownian Motion and Stochastic Calculus, 2nd edn. Springer, Berlin, Heidelberg, New York (1991)
Ladyzenskaja, O.A., Solonnikov, V.A., Ural’ceva, N.N.: Linear and Quasilinear Equations of Parabolic Type. Am. Math. Soc., Providence (1967)
Lions, P.L., Sznitman, A.S.: Stochastic differential equations with reflecting boundary conditions. Commun. Pure Appl. Math. 37, 511–537 (1984)
Nelson, D.B., Ramaswamy, K.: Simple binomial processes as diffusion approximations in financial models. Rev. Financ. Stud. 3, 393–430 (1990)
Nolte, S., Schneider, J.C.: Don’t lapse into temptation: a behavioral explanation for policy surrender. J. Bank. Finance 79, 12–27 (2017)
Peskir, G., Shiryaev, A.N.: Optimal Stopping and Free-Boundary Problems. Lectures in Mathematics. ETH Zürich. Birkhäuser, Basel (2006)
Protter, P.E.: Stochastic Integration and Differential Equations, 2nd edn. Springer, Berlin, Heidelberg, New York (2004)
Rogers, L.C.G., Williams, D.: Diffusions, Markov Processes and Martingales, vol. 2, 2nd edn. Cambridge University Press, Cambridge (2000)
Shanahan, B., Fard, F.A., van der Hoek, J.: Pricing participating policies under the Meixner process and stochastic volatility. Scand. Actuar. J. 2017(7), 559–583 (2017)
Siu, T.K.: Fair valuation of participating policies with surrender options and regime switching. Insur. Math. Econ. 37, 533–552 (2005)
Stabile, G.: Optimal timing of the annuity purchase: a combined stochastic control and optimal stopping problem. Int. J. Theor. Appl. Finance 9, 151–170 (2006)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by Sapienza University of Rome, research project “Life market: a renewal boost for quantitative management of longevity and lapse risks”, grant no. RM11916B8953F292. T. De Angelis gratefully acknowledges support via EPSRC grant EP/R021201/1, “A probabilistic toolkit to study regularity of free boundaries in stochastic optimal control”.
Appendix
Appendix
Proof of Lemma 5.1
Here we borrow arguments from the proof of De Angelis and Kitapbayev [13, Theorem 1]. To keep notation simple, we set \(X_{t}=X^{x_{\alpha }}_{t}\) everywhere in what follows. From the equality
we deduce that
Notice that \(\pi (\, \cdot \,)\) is bounded on \([x_{\alpha }-\varepsilon ,x_{\alpha }+\varepsilon ]\) by a constant \(c_{\pi ,\varepsilon }>0\). Since \(|X_{s\wedge \rho _{\varepsilon }}-x_{\alpha }| \leq \varepsilon \), we get \(1 \ge \varepsilon ^{-p}|X_{s\wedge \rho _{\varepsilon }}-x_{\alpha }|^{p}\) for \(p>0\). Taking expectations and using these two observations gives
The expectation of the absolute value above can be estimated by using the integral form of the SDE for \(X\) and the inequality
for all \(a,b \in \mathbb{R}\). This yields
Now the Burkholder–Davis–Gundy inequality and Doob’s inequality imply that there exists a positive constant \(c_{p}\) such that

Inserting the last inequality into (A.1), we get
for some suitable positive constants \(c_{1}=c_{1}(\varepsilon ,p)\) and \(c_{2}=c_{2}(\varepsilon ,p)\). Since \(p\in (0,1)\), we get for small s > 0 that
because \(\mathbb{P}_{x_{\alpha }} [\rho _{\varepsilon }\leq s]+s^{\frac{1-p}{2}}+s^{ \frac{1+p}{2}}\downarrow 0\) as \(s\to 0\). Given that \(\frac{1+p}{2}\in (\frac{1}{2},1)\), we have \(\lambda (s)>\ell s\) as \(s\downarrow 0\) for any constant \(\ell >0\). This implies the claim of the lemma. □
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chiarolla, M.B., De Angelis, T. & Stabile, G. An analytical study of participating policies with minimum rate guarantee and surrender option. Finance Stoch 26, 173–216 (2022). https://doi.org/10.1007/s00780-022-00471-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00780-022-00471-0
Keywords
- Participating policies
- Minimum rate guarantee
- Surrender option
- Solvency requirement
- Optimal stopping
- Free-boundary problems
- Stop-loss boundary
- Too-good-to-persist boundary