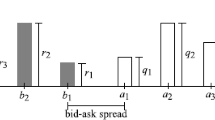Convex duality in optimal investment and contingent claim valuation in illiquid markets

Abstract

This paper develops duality theory for optimal investment and contingent claim valuation in markets where traded assets may be subject to nonlinear trading costs and portfolio constraints. Under fairly general conditions, the dual expressions decompose into three terms, corresponding to the agent’s risk preferences, trading costs and portfolio constraints, respectively. The dual representations are shown to be valid when the market model satisfies an appropriate generalization of the no-arbitrage condition and the agent’s utility function satisfies an appropriate generalization of asymptotic elasticity conditions. When applied to classical liquid market models or models with bid–ask spreads, we recover well-known pricing formulas in terms of martingale measures and consistent price systems. Building on the general theory of convex stochastic optimization, we also obtain optimality conditions in terms of an extended notion of a “shadow price”. The results are illustrated by establishing the existence of solutions and optimality conditions for the nonlinear market models recently proposed in the literature. Our results allow significant extensions including nondifferentiable trading costs which arise, e.g., in modern limit order markets where the marginal price curve is necessarily discontinuous.

1 Introduction

A fundamental problem in financial economics is that of managing investments so that their proceeds cover given liabilities as well as possible. This is important not only in wealth management, but also in the valuation of financial products. Both optimal investment and asset valuation are often analyzed by introducing certain dual variables that appear, e.g., in optimality conditions and valuation operators. Classical references include [29, 30, 41, 18] where the no-arbitrage condition was related to the existence of martingale measures; see [21] for a detailed discussion of the topic. In problems of optimal investment, convex duality has become an important tool in the analysis of optimal strategies; see e.g. [16, 39, 20, 37, 62] and their references.

This article studies convex duality in optimal investment and contingent claim valuation in illiquid markets where one may face nonlinear trading costs and portfolio constraints that hinder transfer of funds between asset classes or through time. Building on the general theory of convex stochastic optimization from [55, 56, 9], we give explicit expressions for the dual objective as well as sufficient conditions for the absence of a duality gap and for the attainment of the dual optimum. The first set of conditions involves multivariate generalizations of the asymptotic elasticity conditions from [39, 64], as well as a condition that generalizes the robust no-arbitrage condition in unconstrained models with proportional transaction costs. The conditions for attainment of the dual optimum are closely related to those of [6, Corollary 5.2] in the context of perfectly liquid market models. The dual solutions provide a natural extension of the notion of a “shadow price” from the unconstrained sublinear market model of [17] to general convex models. Analogously to shadow prices, the optimal dual variables, when they exist, yield pointwise optimality conditions for optimal investment strategies.

Under nonlinear illiquidity effects and nonconical portfolio constraints, the dual objective turns out to be the sum of three nonlinear terms. Like in classical perfectly liquid models, the first term is the conjugate of the primal objective. The two other terms correspond to trading costs and portfolio constraints, respectively. In the classical perfectly liquid model with a cash account, we recover the familiar dual problem over positive multiples of martingale densities. In the absence of a cash account, however, the dual variables become stochastic discount factors that account for uncertainty as well as for the time value of money much like in the numeraire-free conical models of [22, 33, 44, 24, 42, 43, 68]. The introduction of short-sales constraints results in stochastic discount factors that turn the market prices into supermartingales like in [34]. Adding proportional transaction costs, one gets similar conditions for a “shadow price” process that evolves within the bid–ask spread; see [35, 17].

Our model of nonlinear trading costs is closely related to the continuous-time model of [28]. Within the discrete-time framework, we are able to relax the coercivity conditions of [28] so as to allow nondecreasing as well as linear trading costs and thus, to incorporate the classical theory of liquid markets as well. Analogously to [28], we extend the analysis also to contingent claims with physical delivery. It turns out that this is the natural framework of analysis and the results on cash-valued contingent claims are derived from the corresponding results for multivariate claims.

Building on the duality theory of optimal investment, we derive dual expressions for the values of contingent claims that may have several payout dates. As in [52], two widely studied notions of a value will be considered. The first, which we refer to as accounting value, is defined as the least amount of initial cash that is needed to hedge a claim at an acceptable level of risk. In the most risk-averse case, where one does not accept any risk of a loss at maturity, this reduces to the classical superhedging cost. More reasonable versions are obtained by relaxing the superhedging requirement to that of acceptable “risk” associated with the terminal net position. Such valuations have been studied under various names including (but not restricted to) “risk measure” [2, 3], “efficient hedging” [25, 26] or “good-deal bounds” [14]. The second notion of value is that of indifference price which is the natural notion for an agent who considers entering a financial transaction and is interested in how the trade would change her existing financial position; see e.g. [32, 63, 13] and their references.

Dual expressions for the accounting values turn out to have the same general structure as in “good-deal bounds” studied, e.g., in [33] and [14]. The dual representation may also be seen as a multiperiod generalization of the dual representation of a convex risk measure in illiquid markets. In the case of indifference swap rates, we obtain illiquid discrete-time versions of the pricing formulas derived, e.g., in [45, Sect. 7] and [8, Sect. 4].

2 Optimal investment

Consider a financial market where a finite set $J$ of assets can be traded over the dates $t=0,\ldots,T$. As usual, we model uncertainty and information by a filtered probability space $(\varOmega,\mathcal{F},(\mathcal{F}_{t})_{t=0}^{T},P)$. The cost of buying a portfolio $x\in\mathbb{R}^{J}$ at time $t$ and in state $\omega$ is denoted by $S_{t}(x,\omega)$. We assume that $S_{t}:\mathbb{R}^{J}\times\varOmega\to\overline{\mathbb{R}}$ is an $\mathcal{F}_{t}$-measurable convex normal integrand (see the Appendix) such that $S_{t}(0,\omega)=0$. This abstract specification covers, e.g., proportional transaction costs, as well as instantaneous illiquidity effects one faces, e.g., in limit order markets. In the presence of portfolio constraints, the set of portfolios that can be held over $(t,t+1]$ is denoted by $D_{t}(\omega)\subseteq\mathbb {R}^{J}$. We assume that $D_{t}$ is $\mathcal{F}_{t}$-measurable, closed-convex-valued with $0\in D_{t}(\omega)$; see the Appendix. We emphasize that we do not assume a priori the existence of a perfectly liquid numeraire asset that is free of such constraints. Such models can, however, be treated as special cases of the market model $(S,D)$; see Example 2.3 below. More examples with, e.g., proportional transactions and specific instances of portfolio constraints can be found in [47, 50, 49, 52]; see also [67, Sect. 1.2] where it was shown how normal integrands arise naturally as models of financial markets.

In a market without perfectly liquid assets, it is important to distinguish between payments at different points in time; see [52, 42, 68] for further discussion. Accordingly, we describe the agent’s preferences over sequences of payments by a convex normal integrand $V$ on $\mathbb{R}^{T+1}\times\varOmega$. More precisely, the agent prefers to make a random sequence $c^{1}$ of payments over another $c^{2}$ if

$$E[V(c^{1})]< E[V(c^{2})], $$

while she is indifferent between the two if the expectations are equal. A possible choice would be

$$ V(c,\omega)=\sum_{t=0}^{T}V_{t}(c_{t},\omega). $$

(2.1)

In general, the function $V$ can be seen as a multivariate generalization of a “loss function” in the sense of [26, Definition 4.111], where a loss function was a nonconstant nondecreasing function on ℝ. Multivariate utility functions have been studied also in [12] where the utility was a function of a portfolio of assets.

We allow random, nondifferentiable, extended real-valued loss functions $V$ but require the following.

Assumption 1

The loss function $V$ is a normal integrand on $\mathbb{R}^{T+1}\times \varOmega$ such that for almost every $\omega\in\varOmega$, the function $V(\cdot,\omega)$ is convex and nondecreasing with respect to the componentwise order of $\mathbb{R}^{T+1}$, $V(0,\omega)=0$, and for every nonzero $c\in\mathbb{R}^{T+1}_{+}$, there exists an $\alpha >0$ such that $V(\alpha c,\omega)>0$.

The last condition in Assumption 2.1 means that the agent is not completely indifferent with respect to nonzero nonnegative payments. It holds in particular if $V$ is of the form (2.1) and each $V_{t}$ is a convex $\mathcal{F}_{t}$-normal integrand on $\mathbb {R}\times\varOmega$ such that $V_{t}(\cdot,\omega)$ is nonconstant and nondecreasing with $V(0,\omega)=0$.

We study optimal investment from the point of view of an agent who has financial liabilities described by a random sequence $c$ of payments to be made over time. We allow $c$ to take arbitrary real values so it can describe endowments as well as liabilities. In particular, $-c_{0}$ may be interpreted as the agent’s initial endowment. The agent’s problem is to find a trading strategy that hedges against the liabilities $c$ as well as possible as measured by $E[V]$. Denoting the linear space of adapted $\mathbb{R}^{J}$-valued trading strategies by $\mathcal{N}$, we can write the problem as

$$ \mathop{\mathrm{minimize}} E\big[V\big(S(\Delta x)+c\big)\big]\qquad\mathop{\mathrm{over}}x\in{\mathcal{N}}_{D}, $$

(ALM)

where $\mathcal{N}_{D}:=\{x\in{\mathcal{N}}\,:\, x_{t}\in D_{t}\ \forall t\ P\text{-a.s.}\}$ is the set of feasible trading strategies, $\Delta x$ is the process of the increments $\Delta x_{t}:=x_{t}-x_{t-1}$, while $S(\Delta x)$ denotes the process $(S_{t}(\Delta x_{t}))_{t=0}^{T}$ of associated trading costs and $x_{-1}:=0$. Here and in what follows, we define the expectation of a measurable function as $+\infty$ unless the positive part is integrable. For any $z\in\mathbb{R}^{J\times (T+1)}$ and $c\in\mathbb{R}^{T+1}$, we set $V(S(z,\omega )+c,\omega):=+\infty$ unless¹ $z_{t}\in\mathop{\mathrm {dom}} S_{t}(\cdot,\omega)$ for all $t$. Thus, (ALM) incorporates the constraint $\Delta x_{t}\in \mathop{\mathrm {dom}} S_{t}$ almost surely for all $t$, i.e., there may be limits on traded amounts. Assumption 2.1 guarantees that the objective of (ALM) is a well-defined convex function on $\mathcal {N}$; see Corollary A.2 in the Appendix. We assume that $D_{T}(\omega)=\{0\}$, i.e., the agent is required to close all positions at time $T$.

Throughout this paper, we denote the optimum value of ( ALM ) by $\varphi(c)$. The value function $\varphi$ is an extended real-valued function on a linear space ℳ of random sequences of payments. We deviate here slightly from [52] by not insisting that the elements of ℳ are adapted nor that every adapted sequence belongs to ℳ.

Problem (ALM) covers discrete-time versions of many more traditional models of optimal investment that have appeared in the literature. In particular, (ALM) can be interpreted as an optimal consumption–investment problem with random endowment $-c_{t}$ and consumption $-S_{t}(\Delta x_{t})-c_{t}$ at time $t$. Our formulation extends the more common formulations with a perfectly liquid numeraire asset; see e.g. the continuous-time models in [16, 37] and their references. Problem (ALM) is close to [68, Sect. 2], where optimal investment–consumption was studied in a linear discrete-time market model without a perfectly liquid numeraire asset.

By allowing extended real-valued loss functions $V$, we can treat superhedging problems and problems with explicit budget constraints as special cases of (ALM). Indeed, when² $V=\delta_{\mathbb {R}^{T+1}_{-}}$, we have $\varphi=\delta_{\mathcal{C}}$, where

$${\mathcal{C}}:= \{c\in{\mathcal{M}}\,:\,\exists x\in{\mathcal{N}}_{D} \text{ with }S(\Delta x) + c\le0\} $$

is the set of claims that can be superhedged without a cost.

Example 2

When $V$ is of the form

$$V(c,\omega)= \textstyle\begin{cases} V_{T}(c_{T},\omega) & \quad\text{if $c_{t}\le0$ for $t< T$},\\ +\infty&\quad\text{otherwise}, \end{cases} $$

problem (ALM) can be written with explicit budget constraints as

$$ \begin{aligned} &\mathop{\mathrm{minimize}} E[V_{T}(S_{T}(\Delta x_{T})+c_{T})] \qquad \mathop{\mathrm{over}}x\in{\mathcal{N}}_{D}\\ &\mathop{\mathrm{subject\ to}}S_{t}(\Delta x_{t})+c_{t}\le0,\qquad\forall t< T P\text{-a.s}. \end{aligned} $$

(2.2)

This is an illiquid version of the classical problem of maximizing expected utility of terminal wealth. Indeed, since $x_{T}{=}0$ for all $x\in{\mathcal{N}}_{D}$, we have $S_{T}(\Delta x_{T}){=}S_{T}(-x_{T-1})$, which is the cost of closing all positions at time $T$. Alternatively, one may interpret $-S_{T}(-x_{T-1})$ as the liquidation value of $x_{T-1}$.

In models with perfectly liquid cash, problem (2.2) can be written in a more familiar form.

Example 3

Models with perfectly liquid cash correspond to

$$S_{t}(x,\omega) = x^{0} + \tilde{S}_{t}(\tilde{x},\omega)\quad\text{and}\quad D_{t}(\omega) = \mathbb{R}\times\tilde{D}_{t}(\omega), $$

where $x=(x^{0},\tilde{x})$ and $\tilde{S}$ and $\tilde{D}$ are the trading cost and the constraints for the remaining risky assets $J\setminus\{ 0\}$. When $c$ is adapted, one can then use the budget constraint in problem (2.2) to substitute out the cash investments $x^{0}$ from the problem formulation much like in [15, Eq. (2.9)] and [28, Eq. (4)]. Recalling that $x_{T}=0$ for $x\in{\mathcal{N}}_{D}$, problem (2.2) can thus be written as

$$\begin{aligned} &\mathop{\mathrm{minimize}} E\bigg[V_{T}\bigg(\sum_{t=0}^{T}\tilde{S}_{t}(\Delta\tilde{x}_{t})+\sum_{t=0}^{T}c_{t}\bigg)\bigg]\qquad\mathop {\mathrm{over}}x\in{\mathcal{N}}_{D}. \end{aligned} $$

If one specializes further to the perfectly liquid market model where $\tilde{S}_{t}(\tilde{x})= \tilde{s}_{t}\cdot \tilde{x}_{t}$ for a unit price process $\tilde{s}$ that is independent of the trades, one can express the accumulated trading costs in the objective as a stochastic integral of $\tilde{x}$ with respect to $\tilde{s}$, thus recovering a discrete-time version of the classical formulation from, e.g., [39, 20, 40, 7, 8]. Note that in [39, 40, 7], the financial position of the agent was described solely in terms of an initial endowment $w\in\mathbb{R}$ without future liabilities. This corresponds to $c_{0}=-w$ and $c_{t}=0$ for $t>0$. Allowing a general $c\in {\mathcal{M}}$ is the key to the valuation of contingent claims.

3 Contingent claim valuation

This section gives a short review of contingent claim valuation under illiquidity; see [52] for further discussion. The accounting value of the liability of delivering a contingent claim $c\in{\mathcal{M}}$ is defined in terms of the value function $\varphi$ of (ALM) as

$$\pi^{0}_{s}(c) := \inf\{\alpha\in\mathbb{R}\,:\,\varphi(c-\alpha p^{0})\le0\}, $$

where $p^{0}\in{\mathcal{M}}$ is given by $p^{0}_{0}=1$ and $p^{0}_{t}=0$ for $t>0$. The accounting value gives the least amount of initial cash needed to hedge the claim $c$ at an acceptable level of risk as measured by $E[V]$. This extends the notion of “efficient hedging” with minimal shortfall risk from [26, Sect. 8.2] to illiquid markets and claims with multiple payout dates. Alternatively, $\pi ^{0}_{s}(c)$ can be seen as an extension of a “risk measure” from [2] to markets without a perfectly liquid “reference asset”. The function $\pi^{0}_{s}:\mathcal{M}\to\overline{\mathbb{R}}$ is convex and nondecreasing with respect to the pointwise ordering on ℳ. It also has a translation property that extends the one proposed in [2]; see the remarks after [52, Theorem 3.2]. A comprehensive study of risk measures with general translation properties can be found in [43]. Applications of $\pi^{0}_{s}$ in pension insurance are studied in [31]. While $\pi^{0}_{s}(c)$ gives the least amount of initial cash required to construct an acceptable hedging strategy for a liability $c\in{\mathcal{M}}$, the number

$$\pi^{0}_{\ell}(c) := \sup\{\alpha\in\mathbb{R}\,:\,\varphi(\alpha p^{0}-c)\le0\} $$

gives the greatest initial payment one could cover at an acceptable level of risk (by shorting traded assets at time $t=0$ and dynamically trading to close positions by time $t=T$) when receiving $c\in{\mathcal{M}}$. We call $\pi^{0}_{\ell}(c)$ the accounting value of an asset $c\in{\mathcal{M}}$. Clearly, $\pi^{0}_{\ell}(c)=-\pi ^{0}_{s}(-c)$. Accounting values for assets are relevant, e.g., in banks whose assets are divided into a trading book and a banking book. Assets in the banking book are typically illiquid assets without secondary markets. The above definition of $\pi^{0}_{\ell}(c)$ gives a market-consistent, hedging-based value for such assets.

The second notion of a “value” considered in this paper extends the notion of indifference price from [32]. The indifference swap rate of exchanging a claim $c\in{\mathcal{M}}$ for a multiple of a premium sequence $p\in{\mathcal{M}}$ is defined as

$$\pi_{s}(\bar{c},p;c) := \inf\{\alpha\in\mathbb{R}\,:\, \varphi(\bar{c}+c-\alpha p)\le\varphi(\bar{c})\}, $$

where $\bar{c}\in{\mathcal{M}}$ describes the agent’s initial liabilities. The interpretation is that the indifference swap rate gives the least swap rate that would allow the agent to enter the swap contract without worsening her position as measured by the optimum value of (ALM). While accounting values are important in accounting and financial supervision, indifference swap rates are more relevant in trading. The indifference swap rate for taking the other side (“long position”) of the swap contract is given analogously by

$$\pi_{\ell}(\bar{c},p;c) := \sup\{\alpha\in\mathbb{R}\,:\, \varphi (\bar{c}-c+\alpha p)\le\varphi(\bar{c})\}. $$

Note that when $c=(0,\ldots,0,c_{T})$ and $p=p^{0}$, the indifference swap rate reduces to the familiar notion of indifference price.

The following simple facts are from [52] where it was assumed that ℳ consists of adapted sequences and that the agent’s preferences have a time-separable structure. The arguments and the conclusions given there go through unchanged in the present setting. The value function can be expressed as

$$\varphi(c) = \inf_{d\in{\mathcal{C}}}E[V(c-d)]. $$

The functions $\varphi$, $\pi^{0}_{s}$ and $\pi_{s}(\bar{c},p;\cdot)$ are convex functions on ℳ, and they are nonincreasing in the directions of the recession cone

$${\mathcal{C}}^{\infty}:= \{c\in{\mathcal{M}}\,:\,\bar{c} + \alpha c\in {\mathcal{C}}\ \forall\bar{c}\in{\mathcal{C}}, \alpha>0\} $$

of $\mathcal{C}$. Clearly, $\mathcal{C}^{\infty}$ is a convex cone and $\mathcal{C}^{\infty}\subseteq{\mathcal{C}}$ with equality (recall that $0\in{\mathcal{C}}$ since $S_{t}(0)=0$ and $0\in D_{t}$ almost surely, by assumption) when $\mathcal{C}$ is a cone (as is the case, e.g., under proportional transaction costs and conical constraints). Corollary 5.8 below gives an explicit expression for $\mathcal{C}^{\infty}$ in terms of the market model $(S,D)$.

The accounting values can be bounded between the super- and subhedging cost defined by

$$\begin{aligned} \pi^{0}_{\sup}(c) &:= \inf\{\alpha\in\mathbb{R}\,:\,c-\alpha p^{0}\in{\mathcal{C}}\},\\ \pi_{\inf}^{0}(c) &:= \sup\{\alpha\in\mathbb{R}\,:\,\alpha p^{0}-c\in{\mathcal{C}}\}, \end{aligned}$$

respectively. Indeed, if $\pi^{0}_{s}(0)=0$, then by [52, Theorem 3.2],

$$\pi^{0}_{\inf}(c)\le\pi^{0}_{\ell}(c)\le\pi^{0}_{s}(c)\le\pi^{0}_{\sup}(c), $$

with equalities throughout when $c-\bar{\alpha}p^{0}\in{\mathcal{C}}\cap (-\mathcal{C})$ for some $\bar{\alpha}\in\mathbb{R}$, and in this case, $\pi^{0}_{s}(c)=\bar{\alpha}$. Similarly, the indifference swap rates can be bounded by the super- and subhedging swap rates defined by

$$\begin{aligned} \pi_{\sup}(p;c) &:= \inf\{\alpha\in\mathbb{R}\,:\,c-\alpha p\in {\mathcal{C}}^{\infty}\},\\ \pi_{\inf}(p;c) &:= \sup\{\alpha\in\mathbb{R}\,:\,\alpha p-c\in {\mathcal{C}}^{\infty}\}, \end{aligned}$$

respectively. Indeed, if $\pi_{s}(\bar{c},p;0)=0$, then by [52, Theorem 4.1],

$$\pi_{\inf}(p;c)\le\pi_{\ell}(\bar{c},p;c)\le\pi_{s}(\bar{c},p;c)\le \pi_{\sup}(p;c), $$

with equalities throughout if $c-\bar{\alpha}p\in{\mathcal{C}}^{\infty}\cap(-\mathcal{C}^{\infty})$ for some $\bar{\alpha}\in\mathbb{R}$, and in this case, $\pi_{s}(\bar{c},p;c)=\bar{\alpha}$. This last condition extends the classical condition of replicability (attainability) to nonlinear market models. In [42, Sect. 2], elements of $\mathcal{C}^{\infty}\cap(-\mathcal{C}^{\infty})$ are interpreted as “liquid zero cost attainable claims”. Recall that in conical market models, $\mathcal{C}^{\infty}=\mathcal{C}$.

4 Duality in optimal investment

Our overall goal is to derive dual expressions for the value function $\varphi$, the accounting value $\pi^{0}_{s}$ and the indifference swap rate $\pi_{s}(\bar{c},p;\cdot)$, to analyze their properties and to relate them to more specific instances of market models and duality theory that have appeared in the literature. We will use the functional analytic techniques of convex analysis where duality is derived from the notion of a conjugate of a convex function; see [60]. More precisely, we apply the results of [48, 55, 9, 56], where the general conjugate duality framework of Rockafellar was specialized to general convex stochastic optimization problems.

In order to apply conjugate duality in the setting of Sect. 2, we assume from now on that $\mathcal{M}\subseteq L^{0}(\varOmega,\mathcal{F},P;\mathbb{R}^{T+1})$ is in separating duality with another space $\mathcal{Q}\subseteq L^{0}(\varOmega,\mathcal {F},P;\mathbb{R}^{T+1})$ of random sequences under the bilinear form

$$\langle c,q\rangle:= E[c\cdot q], $$

where “⋅” denotes the usual Euclidean inner product. The duality means that $\langle c,q\rangle$ is well defined and finite for all $c\in{\mathcal{M}}$ and $q\in{\mathcal{Q}}$ and that $c=0$ if $\langle c,q\rangle=0$ for all $q\in{\mathcal{Q}}$ (similarly for $q$). We also assume that both ℳ and $\mathcal{Q}$ are decomposable in the sense of [58] and that they are closed under adapted projections. Decomposability means that $c{\mathbb{1}}_A+c^{\prime }{\mathbb{1}}_{\Omega \setminus A}\in \mathcal{M}$ for every $c\in {\mathcal{M}}$, $c'\in L^{\infty}$ and $A\in{\mathcal{F}}$. The adapted projection of $c=(c_{t})_{t=0}^{T}\in{\mathcal{M}}$ is the $(\mathcal {F}_{t})_{t=0}^{T}$-adapted stochastic process $^{a}{c}$ given by $^{a}{c}_{t}:=E_{t}[c_{t}]$. Here and in what follows, $E_{t}$ denotes the conditional expectation with respect to $\mathcal{F}_{t}$. Recall that (see e.g. [11, Lemma 1]) decomposability of ℳ and $\mathcal{Q}$ implies that $L^{\infty}\subseteq{\mathcal{M}}\subseteq L^{1}$ (similarly for $\mathcal{Q}$) and that the pointwise maximum of two elements of ℳ belongs to ℳ. The above setting covers, e.g., classical $L^{p}$-spaces as well as Orlicz spaces (when paired with the associate Morse space).

We denote the space of adapted elements of ℳ and $\mathcal {Q}$ by $\mathcal{M}^{a}$ and $\mathcal{Q}^{a}$, respectively. Since ℳ and $\mathcal{Q}$ are assumed to be closed under adapted projections, $\mathcal{M}^{a}$ and $\mathcal{Q}^{a}$ are in separating duality under $(c,q)\mapsto\langle c,q\rangle$. The elements of $\mathcal{Q}^{a}$ can be interpreted as “stochastic discount factors” (or “state price densities”) that extend the notion of a martingale density from classical market models. In markets without perfectly liquid cash (or other perfectly liquid numeraires), more general dual objects from $\mathcal{Q}^{a}$ are needed in order to bring out the time value of money. In a deterministic setting, the dual variables $q\in {\mathcal{Q}}^{a}$ represent the term structure of interest rates (prices of zero coupon bonds). In [1, Theorem 3.4] and [42, Sect. 3], the dual variables $q\in{\mathcal{Q}}^{a}$ are expressed as products of martingale densities and predictable discount processes; see also [68, Sect. 3.2].

The convex conjugate of $\varphi:\mathcal{M}^{a}\to\overline{\mathbb {R}}$ with respect to the pairing of $\mathcal{M}^{a}$ with $\mathcal {Q}^{a}$ is defined by

$$\varphi^{*}(q) = \sup_{c\in{\mathcal{M}}^{a}}\big(\langle c,q\rangle- \varphi(c)\big). $$

The conjugate of a function on $\mathcal{Q}^{a}$ is defined analogously. If $\varphi$ is closed³ and proper, then $\varphi^{**}=\varphi$; see e.g. [60, Theorem 5]. In other words, we then have the dual representation

$$ \varphi(c) = \sup_{q\in{\mathcal{Q}}^{a}}\big(\langle c,q\rangle- \varphi^{*}(q)\big). $$

(4.1)

If $\varphi$ is not closed, then for some $c\in{\mathcal{M}}^{a}$, the dual optimum value is strictly less than $\varphi(c)$ (there is a “duality gap”). The main result of this section gives an expression for the conjugate $\varphi^{*}$ in terms of the loss function $V$ and the market model $(S,D)$. Section 5 below gives sufficient conditions for the closedness of $\varphi$.

Note that if $V$ is almost surely the indicator function of the nonpositive cone $\mathbb{R}^{T+1}_{-}$, then the value function $\varphi$ coincides with the indicator function $\delta_{\mathcal {C}}$ (of the set $\mathcal{C}$ of claims that can be superhedged without a cost) on $\mathcal{M}^{a}$, and its conjugate $\varphi^{*}$ becomes the support function⁴

$$\sigma_{\mathcal{C}}(q):=\sup_{c\in{\mathcal{C}}}\langle c,q\rangle $$

of $\mathcal{C}$. When $S$ is sublinear (i.e., convex and positively homogeneous) and $D$ is conical, the set $\mathcal{C}$ is a cone as well and $\sigma_{\mathcal{C}}$ becomes the indicator function of the polar cone

$${\mathcal{C}}^{*} := \{q\in{\mathcal{Q}}^{a}\,:\,\langle c,q\rangle\le 0\ \forall c\in{\mathcal{C}}\}. $$

In the classical perfectly liquid market model, the elements of $\mathcal{C}^{*}$ come out as the positive multiples of martingale density processes; see the remarks after Corollary 4.5.

The expression for $\varphi^{*}$ in Theorem 4.3 below applies to loss functions $V$ that exhibit risk aversion with respect to sequences of random payments.

Assumption 1

$E[V(^{a}{c})]\le E[V(c)]$ for all $c\in{\mathcal{M}}$.

Clearly, Assumption 4.1 holds if $\mathcal{F}_{t}=\mathcal{F}$ for all $t$. It holds also if $V$ is of the form (2.1), where each $V_{t}$ is a convex normal $\mathcal{F}_{t}$-integrand such that there exists $q\in{\mathcal{Q}}^{a}$ with $E[V_{t}^{*}(q_{t})]<\infty$ for all $t$. Indeed, in that case, the inequality in Assumption 4.1 is simply Jensen’s inequality for convex normal integrands; see e.g. [48, Corollary 2.1]. At present, we are unaware of interesting cases beyond these two examples.

We use the notation

$$(\alpha S_{t})(x,\omega):= \textstyle\begin{cases} \alpha S_{t}(x,\omega)\quad&\text{if } \alpha>0,\\ \delta_{\mathop{\mathrm{cl}}\mathop{\mathrm{dom}} S_{t}(\cdot,\omega)}(x)\quad&\text{if }\alpha=0. \end{cases} $$

The definition in the case $\alpha=0$ is motivated by the fact that the function $\alpha S_{t}(\cdot,\omega)$ is the epigraphical limit of $\alpha^{\nu}S_{t}(\cdot,\omega)$ as $\alpha^{\nu} \searrow 0$; this follows from [61, Proposition 7.29] and the property that proper closed convex functions are uniformly bounded from below on bounded sets. By [61, Propositions 14.44 and 14.46], $\alpha S$ is a convex normal integrand for every measurable $\alpha\ge0$.

Assumption 2

$S(x,\cdot)\in{\mathcal{M}}^{a}$ for all $x\in\mathbb{R}^{J}$.

Assumption 4.2 is a refinement of the assumption that $S(x,\cdot)\in L^{1}$ for all $x\in\mathbb{R}^{J}$ made in [47]; recall that $\mathcal{M}^{a}\subseteq L^{1}$.

We denote the space of adapted integrable $\mathbb{R}^{J}$-valued processes by $\mathcal{N}^{1}$. To simplify notation in the statements below, we fix a dummy variable $w_{T+1}\in L^{1}(\varOmega,\mathcal {F},P;\mathbb{R}^{J})$. Since $D_{T}\equiv\{0\}$, we have $\sigma_{D_{T}}\equiv0$; so the choice of $w_{T+1}$ does not affect any of the expressions that follow. The proof of the following result is given in Sect. 9.2.

Theorem 3

Under Assumptions 2.1, 4.1 and 4.2, the conjugate of the value function $\varphi$ of (ALM) can be expressed as

$$\varphi^{*}(q) = E[V^{*}(q)] + \inf_{w\in{\mathcal{N}}^{1}}E\bigg[\sum _{t=0}^{T}\big((q_{t}S_{t})^{*}(w_{t}) + \sigma_{D_{t}}(E_{t}[\Delta w_{t+1}])\big)\bigg], $$

where the infimum is attained for every $q\in{\mathcal{Q}}^{a}$.

Note that since $V$ is nondecreasing, we have $\mathop{\mathrm {dom}} V^{*}\subseteq\mathbb{R}^{T+1}_{+}$ almost surely so that $\varphi^{*}(q)=+\infty$ unless $q$ is nonnegative. When $V(\cdot ,\omega)=\delta_{\mathbb{R}^{T+1}_{-}}$ for $P$-almost all $\omega$, Theorem 4.3 gives the following variant of [47, Lemma A.1]. Here and in what follows, $\mathcal{Q}^{a}_{+}$ denotes the nonnegative elements of $\mathcal{Q}^{a}$.

Corollary 4

Under Assumption 4.2,

$$\sigma_{\mathcal{C}}(q) = \inf_{w\in{\mathcal{N}}^{1}}E\bigg[\sum _{t=0}^{T}\big((q_{t}S_{t})^{*}(w_{t}) + \sigma_{D_{t}}(E_{t}[\Delta w_{t+1}])\big)\bigg] $$

for $q\in{\mathcal{Q}}^{a}_{+}$, while $\sigma_{\mathcal{C}}(q)=+\infty$ otherwise, and the infimum is attained for every $q\in{\mathcal{Q}}^{a}$.

Proof

When $V(\cdot,\omega)=\delta_{\mathbb{R}^{T+1}_{-}}$, Assumptions 2.1 and 4.1 clearly hold, and we have $\varphi=\delta _{\mathcal{C}}$ so that $\varphi^{*}=\sigma_{\mathcal{C}}$. Since $V^{*}(\cdot,\omega)=\delta_{\mathbb{R}^{T+1}_{+}}$, Theorem 4.3 gives

$$\varphi^{*}(q) = \inf_{w\in{\mathcal{N}}^{1}}E\bigg[\sum_{t=0}^{T}\big((q_{t}S_{t})^{*}(w_{t}) + \sigma_{D_{t}}(E_{t}[\Delta w_{t+1}])\big)\bigg] $$

for $q\in{\mathcal{Q}}^{a}_{+}$ and $\varphi^{*}(q)=+\infty$ for $q\notin {\mathcal{Q}}^{a}_{+}$. □

Using Corollary 4.4, we can write Theorem 4.3 more compactly as follows.

Corollary 5

Under the assumptions of Theorem 4.3, $\varphi^{*} = E[V^{*} ]+ \sigma_{\mathcal{C}}$.

Corollary 4.5 was given in [51, Lemma 3] under more restrictive assumptions on the loss function. Moreover, the proof of [51, Lemma 3] was based on [48, Theorem 2.2], which suffers from errors that were corrected in [9]; see [53].

When $S$ is sublinear and $D$ is conical, we have $S^{*}_{t}=\delta _{\mathop{\mathrm{dom}} S^{*}_{t}}$, $\sigma_{D_{t}}=\delta _{D^{*}_{t}}$ and $\sigma_{\mathcal{C}}=\delta_{\mathcal{C}^{*}}$, where $\mathcal{C}^{*}$ is the polar cone of $\mathcal{C}$. Under Assumption 4.2, $\mathop{\mathrm{dom}} S_{t}=\mathbb {R}^{J}$ and $(q_{t} S_{t})^{*}=\delta_{q_{t}\mathop{\mathrm{dom}} S^{*}_{t}}$, so Corollary 4.4 gives

$${\mathcal{C}}^{*} =\{q\in{\mathcal{Q}}^{a}_{+}\,:\, \exists w\in {\mathcal{N}}^{1}\text{ with }w_{t}\in q_{t}\mathop{\mathrm{dom}} S^{*}_{t}, E_{t}[\Delta w_{t+1}]\in D_{t}^{*}\ P\text{-a.s.}\}. $$

The polar of $\mathcal{C}$ can also be written as⁵

$${\mathcal{C}}^{*} =\{q\in{\mathcal{Q}}^{a}_{+}\,:\, \exists s\in {\mathcal{N}}^{1}\text{ with }s_{t}\in\mathop{\mathrm{dom}} S^{*}_{t}, E_{t}[\Delta(q_{t+1}s_{t+1})]\in D_{t}^{*}\ P\text{-a.s.}\}. $$

In unconstrained linear models with $S_{t}(x,\omega)=s_{t}(\omega)\cdot x$ and $D_{t}(\omega)=\mathbb{R}^{J}$, we have $\mathop{\mathrm {dom}} S^{*}_{t}=\{s_{t}\}$ and $D_{t}^{*}(\omega)=\{0\}$ so that

$${\mathcal{C}}^{*} = \{q\in{\mathcal{Q}}^{a}_{+}\,:\, \text{$qs$ is a martingale}\}, $$

in consistency with [68, Definition 2.2] in the context of numeraire-free linear models. In unconstrained models with bid–ask spreads, $\mathop{\mathrm{dom}} S^{*}_{t}$ is the cube $[s^{-}_{t},s^{+}_{t}]$ and

$${\mathcal{C}}^{*} = \{q\in{\mathcal{Q}}^{a}_{+}\,:\, \exists s\in {\mathcal{N}}\text{ such that } s^{-}_{t}\le s_{t}\le s^{+}_{t}\text{ and }qs\text{ is a martingale}\}. $$

The processes $s$ above correspond to “shadow prices” in the sense of [17]; see Sect. 7 for more details on this. When short selling is prohibited, i.e., when $D_{t}=\mathbb{R}^{J}_{+}$, the condition $E_{t}[\Delta(q_{t+1}s_{t+1})]\in D_{t}^{*}$ means that $qs$ is a supermartingale. In models with perfectly liquid cash (see Example 2.3), the elements of $\mathcal{C}^{*}$ can be expressed as

$${\mathcal{C}}^{*} = \{q\in{\mathcal{Q}}^{a}_{+}\,:\, \exists Q\in {\mathcal{P}}, \alpha\ge0\text{ with } q_{t}=\alpha E_{t}[dQ/dP]\}, $$

where $\mathcal{P}:= \{Q\ll P\,:\,\exists\tilde{s}\in\tilde {\mathcal{N}}\text{ with }\tilde{s}_{t}\in\mathop{\mathrm{dom}} \tilde{S}^{*}_{t}, E^{Q}_{t}[\Delta\tilde{s}_{t+1}]\in\tilde{D}^{*}_{t}\ Q\text{-a.s.}\}$ and $\tilde{\mathcal{N}}$ denotes the set of adapted $\mathbb{R}^{J\setminus\{0\}}$-valued processes. In unconstrained models, $\mathcal{P}$ is the set of absolutely continuous probability measures $Q$ that admit martingale selectors of $\mathop{\mathrm {dom}} S^{*}_{t}$. In the classical linear model with $S_{t}(x,\omega)=s_{t}(\omega)\cdot x$, we simply have $\mathop{\mathrm {dom}} S_{t}^{*}=\{s_{t}\}$ so that the set $\mathcal{P}$ becomes the set of absolutely continuous martingale measures for $s$.

5 Existence of solutions

This section gives conditions for the closedness of $\varphi$ and thus for the validity of the dual representation $\varphi=\varphi^{**}$. The closedness conditions are given in terms of the asymptotic behavior of the market model and the loss function. As usual, the asymptotic behavior of a proper closed convex function $h$ is described by its recession function $h^{\infty}$ which is the closed sublinear function given by the expression

$$h^{\infty}(x)=\sup_{\alpha>0}\frac{h(\alpha x+\bar{x})-h(\bar{x})}{\alpha}, $$

which is independent of the choice of $\bar{x}\in\mathop{\mathrm{dom}} h$; see [59, Theorem 8.5]. Recall also that the recession cone of a closed convex set $C$ is the closed convex cone

$$C^{\infty}:=\bigcap_{\alpha>0}\alpha(C-x), $$

where the intersection is independent of the choice of $x\in C$; see [59, Theorem 8.3].

Given a market model $(S,D)$, it is easily checked that $S_{t}^{\infty}(\cdot,\omega):=S_{t}(\cdot,\omega)^{\infty}$ defines a convex $\mathcal{F}_{t}$-integrand and $D_{t}^{\infty}(\omega):=D_{t}(\omega )^{\infty}$ defines a convex $\mathcal{F}_{t}$-measurable set. This way, every $(S,D)$ gives rise to a conical market model $(S^{\infty},D^{\infty})$. Similarly, a convex loss function $V$ gives rise to a sublinear loss function $V^{\infty}(\cdot,\omega):= V(\cdot,\omega)^{\infty}$. Note that the growth properties in Assumption 2.1 mean that $V^{\infty}(c,\omega)\le0$ for all $c\in\mathbb{R}^{T+1}_{-}$ and $\{ c\in\mathbb{R}^{T+1}_{+}\,:\, V^{\infty}(c,\omega)\le0\}=\{0\}$. Our closedness result requires the following.

Assumption 1

$\{x\in{\mathcal{N}}_{D^{\infty}}\,:\, V^{\infty}(S^{\infty}(\Delta x))\le0\}$ is a linear space.

If the loss function $V$ satisfies

$$ \{c\in\mathbb{R}^{T+1}\,:\,V^{\infty}(c,\omega)\le0\}=\mathbb{R}^{T+1}_{-}, $$

(5.1)

then Assumption 5.1 means that $\{x\in{\mathcal{N}}_{D^{\infty}}\,:\, S^{\infty}(\Delta x)\le0\}$ is a linear space. This generalizes the classical no-arbitrage condition from perfectly liquid market models to illiquid ones. In particular, when $D\equiv\mathbb{R}^{J}$ (no portfolio constraints), the linearity condition becomes a version of the “robust no-arbitrage condition” introduced in [66] for the currency market model of [36]; see [49] for the details and further examples that go beyond no-arbitrage conditions. The linearity of $\{x\in{\mathcal{N}}_{D^{\infty}}\,:\, S^{\infty}(\Delta x)\le0\}$ can be seen as a relaxation of the condition of “efficient friction”, which in the present setting would require this set to reduce to the origin; see [10] for a review of the efficient friction condition and an extension to a model with dividend payments.

Condition (5.1) clearly implies the growth properties in Assumption 2.1. It holds in particular if $V$ is of the form (2.1), where the $V_{t}(\cdot,\omega)$ are univariate nonconstant loss functions with $V_{t}^{\infty}\ge0$. Indeed, since the $V_{t}$ are nondecreasing, we have $V_{t}^{\infty}\le0$ on $\mathbb{R}_{-}$ while the nonconstancy implies $V_{t}^{\infty}(c_{t},\omega)>0$ for $c_{t}>0$; see [59, Corollary 8.6.1]. Condition (5.1) certainly holds if the $V_{t}$ are differentiable and satisfy the Inada conditions

$$\lim_{c\searrow -\infty}V_{t}'(c,\omega)=0\quad\text{and}\quad\lim _{c\nearrow \infty}V_{t}'(c,\omega)=+\infty, $$

since then $V_{t}^{\infty}\equiv\delta_{\mathbb{R}_{-}}$.

We need one more assumption on the loss functions.

Assumption 2

There exists $\lambda\ne1$ such that

$$\lambda\mathop{\mathrm{dom}} E[V^{*}]\subseteq\mathop{\mathrm {dom}} E[V^{*}]. $$

Assumption 5.2 holds in particular if $V$ is bounded from below uniformly in $c\in\mathbb{R}^{T+1}$ by an integrable function, since then $0\in\mathop{\mathrm{dom}} E[V^{*}]$ so that by convexity, one can take any $\lambda\in(0,1)$. Lemma 5.3 below gives more general conditions. The conditions extend the asymptotic elasticity conditions from [39] and [64] to multivariate, random and possibly nonsmooth loss functions. For a univariate loss function $v$, the conditions can be stated as

Various reformulations of the asymptotic elasticity conditions given for deterministic functions in [39, 64] are extended to random and nonsmooth loss functions in the Appendix. The following lemma gives multivariate extensions.

Lemma 3

If the function $v^{*}(\eta,\omega):=V^{*}(\eta y(\omega),\omega)$ satisfies (RAE₊) for every $y\in \mathop{\mathrm{dom}} E[V^{*}]$, then

$$\lambda\mathop{\mathrm{dom}} E[V^{*}]\subseteq\mathop{\mathrm {dom}} E[V^{*}]\qquad\forall\lambda\ge1. $$

If $v^{*}(\eta,\omega)$ satisfies (RAE₋) for every $y\in\mathop {\mathrm{dom}} E[V^{*}]$, then

$$\lambda\mathop{\mathrm{dom}} E[V^{*}]\subseteq\mathop{\mathrm {dom}} E[V^{*}]\qquad\forall\lambda\in(0,1]. $$

Proof

Given $y\in\mathop{\mathrm{dom}} E[V^{*}]$, the normal integrand $h=v^{*}$ satisfies in both cases the assumptions of Lemma A.4 in the Appendix with $\mathbb{1}\in \mathrm{dom}E[h]$. □

Remark 4

In the univariate case, the radial conditions in Lemma 5.3 are satisfied by loss functions that satisfy the corresponding asymptotic elasticity condition. Indeed, if $V^{*}$ satisfies (RAE₊) and $y\in\mathop{\mathrm{dom}} E[V^{*}]$, then $v^{*}(\eta,\omega):=V^{*}(\eta y(\omega),\omega)$ satisfies (RAE₊) with the same $\lambda$ and $C$, but with $\bar{y}$ replaced by ${\mathbb{1}}_{\{y>0\}}\overline{y}/y$. A similar statement holds for (RAE₋).

We are now ready to state the main result of this section. Besides closedness of the value function $\varphi$ and the existence of optimal trading strategies, it gives an explicit expression for the recession function of $\varphi$. These results turn out to be useful in the analysis of valuations of contingent claims in Sect. 8. The proof of the following result is given in Sect. 9.2.

Theorem 5

Let Assumptions 2.1, 5.1 and 5.2 hold and assume that

$$E[V^{*}(q)] + \inf_{w\in{\mathcal{N}}^{1}}E\bigg[\sum_{t=0}^{T}\big((q_{t}S_{t})^{*}(w_{t}) + \sigma_{D_{t}}(E_{t}[\Delta w_{t+1}])\big)\bigg]< \infty $$

for some $q\in{\mathcal{Q}}$. Then $\varphi$ is $\sigma(\mathcal {M}^{a},\mathcal{Q}^{a})$-closed in $\mathcal{M}^{a}$, the infimum in (ALM) is attained, and

$$\varphi^{\infty}(c) = \inf_{x\in{\mathcal{N}}_{D}}E\big[V^{\infty}\big(S^{\infty}(\Delta x)+c\big)\big] $$

for all $c\in{\mathcal{M}}^{a}$.

Under the assumptions of Theorem 4.3, the last assumption in Theorem 5.5 holds in particular if $\varphi^{*}$ is proper. The assumption that $\varphi^{*}$ be proper holds automatically if $V$ is bounded from below by an integrable function, since then $\varphi$ is bounded as well so that $\varphi^{*}(0)<\infty$. If $V$ is unbounded from below, the properness of $\varphi^{*}$ is a more delicate matter. In the classical linear model, this holds if there exists a martingale measure $Q\ll P$ with a density process $q\in{\mathcal{Q}}^{a}$ with $E[V^{*}(q)]<\infty$. This is analogous to Assumption 1 of [65] where the market was assumed perfectly liquid and the dual problem was formulated over equivalent martingale measures. In general, properness of $\varphi^{*}$ is equivalent to $\varphi$ being bounded from below on a Mackey neighborhood⁶ $U$ of the origin. Indeed, since $x=0$ superhedges $c=0$, we have $\varphi(0)\le 0$ so that the lower boundedness means that the lower semicontinuous hull of $\varphi$ is finite at the origin, which by [60, Theorems 4 and 5] is equivalent to $\varphi^{*}$ being proper. This certainly holds if $\varphi$ is finite and continuous at the origin. Sufficient conditions for that are given in Sect. 7.

We illustrate the use of Theorem 5.5 with two nonlinear market models from the literature.

Example 6

(Çetin and Rogers [15])

Consider Example 2.3 with

$$S_{t}(x,\omega) = x^{0}+s_{t}(\omega)\psi(x^{1}), $$

where $s$ is a strictly positive adapted process and $\psi$ is a real-valued convex function with $\psi(0)=0$. Assuming as in [15] that the function $V_{T}$ is bounded from below, Theorem 5.5 gives the existence of solutions and the lower semicontinuity of the value function as soon as $\{x\in{\mathcal{N}}_{D^{\infty}}\,:\, S^{\infty}_{t}(\Delta x_{t})\le0\}$ is a linear space.

We have

$$S^{\infty}_{t}(x,\omega) = x^{0}+s_{t}(\omega)\psi^{\infty}(x^{1}), $$

where $\psi^{\infty}$ is the recession function of $\psi$. Under Assumption (2.3) of [15], one gets $\psi^{\infty}=\delta _{\mathbb{R}_{-}}$ so that

$$\{x\in{\mathcal{N}}_{D^{\infty}}\,:\, S^{\infty}_{t}(\Delta x_{t})\le0\} = \{x\in{\mathcal{N}}_{D^{\infty}}\,:\,\Delta x_{t}^{0}\le0, \Delta x_{t}^{1}\le 0\}. $$

Since $x_{-1}=0$ by definition and $x_{T}=0$ for $x\in{\mathcal {N}}_{D^{\infty}}$, this set reduces to the origin so that the linearity condition holds. We thus obtain the existence of solutions without imposing the extra conditions used in [15]. Moreover, we also allow portfolio constraints.

Example 7

(Guasoni and Rásonyi [28])

Consider Example 2.3 with

$$S_{t}(x,\omega) = x^{0} + s_{t}(\omega)x^{1} + G_{t}(x^{1},\omega), $$

where $G_{t}$ is a nonnegative $\mathcal{F}_{t}$-measurable convex normal integrand. This is a discrete-time version of the model studied in [28]. If the function $V_{T}$ is bounded from below, then Theorem 5.5 gives the existence of solutions and the lower semicontinuity of the value function as soon as $\{x\in{\mathcal{N}}_{D^{\infty}}\,:\, S^{\infty}_{t}(\Delta x_{t})\le0\}$ is a linear space.

We have

$$S^{\infty}_{t}(x,\omega) = x^{0} + s_{t}(\omega)x^{1} + G^{\infty}_{t}(x^{1},\omega) $$

so that if $\mathop{\mathrm{dom}} G_{t}^{\infty}(\cdot,\omega )\subseteq\mathbb{R}_{-}$, the linearity condition holds just like in Example 5.6 above. By convexity, $G_{t}(x,\omega)/|x|\le G_{t}^{\infty}(x,\omega)$ whenever $|x|>0$, so that we get the existence of solutions in particular if

$$\lim_{x\to\infty}G_{t}(x,\omega)/|x|=\infty, $$

as conjectured in [28, Remark 2.4] in the continuous-time setting. Again, portfolio constraints present no additional difficulty.

When $V=\delta_{\mathbb{R}^{T+1}_{-}}$, the assumptions of Theorem 5.5 are automatically satisfied so that we obtain the following result on the set $\mathcal{C}$ of claims that can be superhedged without a cost.

Corollary 8

If $\{x\in{\mathcal{N}}_{D^{\infty}}\,:\,S^{\infty}(\Delta x)\le0\}$ is a linear space, then $\mathcal{C}$ is closed and its recession cone can be expressed as

$${\mathcal{C}}^{\infty}=\{c\in{\mathcal{M}}^{a}\,:\,\exists x\in{\mathcal {N}}_{D^{\infty}} \textit{ with } S^{\infty}(\Delta x)+c\le0\}. $$

The first part of Corollary 5.8 was given in [49, Sect. 4], where it was also shown that the linearity condition is implied by the “robust no-arbitrage condition”, which reduces to the classical no-arbitrage condition in the classical perfectly liquid market model. Combined with the Kreps–Yan theorem, this gives a quick proof of the famous Dalang–Morton–Willinger theorem from [18].

The recession cone $\mathcal{C}^{\infty}$ of $\mathcal{C}$ plays an important role in contingent claim valuation; see [52] and Sect. 8 below. In particular, the indifference swap rates are uniquely determined by the market model (and are thus independent of the agent’s preferences $V$ and financial position $\bar{c}$) when $c-\alpha p\in{\mathcal{C}}^{\infty}\cap(-\mathcal{C}^{\infty})$ for some $\alpha\in\mathbb{R}$; see [52, Theorem 4.1]. This generalizes the classical notion of “attainability” to illiquid market models. Accordingly, in general market models, the notion of completeness (attainability of all $c\in{\mathcal{M}}^{a}$) extends to the property of $\mathcal{C}^{\infty}\cap(-\mathcal{C}^{\infty})$ being a maximal linear subspace of $\mathcal{M}^{a}$. The maximality means that if $p\notin{\mathcal{C}}^{\infty}\cap(-\mathcal{C}^{\infty})$, then the linear span of $p\cup(\mathcal{C}^{\infty}\cap(-\mathcal{C}^{\infty}))$ is all of $\mathcal{M}^{a}$. Under the conditions of Theorem 5.5 and the mild additional condition that $V^{\infty}\ge0$, the condition $p\notin{\mathcal{C}}^{\infty}$ turns out to be necessary and sufficient for $\pi_{s}(\bar{c},p;\cdot)$ to be a proper lower semicontinuous function on $\mathcal{M}^{a}$; see Theorem 8.2 below.

6 Dual representation of the optimum value

This section summarizes our findings so far. It gives a dual representation for the value function of (ALM) by combining Theorems 4.3, 5.5 and Corollary 4.4 with the general biconjugate theorem for convex functions; see e.g. [60, Theorem 5].

Theorem 1

If Assumptions 2.1–5.2 hold and $\varphi^{*}$ is proper, then

$$\varphi(c) = \sup_{q\in{\mathcal{Q}}^{a}}\big(\langle c,q\rangle- E[V^{*}(q)] - \sigma_{\mathcal{C}}(q)\big), $$

where $\sigma_{\mathcal{C}}$ is given by Corollary 4.4.

The following example specializes Theorem 6.1 to conical market models with perfectly liquid cash.

Example 2

Consider Example 2.3 and assume that $D$ is conical, $S$ is sublinear, and that $\{x\in{\mathcal{N}}_{D}\,:\, S(\Delta x)\le0\}$ is a linear space (which holds in particular under the robust no-arbitrage condition if there are no constraints; see [49, Sect. 4]). If $V_{T}(\cdot,\omega)$ is a nonconstant, convex loss function satisfying $V^{\infty}\ge0$ and either (RAE₊) or (RAE₋), then

$$\begin{aligned} \varphi(c) &= \sup_{\lambda\ge0}\sup_{Q\in{\mathcal{P}}}\bigg(\lambda E^{Q}\bigg[\sum_{t=0}^{T}c_{t}\bigg]-E\bigg[V_{T}^{*}\Big(\lambda E_{T}\Big[\frac{dQ}{dP}\Big]\Big)\bigg]\bigg) \end{aligned}$$

(see the representations of $\mathcal{C}^{*}$ at the end of Sect. 4). This is analogous to the dual problems derived for continuous-time models, e.g., in [45] or [8]. While these references studied optimal investment with random endowment in perfectly liquid markets, the above applies to illiquid markets in discrete time. In the exponential case

$$V_{T}(c) = \frac{1}{\alpha}(e^{\alpha c}-1), $$

the supremum over $\lambda>0$ is easily found analytically and one gets

$$\begin{aligned} \varphi(c) &= \frac{1}{\alpha}\exp\Bigg(\sup_{Q\in{\mathcal {P}}}\bigg(\alpha E^{Q}\bigg[\sum_{t=0}^{T}c_{t}\bigg] -H(Q|P)\bigg)\Bigg)-\frac{1}{\alpha}, \end{aligned}$$

where $H(Q|P)$ denotes the entropy of $Q$ relative to $P$. This is an illiquid discrete-time version of the dual representation obtained in [20]; see also [5].

Much of duality theory in optimal investment has studied the optimum value as a function of the initial endowment only; see e.g. [39] or [38].

Example 3

(Indirect utilities)

The function $v(c_{0})=\varphi(c_{0},0,\ldots,0)$ gives the optimum value of (ALM) for an agent with initial capital $-c_{0}$ and no future liabilities/endowments. We can express $v$ as

$$ v(c_{0}) = \inf_{d\in{\mathcal{C}}(c_{0})}E[V(d)], $$

(6.1)

where $\mathcal{C}(c_{0}) = \{d\in{\mathcal{M}}^{a}\,:\,(c_{0},0,\ldots ,0)-d\in{\mathcal{C}}\}$ is the set of future endowments needed to risklessly cover an initial payment of $c_{0}$. If $\varphi$ is proper and lower semicontinuous (see Theorem 5.5), the biconjugate theorem gives

$$v(c_{0}) = \sup_{q\in{\mathcal{Q}}^{a}}\big(c_{0}q_{0} - \varphi^{*}(q)\big) = \sup_{q_{0}\in\mathbb{R}}\big(c_{0}q_{0}-u(q_{0})\big), $$

where

$$u(q_{0}) = \inf_{z\in{\mathcal{Q}}^{a}}\{\varphi^{*}(z)\,:\,z_{0}=q_{0}\}. $$

If $\mathcal{C}$ is conical, we can use Corollary 4.5 to write $u$ analogously to (6.1) as

$$u(q_{0}) = \inf_{z\in{\mathcal{Y}}(q_{0})}E[V^{*}(z)], $$

where $\mathcal{Y}(q_{0})=\{z\in{\mathcal{C}}^{*}\,:\, z_{0}=q_{0}\}$. Even if $\varphi$ is closed, there is no reason to believe that $u$ would be lower semicontinuous as well nor that the infimum in its definition is attained. In some cases, however, it is possible to enlarge the set $\mathcal{Y}(q_{0})$ so that the function $u$ becomes lower semicontinuous and the infimum is attained; see [17] for a sublinear two-asset model without constraints.

7 Optimality conditions and shadow prices

Under the assumptions of Theorems 4.3 and 5.5, the optimum value of (ALM) equals that of the dual problem

$$\mathop{\mathrm{minimize}}_{q\in{\mathcal{Q}}^{a}, w\in {\mathcal{N}}^{1}} E\bigg[V^{*}(q) + \sum_{t=0}^{T}\big((q_{t}S_{t})^{*}(w_{t}) + \sigma_{D_{t}}(E_{t}[\Delta w_{t+1}]) - c_{t}q_{t}\big)\bigg]. $$

Indeed, Theorem 5.5 gives the validity of the dual representation (4.1), while Theorem 4.3 gives an expression for the conjugate $\varphi^{*}$. The optimal $q\in{\mathcal {Q}}^{a}$, if any exist, are characterized by the equality $\varphi (c)+\varphi^{*}(q)=\langle c,q\rangle$, which means that $q$ is a subgradient of $\varphi$ at $c$, i.e.,

$$\varphi(c')\ge\varphi(c)+\langle c'-c,q\rangle\quad\forall c'\in {\mathcal{M}}^{a}. $$

Dual solutions $q\in{\mathcal{Q}}^{a}$ can thus be interpreted as marginal prices for the claims $c\in{\mathcal{M}}^{a}$. In particular, if $\varphi$ happens to be Gâteaux-differentiable at $c$, then $q$ is the derivative of $\varphi$ at $c$. We denote the subdifferential, i.e., the set of subgradients, of $\varphi$ at $c\in{\mathcal{M}}^{a}$ by $\partial\varphi(c)$.

Much like in the conjugate duality framework of [60], the dual solutions allow us to write down optimality conditions for the solutions of the primal problem (ALM). Given a set $C$, we denote its normal cone at a point $x\in C$ by

$$N_{C}(x) := \{v\,:\,\langle x'-x,v\rangle\le0\ \forall x'\in C\}. $$

For $x\notin C$, $N_{C}(x):=\emptyset$. As usual, a vector is said to be feasible in an optimization problem if it belongs to the domain of the objective function. The proof of the following result is given in Sect. 9.2.

Theorem 1

Let $c\in{\mathcal{M}}^{a}$. If Assumptions 2.1–5.2 hold and $(q,w)\in{\mathcal{Q}}^{a}\times\mathcal{N}^{1}$ solves the dual, then an $x\in{\mathcal{N}}$ solves (ALM) if and only if it is feasible and

$$\begin{aligned} q &\in\partial V\big(S(\Delta x)+c\big),\\ w_{t}&\in\partial(q_{t}S_{t})(\Delta x_{t}),\\ E_{t}[\Delta w_{t+1}] &\in N_{D_{t}}(x_{t}). \end{aligned}$$

Conversely, if $x$ and $(q,w)$ are a feasible primal–dual pair satisfying the above system, then $x$ solves the primal, $(q,w)$ solves the dual, and $\varphi$ is closed at $c$.

In the classical linear model where $S_{t}(x,\omega)=s_{t}(\omega)\cdot x$, the optimality conditions in Theorem 7.1 simplify to

$$\begin{aligned} q &\in\partial V(s\cdot\Delta x+c),\\ E_{t}[\Delta(qs)_{t+1}] &\in N_{D_{t}}(x_{t}). \end{aligned}$$

In the unconstrained case where $D\equiv\mathbb{R}^{J}$, the last condition means that $qs$ is a martingale. If $D\equiv\mathbb{R}^{J}_{+}$ (short selling is prohibited), it means that $qs$ is a supermartingale.

Remark 2

(Shadow prices)

In general, the last condition in Theorem 7.1 means that $w_{t}=q_{t}\bar{s}_{t}$, where $\bar{s}_{t}\in L^{0}(\varOmega,\mathcal {F}_{t},P;\mathbb{R}^{J})$ is such that

$$\bar{s}_{t}\in\partial S_{t}(\Delta x_{t}). $$

Following [17], we call such a process $\bar{s}$ a shadow price. By [59, Theorem 23.5], we can write this as $\Delta x_{t}\in\partial S^{*}_{t}(\bar{s}_{t})$. If $S$ is positively homogeneous like in [17], this becomes

$$\Delta x_{t}\in N_{\mathop{\mathrm{dom}} S^{*}_{t}}(\bar{s}_{t}). $$

In particular, the optimal strategy trades only when $\bar{s}_{t}\notin \mathop{\mathrm{int}}\mathop{\mathrm{dom}} S^{*}_{t}$, and in that case, the increment $\Delta x_{t}$ belongs to the (outward) normal to $\mathop {\mathrm{dom}} S^{*}_{t}$ at $\bar{s}_{t}$. This extends the complementarity condition from [17, Definition 2.2] to multiple assets and general sublinear trading costs. If moreover $S^{*}(\bar{s})\in {\mathcal{M}}^{a}$ and $\bar{x}$ is optimal in (ALM), then it is optimal also in the linearized problem

$$\mathop{\mathrm{minimize}} E[V(\bar{s}\cdot\Delta x+\bar{c})]\qquad\mathop{\mathrm{over}}x\in{\mathcal{N}}_{D}, $$

where $\bar{c}:=c-S^{*}(\bar{s})$. Indeed, if $\bar{x}$, $(\bar{w},\bar{q})$ are optimal in (ALM) and the dual, we have $S(\Delta\bar{x})+S^{*}(\bar{s})=\bar{s}\cdot\Delta\bar{x}$ by the optimality conditions in Theorem 7.1; so they satisfy the optimality conditions for the linearized model for which they are feasible as well, and so the claim follows from the last part of Theorem 7.1.

The condition $\Delta x_{t}\in N_{\mathop{\mathrm{dom}} S^{*}_{t}}(\bar{s}_{t})$ implies that there is no trading when $\bar{s}$ is in the interior of $\mathop{\mathrm{dom}} S^{*}_{t}$, analogously to the “no-transaction region” described in [19]. Note also that if $S$ happens to be strictly convex, $\partial S^{*}$ is (at most) single-valued (see [59, Theorems 26.1 and 26.1]), so that the shadow price characterizes the optimal trading strategy uniquely.

Section 3 of [17] gives an example where shadow prices do not exist and thus the supremum in the dual representation of $\varphi$ is not attained. The following result gives sufficient conditions for the dual attainment. Recall that the Mackey topology on $\mathcal {M}^{a}$ is the strongest locally convex topology compatible with the pairing with $\mathcal{Q}^{a}$.

Theorem 3

Under the assumptions of Theorem 4.3, the dual optimum is attained if $\varphi$ is bounded from above on a Mackey neighborhood of $c$.

Proof

By Theorem 4.3, the optimal $q\in{\mathcal{Q}}^{a}$ in the dual problem coincide with subgradients of $\varphi$ at $c$, while the infimum over $w\in{\mathcal{N}}^{1}$ is attained for every $q\in {\mathcal{Q}}^{a}$. It thus suffices to show that $\partial\varphi (c)\ne\emptyset$. By [60, Theorem 8], the boundedness condition implies that $\varphi$ is continuous at $c$, which by [60, Theorem 11(a)] implies $\partial\varphi(c)\ne\emptyset$. □

Much like in [6, Corollary 5.2], the dual attainment in $\mathcal{Q}^{a}$ can be guaranteed under appropriate continuity assumptions on the expected loss function $E[V]$. Continuity of a convex function is easier to characterize when the underlying space is barrelled, i.e., when every closed convex absorbing set is a neighborhood of the origin. Indeed, by [60, Corollary 8B], a lower semicontinuous convex function on a barrelled space is continuous throughout the algebraic interior (core) of its domain. On the other hand, by [60, Theorem 11], continuity implies subdifferentiability. Fréchet spaces and in particular Banach spaces are barrelled. We say that $\mathcal{M}^{a}$ is barrelled if it is barrelled with respect to a topology compatible with the pairing with $\mathcal{Q}^{a}$.

To illustrate the above results, we derive necessary and sufficient optimality conditions for the model of Çetin and Rogers [15] and for a discrete-time version of the model of Guasoni and Rásonyi [28]. For the latter, sufficient conditions were given already in [28, Theorem 5.5], while for [15] the conditions below seem new. Moreover, we find that the conditions are not just sufficient, but also necessary in many situations.

Example 4

Consider Example 2.3 and assume that $V_{T}$ is strictly increasing. Writing $w=(w^{0},\tilde{w})$, the optimality conditions mean that $q$ is a strictly positive martingale, $w^{0}=q$, $\Delta x^{0}=\tilde{S}(\Delta\tilde{x})+c$ and

$$\begin{aligned} q_{T} &\in\partial V_{T}\bigg(\sum_{t=0}^{T}\tilde{S}_{t}(\Delta\tilde{x}_{t})+\sum_{t=0}^{T}c_{t}\bigg),\\ \tilde{w}_{t}&\in\partial(q_{t}\tilde{S}_{t})(\Delta\tilde{x}_{t}),\\ E_{t}[\Delta\tilde{w}_{t+1}] &\in N_{\tilde{D}_{t}}(\tilde{x}_{t}). \end{aligned}$$

Since $q>0$, this means that there is an adapted process $z$ such that

$$\begin{aligned} q_{T} &\in\partial V_{T}\bigg(\sum_{t=0}^{T}\tilde{S}_{t}(\Delta\tilde{x}_{t})+\sum_{t=0}^{T}c_{t}\bigg),\\ z_{t} &\in\partial\tilde{S}_{t}(\Delta\tilde{x}_{t}),\\ E_{t}[\Delta(qz)_{t+1}] &\in N_{\tilde{D}_{t}}(\tilde{x}_{t}). \end{aligned}$$

When there are no portfolio constraints, the first condition means that $z$ is a martingale under the measure $Q$ defined by $dQ/dP=q_{T}/E[q_{T}]$. We have thus obtained a discrete-time version of the optimality conditions in [28, Theorem 5.5]. Interestingly, the process $z$ coincides with the derivative of the value function in the dynamic programming recursion in [15, Theorem 4.1]. It should be noted that we have not assumed differentiability of $\tilde{S}_{t}$ as in [15, 28]. This is essential in practice where trading costs are nonsmooth due to, e.g., bid–ask spreads. Moreover, the above optimality conditions apply just as well to models with portfolio constraints on $\tilde{x}$. If one wishes to impose constraints or nonlinear trading costs on the cash position $x^{0}$ as well, one can resort to the general formulation in Theorem 7.1.

The above conditions are not just sufficient, but also necessary for the optimality of an $x\in{\mathcal{N}}$, provided $\mathcal{M}^{a}$ is barrelled, $V_{T}(\sum_{t=0}^{T}c_{t})$ is integrable for every $c\in {\mathcal{M}}^{a}$, and either $\varphi$ or $c\mapsto E[V_{T}(\sum _{t=0}^{T}c_{t})]$ is lower semicontinuous on $\mathcal{M}^{a}$; see the discussion before the example. Sufficient conditions for the lower semicontinuity of $\varphi$ are given in Theorem 5.5.

Proof of statements in Example 7.4

In the model of Example 2.3,

$$\begin{aligned} \partial V(c) &= N_{\mathbb{R}_{-}}(c_{0})\times\cdots\times N_{\mathbb {R}_{-}}(c_{T-1})\times\partial V_{T}(c_{T}),\\ \partial S_{t}(x_{t}) &= \{1\}\times\partial\tilde{S}_{t}(\tilde{x}_{t}),\\ N_{D_{t}}(x) &= \{0\}\times N_{\tilde{D}_{t}}(x). \end{aligned}$$

So the optimality conditions mean that $x$ satisfies the budget constraints, $q$ is a strictly positive martingale and that

$$\begin{aligned} q_{T} &\in\partial V_{T}\big(S_{T}(\Delta x_{T})+c_{T}\big),\\ q_{t}&\big(S_{t}(\Delta x_{t})+c_{t}\big) =0,\qquad t< T,\\ \tilde{w}_{t}&\in\partial(q_{t}\tilde{S}_{t})(\Delta\tilde{x}_{t}),\\ E_{t}[\Delta\tilde{w}_{t+1}] &\in N_{\tilde{D}_{t}}(\tilde{x}_{t}). \end{aligned}$$

As to the necessity, it suffices to show that the dual optimum is attained. By Theorem 7.3, this happens if $\varphi$ is bounded from above on a neighborhood of the origin in $\mathcal{M}^{a}$. Choosing $\tilde{x}=0$ gives

$$\varphi(c) \le E\bigg[V_{T}\bigg(\sum_{t=0}^{T}c_{t}\bigg)\bigg]. $$

The claim now follows from the fact that on a barrelled space, finiteness and lower semicontinuity imply continuity. □

8 Duality in contingent claim valuation

The main results of [52] relate the accounting values and indifference swap rates to no-arbitrage bounds and the classical replication-based values. Section 6 of [52] gives conditions on lower semicontinuity and properness of $\pi^{0}_{s}$ and $\pi_{s}(\bar{c},p;\cdot)$. This section refines those conditions and gives dual expressions for $\pi^{0}_{s}$ and $\pi_{s}(\bar{c},p;\cdot)$. Just like in [47], the properties of the valuations are derived from those of the value function $\varphi$ of the optimal investment problem. We start with accounting values.

8.1 Accounting values

The accounting value $\pi^{0}_{s}$ recalled in Sect. 3 extends the notion of a convex risk measure to sequences of payments and markets without a perfectly liquid cash account. This section extends the analogy by giving dual representations for $\pi^{0}_{s}$ which reduce to the well-known dual representations of risk measures when applied in the single-period setting with perfectly liquid cash. We also give general conditions under which the conjugate (“penalty function”) in the dual representation separates into two components, one corresponding to the market model and the other to the agent’s risk preferences. This can be seen as an extension of a corresponding separation in models with perfectly liquid cash; see e.g. [26, Proposition 4.104].

It is clear from the definition in Sect. 3 that the accounting value of a claim $c\in{\mathcal{M}}^{a}$ can be expressed as

$$\begin{aligned} \pi^{0}_{s}(c) &= \inf\{\alpha\,:\, c-\alpha p^{0}\in{\mathcal{A}}\}, \end{aligned}$$

where $\mathcal{A}=\{c\in{\mathcal{M}}^{a}\,:\,\varphi(c)\le0\}$ consists of financial positions which the agent can cover with an acceptable level of risk (as measured by $E[V]$) given the possibility to trade in the market described by $S$ and $D$. This is analogous to the correspondence between convex risk measures and their acceptance sets in [2], where the financial market is described by a single perfectly liquid asset. Besides the market model, another notable extension here is that acceptance sets consist of sequences of payments instead of payments at a single date; see also [33] and [43, Sect. 2.1].

The dual representation for $\pi^{0}_{s}$ below involves the support function of $\mathcal{A}$ which corresponds to the “penalty function” in the dual representation of a convex risk measure; see [26, Chap. 4] and the references therein. Under mild conditions, the support function separates into two terms: the first is the support function of the set

$${\mathcal{B}}= \{c\in{\mathcal{M}}^{a}\,:\,E[V(c)]\le0\}, $$

while the second is the support function of the set $\mathcal{C}$ of claims that can be superhedged without a cost. While ℬ depends only on the agent’s risk preferences, $\mathcal{C}$ depends only on the market model.

Theorem 1

If $\mathcal{F}_{0}$ is the trivial sigma-field, $V^{\infty}\ge0$ and the assumptions of Theorem 5.5 hold, then the conditions

• (1) $\pi^{0}_{s}$ is proper and lower semicontinuous,

• (2) $\pi^{0}_{s}(0)>-\infty$,

• (3) $p^{0}\notin{\mathcal{C}}^{\infty}$,

• (4) $q_{0}=1$ for some $q\in\mathop{\mathrm {dom}}\sigma_{\mathcal{C}}$,

are equivalent and imply the validity of the dual representation

$$\pi^{0}_{s}(c) = \sup_{q\in{\mathcal{Q}}^{a}}\left\{\langle c,q\rangle- \sigma_{\mathcal{A}}(q): q_{0}=1\right\}. $$

If $\inf\varphi<0$, then under the assumptions of Theorem 4.3, $\sigma_{\mathcal{A}}= \sigma_{\mathcal{B}}+ \sigma _{\mathcal{C}}$ and

$$\sigma_{\mathcal{B}}(q) = \inf_{\alpha>0}\alpha E[V^{*}(q/\alpha)]. $$

Proof

The closedness of $\varphi$ in Theorem 5.5 implies the closedness of $\mathcal{A}$. By Lemma A.3 in the Appendix, the dual representation is then valid under the first two conditions which are both equivalent to $p^{0}\notin{\mathcal{A}}^{\infty}$, which in turn is equivalent to the existence of a $q\in\mathop{\mathrm {dom}}\sigma_{\mathcal{A}}$ with $\langle p^{0},q\rangle=1$. Here, $\langle p^{0},q\rangle=q_{0}$ since $p^{0}=(1,0,\ldots,0)$ and $\mathcal{F}_{0}$ is trivial by assumption. By [57, Theorem 3B], $\mathcal{A}^{\infty}=\{c\in{\mathcal {M}}^{a}\,:\,\varphi^{\infty}(c)\le0\}$. When $V^{\infty}\ge0$, the expression for $\varphi^{\infty}$ in Theorem 5.5 yields

$${\mathcal{A}}^{\infty}=\{c\in{\mathcal{M}}^{a}\,:\,\exists x\in{\mathcal {N}}_{D^{\infty}}\text{ with } S^{\infty}(\Delta x)+c\le0\}, $$

which by Corollary 5.8 equals $\mathcal{C}^{\infty}$. Thus the first two conditions are both equivalent to (3). Another application of Lemma A.3 now implies that (3) is equivalent to (4). This finishes the proof of the first claim.

By Lagrangian duality (see e.g. [60, Theorem 17, Example 1”]), the condition $\inf\varphi<0$ implies

$$\begin{aligned} \sigma_{\mathcal{A}}(q) &= \sup_{c\in{\mathcal{M}}^{a}}\{\langle c,q\rangle\,:\,\varphi(c)\le0\}\\ &= \inf_{\alpha>0}\sup_{c\in{\mathcal{M}}^{a}}\big(\langle c,q\rangle -\alpha\varphi(c)\big)\\ &= \inf_{\alpha>0}\alpha\varphi^{*}(q/\alpha)\\ &= \inf_{\alpha>0}\alpha E[V^{*}(q/\alpha)] + \sigma_{\mathcal{C}}(q), \end{aligned}$$

where the last equality comes from Corollary 4.5 and the fact that $\sigma_{\mathcal{C}}$ is positively homogeneous. By Lagrangian duality again,

$$\begin{aligned} \sigma_{\mathcal{B}}(q) &= \inf_{\alpha>0}\alpha\sup_{c\in {\mathcal{M}}^{a}}\big(\langle c,q/\alpha\rangle-E[V(c)]\big). \end{aligned}$$

Under Assumption 4.1, we have for all $q\in{\mathcal{Q}}^{a}$

$$ \sup_{c\in{\mathcal{M}}^{a}}\big(\langle c,q/\alpha\rangle- E[V(c)]\big) = \sup_{c\in L^{1}}\big(\langle c,q/\alpha\rangle- E[V(c)]\big) =E[V^{*}(q/\alpha)], $$

where the last equality comes from the interchange rule [61, Theorem 14.60]. □

The first part of Theorem 8.1 is analogous to Corollary 1 in [24, Sect. 4.3] which was concerned with risk measures in a general single-period setting. The dual representation in the second part is analogous to the one in [26, Proposition 4.104] in the single-period setting with portfolio constraints and linear trading costs. See also [4, Theorem 3.6], which gives a dual representation for the infimal convolution of two convex risk measures.

When $\mathcal{C}$ is a cone, the dual representation in Theorem 8.1 can be written as

$$\pi^{0}_{s}(c) = \sup\{\langle c,q\rangle- \sigma_{\mathcal{B}}(q) : q\in{\mathcal{C}}^{*}, q_{0}=1\}. $$

If in addition $E[V]$ is sublinear, then $\mathcal{B}=\{c\in{\mathcal {M}}^{a}\,:\,E[V(c)]\le0\}$ is a cone and $\sigma_{\mathcal{B}}=\delta _{\mathcal{B}^{*}}$ (the indicator function of the polar cone), so that we get the more familiar expression

$$ \pi^{0}_{s}(c) = \sup\{\langle c,q\rangle:q\in{\mathcal{C}}^{*}\cap {\mathcal{B}}^{*}, q_{0}=1\}. $$

(8.1)

In the completely risk-averse case where $V=\delta_{\mathbb {R}^{T+1}_{-}}$, we have $\mathcal{B}=\mathcal{M}^{a}_{-}$ and $\mathcal{B}^{*}=\mathcal{Q}^{a}_{+}$. Since $\mathcal{C}^{*}\subseteq{\mathcal{Q}}^{a}_{+}$, we thus recover the dual representation of the superhedging cost; see e.g. [49]. In general, ℬ may be interpreted much like the set of “desirable claims” in the theory of good-deal bounds; see [14] and the references therein. In the dual representation above, the polar cone $\mathcal{B}^{*}$ restricts the set of stochastic discount factors used in the valuation of the claim $c$, thus making the value lower than the superhedging cost. This is simply a dual formulation of the no-arbitrage bound obtained by purely algebraic arguments in [52]; see Sect. 3. The general structure is similar also to the models of “two-price economies” in [23, 42] and their references. In particular, expression (8.1) has the same form as the dual representation of the “ask price” in [42, Sect. 3] which addresses conical markets without perfectly liquid numeraire in the context of finite probability spaces.

While Theorem 8.1 is formulated for short positions, it can be immediately translated to accounting values for long positions through the identity $\pi^{0}_{\ell}(c)=-\pi^{0}_{s}(-c)$. In particular, the dual representation of $\pi^{0}_{\ell}$ in the general case becomes

$$\pi^{0}_{\ell}(c) = \inf_{q\in{\mathcal{Q}}^{a}}\left\{\langle c,q\rangle+ \sigma_{\mathcal{A}}(q)\,:\,q_{0}=1\right\}, $$

while in the conical case,

$$ \pi^{0}_{\ell}(c) = \inf\{\langle c,q\rangle: q\in{\mathcal{C}}^{*}\cap {\mathcal{B}}^{*}, q_{0}=1\}. $$

If we ignore the financial market (by setting $S\equiv0$), the last part of Theorem 8.1 gives a multiperiod extension of [27, Theorem 4.115] to extended real-valued random loss functions. Besides the generality, the convex analytic proof above is considerably simpler.

8.2 Indifference swap rates

This section gives a dual representation for the indifference swap rate $\pi_{s}(\bar{c},p;c)$. The arguments involved are very similar to those in the previous section once we notice that the indifference swap rate can be expressed as

$$\pi_{s}(\bar{c},p;c) = \inf\{\alpha\,:\, c-\alpha p\in{\mathcal {A}}(\bar{c})\}, $$

where $\mathcal{A}(\bar{c})=\{c\in{\mathcal{M}}^{a}\,:\,\varphi(\bar{c}+c)\le\varphi(\bar{c})\}$ is the set of claims that an agent with current financial position $\bar{c}\in{\mathcal{M}}^{a}$ deems acceptable given her risk preferences and ability to trade in the illiquid market described by $S$ and $D$.

Analogously to the dual representation for risk measures and accounting values in the previous section, the dual representation for $\pi _{s}(\bar{c},p;\cdot)$ below involves the support function of $\mathcal {A}(\bar{c})$. Under mild conditions, the support function splits again into two terms. One is still the support function of the set $\mathcal {C}$ of claims that can be superhedged without a cost, but now the second is the support function of the set

$${\mathcal{B}}(\bar{c}) = \{c\in{\mathcal{M}}^{a}\,:\,E[V(\bar{c}+c)]\le \varphi(\bar{c})\}. $$

This is the set of claims an agent with financial position $\bar{c}\in {\mathcal{M}}^{a}$ and risk preferences $E[V]$ would deem at least as desirable as the possibility to trade in a financial market described by $S$ and $D$.

Theorem 2

If the assumptions of Theorem 5.5 are satisfied and $V^{\infty}\ge0$, then for every $\bar{c}\in\mathop{\mathrm{dom}} \varphi$ and $p\in{\mathcal{M}}^{a}$, the conditions

• (1) $\pi_{s}(\bar{c},p;\cdot)$ is proper and lower semicontinuous,

• (2) $\pi_{s}(\bar{c},p;0)>-\infty$,

• (3) $p\notin{\mathcal{C}}^{\infty}$,

• (4) $\langle p,q\rangle=1$ for some $q\in\mathop{\mathrm{dom}} \sigma_{\mathcal{C}}$,

are equivalent and imply the validity of the dual representation

$$\begin{aligned} \pi_{s}(\bar{c},p;c) &= \sup_{q\in{\mathcal{Q}}^{a}}\{\langle c,q\rangle - \sigma_{\mathcal{A}(\bar{c})}(q): \langle p,q\rangle=1\}. \end{aligned}$$

If the above conditions hold for some $\bar{c}\in\mathop{\mathrm {dom}}\varphi$, then they hold for every $\bar{c}\in\mathop {\mathrm{dom}}\varphi$. If $\inf\varphi<\varphi(\bar{c})$, then under the assumptions of Theorem 4.3, $\sigma _{\mathcal{A}(\bar{c})}=\sigma_{\mathcal{B}(\bar{c})}+\sigma_{\mathcal {C}}$, where

$$\sigma_{\mathcal{B}(\bar{c})}(q) = \inf_{\alpha>0}\alpha\big(E[V^{*}(q/\alpha)]-\langle\bar{c},q/\alpha\rangle-\varphi(\bar{c})\big). $$

Proof

The closedness of $\varphi$ in Theorem 5.5 implies the closedness of $\mathcal{A}(\bar{c})$, and then $\mathcal{A}^{\infty}(\bar{c})=\{c\in{\mathcal{M}}^{a}\,:\,\varphi^{\infty}(c)\le0\}$ by [57, Theorem 3B]. The first claim is now proved just like in Theorem 8.1.

By Lagrangian duality, the condition $\inf\varphi<\varphi(\bar{c})$ implies

$$\begin{aligned} \sigma_{\mathcal{A}(\bar{c})}(q) &= \sup_{c\in{\mathcal{M}}^{a}}\{ \langle c,q\rangle\,:\,\varphi(\bar{c} + c)-\varphi(\bar{c})\le0\}\\ &= \inf_{\alpha>0}\sup_{c\in{\mathcal{M}}^{a}}\Big(\langle c,q\rangle -\alpha\big(\varphi(\bar{c} + c)-\varphi(\bar{c})\big)\Big)\\ &= \inf_{\alpha>0}\sup_{c\in{\mathcal{M}}^{a}}\Big(\langle c,q\rangle -\alpha\big(\varphi(c)-\varphi(\bar{c})\big)\Big) - \langle\bar{c},q\rangle\\ &= \inf_{\alpha>0}\alpha\big(\varphi^{*}(q/\alpha)-\varphi(\bar{c})\big) - \langle\bar{c},q\rangle\\ &= \inf_{\alpha>0}\alpha\big(E[V^{*}(q/\alpha)]-\varphi(\bar{c})\big) - \langle\bar{c},q\rangle+ \sigma_{\mathcal{C}}(q), \end{aligned}$$

where the last equality comes from Corollary 4.5 and the fact that $\sigma_{\mathcal{C}}$ is positively homogeneous. By Lagrangian duality again,

$$\begin{aligned} \sigma_{\mathcal{B}(\bar{c})}(q) &= \sup_{c\in{\mathcal{M}}^{a}}\{ \langle c,q\rangle\,:\,E[V(\bar{c}+c)]\le\varphi(\bar{c})\}\\ &= \inf_{\alpha>0}\alpha\big(E[V^{*}(q/\alpha)]-\varphi(\bar{c})\big) - \langle\bar{c},q\rangle, \end{aligned}$$

just like in the proof of Theorem 8.1. □

The structure and assumptions of Theorem 8.2 are essentially the same as those in Theorem 8.1. The main difference is in the interpretations. While the accounting value looks for the least amount of initial cash that allows one to find an acceptable hedging strategy, the indifference swap rate compares two financial positions. The difference is reflected in the definitions of the “acceptance sets” ℬ and $\mathcal{B}(\bar{c})$, where the latter compares claims with the current financial position of a rational agent who has access to financial markets.

Specializing to market models with perfectly liquid cash, we obtain illiquid discrete-time versions of pricing formulas obtained in e.g. [45] and [8].

Example 3

(Numeraire and martingale measures)

Let $p=(1,0,\ldots,0)$ and assume that

$$S_{t}(x,\omega) = x^{0} + \tilde{S}_{t}(\tilde{x},\omega)\quad\text{and}\quad D_{t}(\omega) = \mathbb{R}\times\tilde{D}_{t}(\omega) $$

with a sublinear $\tilde{S}$ and conical $\tilde{D}$ as in Example 2.3. Like at the end of Sect. 4, we can then write the dual representation in terms of probability measures as

$$\begin{aligned} &\pi_{s}(\bar{c},p;c) \\ &\quad= \sup_{y\in{\mathcal{C}}^{*}}\{\langle\bar{c}+c,y\rangle- \sigma _{\mathcal{A}(\bar{c})}(y): \langle p,y\rangle=1\}\\ &\quad= \sup_{Q\in{\mathcal{P}}}\sup_{\alpha>0}\Biggl(E^{Q}\bigg[\sum _{t=0}^{T}(\bar{c}_{t}+c_{t})\bigg]-\alpha\bigg(E\bigg[\sum_{t=0}^{T}v_{t}^{*}\Big(E_{t}\Big[\frac{dQ}{dP}\Big]/\alpha\Big)\bigg]-\varphi(\bar{c})\bigg)\Biggr). \end{aligned}$$

This can be seen as an illiquid discrete-time version of the pricing formulas in [45, Sect. 7] and [8, Sect. 4].

9 Contingent claims with physical delivery

In this section, we study problems of the form

$$ \mathop{\mathrm{minimize}} E\big[V\big(S(\Delta x+\theta)+c\big)\big]\qquad\mathop{\mathrm{over}}x\in{\mathcal{N}}_{D}, $$

(ALM+)

where $\theta$ is an $\mathbb{R}^{J}$-valued process that can be interpreted as a contingent claim with physical delivery (portfolio-valued contingent claim) that the agent has to deliver in addition to the cash-settled claim $c$. Superhedging of contingent claims with physical delivery has been studied, e.g., in [36, 54]. Our formulation is close to [28] who studied optimal investment and superhedging under superlinear trading costs in an unconstrained continuous-time market model with perfectly liquid cash.

We denote the optimum value of (ALM+) by $\bar{\varphi}(\theta ,c)$. Clearly, the value function $\varphi$ of (ALM) is simply the restriction of $\bar{\varphi}(0,\cdot)$ to $\mathcal{M}^{a}$. Combined with some functional analytic arguments, this simple identity allows us to derive the main results of the previous sections from corresponding results on $\bar{\varphi}$. The introduction of the extra parameter $\theta$ in fact simplifies the analysis and provides extra information about (ALM).

9.1 Nonadapted claims

We start by analyzing (ALM+) with possibly nonadapted claims $(\theta,c)$. More precisely, we study the optimum value $\bar{\varphi}(\theta,c)$ of (ALM+) on the space

$${\mathcal{U}}:=L^{\infty}(\varOmega,\mathcal{F},P;\mathbb {R}^{J(T+1)})\times\mathcal{M} $$

of claim processes $u=(\theta,c)$ whose physical component $\theta$ is essentially bounded and whose cash component $c$ belongs to ℳ. In most situations, one is interested in adapted claims, but our formulation allows also situations where the investor may remain unaware of the exact claim amounts until a certain future time (as may happen, e.g., in asset management departments of large financial institutions). The space $\mathcal{U}$ is in separating duality with

$${\mathcal{Y}}:=L^{1}(\varOmega,\mathcal{F},P;\mathbb{R}^{J(T+1)})\times \mathcal{Q} $$

under the bilinear form $\langle u,y\rangle:=E[u\cdot y]$. We split the dual variables $y$ into two processes $w$ and $q$ corresponding to the splitting of $u$ into $\theta$ and $c$. One can thus express the bilinear form as

$$\langle u,y\rangle= \langle\theta,w\rangle+ \langle c,q\rangle. $$

The following result shows that under Assumption 2.1, the conjugate of $\bar{\varphi}$ can be expressed in terms of the loss function and the market model. The proof is given in the Appendix.

Theorem 1

If $V$ satisfies Assumption 2.1, then the conjugate of the value function $\bar{\varphi}$ of (ALM+) with respect to the pairing of $\mathcal{U}$ with $\mathcal{Y}$ can be expressed as

$$\bar{\varphi}^{*}(y) = E\bigg[V^{*}(q) + \sum_{t=0}^{T}\big((q_{t}S_{t})^{*}(w_{t}) + \sigma_{D_{t}}(E_{t}[\Delta w_{t+1}])\big)\bigg]. $$

The next result gives sufficient conditions for the closedness of $\bar{\varphi}$ as well as an expression for the recession function $\bar{\varphi}^{\infty}$. The proof can be found in the Appendix.

Theorem 2

If Assumptions 2.1, 5.1 and 5.2 hold and there exists $y\in{\mathcal{Y}}$ such that

$$E\bigg[V^{*}(q) + \sum_{t=0}^{T}\big((q_{t}S_{t})^{*}(w_{t}) + \sigma _{D_{t}}(E_{t}[\Delta w_{t+1}])\big)\bigg]< \infty, $$

then $\bar{\varphi}$ is $\sigma(\mathcal{U},\mathcal{Y})$-closed in $\mathcal{U}$, the infimum in (ALM+) is attained for all $u\in {\mathcal{U}}$ and

$$\begin{aligned} \bar{\varphi}^{\infty}(u) &= \inf_{x\in{\mathcal{N}}}E\big[V^{\infty}\big(S^{\infty}(\Delta x+\theta)+c\big)\big]. \end{aligned}$$

When $V=\delta_{\mathbb{R}^{J+1}_{-}}$, we have $\bar{\varphi}=\delta_{\bar{\mathcal{C}}}$, where

$$\bar{\mathcal{C}}:=\{(\theta,c)\,:\,\exists x\in{\mathcal {N}}_{D}\text{ with }S(\Delta x+\theta)+c\le0\ P\text{-a.s.}\} $$

is the set of multivariate claim processes that can be superhedged without a cost. The closedness result above can then be seen as a discrete-time version of [28, Proposition 3.5] which addresses unconstrained continuous-time models with perfectly liquid cash. When $V=\delta_{\mathbb{R}^{J+1}_{-}}$, the assumptions of Theorem 9.2 reduce to the requirement that

$$\{x\in{\mathcal{N}}_{D^{\infty}}\,:\, S^{\infty}(\Delta x)\le0\} $$

is a linear space; see the discussion after Assumption 5.1 in Sect. 5. This certainly holds under the superlinear growth condition of [28], which (in the notation of Example 2.3) implies that there is a strictly positive adapted process $H$ such that

$$\tilde{S}_{t}(x,\omega)\ge H_{t}(\omega)|\tilde{x}|^{\alpha}\quad\forall \tilde{x}\in\mathbb{R}^{J}. $$

Indeed, this implies that $\tilde{S}_{t}^{\infty}=\delta_{\{0\}}$, and therefore the linearity condition means that $\{(x^{0},0)\in {\mathcal{N}}_{D}\,:\,\Delta x^{0}\le0\}$ is a linear space. But this is obvious since $x_{-1}=0$ and $D_{T}=\{0\}$. Note that unlike the superlinear growth condition, the linearity condition above does allow cost functions $S$ which are decreasing in some directions, which is quite a natural assumption for assets with free disposal.

Under the assumptions of Theorems 9.1 and 9.2, the optimum value of (ALM+) equals that of the dual problem

$$\mathop{\mathrm{minimize}}_{(w,q)\in{\mathcal{Y}}} E\bigg[V^{*}(q) + \sum_{t=0}^{T}\big((q_{t}S_{t})^{*}(w_{t}) + \sigma_{D_{t}}(E_{t}[\Delta w_{t+1}]) - \theta_{t}\cdot w_{t} - c_{t}q_{t}\big)\bigg]. $$

We know from general conjugate duality theory that the dual solutions are then the subgradients of the value function $\bar{\varphi}$ at $u=(\theta,c)$. Much like in [60], the dual variables can be used to give optimality conditions for the solutions of the primal problem (ALM+). The situation here is slightly different, however, since in (ALM+), the primal solutions are sought over the vector space $\mathcal{N}$ that lacks an appropriate locally convex topology. Applying the optimality conditions derived for convex stochastic optimization in [9, Sect. 3], we obtain the following result. The proof is given in the Appendix.

Theorem 3

If $\bar{\varphi}$ is closed at $(\theta,c)$ and Assumption 2.1 holds, then $x\in{\mathcal{N}}$ solves (ALM+) and $y\in{\mathcal {Y}}$ solves the dual problem if and only if they are feasible and

$$\begin{aligned} E_{t}[\Delta w_{t+1}] &\in N_{D_{t}}(x_{t}),\\ q &\in\partial V\big(S(\Delta x+\theta)+c\big),\\ w_{t}&\in\partial(q_{t}S_{t})(\Delta x_{t}+\theta_{t}). \end{aligned}$$

Conversely, if $x$ and $y$ are a feasible primal–dual pair satisfying the above system, then $x$ solves the primal, $(w,q)$ solves the dual, and $\varphi$ is closed at $(\theta,c)$.

9.2 Adapted claims

When the claim process $(\theta,c)$ is adapted and the loss function $V$ satisfies Assumption 4.1, the above results can be expressed in terms of adapted dual variables. We denote the linear subspaces of adapted processes in $\mathcal{U}$ and $\mathcal{Y}$ by $\mathcal{U}^{a}$ and $\mathcal{Y}^{a}$, respectively. In other words,

$${\mathcal{U}}^{a}:=\mathcal{N}^{\infty}\times\mathcal{M}^{a}\quad\text{and} \quad\mathcal{Y}^{a}:=\mathcal{N}^{1}\times\mathcal{Q}^{a}, $$

where $\mathcal{N}^{\infty}$ and $\mathcal{N}^{1}$ denote the essentially bounded and integrable, respectively, $\mathbb{R}^{J}$-valued adapted processes. Since by assumption ℳ and $\mathcal{Q}$ are closed under adapted projections, we have that $\mathcal{U}^{a}$ and $\mathcal{Y}^{a}$ are in separating duality under the bilinear form defined for $\mathcal{U}$ and $\mathcal{Y}$.

We denote the restriction of $\bar{\varphi}$ to $\mathcal{U}^{a}$ by $\bar{\varphi}_{a}$. Since the relative topology $\sigma(\mathcal{U},\mathcal {Y})$ on $\mathcal{U}^{a}$ coincides with $\sigma(\mathcal{U}^{a},\mathcal {Y}^{a})$, the function $\bar{\varphi}_{a}$ is closed with respect to $\sigma(\mathcal{U}^{a},\mathcal{Y}^{a})$ whenever $\bar{\varphi}$ is closed with respect to $\sigma(\mathcal{U},\mathcal{Y})$. It is immediate from the definition of the recession function that $\bar{\varphi}_{a}^{\infty}$ is simply the restriction of $\bar{\varphi}^{\infty}$ to $\mathcal{U}^{a}$. To restrict the dual variables to $\mathcal{Y}^{a}$, only one simple observation is needed.

If $\psi$ is any functional on $\mathcal{U}$ such that $\psi(^{a}{u})\le\psi(u)$ for all $u\in{\mathcal{U}}$, then for any $y\in {\mathcal{Y}}$,

$$\begin{aligned} \psi^{*}(^{a}{y})= \sup_{u\in{\mathcal{U}}}\big(\langle u,^{a}{y}\rangle- \psi(u)\big) \le\sup_{u\in{\mathcal{U}}}\big(\langle ^{a}{u},y\rangle- \psi(^{a}{u})\big) \le\psi^{*}(y). \end{aligned}$$

In particular, if $V$ satisfies Assumptions 2.1 and 4.1, then by the interchange rule, $E[V^{*}(^{a}{q})]\le E[V^{*}(q)]$ so that $V^{*}$ satisfies Assumption 4.1 as well. The following result shows that Assumption 4.1 is inherited by $\bar{\varphi}^{*}$ and thus by the closure of $\bar{\varphi}$ as well.

Theorem 4

If $V$ satisfies Assumptions 2.1 and 4.1, then $\bar{\varphi}^{*}(^{a}{y})\le\bar{\varphi}^{*}(y)$ for all $y\in{\mathcal {Y}}$ and $\bar{\varphi}_{a}^{*}=\bar{\varphi}^{*}$ on $\mathcal{Y}^{a}$. In particular, if $(\theta,c)\in{\mathcal{U}}^{a}$ and $y\in{\mathcal {Y}}$ solves the dual, then $^{a}{y}\in{\mathcal{Y}}^{a}$ solves the dual as well and $x\in{\mathcal{N}}$ solves (ALM+) if and only if it is feasible and satisfies the subdifferential conditions of Theorem 9.3 with $^{a}{y}$.

Proof

Since $S_{t}$ is an $\mathcal{F}_{t}$-measurable convex normal integrand with $S(0)=0$, we have

$$E\big[(q_{t}S_{t})^{*}(^{a}{w}_{t}) + \sigma_{D_{t}}(E_{t}[\Delta ^{a}{w}_{t+1}])\big] \le E\big[(q_{t}S_{t})^{*}(w_{t}) + \sigma_{D_{t}}(E_{t}[\Delta w_{t+1}])\big] $$

by Jensen’s inequality for normal integrands; see e.g. [48, Corollary 2.1]. Since $E[V^{*}(^{a}{q})]\le E[V^{*}(q)]$ under Assumption 4.1, the first claim thus follows from the expression for $\bar{\varphi}^{*}$ in Theorem 9.1. For any $y\in {\mathcal{Y}}^{a}$, the conjugate of $\bar{\varphi}_{a}$ can be expressed (using the fact that the conjugate of the inf-convolution is the sum of the conjugates) as

$$\begin{aligned} \bar{\varphi}_{a}^{*}(y) &= \sup_{u\in{\mathcal{U}}^{a}}\big(\langle u,y\rangle- \bar{\varphi}(u)\big)\\ &= \sup_{u\in{\mathcal{U}}}\big(\langle u,y\rangle- (\bar{\varphi}+\delta_{\mathcal{U}^{a}})(u)\big)\\ &= \mathop{\mathrm{cl}}\inf_{y'\in{\mathcal{Y}}}\big(\bar{\varphi}^{*}(y-y') + \delta_{(\mathcal{U}^{a})^{\perp}}(y')\big)\\ &= \bar{\varphi}^{*}(y), \end{aligned}$$

where the closure is taken with respect to the pairing of $\mathcal{Y}$ with $\mathcal{U}$ and the last equality holds by the first claim. □

The proofs of Theorems 4.3, 5.5 and 7.1 are now simple applications of Theorems 9.2 and 9.4 and the fact that $\varphi$ is the restriction of $\bar{\varphi}(0,\cdot)$ to the space $\mathcal{M}^{a}$ of adapted cash-valued claims.

Proof of Theorem 4.3

Recall that $\varphi=\bar{\varphi}(0,\cdot)$ and let $q\in{\mathcal {Q}}^{a}$. Defining $\gamma_{q}:\mathcal{N}^{\infty}\to\overline{\mathbb {R}}$ by

$$\gamma_{q}(\theta) := \inf_{c\in{\mathcal{M}}^{a}}\big(\bar{\varphi}_{a}(\theta,c) - \langle c,q\rangle\big), $$

we have $\varphi^{*}(q)=-\gamma_{q}(0)$ and $\gamma_{q}^{*}(w)=\bar{\varphi}^{*}_{a}(w,q)$ so that

$$-\gamma_{q}^{**}(0)=\inf_{w\in{\mathcal{N}}^{1}}\bar{\varphi}^{*}_{a}(w,q), $$

where by Theorems 9.1 and 9.4, the right-hand side is the expression for $\varphi^{*}$ in Theorem 4.3. It thus suffices to show that $\gamma_{q}(0)=\gamma _{q}^{**}(0)$ and that the infimum is attained. Applying [60, Theorem 17] to the function $F(c,\theta):=\bar{\varphi}_{a}(\theta,c) - \langle c,q\rangle$, we see that this holds if $\gamma _{q}$ is bounded from above on a Mackey neighborhood of the origin. Choosing $x=0$ and $c=-S(\theta)$, we get

$$\begin{aligned} \gamma_{q}(\theta) &= \inf_{c\in{\mathcal{M}}^{a},x\in{\mathcal {N}}_{D}}E\big[V\big(S(\Delta x+\theta)+c\big) - c\cdot q\big]\le E\bigg[\sum_{t=0}^{T}q_{t}S_{t}(\theta_{t})\bigg]. \end{aligned}$$

Convexity of $S(\cdot,\omega)$ and Assumption 4.2 imply $S(x)\in{\mathcal{M}}$ for all $x\in L^{\infty}$, so that [60, Theorem 22] implies that the last expression is Mackey-continuous on $L^{\infty}$ and thus bounded above on a neighborhood of the origin. □

Proof of Theorem 5.5

Theorem 5.5 follows from Theorem 9.2 once we notice that $\varphi$ is the restriction of $\bar{\varphi}(0,\cdot)$ to $\mathcal{M}^{a}$ and that $\sigma(\mathcal{M}^{a},\mathcal{Q}^{a})$ is the relative topology of $\sigma(\mathcal{U},\mathcal{Y})$ on $\mathcal{M}^{a}$. □

Proof of Theorem 7.1

It suffices to apply Theorem 9.4 with $\theta=0$. □

Appendix

This appendix starts by collecting some definitions and facts from convex analysis. The second section gives the proofs of Theorems 9.1–9.3 by analyzing them in a general stochastic optimization framework. The last section gives sufficient conditions for Assumption 5.2 in terms of asymptotic elasticity.

1.1 Facts from convex analysis

Given a closed convex set $C$ in a topological vector space and an $x\in C$, the set

$$C^{\infty}:= \bigcap_{\alpha>0}\alpha(C-x) $$

is a closed convex cone independent of $x\in C$. It is called the recession cone of $C$. Given a closed proper convex function $h$ and an $\bar{x}\in\mathop{\mathrm{dom}} h$, the function

$$h^{\infty}(x):=\sup_{\alpha>0}\frac{h(\bar{x}+\alpha x)-h(\bar{x})}{\alpha} $$

is a closed sublinear function independent of $\bar{x}\in\mathop {\mathrm{dom}} h$. It is called the recession function of $h$. The proofs of the above facts are given in finite-dimensional spaces in [59, Sect. 8], but the arguments extend to general topological vector spaces.

Given an extended real-valued function $g$ on $\mathbb{R}^{m}$ and an $\mathbb{R}^{m}$-valued function $F$ on a subset $\mathop{\mathrm {dom}} F$ of $\mathbb{R}^{n}$, we define their composition as the extended real-valued function

$$(g\circ F)(x):= \textstyle\begin{cases} g(F(x)) & \quad\text{if $x\in\mathop{\mathrm{dom}} F$},\\ +\infty&\quad\text{if $x\notin\mathop{\mathrm{dom}} F$}. \end{cases} $$

Given a convex cone $K\subseteq\mathbb{R}^{m}$, the function $F$ is said to be $K$-convex if the set

$$\mathop{\mathrm{epi}}\nolimits_{K}F:=\{(x,u)\,:\,x\in\mathop{\mathrm {dom}} F, F(x)-u\in K\} $$

is convex. It is said to be $K$-closed if $\mathop{\mathrm {epi}}_{K}F$ is a closed set. It is easily verified (see the proof of Lemma A.1 below) that if $g$ is convex and $F$ is $K$-convex, then $g\circ F$ is convex if

$$ F(x)-u\in K\implies g\big(F(x)\big)\le g(u)\qquad\forall x\in\mathop {\mathrm{dom}} F. $$

(A.1)

For such compositions, a full subdifferential and recession calculus is available; see [46]. We shall see below that the composition is well behaved also in terms of measurability.

A set-valued mapping $\omega\mapsto C(\omega)\subseteq\mathbb{R}^{n}$ is $\mathcal{F}_{t}$-measurable if the inverse image

$$C^{-1}(U):=\{\omega\in\varOmega\,:\,C(\omega)\cap U\ne\emptyset\} $$

of every open $U\subseteq\mathbb{R}^{n}$ is $\mathcal{F}_{t}$-measurable. An extended real-valued function $f$ on $\mathbb{R}^{n}\times \varOmega$ is a convex normal integrand if the set-valued mapping

$$\omega\mapsto\mathop{\mathrm{epi}} f(\cdot,\omega):=\{ (x,\alpha)\in\mathbb{R}^{n}\times\mathbb{R}\,:\, f(x,\omega)\le \alpha\} $$

is closed-convex-valued and measurable. We refer the reader to [61, Chap. 14] for further details on measurable set-valued maps and normal integrands.

We say that a family $\{F(\cdot,\omega)\}_{\omega\in\varOmega}$ of $K$-closed $K$-convex functions is a random $K$-convex function if $\mathop{\mathrm{epi}}_{K}F(\cdot,\omega)$ is measurable. Throughout, the indicator function of a set $C$ is the extended real-valued function $\delta_{C}$ taking the value 0 on $C$ and $+\infty$ outside of $C$.

Lemma A.1

Let $g$ be a convex normal integrand and $F$ a random $K$-convex function such that (A.1) holds almost surely. If $(-K)\cap \{u\,:\,g^{\infty}(u,\omega)\le0\}$ is linear, then $g\circ F$ is a convex normal integrand on $\mathbb{R}^{n}\times\varOmega$.

Proof

By [61, Example 14.32 and Proposition 14.44],

$$h(x,u,\omega) := g(u,\omega) + \delta_{\mathop{\mathrm {epi}}_{K}F(\cdot,\omega)}(x,u) $$

is a normal integrand. The growth condition gives

$$(g\circ F)(x,\omega) = \inf_{u\in\mathbb{R}^{m}}h(x,u,\omega), $$

while the linearity condition implies by [59, Theorem 9.2] that this expression is lower semicontinuous in $x$ and thus a normal integrand by [61, Proposition 14.47]. □

In the market model of Sect. 2, the function $S(x,\omega):=(S_{t}(x,\omega))_{t=0}^{T}$ with

$$\mathop{\mathrm{dom}} S(\cdot,\omega):=\bigcap_{t=0,\ldots ,T}\mathop{\mathrm{dom}} S_{t}(\cdot,\omega) $$

defines a random $K$-convex function with $K:=\mathbb{R}^{T+1}_{-}$. By [59, Corollary 8.6.1], Assumption 2.1 means that $(-K)\cap\{c\in\mathbb{R}^{T+1}\,:\,V^{\infty}(c,\omega)\le0\}=\{0\}$, so that Lemma A.1 gives the following result.

Corollary A.2

Under Assumption 2.1, the function $(x,c,\omega)\mapsto V(S(\Delta x,\omega)+c)$ is a convex normal integrand and in particular $\mathcal{B}(\mathbb{R}^{J(T+1)}\times\mathbb {R}^{(T+1)})\otimes{\mathcal{F}}$-measurable.

The following was used in the proofs of Theorems 8.1 and 8.2.

Lemma A.3

Let $\mathcal{D}\subseteq{\mathcal{M}}^{a}$ be a closed set containing the origin, let $p\in{\mathcal{M}}^{a}$ and

$$\pi(c)=\inf\{\alpha\in\mathbb{R}\,:\,c-\alpha p\in{\mathcal{D}}\}. $$

Then the conditions

• (1) $\pi(c)$ is closed and proper,

• (2) $\pi(0)>-\infty$,

• (3) $p\notin{\mathcal{D}}^{\infty}$,

• (4) $\langle p,q\rangle=1$ for some $q\in\mathop{\mathrm{dom}} \sigma_{\mathcal{D}}$,

are equivalent and imply the validity of the dual representation

$$\pi^{*}(c) = \sup_{q\in{\mathcal{Q}}^{a}}\{\langle c,q\rangle- \sigma _{\mathcal{D}}(q)\,:\, \langle p,q\rangle=1\}. $$

Proof

This is proved for $\mathcal{D}=\mathcal{C}$ in [50, Proposition 4.2 and Theorem 5.2]. The same arguments work for any convex $\mathcal{D}$; see also [43, Sect. 3.2]. □

1.2 Proofs of Theorems 9.1–9.3

As in [52], we analyze (ALM+) in the general parametric stochastic optimization format from [48, 9]. To this end, we express the value function $\bar{\varphi}$ defined at the beginning of Sect. 9.1 as

$$\bar{\varphi}(u)= \inf_{x\in{\mathcal{N}}}\int f\big(x(\omega ),u(\omega),\omega\big)dP(\omega), $$

where $\mathcal{N}$ is the linear space of adapted $\mathbb {R}^{J}$-valued processes and $f$ is the extended real-valued function on $\mathbb{R}^{J(T+1)}\times\mathbb{R}^{(J+1)(T+1)}\times\varOmega$ defined by (recall that $u=(\theta,c)$)

$$f(x,u,\omega)= V\big(S(\Delta x+\theta,\omega)+c,\omega\big)+\delta _{D(\omega)}(x). $$

Indeed, $f$ is a normal integrand by [61, Propositions 14.44 and 14.45] and Corollary A.2.

The dual expressions involve the associated Lagrangian integrand (recall that $y= (w,q)$)

$$\begin{aligned} &\ell(x,y,\omega) \\ &\quad=\inf_{u\in\mathbb{R}^{(J+1)(T+1)}}\big(f(x,u,\omega)-u\cdot y\big) \\ &\quad= \textstyle\begin{cases} +\infty&\text{if $x\notin D(\omega)$},\\ - V^{*}(q,\omega) + \sum_{t=0}^{T}(\Delta x_{t}\cdot w_{t} - (q_{t}S_{t})^{*}(w_{t},\omega)) &\text{otherwise,} \end{cases}\displaystyle \\ &\quad= \textstyle\begin{cases} +\infty&\text{if $x\notin D(\omega)$},\\ - V^{*}(q,\omega) + \sum_{t=0}^{T}(- x_{t}\cdot\Delta w_{t+1} - (q_{t}S_{t})^{*}(w_{t},\omega)) & \text{otherwise,} \end{cases}\displaystyle \end{aligned}$$

(A.2)

and the conjugate of $f$ given by

$$\begin{aligned} f^{*}(v,y,\omega)&=\sup_{{\scriptstyle x\in\mathbb{R}^{J(T+1)}\atop\scriptstyle u\in \mathbb{R}^{(J+1)(T+1)}}}\big(x\cdot v+u\cdot y-f(x,u,\omega)\big)\\ &=\sup_{x\in\mathbb{R}^{J(T+1)}}\big(x\cdot v-\ell(x,y,\omega)\big)\\ &= V^{*}(q,\omega) + \sum_{t=0}^{T}\big(\sigma_{D_{t}(\omega)}(v_{t}+\Delta w_{t+1}) + (q_{t}S_{t})^{*}(w_{t},\omega)\big). \end{aligned}$$

By [61, Theorem 14.50], $f^{*}$ is a normal integrand as well.

The strategy taken in [9] is first to compute the conjugate of the auxiliary value function

$$\tilde{\varphi}(u):=\inf_{u\in{\mathcal{N}}^{\infty}}E[f(x,u)], $$

where $\mathcal{N}^{\infty}:=\mathcal{N}\cap L^{\infty}$, the essentially bounded adapted trading strategies. Under mild conditions, the conjugate of $\tilde{\varphi}$ coincides with that of $\bar{\varphi}$; see [9, Theorem 2].

Proof of Theorem 9.1

Under Assumption 4.2, $S(x)\in{\mathcal{M}}^{a}$ for every $x\in {\mathcal{N}}^{\infty}$ so that

$$\{x\in{\mathcal{N}}^{\infty}\,:\,\exists u\in{\mathcal{U}}\text{ with } E[f(x,u)]< \infty\}=\{x\in{\mathcal{N}}^{\infty}\,:\,x\in D\}. $$

Thus Theorem 2 of [9] says that the conjugate of $\tilde{\varphi}$ can be expressed as

$$\begin{aligned} \tilde{\varphi}^{*}(y) &= -\inf_{x\in{\mathcal{N}}^{\infty}}E[\ell (x,y)]\\ &= -\inf_{x\in{\mathcal{N}}^{\infty}}E\bigg[\sum_{t=0}^{T}\big(\delta _{D_{t}}(x_{t}) - x_{t}\cdot E_{t}[\Delta w_{t+1}]- (q_{t}S_{t})^{*}(w_{t})\big) - V^{*}(q)\bigg]\\ &= E\bigg[\sum_{t=0}^{T}\big(\sigma_{D_{t}}(E_{t}[\Delta w_{t+1}]) + (q_{t}S_{t})^{*}(w_{t})\big) + V^{*}(q)\bigg], \end{aligned}$$

where the second equality comes from properties of conditional expectations and the last from the interchange rule for integration and minimization; see [61, Theorem 14.60]. Moreover, we have $E[f^{*}(v,y)]=\tilde{\varphi}^{*}(y)$ for any $y\in{\mathcal{Y}}$ as well as $v_{t}=E_{t}[\Delta w_{t+1}]-\Delta w_{t+1}$. Thus by [9, Theorem 2], $\bar{\varphi}^{*}=\tilde{\varphi}^{*}$. □

Proof of Theorem 9.2

By [56, Theorem 5 and Lemma 6], it suffices to show that $\mathcal{L}:=\{x\in{\mathcal{N}}\,:\, f^{\infty}(x,0)\le0\}$ is a linear space and that there exists $(v,y)\in{\mathcal{N}}^{\perp}\times \mathcal{Y}$ with $\lambda(v,y)\in\mathop{\mathrm{dom}} E[f^{*}]$ for two different $\lambda>0$.

By [59, Theorem 9.3] and [46, Theorem 7.3],

$$f^{\infty}(x,u,\omega) =V^{\infty}\big(S^{\infty}(\Delta x+\theta,\omega )+c,\omega\big) + \delta_{D^{\infty}(\omega)}(x), $$

so that ℒ is a linear space under Assumption 5.1. The assumption in the theorem means that $E[f^{*}(v,y)]$ is finite for some $y$ and $v=E_{t}[\Delta w_{t+1}]-\Delta w_{t+1}$. By Assumption 5.1, $E[V^{*}(\lambda q)]$ is finite for some nonnegative $\lambda\ne 1$, and since the other terms in

$$\begin{aligned} E[f^{*}(v,y) ]&= E\bigg[V^{*}(q) + \sum_{t=0}^{T}\big((q_{t}S_{t})^{*}(w_{t}) + \sigma_{D_{t}}(v_{t} +\Delta w_{t+1})\big)\bigg] \end{aligned}$$

are positively homogeneous, we get $\lambda(v,y)\in\mathop{\mathrm {dom}} E[f^{*}]$. □

Proof of Theorem 9.3

By Theorem 9.1, $y$ solves the dual if and only if it maximizes $\langle u,y\rangle-\bar{\varphi}^{*}(y)$. Under the closedness condition, this is equivalent to $y\in\partial\bar{\varphi}(u)$. The assumptions of [9, Theorem 8] are then satisfied with $v_{t}:=E_{t}[\Delta w_{t+1}]-\Delta w_{t+1}$. Thus $x\in{\mathcal{N}}$ and $y\in{\mathcal{Y}}$ are optimal if and only if they are feasible and

$$\begin{aligned} v&\in\partial_{x}\ell(x,w,q),\\ (\theta,c) &\in\partial_{(w,q)} (-\ell)(x,w,q) \end{aligned}$$

almost surely. Looking at the last expression (A.2) for $\ell$, we see that the first inclusion here coincides with the first one in the statement. The second inclusion means that $c\in\partial V^{*}(q)+d$ and $\Delta x+\theta=\eta$ for some $(\eta_{t},d_{t})\in\partial _{q,w}(q_{t}S_{t})^{*}(w_{t})$. Indeed, the subdifferential sum rule [59, Theorem 23.8] applies $\omega$-wise since Assumption 2.1 implies that $\mathop{\mathrm{dom}} V^{*}\cap\mathbb {R}^{T+1}_{++}\ne\emptyset$, while by [59, Theorem 6.6], the relative interior of the domain of the function $(w,q)\mapsto (qS_{t})^{*}(w,\omega)$ contains a $(w,q)$ whenever $q\in\mathbb {R}^{T+1}_{++}$. It is easily checked that $(q_{t}S_{t})^{*}(w_{t})$ is the support function of the set $E_{t}:=\{(\eta,d)\,: \,S_{t}(\eta)+d\le0\}$. By [59, Theorem 23.5 and p. 215], $(\eta_{t},d_{t})\in \partial_{q,w}(q_{t}S_{t})^{*}(w_{t})$ is thus equivalent to $(w_{t},q_{t})\in N_{E_{t}}(\eta_{t},d_{t})$. This means that either $S_{t}(\eta_{t})+d_{t}<0$ and $(w_{t},q_{t})=(0,0)$ or $S_{t}(\eta _{t})+d_{t}=0$ and $w_{t}\in\partial(q_{t}S_{t})(\eta_{t})$. The second inclusion thus means that

$$\begin{aligned} q &\in\partial V(c-d),\\ w_{t}&\in\partial(q_{t}S_{t})(\Delta x_{t}+\theta_{t}) \end{aligned}$$

for some measurable process $d\le-S(\Delta x+\theta)$ such that $q(S(\Delta x+\theta)+d)=0$ almost surely. Since $V$ is nondecreasing, this is satisfied also by $d=-S(\Delta x+\theta)$. □

1.3 Asymptotic elasticity of a random loss function

The main result of [55] was used in [52] to give conditions for the lower semicontinuity of the value function of (ALM). One of the conditions was that the functions $V_{t}$ are bounded from below. While this is satisfied in many cases, it rules out isoelastic utility functions. Theorem 5 in [56] allows us to replace the lower bound by more general “asymptotic elasticity” conditions introduced in [39] and [64]. We extend the conditions of [39, 64] further by allowing nonsmooth and random functions $V_{t}$ and by not imposing the Inada conditions, which can be written as $V_{t}^{\infty}(\cdot,\omega)=\delta_{\mathbb{R}_{-}}$. Indeed, it suffices to have one of the conditions in the following lemma.

Lemma A.4

Let $h$ be a nondecreasing convex normal integrand on the real line. If there exist $\lambda>1$, $\bar{y}\in\mathop{\mathrm{dom}} E[h^{*}]$ and $C\ge0$ such that

$$h^{*}(\lambda y,\omega)\le Ch^{*}(y,\omega)\qquad\forall y\ge\bar{y}(\omega), $$

then (in $L^{0}$)

$$\lambda\mathop{\mathrm{dom}} E[h^{*}]\subseteq\mathop{\mathrm {dom}} E[h^{*}]\qquad\forall\lambda\ge1. $$

If there exist $\lambda\in(0,1)$, $\bar{y}\in\mathop{\mathrm {dom}} E[h^{*}]$ and $C>0$ such that

$$h^{*}(\lambda y,\omega)\le Ch^{*}(y,\omega)\qquad\forall y\in[0,\bar{y}(\omega)], $$

then (in $L^{0}$)

$$\lambda\mathop{\mathrm{dom}} E[h^{*}]\subseteq\mathop{\mathrm {dom}} E[h^{*}]\qquad\forall\lambda\in(0,1]. $$

Proof

Let $y\in\mathop{\mathrm{dom}} E[h^{*}]$. Under the first condition,

$$\begin{array}{rl}{h}^{\ast }(\lambda y)& ={\mathbb{1}}_{\{y\le \overline{y}\}}{h}^{\ast }(\lambda y)+{\mathbb{1}}_{\{y>\overline{y}\}}{h}^{\ast }(\lambda y)\\ & \le {\mathbb{1}}_{\{y\le \overline{y}\}}max(h^{\ast }(y),h^{\ast }(\lambda \overline{y}))+{\mathbb{1}}_{\{y>\overline{y}\}}{h}^{\ast }(\lambda y)\\ & \le {\mathbb{1}}_{\{y\le \overline{y}\}}max(h^{\ast }(y),C{h}^{\ast }(\overline{y}))+{\mathbb{1}}_{\{y>\overline{y}\}}C{h}^{\ast }(y),\end{array}$$

where the first inequality comes from the convexity of $h^{*}$. Since $\bar{y},y\in\mathop{\mathrm{dom}} E[h^{*}]$, the last expression is integrable.

Under the second condition,

$$\begin{array}{rl}E[h^{\ast }(\lambda y)]& =E[{\mathbb{1}}_{\{y\le \overline{y}\}}{h}^{\ast }(\lambda y)]+E[{\mathbb{1}}_{\{y>\overline{y}\}}{h}^{\ast }(\lambda y)]\\ & \le E[{\mathbb{1}}_{\{y\le \overline{y}\}}{h}^{\ast }(\lambda y)]+E[{\mathbb{1}}_{\{y>\overline{y}\}}max(h^{\ast }(y),h^{\ast }(\lambda \overline{y})\left)\right]\\ & \le E[{\mathbb{1}}_{\{y\le \overline{y}\}}C{h}^{\ast }(y)]+E[{\mathbb{1}}_{\{y>\overline{y}\}}max(h^{\ast }(y),C{h}^{\ast }(\overline{y})\left)\right],\end{array}$$

where the first inequality comes from the convexity of $h^{*}$. □

The following lemmas provide some alternative formulations of the conditions in Lemma A.4 which were used in the proof of Theorem 9.2. In both lemmas, the third condition extends the “asymptotic elasticity” conditions introduced in [39] and [64], respectively, for deterministic utility functions.

Lemma A.5

Given a nondecreasing closed convex function $g$ on the real line with $g(0)=0$, the following are equivalent conditions on $\beta>1$ and $\bar{y}$ for which $\partial g^{*}(\bar{y})\subset \mathbb{R}_{+}$:

$$\begin{aligned} g^{*}(\lambda y)&\le\lambda^{\frac{\beta}{\beta-1}}g^{*}(y)\quad\ \ \forall\lambda\ge1, y\ge\bar{y}. \end{aligned}$$

(A.3)

$$\begin{aligned} cy &\le\frac{\beta}{\beta-1} g^{*}(y)\quad\forall y \ge\bar{y}, c\in\partial g^{*}(y). \end{aligned}$$

(A.4)

$$\begin{aligned} cy &\ge\beta g(c)\quad\qquad\ \ \forall c\ge\sup\partial g^{*}(\bar{y}), y\in \partial g(c). \\ \end{aligned}$$

(A.5)

$$\begin{aligned} g(\lambda c) &\ge\lambda^{\beta}g(c)\qquad\quad\forall\lambda\ge1, c\ge\sup\partial g^{*}(\bar{y}). \end{aligned}$$

(A.6)

Proof

Assuming (A.5), we have $g(\lambda c)\ge g(c)+\int_{[c,\lambda c]}\beta\frac{g(s)}{s}ds$, so

$$\begin{aligned} g(\lambda c) &\ge g(c) +\int_{[c,\lambda c]}g(c)\frac{\beta}{s}\exp \bigg(\int_{[s,\lambda c]}\frac{\beta}{r}dr\bigg)ds = \lambda^{\beta}g(c) \end{aligned}$$

by Gronwall’s inequality. For $y\ge\bar{y}(\omega)$, condition (A.6) gives

$$\begin{aligned} g^{*}(y) \ge\sup_{c \in\mathbb{R}}\big(cy-\lambda^{-\beta}g(\lambda c)\big)= \lambda^{-\beta}g^{*}(\lambda^{\beta-1}y), \end{aligned}$$

which implies (A.3). We have for every $\lambda> 1$, $y\ge\bar{y}(\omega)$ and $c\in\partial g^{*}(y)$ that

$$c(\lambda y-y)\le g^{*}(\lambda y)-g^{*}(y) \le(\lambda^{\frac{\beta }{\beta-1}}-1)g^{*}(y), $$

from where we get (A.4) by first dividing by $\lambda-1$ and then letting $\lambda\searrow1$. Using the equivalence

$$c\in\partial g^{*}(y,\omega)\iff y\in\partial g(c)\iff g(c)+g^{*}(y)=cy, $$

we can write condition (A.4) as

$$cy\le\frac{\beta}{\beta-1}\big(cy-g(c)\big)\quad\forall c\ge\sup \partial g^{*}(\bar{y}), y\in\partial g(c), $$

which is equivalent with (A.6). □

Lemma A.6

Given a nondecreasing closed convex function $g$ on the real line with $g(0)=0$, the following are equivalent conditions on $\beta\in(0,1)$ and $\bar{y}$ for which $\partial g^{*}(\bar{y})\subseteq \mathbb{R}_{-}$:

$$\begin{aligned} g^{*}(\lambda y) &\le\lambda^{\frac{-\beta}{1-\beta}} g^{*}(y)\quad\ \,\,\forall\lambda\in(0,1), y\in(0,\bar{y}]. \end{aligned}$$

(A.7)

$$\begin{aligned} cy &\ge\frac{-\beta}{1-\beta} g^{*}(y)\quad \forall y\in(0,\bar{y}], c\in\partial g^{*}(y). \end{aligned}$$

(A.8)

$$\begin{aligned} cy &\ge\beta g(c)\qquad\quad\ \ \forall c\le\inf\partial g^{*}(\bar{y}), y\in \partial g(c). \end{aligned}$$

(A.9)

$$\begin{aligned} g(\lambda c) &\ge\lambda^{\beta}g(c)\qquad\quad \forall\lambda\ge1, c\le\inf\partial g^{*}(\bar{y}). \end{aligned}$$

(A.10)

Proof

Assuming (A.9), we have $g(c)\le g(\lambda c)+\int_{[\lambda c,c]}\beta\frac{g(s)}{s}ds$, so

$$\begin{aligned} g(c) &\le g(\lambda c) +g(\lambda c)\int_{[\lambda c,c]}\frac{\beta }{s}ds =g(\lambda c)\big(1-\ln(\lambda^{-\beta})\big) \le\lambda ^{-\beta} g(\lambda c). \end{aligned}$$

For $y\in(0,\bar{y}]$, condition (A.10) gives

$$\begin{aligned} g^{*}(y) \ge\sup_{c \in\mathbb{R}}\big(cy-\lambda^{-\beta}g(\lambda c)\big)= \lambda^{-\beta}g^{*}(\lambda^{\beta-1}y), \end{aligned}$$

which implies (A.7). We have for every $\lambda\in(0,1)$, $y\in (0,\bar{y}]$ and $c\in\partial g^{*}(y)$ that

$$c(\lambda y-y)\le g^{*}(\lambda y)-g^{*}(y) \le(\lambda^{\frac{-\beta }{1-\beta}}-1)g^{*}(y), $$

from where we get (A.8) by first dividing by $\lambda-1$ and then letting $\lambda\nearrow1$. Using the equivalence

$$c\in\partial g^{*}(y)\iff y\in\partial g(c)\iff g(c)+g^{*}(y)=cy, $$

we can write condition (A.8) as

$$cy\ge\frac{-\beta}{1-\beta}\big(cy-g(c)\big)\quad\forall c\ge\sup \partial g^{*}(\bar{y}), y\in\partial g(c), $$

which is equivalent with (A.9). □