Abstract
It is known that the decision to purchase an annuity may be associated to an optimal stopping problem. However, little is known about optimal strategies if the mortality force is a generic function of time and the subjective life expectancy of the investor differs from the objective one adopted by insurance companies to price annuities. In this paper, we address this problem by considering an individual who invests in a fund and has the option to convert the fund’s value into an annuity at any time. We formulate the problem as a real option and perform a detailed probabilistic study of the optimal stopping boundary. Due to the generic time-dependence of the mortality force, our optimal stopping problem requires new solution methods to deal with nonmonotonic optimal boundaries.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In an ageing world, an accurate management of retirement wealth is crucial for financial well-being. It is important for working individuals to carefully consider the existing offer of financial and insurance products designed for retirement, beyond the state pension. This offer includes for example occupational pension funds and tax-advantaged retirement accounts (e.g. Individual Retirement Account (US)). Most of these products rely on annuities to turn retirement wealth into guaranteed lifetime retirement income. Life annuities provide a lifelong stream of guaranteed income in exchange for a (single or periodic) premium. The purchase of an annuity helps individuals to manage the longevity risk, i.e., the risk of outliving their financial wealth, but it is usually an irreversible transaction. In fact, most annuity contracts impose steep penalties for partial or complete cancellation by the policyholder, especially in the early years of the contract.
Timing an annuity purchase (so-called annuitisation) is a complex financial decision that depends on several risk factors as e.g. market risk, longevity risk, potential future need of liquid funds, and bequest motive. The study of this topic has motivated a whole research field since the seminal contribution of Yaari [19], who showed that individuals with no bequest motive should convert all their retirement wealth into annuities.
After Yaari, several authors have analysed the annuitisation decision under the so-called all-or-nothing institutional arrangement, where a lifetime annuity is purchased in a single transaction (as opposed to gradual annuitisation). Initially, an individual’s wealth is invested in the financial market, and at the time of an annuity purchase, it is converted into a lifetime annuity. The central idea in this literature is to compare the value deriving from an immediate annuitisation with the value of deferring it while investing in the financial market. Therefore, a strict analogy holds with the problem of exercising an American option, and the annuitisation decision can be considered as the exercise of a real option.
Milevsky [12] proposed a model where an individual defers annuitisation for as long as the financial investment’s returns guarantee a consumption flow which is at least equal to the one provided by the annuity payments. In particular, [12] adopts a criterion based on controlling the probability of a consumption shortfall.
Other papers study the optimal annuitisation time in the context of utility maximisation, and formulate the problem as one of optimal stopping and control. The investor aims at maximising the expected utility of consumption (pre-retirement) and of annuity payments (post-retirement).
Assuming a constant force of mortality and CRRA utility, Stabile [18] analytically solves a time-homogeneous optimal stopping problem. He proves that if the individual has the same degree of risk aversion before and after the annuitisation, then an annuity is purchased either immediately or never (the so-called now-or-never policy). On the other hand, if the individual is more risk averse during the annuity payout phase, the annuity is purchased as soon as the wealth falls below a constant threshold (the optimal stopping boundary).
A constant force of mortality is also assumed in Gerrard et al. [7] and Liang et al. [11]. The model in [7] is analogous to the one studied in [18], but with quadratic utility functions, and the authors find a closed-form solution: If \((X_{t})_{t\ge 0}\) represents the individual’s wealth process, then it is optimal to stop when \(X\) leaves a specific interval (hence the optimal stopping boundary is formed by the endpoints of such an interval). In [11], in contrast to the previous papers, the authors assume that the individual may continue to invest and consume after annuitisation. By using martingale methods, explicit solutions are provided in the case of CRRA utility functions. Contrarily to [7], the optimal annuitisation in [11] occurs when the wealth process enters a specific interval, whose endpoints form the optimal stopping boundary.
Assuming a time-dependent force of mortality, Milevsky and Young [13] analyse both the all-or-nothing market and the more general anything-anytime market, where gradual annuitisation strategies are allowed. For the all-or-nothing market, they find that the optimal annuitisation time is deterministic as an artifact of CRRA utility. Thus, the annuitisation decision is independent from the individual’s wealth.
Our work is more closely related to work by Hainaut and Deelstra [9]. They consider an individual whose retirement wealth is invested in a financial fund which eventually must be converted into an annuity. The fund is modelled by a jump-diffusion process and pays dividends at a constant rate. The mortality force is a time-dependent, deterministic function and the individual aims at maximising the market value of future cashflows before and after annuitisation. According to the insurance practice, it is assumed that the individual can only purchase the annuity by a given maximal age. The authors in [9] cast the problem as an optimal stopping one and write a variational inequality for the value function. They then use the Wiener–Hopf factorisation and a time stepping method to solve the variational problem numerically. Hainaut and Deelstra argue that the decision to purchase the annuity should be triggered by either an upper or a lower, time-dependent threshold in the time-wealth plane. Numerical examples are provided in [9] where the annuitisation occurs when the value of the financial fund is high enough or, alternatively, low enough.
In this paper, we perform a detailed mathematical study of the optimal stopping problem associated to an annuitisation decision similar to that considered in [9]. In the interest of a rigorous analysis of the optimal stopping boundary, we simplify the dynamics of the financial fund by considering a geometric Brownian motion with no jumps. As in [9], we look at the maximisation of future expected cashflows for an individual who joins the fund and has the opportunity to purchase an annuity on a time horizon \([0,T]\). Time 0 is the time when the individual joins the fund and time \(T\) is the time by which the individual reaches the maximal age for an annuity purchase. The present value of future expected cashflows, evaluated at the optimum, gives us the so-called value function \(V\).
Notice that a closer inspection of the problem formulation in (2.4) below shows that at time \(T\), the fund is converted into an annuity (the same occurs in [9]). This means that the individual will eventually purchase the annuity at time \(T\), but she also has an option to buy it earlier. One could think of this feature as part of the fund’s contract specifications or as a commitment of the investor at time 0. It is, however, important to remark that the methods developed in this paper apply also to the case \(T=+\infty \), up to some minor changes (see also Remark 3.3 for further details).
One of the key features of the model presented here is the use of a rather general time-dependent, deterministic mortality force. This is a realistic assumption commonly made in the actuarial profession. As in [13], we consider two different mortality forces: a subjective one, used by the individual to weigh the future cashflows (denoted \(\mu ^{S}\)), and an objective one, used by the insurance company to price the annuity (denoted \(\mu ^{O}\)). The interplay between these two different mortality forces contributes to some key qualitative aspects of the optimal annuitisation decision (see Sect. 5 for more details). Interestingly, the generic time-dependent structure of the mortality force constitutes also the major technical challenge in the mathematical study of the problem.
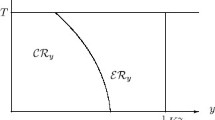
On the one hand, standard optimal stopping results ensure that the time–wealth plane splits into a continuation region \(\mathcal{C}\), where the option to wait has strictly positive value, and a stopping region \(\mathcal{S}\), where the annuity should be immediately purchased. Denoting by \((X_{t})_{t\ge 0}\) the process that represents the fund’s value (or equally, the individual’s retirement wealth), an optimal stopping rule is given by stopping at the first time the two-dimensional process \((t,X_{t})_{t\ge 0}\) enters the set \(\mathcal{S}\). Moreover, under some mild technical assumptions, we prove in Proposition 4.2 that these two sets are split by an optimal boundary (free boundary, in the language of PDEs) which only depends on time, i.e., \(t\mapsto b(t)\).
On the other hand, technical difficulties arise when trying to infer properties of the boundary \(b\). In fact, due to the generic time-dependence of the mortality force, it is not possible to establish any monotonicity of the mapping \(t\mapsto b(t)\). It is well known in optimal stopping and free boundary theory that monotonicity of \(b\) is the key to a rigorous study of the regularity of the boundary (e.g. continuity) and of the value function (e.g. continuous differentiability). The interested reader may consult [15, Chaps. VII and VIII] for a collection of relevant examples, and the introduction in [5] for a deeper discussion.
We overcome this major technical hurdle by proving that the optimal boundary is in fact a locally Lipschitz-continuous function of time. In order to achieve this goal, we rely only on probabilistic methods which are new and specifically designed to tackle our problem. This approach draws from similar ideas in [5], but we emphasise that our problem falls outside the class of problems addressed in that paper (see the discussion prior to Theorem 4.8 below).
Once Lipschitz regularity is proved, we then obtain also that the value function \(V\) is continuously differentiable in \(t\) and \(x\), at all points of the \((t,x)\)-plane and in particular across the boundary of \(\mathcal{C}\). This is a stronger result than the more usual smooth-fit condition, which states that \(z\mapsto V_{x}(t,z)\) is continuous across the optimal boundary. Finally, we find nonlinear integral equations that characterise uniquely the free boundary and the value function.
The analysis in this paper is completed by solving numerically the integral equation for some specific examples and studying their sensitivity to variations in the model’s parameters. It is important to remark that the optimal boundary turns out to be nonmonotonic in some of our examples, under natural assumptions on the parameters. This shows that the new approach developed in this paper is indeed necessary to study the annuitisation problem.
In summary, our contribution is at least twofold. On the one hand, we add to the literature concerning annuitisation problems in the all-or-nothing framework by addressing models with time-dependent mortality force. As we have discussed above and to the best of our knowledge, such models were only considered in [13] (which produces only deterministic optimal strategies) and in [9] (mostly in a numerical way). We provide a rigorous theoretical analysis of the optimal annuitisation strategy in terms of the optimal boundary \(b\). Our study also reveals behaviours not captured by [9] as e.g. lack of monotonicity of \(b\). The latter may reflect the change over time in the investor’s priorities, due to (deterministic) variations in the mortality force. On the other hand, it is rather remarkable that we started by considering an applied problem, with a somewhat canonical and seemingly innocuous formulation, but we soon realised that its rigorous analysis is far from trivial. Therefore we developed methods which are new in the probabilistic literature on optimal stopping and of independent interest.
Finally, in order to relate our work to the PDE literature in this area, it may be worth noticing that [6] (and later [2]) studies a free boundary problem motivated by optimal retirement. In that paper, an investor can decide to retire earlier than a given terminal time \(T\). Early retirement benefits are defined by a function \(\varPsi (t,s)\) of time \(t\) and the current salary \(s\). The problem is addressed exclusively with variational inequalities, and the free boundary depends on time since \(t\mapsto \varPsi (t,s)\) increases linearly. However, contrarily to our model, the mortality force in [6] and [2] is assumed constant.
The rest of the paper is organised as follows. In Sect. 2, we introduce the financial and actuarial assumptions and then the optimal annuitisation problem. In Sect. 3, we provide some continuity properties of the value function and useful probabilistic bounds on its gradient. In Sect. 4, we present sufficient conditions under which the shape of the continuation and stopping regions can be established, and we study the regularity of the optimal boundary. Moreover, we find nonlinear integral equations that characterise uniquely the free boundary and the value function. In Sect. 5, we present some numerical examples to illustrate the range of applicability of our assumptions. In Sect. 6, we provide some final remarks and extensions.
2 Problem formulation
In our model, we consider an individual (or investor) and an insurance company who are faced with two distinct sources of randomness: a financial market and the survival probability of the individual. We assume that the individual and the insurance company have different beliefs about the demographic risk, while they share the same views on the financial market. It is therefore convenient to construct initially two probability spaces: one that models the financial market and another that models the demographic component. The time horizon of the problem is fixed and denoted by \(T<+\infty \).
2.1 Financial and demographic models
For the financial market, we consider a complete probability space \((\varOmega ,\mathcal{F},\mathbb{P})\) carrying a 1-dimensional Brownian motion \((B_{t})_{t\ge 0}\). The filtration generated by \(B\) is denoted by \((\mathcal{F}_{t})_{t\ge 0}\), and it is augmented with ℙ-nullsets. The portion of the individual’s wealth allocated for an annuity purchase and invested in a financial fundFootnote 1 prior to the annuitisation is modelled by a stochastic process \((X_{t})_{t\ge 0}\). Its dynamics reads
where \(\theta \) is the average continuous return of the financial investment, \(\alpha \) is the constant dividend rate and \(\sigma >0\) is the volatility coefficient.
For the demographic risk, we consider another probability space. Given a measurable space \((\varOmega ',\mathcal{F}')\), we let \(\mathbb{Q}^{S}\) and \(\mathbb{Q}^{O}\) denote two probability measures on \((\varOmega ', \mathcal{F}')\) and assume that \((\varOmega ',\mathcal{F}',\mathbb{Q}^{i})\), \(i=S,O\), are both complete. The measure \(\mathbb{Q}^{S}\) is associated with the subjective survival probability of the individual. In contrast, \(\mathbb{Q}^{O}\) refers to the objective survival probability used by the insurance company to price annuities, and it is public information.
The individual is aged \(\eta >0\) at time zero in our problem, and this value is given and fixed throughout the paper. The time of death of the individual is represented by a random variable \(\varGamma _{D}:(\varOmega ', \mathcal{F}')\to (\mathbb{R}_{+},\mathcal{B}(\mathbb{R}_{+}))\), and for \(i=S,O\), we define the hazard functions
with \(s,t\ge 0\). These represent the subjective/objective probability that an individual who is alive at age \(\eta +t\) will survive to age \(\eta +t+s\) (we follow standard actuarial notation for \({}_{s} p^{i} _{\eta +t}\)). Let \(\mu ^{i}:[0,+\infty )\to [0,+\infty )\) for \(i = S,O\) be deterministic functions, representing the subjective and objective mortality forces, respectively. Then for \(i=S,O\), we have
The different survival probability functions adopted by insurer and individual account for the imperfect information available to the insurer on the individual’s risk profile.
Finally, we say that \(\mathcal{M}^{S}:=(\varOmega \times \varOmega ', \mathcal{F}\otimes \mathcal{F}',\mathbb{P}\times \mathbb{Q}^{S})\) is the probability space for the individual and \(\mathcal{M}^{O}:=(\varOmega \times \varOmega ',\mathcal{F}\otimes \mathcal{F}',\mathbb{P}\times \mathbb{Q}^{O})\) the probability space for the insurance company.
Remark 1
The functions \(\mu ^{S}\) and \(\mu ^{O}\) are given at the outset and are not updated during the optimisation. Updating in a nontrivial way would require the use of a stochastic dynamics for the mortality force which in general would lead to a more complex problem.
2.2 The optimisation problem
The insurance company uses its probabilistic model, based on objective survival probabilities, to price annuities. In particular, according to standard actuarial theory, the value at time \(t>0\) of a life annuity that is payable continuously at a rate of one monetary unit per year (purchased by the individual aged \(\eta +t\)) is given by
Here \(\widehat{\rho }>0\) is a constant interest rate guaranteed by the insurer.
In our model, the fund is automatically converted into an annuity at time \(T\), but the individual has the option to annuitise prior to \(T\). If she decides to annuitise at a time \(t\in [0,T]\), with the fund’s value equal to \(X\), then the annuity payout rate is constant and reads
where the constant \(K\) is either a fixed acquisition fee (\(K>0\)) or a tax incentive (\(K<0\)). The case \(K=0\) leads to trivial solutions as explained in Remark 3.2 below. From the modelling point of view, \(T<+\infty \) reflects the fact that insurance companies typically have a maximum age limit for the purchase of an annuity (this is noticed also in [9]).
The optimisation criterion pursued by the individual is the maximisation of the present value of future expected cashflows, via the optimal timing of the annuity purchase under the model \(\mathcal{M}^{S}\). Letting \(\mathbb{E}^{S}[\cdot ]\) be the expectation under the measure \(\mathbb{P}\times \mathbb{Q}^{S}\), if the individual is alive at time \(t\), the optimisation problem reads

where \(\mathcal{T}_{t,T}\) is the set of \((\mathcal{F}_{s})_{s\ge 0}\)-stopping times taking values in \([t,T]\) and \(\rho >0\) is a discount rate. Before annuitisation, i.e., for \(s<\tau \), the individual receives dividends from the fund at rate \(\alpha \). After annuitisation, i.e., for \(s>\tau \), she gets the continuous annuity payment at the constant annual rate \(P_{\eta + \tau }\). In case the individual dies before the time of the annuity purchase, i.e., on the event \(\{\varGamma _{D} \leq \tau \}\), she leaves a bequest equal to her wealth.
Remark 2
Thanks to a result in [1], we show in the Appendix that there is no loss of generality in using stopping times from \(\mathcal{T} _{t,T}\). That is, we obtain the same value in (2.4) as if we were using stopping times of the enlarged filtration \((\mathcal{G} _{t})_{t\ge 0}\), where \(\mathcal{G}_{t}=\mathcal{F}_{t}\vee \sigma ( \{\varGamma _{D}>s\},0\le s\le t)\).
Due to the assumed independence between the demographic uncertainty and the fund’s returns (i.e., \(\varGamma _{D}\) being independent of \((B_{t})_{t\ge 0}\)) and since the optimisation is over \(( \mathcal{F}_{t})_{t\ge 0}\)-stopping times, the value function can be rewritten by using Fubini’s theorem and (2.2) as
where \(\mathbb{E}[\cdot \,]\) is the expectation under ℙ, \(r(t):=\rho +\mu ^{S}(\eta +t)\), \(\beta (t):=\alpha +\mu ^{S}(\eta +t)\), \(G(t,x)=f(t)(x-K)\) and
Here \(a^{S}_{\eta +t}\) is the individual’s subjective valuation of the annuity, i.e.,
The function \(f(\cdot )\) in (2.6) is the so-called “money’s worth”.
Since we are in a Markovian setting, we have \(\mathbb{E}[\cdot \,| \mathcal{F}_{t}]=\mathbb{E}[\cdot \,|X_{t}]\). In particular, if \(X_{t}=x>0\) ℙ-a.s., we find it convenient to use the notation
Moreover, the process \(X\) is time-homogeneous so that
Using the above notations, for any given \((t,x)\in [0,T]\times (0,+ \infty )\), we can rewrite (2.5) as
where we also write \(s_{1}\le \tau \le s_{2}\) for \(\tau \in \mathcal{T}_{s_{1},s_{2}}\) (this should cause no confusion because all stopping times in this paper belong to \(\mathcal{T}_{s_{1},s_{2}}\) for some \(s_{1}\le s_{2}\)).
We notice that the state process in our problem formulation (2.7) is a time–space Markov process \((Y_{s})_{s\in [0,T-t]}\) defined by \(Y_{0}=(t,x)\) and \(Y_{s}:=(t+s,X^{x}_{s})\), \(s \in (0,T-t]\).
2.3 The variational problem
Before closing this section, we introduce the variational problem naturally associated to (2.7). Let ℒ be the second order differential operator associated to the diffusion (2.1), i.e.,
Assuming for a moment that \(V\) is regular enough, by applying the dynamic programming principle and Itô’s formula, we expect that the value function should satisfy the following variational inequality: for \((t,x)\in (0,T)\times \mathbb{R}_{+}\),
with terminal condition \(V(T,x)=G(T,x)\), \(x\in \mathbb{R}_{+}\). In the rest of the paper, we show that (2.8) holds in the a.e. sense with \(V \in C^{1}([0,T) \times \mathbb{R}_{+})\cap C([0,T] \times \mathbb{R}_{+})\) and \(V_{xx}\in L^{\infty }_{\mathrm{loc}}([0,T) \times \mathbb{R}_{+})\). Moreover, we study the geometry of the set where \(V=G\), i.e., the so-called stopping region.
3 Properties of the value function
In this section, we provide some continuity properties of the value function and useful probabilistic bounds on its gradient. In what follows, given a set \(A\subseteq [0,T]\times \mathbb{R}_{+}\), we sometimes write \(A\cap \{t< T\}:=A\cap ([0,T)\times \mathbb{R}_{+})\). Also, we make the next standing assumption in the rest of the paper.
Assumption 1
\(\mu ^{S}(\cdot )\) and \(\mu ^{O}(\cdot )\) are continuously differentiable on \([0,+\infty )\).
To study the optimisation problem (2.7), we find it convenient to introduce the function
which may be financially understood as the value of the option to delay the annuity purchase.
We can easily compute
where
An application of Itô’s formula gives
and therefore it is straightforward to verify (see (2.7)) that
Notice that (3.4) includes a deterministic discount rate which is not time-homogeneous. Optimal stopping problems of this kind are relatively rare in the literature. They feature technical difficulties which are more conveniently handled by considering a discounted version of the problem. Hence we introduce
Since the problem for \(w\) is equivalent to the one for \(v\) and \(V\), we focus from now on on the analysis of (3.5).
From (2.7), it is clear that \(V(t,x) \geq G(t,x)\) for all \((t,x)\in [0,T]\times \mathbb{R}_{+}\) so that \(w\) is nonnegative. Moreover, it is straightforward to check that \(w(t,x)\) is finite for all \((t,x)\in [0,T]\times \mathbb{R}_{+}\), thanks to well-known properties of \(X\) and to Assumption 3.1.
As usual in optimal stopping theory, we let
be the so-called continuation and stopping regions, respectively. We denote by \(\partial \mathcal{C}\) the boundary of the set \(\mathcal{C}\) and introduce the first entry time of \((t+\cdot ,X^{x}_{\cdot })\) into \(\mathcal{S}\), i.e.,
for \((t,x)\in [0,T]\times \mathbb{R}_{+}\).
Since \((t,x)\mapsto H(t,x)\) is continuous, it is not difficult to see that for any fixed stopping time \(\widetilde{\tau }\ge 0\), setting \(\tau :=\widetilde{\tau }\wedge (T-t)\), the map
is continuous as well. It follows that \(w\) is lower semi-continuous and therefore \(\mathcal{C}\) is open and \(\mathcal{S}\) is closed. Moreover, the finiteness of \(w\) and standard optimal stopping results (see [15, Corollary I.2.9]) guarantee that (3.6) is optimal for \(w(t,x)\).
For future frequent use, we introduce here a new probability measure \(\widetilde{\mathbb{P}}\) on \(\mathcal{F}_{T}\) defined by its Radon–Nikodým derivative
and notice that
It is well known that ℙ and \(\widetilde{\mathbb{P}}\) are equivalent on \(\mathcal{F}_{t}\) for all \(t\in [0,T]\).
Remark 2
If \(K=0\) in (2.3), problem (3.5) reduces to a deterministic problem. Noticing that

because \(\{\tau >s\}\) is \(\mathcal{F}_{s}\)-measurable, and thanks to Fubini’s theorem, one has

Then, using \(Z_{\tau }\) to change the measure (cf. (3.7)), we obtain
The latter is equivalent to the deterministic problem of maximising the function
As a result, the optimal annuitisation time only depends on \(t\) (as in [13]).
Remark 3
If we allow \(T=+\infty \) and assume that
then our problem (3.5) remains well posed. We notice that the finite horizon \(T\) only features in (3.5) as part of the definition of the admissible stopping times. Then it is intuitively clear that the major mathematical challenges related to the time-dependence of (3.5) arise from the properties of the map \(t\mapsto e^{-\int _{0}^{t}r(u)\,du}H(t,x)\). Such properties remain the same for \(T = +\infty \); hence the analysis presented below is also informative for the study of the case \(T = +\infty \).
The next proposition starts to analyse the regularity of \(w\) and provides a probabilistic characterisation for its gradient which is crucial for our subsequent analysis of the boundary of \(\mathcal{C}\).
Proposition 4
The value function\(w\)is convex in\(x\)for each\(t \in [0,T]\)and locally Lipschitz-continuous on\([0,T] \times \mathbb{R}_{+}\). Moreover, for almost every\((t,x) \in [0,T] \times \mathbb{R}_{+}\), we have
and there exists a constant\(C > 0\), independent of\((t,x)\), such that
Proof
The proof is divided into several steps.
Step 1 (convexity). Since \(x\mapsto e^{-\int _{0}^{t} r(u)\,du}H(t,x)\) is linear, it is not difficult to show that for \(x,y\in \mathbb{R}_{+}\), \(\lambda \in (0,1)\) and \(x_{\lambda }:= \lambda x+(1-\lambda )y\), we have
for any stopping time \(\tau \). Taking the supremum over \(\tau \in [0,T-t]\), the claim follows.
Step 2 (Lipschitz-continuity). Fix \((t,x)\in [0,T]\times \mathbb{R}_{+}\) and pick \(\varepsilon >0\). First we show that
with \(c>0\) independent of \((t,x)\). Let \(\tau _{*}=\tau _{*}(t,x)\) be optimal in \(w(t,x)\), hence admissible and suboptimal in \(w(t,x+\varepsilon )\), so that we have
where we used (3.8) for the last equality. For the upper bound, we repeat the above argument with \(\tau _{\varepsilon }^{+}:=\tau _{*}(t,x+ \varepsilon )\) optimal for \(w(t,x+\varepsilon )\) and find
Since \(\tau _{*}\) and \(\tau ^{+}_{\varepsilon }\) are smaller than \(T-t\), we have \(|w(t,x+\varepsilon )-w(t,x)|\leq c\, \varepsilon \) for a suitable \(c>0\) independent of \((t,x)\). By applying symmetric arguments, we can also prove that \(|w(t,x-\varepsilon )-w(t,x)|\leq c\, \varepsilon \) so that (3.11) holds. For future reference, we also notice that
Next we show that for all \(\delta >0\), \(x\in \mathbb{R}_{+}\) and any \(t\in [0,T-\delta ]\), we have
for some \(c_{\delta }>0\) only depending on \(\delta \), and for all \(\varepsilon \le T-t\). Let \(\tau _{*}=\tau _{*}(t,x)\) be optimal in \(w(t,x)\) and define \(\nu _{\varepsilon }:=\tau _{*}\wedge (T-t-\varepsilon )\) for \(\varepsilon >0\). Since \(\nu _{\varepsilon }\) is admissible and suboptimal for \(w(t+\varepsilon ,x)\), we get
Now we use that
where the last estimate follows by (3.2), (3.3) and Assumption 3.1, with a uniform constant \(c_{1}>0\) (recall that \(r(\cdot ) \ge 0\)). Plugging the above expression into the first term of (3.15) and using the mean value theorem for the second, we get
where \(\zeta (\omega )\in (\nu _{\varepsilon }(\omega ),\tau _{*}( \omega ))\). Notice that

and from (3.2), one obtains the bound

In conclusion, noticing that \(\nu _{\varepsilon }\le \tau _{*}\) and recalling (3.7) and (3.8), by a change of measure, we have

for a different constant \(C>0\). Using the Markov inequality, we obtain
which plugged back into (3.17) give
By using similar estimates and observing that \(\sigma _{\varepsilon } ^{+}:=\tau _{*}(t+\varepsilon ,x)\) is admissible and suboptimal for \(w(t,x)\), we get
where we have used again (3.16) and the change of measure.
Symmetric arguments then give
and
with \(\sigma _{\varepsilon }^{-}:=\tau _{*}(t,x-\varepsilon )\). Equations (3.18)–(3.21) imply (3.14), and combining (3.11) and (3.14), we conclude that \(w\) is in \(C([0,T]\times \mathbb{R}_{+})\), locally Lipschitz and differentiable a.e. in \([0,T)\times \mathbb{R}_{+}\).
Step 3 (gradient bounds). Let \((t,x)\in [0,T)\times \mathbb{R} _{+}\) be a point of differentiability of \(w\). Dividing (3.12) and (3.13) by \(\varepsilon \) and letting \(\varepsilon \to 0\) gives (3.9), as claimed. Moreover, dividing (3.18) by \(\varepsilon \) and letting \(\varepsilon \to 0\), we obtain the lower bound in (3.10). Finally, dividing (3.20) by \(\varepsilon \) and letting \(\varepsilon \to 0\), we get the upper bound in (3.10). □
The continuity of \(w\) and standard optimal stopping theory guarantee that for all \(t\in [0,T]\), the process
is a continuous supermartingale for all \(s\in [0,T-t]\), and \((W_{s\wedge \tau _{*}})_{s\in [0,T-t]}\) is a martingale.
The next corollary follows by standard PDE arguments used normally in the optimal stopping literature; see e.g. [10, Theorem 2.7.7].
Corollary 5
The function \(w\) is \(C^{1,2}\) inside \(\mathcal{C}\) and solves the boundary value problem
It may appear that (3.23) is given in a slightly unusual form, but one should remember that \(w(t,x)=e^{-\int _{0}^{t}r(u)\,du}v(t,x)\) (see (3.5)) so that for \(v\), we obtain the more canonical expression
The next technical lemma states some properties of \(w\) that will be useful to study the regularity of the boundary \(\partial \mathcal{C}\). Its proof is given in the Appendix.
Lemma 6
Assume\(g(t)< 0\)for\(t\in (0,T)\). Then:
-
(i)
\(x\mapsto w(t,x)\)is nonincreasing for all\(t\in [0,T]\).
-
(ii)
For any\(t\in [0,T]\), we have
$$\begin{aligned} \lim _{x\to \infty }w(t,x)=0. \end{aligned}$$(3.25) -
(iii)
For all\(t_{1}< t_{2}\)in\([0,T]\), we have\(\mathcal{S}\cap ((t_{1},t_{2})\times \mathbb{R}_{+})\neq \emptyset \).
It is worth noticing that (iii) does not exclude that there may exist \(t\in (0,T)\) such that \(\mathcal{S}\cap (\{t\}\times \mathbb{R}_{+})= \emptyset \).
4 Properties of the optimal boundary
In this section, we provide sufficient conditions for the boundary \(\partial \mathcal{C}\) to be represented by a function \(b\) of time. We establish connectedness of the sets \(\mathcal{C}\) and \(\mathcal{S}\) with respect to the \(x\)-variable and finally study Lipschitz-continuity of \(t\mapsto b(t)\). It is worth emphasising that this study is mathematically challenging because of the lack of monotonicity of the map \(t\mapsto b(t)\) and falls outside the scope of the existing probabilistic literature on optimal stopping and free boundary problems. In Sect. 5, we show that the Gompertz–Makeham mortality law (a mainstream model in actuarial science) leads naturally to the set of assumptions that we make below.
An initial insight on the shape of \(\mathcal{C}\) is obtained by noticing that the set
is contained in \(\mathcal{C}\). In fact, if \((t,x)\in \mathcal{R}\), then
with \(\tau _{\mathcal{R}}\) being the first exit time of \((t+s,X^{x} _{s})\) from ℛ. For all \(t\in [0,T]\) such that \(g(t)\neq 0\), the boundary \(\partial \mathcal{R}\) is given by the curve
Moreover, for each \(t\in [0,T]\), we denote the \(t\)-section of ℛ by
Remark 1
(a) Note that if \(g(\cdot )\) and \(K\ell (\cdot )\) in (3.2) have the same sign on \([0,T]\) (i.e., \(\gamma (\,\cdot \,)\le 0\)), then either \(\mathcal{R}=\emptyset \) or \(\mathcal{R}=[0,T]\times \mathbb{R}_{+}\). In the former case, \(\mathcal{S}=[0,T]\times \mathbb{R}_{+}\), while in the latter we have \(\mathcal{C}=[0,T]\times \mathbb{R}_{+}\).
(b) Recall (3.3). Consider \(t\in [0,T)\) such that \(g(t)<0\), or equivalently such that \(\ell (t)-\beta (t)-(\theta -\alpha )f(t)>0\). Then, if \(\theta \ge \alpha \) and \(K>0\), i.e., \(K\) is an acquisition fee, we have \(\mathcal{R}_{t}=[0,\gamma (t))\) and
The latter means that the annuity should not be purchased if the individual’s wealth is less than or equal to \(K\) and the fund’s value has a positive trend (net of dividend payments).
Motivated by (a) in the remark above, we later assume that \(\gamma ( \cdot )>0\) on \([0,T]\).
Now we exhibit sufficient conditions under which the probabilistic representation (3.9) easily provides the shape of the continuation and stopping regions.
Proposition 2
If\(g(\cdot )\)does not change its sign on\([0,T]\), the stopping region is characterised by a free boundary
In particular:
-
(i)
If\(g(t)\ge 0\)for all\(t\in [0,T]\), then\(\mathcal{S}=\{(t,x)\in [0,T]\times \mathbb{R}_{+}: x\le b(t)\}\).
-
(ii)
If\(g(t)\le 0\)for all\(t\in [0,T]\), then\(\mathcal{S}=\{(t,x)\in [0,T]\times \mathbb{R}_{+}: x\ge b(t)\}\).
Proof
In case (i), we have \(w_{x}(t,x)\geq 0\). This implies
and the claim follows. A similar argument applies to case (ii). □
For each \(t\in [0,T]\), we define \(\mathcal{S}_{t}:=\{x\in \mathbb{R} _{+}: (t,x)\in \mathcal{S}\}\) and its complement \(\mathcal{C}_{t}= \mathbb{R}_{+}\setminus \mathcal{S}_{t}\). These are the so-called \(t\)-sections of the stopping and continuation set, respectively. Clearly, \(\mathcal{S}_{t}=[0,b(t)]\) under (i) and \(\mathcal{S}_{t}=[b(t),+ \infty )\) under (ii) of the above proposition.
In the rest of the paper, we make the next standing assumption. This will hold in all the results below without explicit mention. In Sects. 5 and 6, we discuss its range of applicability and some extensions.
Assumption 3
Assume that \(\gamma (t)>0\) for all \(t\in [0,T]\) and also that its limit \(\gamma (T):=\lim _{t\to T}\gamma (t)\) exists (possibly infinite). Moreover, we have
Remark 4
It is worth discussing a financial/demographic interpretation of our assumption. We start by noticing that the money’s worth \(f(\cdot )\) should change slowly as a function of time. Indeed, in models with a deterministic mortality force like ours, it is unreasonable to imagine that the individual or the insurer may have drastic changes in their views on survival probabilities (this could instead be the case in stochastic mortality models). Moreover, it is reasonable that an individual who is healthier than the average of the population at the outset will remain so over time, so that the map \(t\mapsto f(t)-1\) should not change sign (this again would be less reasonable in stochastic mortality models). Finally, we observe that as \(t\to \infty \), one has \(f(t)\to 1\) because eventually the individual and the insurer should agree on the survival probabilities.
As explained, \(f'(\cdot )\) is small; hence the leading terms in \(g(\cdot )\) are those involving \(\beta \) and \(\theta -\rho \) (see (3.3)). In particular, they highlight the interplay between the financial and demographic risk for the individual. On the one hand, \(\beta (t)=\alpha +\mu ^{S}(\eta +t)\) in (2.5) can be interpreted as the dividends arising from the financial investment adjusted by the demographic risk – notice that an individual with high subjective mortality force is less likely to annuitise and would rather enjoy the return on a financial investment; on the other hand, \(\theta -\rho \) is closely related to the risk premium of the financial investment. In \(g(\cdot )\), these two terms are weighted exactly with \(1-f(\cdot )\) and \(f(\cdot )\), respectively. Moreover, \(g(\cdot )\) in (3.4) represents the marginal gain, per unit of investment in the stock, arising from delaying the annuitisation by one time unit.
In light of all considerations so far (recall that \(f(\cdot )-1\) does not change sign and \(f'\) is almost negligible), it is clear from the formula in (3.3) that if \(f(t)>1\) (\(f(t)<1\)) for all \(t\in (0,T)\), i.e., the individual finds the annuity underpriced (overpriced), and \(\theta <\rho \) (\(\theta >\rho \)), then \(g(\cdot )\) remains negative (positive) on \([0,T]\). This conclusion is financially clear because an underpriced annuity and the prospect of a negative risk premium would give the investor a negative marginal gain (per unit of stock) from delaying the annuity purchase (and vice versa).
Finally, if \(f(t)>1\) (\(f(t)<1\)) for all \(t\in (0,T)\) and \(\theta > \rho \) (\(\theta <\rho \)) then \(g(\cdot )\) may change its sign. However, if for example \(t\mapsto \beta (t)\) is monotonic (i.e., the mortality force is monotonic), then the change in sign is unlikely to occur more than once, due to the slow variation in time of the money’s worth \(f\). Motivated by this observation, we conduct numerical experiments in Sect. 5 using Gompertz–Makeham mortality force that suggest that, when a change in the sign of \(g(\cdot )\) occurs, this is likely to be over a time period longer than 20 years. It is therefore mainly for mathematical interest that we allow \(g(\cdot )\) to vanish at time \(T\). Indeed, we will also show in Sect. 6 that this extra flexibility enables us to extend our results to some cases when \(g(\cdot )\) changes its sign once on \((0,T)\).
Remark 5
The positivity of \(\gamma (t)\) in Assumption 4.3 rules out the cases when \(\mathcal{S}=[0,T]\times \mathbb{R}_{+}\) or \(\mathcal{C}=[0,T]\times \mathbb{R}_{+}\) (see point (a) of Remark 4.1).
Conditions (i) and (ii) in Assumption 4.3 are indeed supported by numerical experiments illustrated in Figs. 5.1 and 5.3 in Sect. 5, where \(g(\cdot )\) does not change sign or it changes sign at most once.
Notice that Assumptions 3.1 and 4.3 imply \(\gamma \in C(0,T)\). It is not hard to verify that the following properties hold.
Lemma 6
(a) If\(g(\cdot )>0\)on\((0,T)\), then for each\(t\in (0,T)\), there exists\(g_{0}(t)>0\)such that
(b) If\(g(\cdot )<0\)on\((0,T)\), then for each\(t\in (0,T)\), there exists\(g_{0}(t)>0\)such that
The next simple lemma will be useful in what follows.
Lemma 7
If\(K\ell (t)\le 0\)for all\(t\in [0,T]\), then\(\lim _{x\to 0}w(t,x)=0\)for all\(t\in [0,T]\). Hence\([0,T]\times \{0\}\subseteq \mathcal{S}\).
Proof
Recalling (3.2) and using dominated convergence, we obtain
□
Next we show that the optimal boundary is locally Lipschitz-continuous on \([0,T)\), hence also bounded on any compact interval. Some of the ideas in the proof below are borrowed from Theorem 4.3 in [5]. However, we cannot directly apply results of [5] since Condition (D) therein corresponds to requiring that there exists \(c>0\) such that
The latter bound is clearly impossible in our setting since the left-hand side in the equation above is linear in \(x\).
Theorem 8
The optimal boundary\(b(\cdot )\)is locally Lipschitz-continuous on\([0,T)\).
Proof
In this proof, most of the arguments are symmetric when we consider cases (i) and (ii) of Assumption 4.3.
We start by noticing that in case (i) of Assumption 4.3, Lemma 4.7 holds (because \(\gamma (\cdot )>0\)) and also \(w_{x}> 0\) inside \(\mathcal{C}\) due to (3.9). The free boundary \(b\) is the zero-level set of \(w\); then continuity of \(w\) and Lemma 4.7 imply that for each \(t\in [0,T)\), we can find \(\delta >0\) sufficiently small so that the equation \(w(t,x)=\delta \) has a solution \(x=b_{ \delta }(t)\). The \(\delta \)-level set of \(w\) is locally given by a continuous function \(b_{\delta }\). Moreover, \(b_{\delta }(t)>b(t) \ge 0\). The family \((b_{\delta })_{\delta >0}\) decreases as \(\delta \to 0\) so that its limit \(b_{0}\) exists, is upper semi-continuous as a decreasing limit of continuous functions, and \(b_{0}(t)\ge b(t)\). Since \(w(t,b_{\delta }(t))=\delta \), it is clear that taking limits as \(\delta \to 0\), we get \(w(t,b_{0}(t))=0\) and therefore \(b_{0}(t)\le b(t)\) so that we conclude that
for all \(t\in [0,T)\). Similarly, in case (ii) of Assumption 4.3, we have \(w_{x}<0\). Then \(b_{\delta }(t)< b(t)\) and (4.5) holds (if \(b(t)=+\infty \), the limit is \(+\infty \)). Finiteness of \(b_{\delta }\) is always guaranteed by Lemma 3.6.
Since \((t,b_{\delta }(t))\in \mathcal{C}\) for all \(t\in [0,T)\) and \(w_{x}(t,b_{\delta }(t))\neq 0\) under either (i) or (ii) of Assumption 4.3, an application of the implicit function theorem gives (recall that \(w\) is in \(C^{1}\) in \(\mathcal{C}\))
Next we obtain a bound on \(b'_{\delta }\), which is independent of \(\delta \), for any bounded interval \([t_{0},t_{1}]\subseteq (0,T)\). This allows the use of the Arzelà–Ascoli theorem to extract a sequence \((b_{\delta _{j}})_{j \ge 1}\) such that as \(j\to \infty \), \(b_{\delta _{j}}\) converges uniformly on \([t_{0},t_{1}]\) to a Lipschitz-continuous function. Uniqueness of the limit and (4.5) imply that \(b(\cdot )\) is locally Lipschitz.
To find the uniform bound on \(b'_{\delta }\), we divide the proof into steps.
Step 1. Let us start by observing that \(w_{x}(t,b_{\delta }(t))>0\) in case (i) of Assumption 4.3, so that
To simplify notation, in what follows, we set \(x_{\delta }:=b_{\delta }(t)\) and \(t\) is fixed. To estimate the numerator in (4.7), we use the bound in (3.10), thus obtaining
where \(\tau _{\delta }=\tau _{*}(t,x_{\delta })\) for simplicity. Plugging (4.8) into (4.7), we obtain
A similar estimate but with the denominator replaced by \(-w_{x}(t,x _{\delta })\) can be obtained, up to obvious changes, in the setting of (ii) in Assumption 4.3, i.e.,
At this point, in order to make (4.9) and (4.10) uniform in \(\delta \), we must look at their limits as \(\delta \to 0\). For this, we consider separately cases (i) and (ii) of Assumption 4.3.
Step 2 – Case (i). Here \(\mathcal{S}_{t}=[0,b(t)]\), and since \(b\le \gamma \) and \(\gamma \in C(0,T)\), \(b\) is locally bounded. Notice that under \(\widetilde{\mathbb{P}}\) defined in (3.7), the process \(\widetilde{B}_{s}=B_{s}-\sigma s\), \(s\in [0,T-t]\), is a Brownian motion and the individual’s wealth (2.1) started from \(x_{\delta }\) may be written as
Then for any \(s\in [0,T-t]\), we have
where the inequality uses that
Thus \(\widetilde{\mathbb{E}}[\, \tau _{\delta }]\geq \mathbb{E}[\, \tau _{\delta }]\). Substituting this estimate in the numerator of (4.9) allows us to write
Recalling Assumption 3.1, (3.9) and (4.3), it is now clear that there exists a constant \(c>0\) independent of \((t,x_{\delta })\) such that
Hence plugging the latter into (4.12), we conclude that
with \(c'>0\) a suitable constant and where we used \(b_{\delta }(t) \leq 1+ \gamma (t)\) as \(\delta \to 0\). Then the uniform bound in (4.14) implies that \(b\) is locally Lipschitz as claimed.
Step 2 – Case (ii). Here \(\mathcal{S}_{t}=[b(t),+\infty )\). The analysis in this part is more involved than in the previous case. An argument similar to (4.11) gives \(\mathbb{E}[ \tau _{\delta }]\ge \widetilde{\mathbb{E}}[\tau _{\delta }]\), which unfortunately does not help with the estimate in (4.10). So we need to proceed in a different way.
It follows from (4.10) that in order to find a bound for \(|b'_{\delta }(t)|\), we must find bounds for \(\widetilde{\mathbb{E}}[ \tau _{\delta }]/|w_{x}(t,x_{\delta })|\) and \(\mathbb{E}[\tau _{\delta }]/|w_{x}(t,x_{\delta })|\) (recall that \(w_{x}\le 0\)). The former can be bounded easily by using (3.9) and (4.4), since
with suitable \(c>0\). Then (4.15) implies
The other term requires more work because the expectation in the numerator is taken with respect to ℙ, whereas the one in the denominator uses \(\widetilde{\mathbb{P}}\). Although we can still use (4.15) to estimate the ratio \(\mathbb{E}[\tau _{\delta }]/|w_{x}(t,x _{\delta })|\), now we end up with
Our next task is to find a bound for the ratio \(\mathbb{E}[\tau _{ \delta }]\,/\,\widetilde{\mathbb{E}}[\tau _{\delta }]\).
Due to Assumption 4.3, there exists \(a>0\) such that \(\gamma (t)\ge 2a\) for \(t\in [0,T]\), and we denote
For this part of the proof, it is convenient to think of \(\varOmega \) as the canonical space of continuous paths \(\omega =\{\omega (t),t\ge 0 \}\) and denote by \(\vartheta _{s}\) the shifting operator \(\vartheta _{s} \,\omega = \{\omega (s+t),t\ge 0\}\). Moreover, we recall that \(\widetilde{\mathbb{E}}_{t,x}[\cdot \,]=\widetilde{\mathbb{E}}[ \cdot \,|X_{t}=x]\) and \(\mathbb{E}_{t,x}[\cdot \,]=\mathbb{E}[\cdot \,|X_{t}=x]\). With this notation, we must be careful that for fixed \((t,x_{\delta })\) and any \(s\ge 0\), we have \(\mathbb{P}[\tau _{\delta }>s]=\mathbb{P}_{t,x_{\delta }}[\tau _{*}-t>s]\) and \(\widetilde{\mathbb{P}}[\tau _{\delta }>s]=\widetilde{\mathbb{P}}_{t,x _{\delta }}[\tau _{*}-t>s]\), because
Our first estimate gives
for a suitable constant \(c_{1}>0\), independent of \((t,x_{\delta })\). Next we obtain

The last term can be further simplified via

where we have used that \(\{\tau _{*}< T\}\subseteq \{X_{\tau _{*}}\ge \gamma ({\tau _{*}})\}\) under \(\mathbb{P}_{t,x_{\delta }}\) and \(\gamma ({\tau _{*}})\ge 2a\). The last term in the above expression may be estimated by using iterated conditioning and the strong Markov property as

where

Notice that the strict positivity in (4.22) may be verified by using the known joint law of Brownian motion and its running supremum. Indeed, recalling that \(\gamma (t)\ge 2a\) for all \(t\in [0,T]\), we have


with \(c_{3}=a\wedge c_{2}\). Now we plug the latter into (4.18) and then back into (4.17) and get
with \(c'=c c_{1} c_{3}>0\) a constant independent of \((t,x_{\delta })\). The above expression and (4.16) may now be substituted into (4.10) and give
where \(c''>0\) is a suitable constant.
We recall that in case (ii) of Assumption 4.3, Lemma 3.6 (iii) implies that for any \(0\le t_{0}< t_{1}< T\), we can find \(t_{2}\in (t_{0},t_{1})\) such that \(b_{\delta }(t_{2})\le b(t _{2})<+\infty \). The latter and (4.24) allow us to apply Gronwall’s inequality to obtain that for any \(0\le t_{0}< t_{1}< T\), there exists a constant \(c_{t_{0},t_{1}}>0\) independent of \(\delta \) and such that
The same bound therefore holds for the boundary \(b\), and this shows that \(b\) is bounded on any compact interval. Moreover, (4.24) and (4.25) also give a uniform bound for \(b'_{\delta }\) on \([t_{0},t_{1}]\) as needed. □
Lipschitz-continuity of the boundary has important consequences regarding the regularity of the value function \(w\), which we summarise below.
Proposition 9
The value function\(w\)is continuously differentiable on the set\([0,T) \times \mathbb{R}_{+}\). Moreover, for all\(\varepsilon >0\), the function\(w_{xx}\)is continuous on the closure of the set\(\mathcal{C}\cap \{t< T-\varepsilon \}\).
Proof
Corollary 3.5 tells us that \(w_{t}\) and \(w_{x}\) are continuous at all points in the interior of \(\mathcal{C}\) and of \(\mathcal{S}\), and thus it remains to analyse the regularity of \(w\) across the boundary. In order to do that, it is crucial to observe that since \(t\mapsto b(t)\) is locally Lipschitz, the law of the iterated logarithm implies that \(\tau _{*}\) is indeed equal to the first time \(X\) goes strictly below the boundary, in case (i), or strictly above the boundary, in case (ii). In other words, the first entry time to \(\mathcal{S}\) is equal to the first entry time to its interior part. This is an important fact that can be used to prove that \((t,x)\mapsto \tau _{*}(t,x)\) is continuous ℙ-a.s., and is zero at all boundary points (see e.g. [4, Lemma 5.1 and Proposition 5.2]).
Fix a point \((t_{0},x_{0})\in \partial \mathcal{C}\cap \{t< T\}\) and take a sequence \((t_{n},x_{n})_{n\ge 1} \subseteq \mathcal{C}\) with \((t _{n},x_{n})\to (t_{0},x_{0})\) as \(n\to \infty \). Continuity of \((t,x)\mapsto \tau _{*}(t,x)\) and the discussion above imply that \(\tau _{*}(t_{n},x_{n})\to 0\) ℙ-a.s. as \(n\to \infty \). The latter and (3.9) and (3.10) give \(w_{x}(t_{n},x_{n})\to 0\) and \(w_{t}(t_{n},x_{n})\to 0\). Since \((t_{0},x_{0})\) and the sequence \((t_{n},x_{n})\) were arbitrary, we get \(w\in C^{1}([0,T)\times \mathbb{R}_{+})\).
The continuity of \(w_{xx}\) follows from (3.23). We know from Corollary 3.5 that \(w_{xx}\) is continuous in \(\mathcal{C}\). Moreover, for any \((t_{0},x_{0})\in \partial \mathcal{C}\cap \{t< T\}\), we can take limits in (3.23) as \((t,x)\to (t_{0},x_{0})\) with \((t,x)\in \mathcal{C}\) and use \(w(t_{0},x_{0})=w_{x}(t_{0},x _{0})=w_{t}(t_{0},x_{0})=0\) to obtain
which proves our claim. □
As will be discussed in Sect. 5, for the numerical evaluation of the optimal boundaries, it is important to find the limit value of \(b(t)\) when \(t\to T\). This is analysed in the next proposition. For future use, we introduce the function (recall \(g_{0}\) from Lemma 4.6)
Proposition 10
Recall that\(\gamma (T):=\lim _{t\to T}\gamma (t)\)exists but could be infinite (Assumption4.3). If\(u_{0}\in L^{1}(0,T)\), then\(b(\cdot )\)has the limit
Proof
Let us first consider case (i) in Assumption 4.3. Here we recall the notation \(x_{\delta }=b_{\delta }(t)\), \(\tau _{\delta }=\tau _{*}(t,x _{\delta })\) used in the proof of Theorem 4.8. From (4.6) and the upper bound in (3.10), we get (recall that \(w_{x}>0\))
where the last inequality uses \(\widetilde{\mathbb{E}}[\tau _{\delta }] \ge \mathbb{E}[\tau _{\delta }]\) which follows from (4.11). Employing (4.13) and letting \(\delta \rightarrow 0\), we find
where we have also used that \(b\) is bounded from above by \(\gamma \) (see (4.2)) and \(C'=C/c\). Recalling \(u_{0}(\cdot )\) and setting \(\hat{b}(t)=b(t)+C' \int _{0}^{t} u_{0}(s) \,ds\), the mapping \(t\mapsto \hat{b}(t)\) is increasing. Thus \(\lim _{t\uparrow T} \hat{b}(t) \) exists, and since \(u_{0}\) is integrable and positive on \([0,T]\), the limit \(b(T-) := \lim _{t\uparrow T} b(t)\) exists as well.
Notice that \(b(t)\le \gamma (t)\) for all \(t\in [0,T)\) and therefore \(b(T-)\le \gamma (T)\). Recall that \(\gamma (T)>0\) due to Assumption 4.3. For the proof of (4.27), we follow the approach of [3]. Arguing by contradiction, we assume \(b(T-)<\gamma (T)\). Then we can pick \(a\), \(c\) such that \(b(T-)< a< c<\gamma (T)\) and \(t^{\prime }< T\) such that \((a,c)\times [t^{\prime },T)\subseteq \mathcal{C}\). It is convenient here to work with \(v\) rather than \(w\) (see (3.5)) and to refer to (3.24). Let \(\varphi \in C ^{\infty }(a,c)\) with \(\varphi \geq 0\) and define \(F_{\varphi }(s):= \int _{a}^{c}v_{t}(s,y)\varphi (y)\,dy\). Now, denoting by \(\mathcal{L} ^{*}\) the adjoint of the operator ℒ, we have
since \(v(T,y)=0\) and \(H(T,y)<0\) for \(y\in (a,c)\). From the above, we also deduce that \(F_{\varphi }(\cdot )\) is continuous up to \(T\); thus there exists \(\delta >0\) such that \(F_{\varphi }(s)>0\) for \(s\in [T- \delta ,T]\) and
since \(v(T-\delta ,y)>0\), \(y\in (a,c)\). This is a contradiction.
Consider now case (ii) of Assumption 4.3. Since \(b(t)\ge \gamma (t)\) for all \(t\in [0,T]\), it is obvious that (4.27) holds if \(\gamma (T)=+\infty \). For the case \(\gamma (T)<+\infty \), we recall (4.6) and notice that (3.10) implies
If we now recall (4.16) and (4.23), we find
for a suitable \(c>0\). Since \(u_{0}\in L^{1}(0,T)\) and \(\gamma \in C((0,T])\), the function \(1/g_{0}(t)\) is integrable on \([0,T]\). Gronwall’s lemma applied to (4.28) guarantees that
with \(t_{0}\in (0,T)\) arbitrarily chosen. It was shown in Theorem 4.8 that \(b\) is bounded on any compact subset of \((0,T)\), and therefore taking limits as \(\delta \to 0\) and recalling (4.5), we find that \(b\) is indeed bounded on \([0,T]\). This fact and (4.28) in turn imply that \(b'(t)\le c_{0}/g_{0}(t)\) a.e. on \([0,T]\) for a suitable \(c_{0}>0\) only depending on \(t_{0}\). We can therefore define \(\hat{b}(t):=b(t)-c_{0}\int _{0}^{t} 1/g_{0}(s) \,ds\), and the mapping \(t\mapsto \hat{b}(t)\) is nonincreasing so that \(\hat{b}(T-):= \lim _{t\to T}\hat{b}(t)\) exists. Since \(1/g_{0}(t)\) is integrable and positive on \([0,T]\), \(b(T-) :=\lim _{t\to T}b(t)\) exists, too, is finite and \(b(T-)\ge \gamma (T)\). To prove (4.27), we argue by contradiction, assuming \(b(T-)>\gamma (T)\). Then following analogous arguments to those employed in the proof of case (i) above, we reach the desired contradiction. □
Remark 11
In general, the map \(s\mapsto e^{-\int _{0}^{t+s}r(u)\,du}H(t+s,x)\) is not monotonic. As a consequence, it becomes extremely challenging (if possible at all) to determine whether \(b(\cdot )\) is monotonic or not. For numerical evidence of nonmonotonic boundaries, see Sect. 5.
4.1 Characterisation of the free boundary and the value function
In the next theorem, we find nonlinear integral equations that characterise uniquely the free boundary and the value function. Here we notice that all regularity properties of \(w\) obviously transfer to \(V\) of (2.7), due to (3.1) and (3.5). In particular, we have \(V\in C^{1}([0,T)\times \mathbb{R}_{+})\) and \(V_{xx}\in L^{ \infty }_{\mathrm{loc}}([0,T)\times \mathbb{R}_{+})\), with the only discontinuity of \(V_{xx}\) occurring across \(\partial \mathcal{C}\). It is important to remark that Corollary 3.5 and the remaining properties of \(w\) studied above imply that \(V\) indeed solves (2.8) in the almost everywhere sense (more precisely, at all points \((t,x)\notin \partial \mathcal{C}\)).
Theorem 12
For all\((t,x)\in [0,T]\times \mathbb{R}_{+}\), the value function (2.7) has the representation

Recall (4.26) and assume\(u_{0}\in L^{1}(0,T)\). In case (i) of Assumption4.3 (resp. in case (ii)), the optimal boundary\(b\)is the unique continuous solution, smaller (resp. larger) than\(\gamma \), of the following nonlinear integral equation: for all\(t\in [0,T]\),

with\(b(T-)=\gamma (T)\) (cf. (4.27)).
Proof
Here we only show how to obtain (4.29). Then inserting \(x=b(t)\) in (4.29) and using \(V(t,b(t))=G(t,b(t))\), we get (4.30). The proof of uniqueness is standard in the modern optimal stopping literature and dates back to [14] (for more examples, see [15, Chaps. VII and VIII]). However, we provide the full argument in the Appendix for the interested reader.
Let \(( V^{(n)})_{n \geq 0}\) be a sequence in \(C^{\infty }([0,T)\times \mathbb{R}_{+})\) such that (see [8, Sect. 7.2])
as \(n\uparrow \infty \), uniformly on any compact set, and
Let \(( K_{m})_{m \geq 0}\) be a sequence of compact sets increasing to \([0,T]\times \mathbb{R}_{+}\) and define
Then an application of Itô calculus gives
We want to let \(n\uparrow \infty \) and use (4.31) and (4.32), upon observing that \((t+s,X_{s})\) lies in a compact for \(s\le \tau _{m}\) and that its law is absolutely continuous with respect to Lebesgue measure on \([0,T]\times \mathbb{R}_{+}\). The latter in particular implies \(\mathbb{P}[(t+s,X^{x}_{s})\in \partial \mathcal{C}]=0\) for all \(s\in [0,T-t)\) and enables the use of (4.32). Recall that \(V\), \(V_{x}\), \(V_{t}\) and \(V_{xx}\) are locally bounded. Then dominated convergence and (4.33) yield
Therefore, using (2.8) (or equivalently, Corollary 3.5), we also find

Finally we take \(m\uparrow \infty \), use that \(\tau _{m} \uparrow (T-t)\) and \(V(T,x)=G(T,x)\), and apply dominated convergence to obtain (4.29). □
5 Numerical findings
Here we apply the results obtained in the previous sections to some situations of practical interest. For simplicity, throughout the section, we take \(\rho =\widehat{\rho }\). A standard choice to model the force of mortality is the so-called Gompertz–Makeham law, which corresponds to
where \(A, B, C \in {\mathbb{R}}\) are estimated by statistical data of the population. For simplicity, here we assume \(A=0.00055845\), \(B=0.000025670\), \(C=1.1011\) as in [9].Footnote 2 Time is measured in years, and we consider two different scenarios:
- (a):
-
\(f(t)\equiv f>0\) (see (2.6)) and \(\mu ^{S}(\cdot )= \mu (\cdot )\);
- (b):
-
\(\mu ^{O}(\cdot )=\mu (\cdot )\) and \(\mu ^{S}(\cdot )=(1+\bar{ \mu })\mu ^{O}(\cdot )\) with \(\bar{\mu } \in (-1,+\infty )\).
In the first scenario, the money’s worth function (2.6) is constant. If the individual believes she is healthier than the average in the population, then \(\mu ^{S}(\,\cdot \,) < \mu ^{O}(\,\cdot \,)\) and therefore \(f>1\). Conversely, for an individual who is pessimistic about her health, \(\mu ^{S}(\,\cdot \,) > \mu ^{O}(\,\cdot \,)\) and therefore \(f<1\). It is important to notice that the function \(g\) in (3.3) is monotonic increasing (decreasing) if \(f\) is a constant smaller (greater) than 1.
The second scenario uses the so-called proportional hazard rate transformation, introduced in actuarial science by Wang ([20], see also [13]). If \(\bar{\mu }<0\) (resp. \(\bar{\mu }>0\)), the individual considers herself healthier (resp. less healthy) than the average. The limit case \(\bar{\mu }\to -1\) is not relevant in practice as it corresponds to an individual whose life expectancy is infinite. Similarly, the case \(\bar{\mu }\rightarrow +\infty \) is also irrelevant in practice as it corresponds to an individual who believes she is about to die. An important difference between scenarios (a) and (b) above is that in the latter, the money’s worth \(f\) varies over time. In particular, if \(\bar{\mu }<0\) (resp. \(\bar{\mu }>0\)), then \(f(t)>1\) (resp. \(f(t)< 1\)) for all \(t\in [0,T]\).
We notice that in all our numerical experiments, the function \(\ell (\,\cdot \,)\) of (3.3) is positive on \([0,T]\), so that the sign of \(\gamma \) in (4.2) only depends on that of \(K\) and \(g\). For the reader’s convenience, we also recall the standard numerical algorithm to compute (4.30) (under the assumptions of Theorem 4.12). We take an equally spaced partition \(0=t_{0}< t_{1}< \cdots <t_{n-1}<t_{n}=T\) with \(h:=t_{i+1}-t_{i}\). Starting from \(b(T)=\gamma (T)\), for \(i=1,2,\ldots n\), we solve
where

Notice that the above formula is intended for \(\mathcal{S}_{t}=[0,b(t)]\). To deal with the case \(\mathcal{S}_{t}=[b(t),+ \infty )\), we must change the indicator variable in the last expression in the obvious way.
Unless otherwise specified, in what follows we take \(T=30\), \(\eta =50\), \(\theta =4.5\%\), \(\alpha =3.5\%\), \(\sigma =10\%\) and \(\widehat{\rho }=\rho =4\%\) (we take \(\widehat{\rho }=\rho \) just for simplicity).
Scenario (a). In Fig. 5.1, the function \(g\) in (3.3) is computed for different values of the constant \(f\). As noticed in [9], it is reasonable to expect that the value of \(f\) is close to 1. Notice that if \(f\) is high enough (\(f=1.2\)), \(g\) remains always negative even if \(\theta >\rho \). We observe that \(g\) varies slowly and in most cases it does not change sign, as required in Assumption 4.3. However, if \(g\) changes its sign (at most once, since \(g\) is monotonic), we can still apply our methods as described in more detail in Sect. 6.
Figure 5.2 shows the optimal annuitisation regions and boundaries examining two of the cases considered in Fig. 5.1, where \(g\) is either negative (\(f=1.2\)) or positive (\(f=0.8\)) on \([0,T]\). We note that in the former case, if \(K \leq 0\), then an immediate annuitisation is optimal for all \((t,x)\in [0,T]\times \mathbb{R}_{+}\) (see Remark 4.1). In the presence of a fixed acquisition fee \(K>0\), individuals instead annuitise as soon as the fund’s value exceeds the boundary \(b(\cdot )\) (left plot in Fig. 5.2). On the other hand, in the case \(f=0.8\), if \(K \geq 0\), the annuity is never purchased (Remark 4.1). In the presence of a fixed tax incentive \(K<0\), the annuity is purchased as soon as the fund’s value falls below the boundary \(b(\cdot )\) (right plot in Fig. 5.2).
Scenario (b). In Fig. 5.3, we look at Scenario (b) and the function \(g\) is plotted for different values of the constant \(\bar{\mu }\) for \(\theta <\rho \) (left plot) and \(\theta >\rho \) (right plot). We note that in a right neighbourhood of zero, \(g\) has the same sign as \(\theta -\rho \). For most parameter choices, either \(g\) does not change sign or it changes once. Notice, however, that the change in sign occurs for \(t\approx 22\) years; hence Assumption 4.3 is very reasonable.
The optimal annuitisation regions and their boundaries are presented in Fig. 5.4. Remarkably, we observe a nonmonotonic optimal boundary in the left plot. In the case \(g<0\), an accurate numerical solution of the integral equation for \(b\) needs a very fine partition of the interval \([0,T]\), which results in long computation times. We believe this is due to the steep gradient of \(b\) near \(T\) and to its lack of monotonicity. To simplify our analysis (which is intended for illustrative purposes only), we consider shorter time horizons for the investor than in scenario (a), i.e., \(T=9\) years.
In Fig. 5.5, we also study the sensitivity of the annuitisation boundary with respect to \(\bar{\mu }>0\). Recall that as \(\bar{\mu }\) increases, the individual considers herself increasingly less healthy than the average population. As a result, we observe that the boundary \(b(\cdot )\) is pushed downward and the continuation region expands. This is intuitively clear because annuities are financially less appealing for individuals with shorter (subjective) life expectancy.
6 Final remarks and extensions
As discussed in Remark 4.4, our main technical assumption (Assumption 4.3) is supported by numerical experiments on the Gompertz–Makeham mortality law. The latter is widely used in the actuarial profession; hence it is a natural choice from the modelling point of view. We also notice that Assumption 4.3 allows \(g(T)=0\). This condition is mainly of mathematical interest. Indeed, it enables extensions of our results to cover examples where \(g\) is monotonic on \([0,T]\) and changes sign once. The latter examples are observed in Figs. 5.1 and 5.3 (although the change of sign occurs only on rather long time horizons e.g. \(T>20\) years). On the other hand, it appears that the function \(\ell (\cdot )\) (see (3.3)) is positive in all our numerical experiments.
Here we explain how our results can cover extensions to the case of \(g(\cdot )\) changing sign once. We consider separately the cases \(K<0\) and \(K>0\). From now on, we assume that \(g\) is monotonic and there exists \(t_{0}\in (0,T)\) such that \(g(t_{0})=0\). We also assume that \(\ell (t)> 0\) for \(t\in [0,T]\) and recall ℛ and \(\gamma \) from (4.1) and (4.2).
Case \(K<0\) .
(1) (\(g(\cdot )\)decreasing). In this setting, we have \(\gamma (t)>0\) for \(t\in [0,t_{0})\) with \(\gamma (t)\uparrow +\infty \) as \(t\uparrow t_{0}\). Moreover, ℛ lies above the curve \(\gamma \) on \([0,t_{0})\). For \(t\in [t_{0},T]\), we have \(\mathcal{R}=\emptyset \) and therefore \(\mathcal{S}\cap \{t\ge t_{0} \}=[t_{0},T]\times \mathbb{R}_{+}\) (see Remark 4.1). This implies that \(t_{0}\) is an effective time horizon for our optimisation problem (2.7) since it is optimal to immediately stop for any later time. From a mathematical point of view, this means that we can equivalently study (2.7) with \(T\) replaced by \(t_{0}\). On the effective time interval \([0,t_{0}]\), part (i) of Assumption 4.3 holds and we can repeat the analysis carried out in Sects. 3 and 4.
(2) (\(g(\cdot )\)increasing). In this setting, we have \(\mathcal{R}=\emptyset \) for \(t\in [0,t_{0}]\) while on the interval \((t_{0},T]\), we have \(\gamma (\cdot )>0\) with \(\gamma (t)\uparrow + \infty \) as \(t\downarrow t_{0}\) and ℛ lies above the curve \(\gamma \). We can therefore study problem (2.7) on the restricted time interval \((t_{0},T]\) where our Assumption 4.3 holds. This gives \(\mathcal{S}_{t}=[0,b(t)]\) for \(t\in (t_{0},T]\) and all the results from the previous sections hold.
Moreover, we can show that \(\mathcal{S}_{t}=[0,b(t)]\) also for \(t\in [0,t_{0}]\) (with \(b(t)\) possibly infinite). For that we recall that \(w(t,\,\cdot \,)\) is convex for each \(t\in [0,T]\) (Proposition 3.4) and \(w(t,0+)=0\) (see Lemma 4.7). The latter two properties imply \(\mathcal{S}_{t}=[0,b(t)]\) for \(t\in [0,t_{0}]\) as claimed and \(w_{x}(t,\,\cdot \,)\ge 0\) for all \(t\in [0,t_{0}]\).
In summary, \(\mathcal{S}_{t}=[0,b(t)]\) for all \(t\in [0,T]\) and most of the analysis in Sect. 4 carries over to this setting. However, it should be noted that the methods used in Theorem 4.8 only allow to establish Lipschitz-continuity of \(b\) on \([t_{0},T]\). A complete study of the boundary on \([0,t_{0}]\) requires new methods, and we leave it for future work.
Case \(K>0\) .
(1) (\(g(\cdot )\)decreasing). Here \(\mathcal{R}\cap \{t\le t _{0}\}=[0,t_{0}]\times \mathbb{R}_{+}\), so that it is optimal to delay the annuity purchase at least until \(t_{0}\), regardless of the dynamics of the fund’s value, because \(\mathcal{C}\cap \{t\le t_{0}\}=[0,t_{0}] \times \mathbb{R}_{+}\). On \((t_{0},T]\), we find that \(\gamma (\cdot )>0\) with \(\gamma (t)\uparrow +\infty \) as \(t\downarrow t_{0}\) and ℛ lies below the curve \(\gamma \). From a mathematical point of view, this means that we only need to study our problem (2.7) on the restricted time interval \((t_{0},T]\) where our Assumption 4.3 holds.
(2) (\(g(\cdot )\)increasing). Here \(\mathcal{R}\cap \{t\ge t _{0}\}=[t_{0},T]\times \mathbb{R}_{+}\) so that for \(t\ge t_{0}\), it is optimal to delay the annuity purchase until the maturity \(T\), regardless of the dynamics of the fund’s value, because \(\mathcal{C}\cap \{t \ge t_{0}\}=[t_{0},T]\times \mathbb{R}_{+}\). On \([0,t_{0})\), we find that \(\gamma (\cdot )>0\) with \(\gamma (t)\uparrow +\infty \) as \(t\uparrow t_{0}\) and ℛ lies below the curve \(\gamma \).
This case is much more challenging, and we could not cover it with the methods developed so far. We leave it for future research, but, nevertheless, we should like to make an observation to highlight a key difficulty. Take \(t \in [0,t_{0})\). The martingale property in (3.22) allows us to rewrite problem (3.4) as

where \(v(t_{0},x)\) may be explicitly calculated. In fact, from (3.3) we get
So it is clear that \(v(t_{0},x)=c_{1}+c_{2}x\) with positive constants \(c_{1}\), \(c_{2}\) that depend on \(t_{0}\).
Due to the geometry of ℛ, we should expect that the stopping region lies somewhere above the curve \(\gamma \) for \(t\in [0,t_{0})\). However, if we now compute \(v_{x}\) as in Proposition 3.4, it turns out that

Since \(g(\cdot )<0\) on \([0,t_{0})\) and \(c_{2}>0\), it is no longer obvious that \(v_{x}\) is negative on \([0,t_{0})\times \mathbb{R}_{+}\). This would have been a sufficient condition to guarantee that \(\mathcal{S}_{t}\) and \(\mathcal{C}_{t}\) are connected for all \(t\in [0,t_{0})\).
Noticing that \(H(t,x)\) and \(v(t_{0},x)\) are linear in \(x\), the asymptotic behaviour of \(v(t,x)/x\) as \(x\to \infty \) and convexity of \(v(t,\cdot )\) (see Proposition 3.4) suggest that for a fixed \(t\in [0,t_{0})\), we should have \(\mathcal{S}_{t}=[b_{1}(t),b _{2}(t)]\) with \(b_{2}(t)\) possibly infinite. This, however, leaves open several questions concerning the actual shape of \(\mathcal{S}\) and the regularity of its boundary. A complete answer to these questions requires the use of different methods, and we leave it for future work.
6.1 A comment on the regularity of the optimal boundary
One of the main mathematical challenges in this work was the lack of monotonicity for the optimal boundary, which we managed to overcome by showing that the boundary is indeed locally Lipschitz. While our methodology only relies on stochastic calculus, the idea of looking at the implicit function theorem and to provide bounds on \(b'_{\delta }\) in (4.6) somehow comes from PDEs (we refer to [5] for a more extensive review on the topic). In particular, we were inspired by [17] where a variational inequality associated to an optimal stopping problemFootnote 3 is studied (see Eq. (1.3) therein). Interestingly, our assumptions are weaker than those contained in [17, Sect. 2, Eqs. (2.1)–(2.3)], as we explain in more detail in the next paragraph. In this sense, our probabilistic method extends results which were obtained in [17] with purely analytical tools. The parallel with our notation is better understood if we use the problem formulation (3.5), although using (2.7) is clearly equivalent.
First of all, the problem studied in [17] is for Brownian motion with drift, and both gain function and running cost in the optimal stopping problem are required to be of polynomial growth. This is immediately violated in our case where \((X_{t})_{t\ge 0}\) is the exponential of a Brownian motion with drift and the function \(H\) in (3.5) is linear in \(X\). More importantly, what really is crucial for the proof of Lipschitz-regularity of the free boundary in [17] is that some particular lower bounds on the gradient of the running cost should hold. According to [17], in our Assumption 4.3, we should additionally need
for all \((t,x)\in [0,T]\times \mathbb{R}_{+}\) and some \(c>0\). Since the left-hand side of the above expression is independent of \(x\), it is clear that such a bound cannot hold.
Notes
In what follows, we make no distinction between the fund’s dynamics and the wealth dynamics.
These figures are those used by the Belgian regulator, Arrêté Vie 2003.
A very minor difference with our work is that [17] studies a minimisation problem.
References
Chakrabarty, A., Guo, X.: Optimal stopping times with different information levels and with time uncertainty. In: Zhang, T., Zhou, X. (eds.) Stochastic Analysis and Applications to Finance: Essays in Honour of Jia-an Yan, pp. 19–38. World Scientific, Singapore (2012)
Chevalier, E.: Optimal early retirement near the expiration of a pension plan. Finance Stoch. 10, 204–221 (2006)
De Angelis, T.: A note on the continuity of free-boundaries in finite-horizon optimal stopping problems for one-dimensional diffusions. SIAM J. Control Optim. 53, 167–184 (2015)
De Angelis, T., Ekström, E.: The dividend problem with a finite horizon. Ann. Appl. Probab. 27, 3525–3546 (2017)
De Angelis, T., Stabile, G.: On Lipschitz continuous optimal stopping boundaries. SIAM J. Control Optim. Accepted. Available online at https://arxiv.org/abs/1701.07491
Friedman, A., Shen, W.: A variational inequality approach to financial valuation of retirement benefits based on salary. Finance Stoch. 6, 273–302 (2002)
Gerrard, R., Højgaard, B., Vigna, E.: Choosing the optimal annuitization time post-retirement. Quant. Finance 12, 1143–1159 (2012)
Gilbarg, D., Trudinger, N.S.: Elliptic Partial Differential Equations of Second Order. Springer, Berlin (2001)
Hainaut, D., Deelstra, G.: Optimal timing for annuitization, based on jump diffusion fund and stochastic mortality. J. Econ. Dyn. Control 44, 124–146 (2014)
Karatzas, I., Shreve, S.E.: Methods of Mathematical Finance, 1st edn. Applications of Mathematics, vol. 39. Springer, New York (1998)
Liang, X., Peng, X., Guo, J.: Optimal investment, consumption and timing of annuity purchase under a preference change. J. Math. Anal. Appl. 413, 905–938 (2014)
Milevsky, M.A.: Optimal asset allocation towards the end of the life cycle: to annuitize or not to annuitize? J. Risk Insur. 65, 401–426 (1998)
Milevsky, M.A., Young, V.R.: Annuitization and asset allocation. J. Econ. Dyn. Control 31, 3138–3177 (2007)
Peskir, G.: On the American option problem. Math. Finance 15, 169–181 (2005)
Peskir, G., Shiryaev, A.N.: Optimal Stopping and Free-Boundary Problems. Lectures in Mathematics. ETH Zürich, Birkhäuser (2006)
Protter, P.: Stochastic Integration and Differential Equations, 2nd edn. Springer, Berlin, Heidelberg, New York (2004)
Soner, H.M., Shreve, S.E.: A free boundary problem related to singular stochastic control: the parabolic case. Commun. Partial Differ. Equ. 16, 373–424 (1991)
Stabile, G.: Optimal timing of the annuity purchase: a combined stochastic control and optimal stopping problem. Int. J. Theor. Appl. Finance 9, 151–170 (2006)
Yaari, M.E.: Uncertain lifetime, life insurance and the theory of consumer. Rev. Econ. Stud. 32, 137–150 (1965)
Wang, S.S.: Premium calculation by transforming the layer premium density. ASTIN Bull. 26, 71–92 (1996)
Acknowledgements
We thank three anonymous referees, whose valuable comments helped improving the quality of our paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was financially supported by Sapienza University of Rome, research project “Polizze ‘Deferred Income Annuities’ per la previdenza complementare: un modello stocastico di valutazione”, grant no. RP11615500B7B502. T. De Angelis was also partially supported by the EPSRC grant EP/R021201/1, “A probabilistic toolkit to study regularity of free boundaries in stochastic optimal control”.
Appendix A: Admissible stopping times
Appendix A: Admissible stopping times
Here we use an argument from [1] to confirm that we incur no loss of generality in optimising over \(\mathcal{T}_{t,T}\) instead of using stopping times with respect to \((\mathcal{G}_{t})_{t\ge 0}\), where \(\mathcal{G}_{t}=\mathcal{F}_{t}\vee \sigma (\{\varGamma _{D}>s\},0\le s \le t)\). The key is that for any \((\mathcal{G}_{t})_{t\ge 0}\)-stopping time \(\tau '\), there is an \((\mathcal{F}_{t})_{t\ge 0}\)-stopping time \(\tau \) such that \(\tau \wedge \varGamma _{D}=\tau '\wedge \varGamma _{D}\)\(\mathbb{P}\times \mathbb{Q}^{S}\)-a.s. (see [16, Chap. VI.3, first lemma]). Then, letting \(\mathcal{T}'_{0,T}\) be the set of \((\mathcal{G}_{t})_{t\ge 0}\)-stopping times in \([0,T]\), we have

where the first equality uses \(\{\varGamma _{D}\le \tau '\}=\{\varGamma _{D}= \tau '\wedge \varGamma _{D}\}\) and

The same argument may be repeated for stopping times in \(\mathcal{T}'_{t,T}\) upon conditioning on \(\mathcal{F}_{t}\cap \{ \varGamma _{D}>t\}\).
Proof of Lemma 3.6
Monotonicity of \(w(t,\,\cdot \,)\) follows immediately from (3.9).
We now prove (iii). For that we need a preliminary result, and we introduce
for a fixed \(\delta _{0}>0\). Since \(g(t)<0\) for \(t\in (0,T)\), it is easy to verify that
and \(H(t,x)<-\delta _{0}\) for \(x\in (\gamma _{0}(t),+\infty )\). We define the stopping time
and notice that \(\tau _{0}(t,x)\to T-t\) in probability as \(x\to \infty \). In fact, for any \(\varepsilon >0\), there exists \(\gamma _{\varepsilon }\in (0,+\infty )\) such that \(\gamma _{0}(t+s)\le \gamma _{\varepsilon }\) for all \(s\le T-t-\varepsilon \), therefore
and, clearly, the last term goes to zero as \(x\to \infty \). Notice now that if there exists \(t_{*}< T\) such that \([t_{*},T)\times \mathbb{R} _{+}\subset \mathcal{C}\), then for all \(s\ge t_{*}\), one has
Noticing that
for some \(\xi _{s}\in [0,T-s]\), we immediately conclude that
since \(\ell \in C([0,T])\).
We now proceed in two steps.
Step 1. Here we prove that \(\mathcal{S}\cap ([t,T)\times \mathbb{R}_{+})\neq \emptyset \) for all \(t< T\). Assume the contrary, i.e., there exists \(t_{*}< T\) such that \([t_{*},T)\times \mathbb{R} _{+}\subseteq \mathcal{C}\). Hence for any \(t\in [t_{*},T)\) given and fixed, we have \(\tau _{*}(t,x)=T-t\) ℙ-a.s. for all \(x\in \mathbb{R}_{+}\). In particular, we take \(x>\gamma _{0}(t)\). In order to obtain an upper bound for the value function, we use the martingale property of (3.22) and (A.1) to get

where \(c>0\) is a lower bound for the discount factor. Since \(X^{x}_{\tau _{0}}=\gamma _{0}(t+\tau _{0})\) on \(\{\tau _{0}< T-t\}\) and \(\gamma _{0}(\,\cdot \,)\) is bounded and continuous on \([t,T-\varepsilon ]\), using that \(w\in C([0,T]\times \mathbb{R}_{+})\), we can then find \(c_{\varepsilon }\in [0,+\infty )\) independent of \(x\) and such that
On the other hand, (A.3) implies that
so that (A.4) gives
Taking limits as \(x\to \infty \) and recalling that \(\tau _{0}(t,x) \to T-t\) in probability (see (A.2)), we get
Finally, letting \(\varepsilon \to 0\) and using (A.3), we obtain that \(d_{\varepsilon }\to 0\) and
hence a contradiction. This means that \(\mathcal{S}\cap ([t,T)\times \mathbb{R}_{+})\neq \emptyset \) for all \(t< T\).
Step 2. Here we prove that \(\mathcal{S}\cap ((t_{1},t_{2}) \times \mathbb{R}_{+})\neq \emptyset \) for all \(t_{1}< t_{2}\) in \([0,T]\). Let us argue by contradiction and assume that \(\mathcal{S} \cap ((t_{1},t_{2})\times \mathbb{R}_{+})=\emptyset \) for a given pair \(t_{1}< t_{2}\) in \([0,T]\). Without loss of generality, we can set
and we know from Step 1 above that \(t_{2}< T\). The idea is to show that indeed \(t_{2}=t_{1}\), hence a contradiction.
Fix \(t'\in [t_{2},T)\) such that there exists \(x'\in \mathbb{R}_{+}\) with \((t',x')\in \mathcal{S}\). Since \(w_{x}\le 0\) and \(w(t',x')=0\), we have \(w(t',y)=0\) for \(y>x'\). Hence \(\{t'\}\times [x',+\infty )\in \mathcal{S}\) as well. We define
As in (A.4), we use the martingale property of the process in (3.22) up to the stopping time \(\zeta :=\tau _{*}\wedge \tau _{0}\wedge (t'-t_{1})\), where here \(\tau _{*}=\tau _{*}(t_{1},x)\) and \(\tau _{0}=\tau _{0}(t_{1},x)\). In particular, noticing that \(\mathbb{P}[\tau _{*}\ge t_{2}-t_{1}]=1\) and therefore \(\mathbb{P}[ \zeta \ge \tau _{0}\wedge (t_{2}-t_{1})]=1\), we get

On \(\{\tau _{0}<\tau _{*}\wedge (t'-t_{1})\}\), we have \(\gamma _{0}(t _{1}+\tau _{0})\le \sup _{t_{1}\le s \le t'}\gamma _{0}(s)\le \gamma '\) for some \(0\le \gamma '<\infty \) that depends only on \(t_{1}\) and \(t'\). It follows that \(w(t_{1}+\tau _{0},X^{x}_{\tau _{0}}) \le C\) for some \(C>0\) that also depends only on \(t_{1}\) and \(t'\). Moreover, it also must hold that \(\{t'-t_{1}<\tau _{*}\wedge \tau _{0} \}=\{t'-t_{1}<\tau _{*}\wedge \tau _{0}\}\cap \{\tau '\le t'-t_{1}\}\), as otherwise the process would have crossed the vertical half-line \(\{t'\}\times [x',+\infty )\in \mathcal{S}\). For the same reason, on the event \(\{t'-t_{1}<\tau _{*}\wedge \tau _{0}\}\), one has \(X^{x}_{t'-t _{1}}\le x'\) which then implies \(w(t',X^{x}_{t'-t_{1}})\le C'\) for some \(C'>0\) that only depends on \(t_{1}\), \(t'\) and \(x'\). Collecting these facts, we have from (A.6) that
We now take limits as \(x\to \infty \). From the same argument as in (A.2), we also obtain that \(\mathbb{P}[\tau _{0}\le t'-t_{1}] \to 0\) and \(\mathbb{P}[\tau _{0}>t_{2} -t_{1}]\to 1\) and similarly,
Thus (A.7) leads to a contradiction and we must have \(t_{2}=t_{1}\).
Steps 1 and 2 above give (iii). Finally, we prove (3.25). The limit is obvious for \(t=T\) since \(w(T,x)=0\) for \(x\in \mathbb{R}_{+}\). It is also trivially true for all \(t\in [0,T]\) such that \(\mathcal{S} \cap (\{t\}\times \mathbb{R}_{+})\neq \emptyset \). Therefore it remains to prove it for \(t\in [0,T]\) such that \(\mathcal{S}\cap (\{t\}\times \mathbb{R}_{+})=\emptyset \). Take one such \(t\in [0,T]\) and fix \(t'>t\) such that there exists \(x'\in \mathbb{R}_{+}\) with \((t',x') \in \mathcal{S}\) (this must exist due to (iii)). Recall \(\tau '\) from (A.5); then repeating the martingale argument and the estimates above, we obtain

Taking limits as \(x\to \infty \), (3.25) is easily verified. □
Proof of uniqueness in Theorem 4.12
We give the proof only for the case where \(\mathcal{S}=\{(t,x) : x\le b(t)\}\), as the other case follows by the same arguments. Also, here we assume \(\gamma (T)<+\infty \) for simplicity and notice that the argument below can be easily adapted for \(\gamma (T)=+\infty \).
Suppose there exists a continuous function \(c:[0,T]\to \mathbb{R}_{+}\) with \(c(T)=\gamma (T)\), with \(c(t)\le \gamma (t)\) for all \(t\in [0,T]\) and such that \(c\) solves

Then we define the function

and notice that this is the analogue for \(c\) of the value function \(V\) in (4.29). Notice also that \(U^{c}(T,x)=G(T,x)\) for \(x\ge 0\). Thanks to the strong Markov property, it is not hard to show that the process \((\widehat{U}_{s})_{s\in [0,T-t]}\) is a martingale, where

Then the same argument implies that \((\widehat{V}_{s})_{s\in [0,T-t]}\) is a martingale as well, where

Now we proceed in four steps as it is customary in the literature (see [14] and [15, Chaps. VII and VIII]).
Step 1. First we show that \(U^{c}(t,x)=G(t,x)\) for \(x\le c(t)\), \(t\in [0,T]\). This is trivial for \((t,x)\in \{T\}\times \mathbb{R} _{+}\) or for \(x=c(t)\), as it follows by the definitions of \(c(\cdot )\) and \(U^{c}\). Now take \(t< T\) and \(x< c(t)\), define \(\sigma _{c}:= \inf \{s\ge 0 : X^{x}_{s}\ge c(t+s)\}\wedge (T-t)\) and use the martingale property of \(\widehat{U}\) to obtain
Using that \(U^{c}(t+\sigma _{c},X^{x}_{\sigma _{c}})=G(t+\sigma _{c},X ^{x}_{\sigma _{c}})\) ℙ-a.s., because \(c\) solves (A.8) and \(U^{c}(T,x)=G(T,x)\), we obtain
where the final equality uses \(\beta (t)x-H(t,x)=- (G_{t}+\mathcal{L}G-r( \cdot )G)(t,x)\) and Dynkin’s formula.
Step 2. Now we prove \(V(t,x)\ge U^{c}(t,x)\). The claim is trivial for \(x\le c(t)\), \(t\in [0,T)\) due to Step 1. Similarly, \(U^{c}(T,x)=V(T,x)=G(T,x)\) for \(x\in \mathbb{R}_{+}\). Then fix \(t< T\), take \(x>c(t)\) and denote
Using the martingale property of \(\widehat{U}\) and (A.8), we obtain
Step 3. Here we prove that \(c(t)\ge b(t)\), \(t\in [0,T]\). Assume there is \(t\in [0,T)\) such that \(c(t)< b(t)\), take \(x\le c(t)\) and denote
Using now the martingale property of both \(\widehat{U}\) and \(\widehat{V}\), we obtain

Notice that \(U^{c}(t,x)=V(t,x)\) because \(x\le c(t)< b(t)\) and recall also that \(V(t+\sigma _{b},X^{x}_{\sigma _{b}})\ge U^{c}(t+\sigma _{b},X^{x}_{\sigma _{b}})\). Then subtracting (A.10) from (A.9), we get

Since \(H(t+s,X^{x}_{s})<0\) for \(s\le \sigma _{b}\) (recall that \(H<0\) below \(\gamma (\cdot )\)) and since \(\mathbb{P}[X^{x}_{s}>c(t+s),\, \sigma _{b}>s]>0\) for any sufficiently small \(s\) (thanks to the continuity of \(b\) and \(c\)), the inequality in (A.11) leads to a contradiction. Hence \(c(t)\geq b(t)\).
Step 4. In this final step, we show that \(c(t)\le b(t)\) for \(t\in [0,T]\) so that from Step 3, we conclude that \(c(t)=b(t)\) for \(t\in [0,T]\). Assume that there is \(t\in [0,T)\) such that \(c(t)>b(t)\) and take \(x\in (b(t),c(t))\). Then letting
and using again the martingale property of both \(\widehat{U}\) and \(\widehat{V}\), we get
and

We notice that \(V(t+\tau _{b},X^{x}_{\tau _{b}})=U^{c}(t+\tau _{b},X^{x} _{\tau _{b}})=G(t+\tau _{b},X^{x}_{\tau _{b}})\) due to Steps 3 and 1. Also we recall that \(V(t,x)\ge U^{c}(t,x)\) due to Step 2. Then subtracting (A.13) from (A.12) gives

Since \(c(\cdot )\le \gamma (\cdot )\) and \(c(t)<\gamma (t)\), we get  and this is strictly negative for all \(s\in [0,\tau _{b})\) sufficiently small. Moreover, continuity of \(c(\cdot )\) and \(b(\cdot )\) implies that \(\mathbb{P}[X^{x}_{s}\le c(t+s),\,\tau _{b}>s]>0\) for all \(s>0\) sufficiently small. Hence (A.14) gives a contradiction and we must have \(c(t)\le b(t)\). □
and this is strictly negative for all \(s\in [0,\tau _{b})\) sufficiently small. Moreover, continuity of \(c(\cdot )\) and \(b(\cdot )\) implies that \(\mathbb{P}[X^{x}_{s}\le c(t+s),\,\tau _{b}>s]>0\) for all \(s>0\) sufficiently small. Hence (A.14) gives a contradiction and we must have \(c(t)\le b(t)\). □
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
De Angelis, T., Stabile, G. On the free boundary of an annuity purchase. Finance Stoch 23, 97–137 (2019). https://doi.org/10.1007/s00780-018-00379-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00780-018-00379-8