Butterfly counting and bitruss decomposition on uncertain bipartite graphs

Abstract

Uncertain butterflies are one of, if not the, most important graphlet structures on uncertain bipartite networks. In this paper, we examine the uncertain butterfly structure (in which the existential probability of the graphlet is greater than or equal to a threshold parameter), as well as the global Uncertain Butterfly Counting Problem (to count the total number of these instances over an entire network). To solve this task, we propose a non-trivial exact baseline (UBFC), as well as an improved algorithm (IUBFC) which we show to be faster both theoretically and practically. We also design two sampling frameworks (UBS and PES) which can sample either a vertex, edge or wedge from the network uniformly and estimate the global count quickly. Furthermore, a notable butterfly-based community structure which has been examined in the past is the k-bitruss. We adapt this community structure onto the uncertain bipartite graph setting and introduce the Uncertain Bitruss Decomposition Problem (which can be used to directly answer any k-bitruss search query for any k). We then propose an exact algorithm (UBitD) to solve our problem with three variations in deriving the initial uncertain support. Using a range of networks with different edge existential probability distributions, we validate the efficiency and effectiveness of our solutions.

1 Introduction

Uncertain (or Probabilistic) Networks are graphs aimed at modelling real-world networks in which connections between users or entities can only be assumed with differing levels of uncertainty [3, 37]. Recently, these networks have grown to become a highly interesting area of exploration due to the real-world applications such as modelling influence on social networks [46], fact trustworthiness [49] and uncertain protein-protein interaction [52] to name a few.

Extending on this concept, uncertain bipartite networks are used to examine uncertain networks in which the nodes are separated into two disjoint sets where edges only exist between the two sets. Notable uncertain bipartite network use cases include predicted edges in biological/biomedical networks [9, 25, 40], modelling the likelihood a patient with a disease exhibits a symptom based on historical data [17]. On user-item networks, edges may represent confidence in a recommendation [32] or trust-prediction based on user ratings [16]. Even delivery problems [36, 50] can be modelled as uncertain bipartite networks based on the likelihood the courier can reach a target within a certain time frame.

On deterministic (or certain) bipartite networks, the butterfly (sometimes referred to as a ‘rectangle’ in the literature), a fully connected subgraph containing exactly two nodes from each partition, is perhaps the most important graphlet structure [30, 42, 43]. Butterflies may be used to indicate closely connected nodes, which are useful in tasks such as community search [30], as well as forming the foundation of key community structures such as the bitruss [44, 56] or biclique [51]. In that respect, butterflies play a very similar role to that of the triangle on a unipartite graph [2, 5, 47].

Whilst butterfly counting has been studied on deterministic bipartite networks [30, 42, 43], they have yet to be extended to uncertain bipartite networks which limits their current applicability. This is unlike the triangle (and triangle counting problem) which has already been extended to uncertain scenarios due to similar reasoning [13, 57]. With the structure holding such importance on bipartite graphs, being able to determine the number of butterflies in uncertain bipartite networks can lead to significant insights into the inherent structure and properties of the network.

Use Case Scenario [Host-Parasite]: Host-Parasite networks track which parasites latch onto which hosts in a natural environment. In some work, such uncertain networks have been built which also consider host-parasite combinations which could (but have not been provably shown to) exist based on attributes about each host and comparing them to recorded parasite infections of hosts [40]. As hosts with similar attributes are prone to being ‘targeted’ by the same parasites, naturally, this builds a butterfly structure on the uncertain network as the number of hosts and parasites grows. If the habitat has a high uncertain butterfly count, this poses a great risk if one of the recorded parasites enters as cross-host infection (and subsequently an outbreak) becomes significantly more likely than if the butterfly count is low. Furthermore, it is possible to make plans of action for when uncertain edges become certain (i.e. a host-parasite connection physically appears in the habitat). Additionally, being able to find the count of subgraphs allows for interesting future problems such as partitioning the hosts into separated groups to minimise the total uncertain butterfly count.

Use Case Scenario [Recommendation]: Another use case example is a recommendation user-item network, where edges can exist without certainty where the existential probability is the likelihood a user would enjoy or purchase an item. These recommendation networks can be formed using multiple well-established techniques such as Collaborative Filtering [32]. The uncertain butterflies and their respective count could be used to recommend items which would result in the emergence or reinforcement of strong communities (as we discuss later when describing uncertain bitrusses). Additionally, general statistics such as a bipartite clustering coefficient [19] can be gleamed using the uncertain butterfly count. Furthermore, by comparing the resulting counts of two different recommendation strategies, a relatively cheap method of comparing potential impacts of strategies beyond simply an increased number of edges becomes viable. This becomes even faster if an approximation method which is accurate and fast (like the ones we propose in this work) is utilised.

Another potential use of uncertain butterflies would be for a bitruss structure [44, 56] on uncertain graphs. The bitruss is a popular community structure on bipartite networks as they are able to capture the intrinsic ‘tight’ connections between the set of edges which form the community. The deterministic variation of the k-Bitruss, where each edge in the structure is a part of k butterflies in conjunction with other edges in the subgraph structure, is a popular option as an intermediary between bicliques [51] and $(\alpha , \beta )$-Cores [20].

Once again, this structure has yet to be transported onto the uncertain bipartite space. As a natural progression on the uncertain butterfly counting problem, we introduce the uncertain k-Bitruss. Being able to search for a distinct community structure on uncertain bipartite graphs further opens the level of insights that can be gained from these networks.

Let us first consider the Host-Parasite use case scenario. In this setting, the potential use of this butterfly-based community structure to find a set of host/parasites which are highly likely to cross-transmit is highly relevant. By finding such a community, it is possible to separate the hosts (or simply keep a closer eye on them) to avoid transmission which overall makes the habitat a safer space.

Similarly, the Recommendation Network use case scenario can also strongly benefit from the bitruss community metric. A network operator can observe the effects of any given recommendation strategy on the potential growth of communities in their system by gauging the change in community size pre- and post-implementation. Furthermore, such defined communities may make future recommendations easier (particularly so if the community becomes denser and thus indicative of even higher levels of similarity between individuals). The uncertain bitruss with its polynomial time derivation is practically preferable to a structure like a maximal biclique (which is NP-Hard to enumerate).

Fig. 1

A user-item graph where solid black edges represent known items a user likes and dashed yellow lines represent potential likes with high probability based on recommendation. There exists no bitruss on the black edges only but combining the black and yellow edges forms a 1-bitruss

Let us consider an example of this in Fig. 1, detailing a small user-item purchasing network where the black solid lines describe existing known edges with certain probability and yellow dashed lines describe edges a recommendation system suggests. If a threshold value is selected such that each edge (solid or dashed) would be a part of the final output bitruss we are able to discover a potential community which could form (that does not exist on only the solid edges) if the recommendation strategy was adopted. Using existing bitruss algorithms for certain graphs, in order to find this community, there would have to be a rigid assumption that these dashed edges must exist, something that goes against the spirit of having a probability.

1.1 Our contributions

Fig. 2

An example uncertain bipartite network with a red and blue partition. Each edge has a corresponding existential probability, with the threshold value $t = 0.6$

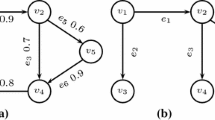
In this paper, we formally define the (global) Uncertain Butterfly Counting Problem (UBFCP), in which we wish to determine the number of butterflies that exist on an uncertain bipartite network with existential probability is greater than or equal to a threshold value t. Figure 2 is an example uncertain bipartite network, where the threshold is set to be $t = 0.6$. The butterflies and both have existential probabilities (the product of the existential probability of their four edges) greater than t (0.72 and 0.63, respectively), whilst the butterfly does not (with probability 0.2). Therefore, the uncertain butterfly count on this network is 2.

Existing butterfly counting techniques on deterministic graphs cannot realistically be transferred directly to this new setting as they treat each edge (and wedge) with equal importance, something that is evidently not true in the uncertain setting. Additionally, in these methods, it is not possible to add in a trivial step in which each butterfly is evaluated as either satisfying or failing the threshold as the deterministic method aggregates a batch of butterflies at the same time. It is possible to enumerate all possible worlds, count the number of certain butterflies in each world and aggregate the result but such an approach is extremely unrealistic in practice.

In this paper, we propose two exact solutions to UBFCP. Firstly, we create a baseline solution UBFC which adapts the current best solution for the Butterfly Counting problem on deterministic graphs and modifies it as necessary such that it is satisfactory to our problem. Then, we propose an improved solution IUBFC which reduces the time complexity (from $O(\sum _{e(u, v) \in E} \min \{deg(u)^2, deg(v)^2 \})$ to $O(\sum _{e(u, v) \in E} \min \{deg(u) \log (deg(u)), deg(v) \log (deg(v)) \})$) without any change in the memory complexity by improving the manner in which wedges are found and combined to find uncertain butterflies. We additionally add heuristics, such as early edge discarding, to further improve the performance of the algorithm.

We also propose two estimation via sampling solutions which trade accuracy in return for significantly improved running time. Minor sacrifices in accuracy in return for major reductions in cost can be highly attractive when a quick examination is needed for recommendation strategies as an example.

Our first algorithm, Uncertain Butterfly Sampling (UBS), samples vertices/edges without replacement determining the number of uncertain butterflies each vertex or edge is a part of. By extrapolating and averaging the solution, we can derive an estimation of the count with high confidence as the sample size increases. Our second algorithm, Proportion Estimation Sampling (PES), estimates the proportion of butterflies with existential probability $\ge t$ and then uses a faster deterministic sampling technique to quickly estimate the number of uncertain butterflies.

The above problem and techniques have been proposed in our preliminary conference version [54], and based on these, we extend our work by introducing a wedge-based sampling method as well as defining and examining our new Bitruss structure on uncertain bipartite graphs. The Uncertain k-Bitruss structure is the one in which each edge in the structure is part of at least k uncertain butterflies. In order to facilitate the usage of the k-Bitruss, we propose the Uncertain Bitruss Decomposition Problem (UBitDP) and provide an online in-memory solution. In this problem, any method would require the initial uncertain support (that being the local uncertain butterfly count) of each edge to be derived, something that cannot be directly adapted from existing methods nor from our global techniques which indiscriminately batch together multiple edges when incriminating the count. By examining different methods with potential benefits and drawbacks, we provide three alternative methods (UBitD-UBFC, UBitD-IUBFC and UBitD-LS) to calculating these initial uncertain supports.

Finally, we demonstrate the effectiveness of our exact solutions by performing experiments on multiple uncertain bipartite networks.

Our contributions are summarised as following:

• We formally define the Uncertain Butterfly and Uncertain Butterfly Counting Problem;

• We propose a non-trivial baseline and introduce an improved algorithm which reduces the time complexity of the solution at no increased memory cost;

• We propose two fast alternate approximation strategies via sampling, each with a variation that is vertex, edge or wedge based;

• We also formally define the Uncertain k-Bitruss as well as the Uncertain Bitruss Decomposition Problem;

• We propose an in-memory algorithm to exactly solve Uncertain Bitruss Decomposition Problem with three initial uncertain support derivation strategies;

• We validate our algorithms via extensive experiments;

To outline the remaining paper, we first examine related works to this topic (Sect. 2) before formally defining the notation and the two problems of Uncertain Butterfly Counting and Uncertain Bitruss Decomposition (Sect. 3). For the global uncertain butterfly counting portion of our work, we introduce a non-trivial baseline exact solution (Sect. 4) and follow up with key improvements which reduce the time complexity of the solution in combination with powerful heuristics (Sect. 5). We also propose two sampling solutions which provide approximate results (Sect. 6). Afterwards, we examine algorithms aimed at solving the problem of Uncertain Bitruss Decomposition efficiently (Sect. 7). Following this, we examine the efficiency and effectiveness of our algorithms (Sect. 8) before concluding the paper (Sect. 9).

2 Related works

Butterflies: The butterfly (sometimes referred to as a rectangle or 4-cycle) [30, 42, 43] is perhaps the most fundamental structure that exists on bipartite networks [55]. Similar to the role that triangles play on unipartite graphs [2, 5, 47], butterflies are utilised in many areas to either quickly gauge information on the network [30] or help to find more complex structures such as the biclique [22, 26], k/$k^*$-Partite Clique [27, 53] and bitruss [44, 45, 56].

There has been a recent boom in the area of butterfly counting. In particular, a baseline deterministic solution for counting the number of butterflies on a regular bipartite network [42] with multiple improvements to that algorithm [30] resulting in the current best solution being a vertex priority approach [43] has been studied.

In addition, the butterfly counting problem has been tackled in different settings with parallel [42] and cache-aware solutions [43] considered and estimation solutions [30] proposed. Furthermore, butterfly counting in a streaming setting has also been a recent area of research [31]. To the best of our knowledge, we are the first to consider the butterfly (and subsequently the butterfly counting problem) on an uncertain setting, and thus, we require different solutions to deal with the increased requirements presented by the new problem.

Bipartite Networks: Bipartite networks in particular have recently seen a surge in research popularity due to the real-world applicability of the network type in modelling information [9, 16, 25, 32, 40]. The problems being studied that closely relate to our work regard in the counting, enumeration or search of a particular subgraph structure in the network.

Such structures include the well-studied biclique [22, 26, 51] in which each node in one partition of the structure must be connected to every node from the other partition. The butterfly is effectively a (2 x 2) biclique (that is a biclique with two nodes in each partition). Another structure is the $(\alpha , \beta )$-core [21] which models the popular k-core on the bipartite setting.

Bitruss: Perhaps the most relevant structure to us is the k-bitruss, a structure in which each edge in the bitruss is a part of k butterflies in the subgraph [56]. Due to the requirement of being able to count butterflies, advancements in butterfly counting can often directly result in improvements to bitruss algorithms. Notable works on bitrusses include an index structure to reduce the cost associated with the peeling stage of the standard bitruss decomposition algorithm [44].

The structure itself is heavily inspired by the k-truss [12, 41], which has been extensively studied. Work in this space recently mainly focuses on scalability via parallel/distributed implementations [7, 8, 14, 35]. Additionally, notably for our work, there exists research on the standard truss structure on uncertain networks [13, 57].

Uncertain Networks: Uncertain (probabilistic) graphs as a sub-genre have received attention from various problems, often by taking traditional graph problems and transferring them into the setting (e.g. k-Nearest Neighbour [28], Core Decomposition [6], Shortest Path [48]). On uncertain graphs, a popular choice is to use Possible World Semantics [1], which breaks the system down into separate instances of the graph with nonzero existential probability. As many problems theoretically require the analysis of all possible worlds, which is expensive, research has been conducted to narrow the scope by finding a good representative possible world [24] or by sampling a set of possible worlds [11, 15, 18] to estimate the result. There does exist one notable work on motif counting (including butterflies) on uncertain (unipartite) networks (LINC) [23]; however, their problem formulation differs from ours (they wish to output the probability mass function of counts across all possible worlds) as ours finds all butterfly instances whose existential probability is above a specific threshold.

3 Problem definition

In this section, we detail the problem setting, that being the uncertain bipartite graph, as well as the structures and concepts that pertain to the Uncertain Butterfly Counting Problem (UBFCP) then the Uncertain Bitruss Decomposition Problem (UBitDP).

Table 1 Key Notation and Definitions

We give most of the key notation used in our paper in Table 1.

3.1 Uncertain butterfly counting problem

Definition 1

Uncertain Bipartite Network: An uncertain bipartite network $G=(V = L \cup R, E, P)$ is a network in which any node $u \in L$ may only be connected to node v given that $v \in R$ or vice versa. $P: E \rightarrow (0, 1]$ maps an edge $e_{u, v} \in E$ to a nonzero existential probability $Pr(e_{u, v}) \in (0, 1]$. We assume there are no multi-edges in our network.

On a given uncertain bipartite network G, a possible world $W_i = (V, E_{W_i})$ is a single possible network outcome after fairly and randomly determining if each edge $e \in E$ exists in $W_i$ based on Pr(e) [1]. Like existing work on uncertain networks [1, 13, 23, 57], we assume the existential probability of each edge is independent of each other. Each possible world $W_i$ on G exists with existential probability $Pr(W_i) = \prod _{e \in E_{W_i}} Pr(e) \cdot \prod _{e \in E {\setminus } E_{W_i}} (1 - Pr(e))$.

For any G, there exists $2^{|E|}$ possible worlds. The set of all possible worlds is defined as ${\mathbb {W}} = \{W_1, \dots , W_{2^{|E|}}\}$ and via the Law of Total Probability $Pr({\mathbb {W}}) = \sum _{i = 1}^{n} Pr(W_i) = 1$. Additionally, we call the possible world in which all edges are selected to exist the backbone graph of G, denoted by $W_{backbone}$. This may also be thought of as the deterministic variant of the network. Furthermore, it can be trivially proven that the total sum of existential probabilities for all worlds a single edge e exists in is equal to Pr(e). That is, given a randomly sampled world $W_i$, the probability $e \in E(W_i)$ is equal to Pr(e).

3.2 Butterfly counting

In certain bipartite networks, butterflies are considered as one of the key fundamental building block graphlet structures due to the cohesive relationships they represent [30, 42, 43]. On certain graphs, we may define the butterfly as following:

Definition 2

Butterfly: Given a bipartite graph $G = (V = L \cup R, E)$, a butterfly consisting of nodes $u_1, u_2 \in L$ and $v_1, v_2 \in R$ exists if and only if there exists edges from $u_1$ to $v_1$ and $v_2$, as well from $u_2$ to $v_1$ and $v_2$.

We may use the notation to denote a butterfly containing nodes $u_1, u_2, v_1, v_2$. We extend the idea of the butterfly to the uncertain bipartite network setting.

Definition 3

Uncertain Butterfly: Given an uncertain bipartite graph $G = (V = L \cup R, E, P)$ and a probability threshold $0 < t \le 1$, an uncertain butterfly consisting of nodes $u_1, u_2 \in L$ and $v_1, v_2 \in R$ exists if and only if there exists edges from $u_1$ to $v_1$ and $v_2$, as well from $u_2$ to $v_1$ and $v_2$, and the resulting product of the existential probabilities of the butterfly is $\ge t$ (i.e. $Pr() \ge t$).

The existential probability of a butterfly can be calculated by .

Fig. 3

Three uncertain butterflies and their corresponding existential probabilities

Definition 4

Certain Butterfly Count: Given a bipartite graph $G = (V, E,)$, the certain butterfly count C is the number of butterflies on that network.

Definition 5

Uncertain Butterfly Count: Given an uncertain bipartite graph $G = (V, E, P)$ and a threshold t, the uncertain butterfly count $C_t$ is the number of uncertain butterflies on that network.

The local deterministic butterfly count of a node $v \in V$ or edge $e \in E$ is denoted as C(v) or C(e) respectively (with the same convention for uncertain butterfly counts $C_t(u), C_t(e)$)

Figure 3 illustrates three uncertain butterflies and their respective existential probabilities. For $t = 0.4$, and would be counted towards the uncertain butterfly count, whilst would not result in a final uncertain butterfly count of 2.

Additionally, we need to introduce the idea of the Wedge and Uncertain Wedge.

Definition 6

Wedge and Uncertain Wedge: A Wedge $\angle (u, v, w)$ is a two-hop path consisting of two different endpoint vertices u, w from the same partition of the uncertain bipartite network and a middle vertex v from the other partition. An Uncertain Wedge $\angle _t$ is a Wedge that, on a randomly sampled world $W_i$, exists with $Pr(\angle _t) \ge t \in [0, 1]$.

Notably, any butterfly consists of four wedges which means butterfly counting techniques often use wedges as one of the building blocks in finding butterflies. If a butterfly contains a wedge $\angle$, we use the notation (and the same for ).

We note that there can be an alternate definition of the uncertain butterfly in which each edge in the butterfly must hold an existential probability greater than some threshold. However, in this scenario, we may simply prune all edges which fail to meet this threshold and then perform any certain/deterministic butterfly counting technique. Additionally, there could be an alternate problem formulation, in a similar vein to [23], in which instead of a threshold value, the mean and variance of the butterfly count over all possible worlds are derived. Due to the removal of the threshold, the problem would become $\#$P-Hard, and as a consequence, this hampers the usability of any exact algorithm in a practical setting.

We formally define the Uncertain Butterfly Counting Problem as following:

Definition 7

Uncertain Butterfly Counting Problem (UBFCP): For an undirected, unweighted bipartite graph $G = (V = L \cup R, E, P)$ and a threshold value t, the Uncertain Butterfly Counting Problem is to determine the count $C_t$ of all uncertain butterflies on G (where ).

The key technical difference between any existing certain algorithm [30, 43] and one that could handle uncertain butterflies is that the certain methods do not need to store previously discovered wedges as it can quickly determine the number of butterflies at this point via the operation $\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ where n is the number of wedges with the same start and end vertices, whereas in the uncertain version, each combination of wedges needs to be examined to check if the resulting butterfly satisfies the probability requirement. This key difference motivates the algorithms which we propose. Furthermore, finding all three-edge paths with satisfactory existential probability and checking if the final edge to complete the uncertain butterfly exists is an expensive endeavour due to the high number of three-edge paths in comparison with edges and wedges.

3.3 Uncertain bitruss decomposition problem

With the foundation of butterfly counting on the uncertain bipartite graph setting defined, we can now define the bitruss structure and related problems on the same setting. Once again, we utilise the same threshold t in order to allow for the user to have a level of control over what they would deem to be a satisfactory uncertainty for the network they operate.

Definition 8

k-Bitruss: Given bipartite graph $G = (V, E)$, a k-Bitruss $B^k$ is a subgraph of a certain graph in which each edge $e \in B^k$ is a member of at least k butterflies in $B^k$ (i.e. $\forall e \in B^k: C(e) \ge k$).

Definition 9

Uncertain k-Bitruss: Given an uncertain bipartite graph $G = (V, E, P)$ and a threshold $0 < t \le 1$, an uncertain k-Bitruss $B^k_t$ is a k-Bitruss in which each edge $e \in B^k_t$ is a member of at least k uncertain butterflies (i.e. $\forall e \in B^k_t: C_t(e) \ge k$).

The number of local butterflies (uncertain butterflies resp.) for each edge e in the current subgraph $G'$ being considered is also referred to as the support (uncertain support resp.) of the edge denoted by $sup(e, G')$ ($sup_t(e, G')$ resp.). Thus, a potential reformulation of the uncertain k-Bitruss $B^k_t$ is $\forall e \in B^k_t: sup_t(e, B^k_t) \ge k$.

We once again note that there can be an alternate definition of the uncertain bitruss (similar to the butterfly) in which each edge in the bitruss must hold an existential probability greater than some threshold, as well as the variation in the mean and variance of the butterfly bitruss is calculated over all possible worlds. Our reasoning for not pursuing these variations remains the same as before.

With this framework in place, we now consider the problem of Uncertain Bitruss Decomposition by first introducing the critical concept of the uncertain bitruss number.

Definition 10

Uncertain Bitruss Number: For an uncertain bipartite graph G and a user-defined threshold value t, the uncertain bitruss number $\phi _t(e)$ for an edge $e \in E$ is the largest number k such that e is still a member of a valid uncertain k-Bitruss $B^k_t$ on G.

It is important to distinguish the difference between the uncertain bitruss number of an edge ($\phi _t(e)$) and the uncertain support of an edge ($sup_t(e, G)$). Due to the nature of the two, it is trivial to see that $\phi _t(e) \le sup_t(e, G)$ as it is possible for an edge to be a part of butterflies which in turn do not contribute to an uncertain $\phi _t(e)$-Bitruss. With that noted, we now formally define the uncertain bitruss decomposition problem.

Definition 11

The Uncertain Bitruss Decomposition Problem (UBitDP): For an undirected, unweighted bipartite graph $G = (V = L \cup R, E, P)$ and a threshold value t, the Uncertain Bitruss Decomposition Problem is to find the Uncertain Bitruss Number for each edge $e \in E$.

4 Uncertain butterfly counting exact algorithms-baseline

In this section, we propose a baseline for exact solutions to the Uncertain Butterfly Counting Problem.

Given no baseline exists specifically for UBFCP, the trivial baseline would be to permute all combinations of four edges and check if it is an Uncertain Butterfly satisfying our threshold, taking $O(E^4)$ time. However, given prior work exists on the deterministic variation of our problem, we will instead utilise a baseline that finds butterflies on the backbone graph and examines if each individually satisfies the existential probability threshold environment.

Our baseline is a modified version of the Vertex Priority Butterfly Counting (BFC-VP) algorithm provided by Wang et al [43] for the deterministic problem, with the critical difference being how wedges are handled in order to find uncertain butterflies. We call our baseline UBFC. A core idea in this algorithm is that of vertex priority.

Definition 12

Vertex Priority [43]: The vertex priority of any node $u \in V$ in comparison with any other node $v \in V$ is defined as $p(u) > p(v)$ if

• 1. $deg(u) > deg(v)$

• 2. $id(u) > id(v)$ if $deg(u) = deg(v)$

where id(u) is the vertex ID of u.

Vertex priority is effectively a method that allows for a structured ranking of all nodes in G to avoid the same butterfly being counted multiple times. Additionally, as shown in [43], the usage of a vertex priority approach reduces the running cost of the algorithm.

Algorithm 1 details the baseline solution. We use the backbone graph $W_1$ (Line 1) in order to extract vertices and edges to find butterflies before checking whether they satisfy the uncertainty threshold. For each node, we sort its neighbours by (increasing) vertex priority (Line 2).

Then, for each node $u \in V_{W_1}$, we perform the baseline uncertain counting algorithm. Firstly, we initialise a Hashmap H which will be used to store all wedges containing u. For each node w, which is a two-hop neighbour of u (thus forming at least one wedge with u), we initialise a list in H which will refer to as H(w) (Line 5). Then, for each nodes $v \in N(u): p(v) < p(u)$, we find its neighbours N(v). For each node $w \in N(v): p(w) < p(u)$, we add v to H(w) since there exists a wedge $\angle (u, v, w)$ (Lines 6-8). The vertex priority constraints ensure no redundancy in our algorithm, that is no wedge will be ever added to any list twice.

As touched upon in Section 3.2, at this point, the certain method quickly calculates the number of butterflies via the operation $\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ where n is the number of wedges with the same start and end vertices, whereas in the uncertain version, each combination of wedges needs to be examined to check if the resulting butterfly satisfies the probability requirement. As a result, the deterministic method does not maintain a list but instead a simple number representing the total number of wedges for each u, w combination. However, given that we need to consider existential probabilities and need to thus know the wedges we keep, our method instead maintains the list H(w). For each combination of two nodes $v_1, v_2 \in H(w), v_1 \ne v_2$, we check if the butterfly is an uncertain butterfly . If it is, we increase $C_t$ (Lines 9-12). This management and combining of wedges sets our baseline algorithm for the uncertain butterfly counting problem apart from the deterministic variant.

Fig. 4

An example of wedges and their uncertainty

Figure 4 demonstrates the principle of uncertain wedges that share the same start and end vertex. If u has the highest vertex priority on this subgraph, it would form three wedges with v passing through nodes a, b and c, respectively, each with the shown existential probability. This forms three butterflies in the list, which are found by checking all combinations. If $t = 0.5$, then the uncertain butterfly count would increase by 2.

4.1 Algorithm complexity

We now examine both the time and space complexity of the baseline algorithm.

Theorem 1

The time complexity of UBFC is $O(\sum _{e(u, v) \in E} \min \{deg(u)^2, deg(v)^2 \})$.

Proof

Wang et. Al proved in their work that for the certain variation of this problem, the algorithm runs in $O(\sum _{e(u, v) \in E} \min \{deg(u), deg(v) \})$ time [43]. Notably, their proof examines the cost of wedge discovery (Algorithm 1 Lines 5-10) which makes up the dominating part of their algorithms time complexity.

In the deterministic variant, the remaining cost of the algorithm is done in O(1) time which is different from our uncertain version. In our uncertain version, we further have to determine the existential probabilities of the subsequent butterflies given the wedges (Algorithm 1 Lines 9-12).

Due to the Vertex Priority approach, we know that the start vertex of any wedge we discover must have a degree of size greater than or equal to the degree of the mid and end vertex. As a result, the total number of wedges that can be uncovered by our algorithm containing a start vertex u and an end vertex w is deg(w), which means the total combination of two wedges containing u and w is $deg(w)^2$. As a result, the cost of determining all wedge combinations of node u and w is $O(deg(w)^2)$. Thus, the time complexity of UBFC is $O(\sum _{e(u, v) \in E} \min \{deg(u)^2, deg(v)^2 \})$. $\square$

Theorem 2

The memory complexity of UBFC is $O(\sum _{e(u, v) \in E} \min \{deg(u), deg(v) \})$.

Proof

As noted in the proof for Theorem 1, the maximum number of wedges discovered for a start vertex u is deg(u). $\square$

5 Uncertain butterfly counting exact algorithms-improvements

In this section, we examine methods of improving the exact solution, ultimately reducing the running time, as well as proposing heuristic techniques to speed up the algorithm in practice.

5.1 Early edge/wedge discarding

One notable area of wasted operations is when examining or considering wedges that are unlikely to, or simply cannot, be a part of any uncertain butterfly for a given t.

Lemma 1

If there exists an edge e with existential probability $Pr(e) < t$, e cannot be a part of any uncertain butterfly.

Proof

Given that all probabilities must be $\le 1$, this can be proven trivially. $\square$

Lemma 1 means that we can simply ignore any edge that exists with probability $<t$. Additionally, this same logic can be applied to any graphlet structure (specifically a wedge) with existential probability $<t$ that can be found within a butterfly. Therefore, a simple pruning heuristic we adopt is that if at any point an edge or wedge has an existential probability lower than the threshold, we ignore it for future considerations.

In the case where no edge $e \in E$ exists with $Pr(e) = 1$, we may adjust the pruning threshold to be higher ($t / \max _{e \in E}\{Pr(e)\}$) to account for the higher required existential probabilities to compensate.

5.2 Improved list management

Another area of improvement over the baseline is in how the list l containing found wedges is handled, noting that currently finding all uncertain butterflies from l is done in $O(|l|^2)$ time, which in turn is a major increase to the runtime of the baseline algorithm acting as one bottleneck.

Lemma 2

To determine if an uncertain butterfly exists, containing nodes $(u_1, u_2, v_1, v_2)$, the only information we need is the existential probability of any two unique wedges sharing the same end points (either $u_1$ and $u_2$ or $v_1$ and $v_2$) and t.

Proof

Firstly, recall that two wedges $\angle _1, \angle _2$ with the same end points that are found in the same butterfly contain all the edges in the butterfly, two from each wedge totalling four unique edges. This is a fundamental truth which serves as the foundation of nearly all butterfly counting techniques [30, 42].

The same extends to the existential probabilities of wedges and butterflies. That is, . With this information and t, we can easily check if an uncertain butterfly exists from these nodes. Given that we are not enumerating, we don’t actually need to store any nodes given that the shared end points are assured and wedge probabilities are stored instead. $\square$

Lemma 2 allows us to modify the content of our lists and our wedge combination algorithm. Firstly, instead of l storing the middle node of the wedge, we instead have it store the existential probability of the wedge. Secondly, we keep the list sorted upon the insertion of a new wedges information.

Before we fully explain the new Uncertain Butterfly Counting algorithm for the sorted list l, we need to note some properties of the list.

Lemma 3

If two wedges $\angle _1, \angle _2: Pr(\angle _1) > Pr(\angle _2)$ form an Uncertain Butterfly, then all wedges before $\angle _1$ in l forms an Uncertain Butterfly with all wedges before $\angle _2$ in l.

Lemma 4

If two wedges $\angle _1, \angle _2: Pr(\angle _1) > Pr(\angle _2)$ do not form an Uncertain Butterfly, then all wedges after $\angle _1$ in l do not form an Uncertain Butterfly with all wedges after $\angle _2$ in l.

Proof

As l is a sorted list by existential probability, both Lemma 3 and 4 can trivially be shown with basic probability theory. $\square$

Both Lemma 3 and 4 allow us to quickly validate the existence of Uncertain Butterflies using l without having to actually calculate their existential probabilities. These ideas form the foundation of our improved algorithm for extracting an Uncertain Butterfly count from l.

Algorithm 2 details our improved technique for determining the number of Uncertain Butterflies from the wedges in l. Given that l is a sorted list of existential probabilities, we initialise $i = 0$ and $j = 1$ to be two indexes on the list. The algorithm continues until $j == |l|$ or another break condition is reached.

If $l[i] * l[j] \ge t$, this implies that the current wedges being represented form an uncertain butterfly, which means determining values for i and j are the key in reducing the runtime of the algorithm. As the algorithm begins, as long as $l[i] * l[j] \ge t$, we increment the count by $i + 1$ (due to Lemma 3) and then increment by i and j by 1 (Lines 9-12).

However, after the first time $l[i] * l[j] < t$, we no longer need to continue to increment i due to Lemma 4. This is reflected in our algorithm by a Boolean flag F (Lines 1, 4, 11-12). When i and j fail to form an uncertain butterfly, we need to find the value of i which can form an uncertain butterfly algorithm with j done by finding a minimum uncertain probability value $target = t / l[j]$ (Line 5). We then give i the largest index (smallest existential probability) in which $l[i] > target$, done via a variation of Binary Search called GTBinarySearch(list, leftIndex, rightIndex, target)

on the existential probabilities in index 0 to $i - 1$ (Line 6). If no such value of i exists, we terminate our algorithm as no further wedges can be found (Line 7-8).

Fig. 5

An example of the operation of our improved list counting method when $t = 0.4$

In Fig. 5, we go through an example of our improved technique. Noting that $t = 0.4$, we have our sorted list with six wedges represented inside. We start our pointers at $i = 0$ and $j = 1$ and calculate that the resulting product of wedge probabilities is 0.72 which is greater than our threshold. As such, we increase the count by 1 and move both pointers down one. The next butterfly (represented by wedges at $i = 1$ and $j = 2$) also passes the existential probability check and the count is increased by 2 ($i + 1$). This continues until $i = 3$ and $j = 4$ in which the represented butterfly has existential probability of 0.3. Thus, i is moved upwards to l[1] which is the lowest probability which still passes the threshold check when multiplied with $l[j = 4]$. This is found using our GT Binary Search method. With the count incremented, we only move j down and the resulting wedge cannot form an uncertain butterfly with any wedge in the list and thus the algorithm terminates with a count of 8.

Theorem 3

Algorithm 2 produces the correct uncertain butterfly count.

Proof

Our algorithm can be thought of as iterating through all values of $0< j < |l|$ and finding the largest value of $i < j$ which forms an uncertain butterfly. Then, using Lemma 3, we know that there exist $i + 1$ uncertain butterflies in l which satisfy the $i < j$ condition for j. This is done for all j which will result in the exact uncertain butterfly count with no redundancy. Furthermore, whenever $l[i] * l[j] < t$, we know that no future value of i can be greater than the current value of i as j increases due to Lemma 4. $\square$

Theorem 4

Algorithm 2 takes time.

Proof

We iterate j from 1 to $|l| - 1$ assuming no early termination which accounts for the O(|l|) portion of the time complexity. If we were to perform GTBinarySearch $|l| - 1$ times on the entire list l, then our time complexity would be $O((|l|-1)\log (|l|)$. However, since the segment of |l| in which GTBinarySearch (GTBS) must operate is capped the first time the function is called and future calls search on an even smaller space due to Lemma 4.

If GTBS is called when $j = |l| - 1$, then the total cost of all GTBS calls is $O(\log (|l| - 1))$. If GTBS is called when $j = |l| - 2$, the total possible cost of all GTBS must be $O(\log (|l|-2) + \log (|l|-3))$. The most number of GTBS calls is capped at when with a total possible cost of . The total possible GTBS cost of any smaller value of j must be smaller than this value.

Given this, the total possible cost of GTBS for list l is time. $\square$

Despite Theorem 4 appearing expensive due to the factorial, it is still distinctly smaller than $O((|l| - 1) \log (|l|) = O((|l| - 1) + \log (|l|^{(|l| - 1)}))$ time which in turn is obviously smaller than the baseline of $O(|l|^2)$. In most realistic scenarios with the early termination clause and the size of the GTBS search space potentially reducing by much more than a single item, the realistic cost of Algorithm 2 can be significantly smaller than the worst case that is Theorem 4. All operations in Algorithm 2 can be done in O(|l|) space, which can be verified trivially.

5.3 Improved algorithm

Adopting all mentioned improvements, we now present our Improved Uncertain Butterfly Counting Algorithm (IUBFC).

Algorithm 3 details our improved algorithm, adopting the previously mentioned improvements. The first deviation from the baseline solution is an additional step after extracting the backbone graph where all edges with $Pr(e) < t$ are removed from $W_1$ for the purposes of wedge (and butterfly) discovery as per Lemma 1 (Line 2).

We sort by vertex priority (Line 3) and then continue using a similar wedge discovery approach as the baseline using the new priority (Lines 5-8). One notable difference from the baseline is the wedge lists store the wedge existential probability value instead of the actual nodes. When a wedge $\angle (u, v, w)$ is discovered, it is inserted (if $Pr(\angle (u, v, w)) \ge t$ (Lemma 1)) such that the list at H(w) remains sorted (Lines 9-10).

Finally, our alternate list management strategy allows us to utilise the improved list count strategy detailed in Algorithm 2 (Lines 11-12).

We now examine the changes to space and time complexity of the algorithm compared to our baseline.

Theorem 5

The time complexity of IUBFC is $O(\sum _{e(u, v) \in E} \min \{deg(u) \log (deg(u)), deg(v) \log (deg(v)) \})$.

Proof

Our proof utilises the observation from Theorem 1 (and thus from the certain algorithm proof by Wang [43]) in which the total number of wedges containing an edge e(u, v) is $\min {deg(u), deg(v)}$, which in turn is the maximum size of a given wedge list l. In turn, the cost of keeping a list sorted via existential probability is $O(|l| \log (|l|))$. As shown in Theorem 4, the time complexity of our improved list combination algorithm (Algorithm 2) is a value which is less than the cost of keeping the list sorted. Thus, via dominant terms in big O notation, the final cost of our algorithm for each wedge list is $O(|l| \log (|l|))$ where $l = \min {deg(u), deg(v)}$. The cost of deriving the wedge list for each edge is $O(\min {deg(u), deg(v)})$ (as per [43]) which is again dominated. Thus, the cost of finding each wedge list and keeping it sorted is $O(\sum _{e(u, v) \in E} \min \{deg(u)\log (deg(u)), deg(v)\log (deg(v)) \})$. $\square$

The memory complexity of IUBFC is unchanged from UBFC (Theorem 2).

5.4 Sorting by vertex priority versus existential probability

Vertex Priority is an important tool in the deterministic variation of this problem as it ensures, in total, each edge is only examined one time for each wedge it is a part of. This not only minimises the cost of the algorithm but also reduces redundancy. However, this idea was formed under the assumption that all butterflies (and wedges) are required in the final solution which is evidently not true in our uncertain variant.

Currently, in our improved solution, nodes are sorted by increasing vertex priority (Algorithm 3 Line 3) and a check is made for each wedge to determine if it satisfies the existential probability constraints (Algorithm 3 Lines 7-10). Of course, since the nodes are sorted by priority, we can terminate the iteration through the neighbour list after the first node which fails the priority check in Lines 7 and 8, which serves as an important part of both the baseline and our improved solution in terms of suppressing the cost in this step.

However, we may consider an approach which comes at this problem from an alternate viewpoint. Instead of sorting by (increasing) vertex priority, we instead sort by (decreasing) edge existential probability. We can leverage the fact if edges $e_1$ and $e_2$ do not form a wedge with existential probability $\ge t$, no edges with existential probability smaller than $Pr(e_2)$ forms a satisfactory wedge with $e_1$ and vice versa using the same logic as Lemma 4. The same is true for wedge combinations with higher existential probability (following Lemma 3). We will refer to the method in which nodes are sorted by vertex priority as VP and the method in which nodes are sorted by edge probability as EP.

Algorithm 4 shows the modified method for wedge discovery assuming sorted EP. For an edge e(u, v), we examine nodes $w \in N(v)$ and determine if $Pr(e(u, v)) * Pr(e(v, w)) \ge t$ (Line 4). If this probability constrain satisfied, we add the wedge if the priority constraint is also satisfied (Line 5-6). If the probability constraint is not satisfied, we know that there are no more satisfactory wedges containing e(u, v) and we move on in our search (Line 7-8).

Using VP, nodes A, B and C are checked in that order with only node A satisfying the existential probability check. Since node D fails the vertex priority requirement, the wedge discovery process is terminated. When using EP on the other hand, nodes E and A are checked in that order with only node A satisfying the vertex priority check. Since node C results in a wedge with lower existential probability than t, the wedge discovery process is terminated.

Both VP and EP ensure that each wedge is only added to a list once during the entire algorithm so the final result will remain the same. What the methods do control is the number of times an edge reaches the alternate check (wedge probability for VP and vertex priority for EP) step. In VP, each edge reaches the alternate check step once for each wedge it is a part of. Alternatively, in EP, each edge reaches the alternate check step twice for each wedge with existential probability $\ge t$ and zero times otherwise.

Theorem 6

The time complexity of EP is $O(\sum _{e(u, v) \in E} \min \{deg(u) \log (deg(u)), deg(v) \log (deg(v)) \} + \Gamma (e))$ where $\Gamma (e)$ is the number of wedges $\angle$ containing e where $Pr(\angle ) \ge t$.

Proof

The numbers of wedges that will be passed into a list, as well as the size of each list, are unchanged from Theorem 5. The only change is that for each edge $e \in E$, it will be checked an additional time for each uncertain wedge it is contained in. $\square$

The memory complexity of EP is unchanged compared to VP.

Of course the better method to use between VP and EP is highly graph and threshold value dependant. The break-point in which EP is the superior method is when less than $50\%$ of the wedges in $W_1$ post-pruning have an existential probability $\ge t$. Furthermore, the larger the percentage favours in one direction indicates the corresponding method is more efficient by that margin. When the percentage skews towards $100\%$, VP is significantly better, and when it skews towards $0\%$, EP is significantly better. Furthermore, it is possible for EP to become more expensive than even the baseline if there is minimal or no pruning and a large percentage of the wedges have an existential probability $\ge t$ due to the nature of reaching the check step twice as opposed to once for each wedges on G than an edge is apart of in the baseline. Thus, it is recommended for low t values relative to the edge probability distributions to select VP.

6 Uncertain butterfly counting sampling algorithms

Whilst exact algorithms are indeed important for determining the exact uncertain butterfly count on a network, approximate solutions may also provide significant insights at a fraction of the time cost. As an example, on a giant user-item network, the operator may be interested in seeing if their recommendation strategy broadly increases the uncertain butterfly count by running an approximation strategy for a few minutes as opposed to waiting hours or days for an exact strategy to provide the specific counts.

In this section, we introduce two local sampling techniques aimed at solving the Uncertain Butterfly Counting problem. The first technique Uncertain Butterfly Sampling (UBS) operates by local sampling the number of uncertain butterflies each vertex is a part of. The second technique Proportion Estimation Sampling (PES) uses a local sampling approach which determines the number of certain butterflies and estimates the proportion of butterflies on G which are uncertain.

6.1 Uncertain butterfly sampling (UBS)

For the first approximate solution, we utilise a local sampling approach to determine the number of uncertain butterflies containing a sampled vertex or edge. We then propagate that number outwards accordingly to the entire network and as the number of samples grows, the average value converges to the true result. This approach is adapted from a local sampling deterministic solution proposed by Sanei-Mehri [30] with the added task of needing to monitor and check existential probabilities to ensure each uncertain butterfly is valid.

Algorithm 5 illustrates a local sampling algorithm for the number of uncertain butterflies containing a selected vertex u. Our algorithm follows the deterministic variation [30] with the key changing being the usage of our ImprovedListCount technique introduced by us in Algorithm 3 (Lines 1-8), in the same way our baseline exact algorithm UBFC was modified from the exact deterministic algorithm.

Theorem 7

The time complexity of Algorithm 5 is $O(d^2 \log (d))$ where $d = \max _{v \in V}\{deg(v)\}$

Proof

As the idea of vertex priority does not apply in local search, the maximum number of wedges for a shared start and end point is the maximum degree of any vertex ($d = \max _{v \in V}\{deg(v)\}$) on G. As proven in Theorem 5, the Improved List Management technique takes $O(d \log (d))$ time thus our final time complexity is $O(d^2 \log (d))$ as any start node can only have $\le d$ end nodes. $\square$

Theorem 8

The memory complexity of Algorithm 5 is $O(d^2)$ where $d = \max _{v \in V}\{deg(v)\}$

Proof

The total number of wedges that any given vertex in G can be a part of is $d^2$. $\square$

With the known number of uncertain butterflies containing u, $C_t(u)$, we extrapolate that number to the entire network $C^e_t(u)$ (Line 9). We can do this as in there deterministic sampling approach, it is shown that ${\mathbb {E}}[C^e(u)] = C$ and $Var(C^e (u)) \le \frac{|V|}{4}(C + p^v)$ where C is the certain butterfly count and $p^v$ is the number of pairs of butterflies in G that share at least a single node [30]. Extending on their proof and excluding butterflies which do not satisfy t, we can trivially show that ${\mathbb {E}}[C^e_{t}(u)] = C_t$ (i.e. the estimator is unbiased) and $Var(C^e_t (u)) \le \frac{|V|}{4}(C_t + p^v_t)$ where $p^v_t$ is the number of pairs of uncertain butterflies in G that share at least a single node. We thus implement this in our algorithm.

Algorithm 6 details our vertex-centric Uncertain Butterfly Sampling (vUBS) method. For a graph G, threshold t and a number of samples sampNum, our method estimates the uncertain butterfly count $\tilde{C_t}$. We sample a node u without replacement and determine $C^e_t (u)$ using vUBLS (Algorithm 5) (Line 4-5). We then adjust $\tilde{C_t}$ accordingly (Lines 6-7). Furthermore, as extended from the deterministic version, if the algorithm is run for $O\left( \frac{|V|}{C_t} (1 + \frac{p_t^v}{C_t})\right)$ iterations, it provides an ($\varepsilon , \delta$)-estimator [30].

Whilst we have only detailed the vertex-centric algorithm, a similar algorithm which is edge-centric is also implemented for the purposes of experimentation. This method holds the same properties and utilises the same algorithm as the vertex-centric approach except with references of vertices replaced with edges.

6.2 Proportion estimation sampling (PES)

Our second sampling approach utilises a different problem formulation as its basis. One notable difference between local certain and uncertain butterfly counting techniques for a selected vertex or edge is that the certain solution is theoretically less expensive in both time and space requirements. As we are interested in a sampling, and thus approximate, solution perhaps an approach in which we leverage the speed of certain sampling and correctly adapt those values to our problem is of interest.

Fig. 6

A Probability Mass Function (PMF) of the existential probabilities of butterflies in a network, split by the threshold value t. $\alpha$ is the proportion of butterflies to the right of t

To accomplish this, let us think of another way of formulating the Uncertain Butterfly Counting problem. Suppose we have the deterministic butterfly count on the Backbone Graph C. Then, the uncertain butterfly count can be formulated as $C_t = \alpha C$ where $\alpha$ is the proportion of butterflies with existential probability $\ge t$. Figure 6 illustrates this idea in the form of the Probability Density Function (PDF) of butterfly existential probabilities on a network.

Using this logic, if we can find $\alpha$, we can use deterministic local sampling approaches to quickly estimate C and thus estimate $C_t$. Essentially, we can think of each butterfly as a Bernoulli trial $Ber(\alpha )$ in regards to succeeding if the existential probability satisfies the threshold t.

Of course determining $\alpha$ exactly is extremely costly and unfeasible as it requires the discovery of all butterflies, which in itself already contains the solution to our problem. Instead, if we can find a way to estimate $\alpha$, we can utilise the deterministic sampling solution to quickly approach the uncertain butterfly count. Our estimation method relies on the following observation.

Lemma 5

The PDF of Butterfly Existential Probabilities (B-PDF) can be thought of as a “random” sample of the PDF of the product of existential probabilities in G for all permutations of four edges (E4-PDF).

Proof

Of course, since a butterfly is a structure which contains exactly four edges, the set of all butterflies is located inside the set of all permutations of four non-identical edges. Noting that edge probabilities are independent, we can think of B-PDF as a sample of size C from E4-PDF. Notably, E4-PFD can be ‘known’ in that all relevant information can be computed in $O(E^4)$ time. That is, no assumptions need to be made about the model distribution. $\square$

Given Lemma 5, using the Margin of Error (in percentage points) statistic for a set of Bernoulli trials [4], we can determine how much the proportion from B-PDF can deviate from the proportion from E4-PDF with a set confidence (i.e. a confidence interval). The Margin of Error (M) equation is as follows:

$$\begin{aligned} \begin{aligned} M&= z \sqrt{\frac{\alpha (1 - \alpha )}{n}} \end{aligned} \end{aligned}$$

(1)

where z is the z-table confidence interval value (e.g. 2.576 for $99 \%$ confidence) and n is the size of the sample set (i.e. C). This essentially means the estimated value of $\alpha$ is within the range $(\alpha - M, \alpha + M)$ $99 \%$ (or other chosen confidence) of the time for a sample of size n.

With this we can calculate, with a confidence interval, the likelihood of a sample set of size C being with a certain Margin of Error using the proportion ${\hat{\alpha }}$ of the $E4-PDF$. Of course we cannot know C with certainty but we can estimate it ${\tilde{C}}$ via a deterministic sampling technique. A quirk of the Margin of Error equation is that small changes in the sample size provide negligible results. It is also known that as the sample size increases, the relative change in the reduction M decreases.

We determine ${\tilde{C}}$ using a vertex-centric deterministic butterfly count and extrapolation sampling technique (vBFC, Algorithm 7) devised by Sanei-Mehri et. al [30]. In this counting technique, the hashmap holds only a single integer for each end-node, and once wedges are discovered, the butterfly counting step can be done in O(1) time. In the same work, it is also shown that ${\mathbb {E}}[C^e(u)] = C$ (i.e. unbiased), $Var(eC(u)) \le \frac{V}{4}(C + p_v)$ where $p_v$ is the pairs of butterflies that share one vertex.

From this, we can estimate the uncertain butterfly count as $\tilde{C_t} = {\hat{\alpha }} {\tilde{C}}$. However, the trivial method of calculating ${\hat{\alpha }}$ is impractical as it checks all combinations of four edges in E. As such, we determine a more reasonable method.

6.2.1 Further proportion estimation sampling

The gains have been made using vPES compared to vUBS in regards to the cost of each sample allowing for vPES to sample more nodes in a shorter timeframe, the trade-off of a $O(|E|^4)$ proportion estimation step is too much in reality without a dedicated system which stores the E4-PDF. In that regard, if we can further estimate $\alpha$, we can adopt the cheaper sampling process with less associated overhead.

We instead estimate the proportion by sampling from the E4-PDF, which results in a trade-off of an increased margin of error for a set confidence in return for a potentially significant decrease in the cost of the process.

To estimate ${\hat{\alpha }}$, given user-defined $M_S$ and z values, it is possible to determine the number of samples required n to have a given confidence (based on the z value). Since the population size is known ($|E|^4$), this equation is $n = \frac{SS}{1 + \frac{SS + 1}{|E|^4}}$ where $SS = \frac{0.25z^2}{{M_S}^2}$. Given the population size of most graphs is a massive number, for a given $M_S$ and z, the sample size is essentially the same for all graphs. Each sample of the E4-PDF trivially takes O(1) time and space, thus the time cost of estimating ${\hat{\alpha }}$ is O(n).

Our vertex-centric Proportion Estimation Sampling (vPES) algorithm is detailed in Algorithm 8. We first calculate the number of samples of the E4-PDF that should be conducted via the method discussed above (Line 1). Then, for each E4-PDF sample required, four random edges in E are sampled and the resulting existential probability is compared to t, which derives ${\hat{\alpha }}$ (Line 2). We sample vertices without replacement (a total of sampNum times) and estimate the deterministic butterfly count ${\tilde{C}}$ (Lines 4-7). Finally, we output our estimated uncertain butterfly count $\tilde{C_t} = {\hat{\alpha }} {\tilde{C}}$ (Line 8). We can then calculate the Margin of Error ${\hat{\alpha }}$ using $\alpha = {\hat{\alpha }}, n = {\tilde{C}}$, with a given confidence value (Eq. 1) then extrapolating this to confidence interval to $\tilde{C_t}$. Following other Monte-Carlo sampling approaches, this method is unbiased.

Once again, a similar edge-centric algorithm exists with minimal adjustment to Algorithms 7 and 8 whose details we have opted to exclude in interest of space.

With the $M_S$ and also the Margin of Error estimated from the B-PDF as described previously (now denoted as $M_B$). The Margin of Error of our final result can be calculated as $M = \sqrt{{M_S}^2 + {M_B}^2}$ assuming the same confidence value was selected for both $M_S$ and $M_B$. It should be noted that via the Law of Large Numbers, the number of samples required is not linear to the number of edges in the graph.

6.3 Wedge-based sampling

Aside from sampling a single vertex or single edge (effectively sampling two vertices), the use of sampling an entire wedge is a known method to estimate the butterfly count [30]. That being said, whilst sampling vertices and edges uniformly is a straightforward process (as a list of all edges are often given as the format of inputting a graph), it is much less trivial to uniformly sample a wedge from a graph without additional pre-processing and/or memory requirements. However, assuming we have a uniform wedge sampling method, it becomes trivial to extend both UBS and PES into a wedge sampling approach.

In order to use a uniform wedge-based sampling method, a simple method would be to enumerate and subsequently store all wedges in the graph, which takes $O(\sum _{v \in V}deg(v)) = O(|E|)$ time but more importantly $O(|\angle |)$ space. Whilst this is fine for smaller networks, for larger graphs, this is a restrictive requirement. Previous works, particularly in the triangle counting space [33], have worked from multiple directions to address this whilst swallowing the additional memory cost and the cost of scalability. The most common of these methods being a weighted sample of pivot vertices based on the number of wedges pivoting at that node, then the uniform sampling of two neighbours of the pivot node [30].

A known method is utilising Walker’s Alias Sampling Method [38] which achieves O(1) sampling time with a $O(\sum _{v \in V} deg(v)) = O(|E|)$ pre-processing step, as well as O(|V|) memory cost [39]. Additionally, given the large or incredibly small numbers that are required for multiplication and particularly division in the pre-processing step, modern machines running standard programming languages may struggle to accurately perform operations on very large graphs.

The method we have chosen to implement for near-uniform wedge sampling is a Monte-Carlo Markov Chain method, or more specifically the Metropolis Hastings algorithm, used in the triangle counting space which requires no additional memory cost but each sample takes $O(deg_{max})$ time [29]. This method becomes more accurate as the sample size increases which means that is less suited for a single sample use case, in which case utilising a node or edge sampling method is our recommendation.

7 Uncertain bitruss decomposition algorithms

In this section, we propose an algorithm designed to perform Uncertain Bitruss Decomposition. Additionally, we delve into the three different algorithms able to compute the support of each edge of the graph, a critical step in bitruss decomposition. These methods aim at dealing with the potential trade-off of theoretical time complexity associated with the algorithm and the hidden constant costs required to implement the algorithms in reality.

Our decomposition algorithm is based off of the certain variation of the Bitruss Decomposition algorithm [44], which in turn was adapted from the foundational framework set via multiple works on Truss Decomposition on unipartite graphs [12, 41, 57]. The key difference between the two is in counting the initial uncertain support of each edge (i.e. the local uncertain butterfly count), a task that largely affects the overall runtime of the algorithm if implemented poorly. As can be inferred from the algorithms, we designed to tackle UBFCP, with the exception of baseline UBFC and edge-based UBS, the methods will batch together multiple edges together when increasing the global count in a way that makes it impossible to update the local support of each edge. Additionally, whilst porting UBFC directly is possible, the method is theoretically and practically much slower than other possible solutions which we will discuss.

Our method for uncertain bitruss decomposition is detailed in Algorithm 9, adapted to our setting from [44]. The first and arguably most critical step is to determine the uncertain support of each edge in the network (Lines 1-2). More details regarding how this is accomplished is discussed later. Then, for the current edge e with the lowest uncertain support $sup_t(e, G)$, that value is reported as the uncertain bitruss number $\phi _t(e) = sup_t(e, G)$ (Lines 3-4). Then, all other edges $e' \ne e$ which share an uncertain butterfly with e have their uncertain supports reduced by one and e is then removed from G (Lines 5-9). This process continues until no edges are left in G implying all edges have been assigned an uncertain bitruss number.

In order to get the edge e with the current lowest $sup_t(e, G)$, this process requires an efficient method. It is not enough to simply sort the list of edges initially and leave the ordering the same afterwards as the uncertain supports of certain edges drop, whilst others remain stable as the algorithm runs. On small graphs or machines with sufficient memory, a common method used in the unipartite variation is a Bin Sort implementation [41]. An implementation of this would require an additional $O(|E| + maxsup_t$) memory cost where $maxsup_t$ is the maximum uncertain support of any edge in G. This method however is inexpensive to build, taking O(|E|) time, and makes selecting the edge with the lowest uncertain support easy and updating the uncertain support of edges after edge removal trivial.

In the case where Bin Sort is not viable due to the memory costs associated with the implementation, it is possible to instead use a Fibonacci Heap [34] to upkeep the uncertain supports of all edges without an uncertain bitruss number. Whilst the Fibonacci Heap takes only O(|E|) memory, less than or equal to Bin Sort, the other associated costs such as the extract-min operation (what would be used to retrieve the edge with the lowest uncertain support) having an amortised cost of O(log(|E|)) per operation [10] make it unappealing if it can be avoided (that is if the memory cost of Bin Sort can be absorbed by the machine being run).

7.1 Deriving initial uncertain supports

Deriving the initial uncertain supports of G is critical to ensuring the entire algorithm for solving the UBitDP to run smoothly. However, it should be noted that finding these uncertain supports cannot be done in the same manner as finding the global uncertain butterfly count using IUBFC. The reason for this is IUBFC batches together butterflies before updating the global count by that size of the batch. However, as no two butterflies share the exact same four edges in our problem setting, we cannot batch in such a manner.

We will examine various different methods which may be used to derive the uncertain support of all edges in a graph, as well as provide analysis and theoretical comparisons between the methods. Firstly, we discuss the two key factors which we must consider when designing and comparing such algorithms.

The first factor is the Big O algorithm time complexity of the method in question, which obviously will largely play a large part in projecting the real running time of the algorithms comparatively.

The second factor we need to consider is more of a cost which is often hidden in Big O notation, that being the number of times an edge has its uncertain support value updated in the process of calculating all uncertain support. As a hashtable is the most obvious structure to use when updating the running uncertain support of all edges during the execution of the method, any time cost of the uncertain support update at any given time is O(1) regardless of how much the count increases by. As a result, especially for large graphs where the uncertain support can be in the thousands or higher, the aim should be to minimise the number of times each uncertain support is updated despite the fact the time complexity may not be noticeably affected.

7.1.1 UBFC-based

Of our existing algorithms, one of the most simple extensions which may be used to answer the initial uncertain support derivation is a trivial extension upon the UBFC algorithm (Algorithm 1, Section 4). Given that this method compares all combinations of two wedges to see if the resulting butterfly is an uncertain butterfly, a simple additional step would be to increment the current uncertain support for each edge in the found uncertain butterfly at the time of discovery. As each uncertain butterfly is discovered once and only once during the operation of UBFC, the correctness of the algorithm is guaranteed. We will henceforth refer to this algorithms as Uncertain Support Calculation-UBFC (USC-UBFC).

Theorem 9

The time complexity of USC-UBFC is $O(\sum _{e(u, v) \in E} \min \{deg(u)^2, deg(v)^2 \})$

Proof

As the cost of increasing the current uncertain support of an edge is O(1), the rest of the proof extends off of the proof for Theorem 1. $\square$

Theorem 10

The total number of times an uncertain support value is modified in USC-UBFC is $\sum _{e \in E}{sup_t(e, G)} = 4C_t$

Proof

When an uncertain butterfly is discovered in this algorithm, the uncertain support of each edge contained in the butterfly increases by 1 (i.e. four modifications of uncertain supports). As the algorithm finds each uncertain butterfly once and only once, it is evident the total number of uncertain support edges is four times the global uncertain butterfly count. $\square$

7.1.2 IUBFC-based

Whilst not all downsides of UBFC compared to IUBFC applies in the initial uncertain support computation variation of the problem (notably not needing to actually visit every pair of two wedges which forms an uncertain butterfly), some areas of improvement do carry over. The most notable area in which improvement can occur is the elimination of useless wedge comparisons, an important motivation behind IUBFC in the global butterfly counting problem. Whilst it is impossible to not at least visit every pair of wedges which form an uncertain butterfly, it is not necessary to validate that the product of the two probabilities is less than t if the sorted property of the Improved List method is observed (Sect. 5.2). Furthermore, the ability to skip wedge pairs which are ruled out using the same properties are still observed in the uncertain support version of our method.

We will first discuss a method of adapting our Improved List Count method (Algorithm 2) in order to account for our problem needing to update uncertain support counts as opposed to just a simple global count. Assume this step executed instead of Line 9 of Algorithm 2. A small modification of the list is that it stores both edges of the wedge in addition to the wedges existential probability. The trivial method would be that once an uncertain butterfly has been identified with pointer i and j pointing, the algorithm reverse iterates through i to 0 (utilising Lemma 3) in order to identify each butterfly and thus update each edge by 1 at that time. As an example assume $i = 4$ and $j = 5$ are identified as forming an uncertain butterfly. Then, the butterfly formed by wedge l[4] and l[5] means we increment the uncertain support of each participating edge by 1. Afterwards, the butterfly formed by wedge l[3] and l[5] increments each edges uncertain support by 1 and so on and so forth until l[0] and l[5] has their edge uncertain support incremented.

Algorithm 10 details an alternative uncertain support updating method for our Improved List Count techniques which further reduces the number of accesses to memory. At Line 9 of Algorithm 2, where i and j have been confirmed to contain an uncertain butterfly, this new algorithm executes. The improved method notices that the wedge at l[j] makes a butterfly with each wedge at l[0] through to l[i] and thus can update the uncertain supports of both edges making up wedge l[j] in the same way the global count algorithm updated the count all at once (Lines 1-3). Unfortunately, as there is no better way to reduce the number of further uncertain support updates without increasing the complexity of the algorithm, the algorithm then iterates through each wedge between l[0] and l[i] and increments the uncertain support of each edge as it appears (Lines 4-8).

USC-IUBFC refers to our new algorithm for deriving the initial uncertain supports adapting IUBFC with our new list counting method.

Theorem 11

The time complexity of USC-IUBFC is $O(\sum _{e(u, v) \in E} \min \{deg(u)^2, deg(v)^2 \})$

Proof

Unlike IUBFC (Algorithm 3), USC-IUBFC may have to access every possible combination of wedges for each list making the time complexity resemble USC-UBFC. $\square$

Whilst USC-IUBFC does not have the same reduction in time complexity that occurs when comparing IUBFC to UBFC in the global counting variation, the method still derives significant benefit from ignoring useless wedge comparisons as well as not needing to verify that every butterfly has an existential probability greater than or equal to t as that information can be inferred via Lemma 3 and Lemma 4.

Theorem 12

The total number of times an uncertain support is modified in USC-IUBFC is $2C_t + 2\sum _{(u, v) \in E}{\mathbb {I}}$ where ${\mathbb {I}} = 1$ if u and v start and end a wedge (which follows vertex priority ordering [Definition 12]) which is a part of an uncertain butterfly and ${\mathbb {I}} = 0$ otherwise.

Proof

For each butterfly, two of the edges are incremented by 1 immediately which accounts for $2C_t$. As a result, we only need to figure out the number of times the algorithm further updates edge uncertain supports (i.e. when a wedge represented by a j pointer is updated). We can find this number by considering that for each pair of nodes u and v which form at least one wedge (following vertex priority) that further forms an uncertain butterfly with the rest of the wedges starting and ending at u and v. Therefore, the two edges of that wedge have their uncertain support updated once (this is a j pointer wedge). $\square$

There is a very rare possibility that no two wedge start/end points u/v are part of more than one uncertain butterfly in which case the total number of uncertain support modifications is once again exactly $4C_t$. However, this is exceedingly unlikely particularly for large real bipartite networks. In general, the total number of uncertain support modifications of USC-IUBFC is in the range of $(2C_t, 4C_t]$ which can never be worse than the $4C_t$ accesses of USC-UBFC.

7.1.3 Systematic local search

Both methods mentioned above follow the logic used to motivate global uncertain butterfly counting in that they aim to find each uncertain butterfly only once and then uses the algorithm structure to try and reduce the number of uncertain support modifications. That is, the minimisation of theoretical time complexity is prioritised over minimisation of the amount of uncertain support modification. Our alternate solution reverses this and aims to prioritise the minimisation of the uncertain support modification.

The absolute minimum number of times the uncertain support of a single edge can be modified is once. That is, the uncertain support of that edge is found and the value is modified from 0 to be its correct value. This means, the minimum possible number of uncertain support modifications over the entire runtime of an algorithm must be |E| exactly (assuming each edge has nonzero uncertain support).

As mentioned in Sect. 6.1, we use a local uncertain butterfly counting method which can find the uncertain butterfly count for a given edge (i.e. the uncertain support). Algorithm 11 provides the details of this method, with largely the same methodology as the vertex-centric version (Algorithm 5). The time complexity of this local count method is also $O(d^2 \log (d))$ where $d = \max _{v \in V}\{deg(v)\}$.

Algorithm 12, henceforth referred to as USC-LS, details the straightforward local search-driven initial uncertain support derivation algorithm. The method is straightforward where for each edge on the graph, local search is conducted in order to find the exact number of uncertain butterflies containing said edge. Then, the uncertain support value is updated all at once in order to minimise accesses to memory.

Theorem 13

The time complexity of USC-LS is $O(|E|d^2 \log (d))$ where $d = \max _{v \in C}\{deg(v)\}$

Proof

Given that the time complexity of local search for any given edge $e \in G$ is $O(d^2 \log (d))$, the remaining proof is trivial. $\square$

To compare the time complexity of USC-LS with USC-UBFC and USC-IUBFC, the latter two may have their time complexity generalised as $O(|E|d^2)$. As a result, it is clear that theoretically USC-LS is more expensive by a factor of O(log(d)).

Theorem 14

The total number of times an uncertain support value is modified is $|E_t|$ number of times where $E_t$ is the set of edges which have nonzero uncertain support

Proof

The value for an edge is derived then the update occurs all at once. This happens for each edge in the entire system. $\square$

It is fairly obvious that USC-LS has the least possible amount of uncertain support updates for a system in which the uncertain support of each edge is stored in its own unique location.

Table 2 Dataset Information (* indicates variable number)

7.2 Complexity analysis

In this section, we examine the complexity analysis of our uncertain bitruss decomposition method. For our analysis, we assume that we are using the Bin Sort method. We refer to the general algorithm framework as UBitD with each variation being referred to as UBitD-UBFC, UBitD-IUBFC or UBitD-LS depending on the selected initial uncertain support derivation method.

Theorem 15

The time complexity of our Uncertain Bitruss Decomposition method is $O({\mathbb {S}} + \sum _{e(u, v) \in E} \sum _{w \in N(v)} \max \{deg(u), deg(w)\})$ where ${\mathbb {S}}$ is the time complexity of the selected initial uncertain support calculation method

Proof

The uncertain bitruss decomposition algorithm UBitD is broken up into two components, the initial uncertain support calculation (Part 1) and the peeling process to determine uncertain bitruss numbers (Part 2). Part 1 depends on the initial uncertain support derivation algorithm selected, with the analysis in the relevant areas in Sect. 7.1. As for Part 2, the peeling component has been utilised in various different bitruss decomposition implementations with the proof being verified by Wang [44]. $\square$

In general, Part 1 will dominate Part 2 in terms of both theoretical and (as we will show in the experiments) practical time cost. It should also be noted that whilst Part 2 is largely the same regardless of which of the three initial uncertain support calculation methods are chosen, the $UBitD-UBFC$ and $UBitD-IUBFC$ variants will require the extra step of needing to re-sort the neighbour lists of each vertex back to ID ordering as opposed to Vertex Priority ordering. Ultimately, this cost can be avoided by storing two neighbour lists in both ordering types but from experimentation, the extra memory cost is largely not worth the relatively minor increase in time cost ($<1\%$ for most large graphs with reasonable t values).

8 Experimentation

In this section, we examine the efficiency and effectiveness of our proposed algorithms on a diverse range of graphs with different edge probability distributions and threshold values. When appropriate, we will preface an algorithm with v if it is vertex-centric, e if it is edge-centric or w if it is wedge-centric (e.g. vUBS is vertex-centric UBS).

8.1 Experiment settings

The datasets used in our experiments are Youtube (YT), Teams (TM), IMDB, Flickr (FL), DBLP, LiveJournal (LJ), Orkut (OR), CiaoDvd (CD) and BookCrossing (BC). Table 2 holds the details of all datasets used in this section. In the Edge Prob. column, if the value is a distribution, this means we assigned a synthetic weight from that distribution to each edge based on the popular Normal (N) and Uniform (U) distributions. Alternatively, for values that say “Collaborative Filtering”, we utilised existing ratings on the network to estimate the likelihood a user would like another item using a Collaborative Filtering Item Recommender [32]. On these networks, we append a number of edges whose probability was estimated to the end for each experiment. For example, if for the CD dataset, our experiment added a million extra edges, we would label the dataset ‘CD1M’. The table also contains the certain butterfly count C as well as the butterfly density ($C/|E|^4$) and average degree of the nodes in each partition as well as combined.

All raw datasets can be found from the Konect project.¹

Our code is written in standard C++11 and compiled using g++. Our experimental environment is an Intel Xeon Gold 6240R CPU @ 2.40GHz with 1007GB of memory.

Table 3 Memory usage

We first briefly touch upon the maximum memory consumption of our methods (denoted by the columns UBFC and IUBFC Memory in Table 3), noting that there is functionally no difference as this is the size of storing the graph in memory. The size of IUBFC drops after pruning edges with probability less than t.

We now examine the Efficiency (Sect. 8.2) and Effectiveness (Sect. 8.3) of our UBFCP algorithms before examining the Efficiency of our UBitDP methods (Sect. 8.4)

8.2 Efficiency of exact UBFCP algorithms

In this section, we examine the efficiency of both variants of IUBFC (IUBFC-VP and IUBFC-EP in Sect. 5) and compare their runtimes with our proposed baseline UBFC (Sect. 4). Since they are exact solutions, the effectiveness need not be compared. If an algorithm did not conclude after 100 h of being run, we terminated it. All instances of this will be noted as required.

Fig. 7

Runtime Comparison of exact algorithms on multiple datasets ($t = 0.8$)

The runtime of each algorithm for a set of datasets is visible in Fig. 7 (where $t = 0.8$). Clearly both our improved algorithms are faster than the baseline (UBFC for LJ and OK both did not finish after 100 h) due to our improvements. Our exact algorithms can take considerable time on the larger datasets, indicating a need for our approximate methods as an alternative if a strictly exact solution is not needed.

Fig. 8

The change in runtime as the threshold value t changes

Figure 8 illustrates that as t approaches 1, the runtime of both IUBFC-VP and IUBFC-EP becomes significantly smaller than the baseline. Notably, the runtime of IUBFC-EP starts higher but drops in a much sharper manner and ultimately becomes faster than IUBFC-VP, as the number of uncertain wedges rapidly diminishes reducing the added costs on IUBFC-EP that do not exist on IUBFC-VP whilst maintaining the benefits (see Sect. 5.4). We observe that the runtime of IUBFC-VP is never slower than UBFC even when t is effectively equal to 0.

Fig. 9

The change in runtime as the threshold value t changes for various distributions

We further examine the effect that the distribution of edge probabilities has on the runtime for varying t values. For the YouTube dataset, we examine the Normal $(\mu = 0.5, \sigma = 0.2)$, Uniform, Exponential and Reverse Exponential ($\lambda = 2$) distributions on Fig. 9.

Fig. 10

The runtime of IUBFC-VP and IUBFC-EP per Edge compared to Butterfly Density and Average Degree (for $t=0.8$)

Figure 10 examines the runtime per edge of our two improved algorithms compared to the butterfly density ($C/|E|^4$) as well as the average degree. We note that there does not appear to be a correlation between runtime and butterfly density, but there is one between runtime and average degree (which makes sense based on our time costs (Theorem 5).

Fig. 11

The change in runtime against the number of edges

Figure 11 examines the change in runtime as the number of edges (and subsequently average degree) changes on our Collaborative Filtering datasets. It is evident that both IUBFC-VP and IUBFC-EP are both much more scalable than the baseline.

8.3 Effectiveness of sampling UBFCP algorithms

We examine the effectiveness of our two sampling algorithms UBS (Sect. 6.1) and PES (Sect. 6.2) using the Further Proportion Estimation method (Sect. 6.2.1). For all PES experiments, we set the desired Margin of Error $M_S$ for Further Proportion Estimation Sampling at 0.01 and z value at 2.56. This experiment takes the mean after 100 samples 500 times.

Fig. 12

The average percentage error after 100 samples as t increases. Corresponding $\alpha$ values are also included

Figure 12 details the change in percentage error as the value of t increases (and subsequently the proportion $\alpha$ decreases). It can be seen that all variants of UBS are highly effective, whilst variants of PES at lower t values are also efficient. Whilst there is no noticeable difference in the three PES variations, it should be noted that wedge-based UBS is less stable which can be attributed to the 100 sample size. Given the use of MCMC to sample wedges ‘uniformly’, an increased sample size would lead to an error more in-line with the other UBS methods.

One noticeable effect is that as t increases and $\alpha$ grows smaller, the error of PES ultimately increases. This is due to the Further Proportion Estimation technique having a set Margin of Error ($M_S$) on ${\hat{\alpha }}$, which in our experimentation was set to 0.01. This of course means that our sampled proportion is allowed to deviate from the true proportion by up to that much, which is not an issue for most $\alpha$ values. However, for small $\alpha$ values, this can allow for a large relative difference in acceptable ${\hat{\alpha }}$ values. For example if the true $\alpha$ value is 0.02, an ${\hat{\alpha }}$ value between 0.01 and 0.03 is within our allowed range despite being able to create up to a 50% change in the estimated uncertain butterfly count. As a result, UBS should be favoured when the $\alpha$ value becomes extremely small. It should be noted that a very high $\alpha$ value will not effect the Error % of the final count in the same way. Both algorithms are similarly effective for larger $\alpha$ values (smaller t values).

8.4 Efficiency of sampling UBFCP algorithms

We now investigate the efficiency of our sampling algorithm and consider situations in which one may be preferred over the other.

Fig. 13

Average running time of a single sample for a dataset with the input threshold in square brackets

The average running cost of single sample of each algorithm on a variety of different datasets and t values is visible on Fig. 13. In general, the cost of a single sample (as evaluated in Theorem 7) scales with the average degree of the network and not the total number of vertices or edges. Therefore, on networks where the majority of edges have a reasonably low degree the algorithm can scale effectively. Even on networks with a high average degree because of ‘hub’ nodes raising the average still means our algorithm scales reasonable (especially when using edge-/wedge-based sampling which can search for uncertain butterflies on the side of the edge/wedge which is not a hub).

Using conventional wisdom, we would expect wedge-based sampling to more efficient than vertex and edge-based sampling as fixing three nodes can significantly reduce the search space compared to fixing only two or even one of the nodes. Whilst this is certainly true on large datasets with a high amount of edges, as well as average degree like ‘LJ’ and ‘OR’, it is noticeably not true for other datasets. This is of course due to the added cost associated utilising the vertex MCMC method to uniformly sampled wedges from our graph, which will take more time on sparser graphs as the algorithm tries to even find a wedge. It is also noticeable that PES sometimes is outperformed by UBS, which is a result that we further explore below.

Fig. 14

The change in runtime per sample as the threshold value t changes

Figure 14 illustrates the effect that an increasing t value (by increments of 0.1) has on the runtime of our sampling algorithms. All PES algorithms have a stable runtime for all t values which is unsurprising given how both methods look at all butterflies regardless of existential probabilities. However, as $t \rightarrow 1$, vertex and edge-based UBS become the faster options due to our improved list management method as well as not adding in any useless edges into any lists. This indicates a strong preference towards UBS algorithms for high t values in the case of vertex and edge-centric methods. On the other hand, wedge-based sampling shows a slightly different story. In general, wedge-based UBS and PES are seen to be stable in runtime as t increases. This suggests that the significant decrease in search space already accounts for most of the savings found by the vertex and edge-centric approach.

One interesting point is that vertex and edge-based approaches can be faster than wedge-based ones (most notable on the IMDB dataset). The reasoning for this is the overhead associated with the Vertex MCMC which we utilise to near-uniformly sample wedges from the network. When vertex and edge-based sampling approaches are naturally fast on a given graph/threshold combination, this overhead becomes apparent in the sampling time of wedges in comparison.

Additionally, wUBS is faster than wPES for all t values (this is also true for CD8M though the scale hides the effect) though this can be attributed to the cost of deriving ${\hat{\alpha }}$, a cost which was not significant in vertex and edge-based approaches but becomes noticeable here.

From our sampling experiments, we can infer that on larger t values, UBS should be favoured due to its improved list management and edge/wedge discarding techniques resulting in a faster runtime than PES. On the other hand, PES may be favoured for lower t values (with an appropriate subsequent $\alpha$ value) as the runtime is stable for all values of t and can be cheaper than UBS as deterministic butterfly counting is less expensive than uncertain butterfly counting even after factoring in the cost associated with Further Proportion Estimation. Additionally, for lower t values, PES does not encounter the problems associated with a very small $\alpha$ value which means the subsequent estimated Uncertain Butterfly Count is similar in accuracy to UBS. Wedge-based methods can be significantly faster than vertex and edge-based techniques, though on sparser graphs, it may perform worse. Ultimately, given the cost of a sample is so minimal, a practical solution in implementation would be to sample each method once and select the one with the smallest runtime to use for a given graph/threshold combination.

8.5 Bitruss effectiveness

In this subsection, we briefly empirically show that our model is able to capture the growth in a community with recommended edges against the existing communities on a recommendation edge-less graph.

Table 4 Increase in bitruss size compared to default graph

Table 4 shows the difference in size of the bitrusses at various k values compared to the bitruss size on the default CiaoDvd and BookCrossing graphs. As baseline BC is sparse, the growth at $k = 1$ is especially noticeable. In comparison, CD is a much denser dataset yet the growth is still noticeable. In general, we are able to capture this growth using the uncertain bitruss structure in a way that the normal bitruss cannot without making rigid assumptions regarding the existence of an edge with probability $<1$.

8.6 Efficiency of UBitDP algorithms

In this section, we examine the efficiency of our uncertain bitruss decomposition techniques. Like when examining exact UBFCP algorithms, we do not need to examine effectiveness as these algorithms are also exact and deterministic. The algorithms we examine are UBitD-UBFC, UBitD-IUBFC and UBitD-LS (Sect. 7 ).

Fig. 15

Runtime Comparison of uncertain bitruss decomposition algorithms on multiple datasets ($t = 0.8$)

The runtime of the three uncertain bitruss decomposition algorithms on a multitude of different datasets is examined in Fig. 15. We can observe that in general that for the given $t=0.8$ parameter, these datasets indicate that UBitD-UBFC is significantly outperformed by both other algorithms which is in-line with our theoretical expectations. The difference in cost between UBitD-IUBFC and UBitD-LS is less pronounced but there exist datasets in which either method outperforms the other which we will further explore later.

Fig. 16

The relative percentage of the runtime that is taken up by the peeling portion (Part 2) of the uncertain bitruss decomposition algorithm. ‘LJ’ and ‘OR’ for UBitD-UBFC are omitted as the algorithms did not terminate after 100 h

In order to understand the costs associated with the two parts of uncertain bitruss decomposition, Fig. 16 details the percentage of the runtime that is taken up by the peeling process (Part 2 of the uncertain bitruss decomposition algorithm). This is the universal algorithm that is run once the uncertain supports are derived. It is evident that, observed in conjunction with Fig. 15, the relative cost of peeling is less than the uncertain support derivation. The percentage is certainly higher for sparser graphs like ‘DBLP’ which makes sense intuitively given our cost analysis.

Fig. 17

The change in runtime of uncertain bitruss decomposition algorithms as t increases

Figure 17 details the change in runtime of the uncertain bitruss decomposition algorithms as the value of t increases. Unlike global uncertain butterfly counting, the baseline in UBitD-UBFC is not static for all t values as a lower t value will result in a more expensive peeling procedure. The two figures do show that as t increases, UBitD-LS outperforms UBitD-IUBFC though when t is smaller, the former is outperformed by UBitD-UBFC, whilst the latter always outperforms that baseline.

From our experiments, we can give the recommendation that for graphs with unknown properties, the recommended uncertain bitruss decomposition algorithm would be UBitD-IUBFC as it will never be outperformed by the baseline. On the other hand, for a graph that is understood by the user as well as an accommodating t value, UBitD-LS could certainly be the most efficient method of the three produced.

9 Conclusion

In this paper, we have examined the Uncertain Butterfly Counting Problem as well as Uncertain Bitruss Decomposition Problem on uncertain bipartite networks. We formally defined both the uncertain butterfly and uncertain wedge as well as proposed a non-trivial baseline for the exact global counting problem based on the state-of-the-art solution for the deterministic variant of the problem. We then proposed two improved algorithms which can drastically reduce the runtime of the algorithm. Additionally, when an efficiency for effectiveness trade-off is desired, we propose two alternate sampling solutions which quickly converge near the true value. For uncertain bitruss decomposition, we propose a framework with three different initial uncertain support derivation methods, two of which may be preferable in different scenarios. Our experiments examine all our algorithms and we also detail in which scenarios one of the methods may be preferred to the other.

In this extension, we explored a practical community leveraging the uncertain butterfly, though further innovation of subgraph structures utilising this building block graphlet is a point of interest. Additionally, given that the runtime of uncertain bitruss decomposition is dominated by the cost of initial uncertain support derivation, a more efficient algorithm to that end could significantly increase the scalability of that method.