Abstract
Frequent queries on semi-structured hierarchical data are Content-and-Structure (CAS) queries that filter data items based on their location in the hierarchical structure and their value for some attribute. We propose the Robust and Scalable Content-and-Structure (RSCAS) index to efficiently answer CAS queries on big semi-structured data. To get an index that is robust against queries with varying selectivities, we introduce a novel dynamic interleaving that merges the path and value dimensions of composite keys in a balanced manner. We store interleaved keys in our trie-based RSCAS index, which efficiently supports a wide range of CAS queries, including queries with wildcards and descendant axes. We implement RSCAS as a log-structured merge tree to scale it to data-intensive applications with a high insertion rate. We illustrate RSCAS’s robustness and scalability by indexing data from the Software Heritage (SWH) archive, which is the world’s largest, publicly available source code archive.
Similar content being viewed by others
1 Introduction
A lot of the data in business and engineering applications is semi-structured and inherently hierarchical. Typical examples are source code archives [2], bills of materials [9], enterprise asset hierarchies [14], and enterprise resource planning applications [15]. A common type of queries on such data are content-and-structure (CAS) queries [25], containing a value predicate on the content of an attribute and a path predicate on the location of this attribute in the hierarchical structure.
CAS indexes are being used to support the efficient processing of CAS queries. There are two important properties that we look for in a CAS index: robustness and scalability. Robustness means that a CAS index optimizes the average query runtime over all possible queries. It ensures that an index can efficiently deal with a wide range of CAS queries. Many existing indexes are not robust since the performance depends on the individual selectivities of its path and value predicates. If either the path or value selectivity is high, these indexes produce large intermediate results even if the combined selectivity is low. This happens because existing solutions either build separate indexes for, respectively, content and structure [25] or prioritize one dimension over the other (i.e., content over structure or vice versa) [6, 11, 41]. Scalability means that even for large datasets an index can be efficiently created and updated, and is not constrained by the size of the available memory. Existing indexes are often not scalable since they rely on in-memory data structures that do not scale to large datasets. For instance, with the memory-based CAS index [42] it is impossible to index datasets larger than 100 GB on a machine with 400 GB main memory.
We propose RSCAS, a robust and scalable CAS index. RSCAS’s robustness is rooted in a well-balanced integration of the content and structure of the data in a single index. Its scalability is due to log-structured merge (LSM) trees [32] that combine an in-memory structure for fast insertions with a series of read-only disk-based structures for fast sequential reads and writes.
To achieve robustness, we propose to interleave the path and value bytes of composite keys in a balanced manner. A well-known technique to interleave composite keys is the z-order curve [30, 33], but applying the z-order curve to paths and values is subtle. Often the query performance is poor because of long common prefixes, varying key lengths, different domain sizes, and data skew. The paths in a hierarchical structure have, by their very nature, long common prefixes, but the first byte following a longest common prefix separates data items. We call such a byte a discriminative byte and propose a dynamic interleaving that interleaves the discriminative bytes of paths and values alternatingly. This leads to a well-balanced partitioning of the data with a robust query performance. We use the dynamic interleaving to define the RSCAS index for semi-structured hierarchical data. The RSCAS index is trie-based and efficiently supports the basic search methods for CAS queries: range searches and prefix searches. Range searches enable value predicates that are expressed as a value range and prefix searches support path predicates that contain wildcards and descendant axes. Crucially, tries in combination with dynamically interleaved keys allow us to efficiently evaluate path and value predicates simultaneously.
To scale the RSCAS index to large datasets and support efficient insertions, we use LSM trees [32] that combine an in-memory RSCAS trie with a series of disk-resident RSCAS tries whose size is doubling in each step. RSCAS currently supports only insertions since our main use case, indexing an append-only archive, does not require updates or deletes. The in-memory trie is based on the Adaptive Radix Tree (ART) [21], which is a memory-optimized trie structure that supports efficient insertions. Whenever the in-memory RSCAS trie reaches its maximum capacity, we create a new disk-based trie. Since disk-based RSCAS tries are immutable, we store them compactly on disk and leave no gaps between nodes. We develop a partitioning-based bulk-loading algorithm that builds RSCAS on disk while, at the same time, dynamically interleaving the keys. This algorithm works well with limited memory but scales nicely with the amount of memory to reduce the disk I/O during bulk-loading.
Main contributions:
-
We develop a dynamic interleaving to interleave paths and values in an alternating way using the concept of discriminative bytes. We show how to compute this interleaving by a hierarchical partitioning of the data. We prove that our dynamic interleaving is robust against varying selectivities (Sect. 5).
-
We propose the trie-based Robust and Scalable Content-and-Structure (RSCAS) index for semi-structured hierarchical data. Dynamically interleaved keys give RSCAS its robustness. Its scalability is rooted in LSM trees that combine a memory-optimized trie for fast in-place insertions with a series of disk-optimized tries (Sect. 6).
-
We propose efficient algorithms for querying, inserting, bulk-loading, and merging RSCAS tries. A combination of range and prefix searches is used to evaluate CAS queries on the trie-based structure of RSCAS. Insertions are performed on the in-memory trie using lazy restructuring. Bulk-loading creates large disk-optimized tries in the background. Merging is applied when the in-memory trie overflows to combine it with a series of disk-resident tries (Sect. 7).
-
We conduct an experimental evaluation with three real-world and one synthetic dataset. One of the real-world datasets is Software Heritage (SWH) [2], the world’s largest archive of publicly-available source code. Our experiments show that RSCAS delivers robust query performance with up to two orders of magnitude improvements over existing approaches, while offering comparable bulk-loading and insertion performance (Sect. 8).
2 Application scenario
As a practical use case, we deploy a large-scale CAS index for Software Heritage (SWH) [13], the largest public archive of software source code and its development history.Footnote 1
At its core, Software Heritage archives version control systems (VCSs), storing all recorded source code artifacts in a giant, globally deduplicated Merkle structure [27] that stores elements from many different VCSs using cryptographic hashes as keys. VCSs record the evolution of source code trees over time, an aspect that is reflected in the data model of Software Heritage [34]. The data model supports the archiving of artifacts, such as file blobs (byte sequences, corresponding to tree leaves), source code directories (inner nodes, pointing to sub-directories and files, giving them local path names), commits (called revisions in this context), releases (commits annotated with memorable names such as “1.0”), and VCS repository snapshots. Nodes in the data model are associated with properties that are relevant for querying. Examples of node properties are: cryptographic node identifiers, as well as commit and release metadata such as authors, log messages, timestamps, etc.
Revisions are a key piece of software development workflows. Each of them, except the very first one in a given repository, is connected to the previous “parent” revision, or possibly multiple parents in case of merge commits. These connections allow the computation of the popular diff representations of commits that show how and which files have been changed in any given revision.
Several aspects make Software Heritage a relevant and challenging use case for CAS indexing. First, the size of the archive is significant: at the time of writing, the archive consists of about 20 billion nodes (total file size is about 1 PiB, but we will not index within files, so this measure is less relevant). Second, the archive grows constantly by continuously crawling public data sources such as collaborative development platforms (e.g., GitHub, GitLab), Linux distributions (e.g., Debian, NixOS), and package manager repositories (e.g., PyPI, NPM). The archive growth ratio is also very significant: the amount of archived source code artifacts grows exponentially over time, doubling every 2 to 3 years [37], which calls for an incremental indexing approach to avoid indexing lag. For instance, during 2020 alone the archive has ingested about 600 million new revisions and 3 billion new file blobs (i.e., file contents never seen before).
Last but not least, short of the CAS queries proposed in this paper, the current querying capabilities for the archive are quite limited. Entire software repositories can be looked up by full-text search on their URLs, providing entry points into the archive. From there, users can browse the archive, reaching the desired revisions (e.g., the most recent revision in the master branch since the last time a repository was crawled) and, from there, the corresponding source code trees. It is not possible to query the “diff”, i.e., find revisions that modified certain files in a certain time period, which is limiting for both user-facing and research-oriented queries (e.g., in the field of empirical software engineering).
With the approach proposed in this paper, we offer functionality to answer CAS queries like the following:
Find all revisions from June 2021 that modify a C file located in a folder whose name begins with “ext”.
This query consists of two predicates. First, a content predicate on the revision time, which is a range predicate that matches all revisions from the first to the last day of June 2021. Second, a structure predicate on the paths of the files that were touched by a revision. We are only interested in revisions that modify files with .c extension and that are located in a certain directory. This path predicate can be expressed as /**/ext*/*.c with wildcard ** to match folders that are nested arbitrarily deeply in the filesystem of a repository and wildcard * to match all characters in a directory or file name.
3 Related work
For related work, two CAS indexing techniques have been investigated: (a) creating separate indexes for content and structure, and (b) combining content and structure in one index. We call these two techniques separate CAS indexing and combined CAS indexing, respectively.
Separate CAS indexing creates dedicated indexes for, respectively, the content and the structure of the data. Mathis et al. [25] use a B+ tree to index the content and a structural summary (i.e., a DataGuide [17]) to index the structure of the data. The DataGuide maps each unique path to a numeric identifier, called the path class reference (PCR), and the B+ tree stores the values along with their PCRs. Thus, the B+ tree stores \((\texttt {value}, \langle \texttt {nodeId}, \texttt {PCR} \rangle )\) tuples in its leaf nodes, where nodeId points to a node whose content is value and whose path is given by PCR. To answer a CAS query, we must look at the path index and the value index independently. The subsequent join on the PCR is slow if intermediate results are large. Kaushik et al. [20] present an approach that combines a 1-index [28] to evaluate path predicates with a B+ tree to evaluate value predicates, but they do not consider updates.
A popular system that implements separate indexing is Apache Lucene [1]. Lucene uses different index types depending on the type of the indexed attributes. For CAS indexing, we represent paths as strings and values as numbers. Lucene indexes strings with finite state transducers (FSTs), which are automata that map strings to lists of sorted document IDs (called postings lists). Numeric attributes are indexed in a Bkd-tree [35], which is a disk-optimized kd-tree. Lucene answers conjunctive queries, like CAS queries, by evaluating each predicate on the appropriate index. The indexes return sorted postings lists that must be intersected to see if a document matches all predicates of a conjunctive query. Since the lists are sorted, the intersection can be performed efficiently. However, the independent evaluation of the predicates may yield large intermediate results, making the approach non-robust. To scale to large datasets, Lucene implements techniques that are similar to LSM trees [32] (cf. Sect. 6).
The problem with separate CAS-indexing is that it is not robust. If at least one predicate of a CAS query is not selective, separate indexing approaches generate large intermediate results. This is inefficient if the final result is small. Since the predicates are evaluated on different indexes, we cannot use the more selective predicate to prune the search space.
Combined CAS indexing integrates paths and values in one index. A well-known and mature technology are composite indexes, which are used, e.g., in relational databases to index keys that consist of more than one attribute. Composite indexes concatenate the indexed attributes according to a specified ordering. In CAS indexing, there are two possible orderings of the paths and values: the PV-ordering orders the paths before the values, while the VP-ordering orders the values first. The ordering determines what queries a composite index can evaluate efficiently. Composite indexes are only efficient for queries that have a small selectivity for the attribute appearing first. In our experiments, we use the composite B+ tree of Postgres as the reference point for an efficient and scalable implementation of composite indexes.
IndexFabric [11] is another example of a composite CAS index. It uses a PV-ordering, concatenating the (shortened) paths and values of composite keys, and storing them in a disk-optimized PATRICIA trie [29]. IndexFabric shortens the paths to save disk space by mapping long node labels to short strings (e.g., map label ‘extension’ to ‘e’). During query evaluation, IndexFabric must first fully evaluate the path predicate before it can look at the value predicate since it orders paths before the values in the index. Since it uses shortened paths, it cannot evaluate wildcards within a node label (e.g., ext* to match extension, exterior, etc.). IndexFabric does not support bulk-loading.
The problem with composite indexes is that they prioritize the dimension appearing first. The selectivity of the predicate in the first dimension determines the query performance. If it is high and the other selectivity is low, the composite index performs badly because the first predicate must be fully evaluated before the second predicate can be evaluated. As a result, a composite index is not robust.
Instead of concatenating dimensions, it is possible to interleave dimensions. The z-order curve [30, 33], for example, is obtained by interleaving the binary representation of the individual dimensions and is used in UB-trees [36] and k-d tries [31, 33, 38]. Unfortunately, the z-order curve deteriorates to the performance of a composite index if the data contain long common prefixes [42]. This is the case in CAS indexing where paths have long common prefixes.
LSM trees [32] are used to create scalable indexing systems with high write throughput (see, e.g., AsterixDB [5], BigTable [10], Dynamo [12], etc.). They turn expensive in-place updates that cause many random disk I/Os into out-of-place updates that use sequential writes. To achieve that, LSM trees combine a small in-memory tree \(R^M_0\) with a series of disk-resident trees \(R_0, R_1, \ldots \), each tree being T times larger than the tree in the previous level. Insertions are performed exclusively in the main-memory tree \(R^M_0\).
Modern LSM tree implementations, see [23] for an excellent recent survey, use sorted string tables (SSTables) or other immutable data structures at multiple levels. Generally, there are two different merge policies: leveling and tiering. With the leveling merge policy, each level i contains exactly one structure and when the structure at level i grows too big, this structure and the one at level \(i+1\) are merged. A structure on level \(i+1\) is T times larger than a structure on level i. Tiering maintains multiple structures per level. When a level i fills up with T structures, they are merged into a structure on level \(i+1\). We discuss the design decisions regarding LSM-trees and RSCAS in Sect. 6.2.
An LSM tree requires an efficient bulk-loading algorithm to create a disk-based RSCAS trie when the in-memory trie overflows. Sort-based algorithms sort the data and build an index bottom-up. Buffer-tree methods bulk-load a tree by buffering insertions in nodes and flushing them in batches to its children when a buffer overflows. Neither sort- nor buffer-based techniques [3, 7, 8] can be used for RSCAS because our dynamic interleaving must look at all keys to correctly interleave them. We develop a partitioning-based bulk-loading algorithm for RSCAS that alternatingly partitions the data in the path and value dimension to dynamically interleave paths and values.
The combination of the dynamic interleaving with wildcards and range queries makes it hard to embed RSCAS into an LSM-tree-based key-value (KV) store. While early, simple KV-stores did not support range queries at all, more recent KV-stores create Bloom filters for a predefined set of fixed prefixes [26], i.e., only range queries using these prefixes can be answered efficiently. SuRF was one of the first approaches able to handle arbitrary range queries by storing minimum-length prefixes in a trie so that all keys can be uniquely identified [45]. This was followed by Rosetta, which stores all prefixes for each key in a hierarchical series of Bloom filters [24]. KV-stores supporting ranges queries without filters have also been developed. EvenDB optimizes the evaluation of queries exhibiting spatial locality, i.e., keys with the same prefixes are kept close together and in main memory [16]. REMIX offers a globally sorted view of all keys with a logical sorting of the data [46]. The evaluation of range queries boils down to seeking the first matching element in a sorted sequence of keys and scanning to the end of the range. CAS queries follow a different pattern. During query evaluation, we simultaneously process a range query in the value dimension and match strings with wildcards at arbitrary positions in the path dimension. The prefix shared by the matching keys ends at the first wildcard, which can occur early in the path. We prune queries with wildcards by regularly switching back to the more selective value dimension.
4 Background
4.1 Data representation
We use composite keys to represent the paths and values of data items in semi-structured hierarchical data.
Definition 1
(Composite Key) A composite key k is a two-dimensional key that consists of a path k.P and a value k.V, and each key stores a reference k.R as payload that points to the corresponding data item in the database.
Given a dimension \(D \in \{P,V\}\), we write k.D to access k’s path (if \(D = P\)) or value (if \(D = V\)). Composite keys can be extracted from popular semi-structured hierarchical data formats, such as JSON and XML. In the context of SWH, we use composite keys k to represent that a file with path k.P is modified (i.e., added, changed, or deleted) at time k.V in revision k.R.
Example 1
Table 1 shows the set \(\mathsf {K}^{1..-9} = \{ \mathsf {k}_1, \ldots , \mathsf {k}_9\}\) of composite keys (we use a sans-serif font to refer to concrete instances in our examples). We write \(\mathsf {K}^{2,5,6,7}\) to refer to \(\{\mathsf {k}_2, \mathsf {k}_5, \mathsf {k}_6, \mathsf {k}_7\}\). Composite key \(\mathsf {k}_2\) denotes that the file /crypto/ecc.h$ was modified on 2019-07-20 in revision \(\mathsf {r}_2\). In the same revision, also file /crypto/ecc.c$ is modified, see key \(\mathsf {k}_3\). \(\square \)
We represent paths and values as byte strings that we access byte-wise. We visualize them with one byte ASCII characters for the path dimension and italic hexadecimal numbers for the value dimension, see Table 1. To guarantee that no path is a prefix of another we append the end-of-string character $ (ASCII code 0x00) to each path. Fixed-length byte strings (e.g., 64 bit numbers) are prefix-free because of the fixed length. We assume that the path and value dimensions are binary-comparable, i.e., two paths or values are <, \(=\), or > iff their corresponding byte strings are <, \(=\), or >, respectively [21]. For example, big-endian integers are binary-comparable while little-endian integers are not.
Let s be a byte-string, then |s| denotes the length of s and s[i] denotes the i-th byte in s. The left-most byte of a byte-string is byte one. \(s[i] = \epsilon \) is the empty string if \(i > |s|\). s[i, j] denotes the substring of s from position i to j and \(s[i,j] = \epsilon \) if \(i > j\).
Definition 2
(Longest Common Prefix) The longest common prefix \(\textsf {lcp}(K,D)\) of a set of keys K in dimension D is the longest prefix s that all keys \(k \in K\) share in dimension D, i.e.,
Example 2
The longest common prefix in the path and value dimensions of the nine keys in Table 1 is \(\textsf {lcp}(\mathsf {K}^{1...9},P) = \texttt {/}\) and \(\textsf {lcp}(\mathsf {K}^{1...9},V) = {{\texttt {\textit{00\,00\,00\,00}}}}\). If we narrow down the set of keys to \(\mathsf {K}^{5,6}\) the longest common prefixes become longer: \(\textsf {lcp}(\mathsf {K}^{5,6},P) = \texttt {/fs/ext}\) and \(\textsf {lcp}(\mathsf {K}^{5,6},V) = \texttt {00 00 00 00 5E}\). \(\square \)
4.2 Content-and-structure (CAS) queries
Content-and-structure (CAS) queries contain a path predicate and value predicate [25]. The path predicate is expressed as a query path q that supports two wildcard symbols. The descendant axis ** matches zero to any number of node labels, while the * wildcard matches zero to any number of characters in a single label.
Definition 3
(Query Path) A query path q is denoted by \(q = /\lambda _1/\lambda _2/\ldots /\lambda _{m}\). Each label \(\lambda _i\) is a string \(\lambda _i \in (A \cup \{\texttt {*}\})^+\), where A is an alphabet and * is a reserved wildcard symbol. The wildcard * matches zero to any number of characters in a label. We call \(\lambda _i = \texttt {**}\) the descendant axis that matches zero to any number of labels.
Definition 4
(CAS Query) CAS query \(Q(q,[v_l,v_h])\) consists of a query path q and a value predicate \([v_l,v_h]\). Given a set K of composite keys, CAS query Q returns the revisions k.R of all composite keys \(k \in K\) for which k.P matches q and \(v_l \le k.V \le v_h\).
Example 3
CAS query \(Q(\texttt {/**/ext*/*.c},\) [2021-06-01, 2021-06-30]) matches all revisions (a) committed in June 2021 that (b) modified a C file located in a folder that begins with name ext, anywhere in the directory structure of a software repository. \(\square \)
4.3 Interleaving of composite keys
We integrate path k.P and value k.V of a key k by interleaving them. Table 2 shows three common ways to integrate k.P and k.V of key \(\mathsf {k}_9\) from Table 1. Value bytes are written in italic and shown in red, path bytes are shown in blue. The first two rows show the path-value and value-path concatenation (\(I_{PV}\) and \(I_{VP}\)), respectively. The byte-wise interleaving \(I_{BW}\) in the third row interleaves one value byte with one path byte. Note that none of these interleavings is well-balanced. The byte-wise interleaving is not well-balanced, since all value-bytes are interleaved with a single label of the path (/Sources).
5 Theoretical foundation: dynamic interleaving
We propose the dynamic interleaving to interleave the paths and values of a set of composite keys K and show how to build the dynamic interleaving through a recursive partitioning that groups keys based on the shortest prefixes that distinguish keys from one another. We introduce the partitioning in Sect. 5.1 and highlight in Sect. 5.2 the properties that we use to construct the interleaving. In Sect. 5.3, we define the dynamic interleaving with a recursive partitioning and develop a cost model in Sect. 5.4 to analyze the efficiency of interleavings.
The dynamic interleaving adapts to the specific characteristics of paths and values, such as common prefixes, varying key lengths, differing domain sizes, and the skew of the data. To achieve this, we consider the discriminative bytes.
Definition 5
(Discriminative Byte) The discriminative byte \(\textsf {dsc}(K,D)\) of keys K in dimension D is the first byte for which the keys differ in dimension D, i.e., \(\textsf {dsc}(K,D) = |\textsf {lcp}(K,D)| + 1\).
Example 4
Table 3 illustrates the position of the discriminative bytes for the path and value dimensions for various sets of composite keys K. Set \(\mathsf {K}^{9}=\{\mathsf {k}_9\}\) contains only a single key. In this case, the discriminative bytes are the first position after the end of \(\mathsf {k}_9\)’s byte-strings in the respective dimensions. For example, \(\mathsf {k}_9\)’s value is eight bytes long; hence, the discriminative value byte of \(\{\mathsf {k}_9\}\) is the ninth byte. \(\square \)
Discriminative bytes are crucial during query evaluation since at their positions the search space can be narrowed down. We alternate in a round-robin fashion between discriminative path and value bytes in our interleaving. Each discriminative byte partitions a set of keys into subsets, which we recursively partition further.
5.1 \(\psi \)-Partitioning
The \(\psi \)-partitioning of a set of keys K groups composite keys together that have the same value at the discriminative byte in dimension D. Thus, K is split into at most \(2^8\) non-empty partitions, one partition for each value (0x00 to 0xFF) of the discriminative byte in dimension D.
Definition 6
(\(\psi \)-Partitioning) The \(\psi \)-partitioning of a set of keys K in dimension D is \(\psi (K,D) = \{ K_1, \ldots , K_m \}\) iff
-
1.
(Correctness) All keys in a set \(K_i\) have the same value at K’s discriminative byte in dimension D:
-
\(\forall k,k' \in K_i \left( k.D[\textsf {dsc}(K,D)] = k'.D[\textsf {dsc}(K,D)] \right) \)
-
-
2.
(Disjointness) Keys from different sets \(K_i \ne K_j\) do not have the same value at K’s discriminative byte in D:
-
\(\forall k \in K_i, k' \in K_j (\) \(k.D[\textsf {dsc}(K,D)] \ne k'.D[\textsf {dsc}(K,D)])\)
-
-
3.
(Completeness) Every key in K is assigned to a set \(K_i\). All \(K_i\) are non-empty.
-
\(K = \bigcup _{1 \le i \le m} K_i \wedge \emptyset \notin \psi (K,D)\)
-
Let \(k \in K\) be a composite key. We write \(\psi _k(K, D)\) to denote the \(\psi \)-partitioning of k with respect to K and dimension D, i.e., the partition in \(\psi (K, D)\) that contains key k.
Example 5
Let \(\mathsf {K}^{1...9}\) be the set of composite keys from Table 1. The \(\psi \)-partitioning of selected sets of keys in dimension P or V is as follows:
-
\(\psi (\mathsf {K}^{1...9},V)=\{\mathsf {K}^{1,4,8,9}, \mathsf {K}^{5,6}, \mathsf {K}^{2,3,7}\}\)
-
\(\psi (\mathsf {K}^{1,4,8,9},P)=\{\mathsf {K}^{1}, \mathsf {K}^{4,8,9}\}\)
-
\(\psi (\mathsf {K}^{4,8,9},V)=\{\mathsf {K}^{4}, \mathsf {K}^{8,9}\}\)
-
\(\psi (\mathsf {K}^{8,9},P) =\{\mathsf {K}^{8}, \mathsf {K}^{9}\}\)
-
\(\psi (\mathsf {K}^{9},V) = \psi (\mathsf {K}^{9},P) = \{\mathsf {K}^{9}\}\)
The \(\psi \)-partitioning of key \(\mathsf {k}_9\) with respect to sets of keys and dimensions is as follows:
-
\(\psi _{\mathsf {k}_9}(\mathsf {K}^{1...9}, V) = \mathsf {K}^{1,4,8,9}\)
-
\(\psi _{\mathsf {k}_9}(\mathsf {K}^{1,4,8,9}, P) = \mathsf {K}^{4,8,9}\)
-
\(\psi _{\mathsf {k}_9}(\mathsf {K}^{4,8,9}, V) = \mathsf {K}^{8,9}\)
-
\(\psi _{\mathsf {k}_9}(\mathsf {K}^{9}, V) = \psi _{\mathsf {k}_9}(\mathsf {K}^{9}, P) = \mathsf {K}^{9}\). \(\square \)
5.2 Properties of the \(\psi \)-partitioning
We work out four key properties of the \(\psi \)-partitioning. The first two properties, order-preserving and prefix-preserving, allow us to evaluate CAS queries efficiently while the other two properties, guaranteed progress and monotonicity, help us to construct the dynamic interleaving.
Lemma 1
(Order-Preserving) \(\psi \)-partitioning \(\psi (K,D) = \{K_1, \ldots , K_m\}\) is order-preserving in dimension D, i.e., all keys in set \(K_i\) are either strictly greater or smaller in dimension D than all keys from another set \(K_j\):
The proofs of all lemmas and theorems can be found in the accompanying technical report [43].
Example 6
The \(\psi \)-partitioning \(\psi (\mathsf {K}^{1...9}, V)\) is equal to the partitions \(\{\mathsf {K}^{1,4,8,9},\) \(\mathsf {K}^{5,6},\) \(\mathsf {K}^{2,3,7} \}\). It is order-preserving in dimension V. The partitions cover the following value ranges (denoted in seconds since the Unix epoch):
-
[0x5D 00 00 00, 0x5D FF FF FF]; approx. 06/2019 – 12/2019
-
[0x5E 00 00 00, 0x5E FF FF FF]; approx. 01/2020 – 07/2020
-
[0x5F 00 00 00, 0x5F FF FF FF]; approx. 08/2020 – 12/2021
The value predicate \([\text {07/2019}, \text {09/2019})\) only needs to consider partition \(\mathsf {K}^{1,4,8,9}\), which spans keys from June to December, 2019, since partitions do not overlap. \(\square \)
Lemma 2
(Prefix-Preserving) \(\psi \)-partitioning \(\psi (K,D) = \{K_1, \ldots , K_m\}\) is prefix-preserving in dimension D, i.e., keys in the same set \(K_i\) have a longer common prefix in dimension D than keys from different sets \(K_i \ne K_j\):
Example 7
The \(\psi \)-partitioning \(\psi (\mathsf {K}^{1...9}, P) = \{\mathsf {K}^{1,4,8,9},\) \(\mathsf {K}^{2,3},\) \(\mathsf {K}^{5,6,7}\}\) is prefix-preserving in dimension P. For example, \(\mathsf {K}^{1,4,8,9}\) has a longer common path prefix \(\textsf {lcp}(\mathsf {K}^{1,4,8,9},P) = \texttt {/Source/}\) than keys across partitions, e.g., \(\textsf {lcp}(\mathsf {K}^{1,4,8,9} \cup \mathsf {K}^{2,3},P) = \texttt {/}\). Query path /Source/S*.go only needs to consider partition \(\mathsf {K}^{1,4,8,9}\). \(\square \)
Lemmas 1 and 2 guarantee a total ordering among the sets \(\psi (K,D) = \{K_1, \ldots , K_m\}\). In our RSCAS index, we order the nodes by the value at the discriminative byte such that range and prefix queries can quickly choose the correct subtree.
The next two properties allow us to efficiently compute the dynamic interleaving of composite keys.
Lemma 3
(Guaranteed Progress) Let K be a set of composite keys for which not all keys are equal in dimension D. \(\psi (K,D)\) guarantees progress, i.e., \(\psi \) splits K into at least two sets: \(|\psi (K,D)| \ge 2\).
Guaranteed progress ensures that each step partitions the data and when we repeatedly apply \(\psi (K,D)\), we eventually narrow a set of keys down to a single key. For each set of keys that \(\psi (K,D)\) creates, the position of the discriminative byte for dimension D increases. This property of the \(\psi \)-partitioning holds since each set of keys is built based on the discriminative byte and to \(\psi \)-partition an existing set of keys we need a discriminative byte that is positioned further down in the byte-string. For the alternate dimension \(\overline{D}\), i.e., \(\overline{D} = P\) if \(D = V\) and \(\overline{D} = V\) if \(D = P\), the position of the discriminative byte remains unchanged or increases.
Lemma 4
(Monotonicity of Discriminative Bytes) Let \(K_i\) be one of the partitions of K after partitioning in dimension D. In dimension D, the position of the discriminative byte in \(K_i\) is strictly greater than in K. In dimension \(\overline{D}\), the discriminative byte is equal or greater than in K, i.e.,
Example 8
The discriminative path byte of \(\mathsf {K}^{1...9}\) is 2 while the discriminative value byte of \(\mathsf {K}^{1...9}\) is 5 as shown in Table 3. For partition \(\mathsf {K}^{1,4,8,9}\), which is obtained by partitioning \(\mathsf {K}^{1...9}\) in the value dimension, the discriminative path byte is 10 while the discriminative value byte is 7. For partition \(\mathsf {K}^{4,8,9}\), which is obtained by partitioning \(\mathsf {K}^{1,4,8,9}\) in the path dimension, the discriminative path byte is 14 while the discriminative value byte is still 7. \(\square \)
Monotonicity guarantees that each time we \(\psi \)-partition a set K we advance the discriminative byte in at least one dimension. Thus, we make progress in at least one dimension when we dynamically interleave a set of keys.
These four properties of the \(\psi \)-partitioning are true because we partition K at its discriminative byte. If we partitioned the data before this byte, we would not make progress and the monotonicity would be violated, because every byte before the discriminative byte is part of the longest common prefix. If we partitioned the data after the discriminative byte, the partitioning would no longer be order- and prefix-preserving. Skipping some keys by sampling the set is not an option, as this could lead to an (incorrect) partitioning using a byte located after the actual discriminative byte.
Example 9
\(\mathsf {K}^{1...9}\)’s discriminative value byte is byte five. If we partitioned \(\mathsf {K}^{1...9}\) at value byte four, we would get \(\{ \mathsf {K}^{1...9} \}\) and there is no progress since all keys have 0x00 at value byte four. The discriminative path and value bytes would remain unchanged. If we partitioned \(\mathsf {K}^{1...9}\) at value byte six, we would get \(\{ \mathsf {K}^{1,4,8,9}, \mathsf {K}^{2,3,6,7}, \mathsf {K}^5 \}\), which is neither order- nor prefix-preserving in V. Consider keys \(\mathsf {k}_3,\mathsf {k}_6 \in \mathsf {K}^{2,3,6,7}\) and \(\mathsf {k}_5 \in \mathsf {K}^{5}\). The partitioning is not order-preserving in V since \(\mathsf {k}_6.V< \mathsf {k}_5.V < \mathsf {k}_3.V\). The partitioning is not prefix-preserving in V since the longest common value prefix in \(\mathsf {K}^{2,3,6,7}\) is 00 00 00 00, which is not longer than the longest common value prefix of keys from different partitions since \(\textsf {lcp}(\mathsf {K}^{2,3,6,7} \cup \mathsf {K}^{5}, V)=\) \( {{\texttt {\textit{00\,00\,00\,00}}}}\). \(\square \)
5.3 Dynamic interleaving
To compute the dynamic interleaving of a composite key \(k \in K\), we recursively \(\psi \)-partition K while alternating between dimension V and P. In each step, we interleave a part of k.P with a part of k.V. The recursive \(\psi \)-partitioning yields a partitioning sequence \((K_1, D_1),\) \(\ldots ,\) \((K_n, D_n)\) for key k with \(K_1 \supset K_2 \supset \dots \supset K_n\). We start with \(K_1 = K\) and \(D_1 = V\). Next, \(K_2 = \psi _k(K_1, V)\) and \(D_2 = \overline{D}_1 = P\). We continue with the general scheme \(K_{i+1} = \psi _k(K_i, D_i)\) and \(D_{i+1} = \overline{D}_i\). This continues until we reach a set \(K_n\) that contains at most \(\tau \) keys, where \(\tau \) is a threshold (explained later). The recursive \(\psi \)-partitioning alternates between dimensions V and P until we run out of discriminative bytes in one dimension, which means \(\psi _k(K_i, D) = K_i\). From then on, we can only \(\psi \)-partition in dimension \(\overline{D}\) until we run out of discriminative bytes in this dimension as well, that is \(\psi _k(K_i, \overline{D}) = \psi _k(K_i, D) = K_i\), or we reach a \(K_n\) that contains at most \(\tau \) keys. The partitioning sequence is finite due to the monotonicity of the \(\psi \)-partitioning (see Lemma 4), which guarantees that we make progress in each step in at least one dimension.
Definition 7
(Partitioning Sequence) The partitioning sequence \(\rho (k,K,D) = ((K_1, D_1), \ldots , (K_n, D_n))\) of a composite key \(k \in K\) is the recursive \(\psi \)-partitioning of the sets to which k belongs. The pair \((K_i, D_i)\) denotes the partitioning of \(K_i\) in dimension \(D_i\). The partitioning stops when \(K_n\) contains at most \(\tau \) keys or \(K_n\) cannot be further \(\psi \)-partitioned in any dimension (\(K_n.D = \bot \) in this case). \(\rho (k,K,D)\) is defined in Fig. 1.
Example 10
Below we illustrate the step-by-step expansion of \(\rho (\mathsf {k}_9,\mathsf {K}^{1...9},V)\) to get \(\mathsf {k}_9\)’s partitioning sequence. We set \(\tau = 2\).
Note the alternating partitioning in, respectively, V and P. We only deviate from this if partitioning in one of the dimensions is not possible. Had we set \(\tau = 1\), \(\mathsf {K}^{8,9}\) would be partitioned once more in the path dimension. \(\square \)
To compute the full dynamic interleaving of a key k, we set \(\tau =1\) and continue until the final set \(K_n\) contains a single key (i.e, key k). To interleave only a prefix of k and keep a suffix non-interleaved we increase \(\tau \). Increasing \(\tau \) stops the partitioning earlier and speeds up the computation. An index structure that uses dynamic interleaving can tune \(\tau \) to trade the time it takes to build the index and to query it. In Sect. 6, we introduce a memory-optimized and a disk-optimized version of our RSCAS index. They use different values of \(\tau \) to adapt to the underlying storage.
We determine the dynamic interleaving \(I_{\text {DY}}(k,K)\) of a key \(k \in K\) via k’s partitioning sequence \(\rho \). For each element in \(\rho \), we generate a tuple with strings \(s_P\) and \(s_V\) and the partitioning dimension of the element. The strings \(s_P\) and \(s_V\) are composed of substrings of k.P and k.V, ranging from the previous discriminative byte up to, but excluding, the current discriminative byte in the respective dimension. The order of \(s_P\) and \(s_V\) in a tuple depends on the dimension used in the previous step: the dimension that has been chosen for the partitioning comes first. Formally, this is defined as follows:
Definition 8
(Dynamic Interleaving) Let \(k \in K\) be a composite key and let \(\rho (k, K, V) = ((K_1, D_1),\) \(\ldots ,\) \((K_n, D_n))\) be the partitioning sequence of k. The dynamic interleaving \(I_{\text {DY}}(k,K) = (t_1, \ldots , t_n, t_{n+1})\) of k is a sequence of tuples \(t_i\), where \(t_i = (s_P, s_V, D)\) if \(D_{i-1} = P\) and \(t_i = (s_V, s_P, D)\) if \(D_{i-1} = V\). The tuples \(t_i\), \(1 \le i \le n\), are determined as follows:
To correctly handle the first tuple, we define \(\textsf {dsc}(K_0,V) = 1\), \(\textsf {dsc}(K_0,P) = 1\) and \(D_0 = V\). The last tuple \(t_{n+1} = (s_P,s_V,R)\) stores the non-interleaved suffixes along with revision k.R: \(\begin{aligned} t_{n+1}.s_P&= k.P[\textsf {dsc}(K_{n},P),|k.P|] \\ t_{n+1}.s_V&= k.V[\textsf {dsc}(K_{n},V),|k.P|] \\ t_{n+1}.R&= k.R \end{aligned}\Box \)
Example 11
We compute the tuples for the dynamic interleaving \(I_{\text {DY}}(\mathsf {k}_9, \mathsf {K}^{1...9}) = (\mathsf {t}_1, \ldots , \mathsf {t}_5)\) of key \(\mathsf {k}_9\) using the partitioning sequence \(\rho (\mathsf {k}_9, \mathsf {K}^{1...9}, V)\) from Example 10. The necessary discriminative path and value bytes can be found in Table 3. Table 4 shows the details of each tuple of \(\mathsf {k}_9\)’s dynamic interleaving with respect to \(\mathsf {K}^{1...9}\). The final dynamic interleavings of all keys from Table 1 are displayed in Table 5. We highlight in bold the values of the discriminative bytes at which the paths and values are interleaved, e.g., for key \(\mathsf {k}_9\) these are bytes  ,
,  , and
, and  . \(\square \)
. \(\square \)
Unlike static interleavings I(k) that interleave a key k in isolation, the dynamic interleaving \(I_{\text {DY}}(k,K)\) of k depends on the set of all keys K to adapt to the data. The result is a well-balanced interleaving (compare Tables 2 and 5).
5.4 Efficiency of interleavings
We propose a cost model to measure the efficiency of interleavings that organize the interleaved keys in a tree-like search structure. Each node represents the \(\psi \)-partitioning of the composite keys by either path or value, and the node branches for each different value of a discriminative path or value byte. We simplify the cost model by assuming that the search structure is a complete tree with fanout o where every root-to-leaf path contains h edges (h is the height). Further, we assume that all nodes on one level represent a partitioning in the same dimension \(\phi _i \in \{P,V\}\) and we use a vector \(\phi (\phi _1, \ldots , \phi _h)\) to specify the partitioning dimension on each level. We assume that the number of Ps and Vs in each \(\phi \) are equal. Figure 2 visualizes this scheme.
To answer a query, we start at the root and traverse the search structure to determine the answer set. In the case of range queries, more than one branch must be followed. A search follows a fraction of the outgoing branches o originating at this node. We call this the selectivity of a node (or just selectivity). We assume that every path node has a selectivity of \(\varsigma _P\) and every value node has a selectivity of \(\varsigma _V\). The cost \(\widehat{C}\) of a search, measured in the number of visited nodes during the search, is as follows:
If a workload is well-known and consists of a small set of specific queries, it is highly likely that an index adapted to this workload will outperform RSCAS. For instance, if \(\varsigma _V \ll \varsigma _P\) for all queries, then a VP-index shows better performance than an RSCAS-index. However, it performs badly for queries deviating from that workload (\(\varsigma _V > \varsigma _P\)). Our goal is an access method that can deal with a wide range of queries in a dynamic environment in a robust way, i.e., avoiding a bad performance for any particular query type. This is motivated by the fact that modern data analytics utilizes a large number of ad hoc queries to do exploratory analysis. For example, in the context of building a robust partitioning for ad hoc query workloads, Shanbhag et al. [40] found that after analyzing the first 80% of a real-world workload the remaining 20% still contained 57% completely new queries. We aim for a good average performance across all queries.
Definition 9
(Robustness) A CAS-index is robust if it optimizes the average performance and minimizes the variability over all queries.
State-of-the-art CAS-indexes are not robust because they favor either path or value predicates. As a result they show a very good performance for one type of query but run into problems for other types of queries. To illustrate this problem, we define the notion of complementary queries.
Definition 10
(Complementary Query) Given a query \(Q = (\varsigma _P, \varsigma _V)\) with path selectivity \(\varsigma _P\) and value selectivity \(\varsigma _V\), there is a complementary query \(Q' = (\varsigma '_P, \varsigma '_V)\) with path selectivity \(\varsigma '_P = \varsigma _V\) and value selectivity \(\varsigma '_V = \varsigma _P\)
Example 12
Figure 3a shows the costs for a query Q and its complementary query \(Q'\) for different interleavings in terms of the number of visited nodes during the search. We assume parameters \(o=10\) and \(h=12\) for the search structure and a dynamic interleaving \(I_{\text {DY}}\) with \(\tau = 1\). \(I_{\text {PV}}\) stands for path-value concatenation with \(\phi _i = P\) for \(1 \le i \le 6\) and \(\phi _i = V\) for \(7 \le i \le 12\). \(I_{\text {VP}}\) is a value-path concatenation (with an inverse \(\phi \) compared to \(I_{\text {PV}}\)). We also consider two additional permutations: \(I_1\) uses a vector \(\phi = (V,V,V,V,P,V,P,V,P,P,P,P)\) and \(I_2\) a vector equal to (V, V, V, P, P, V, P, V, V, P, P, P). They resemble byte-wise interleavings, which usually exhibit irregular alternation patterns with a clustering of, respectively, discriminative path and value bytes. Figure 3b shows the average costs and the standard deviation. The numbers demonstrate the robustness of our dynamic interleaving: it performs best in terms of average costs and standard deviation.
In the previous example, we used our cost model to show that a perfectly alternating interleaving exhibits the best overall performance and standard deviation when evaluating complementary queries. We prove that this is always the case.
Theorem 1
Consider a query Q with selectivities \(\varsigma _P\) and \(\varsigma _V\) and its complementary query \(Q'\) with selectivities \(\varsigma '_P = \varsigma _V\) and \(\varsigma '_V = \varsigma _P\). There is no interleaving that on average performs better than the dynamic interleaving with a perfectly alternating vector \(\phi _{\text {DY}}\), i.e., \(\forall \phi : \widehat{C}(o,h,\phi _{\text {DY}},\varsigma _P,\varsigma _V) + \widehat{C}(o,h,\phi _{\text {DY}},\varsigma '_P,\varsigma '_V) \le \widehat{C}(o,h,\phi ,\varsigma _P,\varsigma _V) + \widehat{C}(o,h,\phi ,\varsigma '_P,\varsigma '_V)\).
Theorem 1 shows that the dynamic interleaving has the best query performance for complementary queries. It follows that for any set of complementary queries \(\mathbf {Q}\), the dynamic interleaving has the best performance.
Theorem 2
Let \(\mathbf {Q}\) be a set of complementary queries, i.e., \((\varsigma _P,\varsigma _V) \in \mathbf {Q} \Leftrightarrow (\varsigma _V,\varsigma _P) \in \mathbf {Q}\). There is no interleaving \(\phi \) that in total performs better than the dynamic interleaving over all queries \(\mathbf {Q}\), i.e.,
This also holds for the set of all queries, since for every query there exists a complementary query. Thus, the dynamic interleaving optimizes the average performance over all queries and, as a result, a CAS index that uses dynamic interleaving is robust.
Corollary 1
Let \(\mathbf {Q} = \{ (\varsigma _P, \varsigma _V) \mid 0 \le \varsigma _P, \varsigma _V \le 1 \}\) be the set of all possible queries. There is no interleaving \(\phi \) that in total performs better than the dynamic interleaving \(\phi _{\text {DY}}\) over all queries \(\mathbf {Q}\).
We now turn to the variability of the search costs and show that they are minimal for dynamic interleavings.
Theorem 3
Given a query Q (with \(\varsigma _P\) and \(\varsigma _V\)) and its complementary query \(Q'\) (with \(\varsigma '_P = \varsigma _V\) and \(\varsigma '_V = \varsigma _P\)), there is no interleaving that has a smaller variability than the dynamic interleaving with a perfectly alternating vector \(\phi _{\text {DY}}\), i.e., \(\forall \phi : |\widehat{C}(o,h,\phi _{\text {DY}},\varsigma _P,\varsigma _V) - \widehat{C}(o,h,\phi _{\text {DY}},\varsigma '_P,\varsigma '_V)| \le \) \(|\widehat{C}(o,h,\phi ,\varsigma _P,\varsigma _V) - \widehat{C}(o,h,\phi ,\varsigma '_P,\varsigma '_V)|\).
Similar to the results for the average performance, Theorem 3 can be generalized to the set of all queries.
Note that in practice the search structure is not a complete tree and the fraction \(\varsigma _P\) and \(\varsigma _V\) of children that are traversed at each node is not constant. We previously evaluated the cost model experimentally on real-world datasets [42] and showed that the estimated and true cost of a query are off by a factor of two on average, which is a good estimate for the cost of a query.
6 Robust and scalable CAS (RSCAS) index
Data-intensive applications require indexing techniques that make it possible to efficiently index, insert, and query large amounts of data. The SWH archive, for example, stores billions of revisions and every day millions of revisions are crawled from popular software forges. We propose the Robust and Scalable Content-And-Structure (RSCAS) index to provide support for querying and updating the content and structure of big hierarchical data. For robustness, the RSCAS index uses our dynamic interleaving to integrate the paths and values of composite keys in a trie structure. For scalability, RSCAS implements log-structured merge trees (LSM trees) that combine a memory-optimized trie with a series of disk-optimized tries (see Fig. 5).
6.1 Structure of an RSCAS trie
RSCAS tries support CAS queries with range and prefix searches. Each node n in an RSCAS trie includes a dimension n.D, a path substring \(n.s_P\), and a value substring \(n.s_V\). They correspond to fields t.D, \(t.s_P\) and \(t.s_V\) in the dynamic interleaving of a key (see Definition 8). Substrings \(n.s_P\) and \(n.s_V\) are variable-length strings. Dimension n.D is P or V for inner nodes and \(\bot \) for leaf nodes. Leaf nodes additionally store a set of suffixes, denoted by \(n.\textsf {suffixes}\). This set contains non-interleaved path and value suffixes along with references to data items in the database. Each dynamically interleaved key corresponds to a root-to-leaf path in the RSCAS trie.
Definition 11
(RSCAS Trie) Let K be a set of composite keys and let R be a trie. Trie R is the RSCAS trie for K iff the following conditions are satisfied.
-
1.
\(I_\text {DY}(k,K) = (t_1,\ldots ,t_m,t_{m+1})\) is the dynamic interleaving of a key \(k \in K\) iff there is a root-to-leaf path \((n_1, \ldots , n_m)\) in R such that \(t_i.s_P = n_i.s_P\), \(t_i.s_V = n_i.s_V\), and \(t_i.D = n_i.D\) for \(1 \le i \le m\). Suffix \(t_{m+1}\) is stored in leaf node \(n_m\), i.e., \(t_{m+1} \in n_m.\textsf {suffixes}\).
-
2.
R does not include duplicate siblings, i.e., no two sibling nodes n and \(n'\), \(n \ne n'\), in R have the same values for \(s_P\), \(s_V\), and D, respectively.
Example 13
Figure 4 shows the RSCAS trie for keys \(\mathsf {K}^{1...9}\). The values at the discriminative bytes are highlighted in bold. The dynamic interleaving \(I_{\text {DY}}(\mathsf {k}_9,\mathsf {K}^{1...9}) =\) \((\mathsf {t}_1, \mathsf {t}_2, \mathsf {t}_3, \mathsf {t}_4, \mathsf {t}_5)\) from Table 5 is mapped to the root-to-leaf path \((\mathsf {n}_1, \mathsf {n}_2, \mathsf {n}_4,\) \(\mathsf {n}_6)\) in the RSCAS trie. Tuple \(\mathsf {t}_5\) is stored in \(\mathsf {n}_6.\textsf {suffixes}\). Key \(\mathsf {k}_8\) is stored in the same root-to-leaf path. For key \(\mathsf {k}_1\), the first two tuples of \(I_{\text {DY}}(\mathsf {k}_1,\mathsf {K}^{1...9})\) are mapped to \(\mathsf {n}_1\) and \(\mathsf {n}_2\), respectively, while the third tuple is mapped to \(\mathsf {n}_3\). \(\square \)
6.2 RSCAS index
The RSCAS index combines a memory-optimized RSCAS trie for in-place insertions with a sequence of disk-based RSCAS tries for out-of-place insertions to get good insertion performance for large data-intensive applications. LSM trees [32, 35] have pioneered combining memory- and disk-resident components and are now the de-facto standard to build scalable index structures (see, e.g., [5, 10, 12]).
We implement RSCAS as an LSM trie that fixes the size ratio between two consecutive tries at \(T=2\) and uses the leveling merge policy with full merges (this combination is also known as the logarithmic method in [35]). Leveling optimizes query performance and space utilization in comparison with the tiering merge policy at the expense of a higher merge cost [22, 23]. Luo and Carey show that a size ratio of \(T=2\) achieves the maximum write throughput for leveling, but may have a negative impact on the latency [22]. Since query performance and space utilization are important to us, while latency does not play a large role (due to batched updates in the background), we choose the setup described above. If needed the LSM trie can be improved with the techniques presented by Luo and Carey [22, 23]. For example, one such improvement is partitioned merging where multiple tries with non-overlapping key ranges can exist at the same level and when a trie overflows at level i, this trie needs only to be merged with overlapping tries at level \(i+1\). Partitioned merges reduce the I/O during merging since not all data at level i needs to be merged into level \(i+1\).
Our focus is to show how to integrate a CAS index with LSM trees. We do not address aspects related to recovery and multi-user synchronization. These challenges, however, exist and must be handled by the system. Typical KV-stores use write-ahead logging (WAL) to make their system recoverable and multi-version concurrency control (MVCC) to provide concurrency. These techniques are also applicable to the RSCAS index.
The in-memory RSCAS trie \(R^M_0\) is combined with a sequence of disk-based RSCAS tries \(R_0, \ldots , R_k\) that grow in size as illustrated in Fig. 5. The most recently inserted keys are accumulated in the in-memory RSCAS trie \(R^M_0\) where insertions can be performed efficiently. When \(R^M_0\) grows too big, the keys are migrated to a disk-based RSCAS trie \(R_i\). A query is executed on each trie individually and the result sets are combined. We only consider insertions since deletions do not occur in the SWH archive.
The size of each trie is bounded. \(R^M_0\) and \(R_0\) contain up to M keys, where M is chosen according to the memory capacity of the system. With an average key length of 80 bytes in the SWH archive, reasonable values of M range from tens of millions to a few billion keys (e.g., with \(M = 10^8\), \(R^M_0\) requires about 8 GB of memory). Each disk-based trie \(R_i\), \(i\ge 1\), is either empty or contains between \(2^{i-1}M\) keys (exclusive) and \(2^iM\) keys (inclusive).
When \(R^M_0\) is full, we look for the first disk-based trie \(R_i\) that is empty. We (a) collect all keys in tries \(R^M_0\) and \(R_j\), \(0 \le j < i\), (b) bulk-load trie \(R_i\) from these keys, and (c) delete all previous tries.
Example 14
Assume we set the number of keys that fit in memory to \(M=10\) million, which is the number of new keys that arrive every day in the SWH archive, on average. When \(R^M_0\) overflows after one day we redirect incoming insertions to a new in-memory trie and look for the first non-empty trie \(R_i\). Assuming this is \(R_0\), the disk-resident trie \(R_0\) is bulk-loaded with the keys in \(R^M_0\). After another day, \(R^M_0\) overflows again and this time the first non-empty trie is \(R_1\). Trie \(R_1\) is created from the keys in \(R^M_0\) and \(R_0\). At the end, \(R_1\) contains 20M keys, and \(R^M_0\) and \(R_0\) are deleted. \(\square \)
An overflow in \(R^M_0\) does not stall continuous indexing since we immediately redirect all incoming insertions to a new in-memory trie \(R^{M'}_0\) while we bulk-load \(R_i\) in the background. In order for this to work, \(R^M_0\) cannot allocate all of the available memory. We need to reserve a sufficient amount of memory for \(R^{M'}_0\) (in the SWH archive scenario we allowed \(R^M_0\) to take up at most half of the memory). During bulk-loading, we keep the old tries \(R^M_0\) and \(R_0, \ldots , R_{i-1}\) around such that queries have access to all indexed data. As soon as \(R_i\) is complete, we replace \(R^M_0\) with \(R^{M'}_0\) and \(R_0, \ldots , R_{i-1}\) with \(R_i\). In practice, neither insertions nor queries stall as long as the insertion rate is bounded. If the insertion rate is too high and \(R^{M'}_0\) overflows before we finish bulk-loading \(R_i\), we block and do not accept more insertions. This does not happen in the SWH archive since with our default of \(M = 10^8\) keys (about 8 GB memory) trie \(R^{M'}_0\) overflows every ten days and bulk-loading the trie on our biggest dataset takes about four hours.
6.3 Storage layout
The RSCAS index consists of a mutable in-memory trie \(R^M_0\) and a series of immutable disk-based tries \(R_i\). For \(R^M_0\), we use a node structure that is easy to update in-place, while we design \(R_i\) for compact storage on disk.
6.3.1 Memory-optimized RSCAS trie
The memory-optimized RSCAS trie \(R^M_0\) provides fast in-place insertions for a small number of composite keys that fit into memory. Since all insertions are buffered in \(R^M_0\) before they are migrated in bulk to disk, \(R^M_0\) is in the critical path of our indexing pipeline and must support efficient insertions. We reuse the memory-optimized trie [42] that is based on the memory-optimized Adaptive Radix Tree (ART) [21]. ART implements four node types that are optimized for the hardware’s memory hierarchy and that have a physical fanout of 4, 16, 48, and 256 child pointers, respectively. A node uses the smallest node type that can accommodate the node’s child pointers. Insertions add node pointers and when a node becomes too big, the node is resized to the next appropriate node type. This ensures that not every insertion requires resizing, e.g., a node with ten children can sustain six deletions or seven insertions before it is resized. Figure 6 illustrates the node type with 256 child pointers; for the remaining node types we refer to Leis et al. [21]. The node header stores the dimension D, the lengths \(l_P\) and \(l_V\) of substrings \(s_P\) and \(s_V\), and the number of children m. Substrings \(s_P\) and \(s_V\) are implemented as variable-length byte vectors. The remaining space of an inner node (beige-colored in Fig. 6) is reserved for child pointers. For each possible value b of the discriminative byte, there is a pointer (possibly NULL) to the subtree where all keys have value b at the discriminative byte in dimension D.
The structure of leaf nodes is similar, except that leaf nodes contain a variable-length vector with references k.R instead of child pointers.
For the memory-optimized RSCAS trie, we set the partitioning threshold \(\tau =1\), meaning that \(R^M_0\) dynamically interleaves keys completely. This provides fast and fine-grained access to the indexed keys.
6.3.2 Disk-optimized RSCAS trie
We propose a disk-resident RSCAS trie to compactly store dynamically-interleaved keys on disk. Since a disk-resident RSCAS trie is immutable, we optimize it for compact storage. To that end, we store nodes gapless on disk and we increase the granularity of leaf nodes by setting \(\tau > 1\). We look at these techniques in turn. We store nodes gapless on disk since we do not have to reserve space for future in-place insertions. This means a node can cross page boundaries, but we found that in practice this is not a problem. We tested various node clustering techniques to align nodes to disk pages. The most compact node clustering algorithm [19] produced a trie that was 30% larger than with gapless storage as it kept space empty on a page if it could not add another node without exceeding the page size. In addition to the gapless storage, we increase the granularity of leaf nodes by setting \(\tau > 1\). As a result the RSCAS index contains fewer nodes, but the size of leaf nodes increases. We found that by storing fewer but bigger nodes we save space because we store less meta-data like node headers, child pointers, etc. In Sect. 8.4.1, we determine the optimal value for \(\tau \).
Figure 7 shows how to compactly serialize nodes on disk. Inner nodes point to other nodes, while leaf nodes store a set of suffixes. Both node types store the same four-byte header that encodes dimension \(D \in \{P,V,\bot \}\), the lengths \(l_P\) and \(l_V\) of the substrings \(s_P\) and \(s_V\), and a number m. For inner nodes, m denotes the number of children, while for leaf nodes it denotes the number of suffixes. Next, we store substrings \(s_P\) and \(s_V\) (exactly \(l_P\) and \(l_V\) bytes long, respectively). After the header, inner nodes store m pairs \((b_i,\text {ptr}_i)\), where \(b_i\) (1 byte long) is the value at the discriminative byte that is used to descend to this child node and \(\text {ptr}_i\) (6 bytes long) is the position of this child in the trie file. Leaf nodes, instead, store m suffixes, and for each suffix, we record substrings \(s_P\) and \(s_V\) along with their lengths and the revision r (20 byte SHA1 hash).
Example 15
The size of \(\mathsf {n}_1\) in Fig. 4 is 30 bytes: 4 bytes for the header, 4 bytes for \(s_V\), 1 byte for \(s_P\), and \(3\times (1+6) = 21\) bytes for the three child pointers and their discriminative bytes. \(\square \)
7 Algorithms
We propose algorithms for querying, inserting, bulk-loading, and merging RSCAS tries. Queries are executed independently on all in-memory and disk-based RSCAS tries and the results are combined. Insertions are directed at the in-memory RSCAS trie alone. Merging is used whenever the in-memory RSCAS trie overflows and applies bulk-loading to create a large disk-optimized RSCAS trie.
7.1 Querying RSCAS
We traverse an RSCAS trie in pre-order to evaluate a CAS query, skipping subtrees that cannot match the query. Starting at the root node, we traverse the trie and evaluate at each node part of the query’s path and value predicate. Evaluating a predicate on a node returns MATCH if the full predicate has been matched, MISMATCH if it has become clear that no node in the current node’s subtree can match the predicate, and INCOMPLETE if we need more information. In case of a MISMATCH, we can safely skip the entire subtree. If both predicates return MATCH, we collect all revisions r in the leaf nodes of this subtree. Otherwise, we traverse the trie further to reach a decision.
7.1.1 Query algorithm
Algorithm 1 shows the pseudocode for evaluating a CAS query on a RSCAS trie. It takes the following parameters: the current node n (initially the root node of the trie), a query path q, and a range \([v_l, v_h]\) for the value predicate. Furthermore, we need two buffers \(\texttt {buff}_{P}\) and \(\texttt {buff}_{V}\) (initially empty) that hold, respectively, all path and value bytes from the root to the current node n. Finally, we require state information s to evaluate the path and value predicates (we provide details as we go along) and an answer set W to collect the results.

First, we update \(\texttt {buff}_{V}\) and \(\texttt {buff}_{P}\) by adding the information in \(s_V\) and \(s_P\) of the current node n (line 1).
For inner nodes, we match the query predicates against the current node. MatchValue computes the longest common prefix between \(\texttt {buff}_{V}\) and \(v_l\) and between \(\texttt {buff}_{V}\) and \(v_h\). The position of the first byte for which \(\texttt {buff}_{V}\) and \(v_l\) differ is lo, and the position of the first byte for which \(\texttt {buff}_{V}\) and \(v_h\) differ is hi. If \(\texttt {buff}_{V}[\texttt {lo}] < v_l[\texttt {lo}]\), we know that the node’s value lies outside of the range; hence, we return MISMATCH. If \(\texttt {buff}_{V}[\texttt {hi}] > v_h[\texttt {hi}]\), the node’s value lies outside of the upper bound and we return MISMATCH as well. If \(\texttt {buff}_{V}\) contains a complete value (e.g., all eight bytes of a 64 bit integer) and \(v_l \le \texttt {buff}_{V} \le v_h\), we return MATCH. If \(\texttt {buff}_{V}\) is incomplete, but \(v_l[\texttt {lo}] < \texttt {buff}_{V}[\texttt {lo}]\) and \(\texttt {buff}_{V}[\texttt {hi}] < v_h[\texttt {hi}]\), we know that all values in the subtree rooted at n match and we also return MATCH. In all other cases, we cannot make a decision yet and return INCOMPLETE. The values of lo and hi are kept in the state to avoid recomputing the longest common prefix from scratch for each node. Instead we resume the search from the previous values of lo and hi.
Function MatchPath matches the query path q against the current path prefix \(\texttt {buff}_P\). It supports symbols * and ** to match any number of characters in a node label, respectively, any number of node labels in a path. As long as we do not encounter any wildcards in the query path q, we directly compare (a prefix of) q with the current content of \(\texttt {buff}_{P}\) byte by byte. As soon as a byte does not match, we return MISMATCH. If we successfully match the complete query path q against a complete path in \(\texttt {buff}_{P}\) (both terminated by $), we return MATCH. Otherwise, we return INCOMPLETE. When we encounter wildcard * in q, we match it successfully to the corresponding label in \(\texttt {buff}_{P}\) and continue with the next label. A wildcard * itself will not cause a mismatch (unless we try to match it against the terminator $), so we either return MATCH if it is the final label in q and \(\texttt {buff}_{P}\) or INCOMPLETE. Matching the descendant-axis ** is more complicated. We store in state s the current position where we are in \(\texttt {buff}_{P}\) and continue matching the label after ** in q. If at any point we find a mismatch, we backtrack to the next path separator after the noted position, thus skipping a label in \(\texttt {buff}_{P}\) and restarting the search from there. Once \(\texttt {buff}_{P}\) contains a complete path, we can make a decision between MATCH or MISMATCH.
The algorithm continues by checking the outcomes of the value and path matching (line 5). If one of the outcomes is MISMATCH, we stop the search since no descendant can match the query. Otherwise, we continue with the matching children of n (lines 6–8). Finding the matching children follows the same logic as described above for MatchValue and MatchPath. If node \(n.D = P\) and we have seen a descendant axis in the query path, all children of the current node match.
As soon as we reach a leaf node, we iterate over each suffix t in the leaf to check if it matches the query using the same functions as explained above (lines 10–14). If the current buffers indeed match the query, we add the reference t.R to the result set.
Example 16
Consider a CAS query that looks for revisions in 2020 that modified a C file in the ext3 or ext4 filesystem. Thus, the query path is \(q=\texttt {{/fs/ext*/*.c\$}}\) and the value range is \(v_l = \textsf {2020-01-01}\) (00 00 00 00 5E 0B E1 00) and \(v_h = \textsf {2020-12-31}\) (00 00 00 00 5F EE 65 FF). We execute the query on the trie in Fig. 4.
-
Starting at \(\mathsf {n}_1\), we update \(\texttt {buff}_V\) to 00 00 00 00 and \(\texttt {buff}_P\) to /. MatchValue matches four value bytes and returns INCOMPLETE. MatchPath matches one path byte and also returns INCOMPLETE. Both functions return INCOMPLETE, so we have to traverse all matching children. Since \(\mathsf {n}_1\) is a value node, we look for all matching children whose value for the discriminative value byte is between 5E and 5F. Nodes \(\mathsf {n}_7\) and \(\mathsf {n}_8\) satisfy this condition.
-
Node \(\mathsf {n}_7\) is a leaf. We iterate over each suffix (there are two) and update the buffers accordingly. For the first suffix with path substring 3/inode.c$ we find that MatchPath and MatchValue both return MATCH. Hence, revision \(\mathsf {r}_4\) is added to W. The next suffix matches the value predicate but not the path predicate and is therefore discarded.
-
Next, we look at node \(\mathsf {n}_8\). We find that
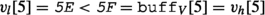 and
and  , thus all values of \(\mathsf {n}_9\)’s descendants are within the bounds \(v_l\) and \(v_h\), and MatchValue returns MATCH. Since \(\mathsf {n}_8.s_P\) is the empty string, MatchPath still returns INCOMPLETE and we descend further. According to the second byte in the query path, \(q[2] = \texttt {{f}}\), we must match letter f; hence, we descend to node \(\mathsf {n}_{10}\), where both predicates match. Therefore, revision \(\mathsf {r}_6\) is added to W.
, thus all values of \(\mathsf {n}_9\)’s descendants are within the bounds \(v_l\) and \(v_h\), and MatchValue returns MATCH. Since \(\mathsf {n}_8.s_P\) is the empty string, MatchPath still returns INCOMPLETE and we descend further. According to the second byte in the query path, \(q[2] = \texttt {{f}}\), we must match letter f; hence, we descend to node \(\mathsf {n}_{10}\), where both predicates match. Therefore, revision \(\mathsf {r}_6\) is added to W.
7.2 Updating memory-based RSCAS trie
All insertions are performed in the in-memory RSCAS trie \(R^M_0\) where they can be executed efficiently. Inserting a new key into \(R^M_0\) usually changes the position of the discriminative bytes, which means that the dynamic interleaving of all keys that are located in the node’s subtree is invalidated.
Example 17
We insert the key  into the RSCAS trie in Fig. 4. First we traverse the trie starting from root \(\mathsf {n}_1\). Since \(\mathsf {n}_1\)’s substrings completely match \(\mathsf {k}_{10}\)’s path and value we traverse to child \(\mathsf {n}_8\). In \(\mathsf {n}_8\), there is a mismatch in the value dimension: \(\mathsf {k}_{10}\)’s sixth byte is 83 while for node \(\mathsf {n}_8\) the corresponding byte is BD. This invalidates the dynamic interleaving of keys \(\mathsf {K}^{2,3,7}\) in \(\mathsf {n}_8\)’s subtree. \(\square \)
into the RSCAS trie in Fig. 4. First we traverse the trie starting from root \(\mathsf {n}_1\). Since \(\mathsf {n}_1\)’s substrings completely match \(\mathsf {k}_{10}\)’s path and value we traverse to child \(\mathsf {n}_8\). In \(\mathsf {n}_8\), there is a mismatch in the value dimension: \(\mathsf {k}_{10}\)’s sixth byte is 83 while for node \(\mathsf {n}_8\) the corresponding byte is BD. This invalidates the dynamic interleaving of keys \(\mathsf {K}^{2,3,7}\) in \(\mathsf {n}_8\)’s subtree. \(\square \)
7.2.1 Lazy restructuring
If we want to preserve the dynamic interleaving, we need to re-compute the dynamic interleaving of all affected keys, which is expensive. Instead, we relax the dynamic interleaving using lazy restructuring [44]. Lazy restructuring resolves the mismatch by adding exactly two new nodes, \(n_{\textsf {par}}\) and \(n_{\textsf {sib}}\), to RSCAS instead of restructuring large parts of the trie. The basic idea is to add a new intermediate node \(n_{\textsf {par}}\) between node n where the mismatch happened and n’s new sibling node \(n_{\textsf {sib}}\) that represents the newly inserted key. We put all bytes leading up to the position of the mismatch into \(n_{\textsf {par}}\), and all bytes starting from this position move to nodes n and \(n_{\textsf {sib}}\). After that, we insert node \(n_{\textsf {par}}\) between node n and its previous parent node \(n_p\).
Example 18
Figure 8 shows the rightmost subtree of Fig. 4 after it is lazily restructured when \(\mathsf {k}_{10}\) is inserted. Two new nodes are created, parent \(n_{\textsf {par}} = \mathsf {n}'_8\) and sibling \(n_{\textsf {sib}} = \mathsf {n}''_8\). Additionally, \(\mathsf {n}_8.s_V\) is updated. \(\square \)
The rightmost subtree of Fig. 4 after inserting key \(\mathsf {k}_{10}\) with lazy restructuring
Lazy restructuring is efficient: it adds exactly two new nodes to \(R^M_0\); thus, the main cost is traversing the trie. However, while efficient, lazy restructuring introduces small irregularities that are limited to the dynamic interleaving of the keys in the subtree where the mismatch occurred. These irregularities do not affect the correctness of CAS queries, but they slowly separate (rather than interleave) paths and values if insertions repeatedly force the algorithm to split the same subtree in the same dimension. Since \(R^M_0\) is memory-based and small in comparison with the disk-based tries, the overall effect on query performance is negligible.
Example 19
After inserting \(\mathsf {k}_{10}\), root node \(\mathsf {n}_1\) and its new child \(\mathsf {n}'_8\) both \(\psi \)-partition the data in the value dimension, violating the strictly alternating property of the dynamic interleaving, see Fig. 8. \(\square \)
7.2.2 Inserting keys with lazy restructuring
Algorithm 2 inserts a key k in \(R^M_0\) rooted at node n. If \(R^M_0\) is empty (i.e., n is \({\textsc {Nil}}\)), we create a new root node in lines 1-3. Otherwise, we traverse the trie to k’s insertion position. We compare the key’s path and value with the current node’s path and value by keeping track of positions \(g_P, g_V, i_P, i_V\) in strings \(k.P, k.V, n.s_P, n.s_V\), respectively (lines 8–11). As long as the substrings at their corresponding positions coincide we descend. If we completely matched key k, it means that we reached a leaf node and we add k.R to the current node’s suffixes (lines 12–14). If during the traversal we cannot find the next node to descend to, the key has a new value at a discriminative byte that did not exist before in the data. We create a new leaf node and set its substrings \(s_P\) and \(s_V\) to the still unmatched bytes in k.P and k.V, respectively (lines 20–22). If we find a mismatch between the key and the current node in at least one dimension, we lazily restructure the trie (lines 15–17).

Algorithm 3 implements lazy restructuring. Lines 1–4 determine the dimension in which \(n_{\textsf {par}}\) partitions the data. If only a path mismatch occurred between n and k, we have to use dimension P. In case of only a value mismatch, we have to use V. If we have mismatches in both dimensions, then we take the opposite dimension of parent node \(n_p\) to keep up an alternating interleaving as long as possible. In lines 5–6, we create nodes \(n_{\textsf {par}}\) and \(n_{\textsf {sib}}\). Node \(n_{\textsf {par}}\) is an inner node of type node4, which is the node type with the smallest fanout in ART [21]. In lines 9–12, we install n and \(n_{\textsf {sib}}\) as children of \(n_{\textsf {par}}\). Finally, in lines 13–15, we place the new parent node \(n_{\textsf {par}}\) between n and its former parent node \(n_p\).

7.3 Bulk-loading a disk-based RSCAS trie
We create and bulk-load a new disk-based RSCAS trie whenever the in-memory trie \(R^M_0\) overflows. The bulk-loading algorithm constructs RSCAS while, at the same time, dynamically interleaving a set of keys. Bulk-loading RSCAS is difficult because all keys must be considered together to dynamically interleave them. The bulk-loading algorithm starts with all non-interleaved keys in the root partition. We use partitions during bulk-loading to temporarily store keys along with their discriminative bytes. Once a partition has been processed, it is deleted.
Definition 12
(Partition) A partition \(L = (g_P,g_V,\textsf {size},\textsf {ptr})\) stores a set K of composite keys. \(g_P = \textsf {dsc}(K,P)\) and \(g_V = \textsf {dsc}(K,V)\) denote the discriminative path and value byte, respectively. \(\textsf {size} = |K|\) denotes the number of keys in the partition. L is either memory-resident or disk-resident, and \(\textsf {ptr}\) points to the keys in memory or on disk. \(\square \)
Example 20
Root partition \(\mathsf {L}^{1...9} = (2,5,9,\bullet )\) in Fig. 9a stores keys \(\mathsf {K}^{1...9}\) from Table 1. The longest common prefixes of \(\mathsf {L}^{1...9}\) are type-set in bold-face. The first bytes after these prefixes are \(\mathsf {L}^{1...9}\)’s discriminative bytes \(g_P = 2\) and \(g_V = 5\). We use placeholder \(\bullet \) for pointer \(\textsf {ptr}\); we describe later how to decide if partitions are stored on disk or in memory. \(\square \)
Bulk-loading starts with root partition L and breaks it into smaller partitions using the \(\psi \)-partitioning until a partition contains at most \(\tau \) keys. The \(\psi \)-partitioning \(\psi (L,D)\) groups keys together that have the same prefix in dimension D, and returns a partition table where each entry in this table points to a new partition \(L_i\). We apply \(\psi \) alternatingly in dimensions V and P to interleave the keys at their discriminative bytes. In each call, the algorithm adds a new node to RSCAS with L’s longest common path and value prefixes.
Example 21
Figure 9 shows how the RSCAS from Fig. 4 is built. In Fig. 9b, we extract \(\mathsf {L}^{1...9}\)’s longest common path and value prefixes and store them in the new root node \(\mathsf {n}_1\). Then, we \(\psi \)-partition \(\mathsf {L}^{1...9}\) in dimension V and obtain a partition table (light green) that points to three new partitions: \(\mathsf {L}^{1,4,8,9}\), \(\mathsf {L}^{5,6}\), and \(\mathsf {L}^{2,3,7}\). We drop \(\mathsf {L}^{1...9}\)’s longest common prefixes from these new partitions. We proceed recursively with \(\mathsf {L}^{1,4,8,9}\). In Fig. 9c, we create node \(\mathsf {n}_2\) as before and this time we \(\psi \)-partition in dimension P and obtain two new partitions. Given \(\tau = 2\), \(\mathsf {L}^1\) is not partitioned further, but in the next recursive step, \(\mathsf {L}^{4,8,9}\) would be partitioned one last time in dimension V. \(\square \)
To avoid scanning L twice (first to compute the discriminative byte; second to compute \(\psi (L,D)\)) we make the \(\psi \)-partitioning proactive by exploiting that \(\psi (L,D)\) is applied hierarchically. This means we pre-compute the discriminative bytes of every new partition \(L_i \in \psi (L,D)\) as we \(\psi \)-partition L. As a result, by the time \(L_i\) itself is \(\psi \)-partitioned, we already know its discriminative bytes and can directly compute the partitioning. Algorithm 6 in Sect. 7.4 shows how to compute the root partition’s discriminative bytes; the discriminative bytes of all subsequent partitions are computed proactively during the partitioning itself. This halves the scans over the data during bulk-loading.
7.3.1 Bulk-loading algorithm
The bulk-loading algorithm (Algorithm 4) takes three parameters: a partition L (initially the root partition), the partitioning dimension D (initially dimension V), and the position in the trie file where the next node is written to (initially 0). Each invocation adds a node n to the RSCAS trie and returns the position in the trie file of the first byte after the subtree rooted in n. Lines 1–3 create node n and set its longest common prefixes \(n.s_P\) and \(n.s_V\), which are extracted from a key \(k \in L\) from the first byte up to, but excluding, the positions of L’s discriminative bytes \(L.g_P\) and \(L.g_V\). If the number of keys in the current partition exceeds the partitioning threshold \(\tau \) and L can be \(\psi \)-partitioned, we break L further up. In lines 5–6, we check if we can indeed \(\psi \)-partition L in D and switch to the alternate dimension \(\overline{D}\) otherwise. In line 8, we apply \(\psi (L,D)\) and obtain a partition table T, which is a \(2^8\)-long array that maps the \(2^8\) possible values b of a discriminative byte (\(\texttt {0x00} \le b \le \texttt {0xFF}\)) to partitions. We write T[b] to access the partition for value b (\(T[b] = {\textsc {Nil}}\) if no partition exists for value b). \(\psi (L,D)\) drops L’s longest common prefixes from each key \(k \in L\) since we store these prefixes already in node n. We apply Algorithm 4 recursively on each partition in T with the alternate dimension \(\overline{D}\), which returns the position where the next child is written to on disk. We terminate if partition L contains no more than \(\tau \) keys or cannot be partitioned further. We iterate over all remaining keys in L and store their non-interleaved suffixes in the set \(n.\textsf {suffixes}\) of leaf node n (lines 16–19). Finally, in line 22 we write node n to disk at the given offset in the trie file.

Algorithm 5 implements \(\psi (L,D)\). We organize the keys in a partition L at the granularity of pages so that we can seamlessly transition between memory- and disk-resident partitions. A page is a fixed-length buffer that contains a variable number of keys. If L is disk-resident, \(L.\textsf {ptr}\) points to a page-structured file on disk and if L is memory-resident, \(L.\textsf {mptr}\) points to the head of a singly-linked list of pages. Algorithm 5 iterates over all pages in L and for each key in a page, line 6 determines the partition T[b] to which k belongs by looking at its value b at the discriminative byte. Next, we drop the longest common path and value prefixes from k (lines 7–8). We proactively compute T[b]’s discriminative bytes whenever we add a key k to T[b] (lines 10–17). Two cases can arise. If k is T[b]’s first key, we initialize partition T[b]. If L fits into memory, we make T[b] memory-resident, else disk-resident. We initialize \(g_P\) and \(g_V\) with one past the length of k in the respective dimension (lines 9–12). These values are valid upper-bounds for the discriminative bytes since keys are prefix-free. We store k as a reference key for partition T[b] in \(\textsf {refkeys}[b]\). If k is not the first key in T[b], we update the upper bounds (lines 13–17) as follows. Starting from the first byte, we compare k with reference key \(\textsf {refkeys}[b]\) byte-by-byte in both dimension until we reach the upper-bounds \(T[b].g_P\) and \(T[b].g_V\), or we find new discriminative bytes and update \(T[b].g_P\) and \(T[b].g_V\).

7.4 Merging RSCAS tries upon overflow
When the memory-resident trie \(R^M_0\) reaches its maximum size of M keys, we move its keys to the first disk-based trie \(R_i\) that is empty using Algorithm 6. We keep pointers to the root nodes of all tries in an array. Algorithm 6 first collects all keys from tries \(R^M_0\), \(R_0,\ldots ,R_{i-1}\) and stores them in a new partition L (lines 2–4). Next, in lines 5–11, we compute L’s discriminative bytes \(L.g_P\) and \(L.g_V\) from the substrings \(s_P\) and \(s_V\) of the root nodes of the i tries. Finally, in lines 12–14, we bulk-load trie \(R_i\) and delete all previous tries.

7.5 Analytical evaluation
7.5.1 Total I/O overhead during bulk-loading
The I/O overhead is the number of page I/Os without reading the input and writing the output. We use N, M, and B for the number of input keys, the number of keys that fit into memory, and the number of keys that fit into a page, respectively [4]. We analyze the I/O overhead of Algorithm 4 for a uniform data distribution with a balanced RSCAS and for a maximally skewed distribution with an unbalanced RSCAS. The \(\psi \)-partitioning splits a partition into equally sized partitions. Thus, with a fixed fanout f the \(\psi \)-partitioning splits a partition into f, \(2 \le f \le 2^8\), partitions.
Lemma 5
The I/O overhead to build RSCAS with Algorithm 4 from uniformly distributed data is
Example 22
We compute the I/O overhead for \(N = 16\), \(M = 4\), \(B = 2\), and \(f=2\). There are \(\lceil \log _2 \lceil \frac{16}{4} \rceil \rceil = 2\) intermediate levels with the data on disk. On each level, we read and write \(\frac{16}{2} = 8\) pages. In total, the disk I/O is \(2 \times 2 \times 8 = 32\). \(\square \)
For maximally skewed data, RSCAS deteriorates to a trie whose height is linear in the number of keys in the dataset.
Lemma 6
The I/O overhead to build RSCAS with Algorithm 4 from maximally skewed data is
Example 23
We use the same parameters as in the previous example but assume maximally skewed data. There are \(16-{\lceil \frac{4}{2} \rceil }2 = 12\) levels before the partitions fit into memory. For example, at level \(i=1\) we write and read \({\lceil \frac{16-1}{2} \rceil } = 8\) pages for \(L_{1,2}\). In total, the I/O overhead is 144 pages. \(\square \)
Theorem 4
The I/O overhead to build RSCAS with Algorithm 4 depends on the data distribution. It is lower bounded by \(O(\log (\frac{N}{M}) \frac{N}{B})\) and upper bounded by \(O((N-M)\frac{N}{B})\).
Note that, since RSCAS is trie-based and keys are encoded by the path from the root to the leaves, the height of the trie is bounded by the length of the keys. The worst-case is very unlikely in practice because it requires that the lengths of the keys is linear in the number of keys. Typically, the key length is at most tens or hundreds of bytes. We show in Sect. 8 that building RSCAS performs close to the best case on real-world data.
7.5.2 Amortized I/O overhead during insertions
Next, we consider the amortized I/O overhead of a single insertion during a series of N insertions into an empty trie. Note that \(M-1\) out of M consecutive insertions incur no disk I/O since they are handled by the in-memory trie \(R^M_0\). Only the Mth insertion bulk-loads a new disk-based trie.
Lemma 7
Let \(\textsf {cost}(N,M,B)\) be the I/O overhead of bulk-loading RSCAS. The amortized I/O overhead of one insertion out of N insertions into an initially empty trie is \(O(\frac{1}{N} \times \log _2(\frac{N}{M}) \times \textsf {cost}(N,M,B)) \).
8 Experimental evaluation
8.1 Setup
Environment We use a Debian 10 server with 80 cores and 400 GB main memory. The machine has six hard disks, each 2 TB big, that are configured in a RAID 10 setup. The code is written in C++ and compiled with g++ 8.3.0.
Datasets We use three real-world datasets and one synthetic dataset. Table 6 provides an overview.
-
GitLab. The GitLab data from SWH contain archived copies of all publicly available GitLab repositories up to 2020-12-15. The dataset contains 914593 archived repositories, which correspond to a total of 120071946 unique revisions and 457839953 unique files. For all revisions in the GitLab dataset, we index the commit time and the modified files (equivalent to “commit diffstats” in version control system terminology). In total, we index 6.9 billion composite keys similar to Table 1.
-
ServerFarm. The ServerFarm dataset [42] mirrors the file systems of 100 Linux servers. For each server, we installed a default set of packages and randomly picked a subset of optional packages. In total, there are 21 million files. For each file, we record the file’s full path and size.
-
Amazon. The Amazon dataset [18] contains hierarchically categorized products. For each product, its location in the hierarchical categorization (the path) and its price in cents (the value) are recorded. For example, the shoe ‘evo’ has path /sports/outdoor/running/evo and its price is 10000 cents.
-
XMark. The XMark dataset [39] is a synthetic dataset that models a database for an internet auction site. It contains information about people, regions (subdivided by continent), etc. We generated the dataset with scale factor 500, and we index the numeric attribute ‘category’.
Previous results In our previous work [44], we compared RSCAS to state-of-the-art research solutions. We compared RSCAS to the CAS index by Mathis et al. [25], which indexes paths and values in separate index structures. We also compared RSCAS to a trie-based index where composite keys are integrated with four different methods: (i) the z-order curve with surrogate functions to map variable-length keys to fixed-length keys, (ii) a label-wise interleaving where we interleave one path label with one value byte, (iii) the path-value concatenation, and (iv) value-path concatenation. Our experiments showed that the approaches do not provide robust CAS query performance because they may create large intermediate results.
Compared approaches This paper compares RSCAS to scalable state-of-the-art industrial-strengths systems. First, we compare RSCAS to Apache Lucene [1], which builds separate indexes for the paths and values. Lucene creates an FST on the paths and a Bkd-tree [35] on the values. Lucene evaluates CAS queries by decomposing queries into their two predicates, evaluating the predicates on the respective indexes, and intersecting the sorted posting lists to produce the final result. Second, we compare RSCAS to composite B-trees in Postgres. This simulates the two possible c-order curves that concatenate the paths and values (or vice versa). We create a table \(\texttt {data}(P,V,R)\), similar to Table 1, and create two composite B+ trees on attributes (P, V) and (V, P), respectively.
Parameters Unless otherwise noted, we set the partitioning threshold \(\tau = 100\) based on experiments in Sect. 8.4.1. The number of keys M that the main-memory RSCAS trie \(R^M_0\) can hold is \(M = 10^8\).
Artifacts The code and the datasets used for our experiments are available online.Footnote 2
8.2 Impact of datasets on RSCAS’s structure
In Fig. 10, we show how the shape (depth and width) of the RSCAS trie adapts to the datasets. Figure 10a shows the distribution of the node depths in the RSCAS trie for the GitLab dataset. Because of its trie-based structure not every root-to-leaf path in RSCAS has the same length (see also Fig. 4). The average node depth is about 10, with 90% of all nodes occurring no deeper than level 14. The expected depth is \(\log _{\bar{f}}\lceil {\frac{N}{\tau }}\rceil = \log _{8}\lceil {\frac{\text {6.9B}}{100}}\rceil =8.7\), where N is the number of keys, \(\tau \) is the partitioning threshold that denotes the maximum size of a leaf partition, and \(\bar{f}\) is the average fanout. The actual average depth is higher than the expected depth since the GitLab dataset is skewed and the expected depth assumes a uniformly distributed dataset. In the GitLab dataset, the average key length is 80 bytes, but the average node depth is 10, meaning that RSCAS successfully extracts common prefixes. Figure 10b shows how the fanout of the nodes is distributed. Since RSCAS \(\psi \)-partitions the data at the granularity of bytes, the fanout of a node is upper-bounded by \(2^8\), but in practice most nodes have a smaller fanout (we cap the x-axis in Fig. 10b at fanout 40, because there is a long tail of high fanouts with low frequencies). Nodes that \(\psi \)-partition the data in the path dimension typically have a lower fanout because most paths contain only printable ASCII characters (of which there are about 100), while value bytes span the entire available byte spectrum.
The shape of the RSCAS tries on the ServerFarm and Amazon datasets closely resemble that of the trie on the GitLab dataset, see the second and third row in Fig. 10. This is to be expected since all three datasets contain a large number of unique paths and values, see Table 6. As a result, the data contain a large number of discriminative bytes that are needed to distinguish keys from one another. The paths in these datasets are typically longer than the values and contain more discriminative bytes. In addition, as seen above, the discriminative path bytes typically \(\psi \)-partition the data into fewer partitions than the discriminative value bytes. As a consequence, the RSCAS trie on these three datasets is narrower and deeper than the RSCAS trie on the XMark dataset, which has only seven unique paths and about 390k unique values in a dataset of 60M keys. Since the majority of the discriminative bytes in the XMark dataset are value bytes, the trie is flatter and wider on average, see the last row in Fig. 10.
8.3 Query performance
Table 7 shows twelve typical CAS queries with their query path q and the value range \([v_l, v_h]\). We show for each query the final result size and the number of keys that match the individual predicates. In addition, we provide the selectivities of the queries. The selectivity \(\sigma \) (\(\sigma _P\)) [\(\sigma _V\)] is computed as the fraction of all keys that match the CAS query (path predicate) [value predicate]. A salient characteristic of the queries is that the final result is orders of magnitude smaller than the results of the individual predicates. Queries \(Q_1\) through \(Q_6\) on the GitLab dataset increase in complexity. \(Q_1\) looks up all revisions that modify one specific file in a short two-hour time frame. Thus, \(Q_1\) is similar to a point query with very low selectivity in both dimensions. The remaining queries have a higher selectivity in at least one dimension. \(Q_2\) looks up all revisions that modify one specific file in a one-month period. Thus, its path selectivity is low, but its value selectivity is high. Query \(Q_3\) does the opposite: its path predicate matches all changes to GPU drivers using the ** wildcard, but we only look for revisions in a very narrow one-day time frame. \(Q_4\) mixes the * and ** wildcards multiple times and puts them in different locations of the query path (in the middle and towards the end). \(Q_5\) looks for changes to all Makefiles, using the ** wildcard at the front of the query path. Similarly, \(Q_6\) looks for all changes to files named inode (all file extensions are accepted with the * wildcard). The remaining six queries on the other three datasets are similar.
Figure 11 shows the runtime of the six queries on the GitLab dataset (note the logarithmic y-axis). We clear the operating system’s page cache before each query (later we repeat the same experiment on warm caches). We start with the runtime of query \(Q_1\) in Fig. 11a. This point query is well suited for existing solutions because both predicates have low selectivities and produce small intermediate results. Therefore, the composite VP and PV indexes perform best. No matter what attribute is ordered first in the composite index (the paths or the values), the index can quickly narrow down the set of possible candidates. Lucene on the other hand evaluates both predicates and intersects the results, which is more expensive. RSCAS is in between Lucene and the two composite indexes. \(Q_2\) has a low path but high value selectivity. Because of this, the composite PV index outperforms the composite VP index, see Fig. 11b. Evaluating this query in Lucene is costly since Lucene must fully iterate over the large intermediate result produced by the value predicate. RSCAS, on the other hand, uses the selective path predicate to prune subtrees early during query evaluation. For query \(Q_3\) in Fig. 11c, RSCAS performs best, but it is closely followed by the composite VP index, for which \(Q_3\) is the best case since \(Q_3\) has a very low value selectivity. While \(Q_3\) is the best case for VP, it is the worst case for PV and indeed its query performance is an order of magnitude higher. For Lucene, the situation is similar to query \(Q_2\), except that the path predicate produces a large intermediate result (rather than the value predicate). Query \(Q_4\) uses the * and ** wildcards at the end of its query path. The placement of the wildcards is important for all approaches. Query paths that have wildcards in the middle or at the end can be evaluated efficiently with prefix searches. As a result, RSCAS’s query performance remains stable and is similar to that for queries \(Q_1, \ldots , Q_3\). Queries \(Q_5\) and \(Q_6\) are more difficult for all approaches because they contain the descendant axis at the beginning of the query path. Normally, when the query path does not match a path in the trie, the node that is not matched and its subtrees do not need to be considered anymore because no path suffix can match the query path. The ** wildcard, however, may skip over mismatches and the query path’s suffix may match. For this reason, Lucene must traverse its entire FST that is used to evaluate path predicates. Likewise, the composite PV index must traverse large parts of the index because the keys are ordered first by the paths and in the index. The VP index can use the value predicate to prune subtrees that do not match the value predicate before looking at the path predicate. RSCAS uses the value predicate to prune subtrees when the path predicate does not prune anymore because of wildcards and therefore delivers the best query runtime.
In Fig. 12, we show the runtime of queries \(Q_7, \ldots Q_{12}\) on the remaining three datasets (again on cold caches). The absolute runtimes are lower because the datasets are considerably smaller than the GitLab dataset, see Table 6, but the relative differences between the approaches are comparable to the previous set of queries, see Fig. 11.
We repeat the same experiments on warm caches, see Fig. 13 (the y-axis shows the query runtime in milliseconds). Note that we did not implement a dedicated caching mechanism and solely rely on the operating system’s page cache. When the caches are hot the CPU usage and memory access become the main bottlenecks. Since RSCAS produces the smallest intermediate results, RSCAS requires the least CPU time and memory accesses. As a result, RSCAS consistently outperforms its competitors, see Fig. 13.
An analysis of the query performance for an RSCAS index with different numbers of levels, i.e., tries, can be found in the accompanying technical report [43].
8.4 Scalability
RSCAS uses its LSM-based structure to gracefully and efficiently handle large datasets that do not fit into main memory. We discuss how to choose threshold \(\tau \), the performance of bulk-loading and individual insertions, the accuracy of the cost model, and the index size.
8.4.1 Calibration
We start out by calibrating the partitioning threshold \(\tau \), i.e., the maximum number of suffixes in a leaf node. We calibrate \(\tau \) in Fig. 14 on a 100 GB subset of the GitLab dataset. Even on the 100 GB subset, bulk-loading RSCAS with \(\tau =1\) takes more than 12 hours, see Fig. 14a. When we increase \(\tau \), the recursive bulk-loading algorithm terminates earlier (see lines 15–21 in Algorithm 4); hence, fewer partitions are created and the runtime improves. Since the bulk-loading algorithm extracts from every partition its longest common prefixes and stores them in a new node, the number of nodes in the index also decreases as we increase \(\tau \), see Fig. 14b. As a result, leaf nodes get bigger and store more un-interleaved suffixes. This negatively affects the query performance and the index size, see Fig. 14c, d, respectively. Figure 14c shows the average runtime of the six queries \(Q_1, \ldots , Q_6\). A query that reaches a leaf node must scan all suffixes to find matches. Making \(\tau \) too small decreases query performance because more nodes need to be traversed and making \(\tau \) too big decreases query performance because a node must scan many suffixes that do not match a query. According to Fig. 14c, values \(\tau \in [10,100]\) give the best query performance. Threshold \(\tau \) also affects the index size, see Fig. 14d. If \(\tau \) is too small, many small nodes are created and for each such node there is storage overhead in terms of node headers, pointers, etc., see Fig. 7. If \(\tau \) is too big, leaf nodes contain long lists of suffixes for which we could still extract common prefixes if we \(\psi \)-partitioned them further. As a consequence, we choose medium values for \(\tau \) to get a good balance between bulk-loading runtime, query performance, and index size. Based on Fig. 14, we choose \(\tau = 100\) as default value. More details on a quantitative analysis on how \(\tau \) affects certain parameters can be found in the accompanying technical report [43].
8.4.2 Bulk-loading performance
Bulk-loading is a core operation that we use in two situations. First, when we create RSCAS for an existing system with large amounts of data we use bulk-loading to create RSCAS. Second, our RSCAS index uses bulk-loading to create a disk-based RSCAS trie whenever the in-memory RSCAS trie \(R^M_0\) overflows. We compare our bulk-loading algorithm with bulk-loading of composite B+ trees in Postgres (Lucene does not support bulk-loading; as a reference point, we include Lucene’s performance for the corresponding point insertions).
Figure 15 evaluates the performance of the bulk-loading algorithms for RSCAS and Postgres. We give the systems 8 GB of main memory. For a fair comparison, we set the fill factor of the composite B+ trees in Postgres to 100% to make them read-optimized and as compact as possible since disk-based RSCAS tries are read-only. We compare the systems for our biggest dataset, the GitLab dataset, in Fig. 15. The GitLab dataset contains 6.9 billion keys and has a size of 550 GB. Fig. 15a confirms that bulk-loading RSCAS takes roughly the same time as bulk-loading the PV and VP composite indexes in Postgres (notice that RSCAS and the PV composite index have virtually the same runtime, thus PV’s curve is barely visible). The runtime and disk I/O of all algorithms increase linearly in Fig. 15a, which means it is feasible to bulk-load these indexes efficiently for very large datasets. Postgres creates a B+ tree by sorting the data and then building the index bottom up, level by level. RSCAS partitions the data and builds the index top down. In practice, both paradigms perform similarly, both in terms of runtime (Fig. 15a) and disk I/O (Fig. 15b).
8.4.3 Insertion performance
New keys are first inserted into the in-memory trie \(R^M_0\) before they are written to disk when \(R^M_0\) overflows. We evaluate insertions into \(R^M_0\) in Fig. 16a and look at the insertion speed when \(R^M_0\) overflows in Fig. 16b. For the latter case, we compare RSCAS’s on-disk insertion performance to Lucene’s and Postgres’.
Since \(R^M_0\) is memory-based, insertions can be performed quickly, see Fig. 16a. For example, inserting 100 million keys takes less than three minutes with one insertion taking 1.7\(\mu \)s, on average. In practice, the SWH archive crawls about one million revisions per day and since a revision modifies on average about 60 files in the GitLab dataset, there are 60 million insertions into the RSCAS index per day, on average. Therefore, our RSCAS index can easily keep up with the ingestion rate of the SWH archive. Every two days, on average, \(R^M_0\) overflows and a new disk-based RSCAS trie \(R_i\) is bulk-loaded.
In Fig. 16b, we show how the RSCAS index performs when \(R^M_0\) overflows. In this experiment, we set the maximum capacity of \(R^M_0\) to \(M = 100\) million keys and insert 600 million keys, thus \(R^M_0\) overflows six times. Typically when \(R^M_0\) overflows we bulk-load a disk-based trie in a background process, but in this experiment we execute all insertions in the foreground in one process to show all times. As a result, we observe a staircase runtime pattern, see Fig. 16b. A flat part where insertions are performed efficiently in memory is followed by a jump where a disk-based trie \(R_i\) is bulk-loaded. Not all jumps are equally high since their height depends on the size of the trie \(R_i\) that is bulk-loaded. When \(R^M_0\) overflows, the RSCAS index looks for the smallest i such that \(R_i\) does not exist yet and bulk-loads it from the keys in \(R^M_0\) and all \(R_j\), \(j<i\). Therefore, a trie \(R_i\), containing \(2^iM\) keys, is created for the first time after \(2^iM\) insertions. For example, after M insertions we bulk-load \(R_0\) (M keys); after 2M insertions, we bulk-load \(R_1\) (2M keys) and delete \(R_0\); after 3M insertions we again bulk-load \(R_0\) (M keys); after 4M insertions we bulk-load \(R_2\) (4M keys) and delete \(R_0\) and \(R_1\), etc. Lucene’s insertion performance is comparable to that of RSCAS, but insertion into Postgres’ B+ tree are expensive in comparison.Footnote 3 This is because insertions into Postgres’ B+ trees are executed in-place, causing many random updates, while insertions in RSCAS and Lucene are done out-of-place.
8.4.4 Evaluating the cost model
We evaluate the cost model from Lemma 5 that measures the I/O overhead of our bulk-loading algorithm for a uniform data distribution and compare it to the I/O overhead of bulk-loading the real-world GitLab dataset. The I/O overhead is the number of page transfers to read/write intermediate results during bulk-loading. We multiply the I/O overhead with the page size to get the number of bytes that are transferred to and from disk. The cost model in Lemma 5 has four parameters: N, M, B, and f (see Sect. 5.4). We set fanout \(f=10\) since this is the average fanout of a node in RSCAS for the GitLab dataset, see Fig. 10a. The cost model assumes that M (B) keys fit into memory (a page). Therefore, we set \(B = {\lceil \frac{16\,\text {KB}}{80\,\text {B}} \rceil } = 205\), where 16 KB is the page size and 80 is the average key length (see Sect. 8.2). Similarly, if the memory size is 8 GB, we can store \(M = {\lceil \frac{8\,\text {GB}}{80\,\text {B}} \rceil } = 100\) million keys in memory.
In Fig. 17a, we compare the actual and the estimated I/O overhead to bulk-load RSCAS as we increase the number of keys N in the dataset, keeping the memory size fixed at \(M=100\) million keys. The estimated and actual cost are close and within 15% of each other. In Fig. 17b, we vary the memory size and fix the full GitLab dataset as input. The estimated cost is constant from \(M=100\) to \(M=400\) million keys because of the ceiling operator in \(\log _f{{\lceil \frac{N}{M} \rceil }}\) to compute the number of levels of the trie in Lemma 5. If we increase M to 800 million keys, the trie in the cost model has one level less before partitions fit entirely into memory and therefore, the I/O overhead decreases and remains constant thereafter since only the root partition does not fit into main memory.
In Fig. 18a, we compare the actual and the estimated I/O overhead to insert N keys one-by-one into RSCAS, setting \(M = 100 \times 10^6\). We compute the estimated I/O overhead by multiplying the amortized cost of one insertion according to Lemma 7 with the number of keys N. We observe a staircase pattern for the actual I/O overhead because of the repeated bulk-loading when the in-memory trie overflows after every M insertions. Next, we fix \(N = 600\) million keys and increase M in Fig. 18b. In general, increasing M decreases the actual and estimated overhead because less data must be bulk-loaded. But this is not always the case. For example, the actual I/O overhead increases from \(M=200\) to \(M=300\) million keys. To see why, we have to look at the tries that need to be bulk-loaded. For \(M=200\), we create three tries: after M insertions \(R_0\) (200 mil.), after 2M insertions \(R_1\) (400 mil.), and after 3M insertions again \(R_0\) (200 mil.) for a total of 800 million bulk-loaded keys. For \(M=300\), we create only two tries: after M insertions \(R_0\) (300 mil.) and after M insertions \(R_1\) (600 mil.) for a total of 900 million bulk-loaded keys.
8.4.5 Index size
Figure 19 shows the size of the RSCAS, Lucene, and Postgres indexes for our four datasets. The RSCAS index is between 30% to 80% smaller than the input size (i.e., the size of the indexed keys). The savings are highest for the XMark dataset because it has only seven unique paths and therefore the RSCAS trie has fewer nodes since there are fewer discriminative bytes. But even for a dataset with a large number of unique paths, e.g., the GitLab dataset, RSCAS is 43% smaller than the input. RSCAS’s size is comparable to that of the other indexes since all the indexes require space linear in the number of keys in the input.
9 Conclusion and outlook
We propose the RSCAS index, a robust and scalable index for semi-structured hierarchical data. Its robustness is rooted in a well-balanced integration of paths and values in a single index using a new dynamic interleaving. The dynamic interleaving does not prioritize a particular dimension (paths or values), making the index robust against queries with high individual selectivities that produce large intermediate results and a small final result. We use an LSM-design to scale the RSCAS index to applications with a high insertion rate. We buffer insertions in a memory-optimized RSCAS trie that we continuously flush to disk as a series of read-only disk-optimized RSCAS tries. We evaluate our index analytically and experimentally. We prove RSCAS’s robustness by showing that it has the smallest average query runtime over all queries among interleaving-based approaches. We evaluate RSCAS experimentally on three real-world datasets and one synthetic data. Our experiments show that the RSCAS index outperforms state-of-the-art approaches by several orders of magnitude on real-world and synthetic datasets. We show-case RSCAS’s scalability by indexing the revisions (i.e., commits) of all public GitLab repositories archived by Software Heritage, for a total of 6.9 billion modified files in 120 revisions.
In our future work, we plan to support deletions. In the in-memory RSCAS trie, we plan to delete the appropriate leaf node and efficiently restructure the trie if necessary. To delete keys from the disk-resident RSCAS trie, we plan to flag the appropriate leaf nodes as deleted to avoid expensive restructuring on disk. As a result, queries need to filter flagged leaf nodes. Whenever a new disk-based trie is bulk-loaded, we remove the elements previously flagged for deletion. It would also be interesting to implement RSCAS on top of a high-performance platform, such as an LSM-tree-based KV-store, the main challenge would be to adapt range filters to our complex interleaved queries.
Notes
As of 2021-11-08, the Software Heritage archive contains more than 11 billion source code files and 2 billion commits, coming from more than 160 million public software projects. The archive can be browsed at: https://archive.softwareheritage.org/.
We measure insertion performance in Postgres by importing a dataset twice: once with index and once without index, and then we measure the difference in runtime.
References
Apache Lucene.: https://lucene.apache.org/ (2021). Accessed September 2021
Abramatic, J., Cosmo, R.D., Zacchiroli, S.: Building the universal archive of source code. Commun. ACM 61(10), 29–31 (2018)
Achakeev, D., Seeger, B.: Efficient bulk updates on multiversion B-trees. PVLDB 6(14), 1834–1845 (2013)
Aggarwal, A., Vitter, J.S.: The input/output complexity of sorting and related problems. Commun. ACM 31(9), 1116–1127 (1988)
Alsubaiee, S., et al.: AsterixDB: a scalable, open source BDMS. PVLDB 7(14), 1905–1916 (2014)
Apache.: Apache Jackrabbit Oak. https://jackrabbit.apache.org/oak/ (2021). Accessed September 2021
Arge, L.: The buffer tree: a technique for designing batched external data structures. Algorithmica 37(1), 1–24 (2003)
den Bercken, J.V., Seeger, B., Widmayer, P.: A generic approach to bulk loading multidimensional index structures. In: VLDB, pp. 406–415 (1997)
Brunel, R., Finis, J., Franz, G., May, N., Kemper, A., Neumann, T., Färber, F.: Supporting hierarchical data in SAP HANA. In: ICDE, pp. 1280–1291 (2015)
Chang, F., Dean, J., Ghemawat, S., Hsieh, W.C., Wallach, D.A., Burrows, M., Chandra, T., Fikes, A., Gruber, R.E.: Bigtable: a distributed storage system for structured data. ACM Trans. Comput. Syst. 26(2), 4:1-4:26 (2008)
Cooper, B.F., Sample, N., Franklin, M.J., Hjaltason, G.R., Shadmon, M.: A fast index for semistructured data. In: VLDB, pp. 341–350 (2001)
DeCandia, G., et al.: Dynamo: Amazon’s highly available key-value store. In: ACM SOSP, pp. 205–220. ACM (2007)
Di Cosmo, R., Zacchiroli, S.: Software heritage: Why and how to preserve software source code. In: iPRES (2017)
Finis, J., Brunel, R., Kemper, A., Neumann, T., Färber, F., May, N.: DeltaNI: an efficient labeling scheme for versioned hierarchical data. In: SIGMOD, pp. 905–916 (2013)
Finis, J., Brunel, R., Kemper, A., Neumann, T., May, N., Färber, F.: Indexing highly dynamic hierarchical data. PVLDB 8(10), 986–997 (2015)
Gilad, E., Bortnikov, E., Braginsky, A., Gottesman, Y., Hillel, E., Keidar, I., Moscovici, N., Shahout, R.: Evendb: Optimizing key-value storage for spatial locality. In: Proceedings of the 15th European Conference on Computer Systems (EuroSys’20) (2020)
Goldman, R., Widom, J.: DataGuides: enabling query formulation and optimization in semistructured databases. In: VLDB, pp. 436–445 (1997)
He, R., McAuley, J.J.: Ups and downs: Modeling the visual evolution of fashion trends with one-class collaborative filtering. In: WWW, pp. 507–517 (2016)
Kanne, C., Moerkotte, G.: The importance of sibling clustering for efficient bulkload of XML document trees. IBM Syst. J. 45(2), 321–334 (2006)
Kaushik, R., Krishnamurthy, R., Naughton, J.F., Ramakrishnan, R.: On the integration of structure indexes and inverted lists. In: SIGMOD, pp. 779–790 (2004)
Leis, V., Kemper, A., Neumann, T.: The adaptive radix tree: ARTful indexing for main-memory databases. In: ICDE, pp. 38–49 (2013)
Luo, C., Carey, M.J.: On performance stability in LSM-based storage systems. Proc. VLDB Endow. 13(4), 449–462 (2019)
Luo, C., Carey, M.J.: LSM-based storage techniques: a survey. VLDB J. 29(1), 393–418 (2020)
Luo, S., Chatterjee, S., Ketsetsidis, R., Dayan, N., Qin, W., Idreos, S.: Rosetta: A robust space-time optimized range filter for key-value stores. In: SIGMOD ’20, pp. 2071–2086 (2020)
Mathis, C., Härder, T., Schmidt, K., Bächle, S.: XML indexing and storage: fulfilling the wish list. Comput. Sci. - R &D 30(1), 1 (2015)
Matsunobu, Y., Dong, S., Lee, H.: MyRocks: LSM-tree database storage engine serving Facebook’s social graph. Proc. VLDB Endow. 13(12), 3217–3230 (2020)
Merkle, R.C.: A digital signature based on a conventional encryption function. In: CRYPTO, vol. 293, pp. 369–378 (1987)
Milo, T., Suciu, D.: Index structures for path expressions. In: ICDT, pp. 277–295 (1999)
Morrison, D.R.: PATRICIA - practical algorithm to retrieve information coded in alphanumeric. J. ACM 15(4), 514–534 (1968)
Morton, G.: A computer oriented geodetic data base; and a new technique in file sequencing. Tech. rep, IBM Ltd (1966)
Nickerson, B.G., Shi, Q.: On k-d range search with patricia tries. SIAM J. Comput. 37(5), 1373–1386 (2008)
O’Neil, P.E., Cheng, E., Gawlick, D., O’Neil, E.J.: The log-structured merge-tree (LSM-Tree). Acta Informatica 33(4), 351–385 (1996)
Orenstein, J.A., Merrett, T.H.: A class of data structures for associative searching. In: PODS, pp. 181–190 (1984)
Pietri, A., Spinellis, D., Zacchiroli, S.: The software heritage graph dataset: Large-scale analysis of public software development history. In: MSR, pp. 138–142 (2020)
Procopiuc, O., Agarwal, P.K., Arge, L., Vitter, J.S.: Bkd-tree: A dynamic scalable kd-tree. In: SSTD, pp. 46–65 (2003)
Ramsak, F., Markl, V., Fenk, R., Zirkel, M., Elhardt, K., Bayer, R.: Integrating the UB-Tree into a database system kernel. In: VLDB, pp. 263–272 (2000)
Rousseau, G., Cosmo, R.D., Zacchiroli, S.: Software provenance tracking at the scale of public source code. Empir. Softw. Eng. 25(4), 2930–2959 (2020)
Samet, H.: Foundations of multidimensional and metric data structures. Morgan Kaufmann series in data management systems. Academic Press (2006)
Schmidt, A., Waas, F., Kersten, M.L., Carey, M.J., Manolescu, I., Busse, R.: XMark: A benchmark for XML data management. In: VLDB, pp. 974–985 (2002)
Shanbhag, A., Jindal, A., Madden, S., Quiané-Ruiz, J., Elmore, A.J.: A robust partitioning scheme for ad-hoc query workloads. In: SoCC, pp. 229–241 (2017)
Shukla, D., et al.: Schema-agnostic indexing with Azure DocumentDB. PVLDB 8(12), 1668–1679 (2015)
Wellenzohn, K., Böhlen, M.H., Helmer, S.: Dynamic interleaving of content and structure for robust indexing of semi-structured hierarchical data. PVLDB 13(10), 1641–1653 (2020)
Wellenzohn, K., Böhlen, M.H., Helmer, S., Pietri, A., Zacchiroli, S.: Robust and scalable content-and-structure indexing (extended version). Tech. rep., CoRR (2022). https://arxiv.org/abs/2209.05126
Wellenzohn, K., Popovic, L., Böhlen, M., Helmer, S.: Inserting keys into the robust content-and-structure (RCAS) index. In: ADBIS, pp. 121–135 (2021)
Zhang, H., Lim, H., Leis, V., Andersen, D.G., Kaminsky, M., Keeton, K., Pavlo, A.: Surf: Practical range query filtering with fast succinct tries. In: SIGMOD ’18, pp. 323–336 (2018)
Zhong, W., Chen, C., Wu, X., Jiang, S.: REMIX: efficient range query for lsm-trees. In: 19th USENIX Conf. on File and Storage Technologies, (FAST’21), pp. 51–64 (2021)
Acknowledgements
We thank the anonymous reviewers and the editor for their insightful and valuable comments and for insisting on precision.
Funding
Open access funding provided by University of Zurich
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wellenzohn, K., Böhlen, M.H., Helmer, S. et al. Robust and scalable content-and-structure indexing. The VLDB Journal 32, 689–715 (2023). https://doi.org/10.1007/s00778-022-00764-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00778-022-00764-y












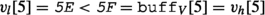 and
and  , thus all values of
, thus all values of 










