Leveraging range joins for the computation of overlap joins

Abstract

Joins are essential and potentially expensive operations in database management systems. When data is associated with time periods, joins commonly include predicates that require pairs of argument tuples to overlap in order to qualify for the result. Our goal is to enable built-in systems support for such joins. In particular, we present an approach where overlap joins are formulated as unions of range joins, which are more general purpose joins compared to overlap joins, i.e., are useful in their own right, and are supported well by B+-trees. The approach is sufficiently flexible that it also supports joins with additional equality predicates, as well as open, closed, and half-open time periods over discrete and continuous domains, thus offering both generality and simplicity, which is important in a system setting. We provide both a stand-alone solution that performs on par with the state-of-the-art and a DBMS embedded solution that is able to exploit standard indexing and clearly outperforms existing DBMS solutions that depend on specialized indexing techniques. We offer both analytical and empirical evaluations of the proposals. The empirical study includes comparisons with pertinent existing proposals and offers detailed insight into the performance characteristics of the proposals.

1 Introduction

Temporal support in relational database systems has gained significant interest during the last years, witnessed by temporal features in the SQL:2011 standard [5, 28, 32] as well as by the numerous database products that offer selected temporal features, such as IBM DB2 [36], Oracle [31], Teradata [1], Microsoft SQL Server [30], and PostgreSQL [35].

Joins are frequent and expensive operations in database systems. Most traditional joins focus on equality constraints for which efficient evaluation techniques exist, such as hash join, sort–merge join, or index join. Overlap joins for temporal data are based on inequalities, making them more demanding to compute efficiently. Not surprisingly, a number of studies have considered the efficient evaluation of overlap joins [6, 9, 12, 18, 34].

Example 1

Consider a relation $\mathbf {emp}$ that records employees working in a department $\text {DNo}$ over a time period $\mathbf {P}$, and a relation $\mathbf {dept}$ that records departments with number $\text {DNo}$ and name $\text {DName}$ that are valid over a time period $\mathbf {P}$. Following the SQL:2011 standard, we use half-open time periods, i.e., $\mathbf {P} =[B, E)$, where $B$ is included and $E$ is excluded, and $B< E$. $\text {DNo}$ forms a temporal primary key [21] in $\mathbf {dept}$, i.e., no tuples may have the same $\text {DNo}$ value and overlapping $\mathbf {P}$ value. This allows values associated with departments, e.g., the department name, to change over time. The SQL:2011 syntax for specifying the temporal primary key is PRIMARY KEY (DNo, P WITHOUT OVERLAPS). Similarly, $\text {DNo}$ in $\mathbf {emp}$ forms a temporal foreign key that references the temporal primary key in $\mathbf {dept}$, i.e., for each time point an entry in $\mathbf {dept}$ with the specific $\text {DNo}$ is required to exist. The SQL:2011 syntax for specifying the temporal foreign key is FOREIGN KEY (DNo, PERIOD P) REFERENCES dept (DNo, PERIOD P).

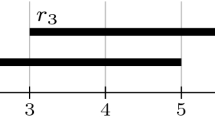
Figure 1a shows instances of the two relations. For example, the first tuple in $\mathbf {emp}$ states that Sam is working in department 2 from January through May. A graphical representation is shown in Fig. 1b, where the time periods are drawn as horizontal lines.

To retrieve employees together with the name of the department they work for, an overlap join is used, which can be expressed as follows in SQL.

The result of this temporal primary key-foreign key join is illustrated in Fig. 2 and contains all pairs of tuples that have the same department and overlapping time periods.

Fig. 1

Example relations $\mathbf {emp}$ and $\mathbf {dept}$ each with a period declaration over two attributes

To evaluate the above query, the DBMSs transform the predicate as follows [28]:

Fig. 2

Result of overlap join of $\mathbf {emp}$ and $\mathbf {dept}$ with equality on department number

This expression is challenging to optimize because it contains two inequality predicates over four different attributes (two from each relation). It is very difficult to find an efficient evaluation mechanisms for such predicates, since each of the four attributes is only bounded on one side, e.g., for $r.B < s.E$, r.B only has an upper bound s.E. Database systems do not offer efficient mechanisms to evaluate joins with such inequality predicates. Traditional join algorithms based on hashing are limited to equality predicates, and join algorithms based on sort–merge or sorted indices are inefficient since no total order on two independent attributes can be established.

Our goal is to support not just overlap predicates and equality predicates, but also their combination. This combination corresponds to temporal primary key-foreign key joins, which generalize conventional primary key-foreign key joins and occur frequently in databases where tuples are valid over a time period. We aim for a simple and general solution that a) facilitates the integration into an actual system, b) efficiently supports the combination of overlap and equality predicates, and c) permits general period boundaries, including closed, open, and half-open periods over discrete and continuous domains.

Our solution uses a novel and effective rewriting of the overlaps predicate into a disjunction of two range predicates¹:

The new predicate has two salient features. First, the two range predicates are disjoint, meaning that they do not produce duplicates in the result and, hence, can be evaluated independently followed by the (duplicate preserving) union of the two results. Second, the range predicates can be evaluated efficiently using sorting, since in each range predicate one attribute is lower and upper bounded, e.g., in $r.B \le s.B< r.E$, s.B has a lower and an upper bound to restrict the search space. Thus, in contrast to predicates that either only lower bound or only upper bound an attribute, a more efficient evaluation mechanism for joins with predicates that both lower and upper bound an attribute can be provided.

We devise a range–merge join algorithm that leverages these properties and joins a point attribute of one relation into a period attribute of the other relation. The overlap join is computed by performing the range join twice with swapped input relations (but the same sorting) followed by a union of the two results. In addition to enabling overlap joins, range joins are more general than overlap joins and thus have additional uses. For example, in click streams, range joins can be used to join users’ IP addresses with the IP address ranges of countries and states. Similarly, in shipping and packaging applications, they can be used to join package weights with weight ranges that determine their price. We show that our overlap join solution based on range joins is as efficient as state-of-the-art main-memory overlap join algorithms. Second, we show how the new predicate can be evaluated efficiently in an existing DMBS, using sorted indices, e.g., B+-trees. Further, we show that this solution is more efficient than join algorithms that rely on complex indexes, such as the R-tree, quadtree, and the relational interval tree.

Our range join solution is appealing from a systems perspective. In particular, in a systems setting where multiple components, e.g., query optimization, indexing, concurrency control, and recovery, interact, simplicity and generality of functionality are crucial since these properties reduce the overall systems complexity. Our index-based solution leverages existing capabilities of DBMSs, which is very attractive, as adding new capabilities is complex and not always possible.

To summarize, the technical contributions are as follows.

• We provide a new and simple rewriting of the overlaps predicate that transforms an overlap join into the union of two independent range joins.

• Our solution supports the combination of the overlaps predicate with nontemporal equality constraints.

• We provide a strict total order for period boundaries over discrete and continuous domains and prove its correctness. This enables support for all common interval definitions for period timestamps as well as relations where tuples might have period timestamps with different interval definitions.

• We show how the rewriting can be used to devise an efficient yet simple main memory algorithm for overlap joins based on the sort–merge join paradigm.

• We show how to evaluate overlap joins in DBMSs by taking advantage of B+-trees.

• An extensive empirical evaluation shows that (a) our main memory algorithm performs on par with the state-of-the-art stand-alone competitors and that (b) the evaluation of the overlap join using B+-trees in an existing DBMS outperforms the state-of-the-art systems competitors.

The rest of the paper is organized as follows. Sect. 2 reviews related work, and Sect. 3 introduces preliminary concepts. Section 4 proceeds to define general period boundaries and a corresponding strict total order. Section 5 introduces our new overlap join transformation while taking into account equality predicates and general period boundaries. This transformation is used in Sect. 6 to design a simple yet efficient main memory join algorithm. This section shows how the new overlap join can be evaluated in an existing DBMS using B+-tree indices. The results of the experimental evaluation are discussed in Sect. 7. Section 8 concludes and points to future work.

2 Related work

We organize the coverage of related work into index-based techniques that are readily available and can be supported directly by existing DBMSs, and pure join algorithms for the overlap join that require modifications to DBMSs in the form of new data structures or processing algorithms. At the end, we cover works that are closely related and can benefit from our approach.

Period timestamps can be represented as “one dimensional” rectangles in a 2D space with the period in one dimension and a point value in the other dimension. Therefore, overlap joins can take advantage of the spatial indices provided by some DBMSs. In the presence of equality attributes, the equality attribute can be integrated into the second dimension. Readily available spatial indices are based on the R-tree [4, 20] or Quadtree [17]. For instance, R-tree indices in PostgreSQL are implemented through the Generalized Search Tree (GiST) [26] index, which has a dedicated implementation for range types [10]² that are used to represent period timestamps. Indices based on the quadtree are implemented through the space-partitioned GiST (SP-GiST) [2] index type. Similarly to GiST, a specific implementation of SP-GiST for range types exists. When retrieving multiple tuples using an index, clustering is a prominent technique for increasing access performance. In contrast to sorted indices, such as B+-trees, clustering techniques for these spatial indices are much less effective.

The relational interval tree by Kriegel et al. [27] is an access structure for interval data that implements Edelsbrunner’s interval tree [15] on top of a standard DBMS. The approach uses two B+-trees to index the period timestamps in a relation, one according to an artificial key and the start point, and the other according to an artificial key and the end point. The artificial keys are assigned to period timestamps such that it is possible to arithmetically determine the set of keys that may overlap a period timestamp. The additional start or end point in the index is used to ensure that only matching period timestamps are retrieved. A query period is first transformed into two sets of keys, which in a second step are joined with the corresponding B+-trees using standard SQL. Join techniques based on the relational interval tree have been proposed by Enderle et al. [16], including the Index-Based Loop Join and several partition-based joins (Up-Down, Down-Down, and Up-Up depending on the tree traversal). Despite using efficient B+-trees, these joins suffer from substantial overhead (see query and query plan in Appendix C.2). In particular, the number of index joins is high (the union of two three-way joins and one two-way join), and the joins rely on unclustered accesses since they use two B+-trees per relation and a relation may only be clustered according to one of these.

Next, we review several recent studies on efficient evaluation algorithms for overlap joins that generally require that the DBMS is extended with new data structures or processing algorithms.

The timeline index by Kaufmann et al. [22, 23] is a main memory index that, in addition to other operations, supports joins with overlap predicates. The time line index stores for each tuple the start and end points in a sorted list. An overlap join is performed by scanning the index of two relations in an interleaved fashion, thereby storing tuples where the start point has been encountered (called active tuples) in a list. The active tuples are joined with tuples of the other relation that become active. Tuples are removed from the active tuple list when their end point is encountered. The bottleneck of this approach is the linked lists for maintaining the active tuples, which is expensive and has been shown to be outperformed by the LEBI join [34], described below, that adopts a gapless hash map.

The overlap interval partition (OIP) join algorithm by Dignös et al. [12] partitions the input relations into groups of tuples with similar timestamps, thereby maximizing the percentage of matching tuples in corresponding partitions. This yields a robust join algorithm that is not affected by the distribution of the data. The partitioning works both in disk-based and main-memory settings. The approach does not support equality predicates in combination with the overlap predicate and has been shown to be outperformed by the approaches described below.

The lazy endpoint-based interval (LEBI) join algorithm by Piatov et al. [34] extends the timeline index approach. Since, for each tuple that becomes active, all active tuples of the other relation must be scanned, a gapless hash map is introduced that keeps all active tuples in memory and is optimized for sequential reads. Additionally, lazy evaluation is used to minimize the number of scans of the active tuple map. This solution does not support equality predicates in combination with the overlap predicate and has been shown to be outperformed by the solution by Bouros and Mamoulis [6] described below.

The disjoint interval partitioning (DIP) join algorithm by Cafagna and Böhlen [9] creates disjoint partitions for each relation, where all tuples in a partition are temporally disjoint. To compute a temporal join, all outer partitions are sort–merge-joined with each inner partition. Since tuples in a partition are disjoint, the algorithm is able to avoid expensive backtracking. This algorithm is only efficient if few tuples in each input relation overlap since the number of partitions is proportional to the maximum number of overlapping tuples.

The O2iJoin by Luo et al. [29] performs an overlap join based on the O2i index, a flat two-level index, where the first level comprises a sorted array containing each endpoint of the relation being indexed and the second level contains inverted lists that approximate the nesting structure of the period timestamps in the relation. Periods may be stored in more than one inverted list. An overlap join is performed by scanning one relation in sorted order and joining all tuples using the O2i index of the other relation. The O2iJoin is much more complex to implement than the state-of-the-art approach by Bouros and Mamoulis [6] that offers comparable runtime.

Bouros and Mamoulis [6] propose a forward-scan (FS)-based plane sweep algorithm [8] for interval joins together with two optimizations that reduce the number of comparisons. First, a grouping step groups consecutive tuples of the same relation and allows to produce join results in batches, which avoids redundant comparisons. Second, a bucket indexing strategy divides the domain into tiles and places start points of periods into the corresponding tiles. This makes it possible to produce the results for all tuples of a tile that is completely covered by a period without comparisons. To further reduce the query time, a parallel evaluation strategy using a domain-based partitioning of the input relations is proposed. The FS algorithm with grouping and bucket indexing is shown to outperform previous approaches, such as the OIP Join [12], the LEBI Join [34] (based on the timeline index [22, 23]), and the DIP Join [9]. The authors further improve their approach [7] by introducing an enhanced loop unrolling, a decomposed data layout, a self-join optimization where pairs of joining tuples are only reported once, and parallelization techniques. We modify the overlap predicate, on which the FS algorithm by Bouros and Mamoulis [6, 7] is based, so that we can split the overlap join into two disjoint range joins. As a result, we only need to implement a join algorithm for range joins, which is a smaller and more general primitive for a DBMS that can be used for other purposes. Our solution computes overlap joins in combination with equality predicates and supports period timestamps with different interval definitions over discrete or continuous domains. Our approach has the same complexity as the FS algorithm, and our empirical study shows that using the smaller range join primitive does not sacrifice query performance. Further, all proposed optimizations (grouping, bucket indexing, and parallelization) are applicable to our solution. Finally, our overlap predicate can be computed efficiently using B+-tree indices in existing systems without altering the DBMS.

The predicates used to formulate the overlap conditions in the introduction are inequality predicates, and the overlap join can be considered as an inequality join. Khayyat et al. [24, 25] point out that contemporary RDBMSs use nested-loop joins for such cases. They propose the IEJoin that, for each relation and join attribute in the inequality, uses a sorted array to find values satisfying the inequality predicates more efficiently. To associate the values sorted in different orders from the same relation with the original tuples, they use permutation arrays and additional data structures to limit the search space. Despite the better efficiency than traditional join algorithms, the complexity of the IEJoin is still quadratic, i.e., ${\mathcal {O}}(n \cdot m)$, where n and m are the cardinalities of the two input relations. While Khayyat et al. focus on joins with general inequality predicates, our approach exploits the additional constraint that the inequalities come from periods, and thus we can device a rewriting that offers a more efficient execution scheme. Additionally, we support separate equality predicates in combination with overlap and range predicates, whereas they rely on traditional hash joins provided by a DBMS for cases where a join involves a separate equality predicate.

The temporal alignment framework [11, 13] provides efficient support for all temporal relational algebra operations over period timestamped data, including aggregations and all forms of join operations. The key idea is to preprocess the input relations depending on the desired algebra operation using two primitives to obtain an intermediate relation, where the tuples are timestamped with the periods of the result tuples. A nontemporal join over the intermediate relations with an appropriate equality constraint computes the result of a temporal join. By reducing temporal operations to their corresponding nontemporal counterparts, existing indexing techniques and query optimization techniques can be reused. This approach and other approaches that rely on SQL rewriting [1, 14] do not provide an efficient mechanism to calculate overlap or range joins, but instead rely on the DBMS, i.e., these approaches benefits from the efficient execution introduced in this paper.

Table 1 summarizes the approaches for the overlap join with information on implementation(s) used in the experiments, and whether the approach has been shown to be outperformed by another approach or has been shown to have the same performance. In our experimental study, we compare our approach with the approaches that have not been outperformed by others, and we also extend these approaches if they do not support equality predicates.

Table 1 Summary of approaches for the overlap join with information on implementations and whether they were shown to be outperformed by another approach

3 Preliminaries

A relational schema is represented as $R = (A_1,\ldots A_m)$, where the $A_i$ are attributes with domain $\varOmega _i$. A tuple r over schema R contains for every $A_i$ a value $v_i\in \varOmega _i$. A relation $\mathbf {r}$ over schema R is a finite multi-set of tuples over R. A relation may contain one or more period attributes, and we denote a relation as a temporal relation if it contains at least one period attribute. A period attribute is either composed of two attributes (according to the SQL:2011 standard) or is a single attribute (e.g., range types in PostgreSQL). Our goal is to provide efficient support for temporal database functionality as defined in SQL:2011, but we do so without constraining the number and type of time dimensions. For notational convenience, we use $\mathbf {P}$ to refer to the period attribute of interest and $B$ and $E$ to denote, respectively, its start and end period boundary. Next, $\circ$ denotes concatenation of tuples, i.e., for a tuple r with schema $R=(A_1,\ldots A_m)$ and a tuple s with schema $S=(A'_1,\ldots , A'_k)$, $r \circ s$ returns a tuple with schema $(A_1,\ldots , A_m, A'_1,\ldots A'_k)$ and the corresponding values from r and s. We use $Ov(\mathbf {P} _1, \mathbf {P} _2)$ to denote the overlap predicate between two time periods $\mathbf {P} _1$ and $\mathbf {P} _2$ that evaluates to true, iff $\mathbf {P} _1$ and $\mathbf {P} _2$ contain at least one common point. We write $a< b < c$ as an abbreviation for $a< b\ \wedge \ b < c$. For two relations $\mathbf {r}$ and $\mathbf {s}$, and a set of common attributes $\mathbf {C} =\{C_1, \ldots , C_k\}$, we use $\mathbf {r}.\mathbf {C} = \mathbf {s}.\mathbf {C}$ to denote the conjunctive equality over all attributes in $\mathbf {C}$. This provides a compact notation for equality joins without loss of generality since users can rename attributes. For cases when $\mathbf {C}$ is empty, we define $\mathbf {r}.\mathbf {C} = \mathbf {s}.\mathbf {C}$ to be true. We use $\uplus$ to denote the multi-set union, i.e., the duplicate-preserving union corresponding to SQL’s UNION ALL.

A range join is an equi-join in which the join predicate additionally specifies that a value from one relation falls into the range between two values from the other relation.

Definition 1

(Range Join) Let $\mathbf {r}$ and $\mathbf {s}$ be relations with schema R and S, respectively; let $\mathbf {C} \in R\, \cap \, S$ be the set of joint attributes; let attributes $B \in R$ and $E \in R$ represent a range (or period) in $\mathbf {r}$; and let attribute $X \in S$ be an attribute with the same domain as B and E. Further $\prec ^{S} \in \{<,\le \}$ and $\prec ^{E} \in \{<,\le \}$. A range join between $\mathbf {r}$ and $\mathbf {s}$ is expressed as:

$$\begin{aligned} \mathbf {r} \bowtie _{\mathbf {r}.\mathbf {C} =\mathbf {s}.\mathbf {C} \,\wedge \,\mathbf {r}.B\prec ^{S} \mathbf {s}.X \prec ^{E} \mathbf {r}.E} \mathbf {s} \end{aligned}$$

The comparison operators $\prec ^{S} \in \{ <, \le \}$ and $\prec ^{E} \in \{<,$ $\le \}$ specify whether X can be equal to $B$ and $E$, respectively.

An overlap join³ is an equi-join in which the join predicate additionally specifies that a period of one relation overlaps the period of the other relation.

Definition 2

(Overlap Join) Let $\mathbf {r}$ and $\mathbf {s}$ be temporal relations with schema R and S, respectively, and let $\mathbf {C} \subseteq R \cap S$ be the set of joint attributes. The overlap join between $\mathbf {r}$ and $\mathbf {s}$ is defined as:

$$\begin{aligned} \mathbf {r} \bowtie ^{Ov(\mathbf {r}.\mathbf {P}, \mathbf {s}.\mathbf {P})}_\mathbf {C} \mathbf {s} = \{r \circ s \mid {}&r \in \mathbf {r} \wedge s \in \mathbf {s} \wedge {} \\&r.\mathbf {C} \!=\! s.\mathbf {C} \wedge Ov(r.\mathbf {P}, s.\mathbf {P}) \} \end{aligned}$$

A summary of the most important notation is provided in Table 2.

Table 2 Frequently used notation

4 General period boundaries

Period timestamps are frequently represented as half-open periods of the form $[B, E)$ where $B< E$. In this section, we show how to support timestamps that have other boundary types over discrete or continuous domains. The period boundary types do not have to be fixed at the schema level. Instead, the boundaries are allowed to be dynamic, i.e., different tuples in a relation may have period values with different boundary types. This is, for instance, allowed for PostgreSQL range types [10, 35], where different tuples may use different period types selected among $[B,E)$ (default), $[B,E]$, $(B,E]$, and $(B,E)$. That is, the range data type allows period values with any combination of period boundary types.

Definition 3

(General periods) Let $\varOmega ^\mathrm{T}$ be a discrete or continuous time domain and let ’[’, ’]’, ’(’, and ’)’ be boundary types. A period timestamp is represented by a pair $\mathbf {P} = (B, E)$ where $B= (v _s,b _s)$ is the start boundary and $E= (v _e,b _e)$ is the end boundary with $v _s, v _e \in \varOmega ^\mathrm{T}$, $b _s \in \{\text {'['}, \text {'('}\}$, and $b _e \in \{\text {']'}, \text {')'}\}$.

Thus, a general period is represented by a start boundary $B= (v _s,b _s)$ and an end boundary $E= (v _e,b _e)$, each of which is composed of a boundary value and a boundary type. The type indicates whether the boundary value is included ($\text {'['}, \text {']'}$) in the period or is excluded ($\text {'('},\text {')'}$). For instance, the period $\mathbf {P} = ((3,\text {'['}), (9, \text {')'}))$ contains all values from 3 (included) to the largest value smaller than 9. In an integer domain, these are the values from 3 to 8. In the domain of real values, the period contains infinitely many numbers, and unlike for an integer domain where $(9, \text {')'}) = 8$, the end time point cannot be explicitly computed or represented. For brevity, we also write $B= \text {'[3'}$ for $\mathbf {P} = ((3,\text {'['})$ and $\mathbf {P} = \text {[3, 9)}$ for $\mathbf {P} = ((3,\text {'['}), (9, \text {')'}))$.

Example 2

Consider a start boundary $B=\text {'(3'}$ and an end boundary $E=\text {'4)'}$. In an integer domain, we have $B> E$ since $B$ represents the successor of 3, which is 4, and $E$ represents the predecessor of 4, which is 3. In the domain of real numbers, however, $B=\text {'(3'}$ is smaller than $\text {'4)'} = E$.

Similarly, we have $\text {'(2'}=\text {'[3'}$ in an integer domain, but $\text {'(2'}<\text {'[3'}$ in the domain of real numbers.

Note that typical implementations use flags to indicate whether a period boundary is a start or an end boundary and whether it is inclusive or exclusive. For instance, PostgreSQL uses one flag each.⁴ Since predicates over period timestamps compare start and end points, we must establish a total order among period boundaries. This is straightforward for discrete domains since all boundaries can be given explicitly so that all periods can be transformed into a uniform representation. In PostgreSQL, for instance, range types for integers (int4range) are internally converted to the default representation $[B,E)$ by using predecessors and/or successor functions, e.g., [3, 4] is converted to [3, 5). Establishing a total order among period start and end points is more challenging for continuous domains, where predecessors and successors cannot be represented explicitly.

We proceed to define an ordering $B_1 < B_2$ for general period boundaries $B_1$ and $B_2$ over continuous domains.

Definition 4

(Binary Relation < on General Period Boundaries over Continuous Domains) Let $\varOmega ^\mathrm{T}$ be a totally ordered continuous domain, and let $B_1 = (v_1, b_1)$ and $B_2 = (v_2, b_2)$ be two period boundaries with $v_1, v_2 \in \varOmega ^\mathrm{T}$ and $b_1, b_2 \in \{\text {'['}, \text {']'}, \text {'('}, \text {')'}\}$. The binary relation < on period boundaries $B_1 < B_2$ is defined using comparison operators on values of domain $\varOmega ^\mathrm{T}$ as follows.

The other comparison operators are defined accordingly, i.e., $B_1 > B_2 \equiv B_2 < B_1$, $B_1 \le B_2 \equiv \lnot (B_2 < B_1)$, $B_1 \ge B_2 \equiv \lnot (B_1 < B_2)$, and $B_1 = B_2 \equiv \lnot (B_1< B_2) \wedge \lnot (B_2 < B_1)$.

Example 3

Consider again the period boundaries $X=\text {'(3'}$ and $Y=\text {'4)'}$, represented as $(v_x,b_x)=(3,\text {'('})$ and $(v_x,b_x)=(4,\text {')'})$, respectively.

• To evaluate $X < Y$, Case 12 applies: $X< Y \equiv v_x< v_y \equiv 3 < 4 \equiv \text {true}$. For an integer domain (cf. Definition 5), we have $X< Y \equiv v_x+1< v_y-1 \equiv 3+1< 4-1 \equiv 4 < 3 \equiv \text {false}$.

• To evaluate $X > Y$, Case 15 applies: $X > Y \equiv Y < X \equiv v_y \le v_x \equiv 4 \le 3 \equiv \text {false}$. For a discrete integer domain in Definition 5, this evaluates to $Y < X \equiv v_y - 1 \le v_x \equiv 4-1 \le 3 \equiv 3 \le 3 \equiv \text {true}$.

Lemma 1

(Strict Total Order over Continuous Domains) The binary relation < in Definition 4 imposes a total order on period boundaries over their continuous linearly ordered domain.

The proof for Lemma 1 is provided in Appendix A.1.

In the following, whenever we compare period boundaries for continuous domains, we assume the comparison operators <, >, $\le$, $\ge$, and $=$ as stated in Definition 4 and Lemma 1. For discrete domains we use Definition 5 Appendix B.

5 Overlap join as a union of two range joins

5.1 A new rewriting of the overlaps predicate

We rewrite the overlaps predicate, $Ov(r.\mathbf {P}, s.\mathbf {P}) \equiv r.B\le s.E\wedge s.B\le r.E$, into a disjunction of two terms with disjoint results (see Sect. 5.2) so that they can be computed independently without producing duplicates. This forms the basis for the efficient join algorithms in Sects. 6.1 and 6.2.

Lemma 2

Assume two tuples r and s, each with a general period attribute $\mathbf {P} =(B,E)$ with starting boundary $B=(v_s, b_s)$ and ending boundary $E=(v_e, b_e)$, where $b_s\in \{\text {'['}, \text {'('}\}$, $b_e\in \{\text {']'}, \text {')'}\}$, and $B\le E$. The overlaps predicate for general boundaries can be expressed as:

$$\begin{aligned}&Ov(r.\mathbf {P}, s.\mathbf {P}) \equiv {}\\&\qquad (r.B\le s.B\le r.E) \vee (s.B< r.B\le s.E), \end{aligned}$$

where < and $\le$ are defined according to Definition 4.

The proof for Lemma 2 is provided in Appendix A.2.

In settings where the period type enforces particular boundary types, including [., .], [., .) (used by SQL:2011), (., .], and (., .), and all tuples use these boundary types, equivalent overlap predicates are provided in Lemma 7 in Appendix B.

5.2 Analysis

First, we prove that the two terms in the disjunction of the overlaps predicate in Lemma 2 are disjoint. That is, both terms cannot be true for a pair of tuples.

Lemma 3

Given two tuples r and s, each with a period attribute $\mathbf {P} = (B, E)$. The two terms $r.B\le s.B\le r.E$ and $s.B< r.B\le s.E$ are disjoint.

Proof

We have to show that the conjunction of the two terms is not satisfiable, i.e., the expression $r.B\le s.B\le r.E\wedge s.B< r.B\le s.E$ is unsatisfiable. This is the case since $r.B\le s.B$ and $s.B< r.B$ lead to a contradiction. $\square$

Lemma 3 forms the basis for evaluating the two terms $r.B\le s.B\le r.E$ and $s.B< r.B\le s.E$ of the overlaps predicate independently. Since the terms are disjoint, the corresponding result sets are disjoint and can be combined to obtain the overlaps join result without introducing duplicates.

Note that an equality predicate can be distributed to the two terms of the overlaps predicate in Lemma 2. This is important since overlap joins often include equality predicates (cf. Definition 2).

Theorem 1 summarizes the above results and shows that the overlap join between two relations with period timestamped tuples can be computed by two independent range joins between a time period and a time boundary, followed by a union with no need for duplicate removal.

Theorem 1

Let $\mathbf {r}$ and $\mathbf {s}$ be relations, each with a period attribute $\mathbf {P} =[B, E)$, and let $\uplus$ denote duplicate preserving union (SQL’s UNION ALL). The overlap join can be expressed as the union of two range joins:

$$\begin{aligned} \mathbf {r} \bowtie ^{Ov(\mathbf {r}.\mathbf {P}, \mathbf {s}.\mathbf {P})}_\mathbf {C} \mathbf {s} \equiv {}&\mathbf {r} \bowtie _{\mathbf {r}.\mathbf {C} =\mathbf {s}.\mathbf {C} \wedge \mathbf {r}.B\le \mathbf {s}.B\le \mathbf {r}.E} \mathbf {s} \uplus {}\\&\mathbf {r} \bowtie _{\mathbf {r}.\mathbf {C} =\mathbf {s}.\mathbf {C} \wedge \mathbf {s}.B< \mathbf {r}.B\le \mathbf {s}.E} \mathbf {s} \end{aligned}$$

Proof

The proof follows directly from Lemmas 2 and 3 and the distributivity of conjunctions over disjunctions. $\square$

6 Evaluation of overlap joins

6.1 A sort–merge-based algorithm

6.1.1 Approach

Our approach to compute overlap joins is based on range joins. Thus, we proceed to provide an efficient algorithm for computing range joins (cf. Definition 1) based on the sort–merge paradigm.

The range–merge join ($\mathrm {RMJ}$) algorithm is shown in Algorithm 1. It takes two sorted input relations, relation $\mathbf {r}$, with start point $B$ and endpoint $E$, and relation $\mathbf {s}$, with attribute X. In addition, it takes optional equality attributes $\mathbf {C}$ and two comparison operators that include or exclude the start and/or end time point in the range join (cf. Definition 1). Input relation $\mathbf {r}$ must be sorted according to equality attributes $\mathbf {C}$ and start time $B$, i.e., $(\mathbf {C}, B)$, and input relation $\mathbf {s}$ must be sorted according to equality attributes $\mathbf {C}$ and attribute X, i.e., $(\mathbf {C}, X)$. The algorithm first reads the first tuple from each relation. Then, as long as the two relations have not yet been fully read, one of the following steps is executed: skip outer, join match, or skip inner. Skip outer (lines 3–5) applies if the equality attributes $\mathbf {C}$ are smaller in r than in s. In this case, the current tuple r is skipped. If $\mathbf {C} =\{\}$, this step is never executed since we assume $r.\mathbf {C} =s.\mathbf {C}$ is true. Join match (lines 6–12) applies if the equality predicates $\mathbf {C}$ match and the start time of r is smaller than (or equal to) the value of attribute X of s, which might produce result tuples. We mark the position of the current tuple in $\mathbf {s}$, as it may also match subsequent tuples in $\mathbf {r}$. Then, the while-loop produces outputs for all subsequent tuples in $\mathbf {s}$ that satisfy the join predicate with r. When all matches for tuple r are produced, the next tuple in $\mathbf {r}$ is retrieved, and the position in $\mathbf {s}$ is set back to the marker. Skip inner (lines 13–14) applies if the equality attributes $\mathbf {C}$ of the current tuple r in $\mathbf {r}$ exceed those in $\mathbf {s}$ or if they are equal and the value of attribute X of s is smaller than the start time point in r. In these cases, we skip the current tuple in $\mathbf {s}$ and move to the next.

We can now use the $\mathrm {RMJ}$ algorithm to compute the overlap join according to Theorem 1 as follows, where R is the schema of relation $\mathbf {r}$, S is the schema of relation $\mathbf {s}$, and we use the start and end time point of one relation and the start point $B$ as attribute X of the other relation.

• 1. Sort $\mathbf {r}$ and $\mathbf {s}$ by $(\mathbf {C}, B)$

• 2. Compute:

  • $\mathrm {RMJ}$ ($\mathbf {r}$, $\mathbf {s}$, $\mathbf {C}$, $B$, $\le$, $B$, $\le$, $E$, $R \circ S$) $\uplus$

    $\mathrm {RMJ}$ ($\mathbf {s}$, $\mathbf {r}$, $\mathbf {C}$, $B$, <, $B$, $\le$, $E$, $R \circ S$)

Note that while for the overlap predicate, we have four attributes, i.e., start (B) and end (E) time points of both input relations, in each of the range predicates, we only have three, i.e., start and end time point of one relation and start of the other relation. Since we reverse the input in the second range join, overall all four attributes are used in the execution scheme, and recall from Theorem 1 that all result tuples of the range joins are part of the result of the overlap join.

Example 4

The overlap join from Example 1 can be computed as follows. First, we sort both input relations by $(\text {DNo}, B)$. Second, we combine the result of $\mathrm {RMJ} (\mathbf {emp}, \mathbf {dept}, \{\text {DNo} \}, B, \le , B, \le , E, R {\circ } S)$ and $\mathrm {RMJ} (\mathbf {dept}, \mathbf {emp}, \{\text {DNo} \}, B, <, B, \le , E, R {\circ } S)$, where R $= (\text {EName}, \text {DNo}, B, E)$ and $S = (\text {DName}, \text {DNo}, B, E)$ are the schemas of the two relations, respectively.

Figure 3a illustrates the processing of the first range–merge join. For the first tuple $e_1$ in sorted order from relation $\mathbf {emp}$, relation $\mathbf {dept}$ is scanned in sorted order from the beginning. Tuples $e_1$ and $d_1$ have the same department value, but the start of $e_1$ is not smaller or equal to the start of $d_1$; thus, $d_1$ is skipped in line 14 (indicated by “-”). Next, tuple $d_2$ is checked. This time, the department value of $e_1$ is smaller than that of $d_2$, so $e_1$ is skipped in line 5 (indicated by “x”), and tuple $e_2$ is fetched. This tuple is skipped for the same reason, and tuple $e_3$ is retrieved that is checked with the current inner tuple $d_2$. They have the same department, and the start time of $e_3$ is smaller than or equal to the start time of $d_2$ (note that we use $\le$ for the start time). Tuple $d_2$ is marked, and since it falls within the period of $e_3$, an output is produced (indicated by “$\checkmark$”), and the inner relation is advanced to tuple $d_3$ (lines 7–10). Tuple $d_3$ has the same department, but its start does not fall within $e_3$’s period. Thus, the next outer tuple $e_4$ is fetched (indicated by “$\bot$”), and the inner relation is restored to tuple $d_2$. Tuples $e_4$ and $d_2$ have the same department, but the start of $d_2$ is before the start of $e_4$, and $d_2$ is skipped. Next, $d_3$ is fetched. It matches $e_4$. Then tuple $d_3$ is marked, and the end of the inner relation is reached. The outer relation is advanced, and the inner relation is restored to tuple $d_3$. Since the outer relation’s end is reached, the algorithm terminates. Overall, this yields two result tuples: $(e_3, d_2)$ and $(e_4, d_3)$.

Fig. 3

Range–merge joins for our running example: $\checkmark$ indicates a match, $\bot$ the end of matches, - an inner skip, and x an outer skip

Other than swapping the two input relations, the processing of the second range–merge join $\mathrm {RMJ} (\mathbf {dept}, \mathbf {emp}, \{\text {DNo} \}, B, <, B, \le , E, R {\circ } S)$ is very similar and is illustrated in Fig. 3b. The main difference is that the comparison operator < is used for the start time instead of $\le$. Thus, for instance, for tuple $d_2$, the inner tuple $e_3$ is skipped, which avoids a duplicated result for $(e_3, d_2)$ that has already been produced in the previous range–merge join.

6.1.2 Complexity

Lemma 4

((Join Time) The complexity of the overlap join using $\mathrm {RMJ}$ is ${\mathcal {O}}(n \cdot \log n + m \cdot \log m + z)$, where n and m are the cardinalities of the two input relations and z is the result size.

Proof

The first step is to sort both relations. Assuming the size of relation $\mathbf {r}$ is n and the size of relation $\mathbf {s}$ is m, this results in ${\mathcal {O}}(n \cdot \log n + m \cdot \log m)$. Then we have to add the complexity of the $\mathrm {RMJ}$ algorithm (cf. Algorithm 1) that is composed of three conditions. Each condition advances the current tuple pointer of one relation by one, resulting in ${\mathcal {O}}(n + m)$. The while loop in lines 8–10 produces result tuples. Assuming we have z result tuples, the loop is executed ${\mathcal {O}}(z)$ times. In total, we get ${\mathcal {O}}(n \cdot \log n + m \cdot \log m) + {\mathcal {O}}(n + m) + {\mathcal {O}}(m + n) + {\mathcal {O}}(z) = {\mathcal {O}}(n \cdot \log n + m \cdot \log m + z)$. $\square$

6.1.3 Considerations for a system implementation

We proceed to cover considerations related to the system implementation of RMJ in PostgreSQL.

A key strength of our approach is the generality and the simplicity of integration into a database system, where implementation and maintenance of code come at a cost. To integrate RMJ into PostgreSQL we had to implement a sort–merge-based algorithm for range joins (Algorithm 1) that is similar to the traditional equality-based sort–merge join already present in these systems. This provides support for range joins as well as overlap joins. PostgreSQL implementations for sorting, reuse of sort orders, as well as exploiting sort orders of available indices to avoid sorting could be leveraged directly. Since the infrastructure for query rewriting and equivalence rules are mature core parts of these systems, the overlap join is a transformation of the overlap query expression into a query expression with two range joins (Theorem 1) that seamlessly fits into the existing query processing architecture.

Another crucial feature in a system implementation, in particular for a database optimizer, is cost estimates. Cost estimates for sorting as well as cardinality estimates for input and output over predicates are already available in these systems. The only missing estimates are cost estimates for the range–merge join (Algorithm 1). Database systems estimate the cost of execution algorithms based on their CPU and IO costs, and they mostly differentiate three cost factors: the CPU cost for attribute comparisons; the cost of sequential access to the data; and the cost of random access to the data.

Assuming that relations are not arbitrarily skewed, and that each tuple in $\mathbf {r}$ produces at least one result tuple, simple CPU (number of attribute comparisons) and IO (number of sequential and random accesses) cost functions are as follows:

$$\begin{aligned} c\_cpu(\mathrm {RMJ} (r, s)) =&(|\mathbf {r} |+|\mathbf {s} |) \cdot |\mathbf {C} | + {}\\&(|\mathbf {r} |+|\mathbf {s} |) \cdot (|\mathbf {C} | +1) + {}\\&(|\mathbf {z} |) \cdot (|\mathbf {C} | +1) \\ c\_io(\mathrm {RMJ} (r, s)) =&|\mathbf {r} | \cdot \text {seq access} + {}\\&|\mathbf {r} | \cdot \text {rand access} + {}\\&|\mathbf {z} | \cdot \text {seq access} \\&|\mathbf {s} | \cdot \text {seq access} \end{aligned}$$

In terms of CPU costs, the first term considers the attribute comparisons when tuples in the outer relation $\mathbf {r}$ or inner relation $\mathbf {s}$ are skipped after producing join results (line 4 in Algorithm 1), the second term considers the attribute comparisons when outer and inner relation have the same equality attributes (line 6 in Algorithm 1), and the third term considers the attribute comparisons needed to produce the result.

In terms of IO costs, the first term considers the sequential reading of the outer relation $\mathbf {r}$ (line 5 in Algorithm 1), the second term considers the backtracking in the inner relation $\mathbf {s}$ (line 12 in Algorithm 1), the third term considers the sequential reading of $\mathbf {s}$ to produce the result, and the last term considers the sequential reading of $\mathbf {s}$ for skipping tuples in $\mathbf {s}$ when they will no longer produce a result.

More advanced cost estimates are based on the cardinality estimates for the predicates (lines 4, 6, and 8 in Algorithm 1) and are part of future work.

6.2 Index-based evaluation for standard dbmss

6.2.1 Approach

Database management systems rely heavily on sorted indices for efficient query processing. One of the most important of such indices is the B-tree [3, 33]. DBMS implementations usually use B+-tree variants, where (in contrast to traditional B-trees) all keys reside in leave nodes, and the intermediate nodes form an index structure on the leaf nodes. To support efficient range searches, leaf nodes are connected by pointers.

While the approach in Sect. 6.1 requires to alter a DBMS and implement a new sort–merge-based algorithm for range joins, in this section, we show how, thanks to the transformation covered in Sect. 5, an overlap join can be formulated that can be evaluated efficiently in existing DBMSs, such as PostgreSQL or Oracle, using B+-trees. Typically, index-based joins are only used for very selective joins. However, for the overlap predicate, there are no efficient alternatives because traditional hash or sorted merge joins are inapplicable. For simplicity and in accordance with the SQL:2011 standard, we use static half-open periods of type $\mathbf {P} = [B, E)$ in the following. For general boundaries, we refer to Appendix C.1.

Lemma 5

An SQL:2011 overlap join query between two relations $\mathbf {r}$ and $\mathbf {s}$ with equality constraints over attributes $\mathbf {C} =\{C_1,\dots ,C_k\}$,i.e.,

is equivalent to the following SQL query:

Proof

The proof follows directly from Theorem 1 with the static predicate from Lemma 7 (case $\mathbf {P} = [v _s, v _e)$). $\square$

The SQL query is composed of the union of two range joins, each of which can be evaluated efficiently using standard indexing technologies available in database systems.

Example 5

By applying Lemma 5, the overlap join in our running example can be rewritten as follows:

Figure 4 shows the PostgreSQL query plan if both relations have a B+-tree index on the combined key $\text {DNo}$ and the tuple’s start time: index e_idx for relation $\mathbf {emp}$ and index t_idx for relation $\mathbf {dept}$. Each join of the query plan scans the outer relation and, for each tuple, applies a range scan on the inner relation using the index. A similar query plan would, for instance, be generated by Oracle DB, where the corresponding query plan terms are a NESTED LOOP between a TABLE ACCESS FULL and an INDEX RANGE SCAN.

Fig. 4

Query plan for the new rewriting approach with B+-trees

We use this example to illustrate how the B+-trees are used for the computation of the two range joins. Figure 5 shows the B+-trees for the two relations together with the index lookups that are indicated by colored lines. For this example, we use the tuple identifiers ($e_1$, ...) from Fig. 3; and for simplicity, we use binary trees, where left descendants store keys that are smaller than or equal to ($\le$) a node’s key, and the right descendants store keys that are larger than (>) a node’s key. Consider now the first join from the query plan in Fig. 4, where the outer relation $\mathbf {emp}$ with the four tuples $e_1$, $e_2$, $e_3$, and $e_4$ is scanned sequentially. For each tuple, the search path in the B+-tree is indicated by a colored line in Fig. 5a. For instance, for tuple $e_3=(Sam, 2, [1, 6))$ (blue line), we have to find all tuples in relation $\mathbf {dept}$ with $\text {DNo} =2$ and start time between 1 (included) and 6 (excluded). This is achieved by identifying the first leaf node with key larger than or equal to (2, 1) and then following the leaf pointer until a node with a key larger than or equal to (2, 6) occurs. All tuples encountered at the leaf level contribute to the result. Similarly, Fig. 5b shows the setting for the second join of the query plan, where $\mathbf {dept}$ is scanned sequentially and, for each of the three tuples $d_1$, $d_2$, and $d_3$, the index on $\mathbf {emp}$ is used to retrieve matching tuples.

Fig. 5

Index joins for our running example

Observe that the query processing here is very similar to the range–merge join described in the previous section. The essential difference is that the range–merge join finds the first matching tuple in the sort order using skipping and backtracking, whereas with the index, the first matching tuple is found by navigating through the levels of the index. The indices required for the range joins may seem specific to this particular join, but as we find in the experimental study, index creation is very efficient and thus may still be beneficial for the purpose of a single join. In addition, such an index is also beneficial to queries retrieving histories. For instance, in our example, such an index can be used to retrieve the history of changes or all employees of a department given its department number, since the department number is a prefix of the index.

The above rewriting of the overlap join, which is based on the new formulation of the overlaps predicate, is the first approach to processing the overlap join in DBMSs that requires only B+-tree indices, without any need for auxiliary tables, functions, or data structures.

6.2.2 Complexity

In this section, we analyze the complexity of our approach.

Lemma 6

((Join Time) The time complexity of the overlap join using B+-trees is ${\mathcal {O}}(n \cdot \log m + m \cdot \log n + z)$, where n and m are the cardinalities of the two input relations and z is the result size.

Proof

We have two independent joins (cf. Fig. 4).

Assuming that one of these joins is between relations with x and y tuples, we have: A scan of the relation with x tuples and ${\mathcal {O}}(x)$ index scans that each traverses the B+-tree on the relation with y tuples once. The height of the B+-tree is ${\mathcal {O}}(\log y)$, and the total is ${\mathcal {O}}(x \cdot \log y)$.

Both joins scan a total of ${\mathcal {O}}(z)$ leaf pages to retrieve ${\mathcal {O}}(z)$ result tuples, and the UNION ALL corresponding to an append has linear complexity ${\mathcal {O}}(z)$.

By substitution and summing up, we have: ${\mathcal {O}}(n \cdot \log m + m \cdot \log n + z)$. $\square$

7 Experimental evaluation

We proceed to evaluate the proposed predicate transformation that enables the computation of overlap joins using general purpose range joins. First, we compare our approach based on range–merge joins from Sect. 6.1 to the state-of-the-art stand-alone overlap join algorithm. Then, we study the computation of overlap joins in DBMSs using our index-based technique presented in Sect. 6.2.

7.1 Setup and datasets

The experiments were run on a machine with an Intel Xeon CPU X5550 with four cores @ 2.67GHz, 8192KB of cache, 50GB RAM, and a 64-bit Ubuntu SMP GNU/Linux with kernel version 3.13.0-117-generic. All stand-alone solutions were implemented in C by the same author and compiled with gcc version 4.8.4 using the following flags: -O3 -march=native -DNDEBUG -std=c99 -D_GNU_ SOURCE -Wall. The tuples used in the experiments contain a start time point and an end time point, as well as two other data attributes, one of which is used for equality predicates. Each result tuple is counted and undergoes a binary XOR operation on the period’s start point [6, 34] and data attributes. The result of the XOR is written to a referenced memory location to simulate a workload. This ensures that the C compiler cannot eliminate portions of the code. For the experiments with a standard DBMS, we use PostgreSQL 10.1 with its default configuration. To measure the execution times of queries, we use EXPLAIN (ANALYZE, TIMING FALSE), which reports the total execution time, excluding the time for sending the result to the client application. This provides a fair comparison for all approaches, since the produced result is the same in all cases. In the experiments, we use integers for the time domain, since one competitor ($\text {RIT}$) requires a discrete domain; and we use integers for the equality attributes, since some competitors ($\text {GiST}$, $\text {SPGiST}$, and $\text {PGIS}$) only support numerical values. For the other approaches, the experiments with other data types (e.g., floats or strings) are slower due to more expensive comparison operations, but the general trend remains the same.

The experiments use synthetic and real-world datasets. We use synthetic datasets to be able to vary a single parameter of the data distribution and keep all other parameters constant. The default parameter values for the synthetic dataset are summarized in Table 3. As the default, we use relations with 10 M tuples, a time domain of $[1,10^8]$, and uniformly distributed start points of periods from the time domain. The period durations are Zipfian distributed with skew parameter $\theta =1.7$ and maximum duration $10^6$. Low values of $\theta$ yield longer periods, and high values yield shorter periods. For the experiments with equality predicates, the default is 10 distinct uniformly distributed values. As workloads for the synthetic dataset, we perform overlap joins with and without equality constraints.

Table 3 Default parameter values for synthetic data

The following three real-world datasets and workloads are used in the experiments, where we use the same dataset for both input relations, as is done in previous work. The incumbent dataset [19] records the history of assignments of employees to departments over a 16-year period at the granularity of days with 83, 857 tuples and 583 departments. On average, a department has around 140 employees assigned with a minimum of 1, a maximum of 2251, and standard deviation of 251. As a workload, we compute the employees that work in the same department at the same time, i.e., an overlap join with equality on the department attribute. The flight dataset contains 684, 838 tuples, each recording the actual time period of a flight from a departure airport (FAP) to a destination airport (DAP). The data ranges over 1 month, has a granularity of minutes, and contains 365 departure and 365 destination airports. On average, 1876 flights started at a given airport, with a minimum of 4, a maximum of 34, 961, and standard deviation of 4, 502. As a workload, we compute the airplanes that are in transit at the same time and have the same destination airport. The webkit dataset [37] records the history of files in the svn repository of the Webkit project over a 13-year period at a granularity of seconds. The dataset captures 1, 547, 419 file changes for 483, 724 different files and 142, 903 revisions. The valid time represents the periods when a file was not changed. On average, 41 files are created within the same revision, with a minimum of 1, a maximum of 46, 153, and standard deviation of 4, 491. As a workload, we compute the evolution of files (files existing at the same time) that were initially created in the same revision. The distributions of time periods on the time line and their durations are shown in Fig. 6.

Fig. 6

Distribution of start time points and distribution of durations for the real-world datasets in % of the domain (histograms with 200 bins)

For the comparison with previous work that does not support equality predicates in combination with overlap predicates, we additionally report the experimental results for the workload on the real-world datasets without equality constraints, i.e., we compute a temporal Cartesian product.

We distinguish between stand-alone join algorithms that run in main memory and standard DBMS solutions that run inside a DBMS. The approaches that are compared are described with the respective experiments.

7.2 Stand-alone join algorithms

In the first set of experiments, we compare the proposed overlap join using range joins to the state-of-the-art approach bgFS [6].

7.2.1 Compared approaches

bgFS is the most recently proposed state-of-the-art competitor [6], a forward scan-based plane sweep algorithm with two optimizations, namely grouping and bucket indexing. The algorithm is similar to our approach based on range–merge joins, but needs only a single pass over the data. To achieve a fair comparison, we extend bgFS to support also equality predicates by integrating the equality attribute into the sort order (similar to our approach), which allows to skip attributes with different equality attributes in a sort–merge fashion (cf. lines 4, 5, 8, and 9 in Algorithm 1).

OMJ is our overlap join, which computes the union of two range–merge joins ($\mathrm {RMJ}$) as shown in Sect. 6.1. To achieve a fair comparison, we include the same optimization techniques grouping and bucket indexing, as used in bgFS, into our $\mathrm {RMJ}$.

7.2.2 Runtime evaluation

In this set of experiments, we are interested in examining how the overhead of our solution based on two more general purpose range joins compares to bgFS, which is specifically tailored for the overlap join, but requires only one join over the input relations.

First, we use the synthetic dataset and vary various parameters. The runtime results for the overlap join without equality predicates are shown in Fig. 7. For each experiment, we also report the number of result tuples. In Fig. 7a, we vary the number of tuples of the inner relation $\mathbf {s}$ from 10 to 200 M, while keeping the size of the outer relation $\mathbf {r}$ at the default value of 10 M tuples. In Fig. 7b, the sizes of both input relations vary from 10 to 100 M; and in Fig. 7c, the duration of period timestamps varies, which is controlled by the skew parameter $\theta$ of the ZIPF distribution. A low value of $\theta$ yields longer period timestamps, and a high value yields shorter period timestamps. The main observation is that the algorithms have comparable runtimes in all settings.

The main difference between the two approaches is in the order they scan and process the data. The bgFS approach scans both input relations in an interleaved fashion, thereby performing join matches and backtracking on the respective other relation. The $\mathrm {RMJ}$ approach performs two joins. In each join, one relation is scanned sequentially, and scanning and backtracking is performed only on the other relation. This improves data locality: the CPU cache can be utilized fully to store tuples of the single backtracking relation. This compensates for having to perform two joins. Whenever bgFS alternates between input relations, due to the start time point of the current tuple of one relation becoming smaller than the start time point of the current tuple in the other relation, it starts scanning for join matches in the other relation. This alternation between scans of the two relations results in the scanned tuples competing for CPU cache storage whenever a switch between the relations occurs. Tuples from one relation that were placed in the cache may be needed later on when backtracking is performed, but they may have been removed from the cache due to a scan of the other relation. The $\mathrm {RMJ}$ approach only scans one relation at a time, so the CPU cache can be devoted exclusively to storing tuples from that relation. This can be observed for data with longer time periods, where in contrast to smaller time period durations, larger jumps in the backtracking need to be performed. For instance, in Fig. 7c, the difference between bgFS and $\mathrm {OMJ}$ becomes even smaller with longer time periods.

Fig. 7

Overlap join without equality predicates on synthetic datasets

For the real-world datasets in Fig. 8, we obtain a similar picture. Since the runtimes for the three datasets are very different, the bar chart shows percentages instead of absolute values, where bgFS corresponds to $100\%$; additionally, the absolute values are shown in the plot. The large runtime of the overlap join on the webkit dataset is due to its output of 556, 428 million result tuples, i.e., approx. 23% of the Cartesian product. As a reference, a single CPU instruction per output tuple on our 2.67 GHz machine increases the runtime by 160 s in total. We can observe that OMJ, which is based on two general purpose range joins, is as efficient as the state-of-the-art algorithm. Also for the real-world datasets, we observe the effect of data locality of $\mathrm {RMJ}$ as compared to bgFS that performs backtracking on both relations at the same time. For the datasets with very small time period durations (cf. Fig. 6), bgFS is slightly more efficient, while for the webkit dataset that contains more tuples with longer durations, $\mathrm {OMJ}$ is more efficient.

Fig. 8

Overlap join without equality predicates on real-world datasets

We repeated the experiments for the case when the overlap join includes equality predicates. The results for the synthetic datasets and using different parameter settings are shown in Fig. 9, while the results for the real-world datasets are shown in Fig. 10. We see that in the presence of equality attributes, our technique based on range merge joins is able to provide the same performance as the state-of-the-art overlap join algorithm.

Fig. 9

Overlap join with equality predicates on synthetic datasets

Fig. 10

Overlap join with equality predicates on real-world datasets

The main conclusion from the above experiments is that the proposed OMJ algorithm is as efficient as the state-of-the-art algorithm bgFS, although OMJ performs two scans over the data, whereas bgFS scans the input relations only once. From a database implementation perspective, OMJ has the advantage that only a range–merge join ($\mathrm {RMJ}$) needs to be implemented that is more general purpose, while the OMJ can be implemented as an execution strategy or equivalence rule that uses range joins.

7.3 Approaches for standard DBMSs

In this section, we analyze the evaluation of overlap joins in existing DBMSs using the SQL query in Lemma 5 and indexing techniques that are available in DBMSs. For all experiments, we use PostgreSQL.

7.3.1 Compared approaches

OMJ $^{\text {i}}$ is our approach with a B+-tree on each relation (cf. Lemma 5 in Sect. 6.2.1). For a fair comparison with the other approaches, we use a user-defined data type⁵ over range types for the start and end time points instead of scalar values. This data type for range boundaries and its sort order⁶ also need to consider inclusion/exclusion for each comparison (cf. Sect. 4). The data type and its associated comparison functions have been implemented as an external dynamically linked C library in PostgreSQL. This incurs some overhead compared to using simple scalar values and is only introduced to enable a fair comparison, since other indices covered (except RIT and PGIS) also work on PostgreSQL range types.⁷ For the clustered experiments we cluster the relation based on the created B+-tree.

RIT is the RI-Tree Up-Down Join [16] based on the relational interval tree [27]. It uses one index table and two B+-trees for each input relation. We extended this approach to handle equality predicates by prepending the equality attributes to the index tables and including the equality into the queries. For the experiments with clustered indices, we cluster the index tables according to one of the indices.

GiST is a one-dimensional R-tree implementation for range types in PostgreSQL using GiST.⁸ [26]. The index supports multi-key indexing but no scalar attributes for the equality predicate. In the experiments with equality predicates, we transform the equality attribute into a range type of duration 1, index it together with the time period, and use an additional overlap predicate for join processing. This index type also supports clustering.

BtGiST is the PostgreSQL extension btree_gist,⁹ which is very similar to GiST, but additionally supports scalar attributes and equality predicates. This approach is only used in experiments with equality predicates, since it is the same as GiST when no equality predicate is used. Also this index type supports clustering.

PGIS is an R-tree implementation for 2D rectangle geometries of PostGIS 2.5 using PostgresSQL’s GiST.¹⁰ We use one dimension of the rectangles for the time dimension and the other for the equality predicate. For fair comparison, and since we are not interested in general geometries, we use the less expensive overlaps predicate && instead of ST_Intersects. Specifically, && uses bounding boxes, and we avoid recalculation of the overlap for the geometry in the bounding box. This index also supports clustering.

SPGiST is a quadtree implementation for range types in PostgreSQL using SP-GiST.¹¹ This index transforms periods into two-dimensional points that are then indexed. PostgreSQL in some cases chooses the index on the smaller relation, which results in higher query times. Thus, we create the index separately on the two relations and report the smaller runtime. The index does not support multi-keys, so for the experiments with equality predicates, we use 2D boxes,¹² which are then transformed into four-dimensional points and indexed by a quadtree. Currently, SPGiST does not support clustering. For the sake of comparison on clustered data, we modify this approach such that it can use index-only scans. This approach for the clustered experiments does not fetch the data from the relation but only provides the joined time periods of the data that are found directly in the index. To ensure that no data is fetched, we perform a VACUUM operation before the query, which ensures that no data is accessed and also check that Heap Fetches (accesses to the data relation) is 0.

The SQL statements for creating indices and queries as well as the corresponding query plans for all approaches are reported in Appendix C.

7.3.2 Runtime for different indexing techniques

Overlap Join Without Equality Predicates. In the next experiment, with results shown in Fig. 11, we analyze the behavior of different indexing techniques. The outer relation $\mathbf {r}$ contains 10 M tuples, and the size of the inner relation $\mathbf {s}$ varies from 1 to 100 M tuples. All other parameters are kept at their default values. $\text {RIT}$ and $\text {GiST}$ are by far the slowest. $\text {OMJ}^{\text {i}}$ is faster than $\text {SPGiST}$, although it also needs to scan the larger relation, while $\text {SPGiST}$ can use the smaller as the outer relation and retrieve matching tuples from the larger relation using the index. When one relation is approximately 15 times larger than the other, $\text {SPGiST}$ becomes slightly faster than $\text {OMJ}^{\text {i}}$. When the relations are clustered, $\text {OMJ}^{\text {i}}$ is much faster than $\text {SPGiST}$. Recall that for the clustered experiments, since $\text {SPGiST}$ clustering is not supported, the number reported is only the time for an index only scan, i.e., the time needed to fetch the actual data is not reported. We also investigated the space consumption and creation time for the indices of the different approaches and provide the numbers for the default parameters (cf. Table 3). $\text {OMJ}^{\text {i}}$ requires two indices of size 214 MB each, for a total of 428 MB. $\text {GiST}$ requires one index of size 458 MB, $\text {SPGiST}$ requires 609 MB, and $\text {PGIS}$ requires 589 MB. The total index creation time is 35 s for $\text {OMJ}^{\text {i}}$, 6 min for $\text {GiST}$, 2 min for $\text {SPGiST}$, and 4 min for $\text {PGIS}$. $\text {RIT}$, needing more than an hour for index creation and requiring an index space of 850 MB, is by far the slowest and most space-consuming approach. This is due to the iterative calculations (for which we use PostgreSQL’s procedural language PL/pgSQL) and additional tables (for which we use SQL) that need to be created. We also experimented with noninteger data types. We use the datasets with default parameters and divide the start and end time by 1000 to measure the overhead of continuous domains for the same result size. For $\text {GiST}$ and $\text {SPGiST}$, we use ranges of numerics, i.e., PostgreSQL’s arbitrary precision numbers, and obtain runtimes that increase by 94% and 100%, respectively, due to the more expensive comparison operations and larger (variable) size data type as compared to integers. For our approach, we use scalars instead of range types for this experiment to also be able to include the overhead caused by the float (double precision, but constant 8 byte size) data type that is not supported by range types. The runtime increases by 25% as compared to using integers when using arbitrary precision numerics; and for the float data type, the overhead is 4%. The overhead of range types, that also need to consider the boundaries, as compared to scalars for the same data type is around $20\%$.

Fig. 11

Overlap join without equality predicates for the synthetic dataset

In Fig. 12, we vary the sizes of both relations from 1 to 50 M. The performances of $\text {RIT}$ and $\text {GiST}$ degenerate very quickly, $\text {SPGiST}$ is more efficient, but $\text {OMJ}^{\text {i}}$ is by far the best approach. In particular for the clustered case, $\text {OMJ}^{\text {i}}$ beats $\text {SPGiST}$ by almost an order of magnitude.

Fig. 12

Overlap join without equality predicates on synthetic dataset, varying number of tuples of both relations

The next experiment, with results shown in Fig. 13, analyzes the impact of the durations of the tuples’ timestamps. For this, we vary the parameter $\theta$ of the Zipf distribution for the timestamp duration: smaller values of $\theta$ produce many long tuples, and larger values of $\theta$ produce shorter tuples. We can observe that for smaller values of $\theta$ (i.e., longer timestamps), the result size is much larger since many more tuples overlap. Again, $\text {OMJ}^{\text {i}}$ is the fastest approach. $\text {GiST}$ is the slowest for small values of $\theta$, but it outperforms $\text {RIT}$ for larger values.

Fig. 13

Overlap join for synthetic data, varying $\theta$ of the Zipf distribution for the period duration

Overlap Join With Equality Predicates. We proceed to analyze the overlap join with additional equality predicates. Our approach and the relational interval tree do not have any restriction on the type of equality attribute. GiST and SPGiST, on the other hand, only support numerical values. For GiST, we use a multi-key attribute composed of two range types, one for the period timestamp and one of duration 1 for the equality attribute. For SPGiST, we use a type box (rectangles) in a similar way.

In the first experiment, we vary the number of tuples of the inner relation $\mathbf {s}$. The number of distinct values for the equality attributes is set to the default 10. The results are shown in Fig. 14. All approaches turn out to be faster when additional equality attributes are used. The gap between OMJ$^{\text {i}}$ and SPGiST is larger than in the case without equality attributes (cf. Fig. 11). Also for the case of equality predicates, we investigated the space consumption and index construction time for the different approaches and provide the numbers for the default parameters (cf. Table 3). $\text {OMJ}^{\text {i}}$ requires two indices of size 301 MB each, for a total of 602 MB. $\text {GiST}$ requires one index of size 680 MB, $\text {SPGiST}$ needs 733 MB, $\text {PGIS}$ needs 518 MB, and $\text {BtGiST}$ needs 560 MB. In terms of index creation time, $\text {OMJ}^{\text {i}}$ takes 37 s for both indices and is by far the fastest approach. The other approaches require several minutes. More specifically, $\text {GiST}$ takes 7 minutes, $\text {SPGiST}$ takes 2 minutes, $\text {PGIS}$ takes 4 minutes, and $\text {BtGiST}$ takes 10 minutes. Also in this case, $\text {RIT}$ takes more than an hour and needs 1.2GB of disk space.

Fig. 14

Overlap join for synthetic data by varying the cardinality of the inner relation

In Fig. 15, we show the results when varying the cardinality of both relations from 1 to 100 M tuples. OMJ$^{\text {i}}$ is by far the fastest. In particular, for the clustered case, it outperforms the other approaches by more than an order of magnitude. All other approaches degenerate quickly.

Fig. 15

Overlap join with equality predicates for synthetic data by varying the cardinality of both relations

Impact of Equality Predicates. To analyze the impact of the selectivity of the equality predicate, we vary the number of distinct values for the equality attributes from 5 to 100—Fig. 16 reports the findings. All approaches benefit from a more selective equality predicate, which is mainly due to the smaller output. None of the competitors has an increased gain that is sufficient to outperform OMJ$^{\text {i}}$. As a comparison, a hash join (faster than a merge join for this case) requires almost 6 h for 1000 distinct values in the equality attributes, which is much more selective than the up to 100 we report here.

Fig. 16

Overlap join with equality predicate for synthetic data by varying the number of distinct equality attributes

The experiment in Fig. 17 shows the effect of the number of equality predicates on the performance. To ensure that the runtime is unaffected by the size of the output, we ensure that all joins have the same result size. This is done by using the same values for all attributes that are involved in the equality predicates. For OMJ$^{\text {i}}$ and RIT, adding an additional equality predicate to the join simply implies adding the attribute in the equality predicate to the index. For the GiST approach, a new range type attribute is added to the index since the index supports multi-key attributes. For PGIS, the dimensionality of the index is increased by one, e.g., one equality predicate and the period timestamp yield a 2D index. PGIS only supports structures up to 3D, so we can only compare to these. SPGiST does not support multi-key attributes, and there is no 3D structure. Thus, we can only show the result for one equality predicate.

For PGIS with two equality predicates, we stopped the execution of the query after it ran for several days. We then reduced the number of input tuples for this approach and performed a join between two relations with 1 M tuples each instead of 10 M tuples. Even for this smaller input, PGIS took more than two days to compute the query with two equality predicates.

Fig. 17

Overlap join with equality predicates for synthetic data by varying the number of equality predicates

Real-World Datasets We proceed to report on experiments with real-world datasets. Since RIT took much longer than all other approaches we omit it from the plots and provide the numbers in the text. Additionally, we provide the runtime of the fastest equi join (hash join or merge join) that exploit the equality predicate and then filter out the matches that do not overlap.

We first consider the incumbent dataset. The results are shown in Fig. 18, and the number of result tuples is about 10 M. RIT is by far the slowest, taking 115 and 113 s for the nonclustered and clustered case, respectively. For better visibility, we omit it from the plot. A hash join took 11.5 s. OMJ$^{\text {i}}$ is fastest for the nonclustered and clustered case. With this dataset, SPGiST is slightly slower than GiST for the nonclustered case. Recall that due do no clustering mechanism for SPGiST for the clustered case, we only provide the numbers of an index-only join that does not fetch the full data.

Fig. 18

Overlap join with equality on the department attribute for the incumbent dataset

Next, results for the flight dataset are shown in Fig. 19, where the number of result tuples is 66 M. For this dataset, RIT took about 14 minutes, with almost no difference between the nonclustered and clustered cases. A hash join took 30 min. OMJ$^{\text {i}}$ is the fastest approach in both cases.

Fig. 19

Overlap join on FAP-DAP for the flight dataset

Finally, the results for the experiments with the webkit dataset are shown in Fig. 20, where the result encompasses 2056 M tuples. Also for this dataset, OMJ$^{\text {i}}$ is the fastest approach. A sort–merge join (faster than hash join for this dataset) took 30 min, and RIT took almost 12 h.

We also measured the index creation time for our approach for these datasets. The total creation time for both B+-tree indices is 180 ms for incumbent, 2.4 s for flight, and 5.4 s for webkit. Hence, our approach when including the creation time for both B+-tree indices in the join remains faster than the other approaches with indices already available. This suggests that even creating the indices for the purpose of the join is beneficial.

Fig. 20

Overlap join on files created at the same time for the webkit dataset

7.3.3 Buffer management

In the next experiment in Fig. 21, we analyze the buffer management by measuring the number of pages that are fetched from the buffer and from disk using PostgreSQL’s EXPLAIN (ANALYZE, BUFFERS) feature. We are particularly interested in understanding to which extent clustering the data helps reduce disk accesses. The buffer size is set to its default value of 128 MB. We keep the size of the outer relation $\mathbf {r}$ at 10 M tuples and vary the number of tuples in the inner relation $\mathbf {s}$ from 1 to 100 M. Figure 21a shows the number of pages fetched during the join from the buffer, disk, and in total when none of the two relations is clustered according to the index. We can see that the numbers of disk fetches and buffer fetches are very similar. As a reference, our relation with 10 M tuples consists of 63,695 pages (497 MB), and our relation with 100 M consists of 636,950 pages (4.97 GB). Figure 21b shows the result when both relations are clustered according to the index. We can observe that the number of disk accesses is very low (1.7 M when $\mathbf {s}$ contains 100 M tuples) and that almost all accesses can be served by the buffer (even with a small buffer of 128 MB). Figure 21c, d shows the result when only relation $\mathbf {r}$ or only relation $\mathbf {s}$ is clustered according to its index. As expected, the impact of clustering on the number of disk fetches is higher when the larger relation is clustered. This is because the index scans on that relation dominate the disk accesses.

Fig. 21

Page access (buffer access and disk access) for the entire join

To gain further insight, we measure the number of page accesses separately for the two range joins, which are evaluated as index nested loop joins (cf. Fig. 4). Figure 22 shows the result for the first join with a sequential scan on $\mathbf {r}$ and an index scan on $\mathbf {s}$. We can observe from Fig. 22b that clustering both relations substantially reduces the number of disk fetches as well as the total number of page accesses when compared to the case where none of the two relations is clustered as shown in Fig. 22a. Figure 22c shows the result when only relation $\mathbf {r}$ is clustered and then scanned sequentially. While the total number of page accesses is the same as for the nonclustered case, the number of disk accesses is reduced, although $\mathbf {r}$ is read only once. The reason is that by clustering $\mathbf {r}$ (i.e., sorting the relation physically on the start time), consecutive tuples in $\mathbf {r}$ match similar tuples in $\mathbf {s}$. Hence, many pages of the index and the relation that are needed for consecutive tuples in $\mathbf {r}$ remain in the buffer. Figure 22d shows the result when clustering only relation $\mathbf {s}$, on which the index scan is performed. We can observe that compared to clustering $\mathbf {r}$, the numbers of disk and buffer accesses are reduced. The reason is that consecutive tuples fetched from the index reside in the same disk page and can be read together. Neither of the individual clusterings achieves the reduction of disk accesses achieved when both relations are clustered. This indicates that clustering both relations has a synergetic effect, i.e., clustering $\mathbf {r}$ reduces disk accesses and clustering $\mathbf {s}$ further reduces disk accesses as well as the total number of buffer accesses.

Fig. 22

Page access for the first range join of the overlap join

Figure 23 analyzes the number of page accesses for the second range join that performs a sequential scan on $\mathbf {s}$ and an index scan on $\mathbf {r}$. The number of page accesses is higher compared to the first join in Fig. 22 since relation $\mathbf {s}$ is larger than relation $\mathbf {r}$. However, the main insight is the same: clustering has a huge impact on the number of disk fetches, resulting in very efficient buffer management.

The result of the overlap join in Fig. 21 is the sum of the two range joins in Figs. 22 and 23.

Fig. 23

Page accesses for the second range join of the overlap join

7.4 Summary

In summary, our approaches based on range joins offer state-of-the-art performance for computing the overlap join. In particular, our stand-alone join technique, OMJ, that is based on applying the $\mathrm {RMJ}$ algorithm twice is on par with the state-of-the-art in all cases, while $\mathrm {RMJ}$ is a more general-purpose, primitive operator for a database system. Our index-based approach, OMJ$^{\text {i}}$, outperforms the previous state-of-the-art indexing approaches for the overlap join that are available in current DBMSs in almost all settings. The only exception is settings where one relation contains very few tuples. Traditional join algorithms based on equality, such as hash and sort–merge joins, are not competitive for the overlap join as they exclusively rely on the equality predicate, which may not be selective for historical data. When the data is clustered, OMJ$^{\text {i}}$ enables very effective buffer management out of the box and outperforms the other approaches by up to an order of magnitude.

8 Conclusion and research directions

We provide a new approach to computing overlap joins as the union of two disjoint range joins. We show how to support relations where tuples are associated with periods that have different period boundary types, and we show how the overlap join approach can support separate, additional equality conditions as needed for primary key/foreign key joins in temporal databases. These two aspects have been largely ignored in previous work. We provide two execution schemes for the overlap join, one that processes tuples in sort–merge fashion and one that uses sorted indices and that can be embedded readily into a DBMS. We show that the proposed sort–merge-based algorithm offers performance on par with the state-of-the-art and, being a smaller primitive, can also evaluate range queries. The DBMS-based evaluation scheme substantially outperforms proposals based on more complex indexing techniques available in some DBMSs.

Several pertinent directions for future work exist. First, it is of interest to develop cost and cardinality estimation techniques for the proposed rewriting. This is a prerequisite for achieving more accurate DBMS query optimization. Second, complete integration of the range–merge join approach into PostgreSQL is an important next step. Third, it is of interest to extend the proposed rewriting of the overlap join to support multiple time dimensions.

Appendices

A Proofs

1.1 A.1 Proof for Lemma 1

Proof

The proof proceeds by considering $B_1 < B_2$ for each of the 16 boundary combinations. In the first step, we transform period boundaries into symbolic values that may or may not be representable. In the second step, we transform the binary relation < on symbolic values into binary relations on values that are representable. We prove that in all cases, we get the order stated in Definition 4.

1st step: We use the symbolic notation $v^-$ for $v\text {)}$, v for $v\text {]}$ and $\text {[}v$, and $v^+$ for $\text {(}v$. For continuous domains, $v^-$ is smaller than v by an infinitely small amount and cannot be represented explicitly. Similarly, $v^+$ is larger than v by an infinitely small amount and cannot be represented explicitly. Replacing boundary types with $v^-$ and $v^+$, we get:

For a continuous domain, we have the time line order

$$\begin{aligned} \langle \ldots , v-\epsilon , \ldots , v^-, v, v^+, \ldots , v + \epsilon , \ldots \rangle , \end{aligned}$$

where, for a representable precision of $\epsilon$, only $v-\epsilon$, v, and $v+\epsilon$ can be represented, while $v^-$ and $v^+$ cannot.

2nd step: We show that after the transformation to representable values, we get the order given in Definition 4.

• Cases 1, 6, 11, and 16: Since the two boundary types are equal (e.g., $B_1 = (v_1$ and $B_2 = (v_2$), we trivially get $B_1< B_2 \equiv v_1 < v_2$.

• Cases 2 and 5: Since for closed boundary types the boundaries are the values $v_i$ (i.e., $[v_i = v_i$ and $v_j] = v_j$), we trivially get $B_1< B_2 \equiv v_1 < v_2$.

• Cases 3 and 7: Since the largest number smaller than $v_2^+$ is $v_2$, we transform $v_1 < v_2^+$ to $v_1 \le v_2$.

• Cases 13 and 14: Since the smallest number larger than $v_1^-$ is $v_1$, we transform $v_1^- < v_2$ to $v_1 \le v_2$.

• Cases 4 and 8: Since the smallest representable value larger or equal to $v_2^-$ is $v_2$, we transform $v_1 < v_2^-$ to $v_1 < v_2$.

• Cases 9 and 10: Since the largest representable value smaller or equal to $v_1^+$ is $v_1$, we transform $v_1^+ < v_2$ to $v_1 < v_2$.

• Case 12: Using Case 4 from above, we transform $v_1^+ < v_2^-$ to $v_1^+ < v_2$. Next, using Case 9 from above, we transform $v_1^+ < v_2$ to $v_1 < v_2$.

• Case 15: Using Case 3 from above, we transform $v_1^- < v_2^+$ to $v_1^- \le v_2$. Next, since the smallest or equal representable value that is larger or equal to $v_1^-$ is $v_1$, we get $v_1 \le v_2$.

$\square$

1.2 A.2 Proof for Lemma 2

Proof

We show that the new predicate is equivalent to the overlaps predicate. We start with the predicate from Lemma 2:

$$\begin{aligned} (r.B\le s.B\le r.E) \vee (s.B< r.B\le s.E) \end{aligned}$$

We transform it into a binary form:

$$\begin{aligned} r.B\le s.B\wedge s.B\le r.E\vee s.B< r.B\wedge r.B\le s.E\end{aligned}$$

We then apply De Morgan’s law to each of the two terms of the disjunction:

$$\begin{aligned} \lnot (r.B> s.B\vee s.B> r.E) \vee \lnot (s.B\ge r.B\vee r.B> s.E) \end{aligned}$$

Next, we apply De Morgan’s law to the entire expression:

$$\begin{aligned} \lnot \big ((r.B> s.B\vee s.B> r.E) \wedge (s.B\ge r.B\vee r.B> s.E)\big ) \end{aligned}$$

Then we distribute disjunction over conjunction:

$$\begin{aligned} \lnot (&(r.B> s.B\wedge s.B\ge r.B) \vee (r.B> s.B\wedge r.B> s.E) \vee {}\\&(s.B> r.E\wedge s.B\ge r.B) \vee (s.B> r.E\wedge r.B> s.E)) \end{aligned}$$

The first disjunct, $r.B> s.B\wedge s.B\ge r.B$, is unsatisfiable and hence can be removed. The second disjunct, $r.B> s.B\wedge r.B> s.E$, is equivalent to $r.B> s.E$, which implies $r.B> s.B$ since by definition, $s.B\le s.E$. The third disjunct, $s.B> r.E\wedge s.B\ge r.B$, can be replaced by $s.B> r.E$. The fourth disjunct can be removed because we now have $r.B> s.E\vee s.B> r.E\vee (s.B> r.E\wedge r.B> s.E) \equiv r.B> s.E\vee s.B> r.E$ due to the equivalence $a \vee b \vee (b \wedge a) \equiv a \vee b$.

This yields

$$\begin{aligned} \lnot (r.B> s.E\vee s.B> r.E) \equiv r.B\le s.E\wedge s.B\le r.E\end{aligned}$$

$\square$

B Period boundaries of discrete domains and static periods

For completeness, we provide the total order over period boundaries for discrete domains. For discrete domains, it is sufficient to express the boundaries $(v, \text {'['})$ and $(v, \text {']'})$ on the time line as v, while $(v, \text {')'})$ and $(v, \text {'('})$ are expressed as the predecessor ($v-1$) and successor ($v+1$) of v, respectively. For simplicity and unification with previous approaches, we apply the equivalences $v_1 < v_2 + 1 \equiv v_1 \le v_2$, $v_1 - 1 < v_2 \equiv v_1 \le v_2$, $v_1 - 1< v_2 - 1 \equiv v_1 < v_2$, and $v_1 + 1< v_2 + 1 \equiv v_1 < v_2$.

Definition 5

(Strict Total Order - Discrete Domains) Let $\varOmega ^\mathrm{T}$ be a discrete domain, and let $B_1 = (v_1, b_1)$ and $B_2 = (v_2, b_2)$ be period boundaries with $v_1, v_2 \in \varOmega ^\mathrm{T}$ and $b_1, b_2 \in \{\text {'['}, \text {']'}, \text {'('}, \text {')'}\}$. Further, let $v-1$ and $v+1$ be the predecessor and successor of v, respectively. The total order on period boundaries $B_1 = (v_1, b_1) < (v_2, b_2) = B_2$ is defined as follows:

The other comparison operators are defined accordingly, i.e., $B_1 > B_2 \equiv B_2 < B_1$, $B_1 \le B_2 \equiv \lnot (B_2 < B_1)$, $B_1 \ge B_2 \equiv \lnot (B_1 < B_2)$, and $B_1 = B_2 \equiv \lnot (B_1< B_2) \wedge \lnot (B_2 < B_1)$.

When considering relations where all tuples have the same period type, but not necessarily only of the form $[v _s, v _e)$, we can use Definition 4, Definition 5, and Lemma 2 to derive overlap predicates that are specific to that type. The time domain can be discrete or continuous, and we use a function p(.) to unify both in a single formula.

Lemma 7

Let two tuples r and s be given, each with a nonempty period attribute $\mathbf {P}$ of the form $[v _s,v _e)$ with $v _s < v _e$, $[v _s,v _e]$ with $v _s \le v _e$, $(v _s,v _e]$ with $v _s < v _e$, or $(v _s,v _e)$ with $p(v _s) < v _e$ over a discrete or continuous domain.

Furthermore, let $p:\varOmega ^\mathrm{T}\rightarrow \varOmega ^\mathrm{T}$ be the following function:

$$\begin{aligned} p(v) = {\left\{ \begin{array}{ll} v-1 &{} \varOmega ^\mathrm{T} \text { is discrete}\\ v &{} \varOmega ^\mathrm{T} \text { is continuous} \end{array}\right. } \end{aligned}$$

The overlap predicate can be expressed as follows:

$$\begin{aligned}&Ov(r.\mathbf {P}, s.\mathbf {P}) \equiv \\&\;\; {\left\{ \begin{array}{ll} (r.v _s \le s.v _s< r.v _e) \vee (s.v _s< r.v _s< s.v _e) &{} \text {if } \mathbf {P} = [v _s, v _e) \\ (r.v _s \le s.v _s< r.v _e) \vee (s.v _s< r.v _s< s.v _e) &{} \text {if } \mathbf {P} = (v _s, v _e] \\ (r.v _s \le s.v _s \le r.v _e) \vee (s.v _s< r.v _s \le s.v _e) &{} \text {if } \mathbf {P} = [v _s, v _e] \\ (r.v _s \le s.v _s< p(r.v _e)) \vee {}\\ \qquad (s.v _s< r.v _s < p(s.v _e)) &{} \text {if } \mathbf {P} = (v _s, v _e) \end{array}\right. } \end{aligned}$$

Note that for the first three static period definitions, the overlap predicate is the same for continuous and discrete domains. For the last period definition (’(.,.)’), there is difference, and we use function p(v) to encode this difference.

Proof

The proof follows directly from Lemma 2 and transforming comparisons on general period boundaries into comparisons of period values using Definition 4 for continuous domains or Definition 5 for discrete domains. For instance, for the case $\mathbf {P} = [v _s, v _e)$, the transformation is the same for continuous and discrete domains, and we have:

$$\begin{aligned} (r.B\le s.B\le r.E) \vee&(s.B< r.B\le s.E) \equiv \\&\big ((r.v _s, \text {'['}) \le (s.v _s, \text {'['}) \le (r.v _e, \text {')'})\big ) \vee \\&\big ((s.v _s, \text {'['}) < (r.v _s, \text {'['}) \le (s.v _e, \text {')'})\big )\\ \end{aligned}$$

We transform the first comparison $(r.v _s, \text {'['}) \le (s.v _s, \text {'['})$ into $\lnot \big ((s.v _s, \text {'['}) < (r.v _s, \text {'['}\big )$ and apply Case 1 of Definition 4, resulting in $\lnot (s.v _s < r.v _s)$ and thus $r.v _s \le s.v _s$. The second comparison $(s.v _s, \text {'['}) \le (r.v _e, \text {')'})$ is transformed into $\lnot \big ((r.v _e, \text {')'}) < (s.v _s, \text {'['})\big )$. Next, applying Case 13 of Definition 4, we get $\lnot (r.v _e \le s.v _s)$ and thus $s.v _s < r.v _e$. For the third comparison $(s.v _s, \text {'['}) < (r.v _s, \text {'['})$, we apply Case 1 and get $s.v _s < r.v _s$. The fourth comparison $(r.v _s, \text {'['}) \le (s.v _e, \text {')'})$ is transformed similarly to comparison 2 (with reversed tuples), and we get $r.v _s < s.v _e$. The final predicate results in:

$$\begin{aligned} (r.v _s \le s.v _s< r.v _e) \vee (s.v _s< r.v _s < s.v _e) \text { for } \mathbf {P} = [v _s, v _e) \end{aligned}$$

The proofs for the other cases follow the same procedure. $\square$

C SQL for approaches in standard DBMS

Here we report the SQL statements for PostgreSQL used for indexing and querying for all approaches compared in the experiments in Sect. 7.3. In all cases, unless stated otherwise, we perform an overlap join between relations and on period attribute (of type range type) . For the overlap join with equality predicates, we use an additional attribute .

1.1 C.1 OMJ$^{\text {i}}$

We first consider the rewriting approach from Sect. 6.2. For a fair comparison with other approaches adopting range types, we implemented two user-defined functions and that extract a user-defined period boundary data type (value and inclusive/exclusive bound) from a range type, and we define their corresponding comparison operators according to Definitions 4 and 5.

Indexing:

Query and query plan:

1.2 C.2 RIT

Next, we consider the RI-Tree Up-Down Join [16]. For this approach, we use two additional tables with already computed fork nodes for each tuple and instead of computing the function each time it is needed, and we index these tables. Similarly, we use tables and with pre-computed left and right queries of fork nodes instead of using more expensive user-defined functions. Additionally, since range boundaries would substantially increase the domain of fork nodes (inclusive and exclusive), we exclusively use static integer boundaries [ts, te] for this approach. When no equality condition exists, is omitted from the indexing and querying.

Indexing:

Query and query plan:

1.3 C.3 GiST

Next, we consider the standard PostgreSQL approach for indexing and querying range types using the general inverted search tree (GiST). This approach allows multiple range types, so the equality attribute is transformed and indexed as a range type of duration 1. When no equality condition exists, is omitted from indexing and querying.

Indexing:

Query and query plan:

1.4 C.4 BtGiST

We proceed to consider the PostgreSQL approach for indexing and querying range types using the btree_gist extension. Unlike the standard GiST, this approach allows additional equality attributes. When no equality condition exists, this approach is the same as GiST.

Indexing:

Query and query plan:

1.5 C.5 PGIS

Next, we consider the R-tree implementation for 2D rectangle geometries of PostGIS 2.5. One dimension of the 2D rectangle is used for the time dimension, and the other is used for the equality predicate. For this approach, we create two new relations and that contain an attribute of type (2D box) encoding the time dimension and the equality predicate. When no equality condition exists, is set to 1 for all tuples, since PostGIS does not support a period data type, but only 2D boxes.

Indexing:

Query and query plan:

1.6 C.6 SPGiST

Finally, we cover the standard PostgreSQL approach for indexing and querying range types using the space partitioned general inverted search tree (SP-GiST). As for PGIS, we use tables and that contain 2D rectangles of type that encode the equality predicate and the time dimension. When no equality condition exists, this indexing mechanism supports range types that can be used directly, similarly to GiST.

Indexing:

Query and query plan: