An innovative EFD using FBG pressure sensors for ship seakeeping

Abstract

This paper examines the acquisition of the measurement data of the spatial distribution of unsteady pressure on a ship advancing in waves. The purpose of the study is to investigate the reliability of the pressure data obtained by the unprecedented experiment and to provide experimental data of unsteady pressure which can be used for validation of arbitrary computation methods. The optical fiber sensing technology, so-called FBG (fiber Bragg gratings) sensing, is employed as the pressure sensors. In the experiment, 379 FBG pressure sensors (version 7; the latest version) in total are attached to the port side surface of ship model and also ordinary strain-type pressure sensors are embedded in the starboard side for validating reliability of FBG pressure sensors by comparing both results. In addition to the pressure distribution, measurement is made for unsteady hydrodynamic forces such as added mass, damping coefficients, and wave exciting forces, and also for ship motions and added resistance. Most of the measurement is repeated at least five times for each condition, and results of measured pressures are evaluated with mean value and standard deviation. Regarding the added resistance, the distribution for estimating added resistance is also extracted from obtained pressure distribution and its pressure contour is illustrated to show visually which hull region affects the added resistance significantly. Validation of the measured pressure with FBG pressure sensors is carried out also by integrating measured pressures over the ship model surface and comparing it with forces directly measured with load cells. The measured pressure distribution is compared with typical calculation results with the Rankine panel method in frequency domain to demonstrate usefulness of the spatial pressure data for validating the calculation method. Through these studies, it is confirmed that the measured unsteady pressures with FBG pressure sensors are accurate enough and valuable as the validation data for any calculation method.

1 Introduction

The research on ship seakeeping has a long history, and numerous studies have been carried out. The strip method, which is still widely used in the practical design, was invented by Korvin-Kroukovsky [1] and Watanabe [2], and arranged in easily usable style by Salvesen, Tuck, and Faltinsen [3]. The slender-ship theory was developed by Ogilvie and Tuck [4] and completed as the unified theory by Newman [5], Sclavounos [6] and Kashiwagi [7]. Thereafter the fully three-dimensional numerical methods in the frequency domain such as the Green function method (GFM) [8, 9] and the Rankine panel method (RPM) [10,11,12,13,14,15,16] were presented in response to the development of the high-performance computers, and the methods have been extended to the time-domain analyses [17,18,19,20,21,22,23,24,25,26,27]. Recently the applications of CFD, which has matured in the research field of ship resistance and propulsion, can be found in some papers [28,29,30,31,32,33,34]. Besides, the development of a fully nonlinear potential method is attempted [35, 36] to calculate fast and solve nonlinear problems instead of CFD.

Most of these estimation methods on ship seakeeping are validated by comparing their numerical results with experimental results such as hydrodynamic forces and/or ship motions; that is, integrated physical quantities. Perhaps, for this reason, we have not seen many results that drastically surpass the strip method. For instance, it may be experienced by many researchers that the strip method sometimes gives more accurate results than the advanced methods if the results are simply compared with hydrodynamic forces and/or ship motions. If the results are compared with local physical quantities, the advanced methods should give better agreement with experiments than the strip method because they take account of three-dimensional effects or some nonlinearities. In view of such background, Ohkusu [37,38,39] and some of the authors [40,41,42,43] have adopted the unsteady wave pattern generated by the ship as one of the local physical quantities, and have carried out a comparison between numerical and measured results. The advantage of the use of an advanced method has been made clear by estimating unsteady wave patterns, which cannot be estimated by the strip method with sufficient accuracy. Although it is easy to measure the unsteady wave pattern with high accuracy and with low cost, which physically indicates the pressure distribution over the free surface, it is difficult to measure in the vicinity of a ship except for ship-side waves. If the unsteady pressure can be measured directly and spatially over the hull surface, it will be the most desirable data for both researchers and designers of ships. And it will drive greater innovation in EFD (experimental fluid dynamics) whose progress seems to be somewhat late compared with CFD.

Up to date, the pressure on the surface of the ship model has been measured using the differential-pressure-type sensors [44,45,46] or strain-type sensors(e.g., [47]). The former cannot be used for the measurement near the free surface where the sensor goes into and out of the water. The latter cannot be set at bow and stern where the breadth of the ship model is too narrow for the sensor to be embedded, and requires one strain meter for each sensor. Both sensors are not appropriate for the multipoint measurement such that the total number of measurement points reaches 300 $\sim$ 400.

This paper proposes a new pressure measurement system that enables us to measure the pressure closely at 400 points simultaneously and to obtain the spatial distribution of the unsteady pressure on the ship model with typical size of $L_{pp}=2.4$ m. The affixed-type FBG (Fiber Bragg Grating) pressure sensor [48,49,50,51] which is one of the optical fiber technologies is employed as the pressure sensor. The latest version, version 7 (ps1000-v7, CMIWS Co., Ltd.) [52], is used. For the validation of the FBG pressure sensors, the ordinary strain-type pressure sensors (SHVR-50k for 50kPa, NTL) are also embedded in the ship model along some ordinates, and the measured results are compared with those obtained by the FBG pressure sensors. In addition, the measurement accuracy by FBG pressure sensors is also evaluated by obtaining the mean value and standard deviation from the repeatedly measured results.

Two types of experiments are conducted. One is free-motion test carried out by towing the ship model in regular head waves and measuring ship motions and added resistance. Another is the forced-motion test carried out by oscillating a ship model forcibly in heave/pitch motions while towing the model in calm water, and the added mass and damping coefficients are measured. Also, wave exciting forces are measured by restraining the motion of the model and towing it in regular head waves. In all cases, the pressure distribution is synchronously measured. In addition to verifying the FBG pressure sensors by comparison with the strain-type pressure sensors described above, another validation of FBG pressure sensors is examined. The resulting spatial pressure distribution is integrated over the hull surface as if it were a numerically calculated pressure distribution, and the obtained forces are compared with the forces measured directly by the load cells or strain gauges.

Regarding the added resistance, ‘added-resistance integrand’, which is the integrand distributed on the wetted surface for estimating the added resistance, gives useful information suggesting which part of the hull dominates the added resistance significantly. Some of the distribution of added-resistance integrand obtained from measured pressure is illustrated to show visually the hull parts that are most sensitive to the added resistance. Numerical calculation by means of RPM is performed and obtained unsteady pressures are compared with measured results. This benchmark test shows how the present measured unsteady pressure distribution is useful for the validation of the numerical method.

2 Principle of FBG sensor

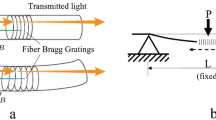
Figure 1 illustrates the principle of a fiber Bragg grating (FBG). The FBG is a type of distributed diffraction grating etched into the fiber core that reflects a particular wavelength of light, called Bragg wavelength, and transmits all others. If the spacing between reflectors changes due to the load, temperature, and the acceleration, the Bragg wavelength also changes. Therefore, the load, etc.  can be measured by measuring the change of Bragg wavelength. It is also possible to arrange many FBGs with different spacing of Bragg grating along one optical fiber, so the simultaneous multipoint measurement can be conducted (see Figs. 2 and 3).

Figure 2 shows a structure of the FBG pressure sensor of ver. 7. The size of the sensor is sufficiently small with diameter of 8.6 mm (pressure-sensitive part: 5 mm), length of 14.8 mm, and thickness of 0.6 mm. Two FBGs with different spacing of Bragg grating are contained in one sensor and they are fixed to the diaphragm so that they do not interfere with each other. The value measured by the temperature-sensitive part is used to eliminate the influence of the temperature on the result measured by the pressure-sensitive part.

Fig. 1

Principle of FBG pressure sensor

Fig. 2

Structure of FBG pressure sensor of ver. 7

Fig. 3

Serial connection of FBG pressure sensor

The initial type of FBG pressure sensor, whose principle is the same as that described above but its size and shape were different, was first applied to measure the steady pressure distribution at bow and stern parts for a ship model with $L_{pp}=4.0$ m [48, 49]. The total number of sensors was only 40 points. Thereafter the improvement and the test for the FBG pressure sensor were repeated and recently reached the latest completed version which enables to measure the steady pressures at 146 points at a time [50, 51]. Note that this sensor is available only for the measurement of steady pressure with a large ship model.

In 2015, a compact-type FBG pressure sensor almost similar to Fig. 2 was newly developed to measure the unsteady pressures on a smaller ship model with $L_{pp}\cong 2.5$ m. The sensor version was ver. 1. The measurement using 28 FBG pressure sensors and 14 strain-type pressure sensors succeeded in clearly illustrating the contour plots of the unsteady pressure distribution near the bow part [53]. The sensor was improved year by year and tested repeatedly while increasing the number attached to the ship model [53,54,55].

The present version of the FBG pressure sensor in Fig. 2 is ver. 7 in which the span is longer compared with the previous version, and the stiffness of the frame and the diaphragm is higher to stabilize the measured value. As a result, the influence of temperature interference can be greatly reduced compared to the previous version. The details are described in the reference [52]. A sensor with a rating of 100 kPa is used in the range of -1 kPa to +4 kPa with an interrogator Si255, and its resolution is 4 Pa (=0.4 mmAq). This rating is large enough to measure gauge pressures even for larger size models such as $L_{pp}=5\sim 6$ m. These FBG pressure sensors can be easily attached to the surface of ship model by double-sided tape. For the data acquisition, two interrogators (Hyperion Si255-16-ST(1000Hz)-160-DP, Micron Optics, Inc., software; Enlight) are used in the present pressure measurement using 379 FBG pressure sensors.

3 Towing tank experiment

3.1 Measurement of pressure distribution

Experiments for measuring the pressure distribution were conducted in the towing tank at RIAM (Research Institute for Applied Mechanics), Kyushu University in 2021. The length, breadth, and depth of the towing tank are 65 m, 5 m and 7 m, respectively. The test ship model is the RIOS bulk carrier that is used in RIOS (Research Initiative on Oceangoing Ships) [56] system. The principal particulars, body plan, and photo of the model are shown in Table 1, Figs. 4 and 5, respectively.

Table 1 Principal particulars of RIOS bulk carrier

Table 2 Target input amplitude and wave steepness $H/\lambda$ for measuring pressure distribution in each test condition ($\lambda$: wavelength. $L\equiv L_{pp}$, K: wavenumber, $K_e$: wavenumber obtained from encounter circular frequency $\omega _e(=\omega +KU)$, H: wave height). The output of incident wave amplitude is about $\pm 10$% of the input $\zeta _a$

Fig. 4

Body plan and positions of pressure sensors. $\varphi$ on bow flare means the line shown by angle, measured from ordinate 9.98 with the stem line ($y=0$) defined as 90$^\circ$. Black circles show sensors above still water and white circles below still water

Fig. 5

Photo of RIOS bulk carrier

For measuring the pressure distribution, 379 FBG pressure sensors ver. 7 (ps1000-v7, CMIWS Co., Ltd.) shown in Fig. 2 were used. While this sensor is considerably improved regarding temperature interference effects [52], the sensor is not completely free from the effect like other conventional sensors. Therefore, the measurements using them were conducted when the temperature difference between air and water was within ±2 $^\circ$C in which the temperature interference effects are small. In addition, the calibration tests of the FBG pressure sensors [52, 57] were carried out each time when the temperature difference changed from the one in the previous calibration test by 2 $^\circ$C. The principle, features including the repeatability, the calibration method for the FBG pressure sensor, and some notes are written in [52] in detail. FBG pressure sensors of 379 in total were attached in 33 sections on the port side as shown on the left of Fig. 4. They also can be seen as black dots in Fig. 5. The pressure data at 379 points were logged through two interrogators. Besides FBG pressure sensors, 19 strain-type pressure sensors (SHVR-50k for 50kPa, NTL) were embedded in three sections on the starboard side for checking the accuracy of outputs by FBG pressure sensors. Their position is shown on the right of Fig. 4.

Fig. 6

Coordinate system and definition of positive direction of motions, forces, and moment

Experiments conducted roughly consist of two tests. One is the measurement of longitudinal ship motions and added resistance (referred to as free-motion test in this paper). This test was carried out by towing the model at constant forward speed in regular head waves (corresponds to $\chi =180$ degrees in Fig. 6). Another is the measurement of unsteady hydrodynamic forces using a forced motion device. This test was carried out by towing the model in calm water. Periodical heave and pitch motions are forced individually and the added mass and damping coefficients are measured (referred to as forced-heave test and forced-pitch test). The amplitude of heave and pitch motions are 10 mm and 1.364 , respectively. Wave exciting forces are also measured by towing the model in regular head waves with the motion of model restricted (referred to as diffraction test). In all tests, the towing speed is 0.18 in Froude number based on $L_{pp}$, and the conditions of incident waves are shown in Table 2. The steepness of incident waves is set to be small so that $H/\lambda < 1/30$ is satisfied (H; wave height, $\lambda$; wavelength). The measurement system is written in [57, 58] in detail. The sampling rate of the data is 200 Hz for the present measurements.

The coordinate system used in the experimental analysis is shown in Fig. 6. The moving coordinate system, o-xyz advancing at the same speed as towing speed U, and the body-fixed coordinate system $\bar{o}$-$\overline{x}\overline{y}\overline{z}$ are defined. Both origins are put at the midship centerline and the ship model is oscillating in surge, heave, and pitch directions periodically with encounter circular frequency around the origin o. Periodical surge, heave, and pitch motions are expressed by $\xi _1(t)$, $\xi _3(t)$ and $\xi _5(t)$, respectively.

3.2 Measurement of ship-side wave profiles

The ship-side wave profiles are very important in the analysis of measured pressure, providing precise timing when the pressure sensor goes into and out of the water surface. Ship-side wave profiles were measured in 2021 and 2022 independently of the pressure measurement using another model with the same hull form and the same size. They were measured by handmade wave probes with capacitance shield wire [59] along the 31 sections illustrated on the left of Fig. 4 except for two bulb sections. The ship-side wave data were obtained in all conditions in Table 2 and towing tests in calm water.

4 Analysis of experimental data

4.1 Ship-side wave profiles

There are two important roles for the use of ship-side wave profiles. The pressure sensors around the still waterline go into and out of water periodically due to ship motions and waves. One role is to detect whether the sensor is exposed to air or not and make the pressure zero when the sensor is in air. This treatment is not necessary if the sensor size is quite small. However, both the present FBG pressure sensor and strain-type pressure sensor have diameters of about 5 mm, and sometimes the measured pressure does not show zero correctly even when the center of the sensor is exposed to air. The effect of surface tension of the water also can be one of the reasons. Another role is to know precisely the boundary of the wetted surface. This role is important to obtain the hydrodynamic forces correctly by integrating measured pressures over the wetted surface, which is explained later in Sect. 4.3.

As already mentioned in Sect. 3, ship-side wave profiles are measured in experiments that are not the same as the tests for getting the pressure distribution. Therefore, assuming repeatability of the experiments of ship-side wave and pressure under the same condition, obtained data of ship-side wave profiles are expanded to the Fourier series, and obtained coefficients are saved for use in the pressure analysis carried out later. The ship-side wave elevation $\zeta (\overline{x};t)$ measured at section $\overline{x}$ along the ship-side can be written in the Fourier series expansion as follows:

$$\begin{aligned} \zeta (\overline{x};t)=\zeta ^{(0)}(\overline{x}) +\textrm{Re}\sum ^N_{n=1} \bigl \{ \zeta _c^{(n)}(\overline{x})-i\zeta _s^{(n)}(\overline{x}) \bigr \}\,e^{i n\omega _e t} \end{aligned}$$

(1)

where $\omega _e$ is the encounter circular frequency. Note that the ship-side wave $\zeta (\bar{{\varvec{x}}};t)$ is defined as the wave elevation from $\overline{z}=0$ to the wave surface, which is measured with capacitance shield wires attached to the hull. The incident regular wave $\zeta _I(t)$ measured at $\overline{x}=0$ (midship) can be written as

$$\begin{aligned}{} & {} \zeta _I(t)\cong \textrm{Re}\Bigl \{ (\zeta _{oc}-i\zeta _{os})\,e^{i\omega _e t} \Bigr \}\nonumber \\{} & {} \hspace{7mm} =\textrm{Re}\Bigl \{ \zeta _{o}\,e^{i\omega _e t} \Bigr \} =\textrm{Re}\Bigl \{ \zeta _{a}\,e^{i\varphi }\,e^{i\omega _e t} \Bigr \} \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \zeta _{o}\equiv \zeta _{oc}-i\zeta _{os} =\zeta _a\,e^{i\varphi }\, \nonumber \\{} & {} \zeta _a=\sqrt{\zeta _{oc}^2+\zeta _{os}^2} \,,\quad \varphi =\tan ^{-1}(-\zeta _{os}/\zeta _{oc}) \end{aligned}$$

(3)

omitting small higher harmonic terms. Here, $\zeta _{oc}$ and $\zeta _{os}$ are cosine and sine components of the 1st harmonic in the Fourier series expansion of measured incident wave. $\zeta _a$ means the incident wave amplitude. The time reference in the experimental analysis is set to $t=0$ when the crest of the incident wave reaches the midship $\overline{x}=0$.

To match the phase of the time-dependent term in the ship-side wave (1) to this reference, that term is divided by the complex amplitude $\zeta _o$ of the incident wave. This corresponds to shifting the phase concerning time. In the case of the 1st-harmonic component of (1), it becomes as follows:

$$\begin{aligned} {\zeta _c^{(1)}(\overline{x})-i\zeta _s^{(1)}(\overline{x})\over \zeta _{o}}\,e^{i n\omega _e t} ={\zeta _c^{(1)}(\overline{x})-i\zeta _s^{(1)}(\overline{x})\over \zeta _{a}}\,e^{i n\omega _e(t-{\varphi \over \omega _e})} \end{aligned}$$

(4)

As confirmed in (4), the time to be shifted is $\varphi /\omega _e \equiv \Delta t$. By applying this time shift $\Delta t$ to the higher harmonic components of (1), the ship-side wave elevation through time shift can be expressed below

$$\begin{aligned}{} & {} \zeta (\overline{x};t)={1\over 2K_0}c_0(\overline{x}) +\zeta _a\,\textrm{Re}\sum ^N_{n=1} c_n(\overline{x})e^{i n\omega _e t} \end{aligned}$$

(5)

$$\begin{aligned}{} & {} \left. \begin{matrix} c_0(\overline{x}) = 2K_0\zeta ^{(0)}(\overline{x}) \\ \displaystyle c_n(\overline{x})={\zeta _c^{(n)}(\overline{x})-i\zeta _s^{(n)}(\overline{x})\over \zeta _o^n} |\zeta _o|^{n-1} \\ \displaystyle \qquad \hspace{1mm} ={\zeta _c^{(n)}(\overline{x})-i\zeta _s^{(n)}(\overline{x})\over \zeta _a}\, e^{-i n\omega _e\Delta t}\quad \\ \end{matrix} \right\} \end{aligned}$$

(6)

where $K_0=g/U^2$, and g is the gravitational acceleration. The coefficients $c_n(\overline{x})$ at 31 sections obtained for all the wave conditions shown in Table 2 are saved. The ship-side wave can be recomposed by substituting $c_n(\overline{x})$ into (5) along with measured $\zeta _a$ in the tests for pressure measurement. In the present analysis, N is set to $N=5$. Needless to say, in the case of forced-heave/pitch tests, the incident wave $\zeta _I(t)$ in (2), which is the time reference, must be replaced with heave motion $\xi _3(t)$ or pitch motion $\xi _5(t)$.

4.2 Pressure

In the experiment, all the signals of sensors including pressure sensors are recorded as initial values at the calm water condition, and they are subtracted from the signals recorded thereafter. The initial signals are usually called zero points. The zero points for the pressure sensors below the still water are set under the hydrostatic loading condition, while the zero points for the pressure sensors above the still water are set under the atmospheric loading condition. Therefore, the measured pressures $p_m(\bar{{\varvec{x}}};t)$ must be corrected to get gauge pressures $p_g(\bar{{\varvec{x}}};t)$ as follows:

$$\begin{aligned} p_g(\bar{{\varvec{x}}};t)= {\left\{ \begin{array}{ll} p_m(\bar{{\varvec{x}}};t) &{}(\overline{z}\ge 0) \\ p_m(\bar{{\varvec{x}}};t)-\rho g \overline{z}&{}(\overline{z}< 0) \\ \end{array}\right. } \end{aligned}$$

(7)

where $\rho$ is the water density.

Fig. 7

Some examples of correction process for pressure data using ship-side wave at ord. 9.0. Red lines are time histories of pressures. Blue lines are pulse-like signals for judging whether sensors are in air or water

The obtained pressure data are processed using ship-side wave data. Some examples of the time history of pressure and the ship-side wave in ord. 9.0 are illustrated in Fig. 7. The pressure data in time history around the still waterline do not show a complete sinusoidal curve as shown in the red lines of two upper figures in Fig. 7, and the signals seem to be periodical sinusoidal pulse. This is because the sensor is periodically exposed to air. In addition, the pressure in air does not show zero exactly as confirmed outside of the analysis region in Fig. 7, where any correction with ship-side wave data is not applied. The FBG pressure sensor has a diameter of 5 mm and a thickness of 0.6 mm, and it is considered that especially the relationship between this thickness and the surface tension of water makes it poor to drain water on the sensor. However, the diameter of the sensor can be one of the reasons, since similar phenomena sometimes occur even for strain-type pressure sensors.

Fig. 8

Four zones for integrating pressure distribution

Table 3 Grid number for each zone ($N_{X\ell }$: number of division in the longitudinal direction, $N_{B\ell }$: number of division along girth)

Fig. 9

An example of interpolated result and measured pressure data $p_m$ in ord. 9.98 at a certain time t. The blue line indicates the position of the still waterline, $\overline{z}=0$

To correct this unnatural pressure when the sensor is in air, the ship-side wave is effectively used. In the beginning, the following preparations are necessary:

• (i) Expand the incident wave data measured together with pressures to the Fourier series in the form (2), in the analysis range usually set like $nT_e$ ($T_e\equiv 2\pi /\omega _e$, n: integer).

• (ii) Obtain the amplitude $\zeta _a$ and phase $\varphi$ in (2). Note that these are different values from those obtained for the incident wave analysis in the measurement of ship-side waves carried out in advance.

• (iii) Shift the time histories of all data including pressure data by $\Delta t=\varphi /\omega _e$. Here, $\Delta t$ indicates the shift of the time history to match it with the time reference based on the incident wave.

• (iv) Regenerate the time history of ship-side wave elevation (5) with $\zeta _a$ obtained in (ii).

With those preparations, first, the ship-side wave recomposed with (5) is synchronized to the time-series pressure data. Second, the pressure sensor is judged whether it is in air or water. Then when the position $\overline{z}$ of the pressure sensor is above $\zeta (\overline{x};t)$, the gauge pressure of the sensor is corrected to be zero in the analysis range.

This correction procedure is shown in the analysis range shown in Fig. 7 (4$T_e$ in the figure). For a sensor at $\theta =99.5$ degrees illustrated on the left of the figure, its vertical position is $\overline{z}=0.024$ m and the corresponding position are illustrated with the dotted line in Fig. 7(d) which shows the time history of ship-side wave elevation on ord. 9.0. The cross points between the dotted line and the time history of ship-side wave elevation indicate the timing when the sensor goes into and out of water, and they are illustrated with the blue line as a pulse signal in Fig. 7(a) and (b) showing the time history of the measured gauge pressure of the sensor. The positive pulse signal indicates the sensor is in air, and the negative pulse signal is in water. Only in the range of negative pulse signal, the gauge pressure is corrected to be zero. For a sensor at $\theta =60$ degrees ($\overline{z}=-0.08$ m), no cross points exist in Fig. 7(d). In this case, no correction is required as shown in Fig. 7(c).

After the correction process using ship-side wave, pressure data in time series are decomposed by the Fourier series expansion in the form

$$\begin{aligned}{} & {} p_m(\bar{{\varvec{x}}};t)= p_m^{(0)}(\bar{{\varvec{x}}}) +\textrm{Re}\sum ^N_{n=1} \bigl \{ p_{mc}^{(n)}(\bar{{\varvec{x}}})-ip_{ms}^{(n)}(\bar{{\varvec{x}}}) \bigr \}\,e^{in\omega _e t} \end{aligned}$$

(8)

$$\begin{aligned}{} & {} p(\bar{{\varvec{x}}}) \equiv p_{mc}^{(1)}(\bar{{\varvec{x}}})-ip_{ms}^{(1)}(\bar{{\varvec{x}}}) \end{aligned}$$

(9)

where the linear complex amplitude is denoted as $p(\bar{{\varvec{x}}})$. In the present analysis, N is set to $N=10$. Once $p_m^{(0)}(\bar{{\varvec{x}}})$, $p_{mc}^{(n)}(\bar{{\varvec{x}}})$ and $p_{ms}^{(n)}(\bar{{\varvec{x}}})$ are obtained, the pressure $p_m(\bar{{\varvec{x}}};t)$ can be recomposed by (8), omitting higher harmonic terms than $N=10$.

4.3 Hydrodynamic forces

A procedure to obtain the time history of hydrodynamic forces $F_i(t)$ $(i=1,3,5)$ acting in i-th direction by integrating measured pressure over the wetted surface is explained here. The pressure integration is performed at every time step.

Although the following explanation uses the free-motion test as an example, a similar procedure is also applied to the forced-heave/pitch test and diffraction test.

• 1) The hull surface is divided into four zones for accurate integration, and the measured pressure at discrete points is interpolated numerically within each zone. The four zones are the stern part, the middle part, the flare part, and the bow part as shown in Fig. 8. Each zone is discretized in the longitudinal and girth directions as shown in Table 3. The numbers of division in both directions are denoted as $N_{X\ell }$ and $N_{B\ell }$ in the table.

• 2) In each cross-section of $\overline{x}$, the position $\overline{z}_w$ of the water surface at instantaneous time t is searched using the ship-side wave data recomposed by (5). This position where the gauge pressure is zero corresponds to the upper boundary of the region in the following pressure analysis. In the analysis below, the pressure data below this position are used. Here, the pressure data of a sensor within 3 mm from this position are not used because those data sometimes show large noise. For the interpolation of the pressure, the girth from the keel up to $\overline{z}_w$ is discretized into $N_{B\ell }$ segments.

• 3) In each cross-section, measured pressure data are smoothed by the least squares method using several adjacent points. This process is for avoiding the poor interpolation affected by uncertain output pressure that sometimes occur locally. The smoothing is applied only to $p_m(\bar{{\varvec{x}}}; t)$ excluding hydrostatic pressure $-\rho g\overline{z}$. Since the pressure distribution excluding $-\rho g\overline{z}$ has a sharp peak at $\overline{z}=0$, the smoothing is carried out by dividing the area into $\overline{z}<0$ and $0\le \overline{z}\le \overline{z}_w$ if $\overline{z}_w>0$.

• 4) In each section, the pressure data after the above procedure are interpolated along the girth. One example of the interpolated curve is illustrated in Fig. 9.

• 5) The pressure data obtained by interpolation along the girth of each cross-section are interpolated in a longitudinal direction.

• 6) The coordinates of grid points for the interpolation are transformed from $\bar{o}$-$\overline{x}\overline{y}\overline{z}$ to o-xyz using ship motions. The measured ship motions by the Fourier series expansion and its linear complex amplitude $X_j$ can be expressed as

  $$\begin{aligned}{} & {} \xi _j(t)=\xi _{j}^{(0)}+\textrm{Re}\sum ^N_{n=1} \bigl \{ \xi _{jc}^{(n)}-i\xi _{js}^{(n)} \bigr \}\,e^{in\omega _e t} \end{aligned}$$

  (10)
  $$\begin{aligned}{} & {} X_j \equiv \xi _{jc}^{(1)}-i\xi _{js}^{(1)} \end{aligned}$$

  (11)

  N is set to $N=10$, the same as the pressure data. Using ship motions $\xi _j(t)$ recomposed by (10) omitting higher harmonic terms than 10-th, the coordinates x, y, z are transformed as follows:

  $$\begin{aligned} x(t)=\alpha _1(\bar{{\varvec{x}}};t) \,,\quad y(t)=\overline{y}\,,\quad z(t)=\alpha _3(\bar{{\varvec{x}}};t) \end{aligned}$$

  (12)
  $$\begin{aligned} \left. \begin{matrix} \alpha _1(\bar{{\varvec{x}}};t)=\xi _1(t)+\overline{x}\cos \xi _5(t)+\overline{z}\sin \xi _{5}(t) \,\,\,\\ \alpha _3(\bar{{\varvec{x}}};t)=\xi _3(t)-\overline{x}\sin \xi _5(t)+\overline{z}\cos \xi _{5}(t) \,\,\,\\ \end{matrix} \right\} \end{aligned}$$

  (13)

  The hull surface divided into $N_{X\ell }\times N_{B\ell }$ in $\ell$-th zone constitutes rectangular panels for pressure integration. Then the normal vector ${\varvec{n}}_k(t)=\{n_{1k}(t),n_{2k}(t),n_{3k}(t)\}$ and its moment component ${\varvec{x}}_k(t)\times {\varvec{n}}_k(t)=\{n_{4k}(t),n_{5k}(t),n_{6k}(t)\}$ in the coordinate system o-xyz are calculated at the k-th panel center. Besides that, the surface area of the panel, $\Delta S_k(t)$, is also calculated.

• 7) The forces $F_i(t)$ acting in i-th direction are now calculated as

  $$\begin{aligned} F_i(t) =-\sum _{\ell =1}^{4} \sum _{k=1}^{N_{P\ell }} {\,p_{gk}(\bar{{\varvec{x}}}_k;t)} \,n_{ik}(t) \,\Delta S_k(t) \quad (i=1,3,5) \end{aligned}$$

  (14)

  where $p_{gk}(\bar{{\varvec{x}}}_k;t)$ denotes the average of gauge pressures (7) at four grid points of the k-th rectangular panel. $N_{P\ell }$ $(=N_{X\ell }\times N_{B\ell })$ indicates the total panel number in $\ell$-th zone.

• 8) By marching the time t and repeating the same procedure from 2) to 7), the time history of $F_i(t)$ can be obtained. Once the time series $F_i(t)$ of the fluid force acting in the i-th direction is obtained as described above, the subsequent analysis can be performed in the same manner as the usual analysis using load cells. For example, applying the Fourier analysis to the data in waves and taking the steady term, the resistance of the steady component is given. By subtracting the resistance obtained in the calm water condition, the added resistance can be obtained.

4.4 Added mass, damping coefficients, and wave exciting forces

In forced-heave/pitch tests, either heave or pitch motion is enforced on the ship model with a forced motion device while towing the model in calm water. The load cells equipped at the fore and aft part of the model measure the reaction forces, and total forces acting at the midship center are obtained finally. On the other hand, the forces can be also estimated by integrating the measured pressure distribution over the model through the same procedure described for the free-motion test in Sect. 4.3. In this case, the j-th motion forced to the model by the device is expanded to the Fourier series as shown in (10) first of all. Since the device accurately enforces the sinusoidal motion to the model, the terms except for the 1st-harmonic term in (10) are almost zero. Thus, the complex motion amplitude $X_j$ in (11) is obtained. In the analysis, this value is used instead of $\zeta _o$ in (2) for the reference of time; $t=0$ in the analysis is defined as the timing when the motion reaches the maximum amplitude. The ship-side wave in the forced-heave/pitch test is regenerated by replacing $\zeta _a$ to $|X_j|$ in (5). Following the same procedure described in Sect. 4.3, the time history of forces $F_i(t)$ is obtained in the form of (14). $F_i(t)$ obtained in this way is expanded to the Fourier series as

$$\begin{aligned}{} & {} F_i(t)=f_i^{(0)} +\textrm{Re}\sum _{n=1}^{N} \big \{ f^{(n)}_{ic}-if^{(n)}_{is} \bigr \}\,e^{i\omega _e t} \end{aligned}$$

(15)

$$\begin{aligned}{} & {} f_i \equiv f^{(1)}_{ic}-if^{(1)}_{is} \end{aligned}$$

(16)

N is set to $N=5$, but higher harmonic terms are not necessary in the subsequent analysis. Using linear complex forces $f_i$ obtained in (16), the added mass $A_{ij}$ and damping coefficients $B_{ij}$, in which i stands for the direction of force and j the direction of forced motion, are calculated. For the forced-heave test, they can be computed as

$$\begin{aligned} \left. \begin{matrix} \displaystyle {A_{13}\over \rho \bigtriangledown } &{}=&{}\displaystyle -{\textrm{Re}\{-f_1/X_3\} \over \omega _e^2\rho \bigtriangledown } \\ \displaystyle {B_{13}\over \rho \bigtriangledown \omega _e} &{}=&{}\displaystyle {\Im \{-f_1/X_3\} \over \omega _e^2\rho \bigtriangledown } \\ \displaystyle {A_{33}\over \rho \bigtriangledown } &{}=&{}\displaystyle {-\textrm{Re}\{-f_3/X_3\}+C_{33}\over \omega _e^2\rho \bigtriangledown } \\ \displaystyle {B_{33}\over \rho \bigtriangledown \omega _e} &{}=&{}\displaystyle {\Im \{-f_3/X_3\} \over \omega _e^2\rho \bigtriangledown } \\ \displaystyle {A_{53}\over \rho \bigtriangledown L} &{}=&{}\displaystyle {-\textrm{Re}\{-f_5/X_3\}+C_{53}\over \omega _e^2\rho \bigtriangledown L} \\ \displaystyle {B_{53}\over \rho \bigtriangledown \omega _e L}&{}=&{}\displaystyle {\Im \{-f_5/X_3\}\over \omega _e^2\rho \bigtriangledown L} \\ \end{matrix} \quad \right\} \end{aligned}$$

(17)

Similarly, for the forced-pitch test, the following results can be calculated:

$$\begin{aligned} \left. \begin{matrix} \displaystyle {A_{15}\over \rho \bigtriangledown L} &{}=&{}\displaystyle -{\textrm{Re}\{-f_1/X_5\}\over \omega _e^2\rho \bigtriangledown L} \\ \displaystyle {B_{15}\over \rho \bigtriangledown \omega _e L}&{}=&{}\displaystyle {\Im \{-f_1/X_5\} \over \omega _e^2\rho \bigtriangledown L} \\ \displaystyle {A_{35}\over \rho \bigtriangledown L} &{}=&{}\displaystyle {-\textrm{Re}\{-f_3/X_5\}+C_{35}\over \omega _e^2\rho \bigtriangledown L} \\ \displaystyle {B_{35}\over \rho \bigtriangledown \omega _e L}&{}=&{}\displaystyle {\Im \{-f_3/X_5\} \over \omega _e^2\rho \bigtriangledown L} \\ \displaystyle {A_{55}\over \rho \bigtriangledown L^2} &{}=&{}\displaystyle {-\textrm{Re}\{-f_5/X_5\}+C_{55}\over \omega _e^2\rho \bigtriangledown L^2}\\ \displaystyle {B_{55}\over \rho \bigtriangledown \omega _e L^2}&{}=&{}\displaystyle {\Im \{-f_5/X_5\}\over \omega _e^2\rho \bigtriangledown L^2} \\ \end{matrix} \quad \right\} \end{aligned}$$

(18)

In (17) and (18), $C_{33}=\rho g A_W$, $C_{35}=C_{53}=-\rho g\, x_f\, A_W$, $C_{55}=\rho g \bigtriangledown \overline{GM}_L$ are the restoring coefficients. $A_W$, $x_f$ and $\overline{GM}_L$ are shown in Table 1.

In the case of diffraction test, the procedure to get the time history of $F_i(t)$ in (14) is the same as described in Sect. 4.3. The treatment for the reference of time using the incident wave is the same. The obtained time history is also expanded to the Fourier series like (15), and $f_i$ in (16) is obtained by extracting the 1st-harmonic component. Using complex force $f_i$, the wave exciting forces $E_i$ are calculated as

$$\begin{aligned} \left. \begin{matrix} \displaystyle {E_1\over \rho g\zeta _a BL} &{}=&{} \displaystyle {f_1/\zeta _o\over \rho g BL} \\ \displaystyle {E_3\over \rho g\zeta _a BL} &{}=&{} \displaystyle {f_3/\zeta _o\over \rho g BL} \\ \displaystyle {E_5\over \rho g\zeta _a BL^2} &{}=&{} \displaystyle {f_5/\zeta _o\over \rho g BL^2} \end{matrix} \quad \right\} \end{aligned}$$

(19)

4.5 Added resistance

The added resistance can be also estimated from the analysis of the time histories (15) obtained by integrating measured pressure distribution at every time step. This is called the ‘time-domain analysis’ in this paper hereafter. In this analysis, the added resistance $R_{AW}$ is simply obtained by

$$\begin{aligned} R_{AW}=-\bigl \{\, f_1^{(0)}-f_{1\,(calm)}^{(0)}\, \bigr \} \end{aligned}$$

(20)

where both $f_1^{(0)}$ and $f_{1\,(calm)}^{(0)}$ stand for $f_1^{(0)}$ in (15), but they are obtained by towing the model in waves and calm water, respectively. The subscript ‘calm’ shows the quantities obtained in the analysis for the experiment towing the model in calm water.

Another method to obtain the added resistance is called the ‘frequency-domain analysis’ in this paper. In this analysis, first the measured pressure is expanded to the Fourier series as in (8), and the zeroth order terms, $p_m^{(0)}(\bar{{\varvec{x}}})$ and $p_{m\,(calm)}^{(0)}(\bar{{\varvec{x}}})$ are obtained discretely at measured points. Next, they are smoothed and interpolated so that they are expressed by continuous curves. Finally, it is integrated over the hull surface multiplying the x component of the normal in the coordinate system o-xyz, to get the added resistance. The difference of attitude of the hull for $p_m^{(0)}(\bar{{\varvec{x}}})$ and $p_{m\,(calm)}^{(0)}$ is taken into account through the difference of the x component in the normal.

Fig. 10

A sample of added pressure distribution $\Delta P_m^{(0)}(\bar{{\varvec{x}}})$ along the girth in a cross-section. The abscissa shows the angle measured from centerline (see Fig. 4). Symbols are the results of measurement at pressure-sensor points, and curves are smoothed and interpolated results of them

That procedure will be explained concretely in what follows. Figure 10 illustrates a sample of pressure distribution of $p_m^{(0)}(\bar{{\varvec{x}}})$ and $p_{m\,(calm)}^{(0)}(\bar{{\varvec{x}}})$ along a girth. The horizontal axis indicates the angle between the keel and the arbitrary position on the girth measured from the centerline (see Fig. 4), and the vertical axis is the nondimensionalized pressure. Symbols are measured pressure with sensors, and curves show smoothed and interpolated pressure distribution with measured pressures. White symbols are pressures in $\overline{z}\le 0$ and closed symbols filled with colors are pressures in $\overline{z}>0$. In the figure, the gauge pressures, $p_g^{(0)}(\bar{{\varvec{x}}})$ and $p_{g\,(calm)}^{(0)}(\bar{{\varvec{x}}})$, are also illustrated as reference. They are defined by (7), and continuous and differentiable even at $\overline{z}=0$. The pressure difference $\Delta p_m^{(0)}(\bar{{\varvec{x}}})$ between $p_m^{(0)}(\bar{{\varvec{x}}})$ and $p_{m\,(calm)}^{(0)}(\bar{{\varvec{x}}})$ is shown by triangle symbol and red curve. $\Delta p_m^{(0)}(\bar{{\varvec{x}}})$ is the so-called added pressure. As confirmed from the red curve in this figure, the curve has a sharp peak at $\overline{z}=\zeta _{(calm)}^{(0)}-\alpha _{3\,(calm)}^{(0)}$ which shows the position of the relative wave elevation of the steady wave. In the smoothing and interpolation of $\Delta p_m^{(0)}(\bar{{\varvec{x}}})$, the region must be divided at this position. The lower and upper regions of this position are divided into $N_{B\ell }$ and $\delta N_{B\ell }\,(=10)$, respectively, in the present analysis. The figure also suggests why the pressure difference becomes large around the ship-side wave of the steady wave.

Fig. 11

Spatial and sectional distributions of steady pressure on RIOS bulk carrier, obtained from measurement in towing test in calm water for RIOS bulk carrier at $F_n=0.18$ and computation by RPM. Results are corrected with steady sinkage and trim taken into account, and the abscissa $\theta$ is defined in Fig. 4

The added resistance can be estimated by integrating $p_m^{(0)}$ and $p_{m\,(calm)}^{(0)}$ separately considering the time-averaged attitude of the hull as follows:

$$\begin{aligned} R_{AW} =-\sum _{\ell =1}^{4} \Bigl \{{} & {} -\sum _{k=1}^{N_{P\ell }+\delta N_{P\ell }} p_{mk}^{(0)}(\bar{{\varvec{x}}})\, n_{1k}^{(0)}\, \Delta S_k \nonumber \\{} & {} +\sum _{k=1}^{N_{P\ell }} p_{mk\,(calm)}^{(0)}(\bar{{\varvec{x}}})\, n_{1k\,(calm)}^{(0)}\, \Delta S_k \Bigr \} \end{aligned}$$

(21)

where $\delta N_{P\ell }=N_{X\ell }\times \delta N_{B\ell }$. $n_{1k}^{(0)}$ and $n_{1k\,(calm)}^{(0)}$ are the x component of normal in the o-xyz system. They are calculated at the center of the k-th panel consisting of adjacent four nodes, and the attitude of the hull is taken into account through the following relation:

$$\begin{aligned} \left. \begin{matrix} n_{1k}^{(0)} &{}=&{}\overline{\nabla }_{1k}\cos \xi _5^{(0)} &{}+\overline{\nabla }_{3k}\sin \xi _5^{(0)} \\ n_{1k\,(calm)}^{(0)}&{}=&{}\overline{\nabla }_{1k}\cos \xi _{5\,(calm)}^{(0)}&{}+\overline{\nabla }_{3k}\sin \xi _{5\,(calm)}^{(0)} \\ \end{matrix} \,\,\, \right\} \end{aligned}$$

(22)

(21) can be expressed in the form

$$\begin{aligned} R_{AW} ={} & {} \sum _{\ell =1}^{4} \sum _{k=1}^{N_{P\ell }} \Bigl \{ p_{mk}^{(0)}\, n_{1k}^{(0)} -p_{mk\,(calm)}^{(0)}\, n_{1k\,(calm)}^{(0)} \Bigr \}\,\Delta S_k \nonumber \\{} & {} +\sum _{\ell =1}^{4} \sum _{k=N_{P\ell }+1}^{N_{P\ell }+\delta N_{P\ell }} p_{mk}^{(0)}\, n_{1k}^{(0)}\Delta S_k \end{aligned}$$

(23)

$$\begin{aligned} \equiv{} & {} \sum _{\ell =1}^{4} \sum _{k=1}^{N'_{P\ell }} \sigma _x(\overline{x})\,\Delta S_k \end{aligned}$$

(24)

where $\sigma _x(\bar{{\varvec{x}}})$ defined by

$$\begin{aligned} \sigma _x(\overline{x})= {\left\{ \begin{array}{ll} p_{mk}^{(0)}\, n_{1k}^{(0)} -p_{mk\,(calm)}^{(0)}\, n_{1k\,(calm)}^{(0)} &{}(1\le k\le N_{P\ell }) \\ p_{mk}^{(0)}\, n_{1k}^{(0)} &{}(N_{P\ell }+1\le k\le N'_{P\ell }) \\ \end{array}\right. } \end{aligned}$$

(25)

is referred to as the added-resistance integrand in this paper. Here, $N'_{P\ell }$ is $N'_{P\ell }=N_{P\ell }+\delta N_{P\ell }$, and (25) is calculated using relation (22).

5 Results and discussion

The pressure distribution measured with FBG pressure sensors is validated by not only the direct comparison with the pressure measured with strain-type pressure sensors but also the comparison of hydrodynamic forces obtained by integrating measured pressures with those obtained by load cells. The results are also compared with typical calculation results with the frequency-domain RPM (Rankine Panel Method) [58, 60]. In the RPM, the linearized free-surface condition based on the double-body flow is used, and the panel-shift method and artificial friction coefficients are employed for satisfying the radiation condition numerically. The comparison is to demonstrate how the spatial distribution of measured pressure is useful for the validation of numerical calculation methods.

5.1 Pressure distribution

Results will be shown for the steady pressure distribution obtained by towing the ship model in calm water without restricting its motion, and the 1st-harmonic unsteady pressure distribution obtained by (9) for four different tests; that is, forced-heave, forced-pitch, diffraction, and free-motion tests. As for the unsteady pressure, the time-varying measured pressure $p_m(\bar{{\varvec{x}}};t)$ in (8) is also shown as some snapshots in one period.

5.1.1 Steady pressure distribution

The spatial distribution of steady pressure $p_{m\,(calm)}^{(0)}$, and its sectional distribution along the girth at ord. 1.5, 5.0, 9.0 and 9.5 are shown in Fig. 11. Here, it should be noted that the measured steady pressure is corrected by adding $\rho g \overline{z}+\rho g \alpha _{3\,(calm)}^{(0)}$ to $p_g(\bar{{\varvec{x}}};t)$ in (7). In order of  5.0, 9.0, and 9.5, the results with strain-type pressure sensors are also illustrated. The abscissa $\theta$ denotes the hull position along the girth, as defined in Fig. 4. The left upper figure is the spatial distribution of steady pressure obtained by experiments, which is an average of 6 times tests. The right one is the computational result of the RPM. After obtaining the numerical solution for the double-body flow based linear BVP (boundary-value problem), the hull surface is discretized again below the calm water considering the obtained sinkage and trim, and the same type of BVP is recalculated by the RPM. Thus, the difference of sinkage and trim between measured and computed is included in these results on pressure distribution. Note that the upper edge in spatial distribution obtained in the experiment indicates the ship-side wave height and experimental data above ship-side wave elevation in sectional distribution are not illustrated.

The results of sectional pressure distribution show that the difference can be seen between the FBG pressure sensor and strain-type pressure sensor and that the RPM predicts the steady pressure measured with strain-type pressure sensor with acceptable accuracy. The difference in results between the FBG and strain-type pressure sensors can be considered to be caused by the thickness of the FBG pressure sensor and optical fibers disturbing the flow field. To decrease these effects, a larger ship model should be used in the experiment. FBG pressure sensors may not be suitable for estimating the steady pressure in calm water unless a large model is used. Although the FBG pressure sensors have that drawback, the spatial distribution of steady pressure with those sensors is useful to grasp the distribution over the hull, as shown in the figure.

5.1.2 Unsteady pressure distribution

In the same manner as Fig. 11, the spatial and sectional distributions of unsteady pressures $p(\bar{{\varvec{x}}})$ [see (9)] in the forced-heave test, forced-pitch test, diffraction test and free-motion test are shown in Figs. 12, 13, 14 and 15, respectively. Unsteady pressures are nondimensionalized by the complex motion amplitude $X_3$ or $X_5$ in (11) for forced-heave or forced-pitch tests and by the complex wave amplitude $\zeta _o$ in (3) for diffraction test and free-motion test. Spatial distribution is illustrated by decomposing into cosine and sine components which correspond to the real and minus imaginary parts respectively, and sectional distribution is shown with amplitude and phase. In these figures, the measured results for the forced-heave test, forced-pitch test, and diffraction test are the average value of two times measurements, and for the free-motion test is over five times measurements. For free-motion test, the standard deviation is also shown in the sectional distribution. In each figure, results for two frequencies corresponding to $\lambda /L=0.5$ and 1.25 in Table 2 are shown. Note that the upper boundary of the contour plot does not show the wetted surface but simply the distribution of the value $p(\bar{{\varvec{x}}})$ in (9) obtained before giving free-surface by ship-side waves.

Sectional pressure distributions in those figures show that the results of FBG pressure sensors generally coincide with those of strain-type pressure sensors in good accuracy. The amplitude of unsteady pressure first increases generally as the depth of the sensor decreases, and next decreases as the position approaches the water surface and converges to zero finally. The RPM based on the linear theory can predict the first part of this tendency, but cannot predict the last two tendencies where a strong nonlinearity appears due to sensors periodically going into and out of water. As a result, the RPM based on the liner theory overestimates the amplitude of unsteady pressure there. The difference between FBG pressure sensors and strain-type pressure sensors also seems to be slightly larger in those nonlinear regions. In regions, the time history of the pressure sensor shows a periodical sinusoidal-pulse wave since the sensor periodically goes out the water surface. At this moment, the thickness of the FBG pressure sensor may prevent quick drain of the water from the sensor surface. This can be one of the reasons for the difference above.

In the results of the free-motion test shown in Fig. 15, the standard deviations of the FBG pressure sensor show almost the same values as those of the strain-type pressure sensor, and they are practically acceptable values. As illustrated in the figure of spatial pressure distribution, the measurement with FBG pressure sensor is effective in acquiring the entire distribution at once over the hull with enough accuracy. This measurement method can be utilized to validate arbitrary computational results. In the present study, the RPM is validated as a test case and it is confirmed that the RPM shows relatively good agreement with measured spatial unsteady pressure distributions in all figures.

Fig. 12

Spatial and sectional distributions of unsteady pressure by measured and computed in the forced-heave test for RIOS bulk carrier ($F_n=0.18$). Each distribution is expressed by decomposing into cosine and sine components, and amplitude and phase, respectively. Abscissa $\theta$ is defined in Fig. 4. See Table 2 for conditions (a) and (b)

Fig. 13

Spatial and sectional distributions of unsteady pressure by measured and computed in the forced-pitch test for RIOS bulk carrier ($F_n=0.18$). Each distribution is expressed by decomposing into cosine and sine components, and amplitude and phase, respectively. Abscissa $\theta$ is defined in Fig. 4. See Table 2 for conditions (a) and (b)

Fig. 14

Spatial and sectional distributions of unsteady pressure by measured and computed in the diffraction test for RIOS bulk carrier ($F_n=0.18$). Each distribution is expressed by decomposing into cosine and sine components, and amplitude and phase, respectively. Abscissa $\theta$ is defined in Fig. 4. See Table 2 for conditions (a) and (b)

Fig. 15

Spatial and sectional distributions of unsteady pressure by measured and computed in the free-motion test for RIOS bulk carrier ($F_n=0.18$). Each distribution is expressed by decomposing into cosine and sine components, and amplitude and phase, respectively. Abscissa $\theta$ is defined in Fig. 4. See Table 2 for conditions (a) and (b)

Fig. 16

Time series of spatial pressure distribution excluding hydrostatic pressure. Condition is $F_n=0.18$, $\lambda /L=1.25\,(K_eL=9.9)$

Fig. 17

Time series of forces and moment. Condition is $F_n=0.18$, $\lambda /L=1.25\,(K_eL=9.9)$

Fig. 18

Added mass and damping coefficients of RIOS bulk carrier at $F_n=0.18$, obtained by load cells and by the integration of measured pressure using FBG pressure sensors

Fig. 19

Wave exciting forces and moment of RIOS bulk carrier at $F_n=0.18$, $\chi =180$ degs, obtained by load cells and by the integration of measured pressure using FBG pressure sensors

Fig. 20

Ship motions of RIOS bulk carrier at $F_n=0.18$, $\chi =180$ degs. White and red circles show the measured results by potentiometers. Green triangles and blue inverted triangles are obtained by solving linear simultaneous motion equations between heave and pitch using measured hydrodynamic forces, $A_{ij}$, $B_{ij}$ and $E_i$ $(i, j=3,5)$. In green triangles, hydrodynamic forces obtained by integrating measured pressures are used. In blue inverted triangles, ones obtained by load cells are used

5.1.3 Time series of pressure distribution

The time series of spatial pressure distribution for four different tests are illustrated in Fig. 16. The incident wave condition is $\lambda /L=1.25$ and this corresponds to $K_eL=9.9$. The illustrated pressure is the recomposed one by (8) with $N=10$, and contains all the components of the pressure except for the hydrostatic component. Besides the pressure, figures also illustrate ship motions and ship-side wave profiles by snapshots of every one-fourth period, where ship motions and ship-side wave profiles are recomposed by (5) and (10), respectively. The results consist only of the measured data and they can be utilized directly for validation such as CFD simulations. On the other hand, the time histories of hydrodynamic forces are obtained by integrating pressures over the wetted surface at every time step.

It should be emphasized that such a figure showing the time-series spatial distribution of the unsteady pressure over the hull surface was obtained using experimental data for the first time in this study.

5.2 Hydrodynamic forces

As one of the validations of measured pressure distribution with FBG pressure sensors, the measured pressure distribution at every time step as shown in Fig. 16 is integrated over the wetted surface, and the time histories of forces are obtained. Then they are expanded to the Fourier series, and the 1st-harmonic component is extracted and compared with forces directly measured by load cells.

Some examples of obtained time histories of forces $F_1, F_3$ and moment $F_5$ are shown in Fig. 17. In the figures, the results of the forced-heave test and forced-pitch test in $K_eL=9.9\,(\lambda /L=1.25)$ are illustrated. Note that $F_3$ in the figure is illustrated by subtracting the buoyancy from $F_3$ obtained in (14). The black lines in the figures show the forces and moment directly measured by load cells, which contain inertia forces. The blue lines are hydrodynamic forces excluding inertia forces, which should be compared with the red lines obtained by the integration of measured pressures.

The blue and red lines show good agreement not only in phase but also in the amplitude. This suggests that the added mass and damping coefficients will show good agreement between results by load cells and by pressure integration. This fact will be confirmed in subsequent figures.

On the other hand, the time-averaged value between the red and blue lines shows a small difference. This might be the effect of thickness of the sensors and optical fibers attached to the hull surface as already described in Sect. 5.1.1.

The obtained forces and moment are expanded to the Fourier series in the form of (15), and its 1st-harmonic component is obtained as (16). The same process is applied to forced motions $\xi _j$ $(j=3,5)$ using Eqs. (10) and (11), and the added mass and damping coefficients are obtained by (17) and (18). The results are shown in Fig. 18. As explained above, the added mass and damping coefficients obtained by direct measurement with load cells and by the pressure integration show good agreement. One of the reasons for the slight difference may be the influence of the parts in the bow and stern where pressure is not measured, as seen in Fig. 8.

A similar analysis is also applied to the wave exciting forces. In this case, the measured incident wave is expanded to the Fourier series in the form of (2), and its 1st-harmonic component is obtained as (3). Then using $\zeta _o$ and measued forces $f_i$ $(i=1,3,5)$, the wave exciting forces $E_1$, $E_3$ and moment $E_5$ are obtained as (19). Two results by load cells and pressure integration also coincide with good accuracy in wave exciting forces and moment.

Those hydrodynamic forces, $A_{ij}$, $B_{ij}$ and $E_i$ $(i,j=3,5)$, are validated furthermore by solving the linear simultaneous coupled motion equations between heave and pitch using them. Figure 20 shows measured results of surge, heave, and pitch motions by potentiometers along with results using RPM. Measured results with potentiometers, which are shown by white and red circles, are in good agreement with computed results using RPM.

Green triangles and blue inverted triangles are obtained by solving linear simultaneous motion equations between heave and pitch using average values of measured hydrodynamic forces, $A_{ij}$, $B_{ij}$ and $E_i$ $(i, j=3,5)$. Note that necessary restoring coefficients are calculated from the principal particulars in Table 1. Besides, the simultaneous motion equations are formulated with only heave and pitch motions because the elements associated with surge motions were not obtained by experiments. In green triangles, hydrodynamic forces obtained by integrating measured pressures are used. Blue inverted triangles are obtained by load cells. Both results agree well and this implies that the pressure measurement with FBG pressure sensor is sufficiently accurate. The slightly larger difference in pitch motion amplitude at $\lambda /L=1.25$ $(K_eL=9.9)$ can be considered to be caused by the small difference seen between the red circle and green triangle in Figs. 18 and 19. It is also noticed that both motions directly measured by potentiometers and computed by solving linear ship-motion equations using measured hydrodynamic forces with load cells coincide in quite good accuracy. This implies that a linear system is still applicable even for the blunt ship treated in this paper.

It is also confirmed that this kind of validation solving the motion equations with measured hydrodynamic forces is very effective as precise validation.

Through these analyses and investigations above, it is evident that the pressure measurement over the entire hull surface with FBG pressure sensors has acceptable accuracy at least in estimation of the 1st-order forces.

Fig. 21

Distribution of added-resistance integrand of RIOS bulk carrier at $F_n=0.18$, $\chi =180$ degs. The black dashed line is the ship-side wave profile in towing test in calm water. The pink dot-dashed line is the bottom line of the ship-side wave elevation in the free-motion test. $C_{AW}$ is the non-dimensional value of added resistance defined by $C_{AW}=R_{AW}/\rho g\zeta _a^2(B^2/L)$

5.3 Added resistance

The added resistance is the 2nd-order hydrodynamic force, which is obtained as the difference of resistance acting in the x direction when the model is towed in waves and calm water.

First, the distribution of the added-resistance integrand $\sigma _x(\bar{{\varvec{x}}})$ over the hull surface is shown in Fig. 21 for 7 wave conditions, which corresponds to the integrand when the added resistance is calculated in the frequency-domain analysis. Only one of the several experimental results in each wave condition is shown as an example. In the caption for each wave condition, the values of non-dimensional added resistance $C_{AW}={R_{AW}}/{\rho g\zeta _a^2(B^2/L)}$ obtained by pressure integration and strain gauge are written as reference. The used steady pressure $p_{mk\,(calm)}^{(0)}$ in (25) is the average of towing tests in calm water carried out 6 times.

In the figure, the ship-side wave height in towing tests in calm water, which is also the average value of several towing tests, is illustrated in a black dashed line. And, the bottom line of the ship-side wave elevation in the free-motion test, which is expressed by $|\zeta (\bar{{\varvec{x}}};t)|_{min}$ in the equation, is shown in a pink dot-dashed line. The upper boundary of the color contour corresponds to $|\zeta (\bar{{\varvec{x}}};t)|_{max}$. The area between $|\zeta (\bar{{\varvec{x}}};t)|_{min}$ and $|\zeta (\bar{{\varvec{x}}};t)|_{max}$ is exposed to air periodically due to ship motions and waves. The area $\delta S$, where the girth is discretized into $\delta N_{B\ell }$ segments, is above the black dashed line (see Fig. 10). It can be seen from the figures that the bow flare part along the ship-side wave profile in calm water is remarkably contributing to the added resistance. This fact is also implied by the CFD calculation [28], and the importance of bow flare shape for the added resistance has been suggested by some researchers so far [61, 62]. Figure 21 supports such facts experimentally.

On the other hand, it is also suggested that some thrust force may be generated from the hull surface around the bow part below the pink dot-dashed line. Now, dividing the wetted surface into two areas by the pink dot-dashed line, the areas above and below the line are expressed by $S_a$ and $S_b$, respectively. The forces by integrating the added resistance integrand over $S_a$, $S_b$ and both are illustrated in Fig. 22. The force by integrating the pressure on both $S_a$ and $S_b$ is the added resistance. These calculations are carried out in the framework of frequency-domain analysis, and the results are expressed by the average and standard deviation of over 5 times tests. In addition to those results based on the frequency-domain analysis, the added resistance estimated by the time-domain analysis in (20) is also shown in the same figure. In Fig. 22, the computational result of enhanced unified theory (EUT) [7, 63] is shown as a reference.

As confirmed in this figure as well, the thrust force is generated on $S_b$ while the resistance acts on $S_a$. This tendency can be also explained by calculation. Simply put, in the calculation by the near field method, the line-integral term along the water line related to the ship-side wave squared is a positive value; which is resistance. On the other hand, the surface-integral term related to the flow velocity squared is a negative value; which is thrust. By summing these dominant terms and the other terms, the added resistance is normally given as resistance. The added resistance of S175 container ship estimated by Kim and Kim [64] with the time-domain RPM also indicates a tendency that the line-integral along the water line shows the resistance and the integral over the hull surface shows the thrust although the line-integral term is not composed of only ship-side wave squared. Zhang et al. [65] also mentioned the same point using the Wigley model. In their calculation, the waterline integration around the bow part shows dominant resistance, and this corresponds to the results in Fig. 21. To reduce the value of added resistance, in addition to the method of reducing the resistance by devising the flare shape near the waterline, it is suggested that there is also a method of increasing the thrust component by changing the shape under the waterline. However, it may be difficult in practice to change the hull shape under the waterline, since the shape is usually determined from a design concept for small resistance in calm water.

The added resistances obtained by both frequency- and time-domain analyses qualitatively agree with the results obtained by the strain gauge. However, quantitative agreement between the two-analysis methods is not necessarily good, although the results of the frequency-domain analysis agree well in a long-wave region with directly measured values. Possible reasons for quantitative disagreement will be discussed below.

At first, the added resistance is the 2nd-order physical quantities and very small. Table 4 shows the non-dimensional and dimensional wave exciting forces and added resistance when the incident wave amplitude is $\zeta _a=10$ mm. In the table, the approximated mean values measured by load cells and strain gauge for each wave condition are indicated. From the table, the added resistance is confirmed as a very small physical quantity compared with the wave exciting force. As a result, analyzed results show a large standard deviation as seen in Fig. 22.

Table 4 Dimensional values of wave exciting force and added resistance when $\zeta _a$ is 10 mm

Fig. 22

Added resistance of RIOS bulk carrier at $F_n=0.18$, $\chi =180$ degs. The computation result is by Enhanced Unified Theory (EUT) [7, 63]. $S_b$ indicates the surface always in water and $S_a$ exposed to air periodically

As already mentioned in Sect. 5.1.1, the flow on the hull surface might be disturbed by the thickness of FBG pressure sensors and optical fibers, and a noticeable measuring error in steady pressure is included as shown in Fig. 11. In fact, the average value of ${f}_{1\,(calm)}^{(0)}$ used in (20) is $+0.12$ N. This indicates a thrust force occurs, which is unrealistic physically. The same influence can appear in the steady component of the measured pressure in towing tests in waves, where the steady component means the zeroth order or time-averaged value in the Fourier series of the measured pressure. Most of this influence to appear in towing tests in calm water and waves may be canceled out by taking the difference between the two, but in reality, slight differences can remain as errors. The difference between the frequency-domain and time-domain analyses is thought to be caused by the difference in how this error appears between the two different analysis procedures. To lessen this error, either a ship model with enough large size which can neglect the effect of sensor thickness should be used, or the thickness of FBG pressure sensor should be made thinner. Although it can be considered that this effect would also affect the unsteady component of measured pressure, its influence on the 1st-harmonic component is negligible as seen in Figs. 18, 19.

6 Conclusion

In this study, an unprecedented experimental data acquisition method for the pressure in the entire ship model surface was examined using FBG pressure sensors. The spatial pressure distributions on the entire hull surface of the RIOS bulk carrier were measured by attaching FBG pressure sensors at 379 points and by carrying out the forced-heave/pitch test, diffraction test, and free-motion test. The pressures measured by FBG pressure sensors were validated by comparing them with measured pressure by strain-type pressure sensors. In addition, the measured pressure was integrated over the wetted surface and hydrodynamic forces were obtained to compare with those measured by load cells and strain gauges. The acquired conclusions are summarized below.

• (1) The steady pressure distribution measured by FBG pressure sensors in the towing test in calm water is slightly different from that measured by the strain-type pressure sensors. The difference might be caused by the flow disturbance due to the thickness of FBG pressure sensors and optical fibers.

• (2) The 1st-harmonic component of measured unsteady pressure by FBG pressure sensors in the forced-heave test, forced-pitch test, diffraction test, and free-motion test was compared with that by strain-type pressure sensors and with computed results using RPM. Pressure distributions measured by FBG pressure sensors and strain-type sensors show good agreement generally. The RPM based on the linear theory overestimates the unsteady pressure amplitude around the free surface where the hull surface periodically goes into and out of water.

• (3) By integrating the pressure distribution on the wetted surface at every time step, the time histories of forces and moments were calculated. Applying the Fourier series expansion to the time histories and extracting the 1st-harmonic component, the added mass and damping coefficients, and wave exciting forces were obtained. The obtained results show good agreement with the results measured by load cells.

• (4) The added-resistance integrand was obtained by taking the zeroth component of the Fourier series of measured pressure in waves and calm water, and by taking their difference. The added-resistance integrand is large along the ship-side wave profile of steady wave, especially near the bow flare region. These regions yield resistance, while the region below the lowest of the unsteady ship-side wave elevation yields a thrust.

• (5) The added resistance was obtained using two methods; time-domain analysis and frequency-domain analysis. Both analysis methods can capture the behavior of the added resistance measured by the strain gauge, but not necessarily accurate enough quantitatively. The reason for this is thought to be that the added resistance is the 2nd-order hydrodynamic force and hence very small, which can be in the same range of measurement error caused by the disturbance flow due to the thickness of the sensor. To improve the accuracy, a larger ship model should be used.

Based on the above results, future work will be to construct a useful database for numerical calculations by conducting pressure measurements in oblique waves and in irregular waves.