1 Introduction

Dynamic positioning (DP) controls the position and heading of a vessel. The horizontal components of the point of interest on the vessel can usually be freely specified, e.g. the position of the tip of a crane boom in a lifting operation, or the center of the drill string in a drilling operation. In some cases the point of interest may have a significant vertical offset from the center of flotation, such that its horizontal motion is strongly influenced by the vessel’s roll and pitch motions when referenced e.g. to an Earth-fixed or inertial coordinate system. Since the thrusters of the vessel are generally located with an offset to the center of gravity, their thrust will create moments about the roll and pitch axes, in addition to the yaw axis. With some exceptions (see below), the vertical offset of the point of interest, and the roll and pitch moments, are usually neglected in dynamic positioning control [3, 17, 18]. The objective of this paper is to study how these effects can be incorporated into the DP control problem formulation to improve the DP controller’s ability to compensate for first order wave-induced motions in surge, sway, roll and yaw. We note that pitch motions could be included in the same framework, while heave compensation should be handled by specific heave compensation equipment since thrusters will usually not provide a significant heave force. We also note that horizontal plane motions of e.g. crane tips could to some extent be compensated for using special mechanisms as an alternative to DP control [6].

Roll and pitch motions are first order wave frequency motions that require rapid thruster responses to compensate. This is in contrast to conventional DP control, where wave filtering is used to remove the effects of first order waves to reduce power consumption, and tear and wear on thrusters and machinery [5].

Especially semi-submersible vessels that have small water plane area and large vertical dimensions, there may be significant couplings between the horizontal and vertical motions. Hence, the roll and pitch motions can be large. In [8, 16], roll and pitch rate damping are proposed as an integral part of the DP control for semi-submersibles to reduce undesired thruster-induced roll and pitch motions, which in some cases also leads to improve positioning control accuracy. Separate roll damping and horizontal plane DP control is considered in [9, 20, 21], while DP control of ships considering all 6 degrees-of-freedom is also considered in [12]. In these references, the main objective is to avoid thruster-induced wave-frequency motions in roll and pitch through a combination of roll damping control and wave filtering. There is no explicit aim to counteract the wave-induced motions in surge, sway and yaw, hence relatively slow thrusters are considered sufficient in these references.

In some applications, it is important to actively compensate for first-order wave-induced motions in surge, sway and yaw. Then the thrusters need to respond quickly to make significant changes in thrust during individual wave periods. For example, Voith-Schneider thrusters have been considered for this purpose [15]. The thrust allocation problem for such thrusters, considering also its roll moment, is studied in [11]. One approach to compensate for first-order wave induced motions is acceleration feedback that commands a force that is opposite to the acceleration to damp oscillatory linear motions by effectively increasing the inertia of the vessel in the surge, sway and yaw axes [10, 13]. In [7], we have compared different approaches to first-order wave motion compensation in DP, including acceleration feedback, feed-forward using wave force prediction, optimally tuned wave filtering, and roll compensation. The results indicated that the combination of wave prediction and roll compensation gave the best results. This has motivated the current paper, that presents some improvements, extensions and deeper analysis of the method of [7]. We propose a systematic DP control design method where the objective is to compensate for the first-order wave-induced motion at an arbitrarily chosen DP point of interest on the vessel. The problem is formulated in terms of the horizontal position and heading, as in conventional DP control, and the effects of the roll angle and moment are included through dynamic models that account for the offset between the center of rotation and the DP point of interest, as well as the moment arm between the center of gravity and the thrusters. The novel contributions, compared to the references reviewed above, are

  • The case study involves a relatively small ship, which has very different hydrodynamics than semi-submersible vessel that have been the focus for most previous references on roll compensation in DP.

  • The dependency between sway and roll motions are modelled and accounted for in a more systematic (less ad.hoc) way in the wave prediction, thrust allocation and controller compared to [7]. The use of a 3-dof thrust vector definition leads to a more clear separation of the control and thrust allocation problems, where we consider the fact that sway and roll motions are inherently dependent and must be carefully modelled to ensure controllability.

  • The wave-force estimation method and its use for wave-prediction feed-forward is reformulated into a form that inherently accounts for the combined effect of feedback and feed-forward. It is also shown that it effectively leads to an increased vessel inertia, similar to acceleration feed-forward.

  • Thruster biasing is used to achieve favourable operating conditions and faster responses of the thrusters, by avoiding operation close to zero thrust.

Section 2 introduces the control model and the feedback and feed-forward control algorithms. Section 3 describes the case study, and the solution to the thrust allocation problem, including thruster biasing, for the specific thruster configuration of the considered ship. It also provides a frequency analysis of the closed loop performance, and simulation results. Conclusions are given in Sect. 4.

2 Control design

2.1 Vessel dynamics

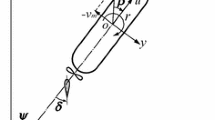
The vessels position and velocity are defined relative to a navigation coordinate frame, which is a Cartesian coordinate system where the first axis is aligned with the desired heading of the vessel, the third axis points down towards the center of the Earth, and the second axis completes the right-handed coordinate system. Consider a reference point that is fixed on the ship, here called CO (center of origin) that defines the origin of the body-fixed coordinate frame that has its first axis to the front, the second axis to starboard, and the third axis down.

The dynamics of a marine vessel can be formulated by its kinematics [3],

$$\begin{aligned} \varvec{{\dot{\eta }}} = \varvec{J(\eta )} \varvec{\nu } \end{aligned}$$
(1)

and kinetics

$$\begin{aligned} {\varvec{M}} \varvec{{\dot{\nu }}} + {\varvec{C}}(\varvec{\nu })\varvec{\nu } + {\varvec{D}}(\varvec{\nu })\varvec{\nu } + {\varvec{g}}(\varvec{\eta }) = \varvec{B^{\prime }}\varvec{\tau } + \varvec{\tau }_\mathrm{{wave}} + \varvec{\tau }_\mathrm{{wind}} + \varvec{\tau }_\mathrm{{curr}} \end{aligned}$$
(2)

where \(\varvec{\eta } = [x,y,z,\phi ,\theta ,\psi ]^T\) is the generalized position of the CO relative to the navigation frame and decomposed in the navigation frame, where the Cartesian coordinates x, y, z define this position. Moreover, \(\varvec{\nu } = [u,v,w,p,q,r]^T\) is the generalized velocity vector of the CO relative to the navigation frame, and decomposed in the body frame. The linear velocity components are u, v, w, the variables \(\phi ,\theta ,\psi \) are the Euler angles (roll, pitch and yaw), and p, q, r are the corresponding angular rates. The block diagonal transformation matrix used in (2) is defined as

$$\begin{aligned} \varvec{J(\eta )} = \text{ blockdiag }[\varvec{{\mathscr {R}}}(\phi ,\theta ,\psi ),\varvec{{\mathscr {T}}}(\phi ,\theta ,\psi )] \end{aligned}$$
(3)

where \(\varvec{{\mathscr {R}}}(\phi ,\theta ,\psi )\) is the standard rotation matrix describing the rotation from the navigation frame to the body frame, and \(\varvec{{\mathscr {T}}}(\phi ,\theta ,\psi )\) is the standard angular velocity transformation matrix [3]. \({\varvec{M}}\) is the inertia matrix, including hydrodynamic added mass, \({\varvec{D}}(\varvec{\nu })\) is the damping matrix, \({\varvec{C}}(\varvec{\nu })\varvec{\nu }\) represents centripetal forces, \(\varvec{B^{\prime }}\) is the control effect matrix, \({\varvec{g}}(\varvec{\eta })\) represents restoring forces, and \(\varvec{\tau }_\mathrm{{wave}}, \varvec{\tau }_\mathrm{{wind}}, \varvec{\tau }_\mathrm{{curr}}\) are vectors with the indicated environmental forces.

The thruster-generated moment in roll is proportional to the sway force from the thrusters and the vertical component of the moment arm of the thrusters, \(\ell _z\), which is assumed to be the same for all thrusters. In this case, the sway force and roll moment cannot be controlled independently, and to achieve controllability in the DP control problem formulation, the thruster control force vector uses only three independent components, \(\varvec{\tau } = [\tau _\mathrm{{surge}}, \tau _\mathrm{{sway}}, \tau _\mathrm{{yaw}}]^T\), since \(\tau _\mathrm{{roll}} = -\ell _z \tau _\mathrm{{sway}}\). We note that [7] also included the roll moment in the control force vector, which lead to loss of controllability and ad.hoc. approaches in the control design and thrust allocation, that are avoided here.

2.2 Control model and LQR problem formulation

The DP control problem can be defined in terms of a different position than the CO. The DP point of interest is therefore defined as an arbitrary point that is considered to be fixed on the ship with an offset defined by a vector \({\varvec{r}}\) that points from the CO to the DP point of interest, e.g. the bearing point of a crane wire, drill string or gangway. This translation defines the DP position coordinate of interest

$$\begin{aligned}{}[x_\mathrm{{DP}}, y_\mathrm{{DP}}, z_\mathrm{{DP}}]^T = [x, y, z]^T + \varvec{{\mathscr {R}}}(\phi ,\theta ,\psi ) {\varvec{r}} \end{aligned}$$
(4)

We consider the station-keeping problem where we assume that variations in the yaw angle are small, and furthermore assume that the navigation coordinate frame is aligned with the desired heading such that \(\psi \) is close to zero. With a small angle approximation we can use \(\sin (\alpha ) \approx \alpha \) and \(\cos (\alpha ) \approx 1\), which leads to the following approximation [3]

$$\begin{aligned} \varvec{\eta }_\mathrm{{DP}}^{\prime } = {\varvec{T}}_\mathrm{{DP}} \varvec{\eta } \end{aligned}$$
(5)

where \(\varvec{\eta }_\mathrm{{DP}}^{\prime } = [x_\mathrm{{DP}},y_\mathrm{{DP}},z_\mathrm{{DP}},\phi ,\theta ,\psi ]^T\), and the constant linear transformation matrix is defined by

$$\begin{aligned} {\varvec{T}}_\mathrm{{DP}} = \begin{bmatrix} {\varvec{I}}_{3x3} &{} \varvec{{\mathscr {S}}}({\varvec{r}})^T \\ {\varvec{0}}_{3x3} &{} {\varvec{I}}_{3x3} \end{bmatrix} \end{aligned}$$
(6)

where \(\varvec{{\mathscr {S}}}({\varvec{r}})\) defines the skew symmetric matrix on SO(3) that implements the vector cross-product \( {\varvec{a}} \times {\varvec{b}} = \varvec{{\mathscr {S}}}({\varvec{b}}) {\varvec{a}}\).

In this paper we will consider only the effects of the roll angle and moment, and neglect the pitch and heave motions. The reasons for this is that the pitch moment that can typically be achieved by thrusters is far less than the pitch moment resulting from environmental forces, i.e. the prospect of influencing pitch motions is much less. Furthermore, thrusters usually do not have much effect on heave, and separate heave compensation systems are commonly used in marine operations. We also remark that while the first assumption above may not hold e.g. for semi-submersible vessels, as reviewed in the introduction, including pitch is rather straight-forward. For simplicity we consider only the vertical offset, such that \({\varvec{r}} = [0,0,d]^T\) with d being the vertical distance from the CO to the DP point of interest. Using (6) leads to

$$\begin{aligned} \begin{aligned}&x_\mathrm{{DP}} = x + d \, \sin (\theta ) \ \approx \ x + d\theta \\&y_\mathrm{{DP}} = y - d \, \sin (\phi ) \ \approx \ y - d\phi \\&z_\mathrm{{DP}} = z + d \, \cos (\theta )\cos (\phi ) \ \approx \ z + d \end{aligned} \end{aligned}$$
(7)

In the control problem formulation we consider the position \(\varvec{\eta }_\mathrm{{DP}} = [x_\mathrm{{DP}}, y_\mathrm{{DP}}, \psi ]^T \in {\mathbb {R}}^{3}\) and generalized velocities \(\varvec{\nu }_\mathrm{{DP}} = [u,v,p,r]^T \in {\mathbb {R}}^{4}\). We note that the roll and pitch angles are not states in the model, but they are implicit in the DP position of interest and their measurements are necessary to compute \(\varvec{\eta }_\mathrm{{DP}}\), see (7). Notice the kinetic model also includes the roll dynamics, and has roll rate as a state. This means that the roll moment will be included in the thruster effect matrix, in addition to the surge force, sway force and yaw moment:

$$\begin{aligned} \varvec{B^{\prime }} = \begin{bmatrix} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} -\ell _z &{} 0 \\ 0 &{} 0 &{} 1 \end{bmatrix} \end{aligned}$$
(8)

where \(\ell _z\) is the vertical moment arm of the thrusters. In this setup the sway control input \({\tau }_\mathrm{{sway}}\) has also a direct effect on the roll moment: \({\tau }_\mathrm{{roll}} = -\ell _z {\tau }_\mathrm{{sway}}\). This matches the definition of the DP sway position of interest \(y_\mathrm{{DP}} = y - d \sin (\phi )\) that is affected by the roll angle \(\phi \), and \({\dot{y}}_\mathrm{{DP}}\) is affected by the roll rate p through

$$\begin{aligned} \dot{\varvec{\eta }}_\mathrm{{DP}} = {\varvec{J}}_\mathrm{{DP}} \varvec{\nu }_\mathrm{{DP}} \end{aligned}$$
(9)

where

$$\begin{aligned} {\varvec{J}}_\mathrm{{DP}} = \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} -d &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \end{bmatrix} \end{aligned}$$
(10)

Integral action is useful to compensate for unknown slowly time-varying environmental disturbances (ocean current, second order waves, and unmeasured wind). The integral error state \({\varvec{z}} \in {\mathbb {R}}^{3}\) is therefore introduced:

$$\begin{aligned} \varvec{{\dot{z}}} = \varvec{\eta }_\mathrm{{DP}} - \varvec{\eta }_\mathrm{{DP}}^\mathrm{{ref}} \end{aligned}$$
(11)

where \(\varvec{\eta }_\mathrm{{DP}}^\mathrm{{ref}}\) is the DP reference point (control setpoint). We assume the navigation coordinate frame is defined such that the desired position of the vessel’s DP point of interest is in its origin. Then the control objective is to regulate \(\varvec{\eta _\mathrm{{DP}}}\) to \(\varvec{\eta }_\mathrm{{DP}}^\mathrm{{ref}} = 0\), and by choosing the state vector \({\varvec{x}} = [ {\varvec{z}},\varvec{\eta _\mathrm{{DP}}}, \varvec{\nu }_\mathrm{{DP}}]^T \in {\mathbb {R}}^{10}\) the following linear state space model is obtained:

$$\begin{aligned} \varvec{{\dot{x}}} = {\varvec{A}}{\varvec{x}} + {\varvec{B}}\varvec{\tau } + {\varvec{E}}\varvec{\tau }_\mathrm{{env}} \end{aligned}$$
(12)

where \(\varvec{\tau }_\mathrm{{env}} = \varvec{\tau }_\mathrm{{wave}} + \varvec{\tau }_\mathrm{{wind}} + \varvec{\tau }_\mathrm{{curr}}\), and the system matrices are defined as

$$\begin{aligned} {\varvec{A}} = \begin{bmatrix} {\varvec{0}}_{3x3} &{} {\varvec{I}}_{3x3} &{} {\varvec{0}}_{3x4} \\ {\varvec{0}}_{3x3} &{} {\varvec{0}}_{3x3} &{} {\varvec{J}}_\mathrm{{DP}} \\ {\varvec{0}}_{4x3} &{} {\varvec{0}}_{4x3} &{} -{\varvec{M}}_\mathrm{{DP}}^{-1}{\varvec{D}}_\mathrm{{DP}} \end{bmatrix} \end{aligned}$$
(13)

and

$$\begin{aligned} {\varvec{B}} = \begin{bmatrix} {\varvec{0}}_{3x3} \\ {\varvec{0}}_{3x3} \\ {\varvec{M}}_\mathrm{{DP}}^{-1}\varvec{B^{\prime }} \end{bmatrix}, \ \ \ \ \ \ {\varvec{E}} = \begin{bmatrix} {\varvec{0}}_{3x3} \\ {\varvec{0}}_{3x3} \\ {\varvec{M}}_\mathrm{{DP}}^{-1} \end{bmatrix} \end{aligned}$$
(14)

In deriving this model based on (2), the following modifications have been made

  • The nonlinear damping has been linearized about zero speed, since there is generally small linear velocity in DP.

  • The centripetal terms have been neglected since these forces are found to be small compared to first order wave forces and thruster forces.

  • \({\varvec{M}}_\mathrm{{DP}}\) and \({\varvec{D}}_\mathrm{{DP}}\) are submatrices of \({\varvec{M}}\) and \({\varvec{D}}\), respectively, corresponding to the variables in \(\varvec{\nu }_\mathrm{{DP}}\).

  • Restoring forces have not been included in the DP model, since the effect of the roll angle is measured through the roll rate in the model, and will thus be considered in the feedback control design.

The control command is defined as

$$\begin{aligned} \varvec{\tau }_c = \varvec{\tau }_\mathrm{{FB}} - \varvec{\tau }_\mathrm{{FF}} \end{aligned}$$
(15)

where \(\varvec{\tau }_\mathrm{{FF}} \in {\mathbb {R}}^{3}\) is a feed-forward term that is designed to compensate for external (environmental) forces, and \(\varvec{\tau }_\mathrm{{FB}} \in {\mathbb {R}}^{3}\) is a feedback control term. With the stated assumptions, the control plant model (12) is linear, time-invariant, and controllable. We use the standard LQR-method to compute a linear state-feedback

$$\begin{aligned} \varvec{\tau }_\mathrm{{FB}} = {\varvec{K}}_{LQ} {\varvec{x}} \end{aligned}$$
(16)

with gain matrix \({\varvec{K}}_{LQ}\) that minimizes the quadratic costs on the states weighted by the positive semi-definite symmetric matrix \({\varvec{Q}}\), and the control input by the positive definite symmetric matrix \({\varvec{R}}\), [1, 3]:

$$\begin{aligned} J_{LQ} = \frac{1}{2}{\varvec{x}}^T{\varvec{Q}}{\varvec{x}} \; + \; \frac{1}{2}\varvec{\tau }_\mathrm{{FB}}^T{\varvec{R}}\varvec{\tau }_\mathrm{{FB}} \end{aligned}$$
(17)

2.3 Feed-forward control

The optional feed-forward control term \(\varvec{\tau }_\mathrm{{FF}}\) is intended to compensate for dynamic disturbances, specifically first order wave forces since wind and current disturbances are less dynamic and can therefore be compensated for using integral action. First order wave compensation will in most practical cases be limited by thrusters’ dynamic response. To compensate for lags in the thrust response, the first order wave feed-forward compensation will strongly benefit from a prediction of the wave-induced forces, using a prediction horizon that matches the thruster lag. Here, we refine the method proposed in [7] that use a linear model-based prediction approach. This method uses acceleration and velocity measurements \(\dot{\varvec{\nu }}_\mathrm{{DP}}\) and \(\varvec{\nu }_\mathrm{{DP}}\) to predict the velocity components induced by the waves by subtracting other known induced velocity components. Under the assumption of linear vessel dynamics, the induced velocity components can be separated into \(\varvec{\nu }_\mathrm{{thr}}\) and \(\varvec{\nu }_\mathrm{{wave}}\) for thruster- and wave-induced velocity components, respectively, by using the superpositioning principle. This gives the following relations

$$\begin{aligned} \varvec{\nu }_\mathrm{{DP}}&= \varvec{\nu }_{thr} + \varvec{\nu }_\mathrm{{wave}} + \varvec{\nu }_\mathrm{{wind}} + \varvec{\nu }_{curr} \end{aligned}$$
(18a)
$$\begin{aligned} {\varvec{B}}^{\prime } \varvec{\tau }&= {\varvec{M}}_\mathrm{{DP}} \dot{\varvec{\nu }}_\mathrm{{thr}} + {\varvec{D}}_\mathrm{{DP}} \varvec{\nu }_\mathrm{{thr}} \end{aligned}$$
(18b)
$$\begin{aligned} \varvec{\tau }_\mathrm{{wave}}&= {\varvec{M}}_\mathrm{{DP}}\dot{\varvec{\nu }}_\mathrm{{wave}}+{\varvec{D}}_\mathrm{{DP}}\varvec{\nu }_\mathrm{{wave}} \end{aligned}$$
(18c)

Assuming \(\dot{\varvec{\nu }}_\mathrm{{wind}}=0\) and \(\dot{\varvec{\nu }}_\mathrm{{curr}}=0\), some manipulation of (18) gives

$$\begin{aligned} \begin{aligned} \varvec{\tau }_\mathrm{{wave}}&= {\varvec{M}}_\mathrm{{DP}} \dot{\varvec{\nu }}_\mathrm{{DP}} + {\varvec{D}}_\mathrm{{DP}} \varvec{\nu }_\mathrm{{DP}} - {\varvec{B}}^{\prime } \varvec{\tau } \end{aligned} \end{aligned}$$
(19)

where the static effects of wind and current are not included in (19). The actual thrust force \(\varvec{\tau }\) is not known, hence we propose to use the commanded control force \(\varvec{\tau _{c}}\) instead. To get a better estimate of the actual thrust force, a lag filter represented by the transfer matrix \({\varvec{H}}(s)\) is used as a first order approximation of the thruster dynamics:

$$\begin{aligned} \varvec{\tau }&= {\varvec{H}}(s) \varvec{\tau }_c \end{aligned}$$
(20a)
$$\begin{aligned} {\varvec{H}}(s)&= \frac{1}{Ts+ 1} {\varvec{I}}_{3 \times 3} \end{aligned}$$
(20b)

The feed-forward is then defined by

$$\begin{aligned} \varvec{\tau }_\mathrm{{FF}}= & {} {\varvec{H}}^{*}(s) {\varvec{G}} \varvec{\tau }_\mathrm{{wave}} \nonumber \\= & {} {\varvec{H}}^{*}(s) {\varvec{G}} ({\varvec{M}}_\mathrm{{DP}} \dot{\varvec{\nu }}_\mathrm{{DP}} + {\varvec{D}}_\mathrm{{DP}} \varvec{\nu }_\mathrm{{DP}}) - {\varvec{H}}^{*}(s) {\varvec{G}} {\varvec{B}}^{\prime } {\varvec{H}}(s) \varvec{\tau }_c \end{aligned}$$
(21)

where

$$\begin{aligned} {\varvec{G}} = \begin{bmatrix} g_\mathrm{{surge}} &{} 0 &{} 0 &{} 0 \\ 0 &{} g_\mathrm{{sway}} &{} g_\mathrm{{roll}} &{} 0 \\ 0 &{} 0 &{} 0 &{} g_\mathrm{{yaw}} \end{bmatrix} \end{aligned}$$
(22)

has non-negative elements that map the wave-induced generalized force to thruster generalized forces. The wave feed-forward \(\varvec{\tau }_\mathrm{{FF}}\) is filtered with an inverse lag filter of the thruster dynamics \({\varvec{H}}^*(s)\) to partly compensate for negative effects due to thruster dynamic lag. The inverse filter is essentially the inverse of \({\varvec{H}}(s)\) defined in (20b) with an added term in the denominator to maintain a proper transfer function:

$$\begin{aligned} {\varvec{H}}^*(s) = \frac{Ts + 1}{\alpha Ts+ 1} {\varvec{I}}_{3 \times 3} \end{aligned}$$
(23)

where \(\alpha \in (0,1)\) is typically small such that

$$\begin{aligned} {\varvec{H}}(j\omega ) {\varvec{H}}^{*}(j\omega ) = \frac{1}{\alpha Tj\omega + 1}{\varvec{I}}_{3 \times 3} \approx {\varvec{I}}_{3 \times 3} \end{aligned}$$
(24)

holds for frequencies \(\omega \) up to an including significant wave frequencies. Using this approximation in (21), the total control input can be rearranged to

$$\begin{aligned} \varvec{\tau }_c = ({\varvec{I}}-{\varvec{G}} {\varvec{B}}^{\prime })^{-1} \left( \varvec{\tau }_\mathrm{{FB}} - \varvec{\tau }_\mathrm{{FF}}^{\prime } \right) \end{aligned}$$
(25)

where it is assumed that \({\varvec{G}}\) is chosen with sufficiently small positive elements such that \({\varvec{I}}-{\varvec{G}} {\varvec{B}}^{\prime }\) is non-singular, and we have defined

$$\begin{aligned} \varvec{\tau }_\mathrm{{FF}}^{\prime } = {\varvec{H}}^*(s) {\varvec{G}} \left( {\varvec{M}}_\mathrm{{DP}}\dot{\varvec{\nu }}_\mathrm{{DP}} + {\varvec{D}}_\mathrm{{DP}}\varvec{\nu }_\mathrm{{DP}}\right) \end{aligned}$$
(26)

The control force \(\varvec{\tau }_c\) is no longer part of the feed-forward term, which makes it causal and implementable. Notice the feed-forward gain matrix is also affecting the output from the LQ controller. The structure of the DP controller is illustrated in Fig. 1.

Fig. 1
figure 1

DP controller structure

Full size image

Rearranging these equations, we get

$$\begin{aligned}&\left( {\varvec{I}} + \varvec{\varDelta } \right) \cdot \left( {\varvec{M}}_\mathrm{{DP}}\dot{\varvec{\nu }}_\mathrm{{DP}} + {\varvec{D}}_\mathrm{{DP}}\varvec{\nu }_\mathrm{{DP}}\right) =\varvec{\tau }_{env} \nonumber \\&\quad + {\varvec{B}}^{\prime } \left( {\varvec{I}} - {\varvec{G}} {\varvec{B}}^{\prime } \right) ^{-1} {\varvec{H}}(s) \varvec{\tau }_\mathrm{{FB}} \end{aligned}$$
(27)

where \(\varvec{\varDelta } = {\varvec{B}}^{\prime } \left( {\varvec{I}} - {\varvec{G}} {\varvec{B}}^{\prime } \right) ^{-1} {\varvec{G}}\). We observe that with suitable \({\varvec{G}}\) that leads to \(\varvec{\varDelta } > 0\), the feed-forward has a similar effect as acceleration feedback with increased inertia, [10, 13].

This control structure is designed to be independent of the specifics of the thruster system. As usual in DP, a thrust allocation algorithm is then used to compute the thrust required from each specific thruster to generate the total desired forces and moments from the controller. We note that in our DP control problem formulation, the coupling between the sway and roll dynamics are accounted for in the controller’s computation of \(\tau _{sway}\) that will consider the combined effect of sway and roll motions on the \(y_\mathrm{{DP}}\) position. Since the roll moment is accounted for in the controller, so it will not be considered by the thrust allocation problem and there will be no conflicting objectives. The thrust allocation can therefore be solved using standard methods, e.g. [3], with the note that the requirement for fast response to counteract wave forces may favour the use of thrust biasing in the thrust allocation.

We note that the proposed controller differs from a conventional DP controller in the following way:

  • The effect of roll in the model used for LQ tuning is neglected in conventional DP controllers, which corresponds to \(\ell _z = 0\) and \(d=0\).

  • There is usually no wave force compensation in conventional DP controllers, i.e. \({\varvec{G}} = 0\).

  • Conventional DP controllers using wave filtering to avoid that thrusters are used to compensate for waves.

3 Case study

A motivating case for this research is illustrated in Fig. 2, with a relatively small exemplary surface ship having a length of 24 m, beam 7.5 m, draft 4.1 m and a mass of about 162 tons. The ship’s operability for launch and recovery of Remotely Operated Vessels (ROVs) for underwater inspection, maintenance and repair (IMR) depends critically on the magnitude of the wave frequency motion of the ship, since large motions increase the risk for damage to the ROV. DP is commonly used during launch and recovery, and the point of interest is the latching point of the LARS which in Fig. 2 is located at the lower end of the moonpool that extends below the keel. Two 500 kW azimuth thrusters with a diameter of 1.9 m and a Bollard pull thrust of 117 kN have been assumed for this study, as illustrated in Fig. 3, with the bow and aft thruster indexed 1 and 2 respectively.

Fig. 2
figure 2

Exemplar illustration of ROV launched and recovered from a relatively small ship. Courtesy Kongsberg Maritime

Full size image
Fig. 3
figure 3

Configuration of azimuth thrusters. Upper part illustrates the horizontal xy-plane (seen from above), while the lower part illustrates the vertical xz-plane (seen from the side)

Full size image

With reference to the models above, in this example the vertical moment arm is \(\ell _z = 2.0 \ m\), and the vertical offset is \(d = 2.32 \ m\). They are therefore significant when compared to the horizontal moment arms \(\ell _{x1} = \ell _{x2} = 9.0 \ m\). The CO is placed midships in the water line.

The purpose of the simulation case study is to compare the proposed controller having roll motion compensation with a conventional DP controller that does not attempt to compensate for wave-induced motions.

3.1 Vessel model and simulator

A realistic simulation model is developed based on the MSS toolbox [4] in Matlab/Simulink, use of WAMIT for hydrodynamic computations [19], and dynamic thruster models [2]. The model is formulated in six degrees of freedom including centripetal terms, restoring forces, current and wind coefficients as well as the frequency-dependent WAMIT coefficients for added mass, damping and fluid memory effects. The frequency-dependent parameters are converted to a linear time-invariant state-space realization of Cummins equation using the method in [14].

3.2 Controller tuning

With the selected state space, the structure of the LQR is equivalent to a PID controller, where the cost matrices are the tuning parameters. The control cost matrix \({\varvec{R}}\) has the following form

$$\begin{aligned} {\varvec{R}} = \text{ diag } \{ r_\mathrm{{surge}}, r_\mathrm{{sway}},r_\mathrm{{yaw}}\} \end{aligned}$$
(28)

The cost parameter for each degree of freedom is found in Table 1, where \(r_\mathrm{{yaw}} = 1/9^2 \) is due to the horizontal moment arms of \(\ell _{x1} = \ell _{x2} = 9 \ m\) to the thrusters, making 1 degree heading error as costly as 1 meter position error. Tuning parameters of the \({\varvec{Q}}\)-matrix are defined similarly to the definitions in [7]. The cost matrix is diagonal and can be split into blocks corresponding to the integral error state, position and velocity, respectively

$$\begin{aligned} {\varvec{Q}} = \text{ blockdiag }\{{\varvec{Q}}_{{\varvec{z}}}, \ {\varvec{Q}}_{\varvec{\eta }}, \ {\varvec{Q}}_{\varvec{\nu }}\} \end{aligned}$$
(29)

where the state cost parameters for each degree of freedom lies in the corresponding block diagonal matrix. Each block matrix is tuned with a control effect cost parameter \(q_i\) for \(i = \{1,2,3\}\) corresponding to integral, proportional, and derivative action of the controller. Additionally, each block matrix is scaled with a cost \(q_ {dof}\) for \({dof} \in \mathrm{\{surge, sway, roll,yaw\}}\). This results in the following matrices

$$\begin{aligned} {\varvec{Q}}_{{\varvec{z}}}&= q_1 \text{ diag }\{q_\mathrm{{surge}} , q_\mathrm{{sway}}, q_\mathrm{{yaw}} \} \end{aligned}$$
(30a)
$$\begin{aligned} {\varvec{Q}}_{\varvec{\eta }}&= q_2 \text{ diag }\{q_\mathrm{{surge}}, q_\mathrm{{sway}}, q_\mathrm{{yaw}} \} \end{aligned}$$
(30b)
$$\begin{aligned} {\varvec{Q}}_{\varvec{\nu }}&= q_3 \text{ diag }\{q_\mathrm{{surge}}, q_\mathrm{{sway}}, q_\mathrm{{roll}}, q_\mathrm{{yaw}} \} \end{aligned}$$
(30c)

Tuning of the controllers is obtained experimentally through time domain simulations throughout the sea states of interest. The tuning parameters for the LQR and the feed-forward gain matrix \({\varvec{G}}\) is found in Tables 1 and 2, respectively.

Summarized, the controllers are tuned equally across the mutual parameters. Hence the roll damping controller is tuned equal to the roll damping with feed-forward but with zero feed-forward gain \({\varvec{G}}\). The same applies for the benchmark controller, which is tuned equal to the roll damping controller, but with \(q_{roll} = 0\).

Table 1 Cost parameters in the LQR
Full size table
Table 2 Feed Forward
Full size table

3.3 Frequency analysis

The performance of the different controllers can be analysed by looking at the frequency responses of the open- and closed-loop transfer functions in surge, sway and yaw respectively. In station-keeping control the focus is on the frequency response from disturbance (ocean waves) to the positioning error. The system model for the frequency analysis is

$$\begin{aligned} \varvec{\dot{\tilde{x}}}= & {} \tilde{{\varvec{A}}} \varvec{\tilde{x}} + \tilde{{\varvec{B}}} \varvec{\tau }_\mathrm{{env}} \end{aligned}$$
(31)
$$\begin{aligned} \varvec{\eta }_\mathrm{{DP}}= & {} \varvec{\tilde{C}} \varvec{\tilde{x}} \end{aligned}$$
(32)

where the state vector is \(\varvec{\tilde{x}} = [ {\varvec{z}}, \varvec{\eta }_\mathrm{{DP}}, \varvec{\nu }_\mathrm{{DP}}, \varvec{\tau }]^T\),

$$\begin{aligned} \tilde{{\varvec{A}}} = \begin{bmatrix} {\varvec{0}}_{3x3} &{} {\varvec{I}}_{3x3} &{} {\varvec{0}}_{3x4} &{} {\varvec{0}}_{3x4} \\ {\varvec{0}}_{3x3} &{} {\varvec{0}}_{3x3} &{} {\varvec{J}}_\mathrm{{DP}} &{} {\varvec{0}}_{3x4} \\ {\varvec{0}}_{4x3} &{} {\varvec{0}}_{4x3} &{} \ \ -{\varvec{M}}_\mathrm{{DP}}^{-1} {\varvec{D}}_\mathrm{{DP}} \ \ &{} {\varvec{M}}_\mathrm{{DP}}^{-1}{\varvec{N}} \\ {\varvec{K}}_{z}/T &{} {\varvec{K}}_{\eta }/T &{} {\varvec{K}}_{\nu }/T &{} -{\varvec{I}}_{3 \times 3}/T \\ \end{bmatrix} \end{aligned}$$
(33)

where \({\varvec{N}} = \left( {\varvec{I}} + \varvec{\varDelta } \right) ^{-1} {\varvec{B}}^{\prime } \left( {\varvec{I}} - {\varvec{G}} {\varvec{B}}^{\prime } \right) ^{-1}\) and

$$\begin{aligned} \tilde{{\varvec{B}}}= & {} \begin{bmatrix} {\varvec{0}}_{3x4} \\ {\varvec{0}}_{3x4} \\ {\varvec{M}}_\mathrm{{DP}}^{-1}\left( {\varvec{I}} + \varvec{\varDelta } \right) ^{-1}\\ {\varvec{0}}_{4x4} \end{bmatrix} \end{aligned}$$
(34)
$$\begin{aligned} \tilde{{\varvec{C}}}= & {} [{\varvec{0}}_{3x3}, \ {\varvec{I}}_{3x3}, \ {\varvec{0}}_{3x4}, \ {\varvec{0}}_{3x4}] \end{aligned}$$
(35)

For station-keeping, the effect of environmental disturbance forces on the position error is of primary concern. The frequency response from the disturbance force \(\varvec{\tau }_\mathrm{{env}}\) to the position error \(\varvec{\eta }_\mathrm{{DP}}\) is shown in Fig. 4. The roll compensating controller performs equally to the benchmark LQ in surge and yaw, which is expected since they are essentially the same controller. The key difference is in sway, where roll compensation outperforms the benchmark controller from 0.1 to 1 rad/s. Considering ocean waves, this corresponds to wave periods from approximately 6–60 s. For a typical ocean wave spectrum the peak wave frequencies is within this frequency band, hence the roll compensation is expected to be superior to the benchmark controller.

The frequency analysis shows the positive effect on the control performance by including the feed-forward term. The magnitude plot in Fig. 4 shows that the feed-forward control reduces the sensitivity to the environmental disturbances at all frequencies, and has a significant effect for typical wave frequencies (0.3–1.0 rad/s).

It can be noted that for frequencies below 0.1rad/s the benchmark LQR is better, suggesting the benchmark controller will handle slow varying drifting disturbances such as ocean current, wind gusts and second order wave drift better than the roll compensating controller. This could be improved by introducing e.g. feed-forward from wind measurements, but this is not pursued any further since the main point of this paper is on wave-frequency motion compensation.

Fig. 4
figure 4

Frequency response from disturbance to position of the USV using different controllers

Full size image

3.4 Thrust allocation

The equations for the desired generalized body forces/moments are

$$\begin{aligned} \underset{ \begin{array}{c} \varvec{\tau _c} \end{array}}{\begin{bmatrix} \tau _\mathrm{{surge}} \\ \tau _\mathrm{{sway}} \\ \tau _\mathrm{{yaw}} \end{bmatrix}} = \underset{ \begin{array}{c} {\varvec{T}}_e \end{array}}{ \begin{bmatrix} 1 &{} 0 &{} 1 &{} 0 \\ 0 &{} 1 &{} 0 &{} 1 \\ 0 &{} \ell _{x1} &{} 0 &{} -\ell _{x2} \end{bmatrix}} \underset{ \begin{array}{c} {\varvec{u}}_e \end{array}}{ \begin{bmatrix} F_{x,1} \\ F_{y,1} \\ F_{x,2} \\ F_{y,2} \end{bmatrix}} \end{aligned}$$
(36)

The commanded generalized thrust in the body frame \(\varvec{\tau }_c\) is described using the extended configuration matrix \({\varvec{T}}_e\) together with the component forces of each thruster: \(F_{x,i}\) and \(F_{y,i}\). Assuming the configuration matrix has full rank, the solution can be found by solving the equation for the thrust components \({\varvec{u}}_e\). The thrust allocation for this case study uses the standard Moore-Penrose pseudo-inverse:

$$\begin{aligned} {\varvec{u}}_e = {\varvec{T}}_e^{\dagger } \; \varvec{\tau }_c \end{aligned}$$
(37)

This simple approach is sufficient for the simulation study that considers conditions where the thrusters do not saturate, and we note that the method can easily be replaced by more advanced method that can optimally handle saturation and other constraints [3].

The azimuth angle of thruster i is found by trigonometry,

$$\begin{aligned} \alpha _i = \text{ atan2 }(F_{y,i},F_{x,i}) \end{aligned}$$
(38)

while the desired thrust is found by solving the thrust allocation problem for the thrust force \({\varvec{u}}\) with a configuration matrix \({\varvec{T}}(\varvec{\alpha })\) from the new desired azimuth angles,

$$\begin{aligned} \underset{ \begin{array}{c} \varvec{\tau _c} \end{array}}{\begin{bmatrix} \tau _\mathrm{{surge}} \\ \tau _\mathrm{{sway}} \\ \tau _\mathrm{{yaw}} \end{bmatrix}} = \underset{ \begin{array}{c} {\varvec{T}}(\varvec{\alpha }) \end{array}}{ \begin{bmatrix} \cos (\alpha _1) &{} \cos (\alpha _2) \\ \sin (\alpha _1) &{} \sin (\alpha _2) \\ \ell _{x1} \sin (\alpha _1) &{} -\ell _{x2} \sin (\alpha _2) \end{bmatrix}} \underset{ \begin{array}{c} {\varvec{u}} \end{array}}{ \begin{bmatrix} F_1 \\ F_2 \end{bmatrix}} \end{aligned}$$
(39)

where \(F_i = \sqrt{F_{x,i}^2 + F_{y,i}^2}\).

For vessels equipped with redundancy in the thruster system it may be beneficial to set the thrusters to deliver forces which cancel each other out, often referred to as thruster biasing. This will result in a higher average thrust corresponding to operating points where the dynamics of the thruster will be faster. Slowly time-varying environmental forces (wind, current and second-order wave component) will also induce such an effect since the integral effect of the DP controller will cancel these forces. Depending on the magnitude of these forces it may be advantageous with an additional thruster bias. With a thruster configuration with two azimuth thrusters, the bias effect from the environmental forces will not apply uniformly for both thrusters when also considering forbidden sectors that should be implemented in the thrust allocation to protect the ROV from the thruster wake during launch and recovery. Figure 5 shows the different response times for the thruster model used in the simulator. By increasing the bias value to 20% the response time is reduced by approximately 80%.

Fig. 5
figure 5

Response time for different thrust levels

Full size image

From a control point of view, the response time should be minimized using thruster biasing. However, the maximum available thrust will be reduced equivalent to the bias value and must be considered. By also considering fuel consumption, the bias value becomes a trade-off between control performance and power consumption. In typical marine operations, the compensation for wave and roll motion is only required for relatively short periods of time, e.g. during launch or recovery of payloads through the wave zone. Since this control mode is usually used in a short time window, the fuel consumption does not need to be prioritized. Another benefit is the reduction of azimuth angles variations. By increasing the force from each thruster, the azimuth angle changes required to generate a given force in a different direction is typically reduced. Consequently, thruster biasing should result in smaller peak values for the azimuth angle.

A thruster biasing effect can be obtained by modifying the extended thruster allocation in (37), and include a bias term. In this case study we want to avoid pointing the thrusters towards the moonpool. The extended thrust configuration matrix is modified with the diagonal weighting matrix \({\varvec{W}}(\tau _\mathrm{{surge}})\)

$$\begin{aligned} {\varvec{W}}(\tau _\mathrm{{surge}}) = \begin{bmatrix} {\mathscr {H}}(-\tau _\mathrm{{surge}}) &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} {\mathscr {H}}(\tau _\mathrm{{surge}}) &{}0 \\ 0 &{} 0 &{} 0 &{} 1 \end{bmatrix} \end{aligned}$$
(40)

where \({\mathscr {H}}(\cdot )\) is the step function that is defined as

$$\begin{aligned} {\mathscr {H}}(x) := \left\{ \begin{array}{cc} 1\; , &{} \quad x \ge 0 \\ 0\; , &{} \quad x < 0 \end{array} \right. \end{aligned}$$
(41)

By post multiplying the extended thrust configuration matrix \({\varvec{T}}_e\) with the weighting matrix in (40), the unbiased thrust vector \({\varvec{u}}_e^{\prime }\) is obtained. The weighting matrix ensures the desired surge force is allocated only to one of the thrusters, hence the thrusters will not be commanded to produce thrust inwards to the moonpool. Positive and negative surge forces are allocated to the aft and bow thruster, respectively. Before calculating the azimuth angles, the thruster bias force \(F_\mathrm{{bias}}\) is added to the extended thrust elements \(F_{x,i}\) with opposite signs, cancelling each other. The complete extended thrust vector becomes

$$\begin{aligned} \begin{aligned} {\varvec{u}}_e&= {\varvec{u}}_e^{\prime } + {\varvec{u}}_\mathrm{{bias}} \\&= ({\varvec{T}}_e {\varvec{W}}(\tau _\mathrm{{surge}}))^{\dagger }\varvec{\tau }_c + [-F_\mathrm{{bias}}, 0 , F_\mathrm{{bias}},0]^T \\ \end{aligned} \end{aligned}$$
(42)

From the biased extended thrust vector \({\varvec{u}}_e\) the azimuth angles are found according to (38). Subsequently, (39) yields a desired thrust which solves the thrust allocation problem while also including a force with magnitude \(F_{bias}\), inwards from each thruster.

3.5 Wave filtering

The benchmark controller has conventional wave filtering where the main effect of first order wave frequency motion is filtered away from the position and motion measurements. The controllers with roll compensation have significantly less wave filtering since the objective is to counteract first order wave frequency motions. The wave filtering effect must be carefully tuned according to the thruster system’s capacity limitations and dynamic responses. We also remark that for larger vessels this is more difficult to achieve, and one must expect to use more wave filtering.

3.6 Implementation aspects

The implementation of the proposed controller in an industrial DP system is considered to be rather straightforward. The computational complexity is not significantly increased, and the main novel element is the need for acceleration measurements for the wave force compensation. Inertial measurements units (IMUs) are commonly used in industrial DP systems to compensate for the effect of roll and pitch motions on position reference systems such as GNSS antennas and hydroacoustic transceivers. The IMU accelerometers can also be used to estimate the ships linear accelerations in the horizontal plane by additional software functions. The proposed control strategy does not require any new hardware compared to what is common in industrial DP systems today.

3.7 Simulation results

The simulations are run with the three different controllers: DP benchmark controller, DP with roll compensation, and DP with roll compensation and feed-forward. The position of the ship relative to an Earth-fixed point is presented together with thrust usage and thruster azimuth angles. A simulation step size of 0.01 seconds is used with Simulink’s ode3 (Bogacki-Shampine) solver.

First, we present typical simulations for a period of 100 second in a sea state with irregular waves simulated with the JONSWAP spectrum with \(H_s = 3.5\) m and \(T_p = 10.5\) s to get some insight into the control strategy. In this scenario the desired heading is towards north, wind is from north with a magnitude that correlates with the sea state, the current is \(0.3 \ m/s\) from north, and the mean wave direction is from north with spreading such that \(75 \ \%\) of the wave energy are distributed within \(\pm 30\) deg of the mean direction. Figure 6 shows the position and angular error with the three controllers, while the commanded control thrust is shown in Figs. 7 (feedback) and 8 (feed-forward). The actual thruster forces and azimuth angles are shown in Figs. 9 and 10, respectively. The simulation results illustrate that the first-order wave induced motion is significantly reduced with the roll compensating control, and that including a feed-forward from the estimated wave forces further reduces the error. This comes at the cost of increased variations in thruster actions (both thrust and azimuth variations), but without significant increase in average thrust usage.

It is also seen from Fig. 9 that the thruster biasing is effective. The simulations are run with a thruster bias of 20%, corresponding to approximately 23 kN of thrust added to each thruster. As the thruster biasing results in the thrusters pointing outwards, the aft thruster must compensate completely for the slow varying drifting forces such as ocean current and wind. This results in a significantly higher thrust usage of the aft thruster. For the same reason, the bow thruster requires a larger azimuth angle to deliver the same amount of thrust sideways as the aft thruster, resulting in larger oscillations in azimuth angle for the bow thruster. Using less than 20% thrust bias have been tested, and found to give significantly reduced roll compensation effect since the thruster system responses are slower.

Fig. 6
figure 6

Position and angular errors

Full size image
Fig. 7
figure 7

Output \(\tau _{fb}\) from feedback controller

Full size image
Fig. 8
figure 8

Output \(\tau _{ff}\) from feed-forward controller compared to wave forces. We note the under-compensation since the feed-forward gains have being chosen less than one

Full size image
Fig. 9
figure 9

Thruster forces

Full size image
Fig. 10
figure 10

Azimuth angle of thrusters

Full size image

A more systematic simulation study considers time series of 1000 seconds each for a number of relevant sea states. The positioning in east/sway and north/surge are presented separately to demonstrate the performance of the different controllers relative to the environmental forces that always comes from north in these simulations. The results are presented in sea chart tables, displaying the results for each sea state. The benchmark DP results are presented as numerical values, while the results from using the roll compensating controllers are displayed in % compared to the benchmark numerical values.

It can be seen in Table 3 that the benchmark DP controller is oscillating within rather small position errors less than 30 cm for the very small sea states with a wave height of 0.5m. As the wave height increases to 1.5m the maximum peak in both north/surge and east/sway is tripled. The roll damping controller outperforms the benchmark controller in positioning, particularly in east/sway (see Tables 4, 5), as could be expected as the roll angle is affecting the DP point of interest that is \(2.32 \ m\) below the CO. The roll compensating controller also performs slightly better in north/surge direction, possibly due to dynamic couplings and wave direction spreading. The position error with the roll compensating controller with feed-forward is presented in Tables 6, 7 and 8. This controller performs significantly better in both surge/north and sway/east.

Although the results cannot be compared directly to [7], because of changes to the hull design and hydrodynamic model as well as DP tuning, we may still compare the relative improvements over the benchmark DP that is in principle the same. The simulations show that the proposed method gives significant performance improvement of 20–45\( \%\) compared to the benchmark DP while [7] reported 0–38\( \%\) improvement compared to a benchmark DP. This implies a performance improvement that is more consistent over all sea states. We note that for the longest wave periods the method in [7] gave insignificant improvements while the present method typically gives 20–30\( \%\) improvements in these cases.

Table 3 Maximum peaks in north/surge position error (meter)—Benchmark DP
Full size table
Table 4 Maximum peaks in east/sway position error (meter)—Benchmark DP
Full size table

We note that the simulation results for heading are not included since they show a similar trend, and are not limiting to the specific marine operation. Simulation results for controller thrust commands and thruster usage are also not tabulated, since they follow similar trends as seen in Figs. 7 to 10.

Table 5 Change in maximum peaks in north/surge position error—roll compensating controller compared to benchmark DP
Full size table
Table 6 Change in maximum peaks in north/surge position error—roll compensating controller with feed-forward compared to benchmark DP
Full size table
Table 7 Change in maximum peaks in east/sway position error—roll compensating controller compared to benchmark DP
Full size table
Table 8 Change in maximum peaks in east/sway position error—roll compensating controller with feed-forward compared to benchmark DP
Full size table

4 Conclusions

It is shown that roll compensation control can improve the DP positioning control when the DP system’s point of interest, and the location of the thrusters, have a significant vertical offset compared to the vertical position of the center of rotation. The proposed control algorithm is demonstrated in a realistic simulation of a relatively small ship during launch-and-recovery of a remotely operated vehicle (ROV) where the DP’s point of interest is at the lower end of the launch-and-recovery-system (LARS) that extends below the keel of the ship. It is shown that the positioning performance can be improved with 20–45\( \%\) reduced error, depending on the sea state. Compared to [7] the performance improvement is more consistent over all sea states, and in particular longer waves. The wave and roll compensation requires some increased variations in thrust magnitude and direction, and the requirements for fast thruster response favours the use of thruster biasing that may increase the average thrust and power consumption.