Abstract
The rudder force, including interference with a ship hull in large drifting conditions, is investigated in this study by captive model tests using a ship model with steering. In the tests, hydrodynamic forces acting on the ship, the rudder normal force, and propeller thrust are measured while changing the hull drift angle \(\beta \) in the range of \(-180^{\circ } \sim 180^{\circ }\), which encompasses forward, lateral, and astern motion. The hull and rudder interaction coefficients, thrust deduction factor, inflow velocity to propeller, and inflow velocity to rudder are obtained in large drifting conditions using the measured hydrodynamic force data. The Maneuvering Model Group (MMG) model (Yasukawa and Yoshimura, 2015) is applicable for estimating the rudder force when the absolute value of \(\beta \) is smaller than \(45^\circ \). In this region, the hydrodynamic force parameters for the inflow velocity to the rudder are nearly constant for any hull drift angle. However, in the region where the absolute value of \(\beta \) is greater than nearly \(45^\circ \), the MMG model cannot be applied. For improving the formula for the longitudinal inflow velocity component to the rudder (\(u_R\)), we propose a new formula that is applicable to any hull drift angle.




















Similar content being viewed by others
Abbreviations
- \(A_R\) :
-
Profile area of movable part of rudder [m\(^2\)]
- \(a_H\) :
-
Rudder force increase factor [–]
- B :
-
Ship breadth [m]
- \(B_R\) :
-
Averaged rudder chord length [m]
- \(C_b\) :
-
Block coefficient [–]
- \(C_{uR0}\) :
-
An experimental constant for longitudinal inflow velocity to rudder when \(u=0\) [–]
- \(D_P\) :
-
Propeller diameter [m]
- d :
-
Mean draft [m]
- \(d_a\) :
-
Aft draft [m]
- \(d_f\) :
-
Fore draft [m]
- \(F_N\) :
-
Rudder normal force [N]
- \(f_{\alpha }\) :
-
Rudder lift gradient coefficient [–]
- \(H_R\) :
-
Rudder span length (rudder height) [m]
- J :
-
Propeller advance ratio in open water [–]
- \(J_P\) :
-
Propeller advance ratio [–]
- \(K_T\) :
-
Propeller thrust coefficient [–]
- \(k_2, k_1, k_0\) :
-
Coefficients representing \(K_T\) in case of \(J\ge 0\) [–]
- \(k_{1R}, k_{0R}\) :
-
Coefficients representing \(K_T\) in case of \(J<0\) [–]
- L :
-
Ship length between perpendiculars [m]
- \(n_0\) :
-
Propeller revolution at model point [rps(s\(^{-1}\))]
- \(n_P\) :
-
Propeller revolution [rps(s\(^{-1}\))]
- \(o-xyz\) :
-
Ship fixed coordinate system taking the origin at midship [–]
- \(O-X_0Y_0Z_0\) :
-
Space fixed coordinate system [–]
- p :
-
Propeller pitch ratio [–]
- r :
-
Yaw rate [rad/s]
- T :
-
Propeller thrust [N]
- \(t_P\) :
-
Thrust deduction factor [–]
- \(t_R\) :
-
Steering resistance deduction factor [–]
- U :
-
Resultant speed (\(=\sqrt{u^2+v_m^2}\)) [m/s]
- \(U_R\) :
-
Resultant inflow velocity to rudder [m/s]
- u :
-
Surge velocity [m/s]
- \(u_R\), \(v_R\) :
-
Longitudinal and lateral inflow velocity components to rudder, respectively [m/s]
- \(v_m\) :
-
Lateral velocity at midship [m/s]
- \(w_P\) :
-
Wake fraction at propeller position [–]
- \(w_R\) :
-
Wake fraction at rudder position [–]
- X, Y, N :
-
Surge force, lateral force, yaw moment around midship [N,N,Nm]
- \(X_H\), \(Y_H\), \(N_H\) :
-
Surge force, lateral force, yaw moment around midship acting on ship hull [N,N,Nm]
- \(X_P\) :
-
Surge force due to propeller [N]
- \(X_R\), \(Y_R\), \(N_R\) :
-
Surge force, lateral force, yaw moment around midship by steering [N,N,Nm]
- \(x_H\) :
-
Longitudinal coordinate of acting point of the additional lateral force component induced by steering [m]
- \(x_R\) :
-
Longitudinal coordinate of rudder position (= \(-0.5L\)) [m]
- Z :
-
Number of propeller blades [–]
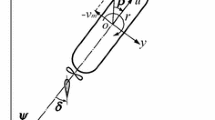
- \(\alpha _R\) :
-
Effective inflow angle to rudder [rad]
- \(\beta \) :
-
Hull drift angle at midship [rad]
- \(\gamma _{R}\) :
-
Flow straightening coefficient [–]
- \(\delta \) :
-
Rudder angle [rad]
- \(\delta _{FN0}\) :
-
Rudder angle where rudder normal force becomes zero [rad]
- \(\eta \) :
-
Ratio of propeller diameter to rudder span (\(=D_P/H_R\)) [–]
- \(\varLambda \) :
-
Rudder aspect ratio (\(=H_R^2/A_R\)) [–]
- \(\kappa \) :
-
An experimental constant for expressing \(u_R\) [–]
- \(\kappa _n\) :
-
An experimental constant for expressing \(u_R\) in new formula [–]
- \(\nabla \) :
-
Displacement volume of ship [m\(^3\)]
- \(\rho \) :
-
Water density [kg/m\(^3\)]
- \(\tau \) :
-
Trim [m]
- \(\varepsilon \) :
-
Ratio of wake fraction at propeller and rudder positions (\(=(1-w_R)/(1-w_P)\)) [–]
- \(\varepsilon _n\) :
-
Ratio of wake coefficients at propeller and rudder positions in new formula [–]
References
Yasukawa H, Yoshimura Y (2015) Introduction of MMG standard method for ship maneuvering predictions. J Mar Sci Technol 20(1):37–52
Kose K, Hinata H, Hashizume Y, Futagawa E (1984) On a mathematical model of maneuvering motions of ships in low speed. J Soc Naval Architects Jpn 155:132–138 (in Japanese)
Oltmann P, Sharma SD (1984) Simulation of combined engine and rudder manoeuvres using an improved model of hull-propeller-rudder interactions. In: Proc. 15th Symposium on Naval Hydrodynamics, Hamburg, pp 83–108
Takashina J (1986) Ship maneuvering motion due to tugboats and its mathematical model. J Soc Naval Architects Jpn 160:93–102 (in Japanese)
Kobayashi E, Asai S (1987) A simulation study on ship manoeuvrability at low speed. In: Proc. international conference on ship manoeuvrability –prediction and achievement, Vol.1, paper 10
Sutulo S, Guedes Soares C (2015) Development of a core mathematical model for arbitrary manoeuvres of a shuttle tanker. Appl Ocean Res 51:293–308
Yumuro A (1988) Some experiments on maneuvering hydrodynamic forces in low speed condition. J Kansai Soc Naval Architects 209:91–101 (in Japanese)
Delefortrie G, Eloot K, Lataire E, Van Hoydonck W, Vantorre M (2016) Captive model tests based 6 DOF shallow water manoeuvring model. In: Proc. 4th International Conference on Ship Manoeuvring in Shallow and Confined Water with Special Focus on Ship Bottom Interaction (4th MASHCON), Hamburg, pp 273–286
Yasukawa H, Hirata N, Matsumoto A, Kuroiwa R, Mizokami S (2019) Evaluations of wave-induced steady forces and turning motion of a full hull ship in waves. J Marine Sci Technol 24(1):1–15
Fujii H, Tuda T (1961) Experimental research on rudder performance (2). J Soc Naval Architects Jpn 110:31–42 (in Japanese)
Hess F (1978) Lifting-surface theory applied to ship-rudder systems. Int Shipbuilding Progress 25(292):299–305
Acknowledgements
This study was supported by JSPS KAKENHI Grant Number JP17H03495. The authors express their sincere gratitude to Mr. T. Yamamoto and Mr. T. Suzuki for their assistance with the tank tests.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Derivation of an equation of \(u_R\)
Appendix: Derivation of an equation of \(u_R\)
In this appendix, we derive an equation for \(u_R\) that is applicable for any hull drift angle. As shown in Fig. 21, there exist two flow fields around the rudder. One is the area where the propeller slip stream makes contact, and the other is the area where the propeller slip stream does not make contact. Here, the representative longitudinal components of the inflow velocity to the rudder area where the propeller slip stream makes contact and does not make contact are denoted \(u_{RP}\) and \(u_{R0}\), respectively. Similarly, the lateral inflow components are denoted as \(v_{RP}\) and \(v_{R0}\).
The representative longitudinal component of the inflow velocity to the rudder \(u_R\) is assumed to be expressed as,
Here, \(A_{RP}\) is the rudder area where the propeller slip stream makes contact and \(A_{R0}\) is the rudder area where the propeller slip stream does not make contact. \(A_R\) is the rudder total area expressed as the sum of \(A_{RP}\) and \(A_{R0}\). The \(u_R\) is expressed by weighting two velocity components \(u_{RP}\) and \(u_{R0}\) with respect to the respective rudder areas. If the rectangular rudder is assumed, \((A_{RP}/A_R)\) can be approximated as \((D_P/H_R)\) where \(D_P\) is the propeller diameter and \(H_R\) is the rudder span length. Therefore, \(u_R\) is expressed in the following form:
where \(\eta \) is \(D_P/H_R\). We consider Eq. (30) as a basic form of \(u_R\).
The \(u_{R0}\) is expressed as
where \(w_R\) is the wake fraction at the rudder position. Note that \(w_R\) should be zero for \(|\beta | > 90^\circ \). According to the MMG model [1], \(u_{RP}\) is expressed as,
where \(k_x \varDelta u\) represents a velocity increase due to the propeller slip stream. \(\varDelta u\) is defined in terms of the difference between \(u_{\infty }\) and the inflow velocity to propeller \(u_P\) (\(\varDelta u = u_{\infty } - u_P\)), where \(u_{\infty }\) is the velocity at the infinite aft position.
The \(u_{\infty }\) is expressed as [1]
Substituting Eqs. (31) and (33) into Eq. (32) yields the following:
Furthermore, substituting Eqs. (31) and (34) into Eq. (30) yields the following:
where \(\varepsilon _n=(1-w_R)/(1-w_P)\), and \(\kappa _n=k_x/\varepsilon _n\). By moving \(u_P\) to the left-hand side of the equation, the boosting ratio of the inflow velocity \(u_R/u_P\) is obtained as follows:
About this article
Cite this article
Yasukawa, H., Ishikawa, T. & Yoshimura, Y. Investigation on the rudder force of a ship in large drifting conditions with the MMG model. J Mar Sci Technol 26, 1078–1095 (2021). https://doi.org/10.1007/s00773-020-00789-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00773-020-00789-4