Wave motion compensation in dynamic positioning of small autonomous vessels

Abstract

Conventional dynamic positioning (DP) systems on larger ships compensate primarily for slowly time-varying environmental forces. In doing so, they use wave filtering to prevent the DP from compensating for the first-order wave motions. This reduces wear and tear of the thruster and machinery systems. In the case of smaller autonomous vessels, the oscillatory motion of the vessel in waves may be more significant, and the thrusters can be more dynamic. This motivates the use of DP to compensate for horizontal wave motions in certain operations. We study the design of DP control and filtering algorithms that employ acceleration feedback, roll damping, wave motion prediction, and optimal tuning. Six control strategies are compared in the case study, which is a small autonomous surface vessel where the critical mode of operation is launch and recovery of an ROV through the wave zone.

1 Introduction

Dynamic positioning (DP) systems achieve station keeping of vessels only using thrusters and a control system. DP systems on larger ships compensate primarily for the slowly time-varying wind, ocean current, and second-order wave drift forces. They employ wave frequency filtering of the position and velocity measurements, so that the DP feedback control does not compensate for first-order wave motions, [6, 16]. One reason for this is that it may not be necessary for many operations, and also that many thrusters do not have a sufficiently fast dynamical response. It would also increase fuel consumption, and fast power load variations cause excessive wear of the machinery system and the thrusters themselves. Moreover, for diesel-electric power systems that do not utilize batteries for peak-shaving, highly dynamic loads may cause variations in electric frequency and voltage that may cause electric power blackout unless mitigating control such as power limitation, reduction, biasing or modulation is implemented in the DP, thruster control, or power management systems [8, 12, 13, 18].

Fig. 1

Exemplar illustration of the ROV launched and recovered from a relatively small USV. Courtesy Kongsberg Maritime

Our research is motivated by new unmanned surface vessels (USV) concepts that are emerging for offshore operations such as inspection, maintenance, and repair (IMR). Some new vessel concepts are designed to be autonomous and much smaller in size than conventional IMR vessels, see Fig. 1 for an example. For smaller and unmanned vessels, the first-order wave-driven oscillatory motion may be large, where we note that crew comfort is not an issue. This motivates the use of DP to actively compensate also for first-order wave-driven horizontal motions in certain operations, for example launch and recovery of an ROV through the wave zone. Usually, such critical operations amount to a very small fraction of the total operational time, and hence, wear on thrusters and machinery is less of a concern. Also, the use of batteries for power peak-shaving is a viable option in new vessel concepts. It should also be mentioned that other DP applications such as shallow-water drilling, well intervention, and pipelay may benefit from compensation of wave-driven horizontal motion, as well. In all these cases, the dynamic response of the thrusters is expected to impose the main limitation on the DP control performance.

This paper’s objective is to study DP systems that can compensate for first-order wave-driven horizontal vessel motions. The study involves DP control and filtering algorithms that use optimally tuned combinations of standard position and velocity feedback using linear quadratic regulation (LQR), [6], together with acceleration feedback, [9, 11], roll damping, [10, 15], and a novel algorithm for wave force prediction. Six control algorithms are compared in a simulation case study considering the exemplar vessel shown in Fig. 1, where the critical operation is the launch and recovery of an ROV through the moonpool. The first control algorithm is a conventional DP with standard wave filtered position and velocity feedback used as a benchmark, while the five others have the goal of reducing first-order wave motions, see Table 1. They are defined by differences in the wave filter, control objective, or tuning compared to the standard DP control algorithms.

One significant contribution in the paper is the method for analysis of DP performance, using a nonlinear multi-body simulator considering the 6-degrees-of-freedom (DOF) rigid-body motion of the autonomous surface vessel, 3-DOF rigid-body motion of the ROV (surge, sway, and heave—assumed to be the most important DOFs as the launch and recovery system (LARS) is deemed capable to compensate for motion in the rotational DOFs), and the vertical position of the water column in the moonpool. The simulations include environmental forces due to wind, waves and ocean current, and hydrodynamic interactions between the autonomous surface vessel and the free-floating ROV just below the USV’s LARS. It is noted that the ROV is not experiencing wind, and somewhat less forces and moments due to waves compared to the USV, since it is more submerged. The ocean current is assumed the same for both the USV and the ROV. The dynamics of thrusters and diesel-electric power system are also included in the simulator. The simulation results consider the effects on the average positioning error, maximum positioning error, peak power consumption, and maximum roll angle.

Table 1 Algorithms compared. LQR—linear quadratic regulator. AFB—acceleration feedback. WFF—wave feed-forward

Fig. 2

Block diagram of the control architecture. Orange arrows are feed-forward terms and blue arrow indicates adapting gains (color figure online)

2 Method

The overall control system architecture can be seen in Fig. 2. It consists of the following modules:

• Vessel and sensors 6-DOF vessel motion model. Measurements include positions and velocities [e.g., using differential global navigation satellite system (GNSS)], orientation (roll, pitch, and yaw), and inertial measurements of acceleration and angular rates.

• Thrusters and diesel-electric power system dynamics Thrust characteristics, including dynamic response and physical limitations in both thrusters and the diesel-electrical power system.

• Environment Forces due to ocean current, wind, and waves. A wind velocity sensor may be used for feed-forward.

• Observer Estimator for position and velocity. This includes estimation of bias corresponding to slowly time-varying unknown environmental disturbances and similar model errors. It may include a wave filter that can be used to partly remove oscillatory motions due to waves from the measured position and velocity, [6]. Inertial navigation techniques might be favourable to get unbiased vessel acceleration and angular rate to support AFB, [4, 9, 14].

• Wave frequency estimation Estimation of the peak wave frequency based on heave measurements. The peak wave frequency is adapting the wave filter’s wave model.

• Wave prediction: Predicts the wave forces in surge and sway, using the vessel velocity and the thruster forces.

• DP controller: Various control algorithms as described in Table 1.

• Thrust allocation An algorithm that allocates the desired forces in surge and sway, and the yaw moment, to thrust and azimuth angle for each thruster.

2.1 Vessel simulation model

Fig. 3

Block diagram of vessel and environment modeling. Blue is waves, yellow is ocean current, orange is wind, and green is vessel (color figure online)

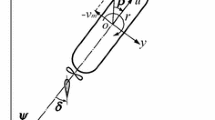
The 6-DOF vessel model illustrated in Fig. 3 is based on [6] and used for simulation:

$$\begin{aligned}&\dot{\eta } = J(\eta )(\nu _r+\nu _c) \end{aligned}$$

(1)

$$\begin{aligned}&M \dot{\nu }_r+C(\nu _r)\nu _r+D\nu _r+D_n(\nu _r)\nu _r+G\eta = \tau +\tau _{\text {env}} \end{aligned}$$

(2)

$$\begin{aligned}&\tau _{\text {env}} = \tau _{\text {wind}}+\tau _{\text {wave}}. \end{aligned}$$

(3)

Equation (1) describes the kinematics, while Eq. (2) describes the kinetics. The position vector $\eta$ contains the three Cartesian coordinates and the Euler angles $\varTheta = (\phi ,\theta ,\psi )$ (roll, pitch, and yaw) relative to these axes. The origin and axes of the local Earth-fixed tangential Cartesian coordinate frame define the desired position and heading for the DP station keeping.

The velocity vector $\nu$ contains the corresponding velocities decomposed in the vessel’s body coordinate frame. The transformation between the coordinate frames of the position and velocity vectors is described by the matrix $J(\eta )$.

The ocean current is modeled as a velocity vector $\nu _c$ that enters the model through the relative velocity of the vessel and the ocean current velocity $\nu _r = \nu - \nu _c$. We note that the ocean current $\nu _c$ is decomposed in the body coordinate frame.

The generalized force vectors $\tau , \tau _{\text {wind}}$, and $\tau _{\text {wave}}$ contains the forces and moments due to thrusters, winds, and waves, respectively. These forces are also decomposed in the body-fixed coordinate frame. The wind is modeled as forces in surge and sway, and yaw moment, according to:

$$\begin{aligned} \tau _{\text {wind}}&= \frac{1}{2}\rho _aV_{w}^2 \begin{bmatrix} -c_x\cos (\gamma _w)A_{Fw} \\ c_y\sin (\gamma _w)A_{Lw} \\ c_n\sin (2\gamma _w)A_{Lw}L_{oa} \end{bmatrix}, \end{aligned}$$

(4)

which is valid for highly symmetrical ships [6]. The constant $\rho _a$ is the air density, $V_w$ is the wind velocity 10 m above the water surface which will vary with the average wave height $H_s$ according to Table 2, and $\gamma _w = \psi - \beta _w - \pi$ is the angle of attack with heading $\psi$ and wind direction $\beta _w$.

Table 2 Average wind speed

The wave forces $\tau _{\text {wave}}$ are represented by a response amplitude operator (RAO), [6], that is computed using numerical tools such as WAMIT. The wave forces are generated with a spreading function, typically with 10 wave direction components. The wave spreading is in the range of $45^\circ$ to each side of the main wave direction. $M = M_{RB} + M_A$ is the mass/inertia matrix, which includes rigid-body mass/inertia $M_{RB}$ and hydrodynamic added mass/inertia $M_A$. $C(\nu _r)$ contains Coriolis terms, D is the linear damping matrix including viscous and potential damping, $D_n(\nu _r)$ is the nonlinear damping, and G is the restoring matrix.

The simulator is implemented in Matlab/Simulink and uses the MSS toolbox [7], where thruster dynamics and diesel-electric power plant models are based on [5]. The thruster dynamics include azimuth, electric motor, and shaft inertia, 4-quadrant propeller characteristics, with static and linear friction, and can compute the produced thrust and consumed electrical power. The diesel-electric system considers the active and reactive power balances to simulate variations in voltage and AC frequency.

2.2 Wave filtering and state estimation

The nonlinear passive observer described in [6] is used for state estimation, bias estimation, and wave filtering. State estimation of velocities is achieved using position and heading measurements, and the vessel model. The bias estimation is tuned to capture ocean current forces, wind forces, and second-order wave forces, while the wave filter is tuned by a damping gain. The damping gain adjusts the amount of oscillatory first-order wave motions that enters the controller. The wave filter includes a wave model, which is from [16]:

$$\begin{aligned} \dot{\xi }_w&= A_w\xi _w + E_ww_w \end{aligned}$$

(5)

$$\begin{aligned} \eta _w&= C_w\xi _w, \end{aligned}$$

(6)

where $\eta _w\in \mathbb {R}^3$ is the position and heading measurement vector, $w_w\in \mathbb {R}^3$ is a zero-mean Gaussian white noise vector, $\xi _w\in \mathbb {R}^6$ is the wave model states, and:

$$\begin{aligned} A_w = \begin{bmatrix} 0_{3\times 3} &{} I_{3} \\ -\varOmega _0^2 &{} -2\varLambda \varOmega _0 \end{bmatrix} , \ C_w = \begin{bmatrix} 0_{3\times 3}&I_{3} \end{bmatrix}, \ E_w = \begin{bmatrix} 0_{3\times 3} \\ K_w \end{bmatrix} \end{aligned}$$

(7)

with the peak wave frequencies $\varOmega _0 =\omega _{0} I_{3}$, relative damping ratios $\varLambda = \text{ diag }\{\zeta _1,\zeta _2,\zeta _3\}$ and disturbance input gain $K_w = \text{ diag }\{K_{w1},K_{w2},K_{w3}\}$. Note that the peak wave frequencies in every DOF will oscillate at the same frequency after some time when the waves are fully excited and the ship dynamics is nonlinear, [6].

The wave estimation technique from [3] is used to estimate the peak wave frequency $\omega _0$ by the use of heave motion measurements. This is a real-time switching-gain estimator based on the fixed-gain estimator in [2]. The estimated peak wave frequency $\hat{\omega }_0$ is then used in (7). We note that alternative methods such as moving data window periodogram can be applied, e.g., [6].

2.3 Postion/velocity feedback controller

The position/velocity feedback controller is an LQR controller in surge, sway, and yaw. As usual in DP control design ([6]), the controller is based on a 3-DOF control model, including integral action and wind feed-forward:

$$\begin{aligned} \dot{z}&= \eta \end{aligned}$$

(8)

$$\begin{aligned} \dot{\eta }&= {\mathscr {R}}\nu \end{aligned}$$

(9)

$$\begin{aligned} M\dot{\nu } + D\nu&= \tau + \tau _{\text {wind}} + \tau _{\text {wave}} + {\mathscr {R}}^T b \end{aligned}$$

(10)

$$\begin{aligned} \tau&= \tau _{lq} -\hat{\tau }_{\text {wind}}. \end{aligned}$$

(11)

With some abuse of notation, the symbols for vectors and matrices that were introduction for the 6-DOF model in Sect. 2.1 are here re-used for convenience of notation in the 3-DOF model. Hence, z $\in \mathbb {R}^3$ is the integral position error state, $\eta = [x,y,\psi ]^T$ is the vessel position and heading error, ${\mathscr {R}} = {\mathscr {R}}(\psi )$ is the rotation matrix which rotates the coordinates from body-fixed coordinates to the Earth-fixed reference frame, and $\tau = [X,Y,N]^T$ is the body-fixed desired forces in surge and sway, and yaw moment, computed by the controller including linear quadratic control input $\tau _{lq}$ $\in \mathbb {R}^{3\times 1}$ and estimated wind feed-forward $\hat{\tau }_{wind}$ $\in \mathbb {R}^{3\times 1}$ using (4) and wind sensors. b in (10) is representing the disturbance forces and moments in the NED coordinate frame due to by unknown ocean current, which is rotated to the body-fixed coordinate frame through ${\mathscr {R}}^T$. Nonlinear damping and Coriolis terms are neglected, since $\nu _r$ is usually small, and the linear damping usually dominates in station keeping. The ramp-up time dynamics of the thrusters and power plant are not included in the control model (8)–(11), which means that the tuning of the controller needs to be robust to account for the limitations on the achievable performance imposed by this unmodeled dynamics. We recall that the NED coordinate frame is aligned with the desired position and heading of the USV, such that for station keeping, the difference between NED and body coordinate frames is small, and hence, the first-order approximation ${\mathscr {R}} \approx I$ can be used for control tuning. Then, the state-space model for (8)–(11) is:

$$\begin{aligned} \dot{x} = Ax + B\tau _{lq} + d, \end{aligned}$$

(12)

where $x=[{\mathscr {R}}^Tz,{\mathscr {R}}^T\eta ,\nu ]^T$, d represents uncompensated environmental disturbances and unmodeled dynamics, and

$$\begin{aligned} A = \begin{bmatrix} 0_{3\times 3} &{} I_{3} &{} 0_{3\times 3} \\ 0_{3\times 3} &{} 0_{3\times 3} &{} I_{3} \\ 0_{3\times 3} &{} 0_{3\times 3} &{} -M^{-1}D \end{bmatrix},&\ \ B = \begin{bmatrix} 0_{3\times 3} \\ 0_{3\times 3} \\ M^{-1} \end{bmatrix}. \end{aligned}$$

(13)

We note that the states of the model (12) used for LQR feedback control synthesis are the velocity error, position error, and the integral of the position error. Since the system matrices (13) are diagonal when formulated in the vessel-parallel coordinate frame, the structure of the LQR feedback controller is identical to the structure of three SISO PID controllers. The control input $\tau _{lq}$ is chosen to minimize the cost function:

$$\begin{aligned} J =&\frac{1}{2}\int _0^\infty \left( x^TQx+\tau _{lq}^TR\tau _{lq} \right) \text {d}t, \end{aligned}$$

(14)

where $Q = Q^T =$ diag{$Q_I,Q_1,Q_2$} $\ge$ 0 $\in \mathbb {R}^{9\times 9}$ is the weight matrix penalizing the states in x and $R = R^T>$ 0 $\in \mathbb {R}^{3\times 3}$ is the input weight matrix. The LQR is defined by the state feedback:

$$\begin{aligned} \tau _{lq}&= -R^{-1}B^TP_{\infty }x, \end{aligned}$$

(15)

where the symmetric matrix $P_{\infty } > 0$ is the solution to the algebraic Riccati equation, [1].

2.4 Roll damping

Roll damping can be achieved when using a DP controller in surge, sway, roll, and yaw. It has a similar structure as described in Sect. 2.3, but the vessel position and orientation vector are in this case augmented with the roll angle $\phi$ and the desired force and moment vector is augmented with the roll moment K.

2.5 Acceleration feedback

Acceleration feedback can be added in conjuncture with position/velocity feedback [11]. The acceleration is in counter phase with oscillatory wave motions, which could be leveraged to minimize first-order wave-driven motions. Acceleration feedback is effectively adding virtual mass/inertia in addition to the mass/inertia matrix M before optimizing the cost function (14). The virtual mass/inertia is chosen as a scaled factor of the actual mass/inertia matrix through $K_m = rM$, where r is a scaling factor [11]. The implemented state feedback control term is:

$$\begin{aligned} \tau _{lq,a}&= \tau _{lq} - \tau _a \end{aligned}$$

(16)

$$\begin{aligned} \tau _a&= K_m\dot{\nu }, \end{aligned}$$

(17)

where $K_m = K_m^T>$ 0 $\in \mathbb {R}^{3x3}$ is the acceleration feedback gain, which effectively increases the mass/inertia in the system and (10) is replaced by:

$$\begin{aligned} (M+K_m)\dot{\nu } + D\nu&= \tau + \tau _{\text {wind}} + \tau _{\text {wave}} + {\mathscr {R}}^Tb. \end{aligned}$$

(18)

The acceleration $\dot{\nu }$ in (17) must be estimated from inertial measurements by appropriate techniques [9, 14]. To partly compensate for the adverse effects of lags due to thruster dynamics, a limited inverse lag filter is recommended to be used on the acceleration measurements to invert the first-order thruster dynamics approximation at low frequencies. This changes (17) to:

$$\begin{aligned} \tau _a&= K_m H(s) \dot{\nu }, \end{aligned}$$

(19)

where the transfer function is given by:

$$\begin{aligned} H(s)&= \frac{1 + Ts}{1 + \alpha Ts}, \end{aligned}$$

(20)

and T is the time constant of a first-order thruster dynamics approximation, and $\alpha$ is a constant typically chosen between 0.1 and 0.2 that is required to achieve a proper transfer function and limit the impact of acceleration measurement noise and vibrations.

2.6 Feed-forward of predicted wave forces

By including feed-forward of predicted wave forces, (11) changes to:

$$\begin{aligned} \tau = \tau _{lq}-\hat{\tau }_{\text {wind}}-G_wH(s)\hat{\tau }_{\text {wave}}, \end{aligned}$$

(21)

where $\hat{\tau }_{\text {wave}}$ is the estimated wave forces in surge/sway, $G_w$ is a feed-forward gain matrix, and H(s) is the limited inverse lag filter (20), which leads to a prediction.

Assuming that the vessel dynamics is linear during operation at low velocity, the velocity of the vessel due to thruster-induced forces $\nu _{\text {thr}}$ and the velocity due to wave-induced forces $\nu _{\text {wave}}$ can be separated, which gives:

$$\begin{aligned} \nu&= \nu _{\text {thr}} + \nu _{\text {wave}} \end{aligned}$$

(22)

$$\begin{aligned} \tau&= M\dot{\nu }_{\text {thr}} + D\nu _{\text {thr}} \end{aligned}$$

(23)

$$\begin{aligned} \hat{\tau }_{\text {wave}}&= M\dot{\nu }_{\text {wave}} + D\nu _{\text {wave}}. \end{aligned}$$

(24)

Equation (22) can be written as:

$$\begin{aligned} \nu _{\text {wave}}&= \nu - \nu _{\text {thr}} \end{aligned}$$

(25)

and $\nu _{\text {thr}}$ is computed by integrating

$$\begin{aligned} \dot{\nu }_{\text {thr}}&= M^{-1}(\tau - D\nu _{\text {thr}}), \end{aligned}$$

(26)

which is then used in Eq. (25) to compute $\nu _{\text {wave}}$, and finally, the estimated wave forces (24) are computed and used as a feed-forward term in Eq. (21).

2.7 Thrust allocation

Allocation of thrust force and azimuth angles to the thrusters is done in an optimal manner to achieve the total force/moment demand in surge, sway, and yaw for the 3-DOF case. The thrust allocation module used in this paper is based on [17] which uses a pseudo-inverse approach with singularity avoidance and saturation.

3 Results

The DP algorithms summarized in Table 1 and described in Sect. 2 are compared in a case study using simulation of the vessel model in Sect. 2.1.

Fig. 4

ROV with exemplar launch and recovery system (LARS) in moonpool. Courtesy Kongsberg Maritime

3.1 Vessel

The USV concept illustrated in Fig. 1 is used in this case study. The study focuses on DP during the launch and recovery of an ROV. In this operation, the ROV is located very close to the water surface and the moonpool of the USV, see Fig. 4. Hence, there are significant hydrodynamic coupling effects between the USV and its moonpool when the ROV is freely floating in the wave zone close to the latching point of the LARS in the moonpool. Various LARSs might be envisaged. The current study assumes one of the simplest forms, comprising a docking head positioned at the lower end of the moonpool during launch and recovery. The simulation model is, therefore, extended and does not only contain the USV motion in 6 DOF as described in Sect. 2, but also the moonpool water column position in 1 DOF (vertical) and ROV in 3 DOF (surge, sway, and heave). The ROV has a neutrally buoyant position underneath the USV, near the LARS latching operation point. This means that the umbilical forces are assumed to be generated by a heave compensation system to compensate for negative buoyancy that is typically resulting from forward thrust during launch and recovery. The ROV is modeled in 3 DOF—surge, sway, and heave—assuming that the LARS will stabilize the rotational DOFs. The mass of the ROV is 2000 kg and its main dimensions are $2150 \times 1160 \times 1174$ mm.

Multi-body wave force RAOs are computed by WAMIT, accounting for the hydrodynamic interactions between the USV, the moonpool, and the ROV. The USV’s mass and linear damping matrices are:

$$\begin{aligned} M_{RB}= & {} \left( \begin{array}{cccccc} 153044 &{} 0 &{} 0 &{} &{} -\,24487 &{} 0 \\ 0 &{} 153044 &{} 0 &{} 24487 &{} 0 &{} 0 \\ 0 &{} 0 &{} 153044 &{} 0 &{} 0 &{} 0 \\ 0 &{} 24487 &{} 0 &{} 952820 &{} 0 &{} 0 \\ -\,24487 &{} 0 &{} 0 &{} 0 &{} 4363200 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 4247800 \end{array} \right) \\ M_{A}= & {} \left( \begin{array}{cccccc} 17557 &{} 0 &{} 0 &{} &{} -\,42170 &{} 0 \\ 0 &{} 151437 &{} 0 &{} -\,197548 &{} 0 &{} 0 \\ 0 &{} 0 &{} 127397 &{} 0 &{} 0 &{} 0 \\ 0 &{} -\,197458 &{} 0 &{} 539082 &{} 0 &{} 0 \\ -\,41436 &{} 0 &{} 0 &{} 0 &{} 2575153 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1261448 \end{array} \right) \\ D= & {} \left( \begin{array}{cccccc} 46912 &{} 0 &{} 0 &{} &{} -\,375519 &{} 0 \\ 0 &{} 402730 &{} 0 &{} 70873 &{} 0 &{} 0 \\ 0 &{} 0 &{} 107085 &{} 0 &{} 0 &{} 0 \\ 0 &{} 63644 &{} 0 &{} 202324 &{} 0 &{} 0 \\ -\,369026 &{} 0 &{} 0 &{} 0 &{} 3665296 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 11098189 \end{array} \right) . \end{aligned}$$

The vessel is equipped with two azimuth thrusters that can rotate using 12 s per revolution, and with azimuth angle limited between $-\,90^\circ$ and $90^\circ$. The rated power for each azimuth thruster is 160 kW, and 37 kN Bollard-pull thrust. The thruster dynamics are tuned with a thrust ramp time of 3 s.

The aerodynamic drag coefficients (wind model) are given by $c_x = 0.70$, $c_y = 0.82$, and $c_n = 0.12$. Moreover, $A_{Fw} = 50$ m$^2$ is the frontal projected area, $A_{Lw} = 100$ m$^2$ is the lateral projected area, and $L_{oa} = 24$ m is the overall length of the vessel.

3.2 Scenarios

In the simulations, we consider Metocean conditions typical to the North Sea. The wave forces and moment vector $\tau _{\text {wave}}$ are generated based on the Joint North Sea Wave Project (JONSWAP) spectrum with a given peak period $T_p$ and significant wave height $H_s$. The 18 wave sea states chosen for simulations are listed in Table 3, which is based on statistical data from the Haltenbanken field in the Norwegian continental shelf.

Table 3 Wave sea states at Haltenbanken field

The following conditions are assumed:

• The environmental loads (wind, current, and waves) are pointing in the same mean direction with spreading.

• The ocean current is set to a mean value of 0.3 m/s.

• The vessel’s bow is pointing toward the environment.

• A blackout of generators is defined as a bus frequency deviation of 10% from the nominal value for more than 1 s.

• No sensor noise.

Fig. 5

Wave prediction of surge and sway oscillatory wave-induced forces with $H_s =$ 5.5 m and $T_p =$ 10.5 s

3.3 Wave prediction validation

Wave force prediction at sea state with $H_s =$ 5.5 m and $T_p =$ 10.5 s is shown in Fig. 5. The wave force prediction $\hat{\tau }_{\text {wave}}$ is slightly different from the actual wave force $\tau _{\text {wave}}$. However, the wave prediction is assuming that we know the mass/inertia matrix M and the linear damping matrix D of the vessel, including the vessel velocity in surge and sway. Due to the capacity limitations of the thrusters and the wave prediction forces, scaled down values are used for control.

3.4 Controller tuning

In this section, the state weight matrix $Q =$ diag{$Q_I,Q_1,Q_2$} in (14) will be presented for each control algorithm. The same controller gains are used for all sea states. The input weight matrix R in (14) is set to:

$$\begin{aligned} R&= \text{ diag }\{1,1,9^{-2}\},\quad \text{ if } \text{ no } \text{ roll } \text{ damping } \end{aligned}$$

(27)

$$\begin{aligned} R&= \text{ diag }\{1,1,2^{-2},9^{-2}\},\quad \text{ if } \text{ roll } \text{ damping } \end{aligned}$$

(28)

for all cases. The choice of the last elements is due to a roll moment arm of 2 m and a yaw moment arm of 9 m. These control weights are, therefore, normalized to thrust units, so the control inputs are directly comparable.

The weights for the elements in $Q_I$, $Q_1$, and $Q_2$ are weighted somewhat differently depending on the algorithm. The matrices have the following structure:

$$ Q_{I} = q_{I} {\text{diag}}\left\{ {{\text{q}}_{{{\text{surge}}}} ,{\text{q}}_{{{\text{sway}}}} ,{\text{q}}_{{{\text{roll}}}} ,{\text{q}}_{{{\text{yaw}}}} } \right\} $$

(29)

$$ Q_{1} = q_{1} {\text{diag}}\left\{ {{\text{q}}_{{{\text{surge}}}} ,{\text{q}}_{{{\text{sway}}}} ,{\text{q}}_{{{\text{roll}}}} ,{\text{q}}_{{{\text{yaw}}}} } \right\} $$

(30)

$$ Q_{2} = q_{2} {\text{diag}}\left\{ {{\text{q}}_{{{\text{surge}}}} ,{\text{q}}_{{{\text{sway}}}} ,{\text{q}}_{{{\text{roll}}}} ,{\text{q}}_{{{\text{yaw}}}} } \right\}, $$

(31)

where $q_{\text {roll}}$ is excluded for the 3-DOF control cases. The weights for each matrix in Q are in general:

$$\begin{aligned} q_{\text {surge}}&= q_{\text {sway}} = 1 \end{aligned}$$

(32)

$$\begin{aligned} q_{\text {roll}}&= \beta _{\text {roll}} \left( \frac{180}{\pi }\right) ^2 \end{aligned}$$

(33)

$$\begin{aligned} q_{\text {yaw}}&= \beta _{\text {yaw}} \left( \frac{180}{\pi }\right) ^2, \end{aligned}$$

(34)

which means that 1 m deviation in surge and sway is considered to be equally important as $1^\circ$ deviation in yaw angle when the tuning parameter $\beta _{\text {yaw}}=1$ is used. We have chosen the tuning parameter $\beta _{\text {roll}} = 3$, such that the roll angle is three times more important that yaw during 4-DOF control with roll damping. For acceleration feedback, wave prediction and roll damping $q_{\text {surge}} = 100$ and $q_{\text {sway}} = 100$ have been used. The LQR design for the acceleration feedback case is using an added mass/inertia matrix which is $r=10$ times larger than the mass/inertia matrix M, i.e., $K_m = 10M$ in (17). This is to achieve an desired trade-off between maneuverability and robustness against disturbances. The wave prediction algorithm is predicting the surge and sway wave forces. The feed-forward gain used for all sea states is $G_w = \text {diag}\{0.25,0.25,0\}$. This means that only 1/4 of the predicted wave forces are compensated with feed-forward. It is noted that a larger percentage of the wave prediction could be used for smaller wave heights, without saturating the thrusters. The scaling weights for the compared controllers are presented for each algorithm in Table 4, with reference to the algorithms described above.

Table 4 LQR scaling weights for the compared DP control algorithm

The benchmark case has relatively small weights, and also the largest amount of wave filtering, such that only the second-order wave motions are accounted for. This corresponds to a classical DP tuning which does not compensate for first-order wave motions.

All cases were tuned based on performance in the sea state with $H_s =$ 5.5 m and $T_p =$ 10.5 s. The velocity weight $q_2$ was chosen large to reduce the imaginary parts of the closed-loop poles, such that the oscillations were minimized.

The wave filter is tuned by adjusting the relative damping ratio $\varLambda$ in (7). For the benchmark case, the relative damping ratio is set large enough to damp out all oscillatory motions. In the optimal wave filter case, the relative damping ratios were set to 1. A sensitivity analysis was conducted to verify that this was the optimal choice, with respect to absolute motions of the surface vessel.

3.5 Absolute motion analysis of autonomous surface vessel

Motion performance in DP is evaluated by the maximum position error peak and the average of maximum position error peaks across a 1000 second simulation time in a stationary state. More specifically, we evaluate the Euclidean distance $e = \sqrt{x^2+y^2}$ from a geo-stationary reference point to the LARS latching point (defined 4.5 m below the water surface), peak roll angle, and thruster peak power consumption. The simulations with the different cases/algorithms are initialized with the same seed in the random number generators used to simulate the stochastic wind, wave, and current processes. This means that the results are directly comparable.

Tables 5, 6, 7 and 8 contain the results from the benchmark case, with conventional wave filtering. Tables 5 and 6 show that the Euclidean distance will increase with the wave height, but decreasing with respect to the wave period. The maximum observed Euclidean distance across all sea states is 2.73 m. This could be too much for the launch and recovery operation.

Table 5 Case 1 (benchmark)—Euclidean distance average peak results in meters

Table 6 Case 1 (benchmark)—Euclidean distance maximum peak results in meters

Table 7 Case 1 (benchmark)—roll angle maximum peak results in degrees

Table 8 Case 1 (benchmark)—thruster power average peak results in kilowatt (kW)

Table 7 shows that the roll angle increases with both wave height and decreasing wave period. Sea state $H_s$ = 4.5 m and $T_p$ = 9.5 s shows that the roll angle can be $6.85^\circ$, which was the observed maximum during simulation. A roll angle of 6.85 degrees will produce a sway deviation $\delta y = 4.5\sin (6.85^\circ )\approx$ 0.54 m of the launch and recovery latching point. Table 8 shows the average peak power consumption by each thruster. It is seen that the power consumption is well within the limit of the thruster (160 kW).

Next, the cases 2–6 in Table 1 are presented based on percentage increase or decrease compared to the benchmark results.

Case 2 (dynamical DP without wave filtering) results are shown in Table 9. It is seen that the dynamical DP algorithm is not providing consistent results. This is mainly due to no filtering techniques being used, such that the control system suffers from the lags in the thrusters. This algorithm (like the others) could, therefore, perform better with faster thruster dynamics.

Table 9 Case 2 (dynamical DP)—Euclidean distance maximum peak in % compared to benchmark

Case 3 (optimal DP) results are shown in Tables 10, 11, 12 and 13. Table 10 shows that the Euclidean average peak distance is reduced in all sea states. This is also reflected in Table 11. This highlights that it is important to tune a wave filter optimally to reduce oscillatory motions. The power consumption in Table 13 indicates that more power is needed with optimal DP compared to the benchmark due to the increased dynamical load. This also applies to the following cases, as they use oscillatory motions directly in the controller. A larger power consumption is allowed as the launch and recovery phase typically takes only about 10 min, as long as the thrusters do not saturate and the power plant does not blackout due to the load variations.

Table 10 Case 3 (optimal DP)—Euclidean distance average peak in % compared to benchmark

Table 11 Case 3 (optimal DP)—Euclidean distance maximum peak in % compared to benchmark

Table 12 Case 3 (optimal DP)—roll angle maximum peak in % compared to benchmark

Table 13 Case 3 (optimal DP)—thruster power average peak in % compared to benchmark

Table 14 Case 4 (acceleration feedback)—Euclidean distance average peak in % compared to benchmark

Table 15 Case 4 (acceleration feedback)—Euclidean distance maximum peak in % compared to benchmark

Table 16 Case 4 (acceleration feedback): roll angle maximum peak in % compared to benchmark

Table 17 Case 4 (acceleration feedback)—thruster power average peak in % compared to benchmark

Case 4 (acceleration feedback) results are shown in Tables 14, 15, 16 and 17. It is seen that acceleration feedback gives a reduction of average Euclidean distance in all sea states from Tables 14 and 15. Table 16 shows that the roll angle is also reduced by the use of acceleration feedback, which could be due to the added virtual mass/inertia in the system.

Table 18 Case 5 (wave prediction): Euclidean distance average peak in % compared to benchmark

Table 19 Case 5 (wave prediction)—Euclidean distance maximum peak in % compared to benchmark

Table 20 Case 5 (wave prediction)—roll angle maximum peak in % compared to benchmark

Table 21 Case 5 (wave prediction)—thruster power average peak in % compared to benchmark

Case 5 (wave prediction) results are presented in Tables 18, 19, 20 and 21. According to the Euclidean maximum peak, this algorithm gives the best performance in most wave heights. The Euclidean distance performance can be seen in Tables 18 and 19. Table 20 also shows that roll is reduced. The reason for this is that sway and roll are coupled, and sway forces from waves are accounted for directly with the feed-forward term.

Table 22 Case 6 (roll damping)—Euclidean distance average peak in % compared to benchmark

Table 23 Case 6 (roll damping)—Euclidean distance maximum peak in % compared to benchmark

Table 24 Case 6 (roll damping)—roll angle maximum peak in % compared to benchmark

Table 25 Case 6 (roll damping)—thruster power average peak in % compared to benchmark

Finally, case 6 (roll damping) results are presented in Tables 22, 23, 24 and 25. It is seen from Tables 22 and 23 that including roll damping in the DP objective will reduce the position error peaks for all sea states. It is noted that the maximum position error peak is the most crucial metric to consider. According to the maximum position error peak, the roll damping algorithm has superior performance in a wave height of 1.5 m and 5.5 m. The reduction of positioning error with roll damping can be explained by that reduced roll imply reduced sway motions in the launch and recovery latching point. Table 24 shows that the roll angle in all sea states is reduced significantly.

Fig. 6

Simulation example of wave prediction algorithm with $H_s =5.5\hbox { m}$ and $T_p =\hbox { 11.5 s}$

Fig. 7

Simulation example of wave prediction algorithm with $H_s = \hbox {5.5 m}$ and $T_p = 11.5\hbox { s}$

A simulation example of the wave prediction algorithm in sea state with $H_s = 5.5\hbox { m}$ and $T_p = 11.5\hbox { s}$ is shown in Figs. 6 and 7. The surge position error is within 2 m, the sway position error is within 1 m, and the heading error is within $0.5^\circ$, while the roll and pitch angles are within 5 degrees. The thruster power consumption in Fig. 7 is not exceeding 160 kW, such that the desired amount of forces and moments can be produced. In the considered scenarios, the bottleneck is not the amount of power which the thruster can produce, but rather the thruster dynamical response time. This leads into the next section, which is considering the thruster dynamics analysis of the surface vessel.

3.6 Thruster dynamics analysis

Wave-compensating DP control will increase the wear and tear of the thrusters and machinery compared to the benchmark, as the variations of the thruster azimuth angle and thrust are increased. This is illustrated in Fig. 8, where the benchmark case, optimal DP, and roll damping algorithm are compared in sea state $H_s = 5.5\hbox { m}$, $T_p = 10.5\hbox { s}$. As can be seen by Fig. 8, the benchmark case has no wave-frequency oscillations in thrust. The optimal DP case has more dynamical behavior due to letting some oscillatory motions through the wave filter. The roll damping case has the same wave filter as optimal DP, but due to direct feedback of roll angle without filtering, this case will be the most dynamic. The maximum position error peak is reduced accordingly with the increase of wave compensation effort. This can be seen by comparing Tables 6, 11, and 23.

Fig. 8

Comparison between benchmark, optimal DP, and roll damping during 200 s in converged state. Sea state is $H_s = 5.5\hbox { m}$, $T_p = 10.5\hbox { s}$

Table 26 shows the thruster ramp time for which the performance of the DP with wave prediction algorithm is the same as the benchmark DP algorithm. This means that for the wave prediction algorithm to get better performance than the benchmark DP algorithm, the thruster ramp times must be smaller than the numbers in the table. The same analysis is made for the roll damping algorithm in Table 27. The metric used to measure performance is the Euclidean average position error peak, since it was found to give the most reliable outcome. Table 26 shows that if the thrusters have a thrust ramp time of less than 7 s (that is, uses less than 7 s from 0 to 100% thrust), the wave prediction algorithm will give a benefit compared to the benchmark DP for all sea states. The roll damping algorithm requires faster thrust ramp time, such that it needs faster thrusters to perform well. The roll damping algorithm needs thrusters with a thrust ramp time of less than 4 s to be better than the benchmark for all sea states.

Table 26 Thrust ramp time in seconds where wave prediction performs equally well as benchmark

Table 27 Thrust ramp time in seconds where roll damping performs equally well as benchmark

A comparative simulation study was done with a thrust ramp time of 2 s and neglected azimuth dynamics. The wave force prediction algorithm was used. Table 28 shows the Euclidean maximum peak results compared to benchmark. Comparing the results with Table 19, we see that more responsive thruster dynamics clearly have a positive impact on performance.

Table 28 Case 5 (wave prediction)—Euclidean distance maximum peak in % compared to benchmark. Thrust ramp time is 2 s

3.7 Relative motion analysis with free-floating ROV

Next, the simulation study considers a neutrally buoyant and passive ROV that is freely floating near the LARS latching point at the bottom of the moonpool of the surface vessel. The relative motion evaluation is divided in two parts:

• 1. Average and maximum relative motion peaks in surge, sway, and heave.

• 2. Time of possible launch and recovery system (LARS) operation in % of the simulation time. Possible LARS operation is defined by the following exemplar criteria on relative positions in surge, sway, and heave:

  $$\begin{aligned} |x_{\text {usv}} - x_{\text {rov}}|&<\text { 0.50 m} \end{aligned}$$

  (35)
  $$\begin{aligned} |y_{\text {usv}} - y_{\text {rov}}|&<\text { 0.50 m} \end{aligned}$$

  (36)
  $$\begin{aligned} |z_{\text {usv}} - z_{\text {rov}}|&<\text { 0.75 m}. \end{aligned}$$

  (37)

  The actual criteria would be subject to the characteristics and performance of the LARS system.

First, the benchmark relative maximum position error peak results in surge, sway, and heave are presented in Tables 29, 30, and 31. The DP algorithm with acceleration feedback gave the best improvements compared to the relative benchmark results. The improvements are shown in Tables 32, 33, and 34. On average, acceleration feedback provides an improvement of 16% in maximum relative surge and 18% in maximum relative sway.

Table 29 Case 1 (benchmark)—relative surge maximum peak in meters

Table 30 Case 1 (benchmark)—relative sway maximum peak in meters

Table 31 Case 1 (benchmark)—relative heave maximum peak in meters

Table 32 Case 4 (acceleration feedback)—relative surge maximum peak in % compared to benchmark

Table 33 Case 4 (acceleration feedback)—relative sway maximum peak in % compared to benchmark

Table 34 Case 4 (acceleration feedback)—relative heave maximum peak in % compared to benchmark

Next, only the benchmark and acceleration feedback case will be considered for the launch and recovery workability analysis. For each sample time, the workability limits are analyzed, and then, the total time where these limits are violated are summed up. The LARS workability results are shown in Tables 35 and 36. It is seen that the workability is increased by utilizing acceleration feedback in the control loop.

Table 35 Case 1 (benchmark)—LARS workability in %

Table 36 Case 4 (acceleration feedback)—LARS workability in %

4 Conclusions and discussion

The DP control algorithms that gave the best results according to the maximum horizontal position error peak were wave prediction and roll damping. Roll damping gave the best results for $H_s =$ 0.5 m and $H_s =$ 5.5 m, and wave prediction gave the best result for the intermediate wave heights. Since no controller is better than all others in all sea states, a hybrid controller can be defined by switching to the best control algorithm in the given sea state. Consider a hybrid controller that optimally switches between wave prediction and roll damping depending on the sea state. Table 37 shows the maximum horizontal position error peak With this hybrid controller, which is reduced by 18% on average across all sea states.

Table 37 Hybrid controller with switching between wave prediction and roll damping control—Euclidean distance maximum peak in % compared to benchmark

Improvements could be achieved with roll damping and wave prediction. However, the simulations show that a conventional diesel-electrical power system having two 180 kW generator sets to feed the thrusters could experience a blackout due to the thruster power variations required to compensate for wave motion. This motivates the use of batteries for peak-shaving when using these algorithms. If batteries are not available to be used for peak-shaving, the optimal DP algorithm could be used. This algorithm did not cause any blackout of the conventional diesel-electrical power system.

Tables 26 and 27 confirm how important fast thruster dynamics are for the performance of the dynamical DP algorithms. Thrusters with a thrust ramp time less than 7 s should be used with the wave prediction algorithm. However, if the hybrid controller is used with the roll damping algorithm for $H_s =$ 5.5 m, thrusters need a thrust ramp time of less than 4 s to be effective for wave compensation, according to Table 27.

Table 28 shows that the thruster dynamics have a large impact on the performance of dynamical DP algorithms and, in this case, the wave prediction algorithm. Faster response of the thrusters will lead to better performance in all sea states.

The relative motions in surge, sway, and heave between the surface vessel and the ROV are quite significant, considering a passive ROV. If an actively controlled ROV is used to follow the surface vessel, the gap could be reduced. With a passive ROV, the acceleration feedback algorithm gave the best relative motion results. This can be seen by comparing the LARS workability in Tables 35 and 36.

The results in this paper are based on state-of-the-art simulation tools and proven DP algorithms. A natural next step could be validation through experimental testing. The use of alternative control design methods is also interesting, such as model predictive control (MPC) [19].