Abstract
In recent years, it has become important to evaluate whether ship propulsive performance achieves the design performance not only in a calm sea condition but also in a seaway. Various on-board monitoring systems have been developed and fitted on-board to check the performance of ships in a seaway. The evaluation can also be fed back to a new ship design. A method for prediction of ship performance in actual seas based on a physical model is described here. Prediction of steady forces in waves, wind forces, drift forces, and steering forces is described from the viewpoint of accurate practical prediction. The prediction of the engine operating point in winds and waves is also treated here. Examples of these prediction methods are illustrated. Performance analysis by an on-board monitoring system using the performance prediction method discussed here is described in the Part 2 of this paper.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
To reduce the greenhouse gas emissions and fuel consumption of ships, improvement of the hull form and the power plant system has been strongly demanded. For this reason, it has become more important to confirm whether propulsive performance achieves the designed performance not only in a calm sea condition, but also in a seaway. The evaluation can also be fed back to a new ship design.
Research on the prediction of ship performance in actual seas has been summarized in many symposiums as technical progress (for example, [1,2,3,4,5,6,7,8,9,10,11]). Studies of performance prediction in actual seas have focused on not only short-term prediction, but also long-term prediction. Thus far, the theoretical frame of the prediction method has reached maturity, and the predicted data can be compared with the ship-scale data monitored on-board.
As ship performance in actual seas includes a very wide range of contents, the meaning of ship performance in actual seas should be clarified first.
According to Naito [9], ship performance when a ship is navigating in a seaway can be categorized as propulsive performance, safety performance, seakeeping performance, and manoeuvering performance. Among these, propulsive performance in actual seas is treated here, since it affects the evaluation of greenhouse gas emissions and fuel consumption of ships. If the weather condition is relatively mild, nominal speed loss occurs due to external forces by winds and waves. On the contrary, under a heavy weather condition, the master gives instruction to reduce speed and change heading deliberately to keep the safety of the crew, cargo and ship itself. The frequency of occurrence of both situations depends on the ship size and weather conditions. As Tasaki and Fujii [5] have pointed out, a weather condition of 6 or 7 on the Beaufort scale of wind (hereafter called BF) will not force the master to order deliberate speed reduction or deliberate heading change in an ocean-going ship. From the long-term statistics of ocean waves, the occurrence probability of BF7 and under accounts for the majority of weather conditions. Figure 1 [12] shows an example of observed frequency of encounter weather. It shows that ships are operated in mild weather.
Cumulative distribution of Beaufort scale [12]
An important classification is made by Hirayama [13]: average weather, which represents mild weather, is determined by ocean statistics, whereas heavy weather is defined by seakeeping performance.
Many experiments and theoretical studies have been carried out so far in connection with ship performance in the mild weather condition. This performance is called ship performance in actual seas in the narrow sense, and is distinguished from ship performance in the heavy weather condition [6], where seakeeping performance will take precedence over propulsive performance. Many evaluations of propulsive performance considering nominal speed loss have been carried out, and the encountered weather is mostly under BF7. The ship performance treated in this paper is based on ship performance in actual seas in the narrow sense.
With respect to ship performance in actual seas, ship-scale performance evaluations based on model tests and theoretical calculations can be compared with abstract logbooks. However, sufficient investigations have not yet been carried out by comparison with on-board monitoring data.
Conventionally, an abstract logbook has been widely used as the report of a voyage. The logbook contains a record of the voyage track, engine operating condition, and weather condition. However, because data are recorded only once a day at noon, the number of data is limited and the weather condition may not represent the whole day. Thus, it is not suitable for comparison of the estimated performance and reported data.
Instead of the abstract logbook, an on-board monitoring system has been developed and diffused recently. Using this system, it is possible to make comparisons between the estimated performance and measured data in various situations.
In this paper, a prediction method for performance in actual seas is described. Performance monitoring and analysis results using the prediction method are described in Part 2 of the concurrent paper. Propulsive performance in actual seas by the prediction method and by monitoring data is compared and discussed.
2 Performance prediction
2.1 Method of performance prediction
Ship performance is a very diverse term, but in this paper, ship speed, engine power, and fuel consumption are treated. The prediction method should be a sufficiently accurate, robust, and reliable one from the practical point of view.
In actual seas, ship speed, engine power, and fuel consumption suffer not only the effects of winds and waves, but also the effects of drift motion and steering. In a heavy weather condition, exceeding the engine torque limit is avoided. Consequently, engine revolution is decreased in such cases. Although ocean currents and tidal currents cause changes in ship speed over ground, the current effect can be excluded, since the ship speed through water is used to evaluate ship performance.
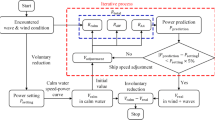
An example of a flow diagram of performance prediction is shown in Fig. 2. In Fig. 2 corresponding section, in which the formulation is described is written; e.g., S.2.2 for Waves. The left column is a typical procedure that has been used in performance prediction in a calm sea condition. The decrease of ship speed varies with the operating mode of the main engine governor. A schematic diagram is shown in Fig. 3. Here, P is main engine power, V is the ship speed through water, V0 is the ship speed in calm sea and Vw1, Vw2 are the ship speed in actual seas in different governor control modes. In addition, the decrease of ship speed is often evaluated under the constant power of main engine for ease of understanding.
Coordinate system for solving ship performance in actual seas is shown in Fig. 4. The origin of the coordinate system is taken as the ship’s center of gravity G.
The equilibrium equations of the forces are set up on the basis of the ship’s course (\(\bar {X}\), \(\bar {Y}\), \(\bar {N}\)). At the condition of constant frequency of engine revolution, for example, the unknowns are the ship speed (V), the drift angle (β ), and the rudder angle (δ ). The unknowns are solved numerically.
The equilibrium equations for longitudinal, lateral and yaw direction are shown in Eq. 1 to 3:
with
where \({R_t}\) is resistance in still water, \({X_{\text{P}}}\) is propeller thrust, \({X_{{\text{drf}}t}}= - \Delta {R_{{\text{drf}}t}}\),\({Y_{{\text{drft}}}}\),\({N_{{\text{drft}}}}\) are hydrodynamic forces and moment due to drift motion, \({X_{{\text{rud}}}}= - \Delta {R_{{\text{rud}}}}\),\({Y_{{\text{rud}}}}\),\({N_{{\text{rud}}}}\) are rudder forces and moment, \({U_{\text{r}}}\) is relative wind speed, \({\gamma _{\text{r}}}\) is relative wind direction (0° is defined as head winds), H is the significant wave height, T is the mean wave period, θ is the primary wave direction (0° is defined as head waves), \({X_{{\text{wind}}}}= - \Delta {R_{{\text{wind}}}}\), \({Y_{{\text{wind}}}}\), \({N_{{\text{wind}}}}\) are wind forces and moment, \(\Delta {R_{{\text{wave}}}}\), \({Y_{{\text{wave}}}}\), \({N_{{\text{wave}}}}\) are added resistance, steady sway force, and steady yaw moment in short crested irregular waves, NP is the frequency of propeller revolution, and \(1 - t\) is thrust deduction coefficient.
2.2 Prediction of added resistance in waves
Added resistance in waves is defined by the difference between the mean resistance value in waves and that in still water. Added resistance in waves is calculated by the component of the radiation effect, diffraction effect, and wave reflection, which are related to the hull form above water.
Ocean waves have irregularities, and these can be expressed in short crested irregular waves by superposition of regular waves having frequency and direction distributions.
According to the theory of small amplitude ship waves, added resistance in regular waves (RAW) is proportion to the square of the wave amplitude (ζa). Added resistance in short crested irregular waves (ΔRwave) is calculated by Eq. 7 with a direction spectrum (E):
where ω is the angular wave frequency and α is the encounter angle between the ship’s heading and component waves. The relationship between the ship’s heading and wave direction is illustrated in Fig. 5, where head waves are defined as 0°.
Many theoretical calculation methods for added resistance in waves have been developed, such as the slender ship theory, three-dimensional panel method, and CFD calculation. These are summarized in Table 1 [14]. The most widespread and practical application in a number of methods is based on Maruo theory [15], where the ship motion is calculated by the strip method and practical correction in short waves is applied.
The strip method agrees relatively well with the experimental values despite the simplicity of the theory, and many ship designers use it in their ship design routine. However, two points related to application should be considered. The first is the treatment of short waves. In relation with the frequency spectrum of ocean waves, the contribution of the added resistance in short waves becomes dominant with increasing ship size. Thus, the accuracy of added resistance in short waves is very important. The second is the treatment of the influence of the hull form above the water surface, since most of the present theoretical methods cannot evaluate the hull form above the water surface.
To solve the first problem, Fujii-Takahashi [16] introduced a semi-empirical correction in short waves for blunt ships. For the second problem, Tsujimoto et al. (hereafter called the NMRI method) [17] integrated the results of tank tests in short waves in calculations. This method not only improves the accuracy of the added resistance in short waves, but can also reflect the hull form above the water surface. The required tank tests are performed at only one frequency with three or more ship speeds, since in short waves, there is almost no ship motion and the frequency response of the added resistance is almost constant. Because the effect of the advance speed is important for the prediction, procedures to determine the coefficient of advance speed of added resistance in short waves are prescribed, as shown in Fig. 6. The coefficient of advance speed of added resistance in short waves (αU) is fitted as proportional to the Froude number (Fr) passing through the origin. An example is shown in Fig. 7, where the tank tests in regular head waves (α = 0°) are carried out at a wave length/ship length ratio (λ/Lpp) of 0.3, where Lpp is the ship length between perpendiculars.
Example of data obtained by tank test in waves (container ship, L = 300 m) [17]
For application to other wave directions, the empirical formula shown in Fig. 8 has been devised [18], where Bf is the bluntness coefficient calculated by the water plane shape and wave direction.
Empirical relationship for estimation of CU [18]
For the semi-empirical correction in short waves, the coefficient of advance speed in short waves (CU) is obtained by the tank tests in short waves or the empirical formula.
The coefficient of advance speed in short oblique waves CU (α) is calculated by Eq. 8:
with
-
1.
\({B_{\text{f}}}(\alpha =0)<{B_{{\text{fc}}}}\) or \({B_{\text{f}}}(\alpha =0)<{B_{{\text{fs}}}}\)
$${F_{\text{S}}}={C_{\text{U}}}(\alpha =0) - 310\left\{ {{B_{\text{f}}}(\alpha ) - {B_{\text{f}}}(\alpha =0)} \right\}$$(10)$${F_{\text{C}}}=Min\left[ {{C_{\text{U}}}(\alpha =0),\;10} \right]$$(11)
-
2.
\({B_{\text{f}}}(\alpha =0) \geqslant {B_{{\text{fc}}}}\) and \({B_{\text{f}}}(\alpha =0) \geqslant {B_{{\text{fs}}}}\)
$${F_{\text{S}}}=68 - 310{B_{\text{f}}}(\alpha )$$(12)$${F_{\text{C}}}={C_{\text{U}}}(\alpha =0)$$(13)where \({B_{{\text{fc}}}}=\frac{{58}}{{310}} \approx 0.187\) and \({B_{{\text{fs}}}}=\frac{{68 - {C_{\text{U}}}(\alpha =0)}}{{310}}\).
The estimation method is validated through on-board measurement [19,20,21,22,23] and is also applied to evaluation of the hull form above the water surface [24]. Verification of the calculation method was carried out at ITTC, and its effectiveness has been confirmed [14].
For quartering and following waves, a correction of NMRI method for the bluntness coefficient (Bf) is proposed in consideration of the relative relationship between the ship speed and the wave propagation by Eqs. 14 and 15:
-
1.
\({B_{\text{f}}}(\alpha )<0\) and \(V+{C_{\text{g}}}\cos (\alpha ) \geqslant 0\)
-
2.
Otherwise
where Cg is the group velocity of waves.
Figures 9 and 10 show the response of added resistance in regular waves and that in short crested irregular waves, respectively, for a container ship using Eqs. 8 and 9 in the NMRI method.
Added resistance in regular waves in full load condition (container ship, L = 300 m) [17]
In addition, Fig. 11 shows the frequency response of added resistance in regular waves in the case of application to the ballast condition [14]. In Fig. 11, STAWAVE1 and STAWAVE2 are the calculation methods developed by the STA group and KAW = RAW/(4ρgζa2Bmax2/Lpp) and NMRI shows the NMRI method. Where ρ is the fluid density, g is the gravitational acceleration, and Bmax is the maximum breadth. Estimation of added resistance in waves in the ballast condition has been considered to be difficult so far, since the bow bulb is exposed above the water surface. However, it can be seen that the added resistance in waves can be estimated practically using the NMRI method.
Added resistance in regular waves in ballast condition (left: bulk carrier, L = 217 m, Fr = 0.188, right: tanker, L = 324 m, Fr = 0.141) [14]
It is known that the hull form above the water surface greatly affects added resistance in waves. Research and development focused on this point have been carried out [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. Evaluations of the effect of the hull form above water by the RANS method have also been carried out in recent years (for example, [43, 44]).
It is possible to understand the performance difference in actual seas from the on-board monitoring data, but for application to ship design, use of an estimation method which can take into account the effect of the hull form above water is important.
In addition, it is also necessary to estimate added resistance in waves under drift motion (ΔRwave). A few studies have examined this, e.g., [45, 46]. As an approximation, it is possible to use Eq. 16, in which the drift effect on added resistance in waves is counted in the change of inflow velocity:
In the calculation of added resistance in short crested irregular waves, the standard spectrum is used for the directional spectrum (E) unless the directional spectrum is measured by a wave buoy or wave radar. When the directional spectrum is not measured, the modified Pierson–Moskowitz-type spectrum is often used as the frequency spectrum (Sf) for wind waves and the JONSWAP spectrum is often used for swells. The expression for standard spectrum by separation of frequency and direction is shown in Eq. 17.
The modified Pierson–Moskowitz-type spectrum is a representation of the open ocean of fully developed waves. The JONSWAP spectrum is a representation of waves of finite fetch length based on wave observations in the North Sea; the bandwidth is narrower than that of the modified Pierson–Moskowitz-type spectrum:
The modified Pierson–Moskowitz-type spectrum is expressed as Eq. 18:
The expression by IACS is shown as
where Γ is the Gamma function.
The expression of the JONSWAP spectrum is shown in Eq. 19:
with \({A_{\text{f}}}=0.072{\left( {\frac{{2\pi }}{T}} \right)^4}{H^2}\), \({B_{\text{f}}}=0.44{\left( {\frac{{2\pi }}{T}} \right)^4}\),
and normally the peak enhancement factor \(\gamma =3.3\) and shape factor \({\sigma _{\text{f}}}=\left\{ {\begin{array}{*{20}{l}} {0.07}&{\left( {\omega \leqslant \frac{{2\pi }}{{1.3T}}} \right)} \\ {0.09}&{\left( {\omega>\frac{{2\pi }}{{1.3T}}} \right)} \end{array}} \right.\) are used.
As the angular distribution function (G) for wind waves, a cosine-squared type is often used, where the spreading parameter (s) is 1 in Eq. 19. For swells, the angular distribution function has a higher concentration than that for wind waves; thus, s = 75 in Eq. 20 is often used:
For evaluation of added resistance in waves, comparison between the standard spectrum and the directional spectrum measured on-board by wave radar has been carried out [47,48,49].
Figure 12 shows a comparison of the added resistance in short crested irregular waves from the directional spectrum measured by wave radar and that from the standard spectrum, in which the significant wave height (H), mean wave period (T), and primary wave direction (θ) are obtained from the directional spectrum. The directional spectrum is measured for about 3 months. The frequency spectrum for the standard spectrum is an IACS spectrum of the modified Pierson–Moskowitz type, and the angular distribution function is the cosine-squared type. The frequency response function of the added resistance in regular waves of a container ship with a length of 300 m is used, as shown previously in Fig. 9.
In Fig. 12, the linear regression line of all the data is shown by the thin line. Since the coefficient of determination (R2) is as high as 0.9, it is observed that ocean waves in the open sea can generally be expressed as a standard spectrum. However, it is also observed that estimation of the added resistance in short crested irregular waves using the standard spectrum has sometimes resulted in over-estimation and under-estimation. Therefore, two typical examples, which are shown 1 and 2 in Fig. 13, are taken up, and the measured directional spectra are shown in Fig. 13, where θ is defined as head waves with an angle of 0°. From Fig. 12, the situation which shows over-estimation and under-estimation is exemplary two directional waves. For the waves having two and more primary wave directions, it was found that the added resistance in short crested irregular waves estimated from the standard spectrum has large error.
The reason for the under/over-estimation is the encounter wave direction. The primary wave direction of Point 1 in Fig. 12 is oblique (θ = 30(°)) and the secondary wave direction is at 100 (°). In this case, the predicted added resistance using standard spectrum is larger than that by measured spectrum, since the component of beam waves in measured spectrum is larger than the standard spectrum. For Point 2, it is the encounter wave direction is quartering [θ = 150(°)] and the secondary wave direction is at 60 (°). This is the opposite case. The predicted added resistance using the standard spectrum is smaller than that by measured spectrum.
Wave steady sway force and yaw moment for a ship having advancing speed are formulated using the ship wave theory [50]. However, these have not been well validated experimentally and by numerical calculations. Therefore, the wave steady sway force and yaw moment are sometimes substituted by a three-dimensional calculation using the singularity distribution of zero forward speed (see Fig. 14 [51]). Here, CYW = YW/(4ρgζa2Bmax2/Lpp) and CNW = NW/(4ρgζa2LppBmax) are non-dimensional coefficient for steady sway force (YW) and steady yaw moment (NW) in regular waves, respectively.
Comparison of experimental and calculation results for steady sway force and steady yaw moment in regular waves and their effects on advance speed [51]
Steady sway force (Ywave) and steady yaw moment (Nwave) in short crested irregular waves are calculated by Eqs. 21 and 22, respectively:
2.3 Prediction of wind resistance
Wind tunnel tests are the most appropriate method of evaluation for prediction of wind resistance, which is required for estimating ship performance in actual seas. However, wind tunnel tests are often difficult from the viewpoints of facility utilization and cost. Therefore, methods using the data set of a similar hull [14] and a regression formula based on the wind tunnel tests have been developed. Various regression formulae have been published [52,53,54,55,56,57]. Figure 15 [14] shows a comparison of the estimated value and the result of a wind tunnel test to determine the wind resistance coefficient as the standard error (\({\overline {{SE}} _{{\text{EST}}}}\)). As the estimated value by the regression formula depends on the database of past wind tunnel tests, it is necessary to be aware of the difference in the shape of the current ship.
Averaged standard errors of longitudinal wind force coefficient (54 ships) [14]
Natural wind is known to have a speed distribution in the height direction, which is caused by the atmospheric boundary layer. In general, this distribution is represented by a logarithmic law or power law shown in Eqs. 23 and 24, respectively:
where Vz is the wind speed at height z, Vh is the wind speed at height h, z0 is the roughness length, and 1/n is an exponent. In the case of the sea, although depending on the sea state, z0 is treated as 0.001 cm, which depends on the wave condition, and the exponent of 1/n is from 1/7 to 1/10 (calm sea condition).
The air resistance caused by self-running even in no wind should be treated in a performance prediction. Incidentally, the speed distribution in the height direction for air resistance is uniform. For a more correct analysis of the increase of wind resistance, it is necessary to convert the wind resistance coefficient by the influence of self-running and natural wind.
2.4 Prediction of hull drifting and steering forces
When the hull is subjected to forces due to wind and waves, the ship is manoeuvered so as not to deviate from the course, but resistance is increased by steering. Moreover, when the rudder force is not sufficient for the forces due to winds and waves, drift motion of the ship occurs.
2.4.1 Hull drifting force
Although the hydrodynamic forces caused by drift motion can be estimated by drift motion tests, a regression formula based on the results of tank tests has also been developed [58]. When the steady navigation condition is assumed in a performance evaluation, the term of yaw rate is omitted. Furthermore, to improve accuracy for the small drift angle, it has been shown that the lift-induced drag given by the small aspect ratio wing theory should be added to the resistance due to drift motion [59].
In this case, the hull drifting forces in the steady condition [resistance (\(\Delta {R_{{\text{drft}}}}\)), sway force (Ydrft) and yaw moment (Ndrft)] are expressed as Eqs. 25 to 28:
where X0′ is a non-dimensional coefficient for still water resistance and Cyβ , Cyββ, Cnβ, and Cnββ are non-dimensional hydrodynamic derivatives, which are calculated by the regression formula.
The non-dimensional expressions for the forces in this section are the following:
where d is the draught and L is the ship length.
If the results of tank tests are used, the resistance due to drift is expressed as Eq. 29, where Cxββ is a non-dimensional coefficient derived from the tank tests:
2.4.2 Steering force
Hydrodynamic forces due to steering [resistance (\(\Delta {R_{{\text{rud}}}}\)), lateral force (Yrud), yaw moment (Nrud)] can be estimated by model tests or regression formulae.
The hydrodynamic forces due to steering are expressed by regression formulae as Eq. 30 to 33 [58]:
where tR is the steering resistance deduction fraction, aH is the rudder force increase factor, \({x_{\text{H}}}^{\prime }={x_{\text{H}}}/L\) is a non-dimensional longitudinal coordinate of the center of the additional lateral force from the center of gravity, AR is the projected rudder area, \({x_{\text{R}}}^{\prime }={x_{\text{R}}}/L\) is a non-dimensional longitudinal coordinate of the rudder position from the center of gravity, δ is the rudder angle, fα is the rudder lift gradient coefficient, UR′ is the non-dimensional resultant inflow velocity to the rudder, and αR is the effective inflow angle to the rudder.
The rudder lift gradient coefficient (fα) is often expressed as Eq. (34), which uses the rudder aspect ratio (ΛR) [60]:
There are various types of expressions for the non-dimensional resultant inflow velocity to the rudder (UR′). The following expression can be used [58]:
where wR0 is the wake fraction at the rudder position in straight moving, w0 is the wake fraction at the propeller position in straight moving, DP is the propeller diameter, HR is the rudder height, γE is a flow straightening coefficient, p is the propeller pitch, and Crud is a correction coefficient for the propeller slipstream [for example, rudder to port (Crud = 1.065) takes a different value from rudder to starboard (Crud = 0.935)].
The empirical formulae for the interaction coefficients tR, aH, xH′, wR0, and γE can be used [61, 62].
Another expression for UR′ is the following [63, 64]:
where w0 is the wake fraction at the propeller position in straight moving, wR is the wake fraction at the rudder position, KT is the thrust coefficient in the open water condition, J is the propeller advance ratio, cw is a constant expressing the wake fraction in drift motion, e.g., − 4.0, and εw is the ratio of the wake coefficient at the propeller and rudder positions, e.g., 1.1, and κw is an experimental constant for expressing the longitudinal inflow velocity to the rudder, e.g., 0.6.
2.4.3 Added resistance due to yaw motion
In case of analysis of on-board monitoring data, the added resistance due to yaw motion (ΔRyaw) may be taken into account [8]. An empirical equation is shown in Eq. 47 for the non-dimensional expression:
where M is the ship mass, CB is the block coefficient, my is the added mass in the lateral direction, and \(\bar {r}\)is the average of the yaw rate.
In case it is hard to obtain \(\bar {r}\) with accuracy, the empirical equation shown in Eq. 48 can be used:
where ψa is the amplitude of yaw motion induced by steering operation and Tψ is the period of yaw motion, which corresponds to the steering period of autopilot.
2.5 Prediction of power
Various methods have been proposed for calculation of main engine power, which varies in actual seas. However, the following five methods are proposed based on tank tests [65, 66].
(1) Direct power method; DPM, (2) torque and revolution number method; QNM, (3) thrust and revolution number method; TNM, (4) resistance and thrust identity method; RTIM, and (5) over load test method; OLTM. These techniques are characterized from the model ship to conversion to the actual ship, as shown in Table 2.
As Naito and Miyake [65] is commentary, it is necessary to consider the rationality of the physics for these methods. It is also necessary to treat wind forces, drift forces, and steering forces.
RTIM is considered to be the most rational of these methods as resistance is used in scaling up.
It is known that the self-propulsion factors in regular waves are different from those in still water. However, in many analyses, the self-propulsion factor in irregular waves is treated as the same as the average factor in still water.
In case of no propeller emersion, it has been shown experimentally that the propeller characteristics in waves can be used as those in still water, but considering the change of the propeller advance ratio.
On the contrary, OLTM [67, 68] can evaluate the self-propulsion factors in waves, but it does not treat the change of self-propulsion factors by ship motion. The treatment of the change of self-propulsion factors by ship motion and a wake scaling method remains as future work.
2.6 Prediction of engine operating point
There is a driving restriction by the torque limit of the main engine. The torque limit usually refers to the restrictions both by the mean effective pressure and by overload protection. In addition, control by constant frequency of engine revolution or constant main engine output is performed by the governor. Control of the limit of the fuel index, which means fuel injection, is applied for fuel economy. There is also a driving restriction by the turbocharger, but its effect is limited to a short time, such as in the steering. Thus, this restriction is not related to steady-state ship operation.
The schematic relationship between the frequency of engine revolution and engine power is shown in Fig. 16.
2.6.1 Limit by mean effective pressure
Shaft power (P) is expressed by Eq. (49) using the propeller characteristic and the mean effective pressure (MEP):
where NP is the frequency of propeller revolution, QP is the propeller torque, η is the propulsion efficiency, ηS is the transmission efficiency, Pme is the mean effective pressure, LS is the stroke length of the cylinder, AC is the bore area, NE is the frequency of engine revolution, ZC is the number of cylinders, and ζcycle is the number of revolutions per cycle (1 for 2-cycle engines and 2 for 4-cycle engines).
From Eq. 35, torque is proportional to MEP. Therefore, the main engine operating limit by MEP is expressed as a linear expression with respect to the frequency of main engine revolution.
2.6.2 Limit by overload protection
The main engine operating limit due to overload protection (OLP) is expressed Eq. 50:
where aOL is a constant determined by OLP, dOL is an exponent determined by OLP, NEOL is the frequency of engine revolution defined as the intersection point between the torque limit by MEP and that by OLP, pOL is the shifting ratio in revolution, and NEMCR is the frequency of engine revolution at maximum continuous rating (MCR). The relationship of these factors is shown in Fig. 16.
Here, Eqs. 52 and 53 are generally used for dOL and pOL by the engine maker:
2.6.3 Limit by fuel index
In normal vessels, both MEP and OLP are used as operation limits. In addition, a limit by the fuel index (FI) is applied for fuel economy. When the operating FI exceeds the limit, the frequency of engine revolution is reduced automatically.
FI is fuel injection, where the value at MCR is 100%. The definition is shown in Eq. 54:
where SFC is the specific fuel consumption and the subscript MCR means SFC at MCR.
It is possible to determine the main engine operating point in accordance with the main engine operating limit line by FI with the frequency of engine revolution.
For example, the performance curves in a head weather condition for P − NE and for P − V are shown in Figs. 17 and 18, respectively. The operating points by the various governor controls, i.e., constant frequency of engine revolution (NE const.), limit by fuel index (FI), and constant main engine power (P const.), are shown in these figures. Figure 19 shows the set value of the upper limit of the fuel index (LimitFI), which can be set arbitrarily.
In this example, the command NE is 90 rpm, and in BF7, the operating points are below the torque limit in all cases. When a ship is operated by NE const. control by the governor, the main engine power is increased. On the contrary, when the ship is operated by P const. control by the governor, the ship speed is lower than that by NE const. control. Looking at the operating point in the case of the FI limit, the FI limit is applied from BF5, and as BF increases, P is reduced and NE and V are significantly reduced.
From this, it is understood that the main engine operating limits cause differences in the ship speed and fuel consumption in actual seas [69].
3 Simulations
Using the performance prediction described in Sect. 2, ship speed and power are evaluated here.
Added resistance in waves is evaluated by the NMRI method. For a tanker, the added resistance in waves is calculated. The principal dimensions are shown in Table 3.
Figure 20 shows the difference of the added resistance in regular waves (RAW) between using Eqs. 14 and 15 and not using them. Figure 21 shows the difference of the added resistance in short crested irregular waves (ΔRwave) between using Eqs. 14 and 15 and not using them.
From these figures, the difference is found in quartering to the following waves. Using Eqs. 14 and 15, the added resistance in quartering to the following waves is increased.
Wave steady sway force and wave steady yaw moment are calculated by the method, as shown in Sect. 2.2 [51]. Wind forces are calculated by Fujiwara et al. [57], drift forces are calculated by Eqs. 11 to 13, and steering forces are calculated by Eqs. 16 to 18 using Eqs. 21 to 25. Added resistance due to yaw motion is not considered.
Using the evaluation of these external forces, ship speed and power is simulated. Power is predicted by RTM and control of the governor is selected for the constant frequency of engine revolution. The main engine is equipped with a low speed diesel. The simulated speed–power relations in quartering waves [θ = 135(°)] are shown in Fig. 22. The weather conditions are shown in Table 4. From Fig. 22, it is found that the engine power is increased using Eq. 2 than not using Eq. 2. This is because the added resistance in waves is increased. Figure 23 shows the difference of the ship speed, the rudder angle (δ ), and the drift angle (β) at BF7 against the wave direction. From the figure, the difference in the prediction of the speed and rudder angle can be seen from the oblique to the following waves. Difference in the drift angle cannot be seen.
4 Conclusions
Analysis of on-board monitoring data leads to an understanding of the performance of the ship for the shipyard. Its feedback to ship design enables the development of ships which display high performance in actual seas. On-board monitoring data are also very useful for ship owners/operators when analyzing factors that increase fuel consumption in actual seas, supporting improvement of ship operation.
The performance prediction method shown in this paper is based on a physical model. Use of a physical model makes it possible to analyze phenomena from a theoretical and physical point of view. It is also possible to introduce the findings from model tests.
Using the performance prediction method, simulation on speed–power relations is performed for a tanker. From the simulation, a correction formula for quartering and following waves of the added resistance in waves is proposed and the effect is investigated. The validation of the method is discussed in Part 2 of this paper.
Based on the prediction of the external forces, it is possible to analyze ship performance in actual seas and to make efforts for improvement of energy efficiency in actual seas.
References
Nakamura S (1964) Elements of seakeeping performance. In: Symposium on seakeeping performance, the society of naval architects of Japan, pp 121–141 (in Japanese)
Shintani A, Naito S (1977) Power increase in waves. In: Symposium on the 2nd seakeeping performance, The Society of Naval Architects of Japan, pp 165–180 (in Japanese)
Takezawa S, Kajita E (1977) Correspondence between result of full-scale measurement and prediction. In: Symposium on the 2nd seakeeping performance, The Society of Naval Architects of Japan, pp 165–180 (in Japanese)
Shintani A, Yamazaki Y (1983) Propulsive performance test in waves. In: Symposium on development of hull form and tank test. The Society of Naval Architects of Japan, pp 189–212 (in Japanese)
Tasaki R, Fujii H (1984) “State of the art”, ship motions, wave loads and propulsive performance in a seaway, 1st marine dynamics symposium, The Society of Naval Architects of Japan, pp 1–12 (in Japanese)
Naito S, Kan M (1984) Speed Loss in a Seaway. In: Ship motions, wave loads and propulsive performance in a seaway, 1st Marine dynamics symposium. The Society of Naval Architects of Japan, pp 81–100 (in Japanese)
Hosoda R, Takahashi T (1984) Sea margin and service performance. In: Motions ship, wave loads and propulsive performance in a seaway, 1st marine dynamics symposium. The Society of Naval Architects of Japan, pp 121–136 (in Japanese)
Miyamoto M, Kadomatsu K, Shimada K (1994) Propulsive performance of a ship in a seaway. In: Applications of ship motion theory to design, 11th marine dynamics symposium. The Society of Naval Architects of Japan, pp 93–146 (in Japanese)
Naito S (1995) Propulsive Performance in waves. In: Propulsive performance of ships at sea, 6th JSPC symposium on propulsive performance of ships at sea. The Society of Naval Architects of Japan, pp 113–129 (in Japanese)
Kajitani H, Naito S, Kohzaki S, Yamano T (1995) Panel discussion on propulsive performance of ships at sea. In: Propulsive performance of ships at sea, 6th JSPC symposium on propulsive performance of ships at sea. The Society of Naval Architects of Japan, pp 189–203 (in Japanese)
Naito S (2003) Evaluation of ship performance at sea. In: 4th symposium on ship performance at sea. The Society of Naval Architects of Japan, pp 1–9 (in Japanese)
Tsujimoto M, Orihara H (2015) Performance prediction of full-scale ship and analysis by means of on-board monitoring. In: Ship performance monitoring in actual seas, marine dynamics symposium, JASNAOE, pp 77–154 (in Japanese)
Hirayama T, Choi Y-H (2001) Consideration on the establishment of rough-sea state-for guaranteeing the ship performances in operating condition. J SNAJ 189:39–46 (in Japanese)
ITTC (2014) Specialist committee on performance of ships in service final report and recommendations to the 27th ITTC. In: Proceedings of 27th ITTC Full Conference, pp 1–72
Maruo H (1963) Resistance in waves, research on seakeeping qualities of ships in Japan. Soc Nav Archit Jpn 8:67–102
Fujii H, Takahashi T (1975) Experimental study on the resistance increase of a ship in regular oblique waves. In: Proceedings of 14th ITTC, vol 4, pp 351–360
Tsujimoto M, Shibata K, Kuroda M, Takagi K (2008) A practical correction method for added resistance in waves. J JASNAOE 8:141–146
Tsujimoto M, Kuroda M, Sogihara N (2013) Development of a calculation method for fuel consumption of ships in actual seas with performance evaluation. In: Proceedings of the ASME 2013 32nd international conference on ocean, offshore and arctic engineering, OMAE2013-11297, pp 1–10
Sogihara N, Ueno M, Hoshino K, Tsujimoto M, Sasaki N (2010) Verification of calculation method on ship performance by onboard measurement. In: Proceedings of 20th international offshore polar engineering conference 2010, vol 4, pp 750–757
Sogihara N, Ueno M, Fujiwara T, Tsujimoto M, Sasaki N (2011) Onboard measurement for verification of a calculation method on decrease of ship speed—for a RoRo Cargo Ship and an Oil Tanker. In: Proceedings of 21st international offshore polar engineering conference 2011, vol 4, pp 975–981
Kuroda M, Tsujimoto M, Sogihara N (2012) Onboard measurement for a container ship in view of container load condition. J JASNAOE 15:29–35
Ichinose Y, Tsujimoto M, Shiraishi K, Sogihara N (2012) Decrease of ship speed in actual seas of a bulk carrier in full load and ballast conditions—model test and onboard measurement. J JASNAOE 15:37–45
Sogihara N, Tsujimoto M, Ando H, Kakuta R, Ueno S (2012) On the estimation of fuel oil consumption for ships in actual seas by embarkation on a large container ship (in Japanese). Conf Proc JASNAOE 14:203–206
Kuroda M, Tsujimoto M, Sasaki N, Ohmatsu S, Takagi K (2010) Relation between added resistance in waves and bow shapes above waterline. In: Proceedings of PRADS2010, pp 256–265
Shibata K, Kogo Y, Ohtagaki Y (1983) A study of tanker design with whale-back shaped bow—for energy saving in rough sea. In: Proceedings of the 2nd international symposium on practical design in shipbuilding, pp 347–352
Ogiwara S, Yamashita S, Mifune M (1996) On resistance increase in waves of short wavelength (in Japanese). J. KSNAJ 225:37–45
Naito S, Kodan N, Takagi K, Matsumoto K (1996) An experimental study on the above-water bow shape with a small added resistance in waves (in Japanese). J KSNAJ 226:91–98
Kihara H, Naito S (1998) Nonlinear hydrodynamic forces acting on slender body ship with large amplitude motion: above water hull form’s effect to added resistance (in Japanese). J KSNAJ 230:185–195
Matsumoto K, Hirota K, Takagishi K (2000) Development of energy saving bow shape at sea. In: Proceedings of 4th Osaka Colloquium, pp 479–485
Kataoka S, Sueyoshi A, Arihama K, Iwashita H, Takaki M (2003) A study on the effect of bow and stern flares on ship seakeeping (in Japanese). Trans West Jpn Soc Nav Archit 105:149–158
Yamasaki K, Matsumoto K, Takagishi K (2003) On the bow shape of full ships with low speed (in Japanese). J KSNAJ 240:101–108
Hirota K, Matsumoto K, Takagishi K, Orihara H, Yoshida H (2004) Verification of Ax-Bow effect based on full scale measurement (in Japanese), J KSNAJ 241:33–40
Hu et al (2013) Development of CFD method for study of above waterline hull form effect on added resistance (in Japanese). Mitsui Zosen Tech Rev 208:1–7
Jeong K-L, Lee Y-G, Yu J-W (2013) A fundamental study on the reduction of added resistance for KCS. In: Proceedings of 12th international symposium on practical design in shipbuilding 2013, pp 23–30
Hwang S, Kim J, Lee Y-Y, Ahn H, Van S-H, Kim K-S (2013) Experimental study on the effect of bow hull forms to added resistance in regular head waves. In: Proceedings of 12th international symposium on practical design in shipbuilding 2013, pp 39–44
Lee J-H, Seo M-G, Park D-M, Yang K-K, Kim K-H, Kim Y-H (2013) Study on the effects of hull form on added resistance. In: Proceedings of 12th international symposium on practical design in shipbuilding 2013, pp 329–337
Ikeda Y, Ibata S, Aoyama Y, He N-V (2013) Development of an appendage to reduce the added resistance in waves for a large blunt ship using CFD (in Japanese). Conf Proc JASNAOE 17:357–360
Yoshida H (2014) Reduction of added resistance in waves by improvement of bow shape (in Japanese). In: Seminar on technologies of reduction of added resistance of ships in waves, JSNAOE, pp 112–123
Izumi T (2014) Efforts on improvement of propulsive performance in actual seas (in Japanese). In: Seminar on technologies of reduction of added resistance of ships in waves, JSNAOE, pp 124–135
Yamashita Y (2014) On the efforts to reduce the added resistance in waves (in Japanese). In: Seminar on technologies of reduction of added resistance of ships in waves, JSNAOE, pp 136–152
Tsujimoto M, Kuroda M, Shiraishi K, Sasaki N, Naito M, Omote M, Nojima N, Kaga M (2014) Development of energy saving device for actual seas STEP (in Japanese). Pap Natl Marit Res Inst 14(2):45–63
Sakurada A, Tsujimoto M, Kuroda M (2016) Development of COVE bow-energy saving bow shape in actual seas. In: Proceedings of PRADS2016, pp 1–9
Orihara H, Miyata H (2003) Evaluation of added resistance in regular incident waves by computational fluid dynamics motion simulation using an overlapping grid system. J Mar Sci Technol 8(3):47–60
Orihara H, Matsumoto K, Yamasaki K, Takagishi K (2008) CFD simulations for development of high-performance hull forms in a seaway. In: Proceedings of 6th Osaka colloquium on seakeeping and stability of ships, pp 58–65
Ueno M, Nimura T, Miyazaki H, Nonaka K (2000) Steady wave forces and moment acting on ships in manoeuvring motion in short waves. J SNAJ 188:163–172 (in Japanese)
Yasukawa H, Adnan F-A (2006) Experimental study on wave-induced motions and steady drift forces of an obliquely moving ship. J JASNAOE 3:133–138 (in Japanese)
Kano T, Kobayashi M, Kan M, Yamazaki E (2009) Estimation on the increase of resistance of a ship in wave by measured directional spectra (in Japanese). Conf Proc JSNAOE 8:145–146
Kano T, Takano S, Matsuura K, Kobayashi M (2010) On the measured wave spectra by coastal vessels and estimated added resistance in wave based on the wave spectra (in Japanese). Conf Proc JSNAOE 11:375–378
Sogihara N, Tsujimoto M, Ando H, Kakuta R (2015) Investigation on the effect of directional wave spectrum for estimation of added resistance in short crested irregular waves (in Japanese). Conf Proc JSNAOE 20:373–376
Kashiwagi M, Ohkusu M (1993) Study on the wave-induced steady force and moment (in Japanese). J Soc Nav Archit Jpn 173:185–194
Tsujimoto M et al (2017) Development on ship performance simulator in actual seas (in Japanese). Pap Natl Marit Res Inst 16(3):17–41
Japan Towing Tank Committee (1944) Proposals of conduct of standard speed trials and analysis method of speed trials (in Japanese). Bull Zosen Kiokai 262:1–12
Isherwood RM (1973) Wind resistance of merchant ships. Trans RINA 115:327–338
Yamano T, Saito Y (1997) An estimation method of wind forces acting on ships (in Japanese). J KSNAJ 228:91–100
Yoneta K, Januma S, Karasuno K (1992) Analysis of vessels’ wind forces through the utilization of a physical–mathematical model-II. J JIN 86:169–177
Fujiwara T, Ueno M, Nimura T (1998) Estimation of wind forces and moments acting on ships. J Soc Nav Archit Jpn 183:77–90
Fujiwara T, Ueno M, Ikeda Y (2006) Cruising performance of a large passenger ship in heavy sea. In: Proceedings of 16th international offshore and polar engineering conference, vol III, pp 304–311
Kijima K, Nakiri Y (2002) On the practical prediction method for ship manoeuvring characteristics” (in Japanese). Trans West Jpn Soc Nav Archit 105:21–31
Sogihara N, Tsujimoto M, Ichinose Y, Minami Y, Sasaki N, Takagi K (2010) Performance prediction of a blunt ship in oblique waves (in Japanese). J JASNAOE 12:9–15
Fujii H, Tuda T (1961) Experimental research on rudder performance. (2) (in Japanese). J Zosen Kiokai 110:31–42
Kijima K, Nakiri Y (1999) Approximate expression for hydrodynamic derivatives of ship manoeuvring motion taking into account of the effect of stern shape (in Japanese), Trans West Jpn Soc Nav Archit 98:67–77
Kijima K, Katsuno T, Nakiri Y, Furukawa Y (1990) On the manoeuvring performance of a ship with the parameter of loading condition. J Soc Nav Archit Jpn 168:141–148
Kose K, Yumuro A, Yoshimura Y (1981) Realization of mathematical model of manoeuvring motion—mutual interference of hull, propeller and rudder and its expression (in Japanese). In: 3rd symposium on manoeuvring performance. The Society of Naval Architects of Japan, pp 27–80
Yasukawa H, Yoshimura Y (2015) Introduction of MMG standard method for ship maneuvering prediction. J Mar Sci Technol 20:37–52
ITTC/RP.7.5-02-07-02.2 (2014) Predicion of power increase in irregular waves from model test, ITTC recommended procedures, pp 1–15
Naito S, Miyake S (2007) Estimation of power increase in actual seas (in Japanese). J JSNAOE 6:121–141
Adachi H (1978) On the theoretical bases and application methods of the propeller load varying test method (in Japanese). J SNAJ 154:109–117
Mizoguchi S, Tasaki R (1983) Investigation into propulsion factors in waves with overload tests of a container ship (in Japanese). J KSNAJ 190:121–129
Tsujimoto M, Sogihara N (2012) Evaluation of fuel consumption for ships in actual seas (in Japanese). J JSNAOE 16:69–75
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Tsujimoto, M., Orihara, H. Performance prediction of full-scale ship and analysis by means of on-board monitoring (Part 1 ship performance prediction in actual seas). J Mar Sci Technol 24, 16–33 (2019). https://doi.org/10.1007/s00773-017-0523-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00773-017-0523-1