Abstract
Underwater gliders, which are profiling autonomous underwater vehicles designed to make oceanographic measurements, are increasingly used in the coastal ocean. As they regularly surface for data transmission, gliders increasingly pose a risk for fast ships. In order to estimate the extent of damage due to collision, 3D finite element simulations of collisions between a glider and a high-speed craft with a glass-fiber reinforced plastic hull are performed. Different collision scenarios such as impact locations, angles of attack and speeds are examined. The results are compared to an analytical solution based on simplifying assumptions. Although both methods reveal consistent results, it is shown that finite element simulations are required to account for the 3D shape of the ship. The results indicate that at ship velocities exceeding 7.5 m/s (14.6 kt) the glider penetrates the ship’s hull causing severe damage to its structure.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Underwater gliders, or gliders for short, are a class of autonomous underwater vehicles propelled by a buoyancy engine. Principle of operation is that the buoyancy engine allows the glider to attain positive or negative buoyancy of the equivalence of about 250 \(\mathrm{cm}^3\) seawater, generating a vertical motion with respect to the ambient water. Wings attached to the side of the hull convert part of the vertical speed into horizontal speed, so that the glider moves through the water column in a zigzag fashion, cf. Fig. 1. Usually, the glider is programmed to come to the surface at regular intervals (hours), where it remains for about 20 min in order to transfer data to a server on land via a satellite communication link.
The low speed of about 0.4 m/s gives the glider its unique endurance of the order of weeks to months, much longer than other classes of autonomous underwater vehicles. The long endurance and relatively low cost of gliders has led to gliders to become more and more ubiquitous as an oceanographic measurement platform. Although most gliders have been deployed in ocean waters, there is an increasing interest to employ gliders in coastal waters for monitoring purposes. In contrast to far off-shore (international) waters, in coastal waters conflicts arise between shipping and free moving unmanned measurement platforms such as gliders. The German Bight (eastern part of the North Sea) for example, is a coastal sea where gliders have been operated as part of the Cosyna observatory [1]. Regulations in the German exclusive economic zone state that operation of gliders is forbidden. However, a request can be filed to the responsible authority to be exempted from this prohibition. Whether to grant the request or not, the authorities take into consideration the risk imposed by operating gliders on shipping and other off-shore activities.
The probability of a ship-glider collision can be estimated with the help of automatic identification system (AIS) data [2]. With a mass of about 50–60 kg, it is clear that in the event of a collision with a large steel ship, no damage will be done to the ship and most likely the glider will be lost. For authorities, the loss of a glider is not of concern. Damage to, or worse, loss of a vessel due to a glider, on the other hand, is a major concern, in particular, if the glider is deployed with the authorities’ consent. Clearly, large steel vessels will not be affected, however, lightweight fast off-shore crafts may suffer damage.
Estimates on the damage caused by ship accidents received attention due to its impact on human lives, environment and the resulting financial consequences [3]. Respective investigations are concerned with ship grounding and stranding, ship–platform collisions, and ship–ship collisions, see [4] for a comprehensive overview. Literature dealing with collisions between ships and objects floating beneath the water surface are, for obvious reasons, scarce, except for ship–container interactions as well as collisions of ships with slender objects. In particular, [5] analysed the collision of a fast cruising single-skin craft using an analytical approach.
The probability of collisions between large vessels was calculated to be 0.516 % per year and ship [6]. In the study mentioned, however, only vessels larger than 4000 gross register tons were considered. To our knowledge, to date no study, neither experimental nor analytical, has been performed on the likelihood of damage to a ship caused by a glider in the event of a collision.
Predictive approaches besides experimental testing were established to anticipate the amount of damage. The problem is commonly divided into two parts: calculation of external mechanical quantities (impulse of a collision), and the determination of internal mechanics (strength or resistance of ship sub-structures) [5]. Depending on the assumptions made for the collision scenario, the details accounted for in the ship’s structure and the underlying material model (constitutive relation), has received considerable attention. Smaller (and faster) ships are made of materials different from steel, such as aluminium or composite materials. Recent work therefore focusses on lightweight vessels [7], the damage behaviour and its interaction [8, 9], the (structural) finite elements to be used [10] and the effect of the damage criterion used [11]. Wisniewski and Kolakowski [12] use an explicit dynamic FE-solver for their analysis based on elastic-plastic shell elements to numerically solve the complete boundary value problem. In order to validate their simulation of a side impact, Karlsson et al. [13] performed laboratory experiments impacting a steel sandwich structure by a rigid punch. Similar to that, Steglich et al. [14] used pre-stretched cruciform specimens to validate damage scenarios caused by a quasistatic punch penetration.
In the current study we explicitly model a collision scenario between glider and sport boat independently from the probability of its occurrence. We consider a typical recreational ship of class B (CE-classification), a glass-reinforced plastic (GRP) hulled powerboat that can be encountered in off-shore waters of coastal seas. It is selected as a “worst case scenario” , as it combines low weight, high cruising speed and a rather fragile ship hull. Rather than employing expensive experiments in which a glider-like object collides with the hull of the design vessel, an analytical and a numerical method based on finite element modelling are exploited to investigate the effects and consequences of various collision scenarios.
2 Analytical approach
Pedersen and Zhang [15] and Zhang [5] introduce an analytical approach to estimate the amount of damage during collision of two vessels in two steps. First, the energy which is to be absorbed during the collision is calculated via the balances of linear and angular momentum. Second, they estimate the amount of energy the hull is capable of absorbing before damage. In this work, we use the results of the Pedersen–Zhang approach for a first estimate of damage.
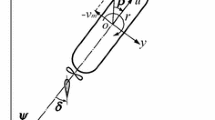
Pedersen and Zhang assume that the ship’s mass is large compared to the mass of the second colliding object, which furthermore does not glide along the hull. In order to derive an analytical solution, they study a two-dimensional simplified problem. We use these premises and apply the methodology to the collision between a ship and a glider, see Fig. 2.
Sketch of the collision scenario following [5] (a) and model of a planar plate (b). 2a and 2b are the distances between two transverse and longitudinal structures, respectively
2.1 Energy to be absorbed during collision
As explained in detail in [16], the energy to be absorbed is split into contributions along the axes of a local coordinate system \(\xi ,\eta\), see Fig. 2a, and reads
with m being the mass of the glider, v the impact speed and \(\beta\) the angle between the ship’s direction of travel and the tangential line of the ship hull in the impact point, see also Fig. 2a. The coefficients \(D_{\xi }\), \(D_{\eta }\), \(K_{\xi }\), \(K_{\eta }\) and \(\mu\)
are functions of the angle \(\alpha\) between the glider and the tangential line in the collision point along the hull, see [16]. Further, Eq. 2 depend on coefficients of relative virtual masses in order to account for hydrodynamical effects of the glider. The coefficients \(m_{x,\mathrm {rel}}\) and \(m_{y,\mathrm {rel}}\) are the relative virtual masses in longitudinal (x, surge) and in lateral (y, sway) direction, respectively, and \(j_{\mathrm {rel}}\) is the relative virtual momentum of inertia with respect to the vertical axis. The relative values can be calculated with the virtual masses/inertia and the actual mass/inertia of the glider (e.g. \(m_{x,\mathrm {rel}}=m_{x}/m\)). The virtual masses/inertia are calculated for an ellipsoid with the dimensions of the glider according to Korotkin [17].
2.2 Energy absorbed by the hull
Zhang [5] assumes that the entire energy is absorbed by a part of the skin bounded by stringers and frames. Figure 2b sketches this part of the hull as a planar plate. Based on this simplification, the collision represents a tensile loading in plane stress conditions. The authors derive expressions for two collinear in-plane strain components \(\varepsilon _1\) and \(\varepsilon _2\). To avoid damage, the sum of both strains \(\varepsilon = \varepsilon _1+ \varepsilon _2\) needs to be smaller than the tensile strain at fracture, \(\varepsilon _f\)
where \(\varepsilon _1\) is the strain caused by the normal component \(F_1\) of the impacting force, \(\varepsilon _2\) the strain caused by the tangential component \(F_2\), cf. Fig. 2b.
Following [5], the energies \(E_\xi\) and \(E_\eta\) to be absorbed due to the orthogonal (\(\xi\)-) and parallel (\(\eta\)-) contribution of the collision force, respectively, are given by
with \({\sigma }_0\) being the yield/fracture stress (elastic–ideal plastic material behaviour assumed), t the hull’s (plate’s) thickness and A the area between stringers (i.e., the area of the plate \(A=4ab\)).
Rewriting Eq. 4 as relations for the strains \(\varepsilon _1\) and \(\varepsilon _2\), inserting Eq. 1 and subsequent substitution into Eq. 3 renders
Equation 5 constitutes a maximum strain criterion and hence allows for an assessment of a loading scenario.
3 Finite element model
To allow for a more comprehensive investigation and to account for a more realistic collision scenario, finite element simulations were performed with the commercial FE-Software Abaqus 6.12. In particular, Abaqus/Explicit was used as it is well suited for dynamic problems involving contact and material failure. The FE-models of the glider and the ship were generated using the ABAQUS CAE software. For the two independent objects, namely glider and ship, shell elements were used to describe the respective hull. In case of the ship, stingers are additionally accounted for by special stiffener (beam) elements. Neither mass scaling nor time scaling was applied in the simulations. The theory of finite deformations was used.
To account for inertia and hydrodynamic effects, non-structural mass and virtual mass have to be introduced to the FE model. A non-structural mass is used to raise the mass of the simplified model (e.g. the ship’s hull including stiffeners but without any interior parts, fuel tank and engines) to the actual mass of the reference object. Virtual mass raises the overall weight of the FE model above the weight of the reference object in reality. This is done to account for hydrodynamic effects of an object which moves mainly below the water surface.
3.1 Glider and ship
The FE-model of the glider was deduced from its axisymmetric structure (1.88 m overall length, 52 kg total mass, wall thickness 9.25 mm), see Fig. 3. The wings and the tail fin are not included in the model, as they will easily break off from the main body in case of a crash. The different sections visible in Fig. 3 refer to the sonar case, solid head, main hull, and tail section (from right to left). For each part a material was assigned: polypropylene (nose), aluminium (main body), and polyester (tail section). The respective physical constants are listed in Table 1. In total, 1200 linear shell elements (S4) were used for the discretisation of the glider. Hydrodynamic effects of the glider were accounted for by adding a virtual mass of 45.3kg, the equivalent of the relative virtual mass \(m_{y,\mathrm {rel}}\) introduced in Eq. 2. While the latter relation considers virtual masses/inertia for each component of motion individually, in the FE analysis no distinction between the different components of virtual mass was done. The highest amount was therefore added, namely \(m_{y}\) [17].
A small vessel (12 m length, 3.7 m width, 7.8 tons weight) is considered as the colliding water vehicle, see Fig. 4, representing a typical recreational motor ship (yacht). The ship’s hull was assumed to be manufactured from E-glass (alumino-borosilicate glass) reinforced polyester, with short-fibre-reinforced as well as woven fabrics laminated in total nine layers. The averaged material properties were calculated for this compound, see Sect. 3.2. The FE-model consists of the ships hulk, a hull (shell elements) reinforced by longitudinal stringers (beam elements). The laminated bulkheads (transverse sections) are modelled by shell elements. The total thickness of all sections was assigned according to the construction plan of the ship, being 10.8 mm. Stringers and bulkheads are considered by their respective hollow cross sections (rectangular profile) and the resulting surface moment of inertia. The masses of the engine and the ships interior structure were accounted for by adding respective concentrated and distributed masses to the model to bring the net mass of the ship to the known value. For the ship no virtual mass (to account for the hydrodynamic effects) was added since we assume that the main part of the ship is above the water surface.
Shell structural elements are used for the discretisation of the ship’s hull and the glider to reduce the computational effort against 3D modelling based on continuum elements. Both objects are thin-walled structures (wall thicknesses of approximately 10 mm being small compared to the other dimensions). Even the laminated bulkheads of the ship can be considered as being thin-walled. Longitudinal stringers of the ship are described by beam elements. The shell elements used have four nodes, six degrees of freedom each and four integration points in plane. Along the thickness direction, five section points with Simpson integration rule are used. Beam elements have two nodes with six degrees of freedom each. Shell and beam elements along the edges of shells share the same nodes. For beams as well for shell elements linear shape functions are used. Therefore, the respective displacement interpolation fields are compatible.
In the region of contact between glider and ship the mesh was refined (not shown in Figs. 4 and 7) for a better spatial resolution of the damage event, using a minimum element length of 10 mm. Different discretisations in the impact region were tested, but not reported here. Mesh convergence was obtained for the considered quantity, i.e. the dissipated energy. In total, 18600 shell elements (S4) and 650 3D beam elements (B31) were used.
The mechanical load was applied by defining an initial velocity on the ship relative to the glider. For describing the contact between glider and ship, the “general contact” algorithm included in ABAQUS was used. The algorithm uses the penalty method to create contact forces that prevent node-into-face and edge-into-edge penetrations, see [18].
3.2 Material behaviour
For each section of the glider and the ship an individual material behaviour was allocated. In case of the glider, all sections are assumed to behave isotropic linear-elastically. The respective parameters (Young’s modulus and Poisson’s ratio) are listed in Table 1.
In case of the ship laminated from polyester with chopped strand mats as well as woven rovings, the properties of a homogeneous material based on an average weight fraction of E-glass fibres of \(w_\mathrm{f}=0.34\) were computed following the procedure given in DIN Deutsches Institut für Normung e.V. [19]. Besides properties of the elastic medium, the maximum allowable strains for various loading conditions can be derived. The respective values of the critical strains are included in Table 2. According to DNV [20], an assessment should be based on these critical (elastic) strains, along with a safety factor. As a matter of course, this procedure leads to conservative results. Moreover, progressive damage leading to energy dissipation is not considered, which in turn affects the global mechanical quantities.
A more realistic material model includes progressive damage, which is expected to occur during collision. The concept of progressive damage accounts for material deterioration and the related energy dissipation. It goes back to the work of Kachanov [21], who first introduced damage as an internal scalar variable into the constitutive relation. It phenomenologically describes the effect of microvoids and microcracks on the stress carrying capacity of the material. Since the millennium, damage mechanics has been widely used and successfully applied to various materials and lengthscales, e.g. concrete [22], pipeline steel [23], laminates [24], and aluminium [25]. Here, we use a simplified version [26] of a more general approach, which is based on the following assumptions. The material deforms elastically until a certain critical strain (fracture strain \(\varepsilon _{ut}\)) is reached. When this strain is exceeded, the stress carrying capability of the point is linearly reduced as shown in Fig. 5, mimicking progressive damage. Plastic deformations are therefore not considered, as they are negligible in glass-reinforced plastics. Therefore, fracture strain and strain at maximum stress are treated as being equal. The parameters E, \(\sigma _y\), and \(\bar{u}\) have to be specified as an input. The respective values calculated according to DIN Deutsches Institut f?ur Normung e.V. [19] are summarised in Table 2. Note that the specific energy dissipated through damage evolution depends on the term \(\bar{u}/L\). The respective value has to be set for the simulation by finding a compromise between physical significance of the material softening, see Fig. 5, and loss of numerical stability of the simulation due to strain localisation effects, see e.g. [27]. A common technique to assess the simulations is to control the artificial strain energy of the model, which should be minimised. In the current investigation, the ratio \(\bar{u}/L\) has been set to 0.1 in order to keep the global artificial strain energy less than 5 \(\%\) of the total internal energy of the system.
Hillerborg’s failure model was used as a built-in feature of the commercial FE-code ABAQUS. Its mode of operation is sketched in Fig. 5. Progressive damage is accounted by linearly reducing the element’s stiffness once the failure strain is reached. Once the stresses become zero, the respective element is removed from the mesh. At this stage it is therefore not visible.
We hereby use a macroscopic (engineering) approach to investigate damage initiation and crack extension in the ship. It is not the aim of the current investigation to account for the micromechanisms causing degradation. It is worth mentioning that the derivation of homogenised quantities from a complex microstructure is generally not straight forward but a current research topic. Hence, a more fundamental assessment might be necessary once purpose-built layers are considered. Here, however, most of the layers are built from chopped strand mats. Hence the global behaviour is expected to be isotropic.
3.3 Collision scenarios
We investigate the influence of three different parameters on the resulting damage of the ship, namely the position of impact, \(\beta\), the impact speed, v, and the angle of impact, \(\alpha - \beta\), cf. Fig. 2a. For all scenarios, the ship was rotated by \(5 ^\circ\) with respect to the horizontal axis to account for the dynamic lift during cruising (trim). The glider was tilted by \(30 ^\circ\) with respect to the waterline in accordance with its orientation at the surface, see Fig. 6. In contrast to the procedure of the analytical solution, the position of impact is studied with respect to structural parts of the ship by means of FE simulations. Figure 7 gives an overview on the different impact locations studied: at the bow along the ship’s centreline, beneath the centre of a skin plate, beneath a longitudinal stringer and beneath a transverse frame element (bulkhead).
4 Results and discussions
4.1 Analytical solution
The ratio of applied strain and failure strain \(\varepsilon /\varepsilon _f\) calculated following Eq. 5 is shown in Fig. 8 using the input data summarised in Table 3. For ratios of \(\varepsilon /\varepsilon _f\) less than one safe operation is guaranteed. It represents a maximum strain (failure) criterion. We first quantify the dependence of the strain ratio on the position of impact \(\beta\). As a collision in the front part of the ship is most likely, \(\beta\) is assumed to lie in the interval 10\(^\circ\) to 35\(^\circ\). The velocity of the ship is set to the maximum possible speed of v = 19 m s\(^{-1}\). A variation of the position angle \(\beta\) leads to small changes of the strain ratio, but the general trend as well as the magnitude does not significantly change with \(\beta\). In case of a collision with a velocity of v = 19 m s\(^{-1}\), the analytical solution reveals that the critical strain ratio is exceeded resulting in failure of the ship. The same analysis preformed for a velocity v = 10 m s\(^{-1}\) reveals its safe operation, as for all angles of attack the strain ratio is less than 1.
4.2 FE simulations
Finite element simulations were carried out using both the elastic and the progressive damage material models. In order to compare the obtained numerical results to those of the analytical solution, it is more appropriate to use the elastic non-damaging model. Hence, the same assessment concept as in the analytical solution can be adopted: comparing the maximum local strain with a (given) failure strain, cf. Table 3. The centre of a skin section, cf. Fig. 7, was selected as the impact position, which corresponds to a position angle of \(\beta =10^\circ\). It can be seen in Fig. 8 that FE-analysis and analytical solution lead to contrasting results. First, the maximum strain ratio occurs at an impact angle of 35\(^\circ\) for the velocity of v = 19 m s\(^{-1}\) rather than at 0\(^\circ\) as in case of the analytical solution. In case of 10 m s\(^{-1}\), the maximum strain criterion reveals unsafe operation, except for the collision angle \(\alpha - \beta =-5^\circ\). Second, the amount of predicted strain is significantly higher in case of the FE simulations. Interestingly, the maximum strain ratio for the lower speed is predicted to be at \(\alpha - \beta =45^\circ\), and therefore at a higher angle of attack compared to the respective scenario for v = 19 m s\(^{-1}\). The discrepancy between analytical and FE-simulation with respect to the angle of attack for maximum strain can be explained by the 3D-shape of the ship, which is not accounted for in the simplified 2D analytical approach. The predicted strain level, however, results from the assumption of elastic material behaviour and leads to unrealistic values.
A second series of finite element simulations were conducted using the damage model as described in Sect. 3.2. With our hardware (Intel Core i5 processor, 4 cores, 3.4 GHz, 8 GB RAM, Windows 7, 64-bit) the simulation took about 30 min. The simulations were evaluated by means of the dissipated energy. This quantity allows to discriminate between collision events causing only elastic deformation (no damage) and those in which material deterioration appears. Moreover, the amount of dissipated energy is a function of the size of the damaged structure. This allows to distinguish between the occurrence of uncritical cracks and large leaks causing the loss of the ship.
In the simulations the impact location (cf. Fig. 7) was varied to study the influence on the extend of damage quantified by the dissipated energy for a given velocity, v = 19 m s\(^{-1}\). The angle of attack \(\alpha - \beta\) was prescribed as 35\(^\circ\) here, which caused the maximum strain ratio as predicted by the FE-strain criterion, cf. Fig. 8. Figure 9 shows that the smallest amount of dissipated energy occurs for the impact at a longitudinal stringer, since the glider is able to slide along the hull preventing a deep penetration. For the remaining three impact locations nearly the same amount of energy is dissipated. In all considered scenarios the glider causes severe damage to the ship.
Considering the impact position being in the centre of the skin section (\(\beta =10^\circ\)), the dissipated energy as a function of the glider’s angle of attack \(\alpha - \beta\) is shown in Fig. 10. At a speed of 19 m s\(^{-1}\) for all angles in the interval between 0\(^\circ\) and 90\(^\circ\) damage occurs. Interestingly, the largest amount of dissipated energy appears at an angle of 15\(^\circ\), when the glider hits the surface normally. This result is different from the one obtained using the maximum strain criterion, cf. Fig. 8. According to the damage analysis, the glider tends to slip off the hull at larger angles, reducing its impact energy. However, at the speed given, even at 90\(^\circ\), the dissipation is non-zero.
Figure 11 shows the effect of the ship’s velocity on the amount of damage for two different angles of attack, namely 15\(^\circ\) and 35\(^\circ\). The former follows from Fig. 10, in which this angle represents the “worst case scenario”. The latter is chosen serving as the respective counterpart deducted from the maximum strain criterion. At smaller speeds only elastic deformations occur, hence the dissipated energy is zero. Damage occurs at impact velocities larger than 7.5 m s\(^{-1}\) (14.6 kt) for the angle of attack \(\alpha - \beta =35^\circ\). In case of the more acute angle of attack, damage is predicted at speeds higher than 10 m s\(^{-1}\) (19.4 kt). With increasing impact velocity more energy is dissipated by the structure. The slope of the dissipated energy functions is different: while the one of \(\alpha - \beta =35^\circ\) linearly increases, the one of \(\alpha - \beta =15^\circ\) evidences a nonlinear sharp increase in the range above 13 m s\(^{-1}\). This leads to the effect that for maximum speed more energy is dissipated at \(\alpha - \beta =15^\circ\) than it is at 35\(^\circ\). In case of the acute angle of attack, the glider is sliding along the hull before penetrating it allowed by the 3D-shape of the ship’s bow. Whereas this effect decreases the risk of damage at lower speeds, it causes the opposite effect at higher speeds, where the glider damages the neighbouring transverse frame. In case of an impact from the side, the glider has less tendency to slide along the ship. This favours its penetration at lower speeds. It is noted that once the glider fully penetrates the hull, a further increase of damage in the interior of the ship (built-in components, installations) is not accounted for.
Snapshots of the ship’s structure during a crash scenario at the maximum speed, \(v =\)19 m s\(^{-1}\), are shown in Fig. 12. In the side view, Fig. 12a, the mesh refinement in the impact region is seen. The top view, Fig. 12b, shows the glider penetrating the skin. The contour plot of the (von Mises) equivalent stress reveals the high stresses in the impact region. Damaged elements are not shown. Hence, a key-hole shaped opening is clearly seen. During the collision, a crack on the left is initiated. Subsequently, the glider passes the hull as the ship continues to move over the glider. At the circumference of the hole the stresses are lower due to the damage evolution, see Fig. 12c.
5 Conclusions
The purpose of the current study was to determine possible damage in a collision scenario between a ship and a glider. The problem was assessed based on a simplified 2D analytical model and based on a fully 3D finite element model. These two assessment procedures, however, lead to different conclusions with respect to the angle of attack and the amount of failure experienced by the ship. The analytical approach is a valuable tool to be used for estimating possible damage scenarios. In the light of the included simplifications, its final result—damage will occur at speeds above 10 m s\(^{-1}\)—lies in a realistic range.
The finite element model captures the geometry and the details of the inner structure of the ship. Hence, it reveals a more realistic description of the mechanical states during the collision. In case of the collision between a glider and a small ship investigated here, the specific shape of the ship’s skin, which is not stipulated in a 2D representation, limits its predictive capabilities. The shape of the underwater ship is complex, which leads to some unexpected results of the 3D finite element simulations for certain collision angles. In particular, the possible slip between glider and ship is relevant for small angles of attack. A more detailed assessment revealed that at an angle of attack of 35\(^\circ\) the glider penetrates the hull at a lower ship’s speed than it does for 15\(^\circ\). Hence, this scenario is more dangerous.
The assessment procedure based on finite element simulations and the maximum strain criterion naturally overestimates the applied strain, as it does not account for energy dissipation due to progressive damage. Consequently, it can be used to judge whether a given failure strain is exceeded or not, but the value of the “overload factor” \(\varepsilon /\varepsilon _\mathrm{f}\) loses its physical significance. Interestingly, even by this criterion, the dependence of the most critical angle of attack on the velocity is captured: the lower the speed, the larger the angle of attack causing the maximum strain ratio.
This study has increased the understanding of what happens when a ship collides with a glider. Still, to reduce the level of complexity, the modelling did not account for the hydrodynamic interaction between ship and glider, nor did it consider the consequences of the glider damaging the propeller or outdrive. Therefore, the results need to be interpreted with care. Also, the study focussed on a particular type of a fast recreational ship. Repeating the simulations for other types of ships will yield different results and conclusions. Nevertheless, the current findings indicate that a ship of a most vulnerable type cruising at speeds less than 7 m s\(^{-1}\) would not be seriously damaged in the event of a collision with a glider, a conclusion that corroborates the estimates of the minimum ship velocity whereby damage may occur resulting from a collision with a 50 kg floating object [5]. Most importantly, the results of this study provide a crucial, but currently lacking, quantitative argument in the discussion on how to regulate the use of gliders in the coastal ocean. It should be mentioned that the conclusions drawn here solely base on numerical prediction. A validation by full-scale tests is desirable, however, difficult to conduct and costly.
References
Riethmüller, Colijn RF, Krasemann H, Schroeder F, Ziemer F (2009) Cosyna, an integrated coastal observation system for northern and arctic seas. Oceans 2009 Conference Proceedings, IEEE, iSBN: 978-1-4244-2523-5
Merckelbach L (2013) On the probability of underwater glider loss due to collision with a ship. J Mar Sci Technol 18(1):75–86
Goerlandt F, Montewka J, Ravn ES, Hänninen M, Mazaheri A (2012) Analysis of the near-collisions using ais data for the selected locations in the baltic sea. Report, Department of Applied Mechanics
Wang G, Spencer J, Chen Y (2002) Assessment of a ship’s performance in accidents. Mar Struct 15:313–333
Zhang S (1999) The mechanics of ship collisions. Phd thesis, Technical University of Denmark
Vanem E, Skjong R (2004) Collision and grounding of passenger ships—risk assessment and emergency evacuations. Int Conf Collis Grounding Ships
Urban J (2003) Crushing and fracture of lightweight structures. Phd thesis, Technical University of Denmark
Haris S (2013) Damage interaction analysis of ship collisions. Phd thesis, Norwegian University of Science and Technology
Sajdak JAW, Brown AJ (2004) Modeling longitudinal damage in ship collisions. Technical report, Department of Aerospace and Ocean Engineering
Abazari A, Ziaei-Rad S, Dalayeli H (2011) Investigation on ship collision phenomena by analytical and finite element methods. World Acad Sci Eng Technol 5:25–34
Ehlers S, Broekhuijsen J, Alsos HS, Biehl F, Tabri K (2008) Simulating the collision response of ship side structures: a failure criteria benchmark study. Int Shipbuild Prog 55(1):127–144
Wisniewski K, Kolakowski P (2003) The effect of selected parameters on ship collision results by dynamic fe simulations. Finit Elem Anal Des 39:985–1006
Karlsson UB, Ringsberg JW, Johnson E, Hoseini M, Ulfvarson A (2009) Experimental and numerical investigation of bulb impact with a ship side-shell structure. Mar Technol 46(1):16–26
Steglich D, Heerens J, Brocks W (2002) Punch test for the simulation of ship hull damage. Adv Eng Mater 4(4):195–200
Pedersen PT, Zhang S (1998b) On impact mechanics in ship collisions. Mar Struct 11:429–449
Pedersen P, Zhang S (1998a) Minimum plate thickness in high-speed craft. In: Oosterveld MWC, Tan SG (eds) Practical design of ships and mobile units, pp 959–965
Korotkin AI (2009) Added masses of ship structures. aktualisierte und revidierte bersetzung ed., Springer Science + Business Media B.V
Dassault Systèmes, 2012: Abaqus 6.12 theory manual
Deutsches Institut DIN für Normung e.V. (2009) Kleine Wasserfahrzeuge—Rumpfbauweise und Dimensionierung—Teil 5: Entwurfsdrücke für Einrumpffahrzeuge, Entwurfsspannungen, Ermittlung der Dimensionierung (iso 12215–5:2008). Beuth Verlag, Berlin
(2009) Rules for classification of high speed, light craft and naval surface craft—hull structural design, fibre composite and sandwich constructions. Det Norske Veritas AS, Norway
Kachanov L (1958) On rupture time under creep conditons. Izv Akad Nauk SSR 8:26–31
Desmorat R, Gatuingt F, Ragueneau F (2007) Nonlocal anisotropic damage model and related computational aspects for quasi-brittle materials. Eng Fract Mech 74(10):1539–1560
Dotta F, Ruggieri C (2004) Structural integrity assessments of high pressure pipelines with axial flaws using a micromechanics model. Int J Pres Ves Piping 81:761–770
Ladeveze P, Allix O, De J-F, Léveque D (2000) A mesomodel for localisation and damage computation in laminates. Comput Methods Appl Mech Eng 183:105–122
Tohgo K, Mochizuki K (2002) Damage mechanics approach to material-dependency of fracture toughness in aluminium alloys. Int J Damage Mech 11:151–170
Hillerborg A, Moder M, Petersson P-E (1976) Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem Concr Res 6:773–782
Steglich D (2004) Structure Damage Simulation, 817–826. Continuum Scale Simulation of Engineering Materials. Wiley-VCH, Weinheim
Acknowledgments
Fruitful discussions with U. Hafner from iYacht GmbH, Hamburg, Germany, are gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Drücker, S., Steglich, D., Merckelbach, L. et al. Finite element damage analysis of an underwater glider–ship collision. J Mar Sci Technol 21, 261–270 (2016). https://doi.org/10.1007/s00773-015-0349-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00773-015-0349-7