Field experiments and new design of a spilled oil tracking autonomous buoy

Abstract

It is important to forecast the location of oil spills to realize effective and adequate oil spill response operations when huge oil spilsl occur. In order to enhance the accuracy of oil drifting simulations, one needs to obtain the meteorological and oceanographic data around the oil slick. In general, the drifting velocity vector of an oil spill contains a wind velocity vector and a water current velocity vector. SOTAB-II was developed for autonomous tracking of oil slicks drifting on the sea surface. It is equipped with a sail whose size and direction are controllable to drift along with the oil slick autonomously. In addition, SOTAB-II transmits its location and necessary measured data around it to the land base in real-time. The results of field experiments using SOTAB-II with a cylindrical hull brought us the effectiveness of the sail and its control. However, the drifting speed of SOTAB-II was lower than a theoretical speed for the oil slick. In order to overcome this problem, SOTAB-II was redesigned. A yacht shape was adopted to reduce the hydrodynamic drag in the water in the advancing direction. Transverse stability, scales of brake board and sail, maneuverability, and performance of tracking spilled oil on the sea surface were considered in the process of the design.

1 Introduction

In recent years, there have been many major sea oil spills. Once the oil spilled from the ship washes ashore, it is difficult to recover it effectively. To prevent oil spills from spreading and causing further damage, it must be recovered while it is drifting on the sea surface. If we can know the real-time location of the oil slick, the recovery operations can be smoothly coordinated.

There exist some methods to deal with the oil spill. Drifting buoys are used to track the oil spill [1]. The weak point of these drifting buoys is that once they are apart from the oil slick, they have no function in tracking it. If the sea condition is fine and safe enough, the vessels can track an oil slick by using the method of the X-band radar detection [2]. A plane can fly over the sea and detect the oil slick. However, at night, it is difficult to detect the spilled oil from the plane. Even though aircraft can apply a fluorescence lidar system [3] to detect the oil slick in the night, the limitation of its endurance can make it impossible to track the oil slick continuously. Satellite remote sensing is available to detect the location of an oil spill [4]. However, this method is not carried out more frequently than the aircraft method.

Meanwhile, the gas and oil blowout accidents from the seabed also unfortunately happen. Similar to the oil spills, these accidents result in long-term damage to the environment and human life. To overcome the weak points of existing oil spill monitoring methods and, moreover, to deal with the gas and oil blowout accidents, we are constructing a marine disaster prevention system. This system consists of the Spilled Oil Tracking Autonomous Buoys (SOTABs) and the land base. Figure 1 shows the concept of this system.

Fig. 1

Concept of spilled oil and gas tracking autonomous buoy system

The underwater autonomous robot named SOTAB-I observes three dimensional distributions of the gas and oil blowing out from the seabed (Measure 1). At the sea surface, the multiple autonomous buoys with controllable sail named SOTAB-IIs observe the oil slick (Measure 2). One of the important roles of SOTAB-I and II is to send the useful real-time data around it to the land base or mother ship. Gas and oil drifting simulation is carried out at the land base (Measure 3). The accuracy of this forecast is enhanced by data assimilation using the real-time data from SOTABs. Then, adequate measures can be taken at coastal areas where the oil slick will drift ashore. With the above three measures, this paper shows the research progress of SOTAB-II.

We developed SOTAB-II for sea trials. It was equipped with the controllable sail, and its hull shape was cylindrical. Some field experiments were carried out using it. The analysis of those experimental results brought to us the efficiency of the sail and its control in drifting with an imaginary oil slick. However, they also brought us the problem that the drifting speed of SOTAB-II was smaller than that of an imaginary oil slick. In order to overcome this problem, SOTAB-II was redesigned in this research. A yacht shape was adopted to reduce the hydrodynamic drag in the water in the advanced direction. Transverse stability, course stability, scales of brake board and sail, maneuverability, and performance of tracking spilled oil on the sea surface were considered in the process of the design.

2 Development of SOTAB-II for the field experiment

2.1 Concept of SOTAB-II

In general, it is said that the drifting velocity vector of an oil spill is the resultant velocity vector of 3.0 % of the wind velocity vector along the wind direction at a 10 m height from the sea surface and the water current velocity vector [5]. SOTAB-II was equipped with a sail whose size and direction are controllable. An oscillating fin and fixed rudder were installed on it for an auxiliary propulsion mechanism. SOTAB-II uses this auxiliary propulsion mechanism only when it moves a long distance. For example, in a case that SOTAB-II tracks not a large oil slick but the other small ones, an operator in a land base sends out a command to SOTAB-II to move to a certain location and track the large oil slick. The intended purpose of the fixed rudder is to support the course stability while SOTAB-II moves with using this auxiliary propulsion mechanism. The oscillating fin oscillates from side to side with this fixed rudder as a center of oscillation. At this stage, a cylindrical shape was adopted for SOTAB-II’s hull so as to rapidly respond to the change in the drifting direction of the oil slick. A GPS receiver and an anemometer were installed on the top side of SOTAB-II, and a current meter was installed on its bottom side. After being dropped into the oil slick, SOTAB-II drifts along with it by controlling the size and direction of its sail autonomously. In this drifting mode, SOTAB-II transmits its location, and the meteorological and oceanographic data around it to the land base in real-time. Meanwhile, an auxiliary propulsion mechanism is used to move into the main oil slick or the location requested from the land base in case SOTAB-II drifts away from the main oil slick. We developed a prototype of SOTAB-II, and some field experiments were carried out using it. However, because of the trouble with the sail control mechanism, only free drifting experiments under different sail sizes were carried out in 2010 [6]. The results of free drifting experiments revealed that the wind speed component of SOTAB-II’s drifting speed was 3.1–3.8 % of the wind speed along the wind direction. In case the sail was completely furled, the difference between the drifting direction of SOTAB-II and that of the simulated oil gradually increased as time passed. That difference was decreased in the case of a completely unfurled sail. These results show the efficiency of the sail for controlling the drifting speed and direction.

Figure 2 shows SOTAB-II developed to evaluate the sail control effects on tracking an oil spill. Its mass is 60 kg. The sail size and sail direction play an important role in gaining wind force to drift along with the oil slick. They are controlled by two different motors. A roller mounted at the bottom of the sail adjusts sail size by rolling up or down. We plan to install an oil detecting sensor, which is based on the fluorescence of oil using a pulsed UV light source that can work even in the night, on SOTAB-II. However, this sensor is under development. If an oil detecting sensor is installed on SOTAB-II, it can monitor oil slicks around itself. Most of the time, SOTAB-II adapts a drifting speed based on the 3 % law as a target to control the sail size. In case the oil detecting sensor detects the edge of the oil slick, SOTAB-II changes the target drifting speed based on the 3 % law as that based on the data from the oil detecting sensor so as to catch up with the oil slick. The effectiveness of the sensor will be discussed using other opportunities.

Fig. 2

Layout plane (left) and picture of the SOTAB-II for sea trial (right)

2.2 The control law of sail size and sail direction

First, we assume a steady drifting situation which means SOTAB-II and oil slicks move into a same current. In this situation, the effect of the current on SOTAB-II is the same as that of the oil slick. Then, the basic law of sail control is as follows. In order to make effectively use of wind force in drifting, the sail direction is required to keep perpendicular to the wind direction. On the other hand, if the drifting speed of SOTAB-II is slower than the oil slick, the sail size must be increased so as to absorb more wind effect. In the case that SOTAB-II drifts faster than the oil slick, the sail size is decreased. The sail size and sail direction are conducted by a PID controller. Figure 3 show the diagram of these PID control systems. In this diagram, V _SW and θ _S are SOTAB-II’s drifting speed in wind direction and actual sail angle of SOTAB-II, respectively. V _T and θ _T are target drifting speeds in wind direction and target sail angle, respectively. These two target values, V _T and θ _T, are calculated as follows.

Fig. 3

Diagram of PID controller for sail size (top) and sail direction (bottom)

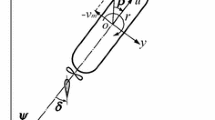
SOTAB-II can obtain its drifting vector $\overrightarrow {V}$ from its GPS data. We define the absolute value of $\overrightarrow {V}$ as V _S, and its direction is α. SOTAB-II can also obtain the relative wind velocity vector $\overrightarrow {Wr}$, relative water current velocity vector $\overrightarrow {Cr}$ in the body fixed coordinate system, and the azimuth angle θ by using equipped devices. Figure 4 shows the relations among these values. In this figure, the body fixed coordinate system and earth coordinate system are represented with O-X′Y′ and O-XY, respectively. The equations $\overrightarrow {Wa}$, β, $\overrightarrow {Ca}$, and ε represent the absolute wind velocity vector, its direction, absolute water current velocity vector, and its direction in O-XY, respectively. These values are calculated by the following relations.

$$ \overrightarrow {Wa} = \left( {Wax, Way} \right) = \left( {\left| {\overrightarrow {Wr} } \right|\cos \left( {\gamma + \theta } \right) + \left| {\overrightarrow {V} } \right|\cos \alpha ,\left| {\overrightarrow {Wr} } \right|\sin \left( {\gamma + \theta } \right) + \left| {\overrightarrow {V} } \right|\sin \alpha } \right), $$

(1)

$$ \beta = \tan^{ - 1} \left( {Way/Wax} \right), $$

(2)

$$ \overrightarrow {Ca} = \left( {Cax, Cay} \right) = \left( {\left| {\overrightarrow {Cr} } \right|\cos \left( {\zeta + \theta } \right) + \left| {\overrightarrow {V} } \right|\cos \alpha ,\left| {\overrightarrow {Cr} } \right|\sin \left( {\zeta + \theta } \right) + \left| {\overrightarrow {V} } \right|\sin \alpha } \right), $$

(3)

$$ \varepsilon = \tan^{ - 1} \left( {Cay/Cax} \right). $$

(4)

Fig. 4

Coordinate system of SOTAB-II (top-view)

Then, the wind component of SOTAB-II’s drifting speed V _SW is calculated by the following equation.

$$ V_{\text{W}} = \left| {\overrightarrow {V} } \right|\cos \left( {\beta - \alpha } \right) + \left| {\overrightarrow {Ca} } \right|\cos \left( {\beta - \varepsilon } \right) $$

(5)

In general, the wind component of an oil slick’s drifting speed is approximately 3.0 % of wind speed along the direction of the wind at a height of 10 m from the sea surface. The anemometer is installed on SOTAB-II at 0.4 m above the water line. Measured wind data should be transformed into those at a height of 10 m from sea surface by using following equations [7].

$$ U_{\left( z \right)} = \frac{{u^{*} }}{\kappa }\log \frac{z}{{z_{0} }}, $$

(6)

$$ z_{0} = 0.0185\frac{{\left( {u^{*} } \right)^{2} }}{g}, $$

(7)

$$ u^{*} = \sqrt {\tau_{\text{s}} /\rho_{\text{a}} } ,$$

(8)

$$ \tau_{\text{s}} = \rho_{\text{a}} C_{\text{f}} U_{(10)}^{2} , $$

(9)

where, z height from the sea surface, U _(z) is wind speed at a z (m) height from sea surface, z ₀ is the roughness coefficient, g is the gravity acceleration, u* is the friction velocity on sea surface, κ is Karman’s constant (=0.40), τ _s is wind stress, ρ _a is air density, and C _f is the friction coefficient $C_{\text{f}} = \left\{ {\begin{array}{*{20}c} {1.4 \times 10^{ - 3} } & {\left( {0 \le \left| {U_{(10)} } \right| < 10} \right)} \\ {\left( {0.49 + 0.065\left| {U_{(10)} } \right|} \right) \times 10^{ - 3} } & {\left( {10 \le \left| {U_{(10)} } \right| < 26} \right)} \\ {2.18 \times 10^{ - 3} } & {\left( {26 \le \left| {U_{(10)} } \right|} \right)} \\ \end{array} } \right.$

From these equations and absolute wind speed at a 0.4 m height from the sea surface, the wind speed at a 10 m height from the sea surface U ₍₁₀₎ is calculated. In this research, we assume that the wind speed component of an oil slick drifting is 3.0 % of U ₍₁₀₎. Finally, U ₍₁₀₎ and the target drifting speed in wind direction V _T are as follows.

$$ U_{(10)} = \frac{{\kappa \left| {\overrightarrow {Wa} } \right|}}{{\sqrt {C_{\text{f}} } \log \frac{z}{{z_{0} }}}}, $$

(10)

$$ V_{\text{T}} = 0.03 U_{(10)}. $$

(11)

Let us define an “imaginary oil slick” that drifts with the resultant velocity vector of the water current velocity vector and 3.0 % of U ₍₁₀₎ vector.

Meanwhile, the sail direction is controlled to be perpendicular to the absolute wind direction at any time to fully utilize the wind force. The target sail angle θ _T is expressed by the following equation.

$$ \theta_{\text{T}} = \beta - \theta + 90. $$

(12)

3 Experiments at a lake

3.1 Purpose of experiments and experimental conditions at the lake

The field experiments at a lake were carried out mainly aimed at confirming the validity of the control systems. They also included the comparisons of SOTAB-II’s drifting characteristics between a free drifting condition without the sail control and the sail controlled condition. These experiments were carried out from September 29th to September 31st, 2011, in Lake Biwa. The average wind speed ranged from 3.5 to 6.3 m/s, and the current speed varied from 0.08 to 0.19 m/s. According to a specification of the anemometer, its resolutions of the wind speed and direction were 0.01 m/s and 1°, respectively. The measurement accuracies of the wind speed and direction were within ±2 % and ±3°, respectively. Concerning the current meter, the resolutions of the current speed and direction were 0.02 cm/s and 0.01°, respectively. The measurement accuracies of the current speed and direction were within ±2 % and ±2°, respectively.

It was reported that the use of thin floating objects is efficient for simulating the drift of the oil slick in the real sea [8]. According to this paper, we used a rubber sheet. The specific gravity of oils is approximately from 0.82 to 0.95. The sheet we used in this research was made of chloroprene rubber and chloroprene rubber sponge, and its specific gravity was 0.85. The rubber sheet was a square, 1.0 m on a side, and it was 3 mm thick. We attached a GPS receiver on this rubber sheet to obtain its trajectories. However, that GPS was not working well. So, we used the rubber sheet as a marker for visual confirmation in lake experiments.

Experimental procedures are as follows. After getting out of the port by ship, SOTAB-II and a rubber sheet were dropped into the water at the same time and roughly in the same position. Three kinds of sail control conditions were investigated. The first condition was free drift with sail furled. The second one was free drift with sail completely unfurled. In this unfurled condition, the sail was fixed parallel to the brake board. In the third condition, the sail size and direction were controlled by a PID controller. Figure 5 shows the overview of these experiments at the lake.

Fig. 5

Overview of the experiment at Biwa lake

3.2 Analysis of experiments at lake

3.2.1 Sail direction control

The sail direction was required to be perpendicular to the absolute wind direction all the time. Figure 6 shows the results of sail direction relative to wind direction under the condition of free drift and sail controlled. The sail direction was in a random angle relative to wind direction under the condition of free drift. On the contrary, we can confirm that the sail direction was always kept perpendicular to the sail direction under the condition of sail control.

Fig. 6

Sail direction relative to absolute wind direction

3.2.2 Effectiveness of sail and sail control

It is expected that when SOTAB-II drifts faster than the target value V _T, the sail is furled to decrease the wind effect. On the other hand, when SOTAB-II drifts slower than V _T, the sail size is unfurled to utilize more wind force. Figure 7 shows the component of SOTAB-II’s drifting speed in wind direction under the different sail conditions. The water current speed in the wind direction was excluded from SOTAB-II’s drifting speed in wind direction. Under the condition of sail control, SOTAB-II’s average drifting speed in wind direction is approximately 70.8 % of the average of V _T. On the other hand, under the condition of free drift with sail unfurled and furled, those percentages decrease to 56.9 and 43.29 %, respectively. Through the whole experiment, SOTAB-II’s drifting speed in wind direction was lower than the target drifting speed in wind direction. This is mainly caused by the additional floats attached on the side of SOTAB-II’s hull to increase the roll stability. The drag force on SOTAB-II should be decreased. Even though SOTAB-II’s drifting speed in wind direction cannot reach the target value, these analyses of experiments at the lake show the efficiency of the sail and sail control.

Fig. 7

Component of SOTAB-II’s drifting velocity in wind direction under the different sail conditions

3.2.3 Trajectories of SOTAB-II

Figure 8 shows the trajectories of SOTAB-II and an imaginary oil slick. The conditions of SOTAB-II are free drift with sail completely furled and sail controlled. The trajectories of SOTAB-II were calculated from the GPS data. Concerning the imaginary oil slick, there are three trajectories. In this study, we assumed that the wind component of the oil slick’s drifting vector was 3 % of the wind vector at a height of 10 m above the sea surface. Based on this assumption, the trajectories of the imaginary oil slick were calculated as follows. The first one is calculated by the effect of only the water current. The second one is calculated by the effect of only 3.0 % of the wind vector at a height of 10 m above sea surface. The last one is the resultant vector by summing the two effects. In these figures, the circles on each trajectory indicate the location of each item every 60 s. We can confirm that the trajectory of SOTAB-II almost lies midway between that of what was calculated by the effect of only the water current and that of the 3.0 % of U ₍₁₀₎. The total length of each line indicates the drifting distance at each experiment. The difference in length between SOTAB-II and the imaginary oil slick under sail control conditions is smaller than that of free drift with sail completely furled. Besides, the gap between the speed of SOTAB-II and the imaginary oil slick under sail control conditions is smaller than that of free drift with sail completely furled. This result also shows the efficiency of SOTAB-II’s sail and sail control to drift along with the oil slick.

Fig. 8

Trajectories of SOTAB-II and that of imaginary oil slick

4 Experiments at sea

4.1 Purpose of experiments and experimental conditions at sea

The experimental results at lake strongly demonstrated the effectiveness of the sail and sail control. SOTAB-II with sail controlled was able to approach in the direction of an imaginary oil slick. However, SOTAB-II was unable to reach the target drifting speed. In experiments at sea, the auxiliary propulsion mechanism and brake board were removed from SOTAB-II to decrease its drag coefficient in water.

The experimental site was Osaka Bay about 7 km away from Awaji Island in Japan. The experimental period was from December 21st to December 23rd, 2011. In this period, the average wind speed ranged from approximately 8.8 to 11.5 m/s, and the water current speed varied from 0.34 to 0.59 m/s, which were 2–3 times as large as those in experiments at Lake Biwa.

For the same as the experiments at the lake, a rubber sheet was first released into the sea, and then SOTAB-II was dropped (Fig. 9). That rubber sheet was equipped with a GPS receiver so that the speed and trajectory of this rubber sheet could be calculated. Three kinds of sail control conditions such as free drift with sail furled, free drift with sail completely unfurled, and sail controlled were investigated. For the same as the experiments at Lake Biwa, the target drifting speed in wind direction was set as 3.0 % of U ₍₁₀₎.

Fig. 9

Overview of the experiment at sea

4.2 Analysis of experiments at sea

4.2.1 Drifting speed of the rubber sheet

The drifting speed of the rubber sheet in wind direction was calculated by subtracting the water current vector from the rubber sheet’s GPS data. As a result, its average was approximately from 1.8 to 1.95 % of the wind speed at the 10 m height above the sea surface. This means it was approximately 60–65 % of the target speed that we set. Figure 10 shows one example of the rubber sheet’s drifting speed in wind direction. SOTAB-II’s drifting speed in wind direction is also plotted in this figure. The drifting condition of SOTAB-II was free drift with sail half furled. From other results, the rubber sheet’s drifting speed in wind direction was smaller than that of SOTAB-II under the completely unfurled sail condition, and it was larger under the furled sail condition. As shown in Fig. 11, even though the auxiliary propulsion mechanism was removed, SOTAB-II’s drifting speed in wind direction couldn’t reach the target value “3.0 % of U ₍₁₀₎”. However, this target value was set according to the general assumption. We should reconsider the percentage of the wind effect because it is not a priori determined and it varies according to the sea conditions. If SOTAB-II is equipped with a sensor to detect the oil slick near itself, it is easy to adjust automatically that target value on site.

Fig. 10

Drifting velocity of rubber sheet in wind direction

Fig. 11

Trajectories of SOTAB-II, rubber sheet, and imaginary oil slick

4.2.2 Trajectories of SOTAB-II and the rubber sheet

Figure 11 shows the trajectories of SOTAB-II, the rubber sheet, and the imaginary oil slick. The conditions of SOTAB-II are free drift with sail completely furled, completely unfurled, and sail controlled. Each trajectory was calculated in the same manner as the analysis of experiments at Lake Biwa. In these figures, the circles on each trajectory indicate the location of each item every 60 s. The trajectories of SOTAB-II and the rubber sheet always lie midway between the trajectory of the water current and that of 3.0 % of U ₍₁₀₎. Besides, in all cases, the trajectories of SOTAB-II and the rubber sheet lie between the trajectory of the water current and that of the imaginary oil slick. This indicates that the percentage of the wind effects on SOTAB-II and the rubber sheet were smaller than 3 % in these experiments.

The difference in length between the trajectory of SOTAB-II and the imaginary oil slick under sail control conditions is smaller than that under the condition of free drift with sail completely furled. Meanwhile, by comparing the drifting distance of SOTAB-II and the rubber sheet, only in the case of sail controlled SOTAB-II does it exceed the rubber sheet. Moreover, in that case, the difference in length between the trajectories of SOTAB-II and the imaginary oil slick is the smallest. This means not only is there the effectiveness of the sail but also the effectiveness of the sail control. It is supposed that SOTAB-II can drift along with the oil slick if its drag force in water acting on SOTAB-II is reduced.

5 Redesign of SOTAB-II

From the analysis of field experiments, it was concluded that the sail control system of SOTAB-II works well, but SOTAB-II with a cylindrical hull can’t reach the target drifting speed. As for the drifting function, SOTAB-II installed with a bigger sail may meet the required drifting speed. However, SOTAB-II has another important function which is to move large distance by using the auxiliary propulsion mechanism. If the drag force on SOTAB-II is so big, the auxiliary propulsion mechanism uses a large amount of electricity to bring SOTAB-II a certain location. Therefore, we designed a new model of SOTAB-II with a yacht shape to reduce the drag coefficient in water. In the process of the design based on an actual yacht shape, transverse stability, course stability, scales of brake board and sail, maneuverability, and performance of tracking spilled oil on a sea surface are considered by using CFD analysis and other methods.

5.1 Selection of ship type and scale

5.1.1 Battery capacity

After being dropped into an oil slick, SOTAB-II is expected to drift along with it at least for 1 week. It is planned to use the same devices used in the former SOTAB-II for the newer SOTAB-II. We calculated time histories of a battery charging rate with and without daily charging by solar cells. The results are shown in Fig. 12. These time histories are simply calculated by using a battery capacity and power consumptions of all electric devices installed on SOTAB-II. Even if we remove the solar cells from SOTAB-II, it doesn’t affect the result of time histories in Fig. 12, because the decrease of the water draft corresponding to the removal of the solar cells will not affect the power consumption of all devices installed on SOTAB-II on a steady drifting condition where a hydrodynamic balance is kept between thrust force by wind and drag force on an underwater body by water inflow for a given wind speed.

Fig. 12

Time histories of the battery power with and without daily charging by solar cells (0.6 m²)

By installing large capacity batteries for main power source and 0.6 m² solar cells for supplemental power generation, SOTAB-II will be operated automatically so as to work for more than 1 week as shown in this figure. However it can work only for 4 days without charging. Mean value of all sunny days in April in Osaka was chosen as the insolation condition for solar cells. In this calculation, the power generating efficiency (13 %), panel loss (87 %), and battery loss (80 %) were considered.

5.1.2 Design of ship form

We chose “KIT34”, shown in Fig. 13 designed by Kanazawa Institute of Technology, for the new body of SOTAB-II [9]. It does fit our concept that the shape is so wide and short that it can hold the amount of batteries and sensors and we can handle it easily.

Fig. 13

Body plan of KIT34

We compared some scale of it to fit the total mass of SOTAB-II. Table 1 shows the principle particulars of KIT34, scale ratios of 1/10, 1/5, 3/10, and 2/5 models. We decided to use 1/5 scale ratio of the original dimensions for new SOTAB-II’s hull.

Table 1 Dimensions of each scale

5.2 Transverse stability of new SOTAB-II

By installing the devices, the gravity center of SOTAB-II goes up and the metacentric height (GM) goes down. It results in the decrease of the righting lever (GZ), and the transverse stability becomes worse. Figure 14 shows GZ curves of SOTAB-II under the unloaded condition and loaded condition. In this figure, the angle of vanishing stability is defined as the angle where GZ becomes zero. That angle is 120° under the unloaded condition. It becomes approximately 100° under the loaded condition. The transverse stability of SOTAB-II can be increased by installing a keel. In order to increase the angle of vanishing stability up to 120°, the keel was designed following the references [10] and [11]. The keel has a cylindrical shape and is made of stainless steel. Its length was fixed as 510 mm, and the distance from ship bottom to the gravity center of cylindrical keel was fixed as 320 mm.

Fig. 14

GZ curve of SOTAB-II under the unloaded condition (top) and loaded condition (bottom)

Then, some patterns of its radius are selected. The distance from the bottom of the mail hull to the gravity center of the keel was also changed in the calculation. Table 2 shows the simulated results of the vanishing stability angle.

Table 2 Calculated results of the vanishing stability angle

The results show that in case keel 4 is installed, the angle of vanishing stability is the biggest among them. However, in case of keel 4, the water line exceeds 2WL because of keel’s weight. In case of keel 3, the angle of vanishing stability is 126°. Then, keel 3 is adapted for the new SOTAB-II.

5.3 Design of brake board and sail

Different from the former SOTAB-II, the new SOTAB-II drifts along with oil slick by controlling its sail size and rudder. According to the required displacement and the transverse stability, the hull form of the new SOTAB-II was determined as explained in the previous section. Therefore, the installation of a brake board should be considered to control the optimum drifting speed of the new SOTAB-II. In this research, CFD software “Fluent” of ANSYS was used in order to simulate the effects of sail and brake board.

Assuming that SOTAB-II and the oil slick are in same water current, then water current effects on them can be ignored. The heading direction of SOTAB-II is along with the downstream water current because it keeps up with the stream of water current. For simplicity, wind on the sail is represented by the wind at the 0.4 m height from the sea surface. This height is determined so that the anemometer is installed on SOTAB-II at 0.4 m above the water line. Wave drag was treated as negligible because SOTAB-II drifts slowly. When SOTAB-II drifts at the speed of 0.03 U ₍₁₀₎, the stream of air and water flow in the posterior direction is at the speed of 0.03 U ₍₁₀₎ in the body fixed coordinate system. Meanwhile, the stream of wind flows in the anterior direction at the speed of U _(0.4)−0.03 U ₍₁₀₎. These relations are shown in Fig. 15. Here “3 %” is used as a typical drifting speed of SOTAB-II in wind direction. Drifting experiments using a thin floating mat brought to us the fact that the value of wind speed effect has a possibility to be increased up to 5 % [12]. So, we assume the wind effect ranges from 2 to 5 % in calculations to cover any situations.

Fig. 15

Relations of Stream around SOTAB-II

SOTAB-II is expected to keep its drifting speed in wind direction as about 3 % of U ₍₁₀₎ under a severe condition such as a very strong typhoon. Therefore, the scale of brake board was designed under the severest condition. So, we assume U ₍₁₀₎ from 0 to 40.0 m/s.Three patterns of brake boards were evaluated to choose the most adequate one. Table 3 shows the scales of these brake boards. In designing the brake board and the sail, the brake force acting on the brake board should be larger than the thrust force acting on the ship body without sail at 2 % of the wind speed to control the speed of the ship by changing the sail area. Then the drag forces at the ship speed of 2 % of wind speed of 40 m/s as the severest condition are compared to design the brake board and the sail.

Table 3 Scales of each brake board

To calculate the hydrodynamic forces exerted by these streams, a 3D model of the new SOTAB-II was constructed by using the 3D modeling software “Gambit”, and two types of double hull models were made (Fig. 16). In these figures, the model on the left-hand side was used to calculate the hydrodynamic force acting on the body part below the water line. In this model, the brake board and its effect are included. The other figure is used to calculate the hydrodynamic force acting on the body part above the water line. The sail and its effect are not considered in this model. The mesh alignment of CFD analysis is shown in Fig. 17. Table 4 shows the calculated hydrodynamic forces on SOTAB-II with the ship speed of 2 % of the wind speed of 40 m/s and with completely furled sail for 3 kinds of the brake boards using CFD analysis. Here, the thrust force acting in the forward direction is expressed by a positive value, and the drag force acting in the backward direction is expressed by a negative value. Judging from these results, the brake board 3 is the best because the drag force acting on the lower part of SOTAB-II in water is larger than the thrust force with completely furled sail.

Fig. 16

SOTAB-II’s Double hull model of lower side (left) and upper side (right)

Fig. 17

Mesh alignment for CFD analysis

Table 4 Comparisons of the Hydrodynamic forces acting on SOTAB-II with different brake boards and without the sail

On the other hand, while SOTAB-II is guided by a thruster, the brake board is not needed because it acts as an unwanted load for guiding. Therefore, two ways of usage for the brake board are taken. In case SOTAB-II is autonomously tracking an oil spill, the brake board is set perpendicular to the longitudinal direction of the main hull to gain the brake force, Table 5. That brake board is set parallel to the longitudinal direction of the main hull in case SOTAB-II is guided to a far target point by using a thruster.

Table 5 Scales of each sail

The sail is expected to generate the thrust force acting on SOTAB-II to drift at any speed from 2 to 5 % of wind speed. The thrust force must be larger than the drag force acting on the lower part of SOTAB-II in water at the maximum size of the sail at any speed. Table 6 shows the calculated results of hydrodynamic forces acting on SOTAB-II with the ship speed of 5 % of the wind speed of 40 m/s and with completely unfurled sail for 3 kinds of the sails. We can see that only sail 3 can gain a positive thrust force that is suitable for SOTAB-II to control its speed.

Table 6 Comparisons of the Hydrodynamic forces acting on SOTAB-II with unfurled sail for three kinds of sails

Then, sail 3 and brake board 3 are evaluated under the other wind conditions with the drifting speed of SOATB-II of 2 to 5 % of the wind speed. Figure 18 shows the calculated hydrodynamic forces acting on the upper and lower part of SOTAB-II with the drifting speed of 2–5 % of the wind speed and with different sail conditions. In this figure, the upper lines show the thrust forces acting on the upper part of SOTAB-II with completely unfurled sail, and the lower lines show those of SOTAB-II with completely furled sail. The middle lines show the drag forces acting on the lower part of SOTAB-II in water, which lie between the upper lines and the lower lines. This indicates that the thrust forces can be adjusted by controlling the sail area to balance with the drag forces acting on the lower part of SOTAB-II in water, corresponding to variation of drifting speed of 2 to 5 % of wind speed ranging from 0 to 40 m/s. From this figure, we can confirm that SOTAB-II can control its speed from 2 to 5 % of wind speed with controlling sail area adequately. And it can carry out the oil spill tracking under any wind velocity condition.

Fig. 18

Hydrodynamic forces acting on the upper and lower part of SOTAB-II with the drifting speed of 2 to 5 % of the wind speed and with different sail conditions

5.4 Maneuverability of new SOTAB-II

SOTAB-II must adjust its rudder to drift along with the oil slick when the wind direction has changed. In order to increase the self-stabilizing function against the change of the wind direction, a jib sail like a weathercock is installed on the front side of SOTAB-II. The shape of the jib sail is a triangle, and its height and width are both 40 mm. If this jib sail works well for turning, it results in saving the energy for rudder control.

Turning performances of new SOTAB-II equipped with and without the jib sail were evaluated. From those results, turning with installing the jib sail takes only half as long as turning without installing the jib sail.

6 Conclusions

In order to overcome the weak points of existing oil spill monitoring methods and deal with the gas and oil blowout accidents, a marine disaster prevention system is being constructed by the authors’ project. The autonomous buoy named SOTAB-II is used in this system. It has two main tasks. The first one is to drift along with oil the slick for the long term after being dropped into the sea. The second one is to send the meteorological and oceanographic data around it to the land base in real-time. Therefore, it needs the ability to track the oil slick autonomously and the capacity to load several sensors. In general, the drifting vector of the oil slick is the resultant vector of the water current vector and about a 3 % vector of the wind at the 10 m height from the sea surface. Based on the assumption that the water current effects on SOTAB-II and oil slick are the same, SOTAB-II controls its drifting speed and drifting direction by controlling the wind effect. To accomplish it, SOTAB-II was equipped with a sail whose size and direction are both controllable. SOTAB-II with a cylindrical hull shape had been developed. This cylindrical shape was selected because SOTAB-II could easily respond to the change of the drifting direction. Some field experiments were carried out by using it. Analysis of the results show the efficiency of the sail installed on SOTAB-II. Besides, it revealed that SOTAB-II had a function to correct the drifting direction and drifting distance by controlling its sail adequately. However, the drifting speed of SOTAB-II was lower than that expected; it is mainly because that the drag force acting on SOTAB-II’s hull becomes large. To overcome this problem, we redesigned SOTAB-II. The yacht shape “KIT34” was adopted for its hull. Its scale was determined through the calculations of operational period and loading capacity. The sizes of brake board and sail were determined by using CFD. The transverse stability and turning ability of the new SOTAB-II were evaluated. Finally, the new SOTAB-II redesigned in this research is shown in Fig. 19. It is planned to develop multiple new SOTAB-IIs, and carry out field experiments by using them.

Fig. 19

Configuration of new SOTAB-II