Numerical study on active wave devouring propulsion

Abstract

The possibility of extracting energy from gravity waves for marine propulsion was numerically studied by a two-dimensional oscillating hydrofoil in this study. The commercially available computational fluid dynamics software FLUENT was used for the unstructured grid based on the Reynolds-average Navier–Stokes equation. The free surface waves and motion of the flapping foil were implemented by customizing the FLUENT solver using a user-defined function technique. In addition, dynamic mesh technology and post processing capabilities were fully utilized. The validation of the model was carried out using experimental data for an oscillation hydrofoil under the waves. The results of the simulation were investigated in detail in order to explain the increase of propeller efficiency in gravity waves. Eight design parameters were identified and it was found that some of them greatly affected the performance of wave energy extraction by the active oscillating hydrofoil. Finally, the overall results suggested that when the design parameters are correctly maintained, the present approach can increase the performance of the oscillating hydrofoil by absorbing energy from sea waves.

1 Introduction

Rising energy bills and intensifying pressure to reduce CO₂ emission have caused increasing demand for alternative energy sources for many sectors including marine propulsion. The ocean waves have long been considered as a substantial source of energy for marine propulsion. However, utilization of wave energy has not been studied extensively because of the complexity of nonlinear oscillatory hydrodynamics.

Several experiments have been performed to examine the possibility of utilizing the energy from ocean waves for marine propulsion (Jakobsen [1], Isshiki et al. [2], Terao [3]). In their concept, one or two hydrofoils were fixed to the ship through a spring system, in a manner that the angle of the hydrofoils could be adjusted as the direction of incoming water is changed. In the meantime, the ship and the hydrofoils are heaving and pitching with incoming waves and produce forward thrust on the hydrofoil.

The corresponding problem with the moving foil oscillating in an unbounded fluid has been studied for several decades. Swimming of slender fish has been treated by Lighthill [4], and the waving motion of a two-dimensional flexible plate has been calculated by Wu [5]. Later, based on the potential flow approach, a series of papers by Wu [6–8] optimized the oscillation motion and shape parameters for two-dimensional flat plates. Furthermore, several theories of an oscillating foil have been developed. Bose [9] has developed a time-domain panel method for analysis of an oscillating foil in unsteady motion. Kubota et al. [10] and Kudo et al. [11] have developed two dimensional linear and nonlinear theories which can estimate propulsive performance of partly flexible as well as rigid oscillating propulsors. They also showed that an aft-half elastic foil reveals 8 % higher efficiency than a rigid foil. Yamaguchi and Bose [12] extended the work of Kubota et al. and Kudo et al. to design rigid and aft-half elastic oscillating foils for a large-scale ship. Their results showed that both oscillating foils can give higher propulsive efficiency than an optimal screw propeller, and the elastic foil gives 5–7 % higher propulsive efficiency than the screw propeller. Early hydrodynamics models were restricted to potential flow assumption. But with the advancement of computers, more sophisticated numerical models have been introduced to analyze the performance of an oscillating foil. Pedro et al. [13] and Guglielmini and Blondeaux [14] have investigated the performance of a low Reynolds number oscillating foil based on a computational fluid dynamics (CFD) approach and promising results have been reported. Other studies (Lai et al. [15], Anderson et al. [16] and Gopalkrishnan et al. [17]) have addressed the thrust producing capability of an oscillating hydrofoil by experimental work. They have shown that the potential efficiency of the oscillation hydrofoil propulsor can compete with that of a conventional rotating propeller. However, an oscillating hydrofoil has not been considered as a practical replacement because of the mechanical complexity even with the improvement of efficiency up to some extent. Because of that, some of them extended their studies on oscillating foils to consider propulsion by using wave energy as described in the following paragraphs.

For the first time in history Wu [18] introduced the theory for extracting energy from surrounding flows by a two-dimensional hydrofoil oscillating through gravity waves in water. According to his theory, it has been found that the energy extraction is impossible if the flow is uniform, and only feasible when the primary flow contains a wave component which has vertical velocity normal to the mean free stream and the wing span. Finally, he was able to obtain the best mode of heave and pitching for extraction of wave energy by passive type wave devouring propulsor.

Later, Isshiki [19] employed Wu’s theory of an oscillating hydrofoil and extended it by introducing a free surface effect for investigating the possibility of wave devouring propulsion by a passive type oscillating hydrofoil. Further, not only theoretically, but also experimentally, Isshiki and Murakami [20] studied the basic concept of passive type wave devouring capability of an oscillating hydrofoil.

In addition, to illustrate the unsteady foil motions and wave devouring capabilities, Grue et al. [21] developed a theory for a two-dimensional flat plate near the free surface using a frequency-domain integral equation approach. The theory in both head and following waves was in good agreement with the experiment conducted by Isshiki and Murakami [20]; however, with lower wave numbers there were systematic discrepancies between the theory and the experimental results as nonlinear effects and free surface effects were not fully accounted for in the theory.

Despite these inviting results by several independent studies, a significant commercial success is yet to be seen. The drawbacks of the concept have added resistance in calm seas as well as mechanical complexity. Although the oscillating foil propulsor is mechanically complex, if the gain by recovering the wave energy is considerable, it may be more attractive than the conventional screw propeller. In the present study, therefore, we propose a new concept of wave energy recovering through a powered oscillating foil propulsor, which is designed to replace the conventional screw propeller. The objectives are to develop a numerical model which can predict the oscillating foil performance in a wave field and to elucidate the physical mechanisms.

2 Problem description and performance indices

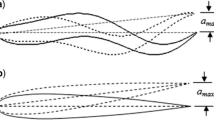
As shown in Fig. 1, the numerical setup is described as a two-dimensional hydrofoil of chord length c, submerged at a mean depth h ₁ underneath the free surface. The basic flow contains the sinusoidal gravity waves of amplitude a and wave length λ. In terms of the body-fixed Cartesian coordinate system (x, y) with the y-axis in the vertical direction and x = 0 fixed at the foil pitching center, the foil oscillates with uniform flow U in the x-direction.

Fig. 1

Body coordinate system for an oscillating hydrofoil under a wave. Cartesian coordinate system (x, y), pitching amplitude θ, heave amplitude h, submergence depth h ₁, total depth H (≫h ₁), advancing speed U

The wave profile of the basic flow can be written as,

$$ \zeta = a\cos (kx - \omega_{0} t) $$

(1)

where wave number k and encounter frequency ω ₀ are given by

$$ k = \frac{2\pi }{\lambda }{\kern 1pt} $$

(2)

$$ \omega_{0} = \sqrt {gk} + kU $$

(3)

In the above equation g is gravitational acceleration.

As shown in Fig. 2, the oscillation motion of the hydrofoil is expressed as harmonic vertical (heave) motion h(t) of amplitude h ₀ and frequency f, and a harmonic angular (pitch) motion at the pitching axis cited as the distance b from leading edge, θ(t) of amplitude θ ₀ and frequency f:

$$ h = h_{0} \sin (2\pi ft + \psi ) $$

(4)

$$ \theta = \theta_{0} \sin (2\pi ft + \psi + \phi ) $$

(5)

where φ and ψ are the phase difference between heave and pitching motion and phase difference between wave and foil motion, respectively.

Fig. 2

Definition of principal motion parameters, heave h(t) and pitch θ(t), for an oscillation foil

Under the above conditions, the foil is subjected to time varying forces F _x , F _y in the –x (thrust) and y (lift) directions, respectively, and a torque of M. The above forces and the moment are non-dimensionalized as follows to provide the thrust coefficient C _x , vertical force coefficient C _y , and moment coefficient C _m .

$$ C_{x} = \frac{{F_{x} }}{{\frac{1}{2}\rho U^{2} c}} $$

(6)

$$ C_{y} = \frac{{F_{y} }}{{\frac{1}{2}\rho U^{2} c}} $$

(7)

$$ C_{m} = \frac{M}{{\frac{1}{2}\rho U^{2} c^{2} }} $$

(8)

where ρ denotes the fluid density. The instantaneous input power P can be defined as,

$$ P = - F_{y} \frac{{{\text{d}}h}}{{{\text{d}}t}} - M\frac{{{\text{d}}\theta }}{{{\text{d}}t}} $$

(9)

We defined the input power coefficient C _p and output power coefficient C _po as,

$$ C_{\text{p}} = \frac{P}{{\frac{1}{2}\rho U^{3} c}} $$

(10)

$$ C_{\text{po}} = \frac{{F_{x} U}}{{\frac{1}{2}\rho U^{3} c}} $$

(11)

The propulsive efficiency η is defined as the ratio of useful power over input power as,

$$ \eta = \frac{{\overline{{F_{x} }} U}}{{\overline{P} }} $$

(12)

where the over-line denotes averaging over one period of oscillation. If T is the period of oscillation, $\overline{X}$ is the time average value of any time varying function X(t).

$$ \overline{X} = \frac{1}{T}\int\limits_{0}^{T} {X(t){\text{d}}t} $$

(13)

3 Modeling of oscillating foil under the wave

Modeling of geometry and meshing were performed by commercially available software called GAMBIT version 2.4. As shown in Fig. 3, the rectangular domain has been divided into three main zones called the numerical zone, air zone and artificial damping zone. The numerical zone again splits into two regions called the inner region and outer region. The inner region was meshed with finer quadrilateral structured O-grid topology, while the outer region was meshed with unstructured triangular mesh. Near the foil, the grid was generated for the wall function based on boundary conditions and thereby the first cell height off the solid foil surface was 1–5 in terms of y ⁺. The foil and the inner region were moved together, while the outer region was deformed in accordance with the foil motion. Triangular unstructured grid based on spring method and dynamic mesh updating techniques were used for deforming the outer region. The other two main zones are the air zone and artificial damping zone which are modeled by using a quadrilateral structured grid. In order to capture more accurate movements of free surface, finer structured mesh was adopted near the free surface level. However, no flow was actually computed in the air zone. The total computational domain ranged −λ ≤ x ≤ 4λ and −3λ/4 ≤ y ≤ λ/4, where λ represents the wave length, as shown in Fig. 3.

Fig. 3

Schematic diagram of numerical wave tank and meshing schemes

The CFD code, FLUENT 6.3 used in this study employs the cell-centered finite volume method that allows the use of computational elements with arbitrary shapes. Free surface deformation was captured using the Volume of Fraction (VOF) method. Reynolds averaging approach with two equations model of k-ω SST model was used for modeling the turbulence. Convective terms were discretized using the second-order accurate upwind scheme, while diffusive terms were discretized using the second-order accurate central differentiation scheme and the volume fraction was discretized with modified high resolution interface capturing (HRIC) option. The velocity pressure coupling and overall solution procedure were based on a SIMPLE type segregated algorithm adapted to structured and unstructured grids. Finally the discretized equations were solved by using point wise Gauss–Seidel iteration.

Boundary conditions were set to simulate the oscillation of the foil under a wave: on the inlet boundary, horizontal and vertical velocity components for generating waves, u and v (Eqs. 14, 15), were imposed with a turbulence intensity of 1 % and pressure extrapolated from inside. On the foil surface, a no-slip condition was imposed, i.e., zero relative velocity with extrapolated pressure. On the outer boundary, the pressure was set to a hydrostatic pressure as a function of depth from the free surface, while all other variables were extrapolated. The first order accurate scheme was used for the extrapolation.

The horizontal and vertical inlet velocity components of wave generation equations are given by Eqs. 14 and 15,

$$ u = U + \sqrt {gk} ae^{ky} \cos (kx - \omega_{0} t) $$

(14)

$$ v = \sqrt {gk} ae^{ky} \sin (kx - \omega_{0} t) $$

(15)

The above wave generation equations and foil motions (in Eqs. 4, 5) are implemented in the FLUENT solver by programming a user defined function (UDF).

Towards the end of the computational domain, an artificial damping zone was applied, so that the wave energy is gradually dissipated in the direction of wave propagation to prevent the wave reflection. The profile and magnitude of the artificial damping have to be designed to minimize the possible wave reflection at entrance of the damping zone and maximize the wave energy dissipation. After comprehensive tests, the length of the damping zone was determined as to be at least three wavelengths. The damping zone was designed by introducing numerical source term into the momentum equation specified by UDF.

x-momentum equation source term S _x ,

$$ S_{x} = - C_{\text{a}} \cdot (u - U) $$

(16)

y-momentum equation source term S _y ,

$$ S_{y} = - C_{\text{a}} \cdot v $$

(17)

where,

$$ C_{\text{a}} = \left\{ \begin{gathered} 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x < X1 \hfill \\ \frac{1}{2}\left[ {1 - \cos \left\{ {\pi \frac{{\left( {x - X1} \right)}}{{\left( {X2 - X1} \right)}}} \right\}} \right]\,\,\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x < X2 \hfill \\ \end{gathered} \right. $$

(18)

u, v, are the velocities in the Cartesian coordinate system, U is the mean flow velocity and, X1 and X2 are the x coordinates of starting and ending points of the damping zone. The performance and efficiency of the artificial damping coefficient C _a were numerically tested and confirmed.

4 Grid dependency study on an oscillating foil under a wave

Verification refers to an estimation of the numerical errors and uncertainties in the process of iteration and grid refinement, which are inevitable issues in the numerical computations. To evaluate the grid dependency, four grids were generated with the same meshing strategy (as described in Sect. 3), but with systematically decreasing the element size on the foil surface and near the free surface. In those four test cases non-dimensional parameters (describe in Sect. 6) were set as, wave phase angle −90°, phase difference of heave and pitch 40°, Froude number 0.87, Reynolds number 5 × 10⁷, non-dimensional heave amplitude 0.5, extended feathering parameter 0.2 and non-dimensional submergence depth 1.28, and further, wave amplitude 1 m and the wave encounter frequency and foil oscillation frequency were kept equal at 0.156 Hz.

The iterative convergence of unsteady flow problems are dependant on time step and number of iterations per time step. The number of iterations per time step was assessed by examining norms of solution changers summed over all grid points. Figure 4 shows the norms of solution of iteration history in the last two time steps. According to Fig. 4, the solution change drops five orders of magnitude per time step of 200 iterations. Then the time step size was assessed through average thrust coefficient solutions on different time step sizes and using the finest grid (grid no. 1). Four different time steps were evaluated by dividing the foil oscillation period with 250, 353, 500 and 707. Finally, by considering the average thrust coefficient errors and uncertainties (calculation procedure omitted) the oscillation period divided by 500 time steps (T/500) is selected for the future computations.

Fig. 4

Iteration history of the last two time steps (norms of solution change on grid no. 1)

Grid convergence is assessed through average thrust coefficient solutions on four systematically refined grids with constant refinement ratio, r = √2 proposed by Stern et al. [22]. The average thrust coefficient values (C _x ) on all four grids are given in Table 1 along with computed solution changers ε _i . The parameter ε _i is the relative difference in the solution obtained at two grid levels and defined in ith grid study ε _i,21 = C _xi,2 − C _xi,1 and ε _i,32 = C _xi,3 − C _xi,2.

Table 1 Grid convergence study for thrust coefficient

Grid studies were conducted using four grids, which enables two separate three-grid studies to be performed and compared. Grid study 1 (GS1) gives estimates for grid errors and uncertainties on grid 1 using the three finer grids 1–3 while grid study 2 (GS2) gives estimates for grid errors and uncertainties on grid 2 using the three coarser grids 2–4.

The verification method proposed by Stern et al. [22] was used in the present grid dependency study. The grid convergence ratio R (Eq. 19), order of accuracy p (Eq. 20), generalized Richardson Extrapolation error δ _RE (Eq. 21), correction factor C (Eq. 23), and uncertainty U _G (Eq. 24) are shown in Table 2.

Table 2 Verification of average thrust coefficient

$$ R = \frac{{\varepsilon_{i,12} }}{{\varepsilon_{i,32} }} $$

(19)

Since 0 < R < 1, both GS1 and GS2 display monotonic convergence as given by condition Stern et al When the grid studies satisfy the monotonic convergence condition, the generalized RE (Richardson Extrapolation) is used to estimate the error δ _RE due to selection of the input grid refinement ratio r and order of accuracy p.

$$ p = \frac{{\ln \left( {{{\varepsilon_{i,32} } \mathord{\left/ {\vphantom {{\varepsilon_{i,32} } {\varepsilon_{i,21} }}} \right. \kern-\nulldelimiterspace} {\varepsilon_{i,21} }}} \right)}}{\ln \left( r \right)} $$

(20)

$$ \delta_{\text{RE}} = \frac{{\varepsilon_{i,12} }}{{r^{p} - 1}} $$

(21)

Correction of Eq. 21 through a multiplication factor C accounts for effects of higher order terms and provides a quantitative metric to determine proximity of the solutions to the asymptotic range

$$ \delta = C\delta_{\text{RE}} = C\left( {\frac{{\varepsilon_{i,12} }}{{r^{p} - 1}}} \right) $$

(22)

where the correction factor is given by

$$ C = \frac{{r^{p} - 1}}{{r^{{p{\text{th}}}} - 1}} $$

(23)

and pth (set to be 2.0 in the present study) is an estimate for the limiting order of accuracy as spacing size goes to zero and the asymptotic range is reached so that C → 1. However, the obtained accuracy (p) of GS1 is much greater than of GS2. As a result, the correction factor C is greater for GS1 than GS2 and both are less than 1. When solutions are far from the asymptotic range, C is sufficiently less than or greater than 1 and only the magnitude of the error is estimated through the uncertainty U _G (Eq. 24).

$$ U_{\text{G}} = \left| {C\delta_{\text{RE}} } \right| + \left| {\left( {1 - C} \right)\delta_{\text{RE}} } \right| $$

(24)

Comparing the estimated grid error through uncertainty U _G, the grid uncertainty is less for GS1 than GS2 and the values (0.1 and 0.17 % grid 1, respectively) are reasonable in consideration of the overall number of grid points used. Therefore, for the rest of the numerical study medium-1 grid is used.

5 Comparison to the experiment

The validation study has been carried out by comparing experimental and numerical results. The present literature survey has shown that the only available experiment about the wave devouring propulsion was carried out by Isshiki et al. [20]. The experiment was carried out in a tank of 25 m × 1 m × 0.71 m (length × breath × depth) with a wave maker at one end of the tank. The foil is attached to the carriage through springs and carriage moves horizontally with constant velocity U. First the carriage and the foil pulled with constant velocity in calm water. Then the resistance of the system was determined as a function of speed. Later, waves were incident upon the foil, which then moves forward solely due to the thrust caused by the waves (free running test). The mean horizontal velocity, heave amplitude, pitching amplitude, and the thrust balancing resistance were obtained by applying the results. The parameters of experimental setup are shown in Table 3.

Table 3 Parameters of experimental setup

Even though the experiment was conducted with passive type oscillation foil, the simulations were carried out by using active type oscillation foil. However, the simulations motion condition of heave amplitude, pitch amplitude, phase differences and oscillation frequencies are kept identical with the experiment, and the oscillation frequency of the foil and the wave encounter frequency are set to be equal. Further, the heave and pitching motions in the free running test were assumed with corresponding sine function and also average advanced velocity of the free running test was assumed for the advance velocity of the active oscillation foil in simulations. The amplitude of the waves observed in the experiment has shown a considerable scattering; therefore, the mean value of the amplitude was chosen for comparison. The size of the numerical domain was the same as the experimental tank and the same meshing strategy as described in Sect. 3 was used for modeling the numerical domain.

The thrust coefficients obtained from the present numerical method were compared with experimental data and linear and nonlinear approximation theories in Fig. 5. A good agreement has been shown between the experiment and simulation results compared with the linear and nonlinear theories in most cases. For long incoming wave lengths (small kc) all three methods have shown good agreement with experimental results. However, when the short wave lengths are presented (large kc), the present numerical method has shown the best agreement with the experiment. It’s reasonable to suppose that the discrepancies are mainly due to the nonlinearity of the formulation which was neglected in the theoretical studies.

Fig. 5

Comparison of non-dimensional thrust (T/ρga ²) between experiment by Isshiki [20], linear theory by Isshiki [19], nonlinear theory by Grue et al. [21] and present numerical results with respect to the kc. Here k is wave number, and c foil chord length

6 Discussions

In order to understand the hydrodynamic behavior and performance of active oscillating foil in wavy flow, eight non-dimensional parameters were identified. Those are phase difference of wave and foil motion ψ, phase difference of heaving and pitching motion φ, submergence depth of foil h ₁/c, non-dimensionalized wave encounter frequency ω ₀/2πf, non-dimensional frequency of oscillation ω ²₀ c/g, heave amplitude h ₀/c, Froude number Fr (Eq. 25) and extended feathering parameter ε (Eq. 26).

$$ Fr = \frac{U}{{\sqrt {gc} }} $$

(25)

$$ \varepsilon = \frac{{\theta_{0} U}}{{\omega_{0} \left( {h_{0} + \frac{gak}{{\omega \omega_{0} }}e^{{ - kh_{1} }} } \right)}} $$

(26)

Although there are eight non-dimensional parameters in the problem, here we show the results of a few parameters for elaboration. The initial conditions of foil and wave motions are given in Table 4.

Table 4 Foil and wave motion condition: basic case for parametric study

6.1 Wave encounter frequency effect

Wu [18] investigated the effect of frequency on extraction of wave energy by his theoretical study. It has been confirmed that when the wave encounter frequency and foil oscillation frequency are equal, the energy gain is maximized. In other words, the energy gain is always accompanied by the increase of the leading-edge suction, suggesting a tendency towards leading edge stall. The above argument has been further investigated numerically by the present study. The non-dimensionalized wave encounter frequency (ω ₀/2πf) was changed from 0.5 to 2, keeping the foil oscillation frequency (f) constant and changing the wave encounter frequency (ω ₀) accordingly. The wave length was changed according to the wave encounter frequency and rest of the parameters were kept constant as Froude number 0.87, wave phase angle −90°, phase difference between heave and pitch 40°, non-dimensional heave amplitude 0.6 and non-dimensional submergence depth 1.28.

Figures 6 and 7 show the variations of average thrust coefficient and propulsive efficiency of oscillating foil propulsor with the non-dimensional wave encounter frequency. Both efficiency and thrust are sharply maximized at ω ₀/2πf = 1 (which means the encounter frequency is equal to the foil oscillation frequency). However, when changing the non-dimensional wave encounter frequency in the vicinity of ω ₀/2πf = 1, the average thrust and propulsive efficiency drop below the average values. Further increasing or decreasing the non-dimensional frequency there are not any significant changes in thrust or efficiency even in harmonic condition of ω ₀/2πf = 2. Because of these reasons, the rest of the parametric study has been carried out by setting the non-dimensional frequency ω ₀/2πf equals to 1.

Fig. 6

Average thrust coefficient versus non-dimensional wave encounter frequency (ω₀/2πf) (φ = 40°, h ₁/c = 1.28, ψ = −90°, Fr = 0.87, h ₀/c = 0.6)

Fig. 7

Propulsive efficiency versus non-dimensional wave encounter frequency (ω₀/2πf) (φ = 40°, h ₁/c = 1.28, ψ = −90°, Fr = 0.87, h ₀/c = 0.6)

6.2 Effect of phase difference between wave and foil motion (ψ)

Phase difference between wave and foil motion is discussed in this section. Nine simulations of different phase angles (ψ) were performed varying from −180° to +180°. The following parameters were set to be constant as Froude number 0.87, phase difference between heave and pitch 105°, non-dimensional heave amplitude 0.6, extended feathering parameter 0.43 and non-dimensional submergence depth 1.28. The physical interpretation of wave phase difference ψ is defined as when the wave frame of reference has been fixed at the wave crest (the vertical component of the wave orbital velocity is about to go downwards), then the wave phase difference is at 0° and 180°, the foil is at the mean position (submergence depth = h ₁) and about to go upwards and downwards with respect to the wave frame of reference respectively. And also when the wave phase difference is −90° and +90°, the foil is at its bottommost position and uppermost position respectively.

Figures 8 and 9 show the thrust coefficient and efficiency versus wave phase difference. When the wave phase difference is at −90°, the maximum thrust and efficiency can be obtained and the thrust and efficiency gains are 25 and 10 % for the case of no incoming wave. As the wave phase angle increases from −90°, a decreasing trend of both thrust and efficiency is observed. The minimum thrust and efficiency has been observed in the phase angle of +90°. Increasing phase angle beyond +90° again increases the thrust and efficiency.

Fig. 8

Comparison of average thrust coefficient between with and without incoming waves as a function of wave phase difference ψ (φ = 105°, h ₁/c = 1.28, ω₀/2πf = 1, ε = 0.43, Fr = 0.87, ω ²₀ c/g = 0.69, h ₀/c = 0.6)

Fig. 9

Comparison of propulsive efficiency between with and without incoming waves as a function of wave phase difference ψ; (φ = 105°, h ₁/c = 1.28, ω₀/2πf = 1, ε = 0.43, Fr = 0.87, ω ²₀ c/g = 0.69, h ₀/c = 0.6)

The reason for this considerable variation has been investigated by observing the instantaneous lift and thrust coefficient for one oscillation cycle as shown in Figs. 10 and 11. In Fig. 10, the lift coefficient variation of phase angle at +90° and −90° shows a significant difference in the amplitude. This makes the input power supply to the foil propulsor near −90° become higher than +90° as the main contribution of input power is the lift component. In Fig. 11, it is clearly shown that the gain of thrust is due to the presence of incoming waves. When the phase angle is at −90°, the vertical component of wave orbital velocity increases the effective angle of attack, thereby shifting the force direction more forward and increasing the thrust. When the phase angle is at +90°, the vertical component of wave orbital velocity adversely affects the effective angle of attack, thereby shifting the force direction more backward and decreasing the thrust. However, the gain of thrust is much higher compared with the increase of power supply to the foil. Thus, when the phase angle −90° displays the maximum propulsive efficiency.

Fig. 10

Comparison of instantaneous lift coefficient in one oscillation period between wave phase angle −90°, +90° and without incoming waves; (φ = 105°, h ₁/c = 1.28, ω₀/2πf = 1, ε = 0.43, Fr = 0.87, ω ²₀ c/g = 0.69, h ₀/c = 0.6)

Fig. 11

Comparison of instantaneous thrust coefficient in one oscillation period between wave phase angle −90°, +90° and without incoming waves; (φ = 105°, h ₁/c = 1.28, ω₀/2πf = 1, ε = 0.43, Fr = 0.87, ω ²₀ c/g = 0.69, h ₀/c = 0.6)

6.3 Phase angle effect between heave and pitching motion (φ)

The previous studies on infinite water oscillating foils suggested that the phase angle between heave and pitching motion is a very sensitive parameter for the efficiency and thrust generation mechanism. Therefore, the thrust generation mechanism of an oscillating foil propulsor under the waves has been investigated in different phase angles. Sixteen simulations were carried out with varying phase angles φ from 0 to 180° while keeping the other design parameters constant as Froude number 0.87, wave phase angle −90°, non-dimensional heave amplitude 0.6, extended feathering parameter 0.43 and non-dimensional submergence depth 1.28. Varying the phase from 90° causes the hydrofoil to have a non-zero pitch angle at the top and bottom positions. If the phase angle is greater than 90° at the lowest position of the heaving motion, the hydrofoil will pitch upwards and, if less than 90° at the same position, the hydrofoil will pitch downwards.

In Fig. 12, the average thrust coefficient shows the minimum trend at the value near 100°, while in Fig. 13 the efficiency shows the maximum trend near the phase angle at 60°. These trends of thrust and efficiency curves are very different from the numerical results obtained in Pedro et al. [13], which studied an oscillating foil in an unbounded fluid.

Fig. 12

Comparison of average thrust coefficient versus phase difference between heave and pitching motion φ; (h ₁/c = 1.28, ω₀/2πf = 1, ψ = −90°, ε = 0.43, Fr = 0.87, ω ²₀ c/g = 0.69, h ₀/c = 0.6)

Fig. 13

Comparison of propulsive efficiency versus phase difference between heave and pitching motion φ; (h ₁/c = 1.28, ω₀/2πf = 1, ψ = −90°, ε = 0.43, Fr = 0.87, ω ²₀ c/g = 0.69, h ₀/c = 0.6)

In the study of low Reynolds number oscillating foils (Pedro et al. [13]), the thrust coefficient increases with phase angle. Below 60°, the average thrust is negative, or in other words, rather drag is created. The present computation with the presence of wave shows completely different behavior of thrust generation. When the phase difference is zero the maximum thrust could be obtained because of high Reynolds number effect and change of effective angle of attack. To get a better understanding of this discrepancy of thrust and efficiency under the wave, the foil position and instantaneous resultant force are plotted against the different phase angles of 20, 60 and 110° as shown in Figs. 14, 15 and 16, respectively.

Fig. 14

Appearance of foil position and resultant force over one period of oscillation at phase angle φ = 20° (h ₁/c = 1.28, ω₀/2πf = 1, ψ = −90°, ε = 0.43, Fr = 0.87, ω ²₀ c/g = 0.69, h ₀/c = 0.6)

Fig. 15

Appearance of foil position and resultant force over one oscillation period at phase angle φ = 60° (h ₁/c = 1.28, ω₀/2πf = 1, ψ = −90°, ε = 0.43, Fr = 0.87, ω ²₀ c/g = 0.69, h ₀/c = 0.6)

Fig. 16

Appearance of foil position and resultant force over one oscillation period at phase angle φ = 110° (h ₁/c = 1.28, ω₀/2πf = 1, ψ = −90°, ε = 0.43, Fr = 0.87, ω ²₀ c/g = 0.69, h ₀/c = 0.6)

In Fig. 14, maximum resultant forces are applied to the foil due to the increase in effective angle of attack. Horizontal components of those resultant forces are much higher and thereby increase the thrust. Also, the vertical component of force is high which results in high instantaneous power supply to the propulsor. As shown in Fig. 15, at the phase angle 60°, the force contribution to the thrust is much higher and the magnitude of instantaneous lift is the smallest. Because of that reason maximum efficiency is achieved near 60°. In Fig. 16, the vertical component of instantaneous force is dominant at phase angle 110°, thus making the higher power input to the foil. Also, the horizontal component gets the minimum values for thrust.

By considering efficiency versus average thrust coefficient graph (Fig. 17), even though 60° phase angle has shown the maximum efficiency, the 40° angle is considered as a realistic phase angle between heaving and pitching motions for the wave devouring foil propulsor, because, when the phase angle is 40°, the foil keeps high efficiency without much sacrifice of thrust force.

Fig. 17

Propulsive efficiency versus average thrust coefficient (h ₁/c = 1.28, ω₀/2πf = 1, ψ = −90°, ε = 0.43, Fr = 0.87, ω ²₀ c/g = 0.69, h ₀/c = 0.6)

6.4 Froude number effect

The Froude number provides a significant contribution to the wave devouring propulsion because the wave encounter frequencies are highly dependent on the advancing velocity of oscillating foil propulsor. In this section, wave devouring performance is numerically investigated by changing the Froude number based on advancing speed of the oscillating foil. The Froude number is changed from 0.6 to 2. In order to change the Froude number, advancing speed and wave length have to change accordingly. Even though the wave length has changed by the simulation, the wave encounter frequency and foil oscillation frequency are kept constant at 0.23 Hz. To keep the extended feathering parameter at 0.2 the pitching amplitude has to change accordingly. Moreover, the other parameters are kept constants as non-dimensional heave amplitude 0.5, wave phase angle −90°, phase difference between heave and pitch 40° and non-dimensional submergence depth 1.28.

Figure 18 shows the variation of thrust coefficient with respect to Froude number. It can be seen that when the Froude number increases from 0.6 to 2, the thrust coefficient exponentially decreases from 0.9 to 0.1 while the efficiency increases from 0.5 to 0.75 as shown in Fig. 19. In an unbounded fluid oscillation, wasted energy of the foil is solely due to the vortex wake formed behind the foil. But when a free surface is presented in addition to the vortex wake, the generated surface waves also transport the considerable amount of energy as a waste. In the present computations, the above wasted energy rate (due to the surface wave generation) is increased with the increase of the foil's advancing speed (due to the increase of Froude number), thereby increasing the so called wave making resistance. Therefore, it’s reasonable to believe that the average thrust coefficient decrement shown in Fig. 18 is mainly because of the wave making resistance increment as a result of Froude number effects. In the meantime, efficiency increases due to the decrease of energy supply to maintain the heaving and pitching motion of oscillation foil. When the Froude number rises above 1, the efficiency slightly increases with a greater sacrifice of thrust coefficient. Thus the authors would like to keep the Froude number in the range of 0.8 and 1 for future studies.

Fig. 18

Average thrust coefficient versus Froude number (Fr); (φ = 40°, h ₁/c = 1.28, ω₀/2πf = 1, ψ = −90°, ε = 0.2, ω ²₀ c/g = 1.5, h ₀/c = 0.6)

Fig. 19

Propulsive efficiency versus Froude number (Fr); (φ = 40°, h ₁/c = 1.28, ω₀/2πf = 1, ψ = −90°, ε = 0.2, ω ²₀ c/g = 1.5, h ₀/c = 0.6)

6.5 Feathering parameter

The extended feathering parameter provides a measure of the relative magnitude of pitch and heave velocities with included vertical wave velocity (Eq. 26). Physically, the feathering parameter is denoted as the ratio of the foil slope to the slope of the path traveled by the pitching axis of the oscillating foil with respect to the space fixed incoming wave profile. In the computation the feathering parameter ε is varied from 0 to 1 while changing the pitching amplitude 0–36° accordingly. The same variation of fathering parameter could be achieved by varying the heave amplitude instead of pitching amplitude. But if we changed the heave amplitude instead of pitching amplitude to match the varying fathering parameter, the foil will operate in different influence of wave orbital velocity range. Because the wave effect (wave orbital velocity) decreases exponentially from the free surface and the most effective height exists in the range of free surface to 80 % of the wave length. Therefore we have kept the heave amplitude as a constant and varied the pitch amplitude to change the feathering parameter. The other parameters that kept constant are, Froude number 0.87, non-dimensional heave amplitude 0.6, wave phase angle −90°, phase difference of heave and pitch 40° and non-dimensional submergence depth 1.71.

Figures 20 and 21 show the variation of thrust coefficient and efficiency with the feathering parameter. Figure 20 shows that, for the thrust force to have a positive mean, ε should be generally less than 1 and the case of ε = 1 corresponds to the pitching angle equals to the gliding angle and minimum effective angle of attack is observed. When the ε is set to zero, the maximum effective angle of attack is obtained, and because of that maximum thrust coefficient is achieved. In Fig. 21, the efficiency initially increases with increasing feathering parameter and attains the maximum near the value of 0.4. Further increase of feathering parameter results in decrease of the efficiency from 0.6 to 0.1. So to obtain a higher efficiency and not sacrifice the thrust, the authors use the value of 0.2 for final investigation on wave energy gain as one of the realistic values.

Fig. 20

Average thrust coefficient versus extended feathering parameter (ε); (φ = 40°, h ₁/c = 1.71, ω₀/2πf = 1, ψ = −90°, Fr = 0.87, ω ²₀ c/g = 0.69, h ₀/c = 0.6)

Fig. 21

Propulsive efficiency versus extended feathering parameter (ε); (φ = 40°, h ₁/c = 1.71, ω₀/2πf = 1, ψ = −90°, Fr = 0.87, ω ²₀ c/g = 0.69, h ₀/c = 0.6)

6.6 Wave amplitude effect

By fixing the parameters determined from the above investigations, i.e., wave phase angle −90°, phase difference of heave and pitch 40°, Froude number 0.8, non-dimensional heave amplitude 0.7, extended feathering parameter 0.2 and non-dimensional submergence depth 1.71, we investigate the wave devouring capability of oscillating propulsor by changing the wave amplitude from 0.5 to 3 m. Simulation parameters are shown in the Table 5.

Table 5 Tabulated data for capability of devouring wave energy with respect to wave amplitude

Even though previous investigations were carried out with non-dimensional heave amplitude of 1.28, the present computations were done with non-dimensional submergence depth of 1.71. To capture the increment of wave amplitude, we had to increase the size of the non-deformed finer structured mesh around the free surface which leads to a decrease in the space between the foil and free surface mesh (mesh generation is described in Sect. 3). Therefore, to avoid the collision between the foil and free surface mesh, the submergence depth had to be increased up to 1.71. However, a series of computations were performed to check the effect of the new submergence depth of 1.71 on best oscillation parameters obtained by previous computations. Surprisingly, the new submergence did not affect the best values of motion parameters obtained previously as wave phase angle −90°, phase difference of heave and pitch 40°, Froude number 0.8, non-dimensional heave amplitude 0.7 and extended feathering parameter 0.2. But, as we predicted, the thrust and efficiencies were bit lower than the previous submergence at 1.28 cases.

On the other hand, to compare the wave amplitude effect on oscillation foil, a series of simulations were carried out without incoming waves to have a bottom line conditions for wave energy capturing.

Figures 22 and 23 show the thrust coefficient and propulsive efficiency variations with the wave amplitude. As the wave amplitude increases, increasing trend of both thrust coefficient and efficiency is observed in those figures since the wave height is proportional to the wave energy (Eq. 27). Figure 24 compares the propulsive efficiency between the presence and absence of incoming waves. For example, when the wave amplitude is 3 m, the efficiency increment is about 18 % compare with absence of incoming waves.

Fig. 22

Average thrust coefficient versus wave amplitude (a); (φ = 40°, h ₁/c = 1.71, ω₀/2πf = 1, ψ = −90°, Fr = 0.8, ω ²₀ c/g = 0.8, h ₀/c = 0.7, ε = 0.2)

Fig. 23

Propulsive efficiency versus wave amplitude (a); (φ = 40°, h ₁/c = 1.71, ω₀/2πf = 1, ψ = −90°, Fr = 0.8, ω ²₀ c/g = 0.8, h ₀/c = 0.7, ε = 0.2)

Fig. 24

Comparison of propulsive efficiencies with different wave amplitudes and without incoming wave as a function of average thrust coefficient of oscillating foil; (φ = 40°, h ₁/c = 1.71, ω₀/2πf = 1, ψ = −90°, Fr = 0.8, ω ²₀ c/g = 0.8, h ₀/c = 0.7, ε = 0.2)

The wave power input P _w, to the oscillating propulsor is defined by the linear theory

$$ P_{\text{w}} = \frac{1}{2}\rho ga^{2} (C_{\text{g}} + U) $$

(27)

where C _g is a group velocity of wave.

$$ C_{\text{g}} = \frac{1}{2}\sqrt {{\raise0.7ex\hbox{$g$} \!\mathord{\left/ {\vphantom {g k}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$k$}}} $$

(28)

Finally, the percentage of wave energy recovery is discussed by plotting the graphs of input power coefficient (Eq. 10) versus output power coefficient (Eq. 11) of the oscillating propulsor. To have the accurate calculation of wave recovery, the input power coefficient range was selected as 5–10 and the output power coefficient versus input power coefficient graph was plotted with different wave amplitudes as shown in Fig. 25. In these calculations, it was assumed that the increment of output power was entirely due to the wave recovery and the calculated data were plotted in the Table 6.

Fig. 25

Comparison of output power coefficients of different wave amplitudes and without incoming wave as a function of input power coefficient of oscillating foil; (φ = 40°, h ₁/c = 1.71, ω₀/2πf = 1, ψ = −90°, Fr = 0.8, ω ²₀ c/g = 0.8, h ₀/c = 0.7, ε = 0.2)

Table 6 Result of wave energy recovery

Recovered wave power P _r is calculated by,

$$ P_{\text{r}} = \left( {\underbrace {{C_{\text{po}} }}_{{{\text{with}}\ {\text{wave}}}} - \underbrace {{C_{\text{po}} }}_{{{\text{without}}\ {\text{wave}}}}} \right) \times \frac{1}{2}\rho U^{3} c $$

(29)

Figure 26 shows the wave energy recovery versus wave amplitude. It can be seen that wave energy recovering capability rapidly decreases with increasing wave amplitude. But in the range of 0.5 to about 1.5 m it can be seen that more than 50 % of wave energy can be recovered by present active type oscillating propulsor.

Fig. 26

Percentage of wave energy recovery by active type oscillation foil versus wave amplitude; (φ = 40°, h ₁/c = 1.71, ω₀/2πf = 1, ψ = −90°, Fr = 0.8, ω ²₀ c/g = 0.8, h ₀/c = 0.7, ε = 0.2)

7 Conclusions

The work presented is an effort towards a systematic understanding of the influence of various motion parameters on thrust generation from an active type oscillation foil in a wave field. The parameters that have been investigated are phase difference between wave and foil motion ψ, phase difference between heave and pitching motion φ, submergence depth of foil h ₁/c, non-dimensional frequency of oscillation ω ²₀ c/g, heave amplitude h ₀/c, non-dimensional wave encounter frequency ω₀/2πf, Froude number Fr and extended feathering parameter ε.

The result of computational verification and validation for an oscillation foil under a wave has been presented. An unstructured grid based Reynolds-averaged Navier–Stokes method was used. First, the effects of oscillating foil frequency and wave encounter frequency were investigated. When the hydrofoil oscillates at the wave encounter frequency, the two motions are correlated and give the peaks of both thrust and efficiency. It was also found that small variation in oscillation frequencies considerably affects the efficiency and thrust. The effects of phase angles between heave and pitch motion and between wave and foil motion were also studied. It was found that when the wave has a −90° phase difference with foil heave motion, the efficiency and thrust reached the maximum due to the high utilization of wave orbital velocity. When selecting the phase angle between heave and pitching motion a design trade-off was found between the efficiency and generated thrust. Then without forfeiting the efficiency or thrust, a value of 40° was found appropriate as the phase angle between heave and pitching motion. Finally, it was observed that increasing wave amplitude increases the efficiency of the propulsor and decreases the percentage of wave energy recovery. It can be seen that 18 % of efficiency increment can be achieved, when the ratio of wave amplitude to foil chord length is 3/7. And when the wave amplitude to foil chord length is less than 1/7, more than 70 % wave energy could be recovered as useful propulsion energy.

The overall results suggest that the present approach (active wave oscillation foil in wavy flow) has the possibility to recover the wave energy for marine propulsion. However, analyzing the interaction between an oscillating propulsor and hull, and developing the hull form suitable for oscillating propulsion could be considered as opportunities for further research.