1 Introduction

In recent years, a ship advancing in waves has become a popular flow case for the users and the developers of interface-capturing methods, e.g. [1–14]. In such a flow case, the interface-capturing methods are advantageous, because they enable modelling the effect of arbitrary free-surface behaviour. In practice, the development of both the interface-capturing methods and the computational resources has been required to run computations on a ship advancing in waves.

The previous publications cover several examples on the computational modelling of a ship advancing in waves. These studies have considered both global [1–9] and more local wave loads [2, 10–13]. As for the harmonic content of these wave loads, the focus has mainly been on the zeroth [3–6, 9] and on the first [2–6] harmonic wave loads, but some examples also on higher harmonic results exist: second and third harmonic wave loads in [11] and spectral analysis of wave loads in [5, 8].

In order to have confidence in computational predictions, they are compared with measured results. However, a computational solution depends on the selected discretisation resolution. Therefore, the behaviour of the numerical solution in this respect should be studied before validating the computations against measured results.

When analysing the solution behaviour as a function of the discretisation, the computations need to be repeated with several discretisation resolutions (usually three in minimum) in order to find out the dependence of solution on the selected resolutions. Previous numerical studies on a ship advancing in waves have been based on the results of three discretisation resolutions [2, 5, 6, 9–11]. Most of these studies have considered the solution behaviour by simply giving or comparing the three results [2, 9–11]. Such comparisons give an idea on the variation of the results within the selected discretisation range and may show sufficiently similar solution behaviour on the selected discretisations.

However, these kinds of qualitative comparisons do not give a quantitative estimate for the difference between the obtained solution and the exact solution of the continuous mathematical model. The difference between the obtained solution and the exact solution of the numerical method is called numerical error. In practice, the numerical error is taken into account as an uncertainty. Estimating this error is important when judging the capability of the method to predict flow behaviour. This is especially important when considering, if the selected models within a method are adequate for predicting certain flow behaviour.

In the case of a ship advancing in waves, little results have been published on the numerical uncertainty. In the studies [5, 6], quantitative uncertainty has been analysed for one very moderate wave condition L w /L pp = 1.5 and kA = 0.025 in the case of a surface combatant. This uncertainty estimation has been restricted to the zeroth harmonic global wave loads and that of the first harmonic results has been omitted due to oscillating results. The choice of the authors of [5, 6] not to give uncertainty estimates for oscillating results relates to the difficulty of treating non-monotonically converging results. The different uncertainty estimation approaches have different attitudes towards such results.

The present study considers the solution behaviour of first–third harmonic wave load distributions on a ship bow area as a function of the discretisation using three discretisation resolutions. The results are studied both by simple comparisons and by estimating the numerical uncertainties of the solution of the fine discretisation resolution. In this case, the encountered waves are steep kA = 0.24 and short in comparison to the ship length L w /L pp = 0.15. Almost similar flow conditions (kA = 0.24, L w /L pp = 0.16) have been applied for a less full bow form in [11] to estimate total forces on the bow area. The focus of this study is in the estimation of the quantitative uncertainty for first–third harmonic wave load distributions and in the encountered challenges of quantifying the uncertainty.

Little knowledge exists on similar computational cases. Both the flow conditions and the load parameters of interest are different from most of the previously published simulations on a ship advancing in waves. It is assumed that the different flow conditions and the interest in higher harmonic components require higher time resolution than in the case of the zeroth and first harmonic wave loads studied previously. Furthermore, the numerical behaviour of the distributions of the predicted wave loads as a function of discretisation resolution has been seldom presented. As regards different harmonic components, there are some indications that having converging results for even the first harmonic global wave loads in moderate conditions can be challenging, see [5, 6]. In the case of the second and third harmonic components, there is even less previous knowledge.

The analysis of the present results differs from the previous similar studies, because of the motivation on the selected wave conditions. This flow case is interesting because it can cause springing vibration. This fact affects the analysis of the numerical uncertainty of the wave loads. Firstly, the wave load is analysed as a longitudinal distribution in the ship bow area. Analysis of the distributions is important when studying springing, because the actual vibratory excitation results from both the longitudinal wave load distribution and the longitudinal distributions of the hull eigenmodes. Secondly, the present analysis of the wave load distribution covers the first–third harmonic components. The second harmonic wave load is the actual load that causes springing in the selected flow case, but the first and the third harmonic components are included to get a more general idea of the solution behaviour. Thirdly, we compare the behaviour of the first–third harmonic single frequency components with the behaviour of the respective components that include the effect of their surrounding frequency components. This is reasonable from the point of view of springing, because several frequencies around the critical frequency contribute to the vibratory excitation. This is reasonable also from the point of view of studying numerical uncertainty, because the wave energy may spread differently in the frequency domain with different discretisation resolutions. Fourthly, the local uncertainties of the load distributions are compared with the uncertainty of the respective global load. This is done to study whether the uncertainty level of a global quantity can represent the uncertainty level of a local quantity.

In this paper, the interface-capturing solution method applied is presented in Sect. 2. The computational case of the study is described in detail in Sect. 3. The approaches used in the analysis of the results are presented in Sect. 4. The results are presented in Sect. 5 and discussed in Sect. 6. Finally in Sect. 7 the conclusions are given.

2 Numerical method

The computations were performed with the commercial flow solver ISIS-CFD. The solver is an unstructured finite volume solver. It includes a volume-of-fluid-type interface-capturing method to simulate free-surface flows. The flow is treated as incompressible and without surface tension. The flow solution (velocity \( \vec{U} \), pressure p and volume fraction c distributions) is obtained for each time step by iterating the solution of the momentum equations, the pressure equation and the volume fraction concentration equation. The numerical method is published in [15] and some further and updated details on it are given in [16]. In the present study, the solver is used as an Euler-solver: in other words the viscosity of the fluid is ignored.

The volume fractions c i of fluids i (e.g. water and air) define the average density ρ in each control volume [15]

$$ \rho = \sum\limits_{i = 1}^{2} {c_{i} \rho_{i} } . $$
(1)

The sum of the volume fractions is always 1 in each control volume. They are solved from the volume fraction conservation equation [15]

$$ \frac{\partial }{\partial t}\int\limits_{V(t)} {c_{i} } \,{\text{d}}V + \int\limits_{S(t)} {c_{i} (\vec{U} - \vec{U}_{\text{d}} ) \cdot \vec{n}\,{\text{d}}S = 0} , $$
(2)

where V(t) denotes the control volume, S(t) its closed surface and \( \vec{U}_{\text{d}} \) the velocity of the surface of the control volume. As the solution contains only two fluids, it is sufficient to use only one volume fraction (the volume fraction of water) because the other volume fraction can be resolved from c 2 = 1 − c 1. In the following, the symbol c is used for the volume fraction of water. The location of the free-surface level is selected to coincide with the isosurface where the volume fraction has the value 0.5. It is not necessary to solve the location within the numerical method, but when necessary it can be resolved during the post-processing of the results.

The velocity \( \vec{U} \) is solved from the momentum conservation equations [15]

$$ \frac{\partial }{\partial t}\int\limits_{V(t)} {\rho \vec{U}\,{\text{d}}V} + \int\limits_{S(t)} {\rho \vec{U}(\vec{U} - \vec{U}_{\text{d}} ) \cdot \vec{n}\,{\text{d}}S} = - \int\limits_{S(t)} {p\vec{n}\,{\text{d}}S} + \int\limits_{V(t)} {\rho \vec{g}\,{\text{d}}V} , $$
(3)

where \( \vec{g} \) is the component of the gravity vector and \( \vec{n} \) the outwards-directed unit normal vector.

The pressure p is solved from the pressure equation, which is derived from the mass conservation equation. The simplified form of the mass conservation equation

$$ \int\limits_{S} {\vec{U} \cdot \vec{n}\,{\text{d}}S} = 0 $$
(4)

is used within the present flow solver, because the phases are considered incompressible with constant densities ρ i .

In the present study, a second order backward discretisation was chosen for the time derivatives. For the velocity and the volume fraction discretisations the second order GDS-scheme and the BICS-scheme [16] were respectively selected. In the numerical method, a special discretisation is used for the pressure to take into account the discontinuity of the density on the interface of the air and water [15].

3 Simulation case

The selected simulation case was chosen because of an interest in the second-order springing excitation. In practice this means that the encounter frequency of the ship and the waves was chosen such that the second harmonic wave load could excite the vertical two-node mode of the full-scale hull. The wave was chosen to be very steep, which should ensure significant higher harmonic excitation. As the main purpose of this paper is to study the behaviour of the numerical solution as a function of the discretisation resolution, the simulation was repeated three times with systematically refined discretisations to enable the uncertainty estimation.

3.1 Case conditions

The frames of the passenger ship are given in Fig. 1 and the model-scale ship main parameters in Table 1. The scale of the model is 1:49. The selected ship speed, 20 kn, is the normal service speed of a cruise ship. Table 1 also includes the wave information.

Fig. 1
figure 1

Ship frames between the ship fore perpendicular and the mid ship

Full size image
Table 1 Ship and wave particulars in the model scale
Full size table

3.2 Spatial domain

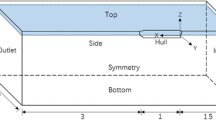
The boundaries of the selected spatial domain are illustrated in Fig. 2 and their locations with respect to the ship fore perpendicular (x FPP, y FPP, z FPP) are given in Table 2. Figure 2b also illustrates the boundaries of the area of the ship hull in which the wave load is analysed.

Fig. 2
figure 2

Coordinate axes, boundaries of the computational domain (x min, x max, y min, y max, z min, z max), boundaries of the refinement boxes b1 and b2 (x bi,1, x bi,2, y bi,1, y bi,2, z bi,1, z bi,2), a xy-level, b xz-level, boundaries of the observation area (x 1, x 2, z 1, z 2)

Full size image
Table 2 Locations of the grid boundaries
Full size table

The selected locations of the boundaries of the spatial domain are related to the applied boundary conditions. The encountered waves are generated with a numerical wave boundary condition on the inlet. The boundary condition is implemented by giving the velocity and the mass fraction distribution on the wave boundary as a function of time. For each cell, whose cell centre is below the instant free-surface level on the boundary, the mass fraction value is set to one (water) and the velocities are set according to the linear Airy wave theory. The distance between the inlet boundary and the ship bow was chosen to be small, because it minimises the simulation time required to transport the waves to the ship bow area. The computational domain includes one half of the hull since the case is symmetric. A symmetry boundary condition is applied on the symmetry wall. The upper and lower boundaries of the grid are set far from the water line to minimise the effect of those boundaries on the solution. The location of the lower boundary is at least 7 times the wave length from the free-surface level in order to prevent the grid bottom boundary affecting the wave properties (shallow water effect caused by grid bottom). For practical reasons, the locations of the upper and lower boundaries are not the same with the three grid densities. It was necessary to make this choice to ensure that the location of the initial free-surface level coincides with a cell face level with each grid. This is a limitation of the hexahedral grid generator, which was used. The boundary conditions applied are given in Table 3.

Table 3 Boundary conditions
Full size table

The computational domain was discretised with the hexahedral grid generator Hexpress. The three grids were generated systematically in a similar way. The refinement ratios were 1.25 for the coarse/medium grid ratio and 1.20 for the medium/fine grid ratio. Figure 3 shows some details of the three grids on the symmetry plane y = 0 and on a plane near the design water line depth.

Fig. 3
figure 3

Grids, a–c y = 0.0-plane, d–f z-directional plane near the design water line, from left to right coarse, medium and fine grid

Full size image

The grids include two refinement boxes: one to transport the waves in the computational domain (b1), and one to refine the domain near the bow in y-direction (b2), Fig. 2. The locations of the boundaries of the refinement boxes are given in Table 4. The length and the height of the cells were equal inside the two refinement boxes. They are given in Table 5. The entire grid was refined in z-direction around the free-surface level with the cell height similar to those in the refinement boxes. The total number of cells in each grid is given in Table 5.

Table 4 Locations of the boundaries of the refinement boxes
Full size table
Table 5 Cell sizes in the refinement boxes, time steps and total number of cells
Full size table

The discretised domain moved during the simulation with the ship velocity along the positive x-axis. The ship hull and the domain were kept fixed in the other degrees of freedom, because the wave-induced ship motions are insignificant in the waves that are very short in comparison to the ship length (about L w /L pp = 0.16).

3.3 Time domain

The length of the simulation in the time domain was chosen such that it ensures a sufficiently long analysis period in the regular waves with the selected ship speed.

The duration of the simulation (0.0–10.8 s) includes three parts: the acceleration ramp for the ship speed with a one half sinusoidal ramp profile (0.0–3.0 s), the time required for the propagation of the waves to the ship bow area (0.0–7.0 s) and the analysed time interval (7.0–10.8 s = 10*T e).

The time steps were chosen such that there are at least 80 time steps per third harmonic period, Table 5. They were refined systematically with the same ratios as the computational volumes.

Within each time step, the convergence of the results is controlled by two input-parameters: maximum number of iterations (10) and orders of magnitude (2) by which the residual is reduced.

3.4 Computational resources

The computations were performed on a high-performance HP CP4000 BL ProLiant supercluster called Murska (CSC—the Finnish IT Center for Science), [17]. Ten processors were used for the coarse-grid, 18 for the medium-grid and 32 for the fine-grid computations. The usage of the computational resources is given in Table 6.

Table 6 Average CPU time/one time step and number of time steps
Full size table

4 Analysing the computational results

The results presented in this paper are mainly derived from the pressures p and volume fractions c on the hull. The wall values of the pressure are the same as the ones in the closest computational volume, in other words the pressure gradient over a wall is set to zero, (Queutey P, personal communication, September 2008). In addition to the pressure and volume fraction values on the faces, the information on the locations of the face central points (x, y, z) is used. The data to be analysed consists of the values at an unstructured set of points without information on the locations of the cells with respect to each other and without information on the location of the corners of faces. For the calculation of the total pressure, the information on the surface area of each face on the wall is also utilised.

4.1 Wave excitation

4.1.1 Frame force

Vertical force is analysed on a set of ship frames. As unstructured grids are used, the grid points are not in practice located on vertical intersections that present frames. Instead, points N p,f within thin vertical sections are selected and used to calculate the instantaneous force on a frame.

The calculation of a vertical frame force history consists of two steps. First, the points N p,f representing the frame need to be organised. In general, the point closest to the ship centre line is chosen to be the point iy = 1, the second closest point is iy = 2 and so forth. The bulb area is an exception. There, the points closest to each other are adjacent. Second, the vertical frame force is calculated using the trapezoidal rule:

$$ F_{z,f} (t) = \frac{1}{2}\sum\limits_{iy = 2}^{{N_{\text{p,f}} }} {(p_{iy} (t) + p_{iy - 1} (t)) \cdot (y_{iy} - y_{iy - 1} )} . $$
(5)

4.1.2 Force on the total observation area

Vertical force on the total observation area of the hull is calculated as an average using the information on the pressure and the vertical surface area A z,i of each face

$$ F_{z,a} (t) = \sum\limits_{i = 1}^{{N_{\text{p,a}} }} {p_{i} (t) \cdot A_{z,i} } . $$
(6)

N p,a indicates the number of cell centres that are situated within the observation area.

4.2 Harmonic components

The force histories are subjected to discrete Fourier transformation DFT (e.g. [18]) to obtain the first–third harmonic amplitudes. The denotation F is used here for a force history from which its mean value F mean has been subtracted.

From the point of view of the signal analysis, the time histories given by the computations are data sequences F = F(n) of discrete times n = 1,2,…,N t . The length of the time history L t  = N t Δt defines the spacing Δω ([Δω] = rad/s) of the frequency domain by Δω = 2π/L t . The total number of points N ω in the frequency domain is limited by the Nyquist frequency π/Δt.

The Fourier series of a real-valued time history F can be written as

$$ F(n) = \sum\limits_{k = 1}^{{N_{\omega } }} {a_{k} \cos \left( {\frac{2\pi k}{{N_{t} }}n} \right)} + \sum\limits_{k = 1}^{{N_{\omega } }} {b_{k} \sin \left( {\frac{2\pi k}{{N_{t} }}n} \right)} $$
(7)

with

$$ a_{k} = \frac{2}{{N_{t} }}\sum\limits_{n = 1}^{{N_{t} }} {p(n)\cos \left( {\frac{2\pi k}{{N_{t} }}n} \right)} $$
(8)

and

$$ b_{k} = \frac{2}{{N_{t} }}\sum\limits_{n = 1}^{{N_{t} }} {p(n)\sin \left( {\frac{2\pi k}{{N_{t} }}n} \right)} . $$
(9)

The focus of the present Fourier analysis is on the components that correspond to the first, second and third harmonic encounter frequencies. As the length of the time histories is 10 times the encounter period, the respective indices in the frequency domain are 10, 20 and 30. Thus, the amplitudes ξsingle,i corresponding to the first, second and third harmonic encounter frequencies are calculated with

$$ \xi_{{{\text{single}},i}} = \sqrt {a_{10i}^{2} + b_{10i}^{2} } . $$
(10)

To study the effect of the discretisation resolution on the energy spreading in the frequency domain, the amplitudes are also calculated using a wider frequency span. The harmonic amplitudes ξspan,i , that include the energy in the frequency span of width ωe around the harmonic frequencies, are calculated with

$$ \xi_{{{\text{span}},i}} = \sqrt {\sum\limits_{k = 10i - 5}^{10i + 4} {(a_{k}^{2} + b_{k}^{2} )} } . $$
(11)

4.3 Uncertainty estimation

Generally speaking, the numerical uncertainty consists of contributions from the iteration number, the grid resolution, the time step, the round-off and the other parameters, e.g. [19]. In the present study, the presented uncertainties include the effect of the grid resolution and of the time step. These two uncertainty sources are studied simultaneously as the Courant number is fixed in the computations. The effect of round-off is assumed to be negligible in comparison to the other sources of uncertainty.

The following ratio R based on the numerical solution of the fine ϕ 1, medium ϕ 2 and coarse ϕ 3 discretisations is used to define the convergence conditions [19]:

$$ R = \frac{{\phi_{2} - \phi_{1} }}{{\phi_{3} - \phi_{2} }}. $$
(12)

The convergence conditions are:

  • Monotonic convergence: 0 < R < 1

  • Oscillatory convergence: −1 < R < 0

  • Divergence: R > 1 or R < −1.

The applied uncertainty estimation approach is presented in [20]. Its application in the present study differs from that in the study [20] by using only three discretisation resolutions. The approach utilises the order of accuracy q, the difference δRE,1 between the fine grid solution ϕ 1 and the estimated exact solution ϕ 0 and the data range ΔM to estimate the uncertainty.

Richardson extrapolation is applied to estimate the exact solution ϕ 0 assuming a single term estimate and dropping the higher order terms. As the grid refinement ratio is not constant in the present case, the order of accuracy q cannot be evaluated analytically. Thus, both the estimated exact solution and the order of accuracy are obtained using the least square fitting on

$$ \phi_{i} - \phi_{0} = \delta_{{{\text{RE}},i}} = \alpha h_{i}^{q} , $$
(13)

where α is a coefficient and h a parameter representing grid cell size.

The definition of the data range is

$$ \Updelta m = \max (|\phi_{j} - \phi_{i} |),\quad 1 \le i,j \le N_{\text{grids}} . $$
(14)

In the case of monotonic convergence, the evaluation of the uncertainty estimate U ϕ depends on the order of accuracy:

  • $$ {\text{For }}0. 9 5\le q \le 2.0 5,U_{\phi } = \, 1.25\delta_{{{\text{RE}},1}} . $$
    (15)
  • $$ {\text{For }}0 \le q \le 0. 9 5,U_{\phi } = { \min }(1.25\delta_{{{\text{RE}},1}} ,1.25\Updelta_{\text{M}} ). $$
    (16)
  • $$ {\text{For}}q \ge 2.0 5,U_{\phi } = { \max }(1.25\delta_{{{\text{RE}},1}}^{*} ,1.25\Updelta_{\text{M}} ). $$
    (17)

\( \delta_{{{\text{RE}},1}}^{*} \) is obtained with Richardson extrapolation using q equal to the theoretical value.

Otherwise (oscillatory convergence, monotonic or oscillatory divergence), the uncertainty is estimated with

$$ U_{\phi } = \, 3\Updelta_{\text{M}} . $$
(18)

4.4 Free-surface levels on the hull

This study includes instant and average free-surface levels on the hull at certain time instants denoted here as t obs. These free-surface levels are obtained by interpolation from the volume fraction distributions. For the average free-surface levels, the average c ave(t obs) of the ten volume fractions c n (t) on each unstructured point is calculated with

$$ c_{\text{ave}} (t_{\text{obs}} ) = \frac{1}{10}\sum\limits_{n = 1}^{10} {c(t_{\text{obs}} + (n - 1)T_{\text{e}} )} . $$
(19)

For the interpolation of the free-surface levels, the hull surface is constructed from the unstructured set of points using Triangle, [21, 22]. (The y-coordinates were ignored during the construction and their effect was added afterwards.) As a result, there is a surface that consists of Delaunay triangulations with corner points that are the central points of the original surface grid. The interpolation of the free-surface levels on the hull is done with the postprocessor tool Ensight.

5 Results

Section 5.1 presents the vertical force distributions given by the three discretisation resolutions, while their uncertainties are given in Sect. 5.2. In addition, Sect. 5.3 studies the source of the largest first harmonic uncertainties.

The observation area is limited between x 1 = 5.20 m = 0.78L pp (close to the ship fore shoulder) and x 2 = 6.63 m = 0.99 L pp (close to the ship fore perpendicular). The length of this observation area is 1.4 times the length of the encountered waves. To have the force distribution as a function of x, 36 equally spaced frames are selected within the observation area. One frame consists of the points, which are within ±0.67 times the cell length on the coarse grid from the specified x-coordinate. This ensures that there are enough points on each frame with each discretisation resolution.

5.1 Force amplitude distributions with the three discretisation resolutions

Figure 4 shows the distributions of the first–third harmonic vertical force amplitudes given by the three discretisation resolutions. These results behave relatively similarly, even if their agreement varies as a function of x. The differences between the resolutions become especially pronounced around x = 5.7 m in the case of the first and the second harmonics.

Fig. 4
figure 4

First–third harmonic vertical force amplitudes on the ship bow. The amplitudes (ξsingle) corresponding to the encounter frequency or its multiples are given with lines, while the amplitudes (ξspan) corresponding to the larger span around the encounter frequency or its multiples are given with dots. a–c amplitudes with the three discretisation resolutions, d–f differences between the resolutions

Full size image

The results in Fig. 4 include both the first–third harmonic amplitudes ξspan,i describing the energy within the frequency spans and the amplitudes ξsingle,i describing the energy of the single frequency components. The differences between the discretisation resolutions given by these two widths of frequency span do not deviate significantly, even if the effect of the frequency span becomes more distinct in some locations the higher the harmonic component is. The amplitude distributions show that the use of the wider frequency span slightly increases the amplitudes in a rather systematic manner for all the three discretisation resolutions.

5.2 Uncertainty of force

The harmonic vertical force amplitudes with the uncertainties for the fine resolution results are given in Fig. 5. The results corresponding to both amplitudes ξspan,i and ξsingle,i are given. The effect of the frequency span on the uncertainties seems to be generally minor, but it becomes more distinguishable the higher the order of the observed harmonic amplitude is. The two uncertainty distributions of the first harmonic amplitude hardly differ from each other. The local uncertainties of the second harmonic amplitude depend slightly on the frequency span. Some local uncertainties of the third harmonics amplitude depend significantly on the frequency span. With the increasing order of the harmonic component, the fact that the wider frequency span gives smaller uncertainties becomes pronounced.

Fig. 5
figure 5

First–third harmonic vertical force amplitudes on the ship bow from the fine discretisation resolution and the uncertainties. a–f ξspan- and ξsingle-distributions with the uncertainty bars. Monotonic and non-monotonic convergences are denoted. g–i Uncertainty distributions (distr.) with their averages (av.) and with the respective uncertainties of the pressure integrated over the observation area (int.). The usage of the lines and dots is described in the caption of Fig. 4

Full size image

The monotonic or non-monotonic convergence of each local result is denoted in Fig. 5. Most (ξspan,i 56% and ξsingle,i 53%) of the local first harmonic amplitudes converge monotonically. The non-converging results are mainly located near the ship fore perpendicular (x FPP = 6.69 m). Some (ξspan,i : 33% and ξsingle,i : 31%) of the second harmonic amplitudes converge monotonically. The converging results are located around x ≈ 5.7 m and in the vicinity of x ≈ 6.3 m. As for the third harmonic results, the results with the monotonic (ξspan,i 50%, ξsingle,i 47%) and the non-monotonic convergence are spread over the observation area.

The local values of the uncertainty distributions of the harmonic amplitudes vary significantly around their average values, Fig. 5. In the case of all three harmonics, the smallest values are located in the vicinity of x = 6.1–6.2 m. The largest values are located near the ship fore perpendicular and towards the rear end of the observation area.

The uncertainty distributions are compared with the respective uncertainties of the harmonic amplitudes of the vertical force integrated over the total observation area in Fig. 5. The first harmonic amplitude of the integrated quantity does not converge monotonically, whereas the second and third harmonic amplitudes do, except ξsingle,2 . The uncertainty of the first harmonic component of the integrated quantity (non-converging) is closest to the average of the uncertainty distribution, but the difference (calculated: (integrated quantity minus average of the distribution) divided by average of the distribution) is still significant (ξspan,i 36% and ξsingle,i 41%). The uncertainties of the second and the third harmonics of the integrated quantity (converging except ξsingle,2) are smaller than almost all the local uncertainties of the respective uncertainty distribution.

5.3 Impact of local flow detail on local uncertainties

The results in Sect. 5.2 show that the uncertainties of the first harmonic force components are especially large around x = 5.7 m. The results in Sect. 5.1 show that this is a consequence of the diminution of the first harmonic force amplitudes with discretisation refinements in this area. This section studies why the first harmonic uncertainties are especially large there.

The force histories at x = 5.7 m with the three discretisation resolutions are presented in Fig. 6. The influence of the diminution of the amplitudes as a function of refining resolution is the most distinct at the minimums and maximums of the time history, e.g. t = 10.41 s. Both an instant period and an average period are shown to demonstrate that their agreement is reasonable.

Fig. 6
figure 6

Vertical force history. a average period, b instant period

Full size image

To find out why these instant forces are different, piezometric pressure distributions at four time instants are shown in Fig. 7. The instants are indicated in the force histories in Fig. 6. The results show that the differences in the piezometric pressure distributions are the largest at t = 10.41 s above z = 0.1 m. The respective mass fraction distributions in Fig. 8j–l show that the higher pressure with the finer discretisations relates to the larger mass fraction of the fluid around the area of different piezometric pressures.

Fig. 7
figure 7

Piezometric pressure distribution on the frame x = 5.7 m. a t = 10.41 s, b t = 10.48 s, c t = 10.56 s, d t = 10.67 s

Full size image
Fig. 8
figure 8

Mass fraction on different cross-section at four time instants. From left to right coarse, medium and fine grids

Full size image

To understand why the mass fraction distributions are different at x = 5.7 m at t = 10.41 s, their propagation to this cross-section is followed according to the ship velocity. The locations of the observed cross-sections on the hull are given in Fig. 9. These results show that the locations follow the propagation of the water splash that originates near the ship fore perpendicular. By the time the water splash has reached the location x = 5.7 m (t 0 + 0.72t e), the water splash has collapsed, but according to Fig. 8 some mixture of water and air remains above the free-surface level. The propagation of the mass fraction distributions in Fig. 8 shows that the splash contains more water the finer the discretisation resolutions. During the propagation of the water splash, this water falls towards the free-surface level. At x = 5.7 m at t = 10.41 s = t 0 + 0.72t e, the area above z = 0.1 m has more mixed water and air the finer the discretisation resolution is.

Fig. 9
figure 9

Free-surface levels on hull

Full size image

6 Discussion

The aim of this study was to estimate the quantitative numerical uncertainty for the first–third harmonic wave load distributions. This section discusses the challenges that were encountered when estimating the uncertainties.

It was decided that the iterative error is ignored, because its definition would have required such significant computational resources. In a time accurate case, estimating iterative error is challenging, because, on one hand, it accumulates from the previous time steps during some time spans of the solution. On the other hand, the oscillatory behaviour of the solution can also diminish it during some other time spans of the solution. In practice, its estimation would have required repeating the computations with several iterative parameters. The comparison of the obtained results would have revealed the iterative error. The omission of the iterative error can make the uncertainty estimates too small.

The reliability of an uncertainty estimate is affected by the convergence behaviour of the solution. The current uncertainty estimation approaches focus mainly on the converging solutions while the estimates for non-converging results are less well justified. The number of non-converging results in this study and the previous observation in e.g. [5, 6] indicate that it is very difficult to avoid non-converging results in a case of a ship advancing in waves. This underlines the need for having uncertainty estimation approaches that would pay more attention to non-monotonically converging results.

It was also demonstrated that having the results of only three discretisation resolutions leaves some uncertainty on the obtained convergence conditions. The present monotonically converging results relates to the largest data ranges while some non-monotonically converging results are even very close to each other. Both in theory and in practice, it is possible that three results that are close to each other oscillate or even diverge, but a larger set of results could show that the general trend is converging. Similarly, three converging results can be a small part of a larger oscillating or diverging set of results. It was also observed that the present monotonically converging results vary significantly from the theoretical order of accuracy. Furthermore, when considering small changes between the results, it should be noted that the smaller the differences between the results of the discretisation resolutions, the larger the effect of small disturbance on the solution behaviour. In the present case, one disturbing factor is the simplistic implementation of the wave boundary condition. Another is that the hexahedral grids may not be fully topologically identical despite the systematic grid refinement.

The above-mentioned issues indicate that the present results may not fully disclose the solution behaviour of this flow case. The only way of confirming the findings would be to repeat the computation with more discretisation resolutions. Then, the solution behaviour could be studied for a larger scale of resolutions and the convergence behaviour could be confirmed. The problem with this kind of option is that a lot of computational resources would be required in order to reveal for instant an oscillatory behaviour of the solution.

A further purpose for increasing the number of the computations would be to confirm the obtained uncertainty estimates. For this purpose, the computations that are used for the uncertainty estimation should be in or close to the asymptotic range due to the uncertainty estimation approach. As already mentioned, reaching the asymptotic range can be very challenging in the case of ship-wave interaction.

In this study, one practical challenge is the requirements for the computational resources, which limited the number of runs to three. In this case, the computational requirements are affected by both the spatial and the time discretisation resolutions. Both of these resolutions were systematically refined between the selected discretisations to keep the Courant number fixed. Often, the spatial discretisation—the number of grid points—is used as a measure for the accuracy level of the computation and for the demand of the computational resources. In the present case, the time discretisation is equally an important measure, because a very fine discretisation (245–368 time steps/encounter period) is used to ensure a meaningful analysis of the second and third harmonic wave loads. From the point of view of running computations, the high time resolution may be a more demanding requirement than the high spatial resolution. With a high spatial resolution, adding number of processors can make the computations faster, even if the increasing inter-processor communications with increasing number of processors limits this benefit. In the case of a high time resolution, it is not possible to accelerate the time stepping by an approach like using multi-processors.

The complexity of the studied flow case, on its part, makes the understanding of the variation of the obtained uncertainty levels challenging. The present results demonstrate that the resolution dependency of an apparently small flow detail can affect significantly local uncertainty levels. In this respect, the amount of the falling mixture of air and water from a water splash was a critical factor that made the first harmonic uncertainties locally significantly larger than elsewhere.

7 Conclusions

The quantitative uncertainty was estimated for ship forward speed diffraction problem in short and steep waves. The present flow case is characterised by a strong deformation of the encountered waves on the hull and by rapidly varying longitudinal excitation distribution on the ship bow area.

The presented results show that the uncertainty levels of the force amplitudes vary significantly along the hull. It was also noticed that the energy around the first and the second harmonic components was quite strictly focused on the main components with all the three discretisations. Thus, the use of a larger frequency span did not have a significant effect on the estimated uncertainties. The local uncertainties are poorly presented by the uncertainties of the global quantities. Firstly, in the case of all the observed harmonic components, any constant would represent the local uncertainties poorly because of the large variation. Secondly, in the case of the second and the third harmonic components, the uncertainties of the global quantities are much smaller than most of the local uncertainties.

It was noticed that estimating quantitative uncertainty is challenging in the present case. From the point of view of the current uncertainty estimation approaches, having several non-monotonically converging results left some uncertainty on the obtained uncertainties. The straightforward solution to this would be to repeat the computations with more discretisation resolutions.

From the point of view of practical application of the present results, their usability can be judged on the basis of the obtained uncertainty levels. In this respect, the conclusions are different for the foremost half and the rearmost half of the observation area. In the foremost half, the uncertainty levels of the first and the second harmonic results are low enough to assess the magnitudes and the ratios of the first and the second force amplitudes. As a practical example, the uncertainties in this area are low enough in order to validate the results against measurements and to take the conclusion whether the selected modelling approach is reasonable for this flow case. In the second half of the observation area, the uncertainties are larger. Even if they are low enough to determine the order of magnitude of the load, which may be sufficient in some cases, decreasing the uncertainty in this area is relevant. Then, the most straightforward task would be to continue refining systematically the discretisation resolutions. However, this could lead to unreasonable computational efforts. Furthermore, it is reasonable to keep in mind that the present results show that the splash behaviour has an important effect on the first harmonic uncertainties. Therefore, we think that one reasonable option is to further study the effect of the spatial discretisation on the splash behaviour. In this connection, the present modelling assumptions, e.g. omitting fluid viscosity and surface tension, should be considered, too.