A practical two-step procedure for taking into account all available information (prior and current) about influence quantities in measurement uncertainty analysis

Abstract

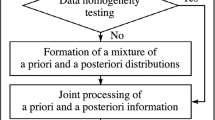
This paper considers the problem of computing the combined standard uncertainty of an indirect measurement, in which the measurand is related to multiple influence quantities through a measurement model. In practice, there may be prior information or current information, or both, about the influence quantities. We propose a practical two-step procedure for taking into account all available information (prior and current) about influence quantities in measurement uncertainty analysis. The first step is to combine prior and current information to form the merged information for each influence quantity based on the weighted average method or the law of combination of distributions. The second step deals with the propagation of the merged information to calculate the combined standard uncertainty using the law of propagation of uncertainty or the principle of propagation of distributions. The proposed two-step procedure is based entirely on frequentist statistics. A case study on the calibration of a test weight (mass calibration) is presented to demonstrate the effectiveness of the proposed two-step procedure and compare it with a subjective Bayesian approach.

Appendix: The law of combination of distributions (LCD)

Consider independent and continuous random variables X_j (j = 1, 2, 3,…N) with probability density function (PDF) ${p}_{j}\left({x}_{j}\right)$ having the same support on the real line, i.e. ${x}_{j}\in (-\infty , +\infty )$. According to the product rule for independent random variables, the joint distribution of X_j, i.e. the multivariate distribution of $\left({x}_{1}, {x}_{2}, {x}_{3}, \dots {x}_{N}\right)$, is written as

$$p\left( {x_{1} , x_{2} , x_{3} , \ldots x_{N} } \right) = \mathop \prod \limits_{j = 1}^{N} p_{j} \left( {x_{j} } \right)$$

(20)

We are interested in a single-variate distribution of X, the same outcome drawn from the multivariate distribution, i.e. ${x=x}_{1}= {x}_{2}{= {x}_{3}\dots =x}_{N}$. Let ${p}_{{\text{c}}}\left(x\right)$ denote the PDF of X. ${p}_{{\text{c}}}\left(x\right)$ can be written as [11]

$$p_{c} \left( x \right) = \frac{{\mathop \prod \nolimits_{j = 1}^{N} p_{j} \left( x \right)}}{{\int {\mathop \prod \nolimits_{j = 1}^{N} p_{j} \left( x \right)dx} }}$$

(21)

where $\int \prod_{j=1}^{N}{p}_{j}\left(x\right)dx$ is the scale factor that ensures the integration of ${p}_{{\text{c}}}\left(x\right)$ to be one.

A similar formula to Eq. (21) was given in [21] (p.230) without the scaling factor. Equation (21) is referred to as the law of combination of distributions (LCD). A demonstartion of the LCD can be found in [11]. The LCD provides a mechanism to combine information (represented by PDFs) from multiple sources.