Introduction

Few topics have generated so many papers, given rise to so many heated discussions, and caused so many disputes about chemical measurement results as “statistics”! — De Bièvre [1]

It may or it may not be just a coincidence that three preeminent statisticians of the twentieth century—in chronological order of their births, John Mandel (1914–2007) [2], John Tukey (1915–2000) [3], and George Box (1919–2013) [4]—started their careers as chemists.

The lessons they taught are strikingly consistent with the remarks that Paul De Bièvre (1933–2016) offered in the Editorial that includes the statement quoted above. None of Paul’s provocative questions would have startled any of those three masters of the statistical arts, even if Paul believed that “these questions will draw fire from classical, non-chemical statisticians” [1]

The assumption most commonly made about observations of the same quantity is that they are a sample from a Gaussian distribution. Both Tukey and De Bièvre have stated emphatically, time and again, that such assumption is very often not warranted, and both Tukey and Box have provided practical guidance for how to cope with this fact [5,6,7].

Paul insisted that “chemists will have to come to grips with an appropriate treatment of their data, and statisticians will have to study the reality of non-normally distributed measurement results in chemistry and develop adequate procedures to handle the data as they are” [1]. This imperative, “to handle the data as they are,” is a directive for the ages, and for all who aim to make a difference with their statistical analyses of empirical data.

For example, the values of the mass fraction of copper in a copper standard solution, measured by the nineteen participants in CCQM-K143 [8], are rather inconsistent with the Gaussian model, as judged by the Anderson–Darling test [9], even though all the participants measured aliquots of a sufficiently homogeneous material, and the ways in which they measured them will have been representative of the state of the art. De Bièvre [1] offers a conjecture as to why: “when a number of measurement results are obtained from using different measurement procedures, don’t they belong to different populations anyway? (Likely answer: probably very much so.)”

In this memorial contribution, we address a general topic that was dear to Paul De Bièvre: evaluating the reliability of chemical measurements.

Interlaboratory comparisons

Interlaboratory comparisons are powerful tools to demonstrate the reliability of chemical measurements. Thus, in such studies competence can be demonstrated rather than just designated, as Paul and his colleagues have so aptly noted [10, 11].

The Mutual Recognition Arrangement of the Comité International des Poids et Mesures (CIPM) [12] is the framework through which National Metrology Institutes demonstrate the equivalence of their measurement standards and measurement capabilities. Key comparisons (KCs) support claims of calibration and measurement capabilities (CMCs) that the National Metrology Institutes make and that are published in the BIPM Key Comparison Database.

These comparisons provide a glimpse of the best available chemical measurements of their time. We often pool measurement results and expect a more adequate reference value from such an operation [13], and the same pooling of data is carried out in KCs, to derive a reference value from the measurement results obtained by the participants. This key comparison reference value (KCRV) is then used as a reliable measure against which other results are compared. The principal tasks in the reduction of results from a KC are: (i) to select the results that will be pooled to produce the KCRV; (ii) to choose and apply a statistical method to compute the KCRV; and (iii) to evaluate the differences of the participants’ reported results from the KCRV, also known as the degrees of equivalence.

The first task should be driven primarily by substantive technical considerations because its purpose is to distinguish the results that are reliable and were obtained in conformity with the KC’s protocol, from results that may be erroneous for some identifiable cause, or that were obtained by means that the participants later deem to be unacceptable.

Much too often purely statistical criteria are used to set measurement results aside just because they do not seem to belong with the bulk of the others. Such practice is unfortunate and logically unfounded because, in the absence of identifiable errors in sample preparation, or in the selection and application of the measurement procedure, or in the evaluation of measurement uncertainty, no measurement result (measured value and associated uncertainty) can confidently be declared to be worse than any other. Paul’s view on such approaches was that “measurement results should not be tortured until they confess” [14].

De Bièvre [1] reflects on such practices that give primacy to statistical considerations and asks these challenging questions:

How many “statistical” procedures have been developed to remove outliers from sets of (chemical) measurement results, whereas there are many well-documented cases where the outliers were later proven to be the (only) correct result? Or where the outlier removal procedures said to aim at arriving to a truly “accurate” measurement result were used to embellish the data set, or, worse, were used to force the set of results to obey “statistical laws”?

Indeed, the mutual agreement of a majority of results offers no assurance that the consensus value corresponding to such happy agreement is correct, especially when that majority employs similar measurement methods. As an example, in key comparison CCQM-K55.b [15] the KCRV for aldrin was determined by the four lowest measured values, out of a group of nineteen, because it became evident that the majority had overestimated the purity of aldrin by missing a hard-to-detect major impurity component!

Application of a conventional (Dixon) outlier detection procedure to the values measured in CCQM-K122, of the mass fraction of the bromide anion in a aqueous solution of sodium chloride, did not reveal any outliers. However, such a test considers only the reported values. When the reported uncertainties are considered as well, using the Cochran’s test, the measurement results listed in Table 1 were found to be mutually inconsistent, but this fact was not taken into account in K122. (Measurement results can be mutually inconsistent without any measured value appearing to be an outlier; it suffices that the measured values be more dispersed than their associated uncertainties suggest that they should be.) Furthermore, the Inorganic Analysis Working Group (IAWG) of the CCQM decided to use the median of the measured values as the KCRV [16] and calculate the uncertainty of the KCRV by ignoring the hard-earned uncertainties reported by the participants.

Table 1 Measurement results for the mass fraction of bromide in NaCl solution from CCQM-K122 key comparison [16]
Full size table

The median is among the most popular choices in summarizing the interlaboratory comparison results of CCQM key comparisons. But there are statistical models that can be used to reduce this and other datasets without ignoring the measurement uncertainties provided by the participants—which formally make up half of the reported data. The following statistical model is able to incorporate both the reported uncertainties and the fact that the measurement results are mutually inconsistent: the value of the mass fraction, \(w_{j}\), measured by participant j, is represented as:

$$\begin{aligned} w_{j} = \omega + \lambda _{j} + \varepsilon _{j} \quad (j=1,\dots ,11), \end{aligned}$$
(1)

where \(\omega\) is the true value of the mass fraction of bromide in the solution, the \(\lambda _{j}\) denote laboratory effects, and the \(\varepsilon _{j}\) represent measurement errors.

The desire to use the weighted median as the KCRV, and not the weighted mean, is another way of saying that the laboratory effects \(\lambda _{j}\) are regarded as a sample from a Laplace, and not a Gaussian probability distribution with mean 0 mg/kg and standard deviation \(\tau\), which is the so-called dark uncertainty [17]:

$$\begin{aligned} \lambda _{j} \sim \text {LAPLACE}\{0, \tau \} \quad (j=1,\dots ,11). \end{aligned}$$
(2)

And the measurement errors \(\varepsilon _{j}\) are modelled as outcomes of independent Gaussian random variables with mean 0 mg/kg and with standard deviations equal to the reported uncertainties, \(u(w_{j})\):

$$\begin{aligned} \varepsilon _{j} \sim \text {GAUSS}\{0, u(w_{j})\} \quad (j=1,\dots ,11). \end{aligned}$$
(3)

The NIST Consensus Builder [18, 19] fits this model to the measurement results using a Bayesian procedure and estimates \(\omega = 3.09\) mg/kg, with associated standard uncertainty \(u(\omega ) = 0.13\) mg/kg. Dark uncertainty, \(\tau\), was estimated as 0.49 mg/kg, which is five times larger than the median of the reported standard uncertainties.

This dark uncertainty can arise, for example, because of the different sample preparation methods employed by the laboratories or because they may be optimistic in their uncertainty evaluations, if for no other reason because they capture only the contribution from lack of repeatability and do not recognize contributions from other sources. Birge [20] was well aware of how prevalent uncertainty underestimation tends to be and proposed a method for correcting the deficiency using a multiplicative factor, which came to be known as the Birge ratio, to achieve both “internal” and “external” consistency of measurement results. Recent years have witnessed a steady adoption of statistical models that have the ability to listen to the data, detect, and propagate dark uncertainty [21, 22]. And this change—away from the simple median or arithmetic mean—has been facilitated by the widespread ability to build interactive web apps using R [23].

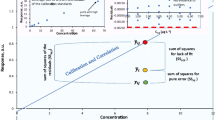
While the aforementioned consensus value is not much different from the simple median (3.15 mg/kg) and its associated uncertainty (0.12 mg/kg) that was adopted for CCQM-K122, as shown in Fig. 1, the consideration of dark uncertainty has a profound impact in determining whether the individual results \(w_{j}\) are consistent with the consensus value \(\omega\), arguably the entire purpose for conducting such intercomparisons. While the choice between Gaussian or Laplace laboratory effects models cannot always be settled from the data alone owing to the small number of participants, the same conclusion (that INTI and KRISS are both consistent with the consensus value) is reached if one adopts the more familiar Gaussian distribution for the laboratory effects.

Fig. 1
figure 1

Statistical modelling of interlaboratory comparisons can have a profound effect in determining whether a reported result is consistent with the consensus value (degree of equivalence). The participants of CCCQM-K122 agreed to employ a simple median for the KCRV [16], which led to the conclusion that the results provided by INTI and KRISS were inconsistent with the consensus value. The laboratory random effects model, however, not only fits the CCQM-K122 data better than the model implicit in the IAWG’s choices, but also leads to the conclusion that these results are consistent with the consensus value. The horizontal bars represent the 95 % coverage intervals

Full size image

De Bièvre [24] suggests that “whether chemists like it or not, most of the ‘error bars’ which accompanied results of chemical measurements in the past, were too small,” and notes that

[this] comes to the surface and becomes clearly visible in interlaboratory comparisons where the results of measurements of the same quantity in the same material are displayed with ‘error bars’ which represent repeatabilities only. All of a sudden, a number of results show up as being ‘bad’ because their ‘error bars’ do not overlap. In many cases they even do not cover the reference value.

The results shown in Table 1 illustrate these perceptive observations cogently. One can inspect the 55 pairwise differences formed from the 11 reported results to note that half of them do not agree with one other at the 95 % confidence level. Yet, all of these results become self-consistent if we allow for the possibility that the reported uncertainties can be underestimated.

The few KCs selected here to illustrate the problems surrounding the reliability of chemical measurements are by no means unique [25]. Our analysis of 197 sets of measured values from 68 KCs of inorganic and organic analyses shows a significant presence of dark uncertainty for the majority (80 %) of them. And even if we stick only to the results that were selected for consensus building, dark uncertainty remains significant in 60 % of the comparisons (Fig. 2). Despite this, it is not yet common for this source of uncertainty to be fully recognized, yet alone utilized in the subsequent work by laboratories as it was done for NRC BOTS-1 reference material [26].

Fig. 2
figure 2

During the last two decades, the Inorganic and Organic Analysis Working Groups of the CCQM organized some 70 key comparisons that relied on consensus building. Even with approx. 10 % data set aside by the participants themselves, the results were still mutually inconsistent in the majority (60 %) of the studies. The overdispersion measure (\(I^{2}\)) estimates the fraction of total variability in the reported results that cannot be explained by their uncertainties alone [27], with the colours turning red when the overdispersion is deemed significant by Cochran’s Q test [28]

Full size image

If we are to learn from the vast number of CCQM key comparisons conducted to date, we must listen to the data instead of resorting to the simple median or mean. And we should not torture the data either, as Paul used to say. As an example, the key comparison CCQM-K95 excluded nearly half of the reported data along with the hard-earned uncertainties before the consensus value was calculated [29]. Hence, we believe analytical chemists are yet to reckon with Paul’s directive to handle the data as they are.

Conclusions

Paul De Bièvre’s insatiable curiosity led him to pursue a wide range of topics in the chemical sciences, and in all these pursuits he made lasting contributions and articulated strong opinions that continue to challenge the scientific community.

We have provided illustrations of the ever widening interface between chemistry, statistics, and computation, in the context of data reductions for interlaboratory studies, key comparisons in particular. Concerning the role of statistical methods at the service of chemistry, Paul De Bièvre’s enlightened view was well aligned with the views of premier statisticians, emphasizing the need “to handle the data as they are,” not as mathematicians pursuing the theory of statistics might have wished them to be.

Paul’s writings will remain a guiding light that allows us to answer with optimism the Quo Vadis? It is the ever tighter embrace between the chemical sciences and the statistical arts that will lead to a better understanding of chemical measurements and, in turn, to better measurements.