A general model for interlaboratory precision accounts for statistics from proficiency testing in food analysis

Abstract

A meta-analysis of statistics from many proficiency tests has demonstrated the wide applicability of a simple model of reproducibility (interlaboratory) standard deviation. The function has already been proposed as a model for uncertainty in an analytical system, that is, a defined method, analyte and matrix type. The function is a two-parameter model with the concentration of the analyte as the single predictor variable. In this study it is applied to statistics derived from results of an international proficiency test covering many different analytes and matrix types in the food analysis sector. In nearly all instances tested the model accounted well for the observed statistics and could be used as a compact description of the performance of the analytical system.

Appendix

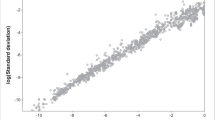
Equation 1 is non-linear in the parameters, which cannot therefore be estimated by simple regression. Several approaches are possible when sufficient data points are available, as in the present study. A straightforward visual interpretation of a graph of σ versus c is an essential preliminary step, and may even provide serviceable estimates. A limitation of visual inspection, however, is that it is difficult to take account of the weights attached to the points, which can differ substantially.

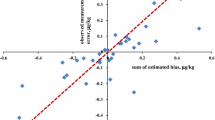
The weights used in regression-type procedures can be calculated as the reciprocals of the variances of the σ _R estimates. For a normally distributed variable x, $\text{var} (s_{x} ) = {\sigma ^{2}_{x} } \mathord{\left/ {\vphantom {{\sigma ^{2}_{x} } {2n}}} \right. \kern-\nulldelimiterspace} {2n}.$ Sample standard deviations, of course, deviate from normality (and robust estimates probably somewhat more so), although the deviation may not be serious when n > 50, as in many proficiency tests. An alternative and asymptotically unbiased (but more time-consuming) estimate can be obtained by using the bootstrap. In the present study, bootstrap estimates were usually found to be similar to those estimated from the normal assumption, but tended to be somewhat larger. In practice the two methods of weighting gave very similar outcomes.

A relatively simple regression approach would be to model the variance rather than the standard deviation, that is, to estimate α ² and β ² directly by regressing σ ² on c ². The present work used non-linear fitting. For that purpose the Taylor Series method up to the first derivative (that is, the Newton–Raphson method) worked well. The standard errors of $\hat{\alpha }$ and $\hat{\beta }$ were estimated by using the bootstrap, although the procedure here was not straightforward as the experimental design had to be conserved in the bootstrap samples, done by sampling the scaled residuals rather than the raw values.