²³Na and ²⁷Al NMR Study of Structure and Dynamics in Mordenite

Abstract

Temperature dependencies of ²⁷Al and ²³Na nuclear magnetic resonance spectra and spin–lattice relaxations in mordenite have been studied in static and magic angle spinning regimes. Our data show that the spin–lattice relaxations of the ²³Na and ²⁷Al nuclei are mainly governed by interaction of nuclear quadrupole moments with electric field gradients of the crystal, modulated by translational motion of water molecules in the mordenite channels. At temperatures below 200 K, the dipolar interaction of nuclear spins with paramagnetic impurities becomes an important relaxation mechanism of the ²³Na and ²⁷Al nuclei.

1 Introduction

The mineral mordenite, Na₈Al₈Si₄₀O₉₆·24H₂O, is a channel-type zeolite [1]. Its framework consists of AlO₄ and SiO₄ tetrahedra linked together via common oxygen atoms (Fig. 1). The mordenite structure exhibits two types of elliptical nanosized channels, both running along the c-axis [2, 3]. The wide channels have aperture of 0.65 × 0.70 nm and are formed by the assemblage of 12-membered rings, each having 12 oxygen atoms. The narrow channels have aperture of 0.26 × 0.57 nm and are built of eight-membered rings, each having eight oxygen atoms. The wide and narrow channels are linked by eight-membered ring channels (aperture 0.34 × 0.48 nm) running along the b-axis [2, 3]. Water molecules and Na⁺ ions are located in the above-mentioned channels [1–3] and possess certain mobility at ambient conditions. While water molecules can be desorbed from the channels, the sodium ions can be substituted by some other ions by means of ionic exchange [1].

Fig. 1

Framework structure of mordenite viewed along the 12-ring channels. The very small and elongated eight-ring channels can also be observed. The eight-ring channels running perpendicular to the large pores are not discernible in this picture

The dynamics of water molecules in mordenite have been studied by nuclear magnetic resonance (NMR) [4, 5]. Analysis of the temperature dependencies of the proton spin-relaxation times in the laboratory and rotating frames (T ₁ and T _1ρ) revealed diffusion of water molecules along the channels above T = 200 K. Temperature dependencies of the ¹ H dipolar spin-relaxation time T _1D showed that the dipolar relaxation in mordenite is responsive to slow 180° reorientations (flips) of water molecules around their second-order symmetry axes.

In the present paper, we report on the NMR study of quadrupolar ²⁷Al and ²³Na nuclei in mordenite. We studied temperature dependencies of the ²⁷Al and ²³Na NMR spectra in static and magic angle spinning (MAS) regimes, as well as the temperature dependencies of the spin–lattice relaxation times of the ²⁷Al and ²³Na nuclei.

2 Experiment

We studied a powder sample of natural mordenite from Nidym, Siberia, with chemical composition Na_0.9Ca_0.05AlSi₅O₁₂.3·1H₂O [4]. The ²⁷Al and ²³Na NMR spectra were measured using a Bruker Avance-400 NMR spectrometer at resonance frequencies of 104.26652 and 105.842 MHz, respectively, in the applied magnetic field of B ₀ = 9.4 T. The MAS rate used in the experiments was 14 kHz. Free induction decay (FID) signals were recorded after applying a single radio-frequency (RF) pulse and 100 signal acquisitions. The NMR spectra of ²³Na and ²⁷Al were obtained by Fourier transformation of the FID signals. Both ²⁷Al (natural abundance 100%, spin I = 5/2) and ²³Na (natural abundance 100%, spin I = 3/2) are quadrupolar nuclei, and their NMR spectra consist of the central transition (+1/2 ⟷ −1/2) and a number of satellites. For a selective excitation of the central transition, the optimal pulse duration is equal to that of a non-selective π/2 pulse divided by (I + 1/2) [6]. In our experiments, the RF pulse of 1.0 μs was used. The spin–lattice relaxation times T ₁ of ²³Na and ²⁷Al nuclei were measured by saturation recovery method. The relaxation processes for ²³Na and ²⁷Al nuclei in mordenite are found to be well described by single exponentials. The Dmfit program [7] was used to simulate the ²⁷Al spectra to extract the isotropic chemical shifts (δ _iso), quadrupolar coupling constants (QCC), and the asymmetry parameters (η _Q ).

3 Results and Discussion

The ²⁷Al NMR spectrum of the powder mordenite is represented by a single line with isotropic chemical shift δ _iso of ~61 ppm. This value is characteristic of ²⁷Al nuclei of AlO₄ groups in different zeolites, in which δ _iso varies in the range of 60 ÷ 63 ppm [1, 8–11]. The lineshape of the quadrupolar ²⁷Al nuclei in mordenite is determined by two contributions, namely by (1) the interaction of nuclear quadrupole moments with electric field gradients (EFG) on the ²⁷Al sites and (2) nuclear dipolar interactions. To determine the contributions of different interactions to the NMR shape of ²⁷Al in mordenite, we measured the ²⁷Al NMR spectra with and without ¹H decoupling and with and without sample spinning at different temperatures.

The ²⁷Al NMR spectra of mordenite obtained at T = 300 K and T = 390 K are shown in Fig. 2. Figure 2a shows the spectra obtained using the ¹H decoupling, which allows to eliminate the effect of the magnetic dipolar coupling between the resonance nuclei (in our case ²⁷Al) and ¹H nuclei. Herewith, the ²⁷Al NMR spectra reveal the same shape and width (Δν = 1.5 kHz) at T = 300 and 390 K (Fig. 2a). Since the dipolar interactions between ¹H and ²⁷Al nuclei are averaged out by the ¹H decoupling and thus only quadrupole interactions are the case, the aforementioned finding means that the temperature variation of electric field gradient (EFG) at the ²⁷Al sites in the region of 300–390 K is slight and actually is not observed in the experiment.

Fig. 2

a ²⁷Al NMR spectra with ¹H-decoupling at T = 300 and T = 390 K; b ²⁷Al MAS NMR spectra at Ω _rot = 14 kHz at T = 300 K and T = 370 K; c ²⁷Al NMR spectra without ¹H-decoupling at T = 300 K and T = 390 K; d ²⁷Al MAS NMR spectra at T = 370 K; Ω _rot = 14 kHz (top) and Ω _rot = 0 kHz (bottom)

The EFG at the ²⁷Al site in the mordenite structure is caused by electric charges of the ions of crystal lattice and by the electric dipolar moments of water molecules. If the latter contribution is considerable, its averaging must be observable in the temperature dependence of ²⁷Al NMR spectra. However, Fig. 2b, c does not show noticeable variations in the temperature range from 300 to 390 K. This means that the contribution of electric dipolar moments of water molecules to the static and MAS ²⁷Al NMR line shapes at 300–390 K is very small. The same conclusion follows from the comparison of the ²⁷Al NMR spectra obtained at T = 300 and 390 K measured with and without ¹H decoupling, which are shown in Fig. 2a, c. These spectra show the same lineshape and width, indicating that the dipolar interactions between of ²⁷Al and ¹H nuclei are very small in the range from 300 to 390 K. This finding is in agreement with the flipping and diffusion of water molecules along the mordenite channels obtained by ¹H NMR [5], which results in an effective averaging of the above-mentioned contribution at T > 300 K.

The rotation of sample at the magic angle leads to complete averaging of the dipolar interaction among ²⁷Al and other nuclei (¹H, ²³Na and, ²⁹Si) in mordenite. In this case, the shape of NMR spectra is determined only by the incompletely averaged by MAS second-order quadrupole effects contributing to the central transition [6].

The second moment of the powder MAS NMR spectrum is defined by equations [6]:

$$M_{2}^{\text{MAS}} = 0.25 \times \nu_{\text{iso}}^{2}$$

(1)

$$\nu_{\text{iso}} = - \frac{{\nu_{Q}^{2} }}{{30\nu_{L} }}\left[ {I\left( {I + 1} \right) - \frac{3}{4}} \right]\left( {1 + \frac{{\eta^{2} }}{3}} \right).$$

(2)

Here, the quadrupole frequency is

$$\nu_{Q} = \frac{{3e^{2} qQ}}{2I(2I - 1)h} \equiv \frac{3}{2I(2I - 1)}C_{\text{qcc}} ,$$

(3)

where ν _L is the Larmor frequency, q is the electric field gradient, η is the asymmetry parameter of EFG, Q is the nuclear quadrupole moment, and $C_{\text{qcc}} = \frac{2I(2I - 1)}{3}v_{Q} \equiv \frac{{e^{2} qQ}}{h}$ is the quadrupole coupling constant (QCC) [6].

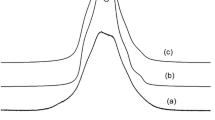
²⁷Al NMR spectra at T = 370 K shown in Fig. 2d reveal noticeable difference in static and MAS regimes, i.e., line width Δν = 1.53 and 0.74 kHz at Ω _rot = 0 and 14 kHz, respectively. These spectra yield $M_{2}^{\text{static}} \approx 2.4\,{\text{kHz}}^{2}$ and $M_{2}^{\text{MAS}} \approx 0.2\,{\text{kHz}}^{2}$, thus $\sqrt {\frac{{M_{2}^{\text{static}} }}{{M_{2}^{\text{MAS}} }}} \approx 3.5$, which is close to the ratio of 3.6 calculated in [6]. Using Eqs. (1–3), we obtain $\nu_{\text{iso}} \approx 0.9\,{\text{kHz}}$, $v_{Q} \sqrt {1 + \frac{{\eta^{2} }}{3}} \approx 0.6\,{\text{MHz}}$, and $C_{\text{qcc}} \sqrt {1 + \frac{{\eta^{2} }}{3}} \approx 4\,{\text{MHz}} .$

The absence of the fine structure in ²⁷Al NMR spectra (Fig. 3) does not allow us to precisely determine parameters C _qcc and η. Using the DMFit program [7], we simulated the shape of the powder ²⁷Al MAS NMR spectrum in mordenite and found the optimal values of C _qcc = 2 (0.2) MHz and η = 0.5 (0.1), as shown in Fig. 3.

Fig. 3

Experimental ²⁷Al MAS NMR spectrum of mordenite measured at T = 300 K and Ω _rot = 14 kHz (bottom) and the simulated one for C _qcc = 2 (0.2) MHz, η = 0.5 (0.1), δ _CSA  = 61.21 (0.07) ppm, and Δν _Lorentz = 460.5 (0.5) Hz

The literature data [1, 6, 8–11] show the QCC (²⁷Al) C _qcc in different zeolites are in the range of 2 ÷ 5 MHz. One can find that our experimental values are within this range. We note that Chae et al. [12] calculated the quadrupole parameters of Al in mordenite with various Si/Al rations using the point change model [13] with the 4 and 20 nearest neighbor oxygen atoms. The coordinates of the atoms surrounding Al sites were taken from the neutron powder diffraction data [14]. However, the obtained value C _qcc ≤ 1 MHz is different from the experimental one obtained in this paper.

The sodium cations in the mordenite structure are mainly located in eight-membered oxygen rings, occupying positions away from the channel center. Some of the cations are also placed in the 12-ring channels [1–3]. The magic angle spinning of the sample results in complete averaging of dipolar interaction of ²³Na spins with the spins of the other nuclei in mordenite, i.e., with ¹H, ²³Na, ²⁹Si, and ²⁷Al. In the case that all sodium nuclei are equivalent, the shape of the central NMR transition would be determined only by the incompletely averaged by MAS second-order quadrupole interaction term [8], which yields a characteristic asymmetric line. Such asymmetric line is observed in the experimental ²³Na MAS NMR spectrum of mordenite at T = 200 K (Fig. 4). In the case in question, however, such lineshape may also be caused by structurally inequivalent sodium ions located in the wide and narrow channels of mordenite. We note that similar asymmetric line was observed by Hunger et al. [15] in one-dimensional ²³Na MAS NMR spectrum of dehydrated mordenitie, while their two-dimensional triple-quantum (2D-3Q) ²³Na MAS NMR spectrum revealed two peaks, attributed to sodium cations located in the side pockets of eight-membered oxygen rings and those on positions in the 12-ring channels. As known, mordenite dehydration leads to some displacements of the cations making their structural positions in dehydrated and non-dehydrated mordenites somewhat different. Anyhow, taking into account an inequivalence of the sodium ion positions, it is worth suggesting that the ²³Na line asymmetry observed is caused by two contributions, namely, by the quadrupole interaction and a superposition of NMR signals coming from the structurally inequivalent sodium atoms with two different populations.

Fig. 4

Experimental ²³Na MAS NMR spectrum of mordenite at T = 200 K and MAS 14 kHz

The temperature dependencies of the ²⁷Al and ²³Na spin–lattice relaxation rates R ₁ in mordenite are shown in Fig. 5.

Fig. 5

Temperature dependencies of the spin–lattice relaxation rates of ²⁷Al (a) and ²³Na (b) nuclei in mordenite. Experimental data are shown by open circles, and simulated contributions of quadrupole interactions and paramagnetic impurities are shown by dashed and dotted lines, correspondingly

There are several contributions to the longitudinal relaxation of the ²³Na and ²⁷Al nuclei [16], namely, (1) interaction of the nuclear quadrupole moment with electric field gradient of the crystal modulated by lattice vibrations (spin–phonon interaction) and motion of cations and water molecules, (2) magnetic dipolar interaction of nuclear spins with paramagnetic impurities, and (3) magnetic dipolar interaction with magnetic moments of the framework ions (²⁷Al, ²⁹Si, ²³Na) and of ¹H nuclei of water molecules [16]. Herewith, cation and water motions are of a hopping-like nature, i.e., these atoms and molecules spent most of time in potential wells corresponding to the equilibrium positions, while the time of molecular jumps between these potential wells is much shorter.

The phonon-based relaxation mechanism is known to be too slow and leads to the relaxation times being by 4–5 orders of magnitude longer than those experimentally obtained for quadrupolar nuclei in zeolites [16]. The spin–lattice relaxation via paramagnetic impurities usually dominates at low temperatures [16] that are beyond the temperature range of our study. Our estimation of the contribution of ¹H–²⁷Al and ¹H–²³Na magnetic dipolar interactions to the ²⁷Al and ²³Na spin–lattice relaxations yield T _1min that is much longer than the experimental values of T _1min varying from 0.5 to 5 s (Fig. 5). Therefore, in the case in question, only quadrupolar mechanism needs to be considered.

For nuclei with I > 1/2, such as ²⁷Al (I = 5/2) and ²³Na (I = 3/2), the energy-level spacings in magnetic field are rendered unequal by quadrupole interaction, and the nuclear spin–lattice relaxation process is described by 2I relaxation times [15–20]. However, usually, the difference between these exponentials in such a multiexponential process can hardly be distinguished and, particularly for selective excitation of the central transition [6], the relaxation is well described by an exponential function [16, 21–25]. This is the case of our experimental ²⁷Al and ²³Na relaxation data in mordenite, which are well described by a single exponential.

Translational and orientational diffusion of water molecules modulates only a part of the EFG tensor governed by electric dipolar moments of water molecules, while the other part of the EFG tensor determined by the electric charges of the ions of lattice remains unchanged. The quadrupolar relaxation related to the former mechanism is described as [15–20]

$$R_{1Q} \equiv T_{1Q}^{ - 1} \cong \alpha \times \overline{{\left(\delta{{C}_{\text{Q}}} \right)}}^{2} \left[ {\frac{{\tau_{c} }}{{1 + \omega_{0}^{2} \tau_{c}^{2} }} + \frac{{4\tau_{c} }}{{1 + 4\omega_{0}^{2} \tau_{c}^{2} }}} \right],$$

(4)

where ω ₀ = 2πν _L is the Larmor frequency of the quadrupole nucleus, $\delta C_{Q} = \frac{{e^{2} \left( {\delta q} \right)Q}}{\hbar }$ describes the fluctuations of the quadrupole coupling constant [20] at the resonant nuclei sites, and $\tau_{c}$ is the correlation time of activated translational and reorientational jumps of electric dipoles of water molecules. Parameter α depends on the asymmetry parameter η and was estimated by us as α ≈ 0.13 ÷ 0.17. The symbol $\overline{\left( \cdots \right)}$ represents an ensemble averaging.

Equation (4) yields $R_{1Q} \sim \tau_{c}$ for $\omega_{0} \tau_{c} < < 1$ and $R_{1Q} \sim {1 \mathord{\left/ {\vphantom {1 {\tau_{c} }}} \right. \kern-0pt} {\tau_{c} }}$ for $\omega_{0} \tau_{c} > > 1$ with a maximum of $R_{1Q}$ (corresponding to the minimum of $T_{1Q}$) in the intermediate region. Since the correlation time τ _c caused by the molecular motion usually follows the Arrhenius-type temperature dependence, $\tau_{c} = \tau_{0} \exp \left( {{{E_{a} } \mathord{\left/ {\vphantom {{E_{a} } {\text{RT}}}} \right. \kern-0pt} {\text{RT}}}} \right)$, the asymptotic behavior of $\log R_{1Q} ({1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0pt} T})$ is represented by a straight line. Just such a behavior is obtained in our experiment in the temperature range from 200 to 390 K (Fig. 5). The deviation from the linear slowdown below T = 200 K is known to be caused by the interaction of nuclear spins with paramagnetic defects and impurities [18, 25, 26]. This contribution, mediated by the dipole–dipole interaction of nuclear spins with unpaired electron spins of paramagnetic defects, is given by expression [25–30]:

$$R_{1ne} \equiv T_{1ne}^{ - 1} = \gamma^{2} \left\langle {H_{L}^{2} } \right\rangle \frac{{\tau_{ce} }}{{1 + (\omega_{0} \times \tau_{ce} )}},$$

(5)

where $\left\langle {H_{L}^{2} } \right\rangle$ is determined as

$$\left\langle {H_{L}^{2} } \right\rangle = \frac{2}{5}\mu_{p}^{2} \frac{{N_{p} }}{N}\sum\limits_{i} {r_{ij}^{ - 6} } .$$

(6)

where $\mu_{p}^{2} = J(J + 1)\gamma_{J}^{2} \hbar^{2}$ is the squared magnetic moment of the paramagnetic defect, N _p is the density of the paramagnetic defects, N is the density of the resonant atoms, $\tau_{ce}$ is the correlation time that describes the reorientation of the electron spin caused by electron spin–lattice relaxation, and r _ij is the distance from the jth paramagnetic center to the ith resonant nucleus. Therefore, the experimental temperature dependences of the spin–lattice relaxation rates in the mordenite are described by expression:

$$R_{1} = T_{1}^{ - 1} = \alpha \times \overline{{\left( {{\delta{C}}_{\text{Q}} } \right)}}^{2} \times \left[ {\frac{{\tau_{c} }}{{1 + \left( {\omega_{0} \tau_{c} } \right)^{2} }} + \frac{{4\tau_{c} }}{{1 + \left( {2\omega_{0} \tau_{c} } \right)^{2} }}} \right] + \gamma^{2} \left\langle {H_{L}^{2} } \right\rangle \frac{{\tau_{ce} }}{{1 + \left( {\omega_{0} \tau_{ce} } \right)^{2} }}.$$

(7)

The experimental temperature dependencies of the spin–lattice relaxation rates and the results of their simulation by function of Eq. (7) are presented in Fig. 5. The obtained adjusting parameters are given in Tables 1 and 2. Figure 5 shows a satisfactory agreement between the experimental data and calculations.

Table 1 Calculated parameters that describe contribution $R_{1Q} \equiv T_{1Q}^{ - 1}$ to the spin–lattice relaxation of ²⁷Al and ²³Na nuclei in mordenite

Table 2 Calculated parameters that describe contribution $R_{1ne} = T_{ne}^{ - 1}$ to the spin–lattice relaxation of ²⁷Al and ²³Na nuclei in mordenite

The obtained activation energy of ~21 kJ/mol suggests that the modulation of quadrupole interactions by means of translational and reorientational jumps of electric dipoles of water molecules [4, 5] is responsible for the relaxation process of the ²⁷Al and ²³Na nuclei. From the data represented in Table 1, the averaged fluctuations of the quadrupole coupling constants are found to be $\sqrt {\overline{{\left(\delta {{C}_{\text{Q}} } \right)}}^{2} \approx 0.03\,{\text{MHz}}}$ for ²⁷Al nuclei and $\sqrt {\overline{{\left( \delta{{C}_{\text{Q}} } \right)}}^{2} \approx 0.16\,{\text{MHz}}}$ for ²³Na nuclei.

Unfortunately, the absence of reliable coordinates of hydrogen atoms and discrepancies in the published coordinates of the other atoms in the mordenite structure does not allow estimation of the contributions of various atoms to EFG. Our rough estimates show that the contributions of charges of oxygen atoms and electric dipole moments of water molecules to EFG of Al and Na atoms are of the same order. Although mordenite structure differs from the structure of natrolite, this finding is consistent with our estimations of the various contributions to the EFG of Al and Na atoms in natrolite [31].

4 Conclusion

Analysis of the temperature dependencies of ²⁷Al and ²³Na NMR spectra show that the shapes of the spectra are mainly determined by the second-order quadrupole interactions, while the dipole–dipole contribution coming from ¹H nuclei is very small. The spin–lattice relaxation of ²⁷Al and ²³Na is governed by the electric quadrupole interaction of nuclei with the crystal electric field gradients modulated by translational motion of H₂O molecules in the mordenite channels. The interaction of the ²⁷Al and ²³Na nuclear spins with paramagnetic impurities becomes to be significant relaxation mechanism at T < 200 K.