Nonlinear pricing, biased consumers, and regulatory policy

Abstract

Recent empirical analyses show consumers in electricity and water markets respond to average price rather than marginal price, calling for information provision policies that help correct the consumers’ bias. This paper characterizes the regulated tariff if the regulator is informed about the average-price response of consumers. I find the regulated tariff for biased consumers promotes equity gains by featuring quantity premia and providing access to utility consumption for a larger population than in the world of rational consumers. The world of biased consumers can also yield higher total welfare. These results bring up the opportunity costs of the information provision programs that help consumers correct the bias.

1 Introduction

Although standard economic theory assumes firms and consumers optimize with marginal prices, recent empirical analyses show it is not the case for electricity consumption (Ito 2014; Shaffer 2020) and water consumption (Ito 2013). They find that given the nonlinearity of the price schedules of electricity and water, consumers respond to average price rather than marginal price.¹ Their findings suggest the suboptimizing behavior would make nonlinear pricing be inefficient and generate welfare loss, compared to the case of rational consumers. However, the comparison assumed rational consumers and biased consumers face the same price schedule. This paper formally examines the welfare comparison between the world of rational consumers and the world of average-price-biased consumers. The key point is I take into account the adjustment in the nonlinear price schedules. What is the efficient price schedule if the regulator were informed about the biased responses of consumers and considered them when designing the price schedule? Would it be better to live in the biased world?

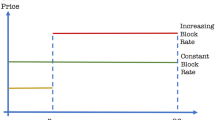
This paper characterizes the optimal regulated price schedule (tariff) that maximizes total surplus subject to a specified net revenue requirement for the utility and that consumers respond to average price rather than marginal price.² I find the optimal regulated tariff features quantity premia even under the consumers’ preferences that lead the tariff for rational consumers to have quantity discounts. This quantity premia feature suggests the regulated tariff for biased consumers supports the equity and conservation goals of increasing block tariffs that a regulator often uses to discourage excessive use of utilities (e.g. electricity and water) and protect low-income consumers from high prices, by charging higher price rates for high consumption.

I also find the regulated tariff in the world of biased consumers provides utility consumption for a larger population than in the world of rational consumers. The population that has access to the utility consumption in the world of biased consumers equals the first-best population in which the utility is priced at marginal cost, whereas consumption in the world of rational consumers is restricted to consumer types that are above the first-best marginal type.

Besides those features that favor the equity and distribution goal, the regulated tariff in the world of biased consumers may offer higher total welfare and consumers’ surplus than in the world of rational consumers. For example, with constant unit costs, quadratic utility preference, and uniformly distributed consumer type, I show the regulated tariffs in the two worlds provide the same total welfare. In the case of Pareto distribution of the consumer type, the total welfare in the world of biased consumers is higher.³ An intuitive reason is the population that can consume the utility is larger in the world of biased consumers than in the world of rational consumers.

This paper is related to a growing literature of behavioral economics and bounded rationality in industrial organization that examines how firms react to and in some cases exploit consumers’ suboptimal responses. These studies consider types of bias apart from average-price bias, such as loss aversion, present bias, overconfidence, or failure to choose the best price due to suboptimal search. Readers can refer to a comprehensive survey by DellaVigna (2009). For example, Courty and Hao (2000), Eliaz and Spiegler (2008), and Grubb (2009) study monopoly screening problems when consumers are overconfident. Heidhues and Kőszegi (2008) and Spiegler (2012) show loss aversion may create kinks in demand curves, which can lead to price rigidities. Carbajal and Ely (2016) and Hahn et al. (2018) characterize price discrimination when a monopolist faces consumers with loss aversion and state-contingent reference points.

My model is built on the literature of nonlinear pricing in Mussa and Rosen (1978) and Maskin and Riley (1984) and regulated tariff (Ramsey pricing) in Brown and Sibley (1986) and Wilson (1989). I depart from the literature by assuming consumers respond to average price instead of marginal price. The paper is closely related to three earlier articles.⁴ Sobel (1984) and Esponda and Pouzo (2016) aim to rationalize average-price bias. Sobel (1984) explains average-price response results from consumers thinking they face a linear price schedule with a constant unit rate. Esponda and Pouzo (2016) introduce a Berk–Nash equilibrium in which agents choose optimal strategies given beliefs and the beliefs put probability one on the misspecified set of subjective distributions over consequences that are closet to the true distribution; so, average-price response is a result of a Berk-Nash equilibrium.

Instead of rationalizing average-price bias, I take the bias as an exogenous feature of consumer decision making and examine the implications. Martimort and Stole (2020) take a similar approach and study monopoly pricing that maximizes net revenue of a monopolist and the implications on the firm’s profit.⁵ On the other hand, I focus on regulatory pricing that maximizes total social welfare subject to a specified net revenue requirement for the utility. This emphasis is important because the empirical evidences of average price responses have been documented in only electricity and water consumption; see Ito (2013, 2014) and Shaffer (2020).⁶ Besides similar results of the tariff shape (quantity premia vis à vis quantity discounts) as in the study of Martimort and Stole (2020), I find regulated tariff in the world of biased consumers offers gains in both equity and efficiency: it provides access to utility consumption for a larger population and may result in higher welfare.

The rest of the paper is organized as follows. Section 2 sets up the model and characterizes the optimal consumption allocation and regulated mark-ups that maximize total surplus subject to a specified net revenue requirement when consumers respond to marginal price (benchmark) and average price. Section 3.1 shows the results of equity gains: quantity premia, consumption population, and consumption distribution. Section 3.2 discusses the gain in welfare and concludes.

2 The model

I consider the standard setting as in the textbook model and the literature on nonlinear pricing (see Tirole (1988); Stole (2007)). The firm’s variable cost is a function of only its total output, C(q), and is increasing, convex, and continuously differentiable. Consumers are heterogeneous by one-dimensional continuous type $\theta$ that is a private information of each individual consumer. Others observe the type distribution according to a differentiable function $F(\theta )$, with density $f(\theta )$ and the support $[\theta _0,\theta _{1}]$. If total price payment a consumer pays for q consumption units is P(q), then the type-$\theta$ consumer’s payoff is $U(q,\theta ) - P(q)$. Let subscripts denote partial derivatives. Standard assumptions on the consumer preference include $U(q,\theta )$ is thrice continuously differentiable, strictly concave in q; $U_{\theta }$ is nonnegative and bounded; and $U_{q\theta }>0$. The last assumption is the familiar single-crossing property that implies higher-type consumers have higher marginal value of consumption. I also assume the outside option is zero: $U(0,\theta )=0$.

2.1 Regulated prices when consumers are rational

I now characterize regulated prices when consumers respond to marginal prices as usual for the benchmark. This is the standard model of Ramsey pricing (Brown and Sibley 1986; Wilson 1989). Specifically, the tariff is designed to maximize total (or consumers’) surplus subject to the constraint that the firm recovers a specified net revenue. The benchmark in this section characterizes the regulated tariff when consumers respond to marginal prices. The next Sect. 2.2, characterizes the regulated tariff when consumers respond to average prices. To distinguish the solutions between the two scenarios, I denote $X^{*}$ for variables in the case of rational consumers and ${\overline{X}}$ for variables in the case of biased consumers.

Formally, the regulated tariff $P^{*}(q)$ is designed to maximize total surplus subject to three conditions:

$$\begin{aligned} ~ \max _{P(\cdot )}&\int _{\theta _0}^{\theta _1} \left\{ U(Q^{*}(\theta ),\theta ) - P(Q^{*}(\theta )) + P(Q^{*}(\theta )) - C(Q^{*}(\theta )) \right\} dF(\theta ) \end{aligned}$$

(1)

$$\begin{aligned} \text {subject to: }&\int _{\theta _0}^{\theta _1} \left\{ P(Q^{*}(\theta )) - C(Q^{*}(\theta )) \right\} dF(\theta ) \ge c_{0} \text { (revenue stability)}, \end{aligned}$$

(2)

$$\begin{aligned}&Q^{*}(\theta ) = \arg \max _{q \ge 0} U(q, \theta ) - P(q) \text { (incentive compatibility)}, \end{aligned}$$

(3)

$$\begin{aligned}&U(Q^{*}(\theta ))- P(Q^{*}(\theta )) \ge 0 \text { (individual rationality)}. \end{aligned}$$

(4)

Constraint (2) refers to the revenue stability that ensures revenues received from utility sales are sufficient to offset fixed costs of operation, maintenance, and delivery system. In other contexts besides utilities, covering fixed costs is also necessary. So, this constraint is just the standard budget balance or break-even constraint in the second-best pricing problem.

The two constraints (3) and (4) follow the standard literature of nonlinear pricing to account for consumers’ behaviors; see Mussa and Rosen (1978) and Maskin and Riley (1984). The incentive compatibility constraint ensures that consumers are motivated to behave in a manner consistent with rationality: the consumer with a higher type consumes his true preferred quantity rather than pretending to be a low type. The other individual rationality constraint means consumers want to consume; that is, they are at least as well off by consuming as they would by not purchasing.

To solve for the regulated tariff, we first rewrite the ex-ante consumer surplus. Define type-$\theta$ consumer surplus $CS^{*}(\theta ) \equiv \max _{q \ge 0} ~ U(q, \theta ) - P(q)$. A result of the envelope theorem implies $\frac{d CS^{*}(\theta )}{d\theta } = U_{\theta }(Q^{*}(\theta ), \theta ) >0$. Hence, the ex-ante consumer surplus is earned from information rent:

$$\begin{aligned} ECS^{*} \equiv \int _{\theta _0}^{\theta _1} CS^{*}(\theta ) dF(\theta ) = \int _{\theta _0}^{\theta _1} \frac{1-F(\theta )}{f(\theta )} \cdot U_{\theta }(Q^{*}(\theta ), \theta ) d F(\theta ) + CS^{*}(\theta _0). \end{aligned}$$

(5)

Let $\lambda \ge 0$ be the multiplier associated with the revenue stability constraint. Substituting the new form of ex-ante consumer surplus in (5) for the one in the regulator’s welfare-maximizing problem and noticing that producer surplus is the difference between total surplus and consumer surplus, we find the optimal consumption $Q^{*}(\theta )$ satisfies

$$\begin{aligned} U_q(Q^{*}(\theta ),\theta ) - C'(Q^{*}(\theta ))&= \frac{\lambda ^{*}}{\lambda ^{*} + 1} \cdot \frac{1- F(\theta )}{f(\theta )} \cdot U_{q\theta }(Q^{*}(\theta ),\theta ). \end{aligned}$$

(6)

Then, the corresponding optimal tariff, $P^{*}(q)$, is uniquely defined from the marginal condition $P^{*'}(q) = U_q(q,\vartheta ^{*}(q))$ and the participation constraint $P(Q^{*}({\underline{\theta }}^{*})) = U(Q^{*}({\underline{\theta }}^{*}))$, where $\vartheta ^{*}(q)$ is the inverse function of the allocation $Q^{*}(\theta )= q$ and ${\underline{\theta }}^{*}$ is the marginal type at which $CS({\underline{\theta }}^{*})=0$.

To see the relation between the regulated tariff and the standard monopolist’s tariff, it is useful to rewrite the optimal consumption Eq. (6) to a mark-up expression. Specifically, we have

$$\begin{aligned} \frac{ P^{*'}(Q^{*}(\theta )) - C^{'}(Q^{*}(\theta ))}{P^{*'}(Q^{*}(\theta ))}&= \frac{\lambda ^{*}}{\lambda ^{*} + 1} \cdot \frac{1}{\epsilon (\theta )}, \end{aligned}$$

(7)

where $\epsilon$ is the price elasticity of demand of type-$\theta$ consumer, $\epsilon (\theta )= \frac{f(\theta )}{1- F(\theta )} \cdot \frac{U_{q}(Q^{*}(\theta ),\theta )}{U_{q\theta }(Q^{*}(\theta ),\theta )}$. This is the basic feature of Ramsey pricing; see Brown and Sibley (1986) and Wilson (1989). $\lambda ^{*}$ is the Lagrange multiplier on the firm’s revenue constraint, measuring the marginal cost (in terms of total surplus) of raising the revenue requirement by $1. The value of $\lambda ^{*}$ is associated with the required revenue $c_{0}$ in the revenue stability constraint, which is set at any non-negative value, depending on the required revenue set by the regulator. Because $\lambda ^{*}\ge 0$, the ratio $r^{*} \equiv \frac{\lambda ^{*}}{\lambda ^{*}+1}$ is a number between 0 and 1, which is so called Ramsey number in the literature or the regulatory degree in this paper. If $\lambda ^{*}=\infty$ or $r^{*}=1$, that is, all the weight is given to the firm’s profit and none to consumers’ surplus, then the regulated tariff will become the (monopolist’s) profit-maximizing tariff. If $\lambda ^{*}=0$ or $r^{*}=0$, or all the weight is given to consumers’ surplus and none to the firm’s profit, then the regulated tariff will be the first-best tariff in which the marginal rate is set at marginal cost.

2.2 Regulated prices when consumers have average-price bias

I now consider the regulated tariff when consumers respond to average prices rather than marginal prices. Similarly to Hô (2017) and Martimort and Stole (2020), the incentive compatibility constraint is replaced by ${\overline{Q}}(\theta ): U_q(q,\theta )=P(q)/q$.⁷ The individual rationality constraint is satisfied as long as the consumption is nonnegative. Hence, the regulated tariff maximizes total (or consumers’) surplus subject to the revenue stability constraint and the average-price response condition:

$$\begin{aligned}&\max _{P(q)} \int _{\theta _0}^{\theta _1} \left\{ U({\overline{Q}}(\theta ),\theta ) - C({\overline{Q}}(\theta ))\right\} dF(\theta ), \\ \text {subject to: }&~ \int _{\theta _0}^{\theta _1} \left\{ P({\overline{Q}}(\theta )) - C({\overline{Q}}(\theta ) ) \right\} dF(\theta ) \ge c_{0} \text { (revenue stability)},\\&~ U_q({\overline{Q}}(\theta ),\theta )=P({\overline{Q}}(\theta ))/{\overline{Q}}(\theta ) \text { (average price response)} . \end{aligned}$$

Let the Lagrangian multiplier associated with the revenue stability constraint be ${\overline{\lambda }}$. The optimal consumption ${\overline{Q}}(\theta )$ satisfies

$$\begin{aligned} U_{q}({\overline{Q}}(\theta ),\theta ) - C'({\overline{Q}}(\theta )) = \frac{{\overline{\lambda }}}{{\overline{\lambda }}+1} \cdot (-{\overline{Q}}(\theta )U_{qq}({\overline{Q}}(\theta ),\theta )). \end{aligned}$$

(8)

Then, the optimal tariff, ${\overline{P}}(q)$, is uniquely defined from the average-bias condition ${\overline{P}}(q) = q\cdot U_{q}(q,{\overline{\vartheta }}(q))$, where ${\overline{\vartheta }}(q)$ is inverse function of ${\overline{Q}}(\theta )$. Marginal type $\underline{{\overline{\theta }}}$ is determined by the break-even profit $P({\overline{Q}}(\underline{{\overline{\theta }}}))-C({\overline{Q}}(\underline{{\overline{\theta }}}))=0$. Assuming the fixed cost is recovered only through the revenue stability constraint, that is, $C(0)=0$, the marginal type is determined by the starting point of consumption: ${\overline{Q}}(\underline{{\overline{\theta }}})=0$.

Rewriting the optimal allocation, we obtain the following formulas for the mark-up ratio:

$$\begin{aligned} \frac{{\overline{P}}({\overline{Q}}(\theta ))/{\overline{Q}}(\theta )- C'({\overline{Q}}(\theta ))}{{\overline{P}}({\overline{Q}}(\theta ))/{\overline{Q}}(\theta )} = \frac{{\overline{\lambda }}}{{\overline{\lambda }}+1} \cdot \frac{1}{\eta (\theta )}, \end{aligned}$$

(9)

where $\eta (\theta ) \equiv \frac{U_{q}({\overline{Q}}(\theta ),\theta )}{-{\overline{Q}}(\theta ) U_{qq}({\overline{Q}}(\theta ),\theta )}$ is the price elasticity of demand.

Similarly to the case of rational consumers, the regulated tariff mark-up in the case of biased consumers is also the ratio of the Ramsey number (${\overline{r}}=\frac{{\overline{\lambda }}}{{\overline{\lambda }}+1}$) to the price elasticity. The regulated tariff mark-up formula covers three regulatory degrees: first-best (${\overline{r}}=0$), strict regulation ($0<{\overline{r}}<1$), and monopoly (${\overline{r}}=1$). However, the regulated tariff mark-up in the case of biased consumers is the difference between average price rate and marginal cost rather than between two marginal rates. The price elasticity in the case of biased consumers also has a different form from the case of rational consumers: the one in the biased-consumer case does not depend on the distribution of the consumer type. Because of the independence of the type distribution, the optimal regulated tariff for average-price consumers may have remarkably different structure from the one for rational consumers. Specifically, it typically features quantity premia and hence, promotes the gains in equity aspect, which is discussed in the following section.

3 Gains from average-price bias

3.1 Equity gains

Regulators often use increasing block tariffs to price electricity and water, because they believe that these tariffs promote conservation and equity (or distributional goal) by charging high marginal prices (and thus, average prices) for large consumption and lower rates for low-type consumers, who consume less and are presumed to be poorer on average; see Gaur (2007) and Borenstein (2012). However, such quantity premia are not justified in the world of rational consumers. As shown above and in Maskin and Riley (1984), the standard monopoly prices that maximize a firm’s profit and the regulated tariff when consumers respond to marginal price depend critically on the distribution of consumer type and typically offer quantity discounts. I now show that the regulated tariff when consumers respond to average price features quantity premia and hence, support the conservation and equity goals of the regulators.

Proposition 1

Assume (i) $U_{q\theta }+qU_{qq\theta }>0$, (ii) $U_{qq}+qU_{qqq}<0$, and (iii) $U_{qq\theta }\le 0$. Then ${\overline{Q}}'(\theta )>0$ and regulatory pricing for average-price biased consumers features quantity premia.

Proof

The main result is the shape of the regulated tariff, but showing and ensuring ${\overline{Q}}'(\theta )>0$ is also useful and important. The reason is ${\overline{Q}}'(\theta )$ is implementable if ${\overline{Q}}'(\theta )>0$, similarly to the case of monopoly pricing in Martimort and Stole (2020). Furthermore, if ${\overline{Q}}'(\theta )>0$ and the tariff has quantity premia, then the price rates (marginal and average rates) will also increase in consumer type.

To begin, I interpret the assumptions by considering the artificial setting of perfect third-degree price discrimination. This is the case in which a firm faces an unbiased consumer of known type $\theta$ but is forced to offer a linear price $P(q|\theta )=p(\theta )q$. The firm’s type-$\theta$ revenue is then $R(q,\theta )=qU_{q}(q,\theta )$. Assumption (i) means increasing marginal revenue in type, $R_{q\theta }>0$. Assumption (ii) means the artificial firm’s revenue is more concave than the consumer utility, $R_{qq}<U_{qq}<0$. Assumption (iii) implies a low-type consumer’s utility is more concave than a high-type consumer’s utility.

I now show that assumptions (i) and (ii) (or a weaker condition $R_{qq}<0$) lead to ${\overline{Q}}'(\theta )>0$. Applying the implicit function theorem for the relation (8), we get $Q'(\theta ) = \frac{-U_{q\theta } - {\overline{r}}qU_{qq}}{U_{qq}-C'' + {\overline{r}}(U_{qq}+qU_{qqq})}$. Using assumption (i) and note that $U_{qq}<0$ and $0\le {\overline{r}}\le 1$, we have $U_{q\theta }+{\overline{r}}qU_{qq}\ge U_{q\theta }+qU_{qq}>0$, and $U_{qq}+{\overline{r}}(U_{qq}+qU_{qqq})\le 2U_{qq}+qU_{qqq} = R_{qq}<0$. Thus, with convex cost, $Q'(\theta )>0$. Note that for monopoly pricing (${\overline{r}}$=1), we have $Q'(\theta ) = \frac{-U_{q\theta } - qU_{qq}}{2U_{qq} -C'' +qU_{qqq}}= \frac{-R_{q\theta }}{R_{qq}- C''}$. In this case, a sufficient condition for $Q'(\theta ) >0$ is $R_{q\theta }>0$ and $R_{qq}<0$ as stated in Martimort and Stole (2020).

To show the tariff features quantity premia, I rewrite the relation (8) in terms of the mark-up difference and using the implicit function theorem to get $(P(q)/q-C'(q))' = -{\overline{r}}[U_{qq}+qU_{qqq}+qU_{qq\theta }{\overline{\vartheta }}']$. This slope of the mark-up difference is positive, as a result of assumptions (ii), (iii), and that ${\overline{\vartheta }}'=1/{\overline{Q}}'>0$. $\square$

The result of Proposition 1 implies that under several utility preferences, the regulated tariff for biased consumers features quantity premia although the one for rational consumers features quantity discounts. The reason is the tariff for rational consumers depends on the distribution of consumer type, in addition to utility preferences. For example, with a quadratic utility preference and convex cost, the tariff for rational consumers will feature quantity discounts if the consumer type is uniformly distributed, whereas it will feature quantity premia if the type follows a Pareto distribution.⁸ On the other hand, the regulated tariff for biased consumers does not depend on the type distribution and thus, will feature quantity premia in the example of the quadratic utility preference, regardless of the type distribution.⁹ Section 3.2 presents the detailed price structure and discusses the welfare comparison.

In addition to the quantity premia feature, the regulated tariff for biased consumers allows more people to consume the utility than in the world of rational consumers. The population of consumers with positive consumption in the biased world equals the first-best population in which utility is priced at marginal cost, regardless of the regulatory degree. On the other hand, the consumption in the world of rational consumers is restricted to above the first-best marginal type.

Proposition 2

Let ${\underline{\theta }}^{*}$ and $\underline{{\overline{\theta }}}$ be the marginal types of consumer in the regulatory pricing schemes for rational consumers and average-price biased consumers, respectively. ${\underline{\theta }}^{\bullet }$ denotes the first-best marginal type. We then have: ${\underline{\theta }}^{\bullet }=\underline{{\overline{\theta }}} < {\underline{\theta }}^{*}$ for any regulatory degrees $r^{*}>0$ and ${\overline{r}}\ge 0$. As the regulator increases the degree of regulation to reduce monopoly power, ${\underline{\theta }}^{*}$ will lower and approach to $\underline{{\overline{\theta }}}$; that is, $\lim _{r^{*} \rightarrow 0} {\underline{\theta }}^{*} = \underline{{\overline{\theta }}}$.

Proof

See Appendix A. $\square$

3.2 Efficiency gain

I now compare the total welfare between the world of biased consumers and the world of rational consumers. Note that the regulated tariffs for biased consumers and rational consumers are associated with the Ramsey numbers ${\overline{r}}$ and $r^{*}$, respectively. These two numbers may be not equal for the same specified net revenue requirement. The reason is that $\lambda ^{*}$ and ${\overline{\lambda }}$, the marginal costs of raising the revenue requirement by $1, may be different because consumers’ surpluses in the case of rational consumers and the case of biased consumers may be different. Hence, when comparing welfare between two worlds, the two worlds need to be comparable by first ensuring that the two Ramsey numbers are associated with the same specified net revenue level $c_{0}$. With such two Ramsey numbers, the two total surpluses (or ultimately the consumers’ surpluses) will then be compared.

Proposition 3

With a quadratic utility preference, constant unit cost, and uniformly distributed type of consumers, regulated tariffs for rational consumers and for biased consumers yield the same total welfare.

Proof

Consider quadratic utility:

$$\begin{aligned} U(q,\theta )&=\theta q -\frac{\gamma }{2} q^2, ~ C(q) =cq,~\text { where } \gamma>0,~ c>0. \end{aligned}$$

Let $\theta$ be uniformly distributed on $[\theta _0,\theta _1]$. Assume $\theta _0<c<\theta _1$. In the standard model where consumers respond to marginal prices,

$$\begin{aligned} Q^{*}(\theta )= \arg \max _{q} u(q,\theta ) - cq - r^{*}(\theta _1 -\theta )q = \max \left\{ 0, \frac{\gamma ((r^{*}+1)\theta -r^{*}\theta _1 -c)}{\gamma } \right\} . \end{aligned}$$

Then the corresponding optimal marginal price and price schedule are

$$\begin{aligned} MP^{*}(q)&=- \frac{\gamma r^{*}}{r^{*}+1} q + \frac{r^{*}\theta _{1} +c}{r^{*}+1} , \\ P^{*}(q)&= -\frac{\gamma r^{*}}{2(r^{*}+1)} q^2 + \frac{r^{*}\theta _{1}+c}{r^{*}+1} q. \end{aligned}$$

The marginal type is ${\underline{\theta }}^{*}=\frac{r^{*}\theta _{1}+c}{r^{*}+1}>c ={\underline{\theta }}^{\bullet }$. Type-specific consumer surplus, ex-ante surplus, profit, and ex ante profit are

$$\begin{aligned} CS^{*}(\theta )&= \frac{((r^{*}+1)\theta -c - r^{*}\theta _{1})^2}{2\gamma (r^{*}+1)}, \\ ECS^{*}&= \int _{\theta ^{*}}^{\theta _{1}}CS^{*}(\theta )f(\theta ) d\theta = \frac{(\theta _1 - c)^{3}}{6\gamma (\theta _1 -\theta _0)(r^{*}+1)^2}, \\ \Pi ^{*}(\theta )&= \frac{[(r^{*}+1)\theta +c -(r^{*}+2)\theta _{1}][-(r^{*}+1)\theta +r^{*}\theta _{1}+c ]r^{*}}{2\gamma (r^{*}+1)} ,\\ E\Pi ^{*}&=\int _{\theta ^{*}}^{\theta _{1}}\Pi ^{*}(\theta ) f(\theta ) d\theta = \frac{r^{*}(\theta _{1}-c)^3}{3\gamma (\theta _{1}-\theta _{0})(r^{*}+1)^2}. \end{aligned}$$

Now consider the average-price-biased-consumer regime; the consumption allocation is

$$\begin{aligned} {\overline{Q}}(\theta ) = \arg \max _{q} qU_{q}(q,\theta ) - cq = \max \left\{ 0,\frac{\theta - c}{\gamma ({\overline{r}}+1)} \right\} . \end{aligned}$$

Then the corresponding optimal average price rate and price schedule are

$$\begin{aligned} {\overline{AP}}(q)&= \gamma {\overline{r}}q +c, \\ {\overline{P}}(q)&= \gamma {\overline{r}} q^2 +cq . \end{aligned}$$

The marginal type is $\underline{{\overline{\theta }}}=c$. Type-specific consumer surplus, ex-ante surplus, profit, and ex ante profit are

$$\begin{aligned} {\overline{CS}}(\theta )&= \frac{(\theta -c)^2}{2\gamma ({\overline{r}}+1)^2} ,\\ {\overline{ECS}}&= \int _{{\overline{\theta }}}^{\theta _{1}} {\overline{CS}}(\theta )f(\theta ) d\theta = \frac{(\theta _{1}-c)^3}{6\gamma (\theta _{1}-\theta _{0})({\overline{r}}+1)^2} , \\ {\overline{\Pi }}(\theta )&= \frac{{\overline{r}}(\theta -c)^2}{\gamma ({\overline{r}}+1)^2} , \\ \overline{E\Pi }&= \int _{{\overline{\theta }}}^{\theta _{1}} {\overline{\Pi }}(\theta )f(\theta ) d\theta = \frac{{\overline{r}} (\theta _{1}-c)^3}{3\gamma (\theta _{1}-\theta _{0})({\overline{r}}+1)^2}. \end{aligned}$$

Because the regulated tariffs in the two worlds of consumers’ behaviors maintain the same net revenue requirement, equal ex-ante profits $E\Pi ^{*}=\overline{E\Pi }$ in the uniform distribution of type implies $r^{*}={\overline{r}}$. With $r^{*}={\overline{r}}$, we then have ${\overline{ECS}}= ECS^{*}$ or total welfare in the two worlds are equal. $\square$

Although total surpluses are the same between the two worlds of consumers’ behaviors, the regulated tariff in the world of biased consumers offers equity gains as noted in Propositions 1 and 2. First, the regulated tariff for biased consumers ${\overline{P}}(q)$ features quantity premia, whereas the tariff for rational consumers $P^{*}(q)$ has quantity discounts. Second, the marginal type in the world of biased consumers is the first-best marginal type, strictly lower than the marginal type in the world of rational consumers.

Proposition 4

With a quadratic utility preference, constant unit cost, and Pareto distribution of consumer type, the regulated tariff for average-price biased consumers yields higher total welfare than the tariff for rational consumers.

Appendix B presents the proof. In this text, I summarize the regulated tariffs, consumption allocation, and provide an intuition how the world of biased consumers yields higher welfare.

Let the consumer type be distributed according to Pareto distribution with scale $s>0$ and shape $\alpha >0$. The probability density function and the cumulative distribution function are

$$\begin{aligned} f(x)= \frac{\alpha s^{\alpha }}{x^{\alpha +1}} \text { and } F(x) = 1 - \frac{s^{\alpha }}{x^{\alpha }}, \text { respectively.} \end{aligned}$$

The distribution has the support $(s,\infty )$ with mean $\frac{\alpha s}{\alpha - 1}$ (for $\alpha >1$), and median $s 2^{1/\alpha }$. The distribution is positively skewed (for $\alpha >3$), has a right long tail and a decreasing hazard rate, $\frac{f(\theta )}{1-F(\theta )} = \frac{\alpha }{\theta }$, in $\theta$. This distribution depicts a society with mostly low-type consumers living with a rare few of extremely high types. For example, if the type represents income, the distribution is well known for the “80–20 law": 80 percent of income in the society is owned by 20 percent of the population.

The regulated tariffs when consumers respond to marginal price and average price are, respectively,

$$\begin{aligned} P^{*}(q)&= \frac{\gamma r^{*}}{\alpha - r^{*}} \frac{q^2}{2} + \frac{\alpha c}{\alpha - r^{*}} q ,\\ {\overline{P}}(q)&= \gamma {\overline{r}} q^2 + cq. \end{aligned}$$

Both regulated tariffs feature quantity premia.

The optimal consumption when consumers respond to marginal price and average price are, respectively,

$$\begin{aligned} Q^{*}(\theta )&= \max \left\{ 0, \frac{(\alpha - r^{*})\theta -\alpha c}{\alpha \gamma } \right\} , \\ {\overline{Q}}(\theta )&= \max \left\{ 0, \frac{\theta -c}{\gamma ({\overline{r}}+1)} \right\} . \\ \end{aligned}$$

As noted in Proposition 2, the marginal type in the world of biased consumers is the first-best marginal type and less than the marginal type in the world of rational consumers: $\underline{{\overline{\theta }}} = c < \frac{\alpha c}{\alpha - r^{*}} ={\underline{\theta }}^{*}$. As the regulator reduces the monopoly power ($r^{*}\searrow 0$), the marginal type in the world of rational consumers will fall to $\underline{{\overline{\theta }}}=c$.

Such gain in the equity aspect provides an intuition why the world of average price bias earns higher welfare than the world of rational consumers. The reason is the regulated tariff for biased consumers provides access to utility consumption for a bigger population, thereby increasing the consumers’ surplus and total welfare of the biased world. Indeed, if the regulated tariff for biased consumers served the population of the rational world (population above the marginal type ${\underline{\theta }}^{*}$ rather than $\underline{{\overline{\theta }}}$), the consumers’ surplus and total welfare would be less than the values of the rational world:

$$\begin{aligned} \int _{{\underline{\theta }}^{*}}^{\infty } {\overline{CS}}(\theta )dF(\theta )&< ECS^{*} \text { but } {\overline{ECS}}= \int _{\underline{{\overline{\theta }}}}^{{\underline{\theta }}^{*}} {\overline{CS}}(\theta )dF(\theta ) + \int _{{\underline{\theta }}^{*}}^{\infty } {\overline{CS}}(\theta )dF(\theta ) > ECS^{*}. \end{aligned}$$

In summary, not only does the regulated tariff for biased consumers offer quantity premia and access to consumption for a larger population, but the tariff may also yield welfare as at least as in the world of rational consumers. The gain in welfare suggests correcting the average-price bias may be costly. Since empirical evidences of bias in consumers’ behaviors has been documented, a growing number of studies have searched for appropriate policies and suggested information provision may help consumers correctly perceive the true price rates. In a randomized controlled trial, Chetty and Saez (2013) find that information provision of nonlinear income tax schedules changes labor supply. Wolak (2011) and Jessoe and Rapson (2014) find information provision also changes the price elasticity of demand for electricity. Nevertheless, the finding in this paper suggests one should consider additional opportunity cost of pricing in the biased world (the welfare gain) when implementing information provision programs that help consumers respond to marginal price.

Appendices

Appendices: Omitted Proofs

A Proof of Proposition 2

Recall that the optimal allocation when consumers respond to marginal price and average price, respectively, must satisfy:

$$\begin{aligned} U_{q}(Q^{*}(\theta ), \theta ) - C'(Q^{*}(\theta )) = r^{*}\cdot \frac{1-F(\theta )}{f(\theta )}\cdot U_{q\theta }(Q^{*}(\theta ),\theta ) , \\ U_{q}({\overline{Q}}(\theta ),\theta ) - C'({\overline{Q}}(\theta )) = - {\overline{r}} \cdot {\overline{Q}}(\theta )\cdot U_{qq}({\overline{Q}}(\theta ), \theta ). \end{aligned}$$

The marginal types ${\underline{\theta }}^{*}$ and $\underline{{\overline{\theta }}}$ satisfy $Q^{*}({\underline{\theta }}^{*})=0$ and ${\overline{Q}}(\underline{{\overline{\theta }}})=0$, respectively.

For biased consumers, the optimal allocation condition implies that at the marginal type at which ${\overline{Q}}(\underline{{\overline{\theta }}})=0$, marginal utility equals marginal cost. Hence, the marginal type under the regulated tariff for biased consumers is the first-best marginal type level (denote ${\underline{\theta }}^{\bullet }$), regardless of the regulatory degree ${\overline{r}}$ and the type distribution.

For rational consumers, I now show $\underline{{\overline{\theta }}}<{\underline{\theta }}^{*}$ for any $r^{*}>0$. Consider the function $g(\theta ;q)$ of $\theta$ with parameter q:

$$\begin{aligned} g(\theta ;q) = U_{q}(q, \theta ) - C'(q) - r^{*}\cdot \frac{1-F(\theta )}{f(\theta )}\cdot U_{q\theta }(q,\theta ). \end{aligned}$$

We have $g(\underline{{\overline{\theta }}};0) = - \frac{1-F(\underline{{\overline{\theta }}})}{f(\underline{{\overline{\theta }}})}\cdot U_{q\theta }(0,\underline{{\overline{\theta }}})<0$ and $g(\theta _{1};0) = U_q(0,\theta _{1}) - C'(0) >0$. Hence, by the intermediate value theorem, the root of the function $g(\theta ;0)$ must lie between $\underline{{\overline{\theta }}}$ and $\theta _{1}$. That is, ${\underline{\theta }}^{*} \in (\underline{{\overline{\theta }}},\theta _{1})$.

If the regulator increases the weight on consumers’ surplus to reduce the monopoly power, the regulatory degree $r^{*}$ will approach toward 0. In that case, utility would be priced at which marginal utility equals marginal cost; so, the marginal type in the world of rational consumers would be the first-best marginal type.

B Proof of Proposition 4

Assume the model of quadratic utility, Pareto distribution of consumer type, and total cost $C(q)= cq$. If consumers respond to marginal prices, the consumption allocation and the price schedule are marginal type, price schedule, consumer surplus, and profits are

$$\begin{aligned} Q^{*}(\theta )&= \max \left\{ 0, \frac{(\alpha - r^{*})\theta -\alpha c}{\alpha \gamma } \right\} , \\ MP^{*} (q)&= \frac{\gamma r^{*} q + \alpha c}{\alpha - r^{*}} , \\ P^{*}(q)&= \frac{\gamma r^{*}}{\alpha - r^{*}} \frac{q^2}{2} + \frac{\alpha c}{\alpha - r^{*}} q , \\ {\underline{\theta }}^{*}&= \frac{\alpha c}{\alpha - r^{*}} > c , \\ CS^{*}(\theta )&= \frac{[(\alpha -r^{*})\theta -\alpha c]^2}{2\gamma \alpha (\alpha - r^{*})} , \\ ECS^{*}&= \int _{{\underline{\theta }}^{*}}^{\infty } CS^{*}(\theta ) f(\theta ) d\theta = \frac{s^\alpha c^{2-\alpha } \left( \frac{\alpha - r^{*}}{\alpha } \right) ^{\alpha - 1}}{\gamma (\alpha -1 ) (\alpha -2)} , \\ \Pi ^{*} (\theta )&= \frac{r^{*}[(\alpha - r^{*})\theta +\alpha c][(\alpha - r^{*})\theta -\alpha c]}{2\gamma \alpha ^2 (\alpha -r^{*})} , \\ E\Pi ^{*}&= \int _{{\underline{\theta }}^{*}}^{\infty } \Pi ^{*}(\theta ) f(\theta ) d\theta = \frac{r^{*}s^{\alpha }c^{2-\alpha } \left( \frac{\alpha - r^{*}}{\alpha }\right) ^{\alpha -1}}{\gamma \alpha (\alpha -2)}. \end{aligned}$$

When consumers respond to average prices, the results are

$$\begin{aligned} {\overline{Q}}(\theta )&= \frac{\theta -c}{\gamma ({\overline{r}}+1)}, \\ {\overline{AP}}(q)&= \gamma {\overline{r}} q + c , \\ {\overline{P}}(q)&= \gamma {\overline{r}} q^2 + cq , \\ \underline{{\overline{\theta }}}&= c , \\ {\overline{\Pi }} (\theta )&= \frac{{\overline{r}}(\theta - c)^2}{\gamma ({\overline{r}}+1)^2}, \\ \overline{E\Pi }&= \int _{\underline{{\overline{\theta }}}}^{\infty } {\overline{\Pi }}(\theta ) f(\theta ) d\theta = \frac{2{\overline{r}}s^{\alpha }c^{2-\alpha }}{\gamma (\alpha -1)(\alpha -2) ({\overline{r}}+1)^2} , \\ {\overline{CS}}(\theta )&= \frac{(\theta -c)^2}{2\gamma ({\overline{r}}+1)^2} , \\ {\overline{ECS}}&= \int _{\underline{{\overline{\theta }}}}^{\infty } {\overline{CS}}(\theta ) f(\theta ) d\theta = \frac{s^{\alpha }c^{2-\alpha }}{\gamma (\alpha -2)(\alpha -1) ({\overline{r}}+1)^2}. \end{aligned}$$

The difference in ex-ante profits between the average-price regime and the marginal-price regime is

$$\begin{aligned} \frac{s^{\alpha }}{\gamma (\alpha -2)c^{\alpha -2}}\left[ \frac{2{\overline{r}}}{(\alpha -1)({\overline{r}}+1)^2}-\frac{r^{*}}{\alpha }\left( 1-\frac{r^{*}}{\alpha }\right) ^{\alpha -1}\right] . \end{aligned}$$

In order for the two regulated tariffs in the two worlds of consumer behaviors to be comparable, the regulatory degrees ${\overline{r}}$ and $r^{*}$ must be such that the profit difference is zero:

$$\begin{aligned} \frac{2{\overline{r}}}{(\alpha -1)({\overline{r}}+1)^2}-\frac{r^{*}}{\alpha }\left( 1-\frac{r^{*}}{\alpha }\right) ^{\alpha -1} = 0. \end{aligned}$$

(10)

This condition implies that ${\overline{r}} < \frac{(\alpha -1)r^{*}}{2\alpha }$.

Now, consider the difference in total welfare. Because profits are equal under the same specified net revenue requirement, the difference in total welfare is the difference in consumers’ surplus. We have the consumers’ surplus in the world of biased consumers is higher than in the world of rational consumers, because

$$\begin{aligned} {\overline{ECS}} - ECS^{*}&= \frac{s^{\alpha }(c-1)^{2-\alpha }}{(\alpha -1)(\alpha -2)}\left( ({\overline{r}}+1)^{-2} - \left( 1-\frac{r^{*}}{\alpha }\right) ^{\alpha -1} \right) \\&= \frac{s^{\alpha }(c-1)^{2-\alpha }}{(\alpha -1)(\alpha -2)} ({\overline{r}}+1)^{-2} \left( 1 - 2 \cdot \frac{{\overline{r}}}{r^{*}}\cdot \frac{\alpha }{\alpha -1}\right) ~~ \text {(using~10)} \\&> 0 ~~ \left( \text {because } {\overline{r}} < \frac{(\alpha -1)r^{*}}{2\alpha } \right) . \end{aligned}$$

We have seen that the consumption population in the world of biased consumers consists of all consumer types above c, whereas the population in the world of rational consumers includes all types above $\frac{\alpha c}{\alpha - r^{*}} >c$. If we restrict the consumption population in the biased world to equal the population in the rational world, then the consumers’ surplus of this population under the tariff for biased world will be lower than the consumers’ surplus of the rational world. That is,

$$\begin{aligned} \int _{{\underline{\theta }}^{*}}^{\infty } {\overline{CS}}(\theta ) f(\theta ) d\theta&< \int _{{\underline{\theta }}^{*}}^{\infty } CS^{*}(\theta ) f(\theta ) d\theta = ECS^{*}, \\ \text {but } {\overline{ECS}} = \int _{\underline{{\overline{\theta }}}}^{{\underline{\theta }}^{*}} CS(\theta ) f(\theta )d\theta + \int _{{\underline{\theta }}^{*}}^{\infty } {\overline{CS}}(\theta ) f(\theta ) d\theta&> \int _{{\underline{\theta }}^{*}}^{\infty } CS^{*}(\theta ) f(\theta ) d\theta = ECS^{*}. \end{aligned}$$

Intuitively, by allowing more consumers to access utility consumption, the regulated tariff in the biased world yields higher welfare than in the rational world.