Abstract
This research explores the welfare implications of vertical licensing when the final goods are produced by multiple complementary inputs. We spotlight the importance of two-part tariff input terms when there is a buyer–seller relationship after vertical licensing, which has different welfare ramifications depending on the product differentiation. When the products are less differentiated, our result shows welfare improving licensing, but when the products are more differentiated, the wholesale price is set above the supplier’s marginal cost through licensing, leading to the problem of double marginalization and reducing welfare. This study offers various policy implications, which go up against conventional wisdom that welfare improving licensing may not be attainable by considering multiple complementary inputs.
Similar content being viewed by others
Notes
Who are Toyota’s Main suppliers? Investopedia (September 22, 2019) (https://www.investopedia.com/ask/answers/060115/who-are-toyotas-tyo-main-suppliers.asp).
Based on data from Toyota’s headquarters, the total value of purchased components is pegged at $300 millions a month.
For example, Boeing purchases jet engines from General Electric and avionics from Honeywell for its product portfolio.
The energy sector or power-generating sector is characterized by oligopolistic competition. As Tyagi (1999) demonstrates, the market for microprocessors, aircraft engines, and many other products are also characterized by oligopolistic competition, emphasizing that input suppliers have significant market power.
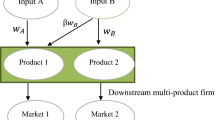
Our paper closely relates to the growing literature on complementary patents such as Shapiro (2001), Lerner and Tirole (2004) and Schmidt (2014). These papers analyze the effects of patent pools and complementary patents with n upstream firms’ technology licensing while we highlight the welfare implications of vertical licensing from a downstream firm when the final goods are produced by multiple complementary inputs. Moreover, the downstream firm in our model can produce a core input in-house while these papers assume the technologies from n upstream firms are essential.
We assume that supplier UB practices uniform input pricing, which naturally could be true, because input price discrimination is not allowed by antitrust law.
We assume that the licensee has the same marginal cost of production as the licensor for simplicity. The licensor has more (less) incentives to license its technology when the licensee is more (less) efficient than the licensor.
In this paper we focus on how the vertical trading contract between the licensor and licensee affects the incentive of vertical licensing. Therefore, we assume that the input price of a complementary input is determined by wholesale input pricing for simplification.
Substituting T into (3), the gross profits (from F) of firm S and firm 1 can be rewritten as \(\pi_{s}^{L} \left( {w_{s} } \right) + T = {\upbeta }\left[ {\pi_{1}^{L} \left( {w_{s} } \right) - \pi_{1}^{N} + \pi_{s}^{L} \left( {w_{s} } \right)} \right]\) and \(\pi_{1}^{L} \left( {w_{s} } \right) - T - \pi_{1}^{N} = \left( {1 - {\upbeta }} \right)\left[ {\pi_{1}^{L} \left( {w_{s} } \right) + \pi_{s}^{L} \left( {w_{s} } \right) - \pi_{1}^{N} } \right]\).
We have \(\left( {\frac{{\partial q_{1}^{L} }}{{\partial w_{B}^{L} }}\frac{{\partial w_{B}^{L} }}{{\partial w_{s} }} + \frac{{\partial q_{1}^{L} }}{{\partial w_{s} }}} \right) = \frac{{ - \left( {6 + r} \right)}}{{4\left( {4 - r^{2} } \right)}} < 0\) in (5).
When \(0 \le r < \overline{r}\), it shows that \(w_{s}^{*} > 0\) due to \(\left( {2 - 2r^{2} - r} \right) > 0\). When \(\overline{r} \le r \le 1\), \(w_{s}^{*} > 0\) if \(c > \frac{{2\left( {1 - c} \right)\left( {2 - r} \right)\left( {2 - 2r^{2} - r} \right)}}{{A_{1} }}\) due to \(\left( {2 - 2r^{2} - r} \right) < 0\). This condition holds if \(c\left( { - 31r^{2} - 4r + 68} \right) > 2\left( {2 - r} \right)\left( {2 - r^{2} - r} \right)\), which is always fulfilled due to \(\overline{r} \le r \le 1\). Therefore, \(w_{s}^{*}\) is positive.
In the case of homogeneous goods, firm S has to subsidize more to firm 1 then captures firm 1’s profit through T due to severe competition. Therefore, the net equilibrium profit of the licensor is not so significant when two products are homogeneous goods. In the case of independent goods, due to less competitive in the downstream market, the subsidy of firm S to firm 1 through T is small, leading a higher net equilibrium profit of the licensor.
When the two products are similar (dissimilar), the gross profit of firm 1 from T (that is, \(\pi_{1}^{L}\)) is significant (less) under licensing and results in \({\text{T}} > \left( < \right){ }0\). Please refer the details in Appendix 2.
Appendix 4 derives the equilibria in the case of no licensing and in the case of vertical licensing.
We have \(\left( {\frac{{\partial q_{1}^{L} }}{{\partial w_{B}^{L} }}\frac{{\partial w_{B}^{L} }}{{\partial w_{s} }} + \frac{{\partial q_{1}^{L} }}{{\partial w_{s} }}} \right) = \frac{{ - \left( {2n + rn + 4} \right)}}{{2\left( {4 - r^{2} } \right)\left( {1 + n} \right)}} < 0\) in (10).
We can confirm that \(\left( {5n + 4} \right) > \sqrt {n\left( {9n + 8} \right)}\) for any n.
References
Arya A, Mittendorf B (2006) Enhancing vertical efficiency through horizontal licensing. J Regul Econ 29:333–342
Arya A, Mittendorf B, Sappington D (2008a) The make-or-buy decision in the presence of a rival: strategic outsourcing to a common supplier. Manag Sci 54:1747–1758
Arya A, Mittendorf B, Sappington D (2008b) Outsourcing, vertical integration, and price vs. quantity competition. Int J Ind Organ 26:1–16
Arya A, Mittendorf B (2011) Supply chains and segment profitability: how input pricing creates a latent cross-segment subsidy. Account Rev 86:805–824
Bakaouka E, Milliou C (2018) Vertical licensing, input pricing, and entry. Int J Ind Organ 59:66–96
Chang RY, Hwang H, Peng CH (2013) Technology licensing, R&D and welfare. Econ Lett 118:396–399
Cournot AA (1938) Researches into the mathematical principles of the theory of wealth, English edition of Researches sur les principles mathematiques de la theorie des richesses. Kelley, New York
Fauli-Oller R, Sandonis J (2002) Welfare reducing licensing. Games Econom Behav 41:192–205
Jansen J (2003) Coexistence of strategic vertical separation and integration. Int J Ind Organ 21:699–716
Kao KF, Peng CH (2016) “Profit improving via strategic technology sharing. B.E. J Econ Anal Policy 16:1321–1336
Kishimoto S (2020) The welfare effect of bargaining power in the licensing of a cost-reducing technology. J Econ 129:173–193
Kitamura H, Matsushima N, Sato M (2018) Exclusive contracts with complementary Inputs. Int J Ind Organ 56:145–167
Kopel M, Loffler C, Pfeiffer T (2016) Sourcing strategies of a multi-input-multi-product firm. J Econ Behav Organ 127:30–45
Kopel M, Loffler C, Pfeiffer T (2017) Complementary monopolies and multi-product firms. Econ Lett 157:28–30
Kuo PS, Lin YS, Peng CH (2016) International technology transfer and welfare. Rev Dev Econ 20:214–227
Laussel D, Resende J (2020) Complementary monopolies with asymmetric information. Econ Theor 70:943–981
Lerner J, Tirole J (2004) Efficient patent pools. Am Econ Rev 94:691–711
Lim WS, Tan SJ (2010) Outsourcing suppliers as downstream competitors: biting the hand that feeds. Eur J Oper Res 203:360–369
Milliou C (2020) Vertical integration without intrafirm trade. Econ Lett 192:109180
Mukherjee A (2003) Licensing in a vertically separated industry. University of Nottingham Discussion Paper No. 03/01
Mukherjee A, Ray A (2007) Strategic outsourcing and R&D in a vertical structure. Manchester Sch 75:297–310
Mukherjee A, Tsai Y (2015) Does two-part tariff licensing agreement enhance both welfare and profit? J Econ 116:63–76
Pack H, Saggi K (2001) Vertical technology transfer via international outsourcing. J Dev Econ 65:389–415
Rey P, Salant D (2012) Abuse of dominance and licensing of intellectual property. Int J Ind Organ 30:518–527
Sappington D (2005) On the irrelevance of input prices for make-or-buy decisions. Am Econ Rev 95:1631–1638
Schmidt KM (2014) Complementary patents and market structure. J Econ Manag Strategy 23:68–88
Shy O, Stenbacka R (2003) Strategic outsourcing. J Econ Behav Organ 50:203–224
Shapiro C (2001) Setting compatibility standards: cooperation or collusion. In: Dreyfuss RC, Zimmerman DL, First H (eds) Expanding the boundaries of intellectual property: innovation policy for the knowledge society. Oxford University Press, Oxford, pp 81–101
Tyagi R (1999) On the effects of downstream entry. Manag Sci 45:59–73
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We are grateful to seminar participants at NTU Trade Workshop for their valuable comments, leading to substantial improvements of this paper. We also thank the Ministry of Science and Technology for funding this study (MOST 107-2410-H-431-001). The usual disclaimer applies.
Appendices
Appendix 1: Outside option for firm 1
In the absence of licensing, firm 1 produces the core input in-house. Each firm chooses its output in order to maximize its profits as \(\pi_{i}^{N} = \left( {1 - q_{i}^{N} - rq_{j}^{N} - c - w_{B}^{N} } \right)q_{i}^{N} , i = 1, 2, i \ne j\), where superscript “N” denotes the equilibrium with no licensing. Solving the resulting system of first-order conditions, we obtain the Cournot-Nash equilibrium quantities, \(q_{1}^{N} = q_{2}^{N} = \frac{{\left( {2 - r} \right) + r\left( {c + w_{B}^{N} } \right) - 2\left( {c + w_{B}^{N} } \right)}}{{4 - r^{2} }}\). In the following stage, supplier UB maximizes the profit, which is \(\pi_{B}^{N} \equiv \pi_{B}^{N} \left( {q_{1}^{N} \left( {w_{B}^{N} } \right),q_{2}^{N} \left( {w_{B}^{N} } \right),w_{B}^{N} } \right) = w_{B}^{N} \left( {q_{1}^{N} + q_{2}^{N} } \right)\), to determine the price of input B. The first-order condition of \(\pi_{B}^{N}\) leads to:
where \(\left( {\frac{{\partial \pi_{B}^{N} }}{{\partial q_{1}^{N} }}\frac{{\partial q_{1}^{N} }}{{\partial w_{B}^{N} }}} \right) = \left( {\frac{{\partial \pi_{B}^{N} }}{{\partial q_{2}^{N} }}\frac{{\partial q_{2}^{N} }}{{\partial w_{B}^{N} }}} \right) = w_{B}^{N} \left( {\frac{r - 2}{{4 - r^{2} }}} \right) < 0\), and \(\frac{{\partial \pi_{B}^{N} }}{{\partial w_{B}^{N} }} = \left( {q_{1}^{N} + q_{2}^{N} } \right) > 0\). Therefore, we have the equilibrium input price of B and the respective equilibrium profits as:
Appendix 2: Two-part tariff input pricing
In the second stage, firm S and firm 1 negotiate over \(\left( {w_{s} ,{\text{ T}}} \right)\) to determine T and \(w_{s}\). Substituting T into (3), it follows that \(w_{s}\) is chosen to maximize the following profits as \({\text{ U}} = \pi_{1}^{L} \left( {w_{s} } \right) + \pi_{s}^{L} \left( {w_{s} } \right) - \pi_{1}^{N}\). The first-order condition of (3) is:
Using the envelop theorem, we derive \(\frac{{\partial \pi_{1}^{L} }}{{\partial q_{1}^{L} }}\left( {\frac{{\partial q_{1}^{L} }}{{\partial w_{B}^{L} }}\frac{{\partial w_{B}^{L} }}{{\partial w_{s} }} + \frac{{\partial q_{1}^{L} }}{{\partial w_{s} }}} \right) = 0\), \(\frac{{\partial \pi_{1}^{L} }}{{\partial w_{s} }} = - q_{1}^{L} < 0\), and \(\frac{{\partial \pi_{s}^{L} }}{{\partial w_{s} }} = q_{1}^{L} > 0\). Therefore, we obtain the first-order condition as (4). Solving (4), we derive the equilibrium wholesale price as (5) and rewrite the wholesale price and equilibrium fixed fee as:
We can easily check that \(w_{s}^{*} > \left( \le \right)c\) if \(0 \le r < \overline{r} \equiv 0.780776\) (\(\overline{r} \le r \le 1\)).
where \(A_{4} = \left( {8r^{4} + 6r^{3} - 27r^{2} - 12r + 20} \right) > \left( \le \right)0\) if \(0 \le r < \overline{r}\) (\(\overline{r} \le r \le 1\)). Therefore, we have \(T^{*} > 0\) due to \(\left( {w_{s}^{*} - c} \right) < 0\) and \(\left[ { - 8\left( {r^{2} - 4} \right)^{2} + \beta A_{4} } \right] < 0\) as \(\overline{r} \le r \le 1\). When \(0 \le r < \overline{r}\), we find \(\left[ { - 8\left( {r^{2} - 4} \right)^{2} + \beta A_{4} } \right] > 0\) if \(\beta > \overline{\beta } \equiv \frac{{8\left( {r^{2} - 4} \right)^{2} }}{{A_{4} }}\), where \(\overline{\beta } > 1\) due to \(0 \le r \le 1\). Therefore, we have \(\left[ { - 8\left( {r^{2} - 4} \right)^{2} + \beta A_{4} } \right] < 0\) due to \(0 \le {\upbeta } \le 1\). Hence, we have \(T^{*} < 0\) due to \(\left( {w_{s}^{*} - c} \right) > 0\) and \(\left[ { - 8\left( {r^{2} - 4} \right)^{2} + \beta A_{4} } \right] < 0\). Moreover, the net equilibrium profit of firm S is:
Appendix 3: Welfare implications
The industry profits in the downstream market and in the upstream market for the in-house case are \((\pi_{1}^{N} + \pi_{2}^{N} ) = \frac{{\left( {2 - r} \right)^{2} \left( {1 - c} \right)^{2} }}{{2\left( {4 - r^{2} } \right)^{2} }}\) and \(\pi_{B}^{N} = \frac{{\left( {2 - r} \right)\left( {1 - c} \right)^{2} }}{{2\left( {4 - r^{2} } \right)}}\), respectively. The total industry profits for the in-house case are \({\Pi }^{N} = (\pi_{1}^{N} + \pi_{2}^{N} ) + \pi_{B}^{N} = \frac{{\left( {1 - c} \right)^{2} \left( {2 - r} \right)^{2} \left( {3 + r} \right)}}{{2\left( {4 - r^{2} } \right)^{2} }}\). The industry profits in the downstream market in the licensing case are \({\Pi }_{D}^{L} = (\pi_{1}^{L} - T^{*} + F) + \pi_{2}^{L} = \pi_{1}^{L} + \pi_{2}^{L} + \pi_{s}^{L} = \frac{{2\left( {1 - c} \right)^{2} \left( {2 - r} \right)\left( { - 3r^{2} - 5r + 14} \right)}}{{\left( {6 + r} \right)A_{1} }}\), and the profit of complementary input supplier B in the licensing case is \(\pi_{B}^{L} = \frac{{2\left( { - 3r^{2} - 5r + 14} \right)^{2} \left( {1 - c} \right)^{2} \left( {2 + r} \right)}}{{A_{1}^{2} }}\), in which the total industry profits in the licensing case are \({\Pi }^{L} \equiv {\Pi }_{D}^{L} + \pi_{B}^{L}\).
Comparing the difference in the profits of the downstream market between the licensing case and the in-house case, we have:
where \(A_{5} = \left( { - 6r^{3} - 21r^{2} + 12r + 44} \right) > 0\) due to \(0 \le r \le 1\). It shows that \({\Pi }_{D}^{L} > \left( \le \right)\left( {\pi_{1}^{N} + \pi_{2}^{N} } \right)\) as \(0 \le r < \overline{r}\) (\(\overline{r} \le r \le 1\)).
Comparing the difference in the profits of complementary input supplier B between the licensing case and the in-house case, we have:
where \(A_{6} = \left( {10r^{4} + 27r^{3} - 106r^{2} - 92r + 232} \right) > 0\) due to \(0 \le r \le 1\). From (18), it shows that \(\pi_{B}^{L} < \left( \ge \right) \pi_{B}^{N}\) if \(0 \le r < \overline{r}\) (\(\overline{r} \le r \le 1\)).
We already showed that \(CS^{L} < \left( \ge \right) CS^{N}\) and \({\Pi }^{L} < \left( \ge \right) {\Pi }^{N}\) if \(0 \le r < \overline{r}\) (\(\overline{r} \le r \le 1\)) in Sect. 4. Therefore, for the difference in social welfare between the licensing case and the in-house case, we find that \(SW^{L} < \left( \ge \right) SW^{N}\) if \(0 \le r < \overline{r}\) (\(\overline{r} \le r \le 1\)).
Appendix 4: Multiple varieties of complementary inputs
The profit functions of two firms with n varieties of complementary inputs when firm 1 produces the core input in-house are:
Using the first-order conditions from (19), we obtain the equilibrium outputs at the final stage. The profit function of complementary input supplier Bv, v = 1, 2, …, n, in the case of in-house is \(\pi_{Bv}^{N} = w_{Bv}^{N} \left( {q_{1}^{N} + q_{2}^{N} } \right)\). The equilibrium wholesale price of input supplier Bv is \(w_{Bv}^{N} = \frac{1 - c}{{\left( {1 + n} \right)}}\). The resulting equilibrium outputs and profits of downstream firms in the in-house case (that is, no licensing) are:
When the licensing agreement has been signed, the resulting equilibrium outputs are:
where \(w_{B1}^{L} = w_{B2}^{L} = \cdots = w_{Bn}^{L} = w_{B}^{L}\) due to symmetry.
Firm 1 and firm S maximize their joint profit. The first-order condition can thus be rewritten as:
From (22), we get the equilibrium wholesale price as (8) and rewrite it as:
It shows that \(w_{s}^{*} > \left( \le \right)c\) if \(0 \le r < \tilde{r} \equiv \frac{{ - n + \sqrt {n\left( {9n + 8} \right)} }}{{2\left( {1 + n} \right)}}\) (\(\tilde{r} \le r \le 1\)). Moreover, we have: \(\frac{{\partial \tilde{r}}}{\partial n} = \frac{{\left( {5n + 4} \right) - \sqrt {n\left( {9n + 8} \right)} }}{{2\left( {1 + n} \right)^{2} \sqrt {n\left( {9n + 8} \right)} }} > 0\).
The equilibrium wholesale price is \(w_{B}^{L} = \frac{{\left( {2 + r} \right)\left( {1 - c} \right)\left[ {n\left( {6 - 2r^{2} - r} \right) + \left( {8 - r^{2} - 4r} \right)} \right]}}{{\left[ {2\left( {2 - r^{2} } \right) + n\left( {6 - 2r^{2} - r} \right)} \right]\left( {rn + 4 + 2n} \right)}}\). The equilibrium outputs are \(q_{1}^{L} = \frac{{\left( {2 - r} \right)\left( {1 - c} \right)}}{{\left[ {2\left( {2 - r^{2} } \right) + n\left( {6 - 2r^{2} - r} \right)} \right]}}\) and \(q_{2}^{L} = \frac{{\left( {1 - c} \right)\left[ {n\left( {8 - 3r^{2} - 2r} \right) + 2\left( {4 - r^{2} - 2r} \right)} \right]}}{{\left[ {2\left( {2 - r^{2} } \right) + n\left( {6 - 2r^{2} - r} \right)} \right]\left( {rn + 4 + 2n} \right)}}\). We now have the equilibrium profits of firm 1 and firm S in the case of licensing.
The net equilibrium profit of firm 1 is:
Using (12), we can derive \(\pi_{1}^{LN} - \pi_{1}^{N} > 0\).
Appendix 5: A wholesale price contract
In the second stage, firm S and firm 1 negotiate over \(w_{s}\) instead of over \(\left( {w_{s} ,{\text{ T}}} \right)\). Under this case, they solve the following generalized Nash bargaining problem:
where \(\pi_{s}^{L} \left( {w_{s} } \right) = \pi_{s}^{L} \left( {q_{1}^{L} \left( {w_{B}^{L} \left( {w_{s} } \right),w_{s} } \right),w_{s} } \right) = \left( {w_{s} - c} \right)q_{1}^{L} \left( {w_{s} } \right)\) is firm S’s profit, and \(\pi_{1}^{L} \left( {w_{s} } \right) = \pi_{1}^{L} \left( {q_{1}^{L} \left( {w_{B}^{L} \left( {w_{s} } \right),w_{s} } \right),q_{2}^{L} \left( {w_{B}^{L} \left( {w_{s} } \right),w_{s} } \right),w_{B}^{L} \left( {w_{s} } \right),w_{s} } \right)\).
Maximizing (25) with respect to \(w_{s}\) and solving the first-order condition, we can derive \(\hat{w}_{s} \left( {\upbeta } \right)\). It shows that \(\hat{w}_{s} \left( {\upbeta } \right) \ge {\text{c}}\) and \(\frac{{\partial \hat{w}_{s} }}{\partial \beta } > 0\). If we assume \(\beta = 1\), then we can derive the wholesale price as:
We then substitute (26) into the profit function of firm S: \(\pi_{s}^{L} = \left( {w_{s} - c} \right)q_{1}\). We can derive the optimal fixed-fee licensing revenue in the first stage as:
Comparing firm 1’s equilibrium profits in the licensing case \(\pi_{1}^{LE}\) with its profits \(\pi_{1}^{N}\) in the no licensing case, we have:
\(\pi_{1}^{LE} - \pi_{1}^{N} = \pi_{1}^{L} \left( {\hat{w}_{s} } \right) + F - \pi_{1}^{N} = \frac{{ - \left( {4r^{2} + 3r + 2} \right)\left( {1 - c} \right)^{2} }}{{16\left( {r + 6} \right)\left( {r + 2} \right)^{2} }} < 0\).
As a result, firm 1 has no incentive to license its core input production technology to firm S with a wholesale price input contract in the extreme case of \(\beta = 1\).
Appendix 6: A two-part tariff or pure royalty licensing contract
In the first stage, firm 1 decides whether to license its input technology to external firm S. We consider the case in which the licensing contract is composed of two-part tariffs,\({ }\left( {k,{ }F} \right)\), instead of a fixed-fee licensing, where k is the royalty rate and F is the fixed fee. Firm S and firm 1 then negotiate over a vertical contract—that is, \(\left( {w_{s} ,{\text{ T}}} \right)\)—to determine T and \(w_{s}\) in the second stage. Following this setting and routine calculation, we substitute T into (3) in the second stage, and it follows that \(w_{s}\) is chosen to maximize the following profits as \({\text{ U}} = \pi_{1}^{L} \left( {w_{s} ,k} \right) + \pi_{s}^{L} \left( {w_{s} ,k} \right) - \pi_{1}^{N}\). The first-order condition is the same as (4). By solving the first-order condition, we derive the equilibrium \(w_{s}^{*}\) and \(T^{*}\) as:
where \(c + \frac{{2\left( {1 - c} \right)\left( {2 - r} \right)\left( {2 - 2r^{2} - r} \right)}}{{A_{1} }}\) is the same as (14), which is the optimal wholesale price under fixed-fee licensing. Here, (27) shows that \(w_{s}^{*}\) is a function of the royalty rate, k, with \(\frac{{\partial w_{s} }}{\partial k} = 1\), and fixed fee \(T^{*}\) is not related to k. Therefore, the royalty rate can be any value even if it is set to zero. By substituting \(k = 0\) into \(w_{s}^{*} \left( k \right)\), we can derive the same \(w_{s}^{*}\) in (5). The results in the first stage and the incentive for licensing are the same as (7). Therefore, it is found that vertical licensing occurs when the licensing contract is a two-part tariff.
In the case of pure royalty licensing in the first stage, which is \(F = 0\), the wholesale price in the second stage is the same as (27). Therefore, the result is similar to the above. We can derive the same \(w_{s}^{*}\) in (5) as \(k = 0\) in (27), and the results in the first stage are the same as (7). Therefore, vertical licensing still occurs when the licensing contract is a pure royalty. However, a royalty licensing cannot extract all the extra profit from firm S. Therefore, pure royalty licensing is inferior to fixed-fee or two-part tariff licensing.
Rights and permissions
About this article
Cite this article
Lin, YJ., Lin, YS. & Shih, PC. Welfare reducing vertical licensing in the presence of complementary inputs. J Econ 137, 121–143 (2022). https://doi.org/10.1007/s00712-022-00782-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00712-022-00782-y
Keywords
- Vertical licensing
- Two-part tariffs
- Input pricing
- Complementary inputs
- Vertically-related market
- Social welfare