Structural studies on synthetic A_2−x[M₂(TeO₃)₃]·nH₂O phases (A = Na, K, Rb, Cs; M = Mn, Co, Ni, Cu, Zn) with zemannite-type structures

Abstract

During a systematic study on formation conditions of new compounds with zemannite-type structures, crystals of ten new oxidotellurate(IV) phases were grown under hydrothermal conditions, partially by employing a drastic reduction of the water content. The crystal structures of the obtained phases were determined by single-crystal X-ray diffraction. Na₂[Ni₂(TeO₃)₃]·2.5H₂O, K₂[Ni₂(TeO₃)₃]·H₂O, K₂[Zn₂(TeO₃)₃]·2H₂O, Rb_1.25[Co₂(TeO₃)₃]·1.5H₂O and Rb_1.24[Mn₂(TeO₃)₃]·2H₂O exhibit a unit-cell with hexagonal symmetry (Z = 2, a ≈ 9.3 Å, c ≈ 7.7 Å), in which most of the other compounds with a zemannite-type structure are known to crystallize. Relative to this unit-cell, K₂[Cu₂(TeO₃)₃]·2H₂O exhibits a twofold superstructure, K₂[Co₂(TeO₃)₃]·2.5H₂O a twofold superstructure with an additional incommensurate modulation, Na₂[Cu₂(TeO₃)₃]·1.5H₂O a threefold superstructure, and Rb_1.5[Mn₂(TeO₃)₃]·1.25H₂O and Cs[Mn₂(TeO₃)₃]·H₂O a fourfold superstructure. Disorder of the alkali metal cations and crystal water molecules in the channels as well as variable water contents complicate modelling and structure refinement.

Introduction

The mineral zemannite was named in honor of Josef Zemann, in recognition of his outstanding work in crystallography, crystal chemistry, optical mineralogy and spectroscopy. The crystal structure of zemannite has originally been determined by Matzat (1967) on a mineral from the Moctezuma mine in Mexico, with an assumed composition of Na_xH_2–x[(Zn,Fe)₂(TeO₃)₃]·yH₂O. Subsequently, it was revealed that in natural zemannite, Fe is present as Fe^III, eliminating the necessity of the proposed H⁺ ions, and Na⁺ was identified as disordered Mg²⁺ cations instead, leading to a revised composition of Mg_0.5[Zn^IIFe^III(TeO₃)₃]·4.5H₂O (Miletich 1995a; Cametti et al. 2017; Missen et al. 2019a). Besides zemannite, several similar mineral phases have been discovered in the meantime and their isotypic structures determined, viz. kinichilite (Mg_0.5[(Mn^II,Zn^II)Fe^III(TeO₃)₃]·4.5H₂O; Hori et al. 1981), ilirneyite (Mg_0.5[Zn^IIMn^III(TeO₃)₃]·4.5H₂O; Pekov et al. 2018) and keystoneite (Mg_0.5Ni^IIFe^III(TeO₃)₃·4H₂O; Missen et al. 2021). They only differ by the nature of the transition metals and the water content.

The first synthetic compounds with zemannite-type structures, K₂[Co^II₂(SeO₃)₃]·2H₂O and K₂[Ni^II₂(SeO₃)₃]·2H₂O, were reported by Wildner (1993) and represent the first oxidoselenates(IV) in this series. The first synthetic tellurium-based zemannite phases, Na₂[Co^II₂(TeO₃)₃]·3H₂O and Na₂[Zn^II₂(TeO₃)₃]·3H₂O, were obtained under mild hydrothermal conditions (Miletich 1995b), similar to those for K₂[Co₂(SeO₃)₃]·2H₂O and K₂[Ni₂(SeO₃)₃]·2H₂O.

In general, compounds with zemannite-type structures can be described by the formula A_x[M₂(XO₃)₃]·nH₂O with A being alkali or alkaline earth metal cations, M being di- and trivalent first-row transition metal cations, and X being Se or Te atoms in the tetravalent state; the value of x can range from 0 for all M being trivalent to 2 for all M being divalent. The zemannite crystal structure is made up from an anionic [M₂(TeO₃)₃]^y− framework, which is permeated by large, hexagonal channels extending along [001]. The A cations inhabit these channels together with the water molecules of crystallization. In the known tellurium- and selenium-containing zemannite-type phases reported so far, A stands for Na⁺ or Mg²⁺ and K⁺ or Ba²⁺, respectively. Most synthetic compounds with zemannite-type structures contain exclusively divalent M cations, leading to A contents of 2 for alkali metal and 1 for alkaline earth metal cations. All known mineral phases and the synthetic Na_x[Fe^III_2–xZn^II_x(TeO₃)₃]·3H₂O (0.55 < x < 1.25) (Missen et al. 2019b) contain a mixture of divalent and trivalent metal cations M, often in an 1:1 ratio. This consequently leads to a reduction of the amount of A cations in the channels. Unit-cell data and space group symmetries for all minerals and numerous synthetic compounds with zemannite-type structures were compiled in a recent report discussing the space-group symmetry of natural zemannite (Effenberger et al. 2023).

The formation of three-periodic framework structures permeated by channels is not uncommon for oxidotellurates(IV) due to the large space consumption of the stereoactive non-bonding 5s² electron pair of Te^IV (Galy et al. 1975). Our recent investigations on the M₃(TeO₃)₂(OH)₂ (M = Mn, Co, Ni, Mg) structure type (Eder et al. 2022b) also showed hexagonal structures formed by a [M₃(TeO₃)₂(OH)_1.5]^0.5+ framework perforated by large channels oriented parallel to [001]. In contrast to zemannite-type structures, these channels host anionic species as counter ions. However, a feature, which zemannite- and M₃(TeO₃)₂(OH)₂-type structures have in common, is the ability to accommodate various other species in their respective channels. M₃(TeO₃)₂(OH)₂ phases can incorporate different kinds of anions (Cl⁻, Br⁻, [NO₃]⁻, [CO₃]²⁻, [SO₄]²⁻ or [SeO₄]²⁻) partially replacing prevalent [OH]⁻, while for zemannite-type phases, their possible cation exchange abilities and zeolitic properties have been in the focus of previous investigations (Matzat 1967; Miletich 1995b). Consequently, the exact water content of zemannite-type phases is variable and not well defined.

We report here on the results of systematic phase formation studies of tellurium-based compounds with zemannite-type structures. Some of the obtained ten new A_x[M₂(TeO₃)₃]·nH₂O phases mark the first representatives with larger alkali metal cations than Na⁺ or K⁺, viz. Rb⁺ and Cs⁺, and/or with distinct superstructures in relation to the usual hexagonal unit-cell with Z = 2.

Experimental

Synthesis

All compounds were obtained from a hydrothermal setup. The educts (Table 1) were weighed into small Teflon vessels with an inner volume of ca. 3 ml and manually mixed. Afterwards, the Teflon container was filled with deionized water (filling degree ≈ 70%), the educts mixed again, and the container closed with a Teflon lid. For several of the batches, the synthesis conditions were modified by a drastic reduction of the water content to only three water droplets (ca. 0.1 ml).

The Teflon containers were subsequently placed inside steel autoclaves, heated to 483 K and held at this temperature for a week. After cooling to room temperature within three hours, the samples were washed with water, ethanol and acetone. Single crystals of zemannite-type phases for X-ray diffraction studies were optically pre-selected under a polarizing microscope. They characteristically form hexagonal prisms ranging from thin needles to thick pillars and sometimes needed to be cut to a smaller size.

Table 1 Details on the hydrothermal syntheses of investigated compounds with zemannite-type structures

X-ray diffraction

Powder X-ray diffraction (PXRD) measurements were conducted on a PANalytical X´Pert II Pro PW 3040/60 diffractometer using CuK_α1,2-radiation and an X’Celerator detector. For phase analysis and refinements of unit-cell parameters, the Highscore Plus software suite was used (Degen et al. 2014).

The majority of single crystal X-ray diffraction measurements was performed with a Stoe STADIVARI diffractometer equipped with an Anton Paar Primux 50 MoK_α microsource and a Dectris EIGER^® 2 R CdTe 1 M detector. Unit-cell determination, optimization of measurement strategies and integration were performed with X-AREA (Stoe & Cie GmbH 2021), absorption correction with LANA (Koziskova et al. 2016), and structure solution and refinement with SHELXT (Sheldrick 2015a) and SHELXL (Sheldrick 2015b), respectively.

The other measurements were done on a Bruker Kappa APEX-II diffractometer with graphite-monochromatized MoK_α-radiation and equipped with a charge-coupled device area detector. APEX-4 (Bruker 2021) and SAINT (Bruker 2016) were used for optimized measurement strategies and integration as well as SADABS (Krause et al. 2015) for absorption correction. For refinement of the incommensurately modulated crystal structure of K₂[Co₂(TeO₃)₃]·2.5H₂O, JANA-2020 (Petříček et al. 2014) was employed.

Atom labels were assigned in accordance with isotypic literature phases, if available. Otherwise, they were assigned after standardization with STRUCTURE-TIDY (Gelato and Parthé 1987). Hydrogen atoms of water molecules could not be located and are excluded from the models but are part of the derived formulas and crystallographic data (absorption coefficient, X-ray density etc.). Graphical representations of selected crystal structures were created with DIAMOND (Brandenburg 2016).

Crystal data, data collection and structure refinement details are summarized in Table 2. Further details of the crystal structure investigations may be obtained from the joint Cambridge Crystallographic Data Centre/FIZ Karlsruhe online deposition service: https://www.ccdc.cam.ac.uk/structures/ by quoting the deposition numbers specified at the end of Table 2.

Table 2 Details on data collections and crystal structure refinements

Crystal structure evaluation

Bond valence sums (BVS; Brown 2002) were calculated based on the parameters by Brese and O’Keeffe (1991). In the case of Te^IV, the revised parameters by Mills and Christy (2013) under consideration of all oxygen contacts within 3.5 Å were used. Because the [MO₆] polyhedra in zemannite-type structures usually deviate from a perfect octahedron, different distortion parameters were calculated using OCTADIST (Ketkaew et al. 2021): the arithmetic mean of interatomic distances d_mean, the distance distortion ζ (1), the tilting distortion Δ (2), the angle distortion Σ (3) and the torsional distortion θ (4).

$$\zeta = \textstyle\sum_{i=1}^{6}\left|{d}_{i}-{d}_{mean}\right|$$

(1)

$$\Delta = \frac{1}{6} \textstyle\sum_{i=1}^{6}(\frac{{d}_{i}-{d}_{mean}}{{d}_{mean}})^{2}$$

(2)

$$\Sigma = \textstyle\sum_{i=1}^{12}\left|{\varphi }_{i}-90\right|$$

(3)

(${\varphi }_{i}$ are the O–M–O angles of neighboring oxygen atoms). For a detailed discussion of the determination of θ_i, see Ketkaew et al. (2021).

$$\theta = \textstyle\sum_{i=1}^{24}\left|{\theta }_{i}-90\right|$$

(4)

For analysis and comparison of the hexagonal channels in zemannite-type structures we used three parameters: D_A describes the distance of the alkali metal cations from the center of the channels. In order to quantify the diameter of the channels, D_C, we calculated the average distance of the oxygen atoms on opposite sides of the channels projected on the plane normal to the channel direction. The channel distortion parameter ξ was computed from distances of the M atoms surrounding the channel to each other. The distances of M atoms being second-next neighbors were chosen, as these M-atoms are located at the same height in the channel direction. Based on these distances, d_M and their mean distance d_mean, ξ is defined as

$$\frac{1}{6}\textstyle\sum_{i=1}^{6}\left|{d}_{i}-{d}_{mean}\right|$$

(5)

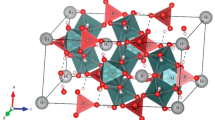
Examples for definition of D_A and the distances used for determination of D_C and ξ are shown in Fig. 1.

Fig. 1

A zemannite-type structure projected on the plane normal to the channel direction, exemplifying the definitions of D_A, D_C and ξ drawn in yellow, grey and blue lines, respectively. A cations are given as yellow, M atoms as blue (with coordination polyhedra), O atoms as red and Te atoms as green spheres with an arbitrary radius

Results and discussion

Synthesis

Our strategy to use a minor amount of water for the hydrothermal set-up changes the role of water from a typical solvent to a mineralizer. This approach has already turned out to be successful for the synthesis of novel mixed alkali/transition metal oxidotellurates(IV) (Eder and Weil 2022a) with some of them exhibiting interesting OD (order–disorder) behavior (Eder et al. 2022a).

As observed frequently for hydrothermal experiments (Weil and Shirkhanlou 2017; Weil et al. 2019), phase mixtures were obtained in nearly all batches. The amounts of intended products obtained during the present study, the nature of by-products and unit-cell parameters refined from PXRD data are listed in Table 3. Obtained secondary phases were the starting materials MO and TeO₂, as well as A₂Te₄O₉·nH₂O (A = Na, K; n ≈ 4) (Julien et al. 1971, 1972). The latter exhibited several very broad reflections in the PXRD patterns most likely originating from the variable water contents located between the planes of these layered structures. For the Co- and Ni-based samples, different M_n(TeO₃)_n–1(OH)₂ phases (M₃(TeO₃)₂(OH)₂, M = Co, Ni; Perez et al. 1976; Co₁₅(TeO₃)₁₄(OH)₂, Eder et al. 2023b) were observed, while for Mn-based samples, Mn₂Te₃O₈ (Cooper and Hawthorne 1996) was the main product. For synthesis of single-phase material, many interdependent parameters (filling degree, temperature, concentration, duration, E_H–pH values, etc.) need to be optimized, which is a very laborious task that was outside the scope of the present study.

Table 3 Refined unit-cell parameters (parental A_2–x[M₂(TeO₃)₃]·nH₂O zemannite structure) and phase analysis of product phases based on PXRD

The parental structure of zemannite in space group P6₃/m

All crystal structures determined during the present study (Tables 2 and 4) can be derived from the same structure model in the hexagonal space group P6₃/m with Z = 2 and unit-cell parameters of a ≈ 9.3 Å and c ≈ 7.7 Å. For further discussion, we will refer to this structure as the zemannite parental structure with a unit-cell volume defined by a_parental and c_parental. The parental structure can be divided into the anionic [M₂(TeO₃)₃]^y– framework, and into the A cations and crystal water molecules located within the channels. The framework is built from four sites: M1 is located at a site with symmetry 3.. (multiplicity 4, Wyckoff letter f), Te1 and O1 at a site with symmetry m.. (6 h) and O2 at a general position (12 i). Atoms at the M1 site (M = Mn^II, Mn^III, Fe^III, Co^II, Ni^II and Zn^II) are coordinated by six oxygen atoms with three of them being at the same distance each as a result of the 3.. site symmetry. They form a slightly distorted [MO₆] octahedron, which is connected to one neighboring octahedron by plane-sharing, thus forming [M₂O₉] dimers. The Te^IV atoms are coordinated by three oxygen atoms with typical distances between 1.85 and 1.90 Å (Christy et al. 2016; Zemann 1971). The formed [TeO₃] units are isolated from each other; the Te^IV atoms do not have additional contacts to oxygen atoms within ~ 2.9 Å, therefore their connectivity is defined as Q³⁰⁰⁰ (Christy et al. 2016). The electron lone pairs of the Te^IV atoms are directed towards the hexagonal channels. Within the framework, [TeO₃] and [M₂O₉] groups are isolated from their own kind but are linked by corner-sharing to the other type of building block.

The A cations in the parental structure are either alkali (Na⁺, K⁺) or alkaline earth metal cations (Mg²⁺, Ba²⁺). If the radius of A cations is small enough, the A sites are located directly at the center of the channels (Fig. 2a) at a site with symmetry 3.. (4 e). This is the case for mixed M^II/M^III phases with A being a small divalent cation (usually Mg²⁺), like in the mineral phases zemannite, ilirneyite or keystoneite. Otherwise, larger A cations in the channels are located at a general position (12 i), in a distance of up to 2 Å from the center of the channels, like in Na₂[Co₂(TeO₃)]·3H₂O (Miletich 1995b; Fig. 2b). The P6₃/m symmetry leads to artificially short distances of about 1.2 Å for the A cations to their symmetry-equivalent positions. Hence, the A1 site cannot be fully occupied. Its site occupation factor (s.o.f.) depends on the charge of the [M₂(TeO₃)₃]^y– framework and cannot exceed a value of $^1/_3$, which corresponds to a maximum amount of two A counter cations for the negatively charged framework. The oxygen sites O3, O4 and O5 correspond to water molecules of crystallization. They are located at sites with symmetry m.. (6 h) for O3, and at a general position (12 i) for O4 and O5, respectively. Like the A cations, these O atoms show occupational disorder, resulting in variable amounts of the water content n in A_2−x[M₂(TeO₃)₃]·nH₂O compounds.

Fig. 2

The crystal structures of (a) Mg_0.45[(Fe_1.12Zn_0.80Mn_0.08)(TeO₃)₃]·4.08H₂O (Miletich 1995a) and (b) Na₂[Co₂(TeO₃)₃]·2.97H₂O (Miletich 1995b) viewed along [00$\overline{1 }$]. Color codes refer to Fig. 1

Based on mineral samples of zemannite, the parental structure has alternatively been refined in space groups with lower symmetry. Although the [M₂(TeO₃)₃]^y– framework exhibits P6₃/m symmetry, the disordered content within the channels causes a symmetry reduction to space group P6₃ (Cametti et al. 2017; Missen et al. 2019a) or even to P3 (Effenberger et al. 2023). We likewise considered symmetry reductions for modelling the parental structure for some of the synthetic phases obtained during the present study. In contrast to mineral phases where the counter cations are located at the center of the channel, the presence of alkali metal cations located outside the center leads to a further symmetry reduction, i.e. to the monoclinic or even to the triclinic crystal system. Alternative models to resolve the disorder are presented in the following, and corresponding structure data for the alternative models are available in form of crystallographic information files (CIFs) in the electronic supplementary information (ESI).

Diffraction patterns shown as reconstructed sections of reciprocal space are given for each of the compounds in Fig. 3. Some interdependent structural features and the associated challenges in space group assignment, as well as problems during modelling and refinement occurred similarly for several of the zemannite-type phases and are discussed in the following. Special features are discussed separately for each structure.

Fig. 3

Reconstructed reciprocal lattice planes of the investigated crystals. Reciprocal lattice vectors refer to the zemannite parental structure. *A different plane than given at the top was chosen for better visibility of the superstructure reflections for b (h + k)0 l (right), d hk1 (left) and h1l (right), e h$\overline{1 }$l (right)

The parental structure of A _2−x[M ₂(TeO₃)₃]·nH₂O phases in P6₃/m

The sizes of the unit-cells for Na₂[Co₂(TeO₃)₃]·3H₂O, Na₂[Ni₂(TeO₃)₃]·2.5H₂O, K₂[Ni₂(TeO₃)₃]·H₂O, K₂[Zn₂(TeO₃)₃]·2H₂O, Rb_1.25[Co₂(TeO₃)₃]·1.5H₂O and Rb_1.24[Mn₂(TeO₃)₃]·2H₂O (Table 2) correspond to the parental structure with Z = 2, with the diffraction patterns of the latter two phases showing deviations from the P6₃/m symmetry. However, on basis of the present diffraction data, we cannot make an unambiguous statement on the arrangement of the contents in the channels. Caused by the hexagonal symmetry imposed by the framework, an averaged structure within the channels results. Although a significant broadening of reflections or the presence of diffuse scattering frequently accompanies such a phenomenon, we did not observe such features, here in the nkl/hnk planes along the channel direction. This is not surprising as the anionic [M₂(TeO₃)₃]^y─ framework is highly ordered and unaffected by the distribution of the channel contents. Most of the scattering intensity originates from the framework, so potential superstructure reflections or diffuse scattering can be rather weak, if A = Na⁺, K⁺, Mg²⁺ like for most structures that have been investigated up to now. Eventually, for all these phases we have to accept the parental structure in space group P6₃/m as the best model because alternative models with lower space group symmetry that resolve the disorder in the channels have even stronger deficiencies.

Formation of superstructures

The formation of a fourfold superstructure (a = 2a_parental, b = 2b_parental) with space group symmetry P6₃ was observed for Rb_1.5[Mn₂(TeO₃)₃]·1.25H₂O and Cs[Mn₂(TeO₃)₃]·H₂O (Fig. 3i, k), in analogy with Ba[M₂(SeO₃)₃]·3H₂O (M = Mg, Mn, Co) (Johnston and Harrison 2011). In contrast to Na⁺ and K⁺ cations, the Rb⁺, Cs⁺ or Ba²⁺ cations are too large to be placed easily in the small channels of the parental structure. They cause a distortion of the framework in the direction of the cations under formation of a larger unit-cell and a reduction of the symmetry. Nevertheless, also superstructure formation involving the smaller Na⁺ and K⁺ cations occurred. We assume that the water content inside the channels plays a major role in this regard. For the incommensurately modulated structure of K₂[Co₂(TeO₃)₃]·2.5H₂O, the modulation is associated with the partial occupancy of an O position corresponding to a crystal water molecule. For K₂[Cu₂(TeO₃)₃]·2H₂O and Na₂[Cu₂(TeO₃)₃]·1.5H₂O, superstructures were only/primarily observed on basis of data collections under dry nitrogen flow at 300 K, but not/only very weak for those at 100 K or 300 K without the gas stream. This behavior indicates a (partial) dehydration that affects the symmetry and ordering of the structure. For most of the structures, another possible cause for superstructure formation is the peculiar crystal chemistry of Cu^II and Mn^III determined by the Jahn–Teller effect (Falvello 1997). The strong axial distortion of the [CuO₆] and [MnO₆] units to give tetragonal bipyramids possibly results in a distortion of the complete framework, which relaxes under symmetry reduction. An example for this behavior is the mixed-valent zemannite-type phase K[(Cu^II,Mn^II,Mn^III)₂(TeO₃)₃]·2H₂O comprising both types of Jahn–Teller-active cations and forming a twofold monoclinic superstructure (Eder et al. 2023a). In comparison with the parental structure, the localization of all sites corresponding to crystal water molecules was difficult in lower-symmetric space groups or in superstructures, which had the effect that the overall amount of determined water is smaller in some cases.

Further disorder of large A cations

For Rb_1.25[Co₂(TeO₃)₃]·1.5H₂O, Rb_1.24[Mn₂(TeO₃)₃]·2H₂O and Cs[Mn₂(TeO₃)₃]·H₂O, modelling the very large Rb⁺ and Cs⁺ cations with partial occupancies resulted in rather unsatisfactory refinements with high reliability factors, significant remaining electron densities or physically meaningless displacement parameters. These features indicate additional positional A site disorder that could not be resolved for the present cases. It is obvious that disorder phenomena involving heavy atoms generally lead to more serious problems in the refinement than of lighter atoms. Hence, it remains unclear whether this kind of additional disorder is also present in the structures with lighter alkali atoms.

Variable water contents

Zemannite-type phases are known for their zeolitic behavior and the concomitant variability of the crystal water content (Miletich 1995b). This led to complications during some measurements, where the unit-cell volume gradually decreased by up to 2% during the data collection using a dry stream of nitrogen constantly surrounding the crystal. For example, crystals of Na₂[Cu₂(TeO₃)₃]·1.5H₂O from the same batch were measured at 100 K and at room-temperature (RT; refinement based on the RT measurement is presented in 3.8.2.), with the crystal at 100 K exhibiting a greater unit-cell volume (579 ų) than that at room-temperature (572 ų at RT). Such a decrease with increasing temperature contradicts general experience and points to partial dehydration, in this case also with ordering phenomena under formation of weak superstructure reflections. A similar behavior was observed for K₂[Cu₂(TeO₃)₃]·2H₂O. The data collected at 100 K (V = 578 ų) do not indicate a superstructure, whereas the data at 300 K (V = 569 ų) reveal a twofold superstructure. Aside from that, the diffraction data of another K₂[Cu₂(TeO₃)₃]·2H₂O crystal measured at RT without the dry-air unit turned on showed only a small decrease of the unit cell volume during the measurement. The final unit-cell volume (V = 577 ų) was still significantly greater than that determined from the other room-temperature study, which provides evidence that the dry gas stream leads to a higher degree of dehydration. It is noteworthy that no superstructure reflections were observed for the latter measurement.

The gradual loss of water over the course of the diffraction experiment not only affects the (refined) composition, but the structure model and its quality in general, in particular because dehydration products frequently have disordered structures. To complicate matters, an accurate determination of the water content from diffraction data is not possible due to strong correlations between occupancy and displacement parameters of the (disordered) oxygen sites inside the channels. In the present cases, the occupancies of the crystal water O sites were constrained to values based on symmetry considerations and reasonable interatomic distances, as well as meaningful displacement parameters. In general, the indicated water contents in the presented phases are only approximations and were estimated to multiples of ½. A thorough determination of the water content of compounds with zemannite-type structures is possible only by complementary analytical methods like thermogravimetry. However, this requires the presence of larger amounts of single-phase material, which could not be accomplished so far.

Structural parameters

The incorporation of larger monovalent A cations such as K⁺, Rb⁺ or Cs⁺ into the channels of tellurium-based zemannite type phases is enhanced by widening of the anionic framework in the first place. The sizes of the channel diameters D_C (Table 5) follow the trend of the ionic radii (Shannon 1976) of the M cations present in the framework: Ni^II < Co^II < Cu^II < Zn^II < Mn^II, although the size of the Mn^II-frameworks is reduced by the partial presence of smaller Mn^III. This partial oxidation of M^II to M^III in the framework has another beneficial effect, as the total possible number of cations present in the channels decreases in view of the required electroneutrality. In this regard, Mn appears to be the ideal candidate as it fulfills both conditions with its rather large ionic radius and its peculiar redox behavior. The partial oxidation of some Mn^II atoms in the corresponding structures is confirmed by computing their BVS values, which are considerably higher than 2 (Table 5).

The size of the A cation itself influences its position inside the channels. The smaller the cation, the farther away from the center of the channel it is located, resulting in the highest D_A values for the smallest alkali cation Na⁺. Concurrently, the distance between neighboring Na⁺ sites is longer than for larger cations. In order to increase the distance between larger A cations, the structure can adapt through a distortion of the hexagonal channels under formation of a superstructure (see "Formation of superstructures"), leading to higher D_A values in Rb_1.5[Mn₂(TeO₃)₃]·1.25H₂O or Cs[Mn₂(TeO₃)₃]·H₂O. These two structures exhibit by far the greatest channel distortion parameter ξ of all phases obtained during the present study.

The octahedral distortion parameters for [MO₆] units in the anionic framework (Table 5) show two trends: They increase for larger A cations and for superstructures with lower symmetry. Generally, it has to be noted that most refinements of superstructures were of poorer quality with respect to reliability factors, interatomic distances and their standard deviations etc. than refinements of the parental family structure. Nevertheless, on basis of the comparably high-quality data of Rb_1.5[Mn₂(TeO₃)₃]·1.25H₂O, the [MnO₆] units (tetragonal bipyramids) show distinct higher distortions caused by the Jahn–Teller effect of the partially included Mn^III and the deformation of the channel cross-sections in order to accommodate the Rb⁺ cations. Within the framework, the two Mn sites with symmetry 3.. (2 b) expectedly show smaller distance distortions ζ and tilting distortions Δ than those located at the general 6 c position (Table 5).

The degree of the channel distortion ξ is likewise influenced by the symmetry of the structure, as it is 0 in the hexagonal P6₃/m parental structure. In the structures with lower symmetry and/or superstructures, two values for ξ were calculated. One corresponds to the three distorted channels with ordered A cations, the other to the hexagonal channels with disordered A cations.

Special features

Na₂[Co₂(TeO₃)₃]·3H₂O

Crystals of Na₂[Co₂(TeO₃)₃]·3H₂O showed the best performance in terms of reflection intensities and overall quality of the diffraction data. Therefore, the Na–Co phase was chosen as a model compound for structure refinements with the intention to resolve the disorder of the channel contents in space groups with lower symmetry.

The Na–Co phase has already been investigated by Miletich (1995b) with a refined composition of Na₂[Co₂(TeO₃)₃]·2.97H₂O. In the current P6₃/m model, we were able to assign three crystal water molecules per formula unit. Our investigated Na–Co zemannite phase has a very similar unit cell volume of 584 ų compared to 588 ų of the literature phase.

Two alternative models with reduced space group symmetry are proposed: a) P112₁/m considering a threefold twin and b) $P\overline{1 },$ considering a sixfold twin. The parental structure and the two alternative structure models are visually compared in Fig. 4. The unit-cell data of the alternative models are collated in Table 4.

Fig. 4

The crystal structure of Na₂[Co₂(TeO₃)₃]·3H₂O viewed along the channel direction (left) and normal to the channel direction (right). Color codes refer to Fig. 1. a The disordered parental structure; b, c alternative models in lower-symmetric space groups trying to resolve the disorder within the channels

Table 4 Unit-cell data for alternative refinements of A_2–x[M₂(TeO₃)₃]·nH₂O structures in models with lower space group symmetry

Table 5 Structural parameters for A_2–x[M₂(TeO₃)₃]·nH₂O zemannite-type phases

The P112₁/m case

The symmetry reduction from P6₃/m to P112₁/m splits every atomic position except for Co1 into three sites, resulting in thirteen sites being present in the asymmetric unit, viz. three Te, one Co, one Na and eight O. The three Te atoms and four O atoms are located on mirror planes (2 e); all other atoms are at a general position (4 f). The disorder of the cations over Na sites is resolved, with the Na⁺ cations being located on opposite sides of the channel. One oxygen site (O4), corresponding to a crystal water molecule, is not fully occupied (s.o.f. = 0.5). This O4 site has a rather small distance of 2.36(4) Å to its own symmetry-related equivalent. The crystal water content in the P112₁/m model was determined to be 2, with O6 corresponding to the O3 site (one water molecule) in the parental structure and O4 to the O4 site in the parental structure, respectively.

The asymmetric arrangement within the channels does not become notable in a significant distortion of the surrounding framework and without visible splitting of reflections (Fig. 3a). The twin operation is a threefold rotation by the former hexagonal axis, oriented along the c direction of the monoclinic model; the twin ratios refined to values close to $^1/_3$, viz. 0.372(4), 0.318(4) and 0.310(4). The ordering of Na⁺ cations in the channels results in a rather close Na···Na contact of 3.299(9) Å. The P112₁/m model is only feasible for Na-based zemannite-type structures.

The ${\varvec{P}}\mathbf{\overline{1 }}$ case

The second symmetry-reduced model in $P\overline{1 }$ is based on the ordering of both Na⁺ cations and crystal water molecules. Two of the three possible orientations of pairs of neighboring Na⁺ cations and adjacent crystal water molecules are realized, with the two Na-pairs in the unit-cell being oriented in different directions. The ordered crystal water molecules play an important role in maintaining the ordering of the Na⁺ cations. This model leads to a significantly larger minimum Na···Na distance of 4.110(13) Å compared to the P112₁/m model, which makes it more realistic for structures containing larger A cations than Na⁺.

However, the symmetry loss from P6₃/m to P$\overline{1 }$, accompanied with the presence of six twin domains with a sixfold rotation along the channel axis as twin operation (refined contents between 0.130(4)–0.193(5)), resulted in problems during refinement. Placing the first of the two Na sites into the channels with maximum occupancy is straightforward. The second Na site, however, cannot be located unambiguously because positive difference-Fourier density peaks corresponding to all possible Na locations inside the channels are present. Furthermore, the highest electron densities are unrealistically close (ca. 2 Å) to the first Na site. Placing Na sites on realistic positions with lower remaining electronic density led to heavily enlarged displacement parameters, often in combination with movement of the atom to a completely different position in the channel. Additionally, the refinement did not converge because atomic coordinates of several framework O atoms were alternating between two values even after several hundred refinement cycles. For the final refinement, several constraints had to be used. The displacement parameters of all channel contents (two Na and three O sites) were fixed to U_iso = 0.05 and their s.o.f.s to 1. Furthermore, convergence of the refinement was only reached by imposing a stronger dampening term (DAMP 100 command) in SHELXL (Sheldrick 2015b).

Na₂[Cu₂(TeO₃)₃]·1.5H₂O

Refinement of the Na–Cu-phase in the P6₃/m parental structure led to larger ADPs with rather unequal shapes for the atoms at the Na sites, and a crystal water content of ca. 1.5 was determined. The O3 site shows an occupancy of about a half compared to the symmetrically allowed maximum.

The diffraction pattern of Na₂[Cu₂(TeO₃)₃]·1.5H₂O exhibits weak superstructure reflections in the hk(n + $^1/_3$) and hk(n – $^1/_3$) planes (n ∈ ℤ) relative to the parental structure (Fig. 3b), with reflections being present for h = n ± $^1/_3$ (n ∈ ℤ) and k = m ± $^1/_3$ (m ∈ ℤ) in these planes. A close inspection of the diffraction pattern revealed a rhombohedral cell (instead of a hexagonal supercell with a = $\sqrt{3}$ a_parental, b = $\sqrt{3}$ b_parental, c = 3c_parental as first suggested by the indexing software) under consideration of twinning by reticular merohedry (“obverse/reverse twinning”).

The triplication of the c axis relative to the parental structure indicates a distinct and different distribution of the Na⁺ cations and/or water molecules inside the channels compared to parental structure phases. In analogy with the symmetry-reduced models for Na₂[Co₂(TeO₃)₃]·3H₂O, the Na⁺ cations form pairs located on opposite sides of the channel. The direction of a neighboring pair is rotated by 120° along c combined with a translation by 0.5c_parental. Hence, the channel has a (pseudo-)translational period of 1.5c_parental, while the anionic framework still has a (pseudo-)translational symmetry of c_parental. As a result, the translational symmetry of the whole crystal then amounts to 3c_parental in the directions of the channels. Each hexagonal channel has six neighboring channels. In the rhombohedral model, neighboring channels never share the same arrangement of Na⁺ cations, as the rhombohedral lattice-centering leads to a translation of the contents of a neighboring channel by ± c_parental.

Based on coordinates obtained by transformations from the parental structure using JANA-2020 (Petříček et al. 2014), we constructed a model with an ordered arrangement of Na⁺ cations (Fig. 5). The space group symmetry of the resulting structure is $R3$ with the threefold rotation axes going through half of the Cu sites and the ${3}_{1}$ and ${3}_{2}$ screw axes being located inside the channels and passing through the other half of the Cu sites. However, in our refinements based on the actual diffraction data, a model in R$3$ with the $3$ axis running through the channels was the most feasible one.

Fig. 5

Assumed model of the crystal structure of Na₂[Cu₂(TeO₃)₃]·1.5H₂O viewed along [00$\overline{1 }$]. Color codes refer to Fig. 1; crystal water molecules were omitted for clarity. Na atoms located at different z values are drawn in different colors (yellow, orange and brown)

Na₂[Ni₂(TeO₃)₃]·2.5H₂O

The small crystal size led to only weak intensities in the diffraction pattern that correspond to the zemannite parental structure (although this might be a consequence of the small crystal size). In the P6₃/m model, only the Te1 and Ni1 atoms could be refined with ADPs, the remaining atoms were refined with isotropic displacement parameters. Besides the disordered Na⁺ cations, three oxygen sites corresponding to 2.5 water molecules per formula unit could be assigned. They are located at similar positions as the respective O3, O4 and O5 sites in Na₂[Co₂(TeO₃)₃]·3H₂O (Miletich 1995b), but with only half the s.o.f. for O4.

K₂[Co₂(TeO₃)₃]·2.5H₂O

The diffraction pattern of the K–Co-phase showed two interesting features. First, the presence of superstructure reflections hinting at a doubling of the parental structure along a, b or –a – b, combined with a symmetry loss to monoclinic P112₁/m symmetry under consideration of a trifold twin by rotation of 120° about the former hexagonal axis (c in the monoclinic model). Second, the appearance of diffuse scattering in form of streaks with distinct maxima located at irrational k values, indicating an incommensurate modulation along the channel direction. The q-vector was determined to a value of 0.3886(5) c*. Besides the clearly visible first order satellites, also weaker ones of second order were observed (Figs. 3d and 6).

Fig. 6

Small section of the reconstructed h1l plane of K₂[Co₂(TeO₃)₃]·2.5H₂O. The reciprocal channel direction c* is drawn vertically

Modelling of the parental structure in P6₃/m was satisfactory, with a refined crystal water content of ca. 2.5. Within the channels, three oxygen sites and the K site are all partially occupied. In comparison with Na₂[Co₂(TeO₃)₃]·3H₂O (P6₃/m model), the positions of the O sites are similar, but those of Na1 and K1 differ somehow. For the distribution of the channel contents, considerations like for the $P\overline{1 }$ model in Na₂[Co₂(TeO₃)₃]·3H₂O were made. The possibilities for distribution of the atoms inside the channels are shown in Fig. 7b. For each K site, the corresponding site on the opposite side of the channel must be occupied, whereas the site positioned directly above and below cannot be occupied simultaneously, leading to two possible arrangements of the next K-pair. Without consideration of the crystal water molecules, the two resulting possible contacts are symmetrically equivalent, and the distribution of the K sites and their adjacent crystal water molecules is a probable reason for the diffuse scattering along the c* rods. The two adjacent K positions also influence the occupancy of O3, which exhibits an s.o.f. of ca. $^1/_6$ rather than $^1/_3$, the highest possible value based on interatomic distances to its symmetry-equivalent positions. Like in the $P\overline{1 }$ model of Na₂[Co₂(TeO₃)₃]·3H₂O, the presence of the O3 site plays an important role in maintaining the order of the A-pairs and crystal water molecules within the channels, and its presence/absence can lead to disorder in the distribution of the K⁺ cations. The crystal water content is estimated to be 2.5 and, in principle, could be any similar (also irrational) value. It is reasonable to assume that the supposedly incommensurately modulated occupancy of the O3 site causes the rest of the channel contents to relax into the resulting empty spaces.

Fig. 7

The crystal structure of K₂[Co₂(TeO₃)₃]·2.5H₂O (parental structure) viewed along [0$\overline{1 }$0]. Colour codes refer to Fig. 1. a All disordered channel contents are displayed; b based on the central Na-pair, all ineligible neighboring sites are omitted

The occupancies of the O4 and O5 sites are at least partially determined by the K-pairs on opposite sides of the channel, because a K-pair allows two pairs of O4/O5 positions with exactly one position of each pair being occupied, like in Na₂[Co₂(TeO₃)₃]·3H₂O. The s.o.f.s of O4 and O5 refine to almost the same value very close to $^1/_6$.

The twofold superstructure was modelled in the space group P112₁/m (Fig. 8) using the transformation matrix

Fig. 8

The average structure on basis of the monoclinic P112₁/m superstructure refinement of K₂[Co₂(TeO₃)₃]·2.5H₂O viewed along [0$\overline{1 }$0]; the incommensurate modulation is ignored. Color codes refer to Fig. 1

$$\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right).$$

Here, the different atoms within the channels could not be located as easily as in the parental structure. One crystal water site corresponding to $^1/_6$ H₂O per formula unit did not stay stable in the refinement and was forced on its position. The K⁺ cations show a significant displacement from their corresponding “higher-symmetric” sites. These issues resulted in a non-converging refinement when trying to model the incommensurate modulation (JANA-2020; Petříček et al. 2014) in the superspace group P112₁/m(00γ)s0, because some contents of the channels did not stay stable at their positions. Therefore, a more thorough investigation of the incommensurate modulation behavior based on better-resolved and high-intensity data sets is necessary.

K₂[Cu₂(TeO₃)₃]·2H₂O

Crystals of K₂[Cu₂(TeO₃)₃]·2H₂O showed a peculiar behavior. When measured at 100 K, only reflections of the parental structure in P6₃/m (a = 9.3410(5) Å, c = 7.6463(4) Å, V = 577.79(5) Å³) were observed, leading to a refined crystal water content of ca. 2. Measurement of a crystal at 300 K under a constant stream of dry nitrogen led to a significant reduction of the unit-cell volume (a = 9.2806(5) Å, c = 7.6336(4) Å, V = 569.39(7) ų) despite the higher measurement temperature. Additionally, superstructure reflections at h, k = n + ½ (n ∈ ℤ) appeared in the diffraction pattern at 300 K, similar to the commensurate part of the superstructure of K₂[Co₂(TeO₃)₃]·2.5H₂O. The resulting twofold monoclinic superstructure (Table 4 and Fig. 8) was refined in the space group P112₁/m, whereby the model does not resolve the disorder of the channel contents. Allocation of the same amount of crystal water molecules as in the parental structure refinement proved to be problematic again, like for Na₂[Cu₂(TeO₃)₃]·1.5H₂O.

K₂[Ni₂(TeO₃)₃]·H₂O

The very thin needles of K₂[Ni₂(TeO₃)₃]·H₂O produced data sets with low-intensity reflections corresponding to the parental P6₃/m structure. As detailed for the Na–Ni-compound, Ni creates the smallest zemannite frameworks of all investigated M cations (Tables 2 and 4). Only one crystal water molecule resulted from the refinement as compared to 2.5 for Na₂[Ni₂(TeO₃)₃]·2.5H₂O. The different crystal water content of the two compounds most likely is a result of the larger ionic radius of K⁺ compared to Na⁺ (1.60 Å and 1.26 Å for CN7; Shannon 1976) with the two structures having similar unit-cell dimensions and channel diameters D_C.

K₂[Zn₂(TeO₃)₃]·2H₂O

Only reflections of the zemannite parental structure were observed for K₂[Zn₂(TeO₃)₃]·2H₂O. For the P6₃/m model, all sites except the two O atoms of crystal water molecules could be refined with ADPs.

Miletich (1993) has already reported a zemannite-type K–Zn phase, but with higher water content, K₂[Zn₂(TeO₃)₃]·3H₂O. The latter was obtained under similar hydrothermal conditions but twinning inhibited structure solution at that time. PXRD data revealed a splitting of reflections, indicating a symmetry reduction from hexagonal to monoclinic symmetry with refined unit-cell parameters of a = 9.474(5) Å, b = 7.738(4) Å, c = 9.406(5) Å, β = 119.66(4)° and an assumed space group P2₁/m (Miletich 1993). Such a significant deviation from a metrically hexagonal cell was not discernible on basis of the current single crystal data (Fig. 3g) or powder data of K₂[Zn₂(TeO₃)₃]·2H₂O.

Rb_1.25[Co₂(TeO₃)₃]·1.5H₂O

The symmetry of the Rb–Co zemannite-type structure (Fig. 9) is hexagonal with Z = 2, but with a space group change from centrosymmetric P6₃/m for the parental structure to non-centrosymmetric $P\overline{6 }$, resulting in the splitting of all sites. In the channel, Rb1 is located at the general 6 l position and has an s.o.f. of $^1/_3$ (the maximal possible value for simultaneous occupation), while the s.o.f. of Rb2 (site symmetry m..; 3 j) refined to a value close to $^1/_6$. For the final refinement, this value was fixed, resulting in an overall Rb content of 1.25 atoms per formula unit. Three oxygen atoms, corresponding to 1.5 water molecules per formula unit, were assigned in the channel. The O6 site is located very close to the center of the channel and exhibits a negative U_iso parameter when its occupancy is fixed to $^1/_3$ (the maximal possible value for simultaneous occupation), together with significant remaining positive and negative electron densities near this site.

Fig. 9

The crystal structure of Rb_1.25[Co₂(TeO₃)₃]·1.5H₂O viewed along [00$\overline 1$]. Color codes refer to Fig. 1

In comparison with other phases, such as K₂[Co₂(TeO₃)₃]·2.5H₂O, both the alkali and the water content are reduced whereas the size of the unit-cell and the channel diameter D_C are similar (Tables 4 and 5). The [Co₂(TeO₃)₃]^y– framework is rather rigid and cannot expand in order to accommodate the larger Rb⁺ cations and the same amount of water molecules. The reduced Rb⁺ content of Rb_1.25[Co₂(TeO₃)₃]·1.5H₂O requires a partial oxidation of Co^II to Co^III and/or a partial protonation of the anionic framework. However, both assumptions are difficult to prove since a partial oxidation was not observed for the corresponding Na- and K-compounds, the BVS values of the two Co sites (1.80 and 2.07 v.u.) rather point to Co^II in the framework, and a (partial) protonation of the framework seems unlikely because the synthesis was performed under strong alkaline conditions using an excess of Rb₂CO₃. All these features and the comparatively high reliability factors make it necessary to improve the current disorder model of Rb_1.25[Co₂(TeO₃)₃]·1.5H₂O.

Rb_x[Mn₂(TeO₃)₃]·nH₂O

For Rb–Mn-zemannites, we obtained two phases with different compositions and crystal structures in separate batches, even though the same ratios of educts were used. Rb_1.5[Mn₂(TeO₃)₃]·1.25H₂O was obtained in form of thick, dark brown pillars. Reproduction of the first batch instead yielded thinner brown needles of Rb_1.24[Mn₂(TeO₃)₃]·2H₂O with a considerable deviation from the hexagonal symmetry.

The Rb_1.5Mn₂(TeO₃)₃·1.25H₂O case

The unit-cell has four times the size of the zemannite parental structure (a = 2a_parental, b = 2b_parental). Just like in the related hexagonal Ba[M₂(SeO₃)₃]·3H₂O (M = Mg, Mn, Co) series (Johnston and Harrison 2011), the space group symmetry is reduced to $P{6}_{3}$. The asymmetric unit comprises four Te, four Mn, four Rb and fifteen O sites. With the exception of Mn3 and Mn4, which are located at sites with symmetry 3.. (2 b), all atoms are located at the general 6 c position. Atom labels for the framework were assigned in analogy to the related Ba[M₂(SeO₃)₃]·3H₂O structures. The main differences to the latter pertain to the content of the channels as there are more (four compared to two) A sites, but less O sites (related to crystal water molecules) present.

The crystal structure comprises two types of channels in a ratio of 3:1. Caused by the 6₃ screw axis, the first are symmetrically equivalent and show a significant distortion of the channel due to a unidirectional position of the Rb⁺ cations on two opposite ends (Fig. 10), like in the P112₁/m model of Na₂[Co₂(TeO₃)₃]·3H₂O. The degree of channel distortion ξ is 0.4902 Å for Rb_1.5[Mn₂(TeO₃)₃]·1.25H₂O, while it is only 0.0431, 0.0538 and 0.0392 Å for the literature phases Ba[M₂(SeO₃)₃]·3H₂O (M = Mg, Mn, Co). This can be explained by the fact that more A cations populate the channels and therefore need to be located farther away from the center, which leads to a stronger distortion. The twofold superstructure of zemannite-type K[(Cu^II,Mn^II,Mn^III)₂(TeO₃)₃]·2H₂O (Eder et al. 2023a) also exhibits a significant deformation of the channels (ξ = 0.2584, 0.2276 Å), despite the presence of only one A cation per formula unit. This underlines the strong influence of Jahn–Teller-active cations on the distortions of the [MO₆] units and, consequently, the channels.

Fig. 10

The crystal structure of Rb_1.5[Mn₂(TeO₃)₃]·1.25H₂O viewed along [00$\overline{1 }$]. Color codes refer to Fig. 1

The fourth channel, which extends along the 6₃ screw axis, cannot be unidirectionally distorted due to symmetry restrictions. The involved Rb⁺ cations (Rb3, Rb4) and crystal water molecules (corresponding to O14 and O15) are disordered like in the hexagonal parental structure. In this type of channel, more water O sites were assigned than in the other type of channel, resulting in an overall content of 1.25 water molecules per formula unit.

All Rb sites show s.o.f.s < 1, the refined value being close to 0.75 for each of the four sites. For the final refinement, the s.o.f.s were refined with a common variable resulting in a value of 0.753(4), which corresponds to 1.5 Rb atoms per formula unit. Similar to Rb_1.25[Co₂(TeO₃)₃]·1.5H₂O, the low alkali content can be caused by a partial oxidation of the transition metal or a partial protonation of the framework. Here, the first explanation appears more likely because a significant amount of Mn^III in the structure should be recognizable from BVS values of individual atoms. In fact, the individual BVS values (using parameters for Mn^II–O) of the four Mn sites amount to 2.25 (Mn1), 2.32 (Mn2), 2.60 (Mn3) and 2.04 (Mn4) v.u., which corresponds to an average BVS value of 2.29 v.u.. This value reflects the required averaged positive charge of 2.25 per Mn atom to reach an electroneutral compound. It should be noted that a partial oxidation of Mn^II to Mn^III is a common feature observed under hydrothermal reaction conditions. Investigation of the hydrothermal phase formation behavior between Mn^II salts and TeO₂ under alkaline conditions (Eder and Weil 2022b) frequently yielded variable amounts of the mixed-valent phase Mn₃O₄ and small amounts of elemental Te. Hence, a partial oxidation of Mn^II under similar conditions is not unexpected, thus leading to Rb_2–x[Mn^II_2–xMn^III_x(TeO₃)₃]·nH₂O phases with a reduced Rb content.

The Rb_1.24[Mn₂(TeO₃)₃]·2H₂O case

Only reflections corresponding to the unit-cell volume of the zemannite parental structure were observed, however with a clear splitting of reflections in the hkn planes, indicating the presence of three domains, two with similar intensities and one with much weaker intensities (Fig. 3j). In general, the reflections become very diffuse at higher diffraction angles and frequently show an overlap, which made a clear separation of the distinct domains impossible during the integration process. Alternatively, an increased box size was used for integrating to properly collect intensity data of the reflections simultaneously, leading to averaged intensity statistics. The notional twinning together with the presence of diffuse reflections yielded a data set of substandard quality. Structure refinement was eventually performed in the hexagonal P6₃/m parental structure. Like in Rb_1.5[Mn₂(TeO₃)₃]·1.25H₂O, the Rb sites are not fully occupied, coupled with a partial oxidation of Mn^II to Mn^III in the framework (BVS of the unique Mn1 is 2.35 v.u. using the parameters for Mn^II–O bonds). The occupancy of the Rb1 site refined to a value of 0.620(3). The refined content of crystal water is higher than that for Rb_1.5[Mn₂(TeO₃)₃]·1.25H₂O. This difference is reflected in the unit-cell volumes. Rb_1.24[Mn₂(TeO₃)₃]·2H₂O at 100 K has a volume of 617 ų, which is significantly larger than the volume of Rb_1.5[Mn₂(TeO₃)₃]·1.25H₂O (2409 / 4 ≈ 602 ų) at room temperature (neglecting the different measurement temperatures).

Cs[Mn₂(TeO₃)₃]·H₂O

The diffraction pattern of the Cs–Mn-zemannite indicates a hexagonal unit-cell with a fourfold volume relative to the parental structure (a = 2a_parental, b = 2b_parental) without splitting of reflections in the hkn planes. The crystal structure of Cs[Mn₂(TeO₃)₃]·H₂O resembles that of Rb_1.5[Mn₂(TeO₃)₃]·1.25H₂O or those of the Ba[M₂(SeO₃)₃]·3H₂O (M = Mg, Mn, Co) series (Johnston and Harrison 2011) and was refined in the space group $P{6}_{3}$. The low cesium content indicates a large amount of Mn^III in the structure, which is visible in the average BVS of 2.59 v.u. (based on the parameters of Mn^II–O) of the Mn atoms. The two sites associated with Cs⁺ cations in the distorted channels were refined with split positions in close ± z vicinity under consideration of half-occupation for each pair. Depending on reasonable interatomic distances, the crystal water content was fixed to one molecule present per formula unit. Refinements in space groups with lower symmetry led to unrealistic interatomic distances of the anionic framework and thus were discarded.

Conclusions and outlook

We successfully synthesized several new tellurium-based zemannite-type phases with the composition A_2–x[M₂(TeO₃)₃]·nH₂O (A = Na, K, Rb, Cs; M = Mn, Co, Ni, Cu, Zn) using either mild hydrothermal conditions or a modification of such by a drastic reduction of the water content. During our investigations, we focused only on one alkali metal cation and one M species per batch. With regard to natural samples that comprise mixtures of M species in the framework, it is very likely that that the pool of synthetic compounds with zemannite-type structures can be extended if alkali cations, alkaline earth cations and/or various combinations of transition metals are simultaneously available in the reaction mixture.

Although we were able to present structure models for all new synthesized phases, the results are afflicted with shortcomings that could not be resolved on basis of the present single-crystal X-ray diffraction data. For compounds refined in the parental P6₃/m structure, an averaged model reflects the distribution of the species in the channels. Diffraction data with much better resolution and quality are necessary to get the full particulars. Complementary HR-TEM studies might give deeper insight into the presence and distribution of potential (twin) domains, whereby the stability of the crystals, which are prone to lose water, is certainly a challenging aspect under the required vacuum conditions.

Formations of various superstructures, probably determined by the size of the A cation, a variable crystal water content and/or a peculiar crystal-chemistry (Jahn–Teller distortions for Cu^II and Mn^III) leave space for broad follow-up investigations. By employing different ratios of M^II and M^III in the mixtures, it might be possible to tune the resulting phases to different A contents under formation of distinct crystal structures. Such studies need to be accompanied by thorough chemical analysis, e.g. by SEM–EDS measurements. The incommensurate superstructure of K₂[Co₂(TeO₃)₃]·2.5H₂O still requires more thorough modelling of the modulation, including a potential temperature-dependence. The uncertainties concerning the content of water in the channels of zemannite-type phases might be resolved using thermogravimetry as soon as single-phase products are available, followed by investigations of the de- and potential re-hydration behavior of these phases.

In summary, we showed that compounds crystallizing with zemannite-type structures can exhibit different types of superstructures and modulations based on the hexagonal parental structure (P6₃/m symmetry), which has been reported more than fifty years ago. Given the relatively easy accessibility of these phases through (modified) hydrothermal synthesis, there is a plethora of possibilities for modification of the composition and consequently of the crystal structure. Hence, phases with zemannite-type structures still are fruitful but challenging systems under the aspects of crystal-engineering, structural chemistry and crystallography.