Introduction

Feldspars are rock-forming minerals, on Earth and on other terrestrial planetary bodies. In the Earth’s crust, they account for more than 50 vol% (Okrusch and Matthes 2014). Lunar highlands, which cover approximately 83% of the lunar surface (Jolliff et al. 2006), are composed mostly of anorthosites and gabbros with a large amount of anorthite (Wood et al. 1970). Furthermore, Mercury’s crust is feldspatic with a labradorite-like composition predicated on the basis of Earth-based infrared emission spectroscopy by Sprague et al. (1997), who measured a Christiansen feature (CF) at 8 μm (1250 cm− 1) near the equator at approximately 120∘ longitude. After spectral unmixing of Earth-based observations, Mercury’s surface is thought to contain potassium-rich feldspar (Sprague et al. 2009).

Direct sampling of Solar System bodies other than Earth requires landing on the surface and returning samples, which is extremely expensive and currently not feasible for most objects. Thus, remote sensing data of planets and moons are necessary to provide the missing information.

Between 2011 and 2015, the MESSENGER (MErcury Surface, Space ENvironment, GEochemistry and Ranging) mission investigated the hermean surface (see Solomon et al. 2018, for a detailed description). The gamma-ray spectrometer (GRS) onboard the MESSENGER mission measured high Mg/Si and low Al/Si and Ca/Si contents, which excludes an anorthite-rich feldspatic crust like the lunar highlands (Nittler et al. 2011). GRS detected relatively high abundances of sodium, which suggest that albite is a major mineral on the surface of Mercury (Evans et al. 2012).

In October 2018, the ESA/JAXA BepiColombo spacecraft was launched to investigate the innermost planet of our Solar System via remote sensing. Among several other instruments, MERTIS (MErcury Radiometer and Thermal Infrared Spectrometer) will investigate Mercury’s surface in the mid-infrared (mid-IR) wavelength region (Hiesinger et al. 2010; H. Hiesinger and co-workers, in preparation). The goals of MERTIS are to study the surface mineralogy and composition, to map the mineralogy, and to measure the surface temperatures as well as the thermal inertia (Hiesinger et al. 2010; H. Hiesinger and co-workers, in preparation). To achieve these goals, MERTIS operates in the wavelength region from 7 μm to 14 μm (Spectrometer Channels/TIS 1429 cm− 1 to 714 cm− 1) and from 7 μm to 40 μm (Radiometer Channels/TIR 1429 cm− 1 to 250 cm− 1) (Hiesinger et al. 2010; H. Hiesinger and co-workers, in preparation).

Reflectance and absorption are not directly convertible (e.g., Kirkland et al. 2002; Thomson and Salisbury 1993). Therefore to apply spectral deconvolution algorithms we need reflectance spectra, which are comparable to remotely acquired data for the remote sensing applications.

For the interpretation of data returned from space missions, laboratory work is essential. Known factors which control reflectance and emission mid-IR data are, for example, the chemical composition, grain size distribution, bulk sample density, viewing geometry, pressure, and temperature (e.g., Pieters and Englert 1993). In this context, analyses of different grain sizes are necessary, because the surfaces of atmosphereless planetary bodies, like Mercury, are highly affected by larger and smaller impacts, which cause the formation of a poorly-sorted regolith.

To setup our spectral database that is valuable for remote sensing of various Solar System bodies, it is necessary to investigate well characterized samples of the alkali feldspar system. This includes both chemical composition and degree of Al,Si order in addition to other known factors controlling the shape of mid-IR spectra (Weber et al. 2018).

The study of feldspars includes their formation conditions, occurrences, chemical, and physical behaviors. Alkali feldspars are solid solutions of the end-members K[AlSi3O8] (Or) and Na[AlSi3O8] (Ab). They mostly contain small amounts of Ca[Al2Si2O8] (An). In addition to their chemical compositions, they are characterized by the specific distributions of Al and Si onto the tetrahedral sites of their framework structures (“structural state”). The most common rock-forming alkali feldspars, ranging in composition from Or100Ab0 to Or30Ab70, occur in two different modifications. Monoclinic sanidine (K,Na)[AlSi3O8] is the stable modification at high temperatures. The Al and Si atoms (1 Al plus 3 Si per formula unit) are distributed in a highly disordered, but not completely random manner onto two T1 and two T2 tetrahedral sites. The larger Al atom slightly prefers the T1 over the T2 site (Scambos et al. 1987), denoted by t1 > t2 with t = Al/(Al + Si) of the respective site (Kroll 1973). Provided a rate-enhancing influence being present, such as a fluid phase, mineral-fluid replacement processes lead at T ≤ 450 ∘C - 480 ∘C to the triclinic modification of microcline that under the polarizing microscope shows a characteristic tartan twinning reflecting the loss of monoclinic symmetry elements (Parsons 1978). The phase transition causes the T1 and T2 sites to split into T10, T1m and T20, T2m sites, respectively. Aluminum concentrates in the T10 site so that at full order t10 = 1, t1m = t20 = t2m = 0. At less favorable conditions, due to the high kinetic Al,Si exchange barrier, the transition results in a kinetically stranded, metastable pseudomorph called orthoclase. On a submicroscopic scale, orthoclase consists of intimately intergrown triclinic domains. All textural stages between orthoclase and microcline may be present in one and the same morphological unit. Na-rich alkali feldspars are as well symmetrically monoclinic at high temperature (monalbite). Changes to triclinic symmetry are induced during cooling through two different, though coupled mechanisms: A displacive transition at 980 ∘C, followed by a continuous Al,Si ordering process (Salje et al. 1985). On slow cooling, Al,Si ordering proceeds at T < 980 ∘C in the triclinic state with Al gradually enriched in the T10 site while leaving the other three sites so that in the end t10 = 1, t1m = t20 = t2m = 0 like in microcline. By contrast, when rapidly cooled, monalbite collapses to triclinic metastable analbite because the Na ion is too small to prevent structural collapse in contrast to the larger K ion in sanidine. The terms high albite and low albite denote different states of order.

At high temperatures, the solid solution series between monalbite and sanidine is continuous. A wide miscibility gap opens at lower temperatures, leading to the formation of intimately intergrown phase segregation textures of which perthites (Na-feldspar in a matrix of K-feldspar) are most common (Okrusch and Matthes 2014, and referenes therein).

Characteristics of alkali feldspars concerning the structure, formation conditions, exsolution processes, and behavior at high temperatures are well known (e.g., Ribbe 1983). Previous infrared spectroscopy work on the feldspar system shows that changes in absorption spectra occur according to chemical composition and degree of Al,Si order (e.g., Laves and Hafner 1956; Hafner and Laves 1957; Martin 1970; Zhang et al. 1996, 1997). Hecker et al. (2010) gave a review of different infrared techniques and their usefulness for remote sensing application. Iiishi et al. (1971) correlated single bands in K-feldspar absorption spectra between 8.7 μm and 23.3 μm (1150 cm− 1 and 430 cm− 1) with specific stretching, bending, translation, and expansion/contraction vibrations of Si-O, Si-Si, and Si-O-Si bonds, which are controlled by the state of Al,Si order. However, most of the bands described by Iiishi et al. (1971) cannot be observed as single peaks in powder reflectance spectra.

The objective of our study is to measure mid-IR powder reflectance spectra of well characterized alkali feldspar samples to build a database for remote sensing applications. This database is necessary especially for MERTIS.

Samples and analyses

Samples

To differentiate and quantify controlling factors of the powder mid-IR reflectance spectra, the analyzed samples must be well characterized. Natural alkali feldspars were used as raw materials, which were first thoroughly characterized and then treated in different ways described in the subsection “Sample Treatment”. All samples presented in this study, both natural and treated, have an internal database identification number (ID, Table 1), which refers to our database which is accessible at www.uni-muenster.de/Planetology (Weber et al. 2018). Our starting material included sanidine from Volkesfeld, Eifel, Germany (ID 73), microcline from Prilep, North Macedonia (ID 151), and albite from Cazadero, California (ID 125). ID 73 sanidine, (Na15K85)[AlSi3O8], is of gem-stone quality, being transparent. Its Al,Si order is low, 2t1 = 0.61 (Kroll and Knitter 1991). ID 151 microcline, (Na5K95)[AlSi3O8], is a light greenish powder sample fraction (100 μm to 125 μm) prepared from the original perthitic microcline (amazonite) from Prilep, which contains some exsolved albite. The Al content of the T10 site is 0.99 (Strob 1983). ID 125 albite has a white color and represents an endmember of the alkali feldspar solid solution in terms of Ab content (Ab99.9) and Al,Si order (t10 = 1.00) (Wenk and Kroll 1984). These natural samples were treated in different ways as described in section sample treatment.

Table 1 Overview of the used samples, their treatment, lattice parameters, Ab-Or content, and degree of order
Full size table

Sample characterization

Natural as well as commercially available minerals are often impure. We checked for impurities using light microscopy of thin sections, which also allowed us to distinguish between different compositions and states of order.

To determine the degree of Al,Si order, XRD patterns were obtained with a Philips X’Pert powder diffractometer, equipped with a primary Ge monochromator and with a Bruker D8 ADVANCE. For the XRD measurements, some sample material was crushed in an agate mortar to receive a “X-ray fine” grain size (approx. 1 μm to 10 μm), controlled by light microscopy. The powder was mixed with Si powder as internal standard to correct the zero shift of the X-ray diffractometers. Rietveld analysis of the XRD patterns were performed with the FULLPROF software (Rodriguez-Carvajal 2005) to refine the lattice parameters. Atomic coordinates and lattice parameters for albite were taken from Wenk and Kroll (1984), for microcline from Strob (1983), and for sanidine from Kroll et al. (1986). Based on the obtained lattice parameters, Al,Si site occupancies were derived from equations given by Kroll and Ribbe (1987) (Table 1).

Sample treatment

For our investigation we needed alkali feldspars with endmember compositions, which possess a maximum spread of ordering states. Natural feldspars do not fulfill these requirements. Therefore, we performed annealing experiments to vary the state of order as well as alkali exchange experiments to change compositions. Volkesfeld sanidine, ID 73, has been heated at 850 ∘C for 11 d (days), thereby slightly decreasing its state of order. Much larger changes were obtained for the Cazadero low albite. A portion of ID 125 was filled in platinum tubes (ca. 1g per tube) and sealed in evacuated silica glass tubes together with gibbsite (=hydrargillite, Al(OH)3). The samples were heated at 1060 ∘C to produce increasing states of disorder (see Tab. 1 for details). H2O released by gibbsite acts as a flux that promotes disordering. The amount of gibbsite was chosen so that the H2O pressure was about 7 bar. The samples were recovered after 8 d (ID 163), 15 d (ID 164), 18 d (ID 165), 47 d (ID 166) and finally after 92 d (ID 167). While Cazadero low albite is a pure Na-feldspar endmember, Volkesfeld sanidine and Prilep microcline contain some Ab component. They were thus treated by the alkali exchange method to produce K-feldspar endmembers (Kroll et al. 1986). Charges of ID 73, ID 129 (63 μm to 125 μm) and ID 151 (100 μm to 125 μm) were heated at 850 ∘C for 5 h in an excess of molten KCl in a covered Pt crucible in order to exchange Na ions by K ions. The weight ratio sample/KCl was set at 1:4.5 (ID 73 → ID 129), 1:70 (ID 129 → ID 150), and 1:5 (ID 151 → ID 152). Both small and large weight ratios led to the desired results. After the experiments, the samples were washed with distilled water, filtered and then dried at 50 ∘C for several hours. The Or contents of the exchange products were determined from the position of the composition-sensitive (\(\bar {2}01\)) reflection in X-ray powder diagrams (Kroll et al. 1986, their Table 9) resulting in Or99 and Or100, respectively (Table 1).

Infrared and analysis procedure

For the IR measurements, all samples were crushed in a steel mortar and/or agate mortar and sieved to grain sizes < 25 μm, 25 μm to 63 μm, 63 μm to 125 μm, 125 μm to 250 μm, and grains greater than 250 μm. Mid-infrared measurements were performed with a Bruker 70v FTIR spectrometer with a spectral resolution of 4 cm− 1 using a grazing angle unit A513. We used a liquid nitrogen cooled MCT (mercury cadmium telluride) detector, and all measurements took place at pressures of 2 hPa at room temperature (ca. 23 ∘C). For the background spectrum we used a commercially available diffuse gold standard (INFRAGOLDTM). The powder samples were placed in an aluminum sample holder, 1cm in diameter and 1.5 mm in depth, and flattened with a spatula. Each grain size fraction was measured at two different geometries, with an incident angle (i) of 20∘ and emergent angle (e) of 30∘ (i20∘ e30∘) and with an incident and emergent angle of 30∘ (i30∘ e30∘). For each sample and background measurement, 512 single interferogram scans in double sided foreward-backward scan mode were summed up, and the spectrum was calculated through Fourier transformation. In the wavelength region we measured, silicates show characteristic spectral features: (1) The Christiansen Feature (CF), which is a reflectance minimum at which the sample is mostly transparent for the infrared radiation because there is a rapid change of the real part of the refractive index in the sample (Conel 1969). This feature is diagnostic for the mineralogy (Conel 1969). (2) The Reststrahlen Bands (RB), as a result of dominating surface scattering of photons. RBs arise from the Si-O and Al-O stretching (e.g., Pieters and Englert 1993; Iiishi et al. 1971). (3) The Transparency Feature (TF) results from increased volume scattering of the infrared radiation and is only visible in samples with small grain sizes (< 25 μm) (Pieters and Englert 1993).

Because peak fitting is complex (Malcherek et al. 1999), especially in powder reflectance spectra with broad and overlapping peaks, we decided to use the autocorrelation method, which gives us a measure of the peak widths. This method was used successfully to determine the degree of order in cordierite and Al,Ge ordering in Ba[Al2Ge2O8] feldspar (e.g., Malcherek et al. 1995; Salje et al. 2000). Following this, we analyzed the feldspar infrared spectra not only in terms of band positions but also with autocorrelation of specific band regions. For this we had to slightly modify the method given by Salje et al. (2000) and calculated the following correlations. From the autocorrelation function we used the FWHM (Full Width at Half Maximum) of the complete autocorreleation function for two specific band regions from 8 μm to 9 μm and from 9 μm to 10 μm, because of the remarkable changes in the spectra in these bands without baseline correction. Gaussian fits to the central part of the autocorrelation function from 7.27 μm to 12.11 μm were calculated with a constant offset around zero considering our spectral resolution (Offset values for fitting: -26 cm− 1 and 26 cm− 1. From this fit to the central part of the autocorrelation function we used the width ω, which corresponds with k2 in Salje et al. (2000).

Results

X-ray diffraction

Heating of the Volkesfeld sanidine (ID 73) for eleven days at 850 ∘C led to further disorder resulting in a final value of \(\sum \mathrm {t_{1}}=0.58\) (ID 129). Heating of samples ID 73 and ID 129 in molten KCl lead to an Or content of 100% in the samples ID 149 and ID 150. The degree of order remained unchanged. After ion exchange of the Prilep Microcline ID 151 in molten KCl, the produced sample (ID 152) had an Or content of 99% with no observable Ab component in the XRD diagram. The calculated degree of order was also unchanged within the range of uncertainty (Table 1).

The degree of order in the low albite sample ID 163 that had been heated for 8 days at 1060 ∘C decreased from \(\sum \mathrm {t_{1}} = 1\) to 0.90; after 15 d it was down to 0.86 (ID 164). In the experiment that lasted 18 d (ID 165), the silica glass tube was bulging and was possibly broken, most likely because of a too high water vapor pressure. The crystals, however, were not molten. XRD analysis showed two albite populations, 32% of the original low albite had not yet started to disorder, 68% were high albite with \(\sum \mathrm {t_{1}} = 0.69\). An average value of \(\sum \mathrm {t_{1}}= 0.79\) was assigned to the sample. The silica glass tube of sample ID 166 also strongly bulged but did not break and for this sample, the degree of order was determined from XRD refinment to \(\sum \mathrm {t_{1}}=0.77\). For sample ID 167, after opening the tube a small hole near the weld seam was noticed. At this position the tube wall was probably thinner because of welding and therefore a hole could form due to the water vapor pressure. The calculation of the degree of order gave a highly disordered \(\sum \mathrm {t_{1}}=0.55\). All samples, their precursor material, treatment, refined XRD data, Ab-Or-content, as well as degree of Al,Si order are listed in Table 1 (compare section results).

Infrared

Our main goal was to investigate the spectral range between 7 μm and 14 μm (marked by a gray background in Figs. 1 and 2 /≈ 1429 cm− 1 to 714 cm− 1), which corresponds to the measurement range of the MERTIS instrument. The overall reflectance of our samples decreases with decreasing particle size because surface scattering is decreased compared to volume scattering. The autocorrelation function was used for the analysis of this spectral range (ranges of autocorrelation calculations: 8 μm to 9 μm (1250 cm− 1 to 1111 cm− 1), 9 μm to 10 μm (1111 cm− 1 to 1000 cm− 1), and 7.27 μm to 12.11 μm (825 cm− 1 to 1376 cm− 1).

Fig. 1
figure 1

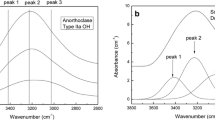
a Spectra of all samples with Ab100 with different degree of order and grain sizes between 63 μm and 125 μm (i20∘, e30∘). The gray region indicates the measurement range of MERTIS. The black lines indicate a feature shifting with \(\sum \mathrm {t_{1}}\) and Or content. The dashed lines indicate the borders of the region for autocorrelation analysis and the associated fit analyzes to determine the degree of order. The dashed-dotted lines indicates the bands for autocorrelation analyzes for the determination of the Or content. b The same as in a but for samples with Or100 to Or85

Full size image
Fig. 2
figure 2

a Spectra of all samples with Ab100 with different degree of order and grain sizes smaller 25 μm (i20∘, e30∘). The gray region indicates the measurement range of MERTIS. The black lines indicate a feature shifting with \(\sum \mathrm {t_{1}}\) and Or content. The dashed lines indicate the borders of the region for autocorrelation analysis and the associated fit analyzes to determine the degree of order. The dashed-dotted lines indicates the bands for autocorrelation analyzes for the determination of the Or content. b The same as in a but for samples with Or100 to Or85

Full size image

Figure 1 shows the spectra of samples with a grain size of 63 μm to 125 μm, measured at i20∘ and e30∘ for samples with compositions Ab100 (Fig. 1a) and Or100 to Or85 (Fig. 1 b). The spectra change with the degree of Al,Si order. RB peaks, which are related to Si-O and Al-O stretching (Iiishi et al. 1971), broaden and disappear with increasing disorder. In the ordered species (ID 151, 152, 125), four clear bands and one to two shoulders can be distinguished between 8 μm (1250 cm− 1) and 10.5 μm (952 cm− 1) in the region of the RBs. In contrast, the spectra of disordered species show only two or three broad peaks and two or three shoulders. Spectral differences resulting from the varying Or content in the disordered samples (ID 73, 129, 149, 150) are only minor. The absolute intensities of the RB peaks change with the degree of order as well. There are no observable RB shifts resulting from Al,Si distribution changes. The mean wavelength of the CFs is ca. 7.83 μm (1277 cm− 1) for the Or-rich samples (ID 73, 129, 149, 150, 151, 152) compared to 7.72 μm (1295 cm− 1) for the Ab100 samples (ID 125, 163, 164, 165, 166, 167). As an effect of small grain sizes, spectral contrast and overall reflectance are reduced (Fig. 2). Thus, the peaks in the spectral region of the RB in samples with a high Al,Si order are weak but still distinguishable. In the spectra of the more disordered species (ID 73, 129, 149, 150, 165, 166, 167), the small grain sizes also led to a decrease of the RB bands, so that the spectra are difficult to distinguish. In addition, the TF is clearly visible in the spectra as a large broad peak between 11 μm and 12 μm (909 cm− 1 and 833 cm− 1).

Discussion

General remarks

In the following, we discuss the infrared powder reflectance spectra results in terms of peak shift and the autocorrelation analyzes for the three different grain size fractions. In addition, we debate implications that arise for remote sensing.

IR absorption spectra show decreasing band intensities, increasing linewidths, and shifts of bands with decreasing Al,Si order (e.g., Zhang et al. 1997). Our powder reflectance spectra exhibit the same changes. Zhang et al. (1997) correlated peak positions and linewidths of absorption spectra above 16.6 μm (below 600 cm− 1) and in the far infrared around 33 μm (300 cm− 1) with Or content and degree of order of alkali feldspars. In contrast, our study focused on the mid-IR, especially the wavelength region from 7 μm to 14 μm (1429 μm to 714 cm− 1), which is the measurement range of the MERTIS experiment (Hiesinger et al. 2010; H. Hiesinger and co-workers, in preparation).

Following the classification of Iiishi et al. (1971), the IR bands between 8.6 μm (1162 cm− 1) and 17.2 μm (580 cm− 1) should only depend on stretching and bending of the bonds between Si or Al and O-ions. In contrast, we found in our analysis, that this wavelength region is also affected by the Or-content. This is probably associated with the change of the bond length <T-O> in the alkali feldspar crystal structure due to the Or-content (Ribbe 1983).

Feature shift analysis

In Fig. 3, the position of the maximum of the spectral feature, denoted as 15.48 μm (646 cm− 1) feature thereafter, that is bounded by two black lines in Figs. 1 and 2 is plotted versus the degree of order, \(\sum \mathrm {t_{1}}\). The marked feature shifts from 15.26 μm (655 cm− 1) in pure low albite to 15.40 μm (649 cm− 1) in disordered high albite. These results are in agreement with the peak shifts in absorption spectra reported by Zhang et al. (1996) for low albite but for the high albite sample it is shifted around Δ = 0.12 μm towards shorter wavelengths (higher wavenumbers; Δ = 5 cm− 1). In microcline with Or100 the feature is at 15.41 μm (649 cm− 1) and shifts to 15.69 μm (637 cm− 1) in highly disordered sanidine with Or100 (Fig. 3). Zhang et al. (1996) reported an absorption feature in microcline also at around 15.43 μm (648 cm− 1) and for highly disordered sanidine with Or100 at around 15.67 μm (638 cm− 1), which is in agreement with our reflectance data. These discussed features in the spectral range around 15.48 μm (646 cm− 1) should be originating from bending of O − Si(Al) − O bonds (Zhang et al. 1996). The intensity of this bond depends on the degree of order (Iiishi et al. 1971). Our results confirm these findings as seen in Fig. 3a. In addition, the Or-Ab content also affects shape and position of the analyzed feature in reflectance spectra. Therefore, we fitted the wavelength of the 15.48 μm (646 cm− 1) feature to the degree of Al,Si order of the samples with Or100 and Ab100, respectively. The 15.48 μm (646 cm− 1) feature in the spectra of samples with grain sizes smaller than 25 μm (Fig. 3b) is not as well resolved as in the spectra for the larger grain sizes (Fig. 3a). In the microcline-sanidine series (ID 73, 129, 149, 150, 151, 152) the 15.28 μm (646 cm− 1) feature is only visible as a shoulder. In these cases, fitting of the spectral region of interest was done with a function of the form \(R(\lambda )=a\cdot \left (b-\lambda \right )^{3}+d\cdot \lambda +c\) (R reflectance, λ wavelength in μm). The variation of the band position with \(\sum \mathrm {t_{1}}\) is about the same for both grain size fractions (Fig. 3). The slopes and intercepts with the y-axis of the straight lines are, however, affected by the grain size, which highlights the need of powder reflectance spectra for remote sensing (Table 2). The 15.28 μm (646 cm− 1) feature shifts slightly (mean deviation Δ125 − 25 ≈ 0.06 μm) to shorter wavelengths in the sample fraction with smaller grain sizes. This deviation is 0.01 μm larger than our estimated upper bound of the uncertainty of the feature wavelength of 0.05 μm. In particular, two microcline samples (ID 151, 152) and the albite sample (ID 125) show larger deviations (Δ125 − 25,MICRO,ALB ≈ 0.12 μm) from the large to the small grain sizes. For all other samples, the mean deviation is at the upper bound of uncertainty; therefore, the grain size-dependent shift of the feature could be neglected. Based on our study we conclude, that with the feature shift analysis of the 15.28 μm (646 cm− 1) feature, the degree of order of an alkali feldspar can be estimated if the chemical composition is known.

Fig. 3
figure 3

a Band position of the feature marked in Fig. 1 for grain sizes between 63 μm and 125 μm. Dashed-dotted line Or100 fit; dotted line Ab100 fit. b Same as a for figure but for grain sizes smaller 25 μm

Full size image
Table 2 Functions of the different fits calculated with the software gnuplot v.5.2
Full size table

Autocorrelation analysis

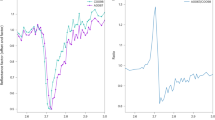
The calculations of the autocorrelation analyses were related to the degree of order and the Or content. Figure 4 shows a typical autocorrelation function. We tested several different ways of combining autocorrelation analyses (linear, polynomial, and ratio correlations) and degree of order as well as Or content. Ratios of different spectral regions are a common way in multi- or hyperspectral data analysis to identify distinct chemical compositions (e.g., Vincent and Thomson 1972; Kirland et al. 2002). In Fig. 5, the ratio FWHM of the autocorrelation function of the spectral range from 8 μm to 9 μm (1250 μm to 1111 cm− 1) to that of the spectral range from 9 μm to 10 μm (1111 μm to 1000 cm− 1) (denoted as Ψ thereafter) is plotted against the Or content for all analyzed samples and grain size fractions. Samples with smaller Or contents have a larger Ψ value than Or-rich samples.

Fig. 4
figure 4

Typical autocorrelation function (Auto.corr. is the value of the autocorrelation function) with marked FWHM and fit to the central peak between -26 cm− 1 and 26 cm − 1 (inset with ω of the Gaussian fit): ID 125 albite, spectral range 7.27 μm to 12.11 μm

Full size image
Fig. 5
figure 5

Correlation between Or content and Ψ, which is defined as the ratio of the FWHM of the autocorrelation function of the spectral range from 8 μm to 9 μm to that of the spectral range from 9 μm to 10 μm (see dashed-dotted lines in Figs. 2 and 3) a Grain sizes of 63 μm to 125 μm; b Grain sizes from 25 μm to 63 μm, and c Grain sizes smaller than 25 μm. The yellow data point is sample ID 12 with Or62. Although it supports the linear trend between the endmembers it was not used for the fit because of contamination with quartz

Full size image

One measured sample with an intermediate chemical composition between Or and Ab (Or62) suggest a linear relationship of Ψ value and Or content (yellow data point in Fig. 5). However, because of some accessory minerals contained in the sample, it was not suitable for exact spectral analysis. To prevent uncertainties resulting of this contamination we fitted our data with a linear function, without using of the data of the sample with intermediate composition. The slope of the fitted straight line and its intercept with the y-axis increase with decreasing grain sizes, but the overall behavior is the same for all fractions (Table 2). The respective fit functions are Or(mol%) = − 321 ⋅Ψ + 403 for samples with grain sizes between 63 μm and 125 μm, Or(mol%) = − 360 ⋅Ψ + 454 for samples with grain sizes between 25 μm and 36 μm, and Or(mol%) = − 428 ⋅Ψ + 568 for the smallest grain size fraction.

In Fig. 6, the width \(\omega =FWHM/\sqrt {\ln 4}\) of a Gaussian fit (note: this FWHM is from the Gaussian fit and therefore something different as the FWHM from above) to the central peak from -26 cm− 1 to 26 cm− 1 on the x-coordinate of the autocorrelation function of the spectral band region from 7.27 μm to 12.11 μm (1376 μm to 826 cm− 1) is plotted versus the degree of order. The black line in Fig. 6a is a quadratic fit to all the samples with a grain size ranging from 63 μm to 125 μm. The fit function to the dependence of the width ω of the Gaussian fit curve on \(\sum \mathrm {t_{1}}\) is given by \(\sum \mathrm {t_{1}}=-0.0005\cdot \left (26-\omega \right )^{2} +1.02\) (Fig. 6a). In Fig. 6b and c, the results for the grain size fractions from 25 μm to 63 μm and smaller than 25 μm are plotted. The analyses of the smaller grain size fractions led to a split in the correlation of ω and and degree of order for Or-rich samples and Ab-rich samples (\(\sum \mathrm {t_{1}}\mathrm {Or_{100}}=-0.032\cdot \omega + 1.9\) and \(\sum \mathrm {t_{1}}\mathrm {Ab_{100}}=-0.016\cdot \omega +1.5\) for grain sizes from 25 μm to 63 μm and \(\sum \mathrm {t_{1}}\mathrm {Or_{100}}=-0.12\cdot \omega + 4.3\) and \(\sum \mathrm {t_{1}}\mathrm {Ab_{100}}=-0.06\cdot \omega +2.8\) for the smallest grain size fraction). This implies that the grain size distribution has a large effect on the form of the autocorrelation function in the regions of the RB (Table 2). This is probably an effect of the reduced spectral contrast in combination with decreasing reflectance in spectra of samples with smaller grain sizes compared to those with larger grain sizes. The combination of the effects leads to a reduced FWHM of the peaks which is visible through the calculation of the autocorrelation function.

Fig. 6
figure 6

Correlation between ω of Gaussian fit to the central part of the autocorrelation function of the wavelength region from 7.27 μm to 12.105 μm (see dashed lines in Figs. 2 and 3) and the degree of order (\(\sum \mathrm {t_{1}}\)). a Grain size range from 63 μm to 125 μm. The black line is a quadratic fit to all samples. b Grain size range from 25 μm to 63 μm. Dashed-dotted line Or100 fit; Dashed line Ab100 fit, and c Same as b but with grain size smaller than 25 μm

Full size image

Iiishi et al. (1971) stated that the mid-IR spectral region of alkali feldspars is unaffected by alkali ions and only affected by the degree of order. In contrast, with the autocorrelation analysis we can distinguish not only the degree of order within infrared reflectance spectra between 7 μm and 14 μm but also the Or content. Nevertheless, the reflectance spectral behavior is more complex, because the analyzed grain size fractions have an influence on the RBs, which in turn have an influence on the autocorrelation function. Therefore, knowing the grain sizes of the samples is necessary for accurate determinations of Or content and degree of order from the spectra. Best results were obtained from samples with a grain size between 63 μm to 125 μm.

Conclusions

We investigated reflectance mid-IR powder spectra of endmember alkali feldspars with respect to their Ab-Or content and their Al,Si distribution which were derived from XRD analysis. The results of this study showed that the Al,Si degree of order as well as the Or content can be determined by reflectance spectroscopy. Thus, these results are important and applicable for future space missions carrying TIR spectrometers.

Mid-infrared spectra of alkali feldspars are strongly affected by the distribution of Al and Si on the non-equivalent tetrahedral sites of the frame-work structure and are less affected by the amount of K and Na. Previous work showed that the positions of specific absorption bands are related to the Al,Si distribution (e.g., Martin 1970). On the basis of our study, we demonstrate that a specific feature found in all of our investigated spectra around 15.48 μm (646 cm− 1), which is in the same spectral region as investigated by Martin (1970), is a measure of the state of order. This feature shifts from 15.26 μm (655 cm− 1) in pure low albite to 15.40 μm (649 cm− 1) in disordered high albite and from 15.41 μm (649 cm− 1) in microcline to 15.69 μm (637 cm− 1) in highly disordered sanidine (Fig. 3). As different means to investigate the degree of order, Malcherek et al. (1995) introduced the autocorrelation analysis of absorption spectra. In contrast to the feature shift analysis discussed above, the autocorrelation analysis, which provides insights into the chemical composition as well as the degree of order, can be applied to the measurement range of MERTIS. We used the autocorrelation analysis on reflectance spectra for different spectral regions. The ratio of FWHM of the autocorrelation function of 8 μm to 9 μm (1250 μm to 1111 cm− 1) to the autocorrelation function of 9 μm to 10 μm (1111 μm to 1000 cm− 1), called Ψ, is linearly dependent on the Or content (Fig. 5). Iiishi et al. (1971) predicted that the alkali ions do not affect the region of the RB in absorption spectra of alkali feldspar. With our approach it is possible to determine the Or content of (pure) alkali feldspars from their reflectance spectra. Salje et al. (2000) suggested autocorrelation of the absorption spectra from 12.11 μm to 7.27 μm (825 cm− 1 to 1376 cm− 1) for cordierite and fitting of the central peak of the autocorrelation function with a Gaussian curve to investigate the degree of order. We used the same approach to analyze our powder reflectance spectra because MERTIS measures in the same spectral range and we are also observing spectral changes in these wavelength region. For samples with grain sizes between 63 μm and 125 μm the correlation of \(\sum \mathrm {t_{1}}\) and the width ω of a Gaussian fit to the central part of the autocorrelation function is independent of the Or-content of the samples and thus allows to identify the degree of order without previous determination of the chemical composition. For samples with a grain size below 63 μm, however, the relation between ω and \(\sum \mathrm {t_{1}}\) becomes dependent on the Or content.

Depending on the spectral deconvolution of data returned from MERTIS, it will be possible not only to determine the degree of order of an alkali feldspar, but also its chemical composition. The data gained in this study as well as the calculated correlations are the basis for further investigations of the feldspar system, especially for remote sensing of other planetary surfaces. Further work on the alkali feldspar system will include samples with intermediate chemical compositions plus mechanical mixtures with the same bulk composition.