Effect of the porous structure on the hygrothermal vibration analysis of functional graded nanoplates using nonlocal high-order continuum plate model

Abstract

This study delves into the thermomechanical vibration behavior of functionally graded porous nanoplates under extreme thermal temperature and humidity conditions. The equation of motion of the nanoplate was derived using advanced theories in elasticity and deformation. The nanoplate consists of metal (SUS304) on the bottom surface and ceramic (Ni₃S₄) on the top surface, with the material distribution changing according to the power law across the plate thickness. The nanoplate was modeled with uniform and symmetric distributions of porosity reaching as high as 60%. Upon incorporating the thermal and moisture loads from the humid surroundings into the equations of motion derived from Hamilton's principle, the equations were solved using Navier's method and simplified to the eigenvalue equation. Analyzed within a broad framework are the thermomechanical vibration behavior of the nanoplate, temperature impact, humidity influence, porosity and its distribution, material grading parameter effects, and nonlocal integral elasticity effects. Observations indicate that variations in thermal temperature, humidity, and nonlocal parameters can lower the thermomechanical vibration frequency of the nanoplate, whereas porosity has the opposite effect. The effects mentioned are influenced by factors, such as the porosity ratio, porosity distribution, material ratios, and the size of the nonlocal parameter in the plate. The primary objective of this work is to uncover the nonlinear frequency response of nanoplates with high porosity in conditions characterized by high temperature and humidity.

1 Introduction

In recent years, functionally graded materials (FGMs) have been used in so many engineering applications. FGM is often used in applications that involve the integration of ceramic and metal components. The integration of metal components with high fracture toughness and ceramic components with high heat resistance and low thermal conductivity offsets the limits of each other, leading to a material with substantially improved capacity. The bending analysis of a sandwich plate using the first-order shear deformation theory and nonlocal strain gradient theory is investigated [1]. Bending and buckling studies are analyzed for a rectangular nanoplate made of BiTiO3–CoFe2O4 [2]. Using the quasi-3D sinusoidal shear deformation plate theory and the nonlocal strain gradient theory (NSGT) dynamic instability of viscoelastic porous functionally graded (FG) nanoplates under biaxially oscillating loads and longitudinal magnetic field have been examined [3]. Vibrations and buckling behavior of thin laminated composite nanoplates in a hygrothermal environment, employing the second-order strain gradient theory have been studied [4]. The buckling characteristics of porous double-layered functionally graded nanoplates in a hygrothermal environment have been investigated under different conditions [5]. Under sinusoidal and uniform loads in a hygrothermal environment the flexural response of nanoplates has been examined [6]. The nonlocal strain gradient theory (NSGT) has been used for examining the dynamic behavior of bi-directional (2D) functionally graded (FG) porous nanoplates supported by Winkler and Pasternak elastic foundations [7]. The static bending and free vibration response of organic nanoplates have been investigated using nonlocal theory and different shear strain theories [8]. A computational method has been developed for forecasting the mechanical properties of nanoplates made of functionally graded triply periodic minimum surface (FG-TPMS) material, reinforced with graphene platelets (GPLs) [9]. Uninterrupted shear function for the analysis of the natural vibration of functionally graded (FG) nanoplates that contain internal porosity by using isogeometric analysis (IGA) has been investigated [10]. For the structural elements, the nonlocal equations and modified boundary conditions have been examined separately with generalized differential quadrature method [11]. The isogeometric analysis (IGA) have been examined using the modified nonlocal couple stress theory (MNCST) to investigate the bending and free vibration properties of functionally graded (FG) nanoplates supported by an elastic foundation (EF) [12]. The thermomechanical vibration characteristics of sandwich nanoplates composed of a foam or solid core layer and smart surface layers have been investigated under different conditions [13]. The propagation of bending waves in porous functionally graded embedded nanoplates have been studied under thermal and magnetic conditions using high-order plate and nonlocal strain gradient elasticity theories [14]. The thermal vibration of a foam core nanoplate made of ceramic silicon nitride (Si3N4) and metal biomaterial (Ti–6Al–4 V) in the core layer, and cobalt-ferrite (CoFe2O4) and barium-titanate (BaTiO3) in the face layers have been investigated [15].

The influence of different factors on the natural frequencies of magneto-electro-viscoelastic functionally graded (FG) nanobeams are investigated under various boundary conditions [16]. Bending behavior of a simply supported functionally graded piezoelectric plate has been examined for different conditions under an in-plane magnetic field [17]. The active vibration control of a host structure that is bonded with a layer of functionally graded piezoelectric material (FGPM) serving as both a sensor and an actuator has been studied [18]. Buckling behavior of functionally graded (FG) nanobeams which are supported by an elastic foundation and exposed to a unidirectional magnetic field has been investigated under humidity and heat stresses [19]. Considering refined plate theory (RPT) and small-scale effects the free vibration behavior of nanoscale FG rectangular plates has been examined and results show that RPT does not demand a shear correction factor [20]. Dispersion and attenuation characteristics of thermoelastic Lamb waves in functionally graded material nanoplates have been investigated considering integral form of the modified nonlocal theory and according to obtained results escape frequency does not exist [21]. Propagating and evanescent waves in functionally graded (FG) nanoplates with the consideration of nonlocal effect have been analyzed [22]. Using nonlocal theory for the dynamic analysis of the functionally graded porous (FGP) L-shape nanoplate upon the elastic foundation (EF) have been studied with a finite element method (FEM) [23]. The free vibration behavior of functionally graded (FG) porous doubly curved shallow nanoshells under variable nonlocal parameters has been investigated using modified the classical Eringen’s nonlocal elasticity theory [24]. Using the new higher order deformation theory and nonlocal strain gradient elasticity theory thermomechanical buckling behavior of sandwich nanoplates that include foam core layers has been studied [25]. The thermal buckling characteristics of sandwich porous plates composed of metal-ceramic functionally graded material (FGM) components has been analyzed with a novel sinusoidal high-order shear theory [26]. The geometrically nonlinear dynamic response of a joint shell which made of functionally graded material conical–cylindrical–conical has been examined under the effect of rapid surface heating [27]. Using a quasi-3D plate theory, axisymmetric free vibration has been studied for the functionally graded (FG) sandwich annular plates [28]. Using the Newton–Raphson iterative approach and β-Newmark time estimate approach the geometrically nonlinear dynamic response of hermetic capsule construction made of functionally graded materials subjected to thermal shock has been examined [29]. For a conical panel which made of functionally graded materials, the phenomenon of thermally induced vibrations has been investigated by considering the thermal and mechanical characteristics of the panel are uniformly distributed in the thickness direction [30]. Using the modified couple stress theory, the nonlinear bending behavior of elastic tubes composed of functionally graded porous material has been studied [31].

A study which equation of motion for the beam model is determined to be two orders of magnitude greater than that of the conventional Euler–Bernoulli model using magneto-electro-elastic (MEE) properties for nanomaterials has been carried out [32]. An analytical model has been created using the equivalent layered technique to assess the effective properties of magneto-electro-elastic (MEE) composites, in which the fibers are responsive to both electrical and magnetic domains. According to results that the model calculations exhibited a satisfactory level of concordance with other proposed models [33]. A study has been proposed a higher-order model to analyze the static and free vibration characteristics of magneto-electro-elastic plates, both thin and thick. Results were compared with several models for static and free vibration conditions [34]. A novel analytical buckling solution for a cylindrical shell composed of two-phase magneto-electro-thermo-elastic (METE) composites, subjected to multiple physical fields, has been derived using a Hamiltonian-based method. The proposed solution was thoroughly compared to provide a full evaluation, and the results show a high level of agreement with other studies [35]. For studying the nonlinear magneto-electro-elastic vibration of a smart sandwich plate an analytical methodology has been presented [36]. In a hygrothermal environment an analytical method has been presented for analyzing the linear vibrations and buckling of nanoplates [37]. The time-dependent behavior of magneto-electro-elastic (MEE) structures in a hygrothermal environment has been conducted using the cell-based smoothed finite element method (CS-FEM) in combination with the modified Newmark scheme [38]. Using finite element method, the impact of the hygrothermal environment on the free vibration properties of magneto-electro-elastic (MEE) plates has been investigated [39]. A nonlocal modified sinusoidal shear deformation plate theory including the thickness stretching effect has been studied for the free vibration and buckling responses of functionally graded nanoplates with magneto-electro-elastic coupling [40]. An investigation has been conducted on the free vibration characteristics of a composite beam made of BaTiO3–CoFe2O4, which is multiphase and layered, and possesses magneto-electro-elastic properties [41]. The free vibration of simply supported and multilayered magneto-electro-elastic plates has been analyzed using a hybrid approach that combines the state space approach (SSA) and the discrete singular convolution (DSC) algorithm [42]. An investigation has been presented for free vibrations in functionally graded, anisotropic, and linear magneto-electro-elastic plates using a semi-analytical finite element method [43]. Vibrations of a voids cylinder that is rigidly fixed electro-magneto nonlocal elastic with generalized thermo-elasticity has been presented [44]. The solution of deformations in a magneto-electro-elastic plate with non-uniform materials has been investigated using the scaled boundary finite element technique (SBFEM) [45]. The asymptotic homogenization method (AHM) has been utilized to analyze a set of boundary value problems involving linear thermo-magneto-electro-elastic (TMEE) heterogeneous material [46]. Using the finite element (FE) approach the static response of a magneto-electro-elastic (MEE) plate under hygrothermal loads has been examined [47]. A computational model has been proposed for the solution of magneto-electro-elastic (MEE) shell structures [48]. Finite element (FE) methods have been utilized to anticipate how the spatial arrangement of two-phase Barium Titanate (BaTiO₃) and Cobalt Ferric Oxide (CoFe₂O₄) particulate composites affects the static response of magneto-electro-thermo-elastic (METE) plates [49]. For free vibration and transient dynamic problems of the composite magneto-electro-elastic (MEE) cylindrical shell the scaled boundary finite element method (SBFEM) has been explored [50]. To calculate effective elastic constants of generally anisotropic multilayer composites an exact matrix method has been proposed and results calculated for a composite which made of BaTiO3–CoFe2O4 [51]. Theoretical modeling of a new nano-mass sensor system consists of a smart core that is combined with graphene layers on both its top and bottom surfaces has been studied [52]. Wave propagations have been analyzed in a transversely isotropic thermo-electro-magneto-elastic circular fiber [53]. The nonlinear vibration and bending problems have been studied for magneto-electro-elastic laminated beams in thermal environments [54]. Using nonlocal third-order shear deformable beam model, the forced vibration behavior of magneto-electro-thermo-elastic (METE) nanobeams has been investigated based on the nonlocal elasticity theory with the von Karman geometric nonlinearity [55]. The frequency response of functionally graded carbon nanotube with magneto-electro-elastic (FG-CNTMEE) plates has been examined under open and closed electro-magnetic circuit conditions [56]. A finite element (FE) formulation has been proposed for the calculating porosity effects on the static responses and free vibration of functionally graded skew magneto-electro-elastic (FGSMEE) plate [57]. Under the multi-field coupled loadings effect, the post‐buckling analysis of magneto‐electro‐elastic (MEE) composite cylindrical shells has been performed [58]. An investigation has been conducted on the vibration and buckling characteristics of a single-layer cylindrical nano-shell, which is subjected to thermo-electro-magneto-elastic effects and rests on a Winkler base [59]. The thermo-electro-magnetic mechanical properties of a flexoelectric nanoplate have been studied by employing a modified flexoelectric theory and applying the classical Kirchhoff plate theory [60]. Under the thermal environment condition for a multilayered magneto-electro-elastic (MEE) beam a three-dimensional finite element (FE) formulation has been proposed [61]. A cell-based smoothed finite element method (CS-FEM) has been suggested for qualify the steady-state magneto-electro-elastic (MEE) structures combining of the coupling among elastic, electric, magnetic, and thermal properties in the thermal environment [62]. The size-dependent response of magneto-electro-thermo-elastic (METE) nanobeams under effect of propagating wave has been studied by using sinusoidal shear deformation beam theory (SSDBT) [63]. With various edge supports, size-dependent post-buckling behavior of magneto-electro-thermo-elastic (METE) nanobeams has been studied [64]. A magneto-electro-thermo-elastic (METE) nanobeam model with nonlocal geometrically that under the influence of external electric voltage, external magnetic potential, and uniform temperature increase has been proposed [65]. Considering nonlocal and surface effects based on the principle of virtual work and Mindlin’s theory, a two-dimensional (2D) magneto-electro-thermo-elastic (METE) laminated plate theory has been suggested [66]. Using Timoshenko beam theory with the von Kármán geometric nonlinearity, the thermal post-buckling behaviors of magneto-electro-elastic laminated beams have been studied [67]. Using free energies, state variables, and state equations a new thermo-electro-magneto-mechanical (TEMM) model has been proposed for understand to behavior in the finite-deformation regime [68]. Using Kirchhoff's plate theory and nonlocal theory, thermo-electro-magneto-mechanical bending behaviors have been studied for a sandwich nanoplate [69]. A meshless approach has been proposed for analyzing the stresses and deflections in an advanced smart lightweight sandwich plate (ASLSP) under thermo-electro-mechanical loads [70]. Displacements and electro-magnetic potentials have been studied using a trigonometric method with strain gradient nonlocal procedure [71]. A unified model that formulated by first-order shear deformation theory (FSDT) combing with the Voigt model and modified power-law distribution has been suggested to understand the vibration and acoustic radiation behaviors of magneto-electro-thermo-elastic functionally graded porous plates (METE-FGPPs) [72]. Consisting of Barium Titanate (BaTiO₃) and Cobalt-Ferric oxide (CoFe₂O₄) a cantilever beam have been modeled for the effect of volume fraction [73]. The size-dependent vibrational behaviors of functionally graded (FG) magneto-electro-viscoelastic nanobeams have been investigated via Timoshenko beam theory in conjunction with the Kelvin–Voigt viscoelastic model [74]. Using Timoshenko beam model, wave propagation analysis of a nanobeam made of functionally graded magneto-electro-elastic materials with rectangular cross section rest on Visco-Pasternak foundation has been explored for the axial, rotation, and transverse deformations [75]. The propagation of waves in magneto-electro-elastic (MEE) nanoshells has been studied based on the Kirchhoff–Love shell theory and the first-order shear deformation (FSD) shell theory, respectively [76]. The dispersion behavior of waves has been studied for magneto-electro-elastic (MEE) nanobeams that modeled as Euler nanobeam model and Timoshenko nanobeam model [77]. As a novel semi-analytical technique, the wave-based method (WBM) has been proposed for studying the wave propagation properties of magneto-electro-thermo-elastic nanobeams with arbitrary boundary conditions [78]. A new method that uses meshfree techniques has been presented to analyze the free vibrations of magneto-electro-elastic (MEE) functionally graded (FG) nanoplates, considering their size-dependence [79]. A nonlocal strain gradient isogeometric model, which is based on the higher-order shear deformation theory, nonlocal strain gradient theory, and isogeometric analysis method, has been investigated to analyze free vibration of functionally graded (FG) nanoplates made of magneto-electro-elastic (MEE) materials [80]. Energy dissipation of plane waves in sandwiched functionally graded material (FGM) nanoplates has been examined using the Lord-Shulman thermo-electric-elastic (TEE) theory and the nonlocal integral elasticity effect [81]. Analysis of the thermal vibration and buckling behavior has been studied for a functionally graded nanoplate [82]. Zhu et al. has conducted an investigation on the correlation between the nonlinear free vibration behavior and the nonlinear forced vibration behavior of viscoelastic plates [83]. He et al. [84] conducted a study on the free vibration of piezoelectric semiconductor plates and found that the natural frequency and damping characteristic are significantly influenced by the nonlocal parameter and geometric properties.

As summarized above, studies on the thermomechanical behavior of nanoplates intended to operate in high temperature and humidity environments are limited in the literature. In this study, a porous FGM metal (SUS304)-ceramic (Si₃N₄) nanoplate with potential for use in high temperature and humidity environments was modeled using high-order shear deformation theory and nonlocal integral elasticity, with the addition of stretching effects. The modeling has been created to provide the highest level of precision, considering all effects. The results of this study will be beneficial in advanced industrial applications such as nano-sensor carrier plates that will operate in high thermal loads and humidity environments, soft robotic applications, nanodrug delivery applications, and gas sensing applications in high temperature environments. The primary objective of this work is to uncover the nonlinear frequency response of nanoplates with high porosity in conditions characterized by high temperature and humidity. Furthermore, an investigation was conducted to analyze the impact of the porosity distribution function on the frequency response, considering the symmetrical and uniform distribution of porosity throughout the height of the nanoplate, as well as the significant presence of a 60% porosity content. The incorporation of the nanosize effect was achieved by combining Eringen's nonlocal integral elasticity theory with high-order plate theory, resulting in more accurate and realistic analytical outcomes.

Figure 1 shows a nanoplate with functionally graded (FGM) porosity located in a hygrothermal environment. Nanoplate consists of materials that SUS304 (metal) on the bottom surface and silicon Nitride Si₃N₄ (ceramic) on the top surface. The material distribution of the nanoplate between the forehead and the upper surface is determined by a power law.

Fig. 1

Configuration of a thick FGM porous nanoplate in hygrothermal fields

2 Temperature-dependent material properties

In this study, it is assumed that the properties of the metal and ceramic materials forming the nanoplate change depending on temperature, and the effective material properties are defined as follows [83]:

$$P\left( T \right) = P_{0} \left( {P_{ - 1} T^{ - 1} + 1 + P_{1} T + P_{2} T^{2} + P_{3} T^{3} } \right).$$

(1)

Table 1 shows the P₀, P_-1, P₁, P₂, and P₃ values of S₃N₄ and SUS304 in Eq. (1), which defines the temperature-dependent material properties $P(T)$ [84].

Table 1 Temperature-dependent coefficients of the properties

At T₀ = 300 K, the nanoplate is stress-free and temperature is uniform throughout the thickness of the material, Eq. (2), linear Eq. (3) [85] and nonlinear Eqs. (4a, 4b) case are discussed [86].

$$\Delta T=T-{T}_{0}.$$

(2)

$$T(z)={T}_{m}+({T}_{c}-{T}_{m})\left(\frac{h+2z}{2h}\right).$$

(3)

$$-\frac{d}{dz}\left(\psi (z)\frac{dT}{dz}\right)=0,T\left(\frac{h}{2}\right)={T}_{c},\hspace{0.33em}\hspace{0.33em}T\left(-\frac{h}{2}\right)={T}_{m}.$$

(4a)

$$T = T_{m} + \frac{{\left( {T_{c} - T_{m} } \right)}}{{\int_{{\frac{ - h}{2}}}^{\frac{h}{2}} {\frac{1}{\psi \left( z \right)}dz} }}\int\limits_{{\frac{ - h}{2}}}^{z} {\frac{1}{\psi \left( z \right)}} dz.$$

(4b)

The temperature of the bottom surface is symbolized as T_m, the linear change of temperature along the thickness is symbolized as T_c, and the temperature of the upper surface is symbolized as T_t. ${T}_{0}=300 K$ indicates the room temperature and $\psi \left(W/mK\right)$ indicates the thermal conductivity. While calculating the effective material properties $P(z)$ properties along the plate thickness considering uniform temperature rise, the effective temperature along the plate height is calculated as $T={T}_{0}+\Delta T$ using Eq. (2). In case of linear temperature rise, $T(z)$ is calculated using Eq. (3). In case of nonlinear temperature rise, $T(z)$ is calculated from Eq. (4b) using the boundary conditions $T\left(h/2\right)={T}_{c},\hspace{0.33em}T\left(-h/2\right)={T}_{m}$ specified in Eq. (4a).

3 Porosity models and effective properties

The effective material properties ${P}_{e}$ along the height of the plate are calculated using the material properties ${P}_{c}, {P}_{m}$ and volume fractions ${V}_{c}, {V}_{m}$ of the ceramic and metal components forming the plate, as shown in Eq. (5) [87]:

$${P}_{e}={{P}_{c}V}_{c}+{{P}_{m}V}_{m}.$$

(5)

Here, ${V}_{c}$ is the volumetric fraction of the ceramic component and is defined according to a power law along the plate thickness as in Eq. (6) [87]:

$${V}_{c}={\left(\frac{z}{h}+\frac{1}{2}\right)}^{p}, {V}_{m}=1-{V}_{c}, 0\le p<\infty .$$

(6)

In Eq. (6), $p$ is the power law index (material gradation index). According to Eq. (5) elasticity modulus $E\left(z\right)$, shear modulus $G\left(z\right)$, Poisson ratio $\nu \left(z\right)$, thermal expansion coefficient $\alpha \left(z\right)$, thermal conductivity coefficient $\psi \left(z\right)$ and material density $\rho \left(z\right)$ are calculated as in Eq. (7) [84]:

$$P\left(z\right)={P}_{m}+\left[{P}_{c}-{P}_{m}\right]{V}_{c}.$$

(7)

In this study, two types of porosity distributions across the thickness are considered as given in Fig. 2. Accordingly, effective material properties are obtained by substituting the total volume fraction (α) of porosity in Eq. (6). Thus, Eqs. (8) and (9) are obtained for Models 1 and 2.

Fig. 2

Two models of porosity distribution across the thickness

In this study, it is assumed that there is porosity within the nanoplate, and that the porosity is distributed throughout the thickness of the plate in two different ways, as shown in Fig. 2. The amount of porosity in the material is symbolized as porosity volume fraction (α). Accordingly, the effective material properties given in Eq. (7) are defined as follows in case of uniform porosity [14].

$$P\left(z\right)=\left[{P}_{c}-{P}_{m}\right]{V}_{c}+{P}_{m}-\frac{\alpha }{2}\left[{P}_{c}+{P}_{m}\right].$$

(8)

Effective material properties in symmetrical porosity distribution, assuming that the porosity distribution is a trigonometric function [14]:

$$P\left(z\right)=\left\{\left[{P}_{c}-{P}_{m}\right]{V}_{c}+{P}_{m}\right\}\left\{1-\alpha cos\left[\pi \frac{z}{h}\right]\right\}.$$

(9)

4 Summary of the nonlocal elasticity theory

In this study, the nonlocal elasticity theory (NET) proposed by Eringen [88,89,90] was used to account for nonlocal effects. According to this theory, the stress–strain relationship for an elastic solid is defined as follows:

$${\sigma }_{ij}=\underset{V}{\overset{ }{\iiint }}\vartheta \left(\left|x-{x}^{\prime}\right|,\eta \right){\sigma }_{ij}^{c}dV.$$

(10)

Here, ${\sigma }_{ij}$ and ${\sigma }_{ij}^{c}$ denotes the nonlocal and classical stress tensors. Containing the small-size effects, the symbol $\vartheta$ defines the nonlocal modulus in the three dimensions of the volume. And the term $\left|x-{x}^{\prime}\right|$ defines the distance point $x$ from the point ${x}^{\prime}$. The symbol $\eta$ is the material constant described as follows:

$$\eta =\frac{{e}_{0}{l}_{i}}{L}.$$

(11)

Here, external, and internal specific lengths are defined by ${l}_{i}$ and $L$, respectively. Validating of nonlocal models, parameter ${e}_{0}$, which value calculated as 0.39 by [88] for matching the dispersion curves based on atomic model, is critical. Until recently in the literature, this value has been used ranging between 0 and 2 nm for the analysis of nanoplates by most researchers. To solve nonlocal elasticity problems, using Eq. (10) has some difficulties, and thus more general used differential form as follows:

$${\sigma }_{ij}-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}{\sigma }_{ij}=C:\varepsilon .$$

(12)

Here, $\varepsilon$ and $C$ are strain tensors and fourth-order elasticity, respectively, while double dot product is symbolized by ‘$:$’. And $\nabla =\partial /\partial x+\partial /\partial y$ is the Laplacian operator.

5 Constitutive equations

In this study, a high-order shear deformation theory (HSDT) is used for vibration analysis of the nanoplate (Fig. 1). Here, shear stresses are assumed to vary parabolic throughout the thickness and shear stresses satisfy the following boundary conditions:

$${\tau }_{xz}={\tau }_{yz}=0 \text{at }z=\pm \frac{h}{2}.$$

(13)

According to the above assumption, the displacement field in the nanoplate is as follows [20]:

$$U\left(x,y,z,t\right)=u\left(x,y,t\right)-z\frac{\partial {w}_{b}}{\partial x}-z{\varphi }_{1}\left(z\right)\frac{\partial {w}_{s}}{\partial x},$$

(14)

$$V\left(x,y,z,t\right)=v\left(x,y,t\right)-z\frac{\partial {w}_{b}}{\partial y}-z{\varphi }_{2}\left(z\right)\frac{\partial {w}_{s}}{\partial y},$$

$$W\left(x,y,z,t\right)={w}_{d}\left(x,y,t\right)+{w}_{b}\left(x,y,t\right)+{w}_{s}\left(x,y,t\right).$$

where,

$${\varphi }_{1}\left(z\right)=-\frac{1}{4}+\frac{5{z}^{2}}{3{h}^{2}}, {\varphi }_{2}\left(z\right)=-5\frac{{z}^{2}}{{h}^{2}}+\frac{5}{4}.$$

(15)

Here, $u, v, w$ represent the displacements of the plane on the neutral axis of the nanoplate in the x-, y- and z-axes, respectively, while the symbols ${w}_{\text{d}}, {w}_{\text{s}}, {w}_{\text{b}}$ represent the displacements caused by the effect of stretch, shear and bending along the z-axis, respectively. The strains for the displacement field in Eq. (14) are described as follows:

$$\left\{\varepsilon \right\}=\left\{{\varepsilon }^{0}\right\}+z\left\{{\kappa }^{b}\right\}+z{\varphi }_{1}\left(z\right)\left\{{\kappa }^{s}\right\},$$

(16)

$$\left\{\gamma \right\}=\left\{{\chi }^{e}\right\}+{\varphi }_{2}\left(z\right)\left\{{\chi }^{s}\right\}.$$

Here,

$$\left\{\varepsilon \right\}=\left[\begin{array}{c}{\varepsilon }_{x} \\ {\varepsilon }_{y}\\ {\gamma }_{xy}\end{array}\right], \left\{{\varepsilon }^{0}\right\}=\left[\begin{array}{c}\frac{\partial u}{\partial x}\\ \frac{\partial v}{\partial y}\\ \left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\end{array}\right], \left\{{\kappa }^{b}\right\}=-\left[\begin{array}{c}\frac{{\partial }^{2}{w}_{b}}{\partial {x}^{2}}\\ \frac{{\partial }^{2}{w}_{b}}{\partial {y}^{2}}\\ \left(2\frac{{\partial }^{2}{w}_{b}}{\partial x\partial y}\right)\end{array}\right], \left\{{\kappa }^{s}\right\}=-\left[\begin{array}{c}\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}\\ \frac{{\partial }^{2}{w}_{s}}{\partial {y}^{2}}\\ \left(2\frac{{\partial }^{2}{w}_{s}}{\partial x\partial y}\right)\end{array}\right],$$

(17)

$$\left\{\gamma \right\}=\left\{\begin{array}{c}{\gamma }_{yz}\\ {\gamma }_{xz}\end{array}\right\}, \left\{{\chi }^{d}\right\}=\left[\begin{array}{c}\frac{\partial {w}_{d}}{\partial y}\\ \frac{\partial {w}_{d}}{\partial x}\end{array}\right], \left\{{\chi }^{s}\right\}=\left[\begin{array}{c}\frac{\partial {w}_{s}}{\partial y}\\ \frac{\partial {w}_{s}}{\partial x}\end{array}\right].$$

Force resultants M, N, and Q can be expressed as follows:

$$\begin{aligned} \left( {M_{x}^{b} ,M_{y}^{b} ,M_{{xy}}^{b} } \right) = & \int\limits_{{ - h/2}}^{{h/2}} {\left( {\sigma _{x} ,\sigma _{y} ,\sigma _{{xy}} } \right)zdz,} \\ \left( {M_{x}^{s} ,M_{y}^{s} ,M_{{xy}}^{s} } \right) = & \int\limits_{{ - h/2}}^{{h/2}} {\left( {\sigma _{x} ,\sigma _{y} ,\sigma _{{xy}} } \right)f_{1} \left( z \right)zdz,} \\ \left( {N_{x} ,~N_{y} ,~N_{{xy}} } \right) = & \int\limits_{{ - h/2}}^{{h/2}} {\left( {\sigma _{x} ,\sigma _{y} ,\sigma _{{xy}} } \right)dz,} \\ \left( {Q_{{xz}}^{d} ,Q_{{yz}}^{d} } \right) = & \int\limits_{{ - h/2}}^{{h/2}} {\left( {\sigma _{{xz}} ,\sigma _{{yz}} } \right)dz,} \\ \left( {Q_{{xz}}^{s} ,Q_{{yz}}^{s} } \right) = & \int\limits_{{ - h/2}}^{{h/2}} {\left( {\sigma _{{xz}} ,\sigma _{{yz}} } \right)f_{2} \left( z \right)dz.} \\ \end{aligned}$$

(18)

Including the nonlocal effect in Eq. (12) and the strain and stresses in Eqs. (17 and 18), the constitutive equation of nanoplate is as follows:

$$\left\{ {\begin{array}{*{20}l} {\sigma _{{xx}} } \hfill \\ {\sigma _{{yy}} } \hfill \\ {\sigma _{{xy}} } \hfill \\ {\sigma _{{yz}} } \hfill \\ {\sigma _{{xz}} } \hfill \\ \end{array} } \right\} - \left( {e_{0} a} \right)^{2} \nabla ^{2} \left\{ {\begin{array}{*{20}l} {\sigma _{{xx}} } \hfill \\ {\sigma _{{yy}} } \hfill \\ {\sigma _{{xy}} } \hfill \\ {\sigma _{{yz}} } \hfill \\ {\sigma _{{xz}} } \hfill \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}l} {C_{{11}} } \hfill &\quad {C_{{12}} } \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill \\ {C_{{12}} } \hfill &\quad {C_{{22}} } \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad {C_{{66}} } \hfill &\quad 0 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad {C_{{44}} } \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad {C_{{55}} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\varepsilon _{{xx}} } \hfill \\ {\varepsilon _{{yy}} } \hfill \\ {\varepsilon _{{xy}} } \hfill \\ {\varepsilon _{{yz}} } \hfill \\ {\varepsilon _{{xz}} } \hfill \\ \end{array} } \right\}.$$

(19)

Here, the elastic coefficients ${C}_{ij}$ can be described as follows:

$${C}_{11}=\frac{E\left(z\right)}{1-{\upsilon }^{2}}, {C}_{12}=\frac{\upsilon E\left(z\right)}{1-{\upsilon }^{2}}, {C}_{22}=\frac{E\left(z\right)}{1-{\upsilon }^{2}}, {C}_{66}=G\left(z\right), {C}_{44}=G\left(z\right), {C}_{55}=G\left(z\right).$$

(20)

Using the strain components and the nonlocal stresses the following force resultants equations are obtained.

$$\left\{N\right\}-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\left\{N\right\}=\left[{B}^{0}\right]\left\{{\varepsilon }^{0}\right\}+\left[{B}^{1}\right]\left\{{\kappa }^{b}\right\}+\left[{B}^{1,s}\right]\left\{{\kappa }^{s}\right\}.$$

(21a)

$$\left\{{M}^{s}\right\}-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\left\{{M}^{s}\right\}=\left[{B}^{1,s}\right]\left\{{\varepsilon }^{0}\right\}+\left[{B}^{2,s}\right]\left\{{\kappa }^{b}\right\}+\left[{B}^{6,s}\right]\left\{{\kappa }^{s}\right\}.$$

(21b)

$$\left\{{M}^{b}\right\}-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\left\{{M}^{b}\right\}=\left[{B}^{1}\right]\left\{{\varepsilon }^{0}\right\}+\left[{B}^{2}\right]\left\{{\kappa }^{b}\right\}+\left[{B}^{2,s}\right]\left\{{\kappa }^{s}\right\}.$$

(21c)

$$\left\{{Q}^{s}\right\}-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\left\{{Q}^{s}\right\}=\left[{J}^{0,s}\right]\left\{{\chi }^{d}\right\}+\left[{J}^{0,s}\right]\left\{{\chi }^{s}\right\}.$$

(21d)

$$\left\{{Q}^{d}\right\}-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\left\{{Q}^{d}\right\}=\left[{J}^{0}\right]\left\{{\chi }^{d}\right\}+\left[{J}^{0,d}\right]\left\{{\chi }^{s}\right\}.$$

(21e)

where,

$$\left\{N\right\}=\left\{\begin{array}{c}{N}_{x}\\ {N}_{y}\\ {N}_{xy}\end{array}\right\},\left\{{M}^{b}\right\}=\left\{\begin{array}{c}{M}_{x}^{b}\\ {M}_{y}^{b}\\ {M}_{xy}^{b}\end{array}\right\},\left\{{M}^{s}\right\}=\left\{\begin{array}{c}{M}_{x}^{s}\\ {M}_{y}^{s}\\ {M}_{xy}^{s}\end{array}\right\},\left\{{Q}^{d}\right\}=\left\{\begin{array}{c}{Q}_{yz}^{d}\\ {Q}_{xz}^{d}\end{array}\right\},\left\{{Q}^{s}\right\}=\left\{\begin{array}{c}{Q}_{yz}^{s}\\ {Q}_{xz}^{s}\end{array}\right\}.$$

(22)

where, ${B}_{ij}, {J}_{ij}$, etc., are plate stiffness defined by

$$\begin{gathered} \left[ {B^{0} } \right] = \left[ {\begin{array}{*{20}c} {F_{11}^{0} } &\quad {F_{12}^{0} } &\quad {F_{16}^{0} } \\ {F_{12}^{0} } &\quad {F_{22}^{0} } &\quad {F_{26}^{0} } \\ {F_{16}^{0} } &\quad {F_{26}^{0} } &\quad {F_{66}^{0} } \\ \end{array} } \right], \left[ {B^{1} } \right] = \left[ {\begin{array}{*{20}c} {F_{11}^{1} } &\quad {F_{12}^{1} } &\quad {F_{16}^{1} } \\ {F_{12}^{1} } &\quad {F_{22}^{1} } &\quad {F_{26}^{1} } \\ {F_{16}^{1} } &\quad {F_{26}^{1} } &\quad {F_{66}^{1} } \\ \end{array} } \right], \left[ {B^{2} } \right] = \left[ {\begin{array}{*{20}c} {F_{11}^{2} } &\quad {F_{12}^{2} } &\quad {F_{16}^{2} } \\ {F_{12}^{2} } &\quad {F_{22}^{2} } &\quad {F_{26}^{2} } \\ {F_{16}^{2} } &\quad {F_{26}^{2} } &\quad {F_{66}^{2} } \\ \end{array} } \right], \hfill \\ \left[ {B^{1,s} } \right] = \left[ {\begin{array}{*{20}c} {F_{11}^{1,s} } &\quad {F_{12}^{1,s} } &\quad {F_{16}^{1,s} } \\ {F_{12}^{1,s} } &\quad {F_{22}^{1,s} } &\quad {F_{26}^{1,s} } \\ {F_{16}^{1,s} } &\quad {F_{26}^{1,s} } &\quad {F_{66}^{1,s} } \\ \end{array} } \right], \left[ {B^{2,s} } \right] = \left[ {\begin{array}{*{20}c} {F_{11}^{2,s} } &\quad {F_{12}^{2,s} } &\quad {F_{16}^{2,s} } \\ {F_{12}^{2,s} } &\quad {F_{22}^{2,s} } &\quad {F_{26}^{2,s} } \\ {F_{16}^{2,s} } &\quad {F_{26}^{2,s} } &\quad {F_{66}^{2,s} } \\ \end{array} } \right], \left[ {B^{6,s} } \right] = \left[ {\begin{array}{*{20}c} {F_{11}^{6,s} } &\quad {F_{12}^{6,s} } &\quad {F_{16}^{6,s} } \\ {F_{12}^{6,s} } &\quad {F_{22}^{6,s} } &\quad {F_{26}^{6,s} } \\ {F_{16}^{6,s} } &\quad {F_{26}^{6,s} } &\quad {F_{66}^{6,s} } \\ \end{array} } \right]. \hfill \\ \end{gathered}$$

(23a)

$$\left[{J}^{0}\right]=\left[\begin{array}{cc}{F}_{44}^{0}&\quad {F}_{45}^{0}\\ {F}_{45}^{0}&\quad {F}_{55}^{0}\end{array}\right], \left[{J}^{0,e}\right]=\left[\begin{array}{cc}{F}_{44}^{0,e}&\quad {F}_{45}^{0,e}\\ {F}_{45}^{0,e}&\quad {F}_{55}^{0,e}\end{array}\right], \left[{J}^{0,s}\right]=\left[\begin{array}{cc}{F}_{44}^{0,s}&\quad {F}_{45}^{0,s}\\ {F}_{45}^{0,s}&\quad {F}_{55}^{0,s}\end{array}\right].$$

(23b)

$${F}_{ij}^{n}=\underset{-h/2}{\overset{h/2}{\int }}{C}_{ij}{z}^{n}dz\; \left(i,j=\text{1,2},6, n=\text{0,1},\text{2,3},\text{4,6}\right).$$

(24a)

$${F}_{ij}^{1,s}=-\frac{1}{4}{F}_{ij}^{1}+\frac{5}{3{h}^{2}}{F}_{ij}^{3}\; \left(i,j=\text{1,2},6\right).$$

(24b)

$${F}_{ij}^{2,s}=-\frac{1}{4}{F}_{ij}^{2}+\frac{5}{3{h}^{2}}{F}_{ij}^{4} \;\left(i,j=\text{1,2},6\right).$$

(24c)

$${F}_{ij}^{6,s}=-\frac{1}{16}{F}_{ij}^{2}+\frac{5}{6{h}^{2}}{F}_{ij}^{4}+\frac{25}{9{h}^{4}}{F}_{ij}^{6}\; \left(i,j=\text{1,2},6\right).$$

(24d)

$$\left({F}_{ij}^{0}, {F}_{ij}^{2},{F}_{ij}^{4}\right)=\underset{-h/2}{\overset{h/2}{\int }}{C}_{ij}\;\left(1,{z}^{2},{z}^{4}\right)dz \left(i,j=\text{4,5}\right).$$

(24e)

$${F}_{ij}^{0,e}=\frac{5}{4}{F}_{ij}^{0}-\frac{5}{{h}^{2}}{F}_{ij}^{2}\; \left(i,j=\text{4,5}\right).$$

(24f)

$${F}_{ij}^{0,s}=\frac{25}{16}{F}_{ij}^{0}-\frac{25}{2{h}^{2}}{F}_{ij}^{2}+\frac{25}{{h}^{4}}{F}_{ij}^{4} \;\left(i,j=\text{4,5}\right).$$

(24g)

Deformation energy

$$V=\frac{1}{2}\underset{V}{\iiint }\left(1-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\right)\left[{\sigma }_{xx}{\varepsilon }_{xx}+{\sigma }_{yy}{\varepsilon }_{yy}+{\tau }_{xy}{\gamma }_{xy}+{\tau }_{xz}{\gamma }_{xz}+{\tau }_{yz}{\gamma }_{yz}\right]dV.$$

(25)

Kinetic energy

$${T}_{e}=\frac{1}{2}{\int }_{0}^{a}{\int }_{0}^{b}\int_{-h/2}^{h/2}\rho (z)\left[({\dot{u}}^{2}+{\dot{v}}^{2}+{\dot{w}}^{2})\right]dzdydx.$$

(26)

The external potential energy of transverse external load $q(x,y,t)$ and thermal loads is defined as follows:

$$\begin{aligned} U &= \mathop \int \limits_{\Omega } \left[ {q\left( {x,y,t} \right)\left( {w_{d} + w_{b} + w_{s} } \right) - N_{xx}^{T} \frac{{\partial^{2} \left( {w_{b} + w_{s} } \right)}}{{\partial x^{2} }} - N_{yy}^{T} \frac{{\partial^{2} \left( {w_{b} + w_{s} } \right)}}{{\partial y^{2} }} - N_{xx}^{H} \frac{{\partial^{2} \left( {w_{b} + w_{s} } \right)}}{{\partial x^{2} }}} \right. \hfill \\ & \quad \left. { - N_{yy}^{H} \frac{{\partial^{2} \left( {w_{b} + w_{s} } \right)}}{{\partial y^{2} }} - N_{zz}^{T} \frac{{\partial^{2} \left( {w_{d} } \right)}}{\partial x\partial y} - N_{zz}^{H} \frac{{\partial^{2} \left( {w_{d} } \right)}}{\partial x\partial y}} \right]d\Omega . \hfill \\ \end{aligned}$$

(27)

Here ${N}_{xx}^{T}$ and ${N}_{yy}^{T}$ are thermal and ${N}_{xx}^{H}$ and ${N}_{yy}^{H}$ are humidity force resultants. They can be calculated as follows:

$${N}_{xx}^{T}=b\int_{-h/2}^{h/2} E(z)\alpha (z)\Delta Tdz.$$

(28a)

$${N}_{yy}^{T}=a\int_{-h/2}^{h/2}E(z)\alpha (z)\Delta Tdz.$$

(28b)

$$N_{xx}^{H} = b\mathop \int\limits_{ - h/2}^{h/2} E\left( z \right)\beta \left( z \right){\Delta C}dz.$$

(28c)

$$N_{yy}^{H} = a\mathop \int \limits_{ - h/2}^{h/2} E\left( z \right)\beta \left( z \right){\Delta C}dz.$$

(28d)

$$N_{zz}^{T} = ab\int_{-h/2}^{h/2}E\left( z \right)\alpha \left( z \right){\Delta T}dz.$$

(28e)

$$N_{zz}^{H} = ab\int_{-h/2}^{h/2} E\left( z \right)\beta \left( z \right){\Delta C}dz.$$

(28f)

In Eqs. (28c, 28d), $\beta (z)$ is the moisture coefficient and ΔC is the moisture rise. The effective moisture coefficient can be calculated using Eq. (7). In this study, ${\beta }_{m}=0.0005, {\beta }_{t}=0$ are used.

For the governing equations, the Hamilton’s principle is implemented as follows:

$$\underset{0}{\overset{t}{\int }}\delta \left({T}_{e}-V+U\right)dt=0.$$

(29)

Here ${T}_{\text{e}},V$ and $U$ denote the kinetic energy, the strain energy, and the work by done external forces of the plate, respectively. After substituting the energy and work terms into Eq. (29) and making variation and integrated by part and rearranging the result equation for the displacement coefficients the following equations for each coefficient $\delta u, \delta v,\delta {w}_{b},\delta {w}_{s}$ and $\delta {w}_{e}$ are derived:

$$\delta u:\frac{\partial {N}_{s}}{\partial x}+\frac{\partial {N}_{xy}}{\partial y}={I}_{0}\frac{{\partial }^{2}u}{\partial {t}^{2}}.$$

(30a)

$$\delta v:\frac{\partial {N}_{y}}{\partial y}+\frac{\partial {N}_{xy}}{\partial x}={I}_{0}\frac{{\partial }^{2}v}{\partial {t}^{2}}.$$

(30b)

$$\begin{aligned} & \delta w_{b} :\left[ {\frac{{\partial^{2} M_{x}^{b} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} M_{xy}^{b} }}{\partial x\partial y} + \frac{{\partial^{2} M_{y}^{b} }}{{\partial y^{2} }} - N_{xx}^{T} \frac{{\partial^{2} \left( {w_{b} } \right)}}{{\partial x^{2} }} - N_{yy}^{T} \frac{{\partial^{2} \left( {w_{b} } \right)}}{{\partial y^{2} }} - N_{xx}^{H} \frac{{\partial^{2} \left( {w_{b} } \right)}}{{\partial x^{2} }} - N_{yy}^{H} \frac{{\partial^{2} \left( {w_{b} } \right)}}{{\partial y^{2} }}} \right] \hfill \\ & \quad = I_{0} \left( {\frac{{\partial^{2} w_{d} }}{{\partial t^{2} }} + \frac{{\partial^{2} w_{b} }}{{\partial t^{2} }} + \frac{{\partial^{2} w_{s} }}{{\partial t^{2} }}} \right) - I_{0} \nabla^{2} \frac{{\partial^{2} w_{b} }}{{\partial t^{2} }}. \hfill \\ \end{aligned}$$

(30c)

$$\begin{aligned} & \delta {w}_{s}:\left[\frac{{\partial }^{2}{M}_{x}^{s}}{\partial {x}^{2}}+2\frac{{\partial }^{2}{M}_{xy}^{s}}{\partial x\partial y}+\frac{{\partial }^{2}{M}_{y}^{s}}{\partial {y}^{2}}+\frac{\partial {Q}_{yz}^{s}}{\partial x}+\frac{\partial {Q}_{yz}^{s}}{\partial y}-{N}_{xx}^{T}\frac{{\partial }^{2}\left({w}_{s}\right)}{\partial {x}^{2}}-{N}_{yy}^{T}\frac{{\partial }^{2}\left({w}_{s}\right)}{\partial {y}^{2}}-{N}_{xx}^{H}\frac{{\partial }^{2}\left({w}_{s}\right)}{\partial {x}^{2}}-{N}_{yy}^{H}\frac{{\partial }^{2}\left({w}_{s}\right)}{\partial {y}^{2}}\right]\\ &\quad ={I}_{0}\left(\frac{{\partial }^{2}{w}_{d}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}\right)-\frac{{I}_{2}}{84}{\nabla }^{2}\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}.\end{aligned}$$

(30d)

$$\delta {w}_{d}:\frac{\partial {Q}_{xz}^{d}}{\partial x}+\frac{\partial {Q}_{yz}^{d}}{\partial y}-{N}_{zz}^{T}\frac{{\partial }^{2}\left({w}_{d}\right)}{\partial x\partial y}-{N}_{zz}^{H}\frac{{\partial }^{2}\left({w}_{d}\right)}{\partial x\partial y}={I}_{0}\left(\frac{{\partial }^{2}{w}_{d}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}\right).$$

(30e)

Here, the inertias ${I}_{0}$ and ${I}_{2}$ are defined by

$$\left({I}_{0},{I}_{2}\right)=\underset{-h/2}{\overset{h/2}{\int }}\left(1,{z}^{2}\right)\rho dz.$$

(31)

in which, $\rho$ is the mass of nanoplate density. Substitution of Eqs. (21a–21e) and (24a–24g) into Eqs. (30a–30e) yields the following governing equations in terms of the displacements:

$$\delta u:{C}_{11}h\frac{{\partial }^{2}u}{\partial {x}^{2}}+{C}_{12}h\frac{{\partial }^{2}v}{\partial x\partial y}+{C}_{66}h\left(\frac{{\partial }^{2}v}{\partial x\partial y}+\frac{{\partial }^{2}u}{\partial {y}^{2}}\right)={I}_{0}\frac{{\partial }^{2}u}{\partial {t}^{2}}-{\left({e}_{0}a\right)}^{2}{I}_{0}{\nabla }^{2}\left(\frac{{\partial }^{2}u}{\partial {t}^{2}}\right).$$

(32a)

$$\delta v:{C}_{22}h\frac{{\partial }^{2}v}{\partial {y}^{2}}+{C}_{12}h\frac{{\partial }^{2}v}{\partial x\partial y}+{C}_{66}h\left(\frac{{\partial }^{2}u}{\partial x\partial y}+\frac{{\partial }^{2}v}{\partial {x}^{2}}\right)={I}_{0}\frac{{\partial }^{2}v}{\partial {t}^{2}}-{\left({e}_{0}a\right)}^{2}{\nabla }^{2}\left({I}_{0}\frac{{\partial }^{2}v}{\partial {t}^{2}}\right).$$

(32b)

$$\begin{aligned} & \delta {w}_{b}:-\left[{F}_{11}\frac{{\partial }^{4}{w}_{b}}{\partial {x}^{4}}+2\left({F}_{12}+2{F}_{66}\right)\frac{{\partial }^{4}{w}_{b}}{\partial {x}^{2}\partial {y}^{2}}+{F}_{22}\frac{{\partial }^{4}{w}_{b}}{\partial {y}^{4}}-{N}_{xx}^{T}\frac{{\partial }^{2}\left({w}_{b}\right)}{\partial {x}^{2}}-{N}_{yy}^{T}\frac{{\partial }^{2}\left({w}_{b}\right)}{\partial {y}^{2}}-{N}_{xx}^{H}\frac{{\partial }^{2}\left({w}_{b}\right)}{\partial {x}^{2}}-{N}_{yy}^{H}\frac{{\partial }^{2}\left({w}_{b}\right)}{\partial {y}^{2}}\right]\\ &\quad ={I}_{0}\left(\frac{{\partial }^{2}{w}_{d}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}\right)-{I}_{2}{\nabla }^{2}\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}-{\left({e}_{0}a\right)}^{2}{I}_{0}{\nabla }^{2}\left(\frac{{\partial }^{2}{w}_{d}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}\right)-{\left({e}_{0}a\right)}^{2}{I}_{0}{\nabla }^{4}\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}.\end{aligned}$$

(32c)

$$\delta {w}_{s}:-\frac{1}{84}\left[{F}_{11}\frac{{\partial }^{4}{w}_{s}}{\partial {x}^{4}}+2\left({F}_{12}+2{F}_{66}\right)\frac{{\partial }^{4}{w}_{s}}{\partial {x}^{2}\partial {y}^{2}}+{F}_{22}\frac{{\partial }^{4}{w}_{s}}{\partial {y}^{4}}\right]+\frac{5}{6}{C}_{55}h\left(\frac{{\partial }^{2}{w}_{d}}{\partial {x}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}\right)+\frac{5}{6}{C}_{44}h\left(\frac{{\partial }^{2}{w}_{d}}{\partial {y}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {y}^{2}}\right)-{N}_{xx}^{T}\frac{{\partial }^{2}\left({w}_{s}\right)}{\partial {x}^{2}}-{N}_{yy}^{T}\frac{{\partial }^{2}\left({w}_{s}\right)}{\partial {y}^{2}}-{N}_{xx}^{H}\frac{{\partial }^{2}\left({w}_{s}\right)}{\partial {x}^{2}}-{N}_{yy}^{H}\frac{{\partial }^{2}\left({w}_{s}\right)}{\partial {y}^{2}}={I}_{0}\left(\frac{{\partial }^{2}{w}_{d}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}\right)-\frac{{I}_{2}}{84}{\nabla }^{2}\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}-{\left({e}_{0}a\right)}^{2}{I}_{0}{\nabla }^{2}\left(\frac{{\partial }^{2}{w}_{d}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}\right)-{\left({e}_{0}a\right)}^{2}\frac{{I}_{2}}{84}{\nabla }^{4}\left(\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}\right).$$

(32d)

$$\delta {w}_{d}:{C}_{55}h\frac{{\partial }^{2}{w}_{d}}{\partial {x}^{2}}+\frac{5}{6}{C}_{55}h\frac{{\partial }^{2}{w}_{s}}{\partial {x}^{2}}+{C}_{44}h\frac{{\partial }^{2}{w}_{d}}{\partial {y}^{2}}+\frac{5}{6}{C}_{44}h\frac{{\partial }^{2}{w}_{s}}{\partial {y}^{2}}-{N}_{zz}^{T}\frac{{\partial }^{2}\left({w}_{d}\right)}{\partial x\partial y}-{N}_{zz}^{H}\frac{{\partial }^{2}\left({w}_{d}\right)}{\partial x\partial y}={I}_{0}\left(\frac{{\partial }^{2}{w}_{d}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}\right)-{\left({e}_{0}a\right)}^{2}{I}_{0}{\nabla }^{2}\left(\frac{{\partial }^{2}{w}_{d}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{b}}{\partial {t}^{2}}+\frac{{\partial }^{2}{w}_{s}}{\partial {t}^{2}}\right).$$

(32e)

It should be noted that when the nonlocal parameter is set to zero, $\left({e}_{0}a\right)=0$, Eq. (32a-e) reduces to that of the classical equation [20].

6 Analytical solution

For the solution of motion Eqs. (32a–32e) the Navier’s method is implemented in this study for simply supported geometric boundary conditions and natural boundary conditions given in Eqs. (33a-33b).

At edges x = 0 and x = a

$$v={w}_{d}={w}_{b}={w}_{s}=\partial {w}_{d}/\partial y=\partial {w}_{b}/\partial y=\partial {w}_{s}/\partial y={N}_{xx}={M}_{xx}^{b}={M}_{xx}^{s}=0.$$

(33a)

and y = 0 and y = b;

$$u={w}_{d}={w}_{b}={w}_{s}=\partial {w}_{d}/\partial x=\partial {w}_{b}/\partial x=\partial {w}_{s}/\partial x={N}_{yy}={M}_{yy}^{b}={M}_{yy}^{s}=0.$$

(33b)

The displacements $u\left(x,y,t\right), v\left(x,y,t\right), {w}_{b}\left(x,y,t\right), {w}_{s}\left(x,y,t\right),{w}_{d}\left(x,y,t\right)$ can be approximated using the following Fourier Series.

$$u=\sum_{m=1}^{\infty }\sum_{n=1}^{\infty }{U}_{mn}\text{cos}\left(\alpha x\right)\text{sin}\left(\beta y\right){e}^{-i\omega t}.$$

(34a)

$$v=\sum_{m=1}^{\infty }\sum_{n=1}^{\infty }{V}_{mn}\text{sin}\left(\alpha x\right)\text{cos}\left(\beta y\right){e}^{-i\omega t}.$$

(34b)

$${w}_{b}=\sum_{m=1}^{\infty }\sum_{n=1}^{\infty }{W}_{bmn}\text{sin}\left(\alpha x\right)\text{sin}\left(\beta y\right){e}^{-i\omega t}.$$

(34c)

$${w}_{s}=\sum_{m=1}^{\infty }\sum_{n=1}^{\infty }{W}_{smn}\text{sin}\left(\alpha x\right)\text{sin}\left(\beta y\right){e}^{-i\omega t}.$$

(34d)

$${w}_{d}=\sum_{m=1}^{\infty }\sum_{n=1}^{\infty }{W}_{dmn}\text{sin}\left(\alpha x\right)\text{cos}\left(\beta y\right){e}^{-i\omega t}.$$

(34e)

When the displacements in Eqs. (34a–34e) are substituted into Eq. (32a–32e) and after rearranging the resulting equations, one can derive the following matrix equation for the free vibration of the FG porous nanoplate:

$$\left({\left[K\right]}_{5x5}-{\omega }_{mn}^{2}{\left[M\right]}_{5x5}\right){\left\{\overline{\Delta }\right\} }_{5x1}=0.$$

(35)

Here, Eq. (35) is an eigenvalue equation and ${\omega }_{mn}$ is the natural frequencies of the modes $\left(m,n\right)$, and $K$ is the stiffness matrix, $M$ is the mass matrix; and $\overline{\Delta }={\left({U}_{mn} {V}_{mn} {W}_{bmn} {W}_{smn} {W}_{dmn}\right)}^{T}$ is the vector of unknowns to be determined. The coefficients of the matrices $\mathbf{K}$ and $\mathbf{M}$ are given as follows:

$$\begin{aligned} K_{11} = & F_{11}^{0} \alpha^{2} + F_{66}^{0} \beta^{2} , \\ K_{12} = & \alpha \beta \left( {F_{12}^{0} + F_{66}^{0} } \right), \\ K_{13} = & - F_{13}^{1} \alpha^{3} , \\ K_{14} = & - F_{11}^{1,s} \alpha^{3} , \\ K_{22} = & F_{66}^{0} \alpha^{2} + F_{22}^{0} \beta^{2} , \\ K_{23} = & - F_{11}^{1} \beta^{3} , \\ K_{24} = & - F_{11}^{1,s} \beta^{3} , \\ K_{33} = & F_{11}^{2} \alpha^{4} + 2\left( {F_{12}^{2} + 2F_{66}^{2} } \right)\alpha^{2} \beta^{2} , \\ K_{34} = & F_{11}^{2,s} \alpha^{4} + 2\left( {F_{12}^{2,s} + 2F_{66}^{2,s} } \right)\alpha^{2} \beta^{2} + F_{22}^{2,s} \beta^{4} , \\ K_{44} = & F_{11}^{6,s} \alpha^{4} + 2\left( {F_{12}^{6,s} + 2F_{66}^{6,s} } \right)\alpha^{2} \beta^{2} + F_{22}^{6,s} \beta^{4} + F_{55}^{0,s} \alpha^{2} + F_{44}^{0,s} \beta^{2} , \\ K_{45} = & F_{55}^{0,d} \alpha^{2} + F_{44}^{0,d} \beta^{2} , \\ K_{55} = & F_{55}^{0} \alpha^{2} + F_{44}^{0} \beta^{2} , \\ M_{11} = & M_{22} = M_{34} = M_{35} = M_{45} = M_{55} = I_{0} + I_{0} \left( {ea} \right)^{2} \left( {\alpha^{2} + \beta^{2} } \right), \\ M_{33} = & \left[ {1 + \left( {ea} \right)^{2} \left( {\alpha^{2} + \beta^{2} } \right)} \right]\left[ {I_{0} + I_{2} \left( {\alpha^{2} + \beta^{2} } \right)} \right], \\ M_{44} = & \left[ {1 + \left( {ea} \right)^{2} \left( {\alpha^{2} + \beta^{2} } \right)} \right]\left[ {I_{0} + \frac{{I_{2} }}{84}\left( {\alpha^{2} + \beta^{2} } \right)} \right], \\ M_{12} = & M_{13} = M_{14} = M_{15} = M_{21} = M_{23} = M_{24} = M_{25} = M_{31} = M_{32} = M_{41} = M_{42} = M_{51} = M_{52} = 0. \\ \end{aligned}$$

(36)

7 Results and discussions with numerical solution

7.1 Validation

Comparisons are conducted between the acquired findings and alternative hypotheses for the orthotropic plate ${e}_{0}a=0$ to validate the results. In this study, the boundary conditions on all four edges are considered as simply supported. The orthotropic nanoplate's material characteristics are derived from reference [91]. Tables 2 and 4 compare the non-dimensional natural frequencies obtained using theory in this paper with those derived using CPT, FSDT, TSDT, and RPT for orthotropic and isotropic graphene sheets with certain material and geometrical parameters, respectively [20]. The material parameters of the FG nanoplate are listed in Table 3.

Table 2 Comparison of the non-dimensional naturel frequencies $\Omega =\omega h\sqrt{\rho /{C}_{11}}$ of an orthotropic square plate

Table 3 Material properties of the nanoplate [20]

When the non-dimensional frequencies obtained with the presented in this study are compared with other studies given in Tables 2 and 4, it is seen that similar results are obtained.

Table 4 Comparison of the non-dimensional naturel frequencies $\Omega =\omega h\sqrt{\rho /{C}_{11}}$ of an isotropic square nanoplate

7.2 Numerical results

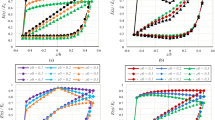
Figure 3 shows the change in the dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ of the nanoplate depending on the material grading index and temperature increase. Here, humidity is $\Delta C=0$, porosity ratio $\alpha =0$, thickness ratio $h=\text{a}/10$ and thickness $a=10\text{ nm}$. The material of the nanoplate consists of functional gradation of metal (SUS304) on the lower surface and silicon nitride (Si₃N₄) on the upper surface, according to the power law given in Eq. (1). According to the power law in Eq. (1) at $p=0$ the nanoplate consists entirely of ceramic. At $p=1$, in addition to the change in the material of the nanoplate depending on the height, 50% is ceramic and 50% is metal. At $p=6$, %14.3 consists of ceramics and 85.7% consists of metal. For $\Delta T=0$, at $p=0$ it has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.046$, at $p=1$ it decreases by 35% reaching ${\lambda }_{\left(\text{1,1}\right)}=9.173$ and, at $p=6$ it decreases by 52% reaching ${\lambda }_{\left(\text{1,1}\right)}=7.157$. For $\Delta T=75$, at $p=0$ it has a value of ${\lambda }_{\left(\text{1,1}\right)}=14.771$, at $p=1$ it decreases by 39% reaching ${\lambda }_{\left(\text{1,1}\right)}=8.971$ and, at $p=6$ it decreases by 53% reaching ${\lambda }_{\left(\text{1,1}\right)}=6.983$. For $\Delta T=150$, at $p=0$ it has a value of ${\lambda }_{\left(\text{1,1}\right)}=14.486$, at $p=1$ it decreases by 40% reaching ${\lambda }_{\left(\text{1,1}\right)}=8.744$ and, at $p=6$ it decreases by 53% reaching ${\lambda }_{\left(\text{1,1}\right)}=6.772$. For $\Delta T=225$, at $p=0$ it has a value of ${\lambda }_{\left(\text{1,1}\right)}=14.191$, at $p=1$ it decreases by 40% reaching ${\lambda }_{\left(\text{1,1}\right)}=8.490$ and, at $p=6$ it decreases by 54% reaching ${\lambda }_{\left(\text{1,1}\right)}=6.525$. In general, as the material grading index $p$ increases, the metal ratio in the nanoplate increases and the ceramic ratio decreases. Therefore, at high values of $p$, the dimensionless fundamental frequency is lower than at values of $p$ close to zero. Since the ceramic ratio is high at $p$ values close to zero and ceramics are less affected by temperature than metal, the temperature-dependent change curves are close to each other. However, at $p$ values where the metal ratio is high, the temperature-dependent change is more noticeable, as given above.

Fig. 3

Comparison of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on material gradation index $p$, and temperature rise $\Delta T=0, 75, 150, 225 K$, for $\Delta C=0$, nonlocal parameters ${e}_{0}a=0 nm$, thickness ratio $\text{h}=\text{a}/10$, porosity index $\alpha =0$

Figure 4 shows the change in dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on humidity and temperature increase. Here, the nonlocal parameter ${e}_{0}a$, material gradation index $p$ and porosity index $\alpha$ are considered as zero, and the thickness ratio is assumed to be $\text{h}=a/10$. For $\Delta T=0$ case, it changes from $\Delta C=0$ to $\Delta C=6$, while the dimensionless fundamental frequency remains constant at ${\lambda }_{\left(\text{1,1}\right)}=15.046$. For $\Delta T=75$ case, while it changes from $\Delta C=0$ to $\Delta C=6$, the dimensionless fundamental frequency decreases by 1.823% compared to the degree at $\Delta T=0$ and remains constant at ${\lambda }_{\left(\text{1,1}\right)}=14.771$. For $\Delta T=150$ case, while it changes from $\Delta C=0$ to $\Delta C=6$, the dimensionless fundamental frequency decreases by 3.722% compared to the degree at $\Delta T=0$ and remains constant at ${\lambda }_{\left(\text{1,1}\right)}=14.486$. For $\Delta T=225$ case, while it changes from $\Delta C=0$ to $\Delta C=6$, the dimensionless fundamental frequency decreases by 5.683% compared to the degree at $\Delta T=0$ and remains constant at ${\lambda }_{\left(\text{1,1}\right)}=14.191$.

Fig. 4

Comparison of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on humidity $\Delta C$, and temperature rise $\Delta T=0, 75, 150, 225 K$, for nonlocal parameters ${e}_{0}a=0 nm$, thickness ratio $\text{h}=a/10$, material gradation index $p=0$, porosity index $\alpha =0$

Figure 5 shows the change of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on nonlocal parameters and temperature increase. Here, humidity $\Delta C$, material gradation index $p$ and porosity index $\alpha$ are accepted as zero and thickness ratio is considered $h=a/10$ and thickness is $\text{a}=10\text{ nm}$. For $\Delta T=0$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.046$ while at ${e}_{0}a=0$, it decreases by 2.38% has a value ${\lambda }_{\left(\text{1,1}\right)}=14.688$ at ${e}_{0}a=0.05$, and decreases by 25.24% reaching ${\lambda }_{\left(\text{1,1}\right)}=11.248$ at ${e}_{0}a=0.2$. For $\Delta T=75$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=14.771$ while at ${e}_{0}a=0$, it decreases by 2.438% has a value ${\lambda }_{\left(\text{1,1}\right)}=14.411$ at ${e}_{0}a=0.05$, and decreases by 25.9% reaching ${\lambda }_{\left(\text{1,1}\right)}=10.946$ at ${e}_{0}a=0.2$. For $\Delta T=150$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=14.486$ while at ${e}_{0}a=0$, it decreases by 2.49% has a value ${\lambda }_{\left(\text{1,1}\right)}=14.125$ at ${e}_{0}a=0.05$, and decreases by 26.67% reaching ${\lambda }_{\left(\text{1,1}\right)}=10.622$ at ${e}_{0}a=0.2$. For $\Delta T=225$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=14.191$ while at ${e}_{0}a=0$, it decreases by 2.57% has a value ${\lambda }_{\left(\text{1,1}\right)}=13.827$ at ${e}_{0}a=0.05$, and decreases by 27.61% reaching ${\lambda }_{\left(\text{1,1}\right)}=10.273$ at ${e}_{0}a=0.2$. As seen in Fig. 5, these decreases are not linear but curvilinear. This shows that the nonlocal parameter makes a softening effect on the nanoplate. Increasing the temperature also makes a softening effect on the nanoplate and reduces the dimensionless fundamental frequencies, as seen in the Fig. 5.

Fig. 5

Comparison of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on nonlocal parameters ${e}_{0}a ({nm}^{2})$ and temperature rise $\Delta T=0, 75, 150, 225 K$, for $\Delta C=0$, thickness ratio $\text{h}=a/10$, material gradation index $p=0$, porosity index $\alpha =0$

Figure 6 demonstrates the change of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on porosity and temperature increase. Where, humidity $\Delta C$, material gradation index $p$ and nonlocal parameter ${e}_{0}a$ are accepted as zero, and thickness ratio is considered $\text{h}=a/10$, and thickness is $\text{a}=10\text{ nm}$. In Fig. 6a, the results have been obtained according to the uniform porosity condition. According to these results, for $\Delta T=0$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.046$ while at $\alpha =0$, it increases by 21.8% has a value ${\lambda }_{\left(\text{1,1}\right)}=18.328$ at $\alpha =0.2$, and increases by 143.3% reaching ${\lambda }_{\left(\text{1,1}\right)}=36.605$ at $\alpha =0.4$. For $\Delta T=75$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=14.770$ while at $\alpha =0$, it increases by 22.2% has a value ${\lambda }_{\left(\text{1,1}\right)}=18.044$ at $\alpha =0.2$, and increases by 144.7% reaching ${\lambda }_{\left(\text{1,1}\right)}=36.143$ at $\alpha =0.4$. For $\Delta T=150$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=14.486$ while at $\alpha =0$, it increases by 22.6% has a value ${\lambda }_{\left(\text{1,1}\right)}=17.762$ at $\alpha =0.2$, and increases by 146.6% reaching ${\lambda }_{\left(\text{1,1}\right)}=35.718$ at $\alpha =0.4$. For $\Delta T=225$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=14.191$ while at $\alpha =0$, it increases by 23.2% has a value ${\lambda }_{\left(\text{1,1}\right)}=17.481$ at $\alpha =0.2$, and increases by 148.9% reaching ${\lambda }_{\left(\text{1,1}\right)}=35.324$ at $\alpha =0.4$. In Fig. 6b, the results have been obtained according to the symmetric porosity condition. According to these results, for $\Delta T=0$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=19.079$ while at $\alpha =0$, it decreases by 0.089% has a value ${\lambda }_{\left(\text{1,1}\right)}=19.062$ at $\alpha =0.2$, and decreases by 0.168% reaching ${\lambda }_{\left(\text{1,1}\right)}=19.047$ at $\alpha =0.4$. For $\Delta T=75$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=18.733$ while at $\alpha =0$, it increases by 0.048% has a value ${\lambda }_{\left(\text{1,1}\right)}=18.742$ at $\alpha =0.2$, and increases by 0.091% reaching ${\lambda }_{\left(\text{1,1}\right)}=18.750$ at $\alpha =0.4$. For $\Delta T=150$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=18.245$ while at $\alpha =0$, it increases by 0.36% has a value ${\lambda }_{\left(\text{1,1}\right)}=18.310$ at $\alpha =0.2$, and increases by 0.67% reaching ${\lambda }_{\left(\text{1,1}\right)}=18.368$ at $\alpha =0.4$. For $\Delta T=225$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=17.563$ while at $\alpha =0$, it increases by 0.93% has a value ${\lambda }_{\left(\text{1,1}\right)}=17.727$ at $\alpha =0.2$, and increases by 1.74% reaching ${\lambda }_{\left(\text{1,1}\right)}=17.868$ at $\alpha =0.4$. According to obtained results demonstrated in Fig. 6a for uniform porosity case, value of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ increase with the porosity increase as curvilinear. Figure 6b shows the symmetric porosity case and value of dimensionless frequency ${\lambda }_{\left(\text{1,1}\right)}$ is not affected much by the increase of the porosity value.

Fig. 6

Comparison of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on porosity index $\alpha$, and temperature rise $\Delta T=0, 75, 150, 225 K$, for $\Delta C=0$, nonlocal parameters ${e}_{0}a=0 nm$, $\text{h}=\text{a}/10$, material gradation index $p=0$; a results of uniform porosity; b results of symmetric porosity

Figure 7 shows the change of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on nonlocal parameters and humidity. Where, temperature $\Delta T$, material gradation index $p$ and porosity index $\alpha$ are accepted as zero and thickness ratio is considered $h=a/10$ and thickness is $a=10\text{ nm}$. According to obtained results that shown in Fig. 7, change of the humidity value has no effect on dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ but increase of the nonlocal parameter decreases of the dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$. Dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.05$ while ${e}_{0}a=0,$ it decreases by 8.64% reaching ${\lambda }_{\left(\text{1,1}\right)}=13.75$ at ${e}_{0}a=0.1$, and decreases by 25.25% reaching ${\lambda }_{\left(\text{1,1}\right)}=11.25$ at ${e}_{0}a=0.2$.

Fig. 7

Comparison of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on nonlocal parameters ${e}_{0}a \left(nm\right)$, and $\Delta C=0, 3, 5, 7$, for temperature rise $\Delta T=0 K$, thickness ratio $\text{h}=a/10$, material gradation index $p=0$, porosity index $\alpha =0$

Figure 8 shows the change of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on material gradation index and humidity. Where, temperature $\Delta T$, nonlocal parameter ${e}_{0}a$ and porosity index $\alpha$ are accepted as zero and thickness ratio is considered $h=a/10$ and thickness is $a=10\text{ nm}$. The material of the nanoplate consists of functional gradation of metal (SUS304) on the lower surface and silicon nitride (Si₃N₄) on the upper surface, according to the power law given in Eq. (1). According to the power law in Eq. (1), at $p=0$ the nanoplate consists entirely of ceramic. At $p=1$, in addition to the change in the material of the nanoplate depending on the height, 50% is ceramic and 50% is metal. At $p=6$, 14.3% consists of ceramics and 85.7% consists of metal.

Fig. 8

Comparison of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on material gradation index $p$, and $\Delta C=0, 3, 5, 7$, for temperature rise $\Delta T=0 K$, nonlocal parameters ${e}_{0}a=0 nm$, thickness ratio $h=a/10$, porosity index $\alpha =0$

For $\Delta C=0$, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.046$ while at $p=0$, it decreases by 35% reaching ${\lambda }_{\left(\text{1,1}\right)}=9.173$ at $p=1$, and it decreases by 52% reaching ${\lambda }_{\left(\text{1,1}\right)}=7.157$ at $p=6$. For $\Delta C=3$, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=14.771$ while at $p=0$, it decreases by 39% reaching ${\lambda }_{\left(\text{1,1}\right)}=8.971$ at $p=1$, and it decreases by 53% reaching ${\lambda }_{\left(\text{1,1}\right)}=6.983$ at $p=6$. For $\Delta C=5$, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=14.486$ while at $p=0$, it decreases by 40% reaching ${\lambda }_{\left(\text{1,1}\right)}=8.744$ at $p=1$, and it decreases by 53% reaching ${\lambda }_{\left(\text{1,1}\right)}=6.772$ at $p=6$. For $\Delta C=7$, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=14.191$ at $p=0$, it decreases by 40% reaching ${\lambda }_{\left(\text{1,1}\right)}=8.490$ at $p=1$, and it decreases by 54% reaching ${\lambda }_{\left(\text{1,1}\right)}=6.525$.

Depending on the increase of the material grading index $p$, the metal ratio in the nanoplate increases and the ceramic ratio decreases. Therefore, at high values of $p$, the dimensionless fundamental frequency is lower than at values of $p$ close to zero. Since the ceramic ratio is high at $p$ values close to zero and ceramics are less affected by humidity than metal, the humidity change curves are close to each other. However, at $p$ values where the metal ratio is high, the humidity-dependent change is more noticeable, as given above.

Figure 9 shows the change of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on porosity and humidity. In Fig. 9a, the results have been obtained according to the uniform porosity condition. Where, temperature $\Delta T$, nonlocal parameter ${e}_{0}a$ and material gradation index $\text{p}$ are accepted as zero and thickness ratio is considered $h=a/10$ and thickness is $a=10\text{ nm}$. According to these results, for $\Delta C=0$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.046$ while at $\alpha =0$, it increases by 22.6% has a value ${\lambda }_{\left(\text{1,1}\right)}=18.444$ at $\alpha =0.2$, and increases by 146.4% reaching ${\lambda }_{\left(\text{1,1}\right)}=37.073$ at$\alpha =0.4$. For $\Delta C=3$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.046$ while at$\alpha =0$, it increases by 22.4% has a value ${\lambda }_{\left(\text{1,1}\right)}=18.411$ at $\alpha =0.2$, and increases by 145.5% reaching ${\lambda }_{\left(\text{1,1}\right)}=36.941$ at $\alpha =0.4$. For $\Delta C=5$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.046$ while at$\alpha =0$, it increases by 22.2% has a value ${\lambda }_{\left(\text{1,1}\right)}=18.378$ at $\alpha =0.2$, and increases by 146.6% reaching ${\lambda }_{\left(\text{1,1}\right)}=36.807$ at $\alpha =0.4$. For $\Delta C=7$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.046$ while at $\alpha =0$, it increases by 21.8% has a value ${\lambda }_{\left(\text{1,1}\right)}=18.328$ at $\alpha =0.2$, and increases by 143.3% reaching ${\lambda }_{\left(\text{1,1}\right)}=36.605$ at $\alpha =0.4$. In Fig. 6b, the results have been obtained according to the symmetric porosity condition and material gradation index selected as $p=5$. According to these results, for $\Delta C=0$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=7.269$ while at$\alpha =0$, it decreases by 0.165% has a value ${\lambda }_{\left(\text{1,1}\right)}=7.257$ at $\alpha =0.2$, and increases by 0.014% reaching ${\lambda }_{\left(\text{1,1}\right)}=7.268$ at $\alpha =0.4$. For $\Delta C=3$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=7.033$ while at $\alpha =0$, it increases by 0.3% has a value ${\lambda }_{\left(\text{1,1}\right)}=7.054$ at $\alpha =0.2$, and increases by 0.88% reaching ${\lambda }_{\left(\text{1,1}\right)}=7.095$ at $\alpha =0.4$. For $\Delta C=5$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=6.878$ while at$\alpha =0$, it increases by 0.59% has a value ${\lambda }_{\left(\text{1,1}\right)}=6.919$ at $\alpha =0.2$, and increases by 1.48% reaching ${\lambda }_{\left(\text{1,1}\right)}=6.980$ at $\alpha =0.4$. For $\Delta C=7$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=6.722$ while at $\alpha =0$, it increases by 0.92% has a value ${\lambda }_{\left(\text{1,1}\right)}=6.784$ at $\alpha =0.2$, and increases by 2.13% reaching ${\lambda }_{\left(\text{1,1}\right)}=6.865$ at $\alpha =0.4$. In general, it is seen that when porosity increases uniformly, dimensionless fundamental frequencies increase significantly curvilinearly, but the effect of humidity on this increase is very limited. In the case of a symmetric increase in porosity, it is obtained from the graphs that the increases in dimensionless fundamental frequencies are quite limited, but the increases in humidity have an effect on reducing dimensionless fundamental frequencies.

Fig. 9

Comparison of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on porosity index $\alpha$, and $\Delta C=0, 3, 5, 7$, for temperature rise $\Delta T=0 K$, nonlocal parameters ${e}_{0}a=0 nm$, thickness ratio $h=a/10$, material gradation index $p=0$

Figure 10 demonstrates the change of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on temperature increase and nonlocal parameter. Where, humidity $\Delta C$, material gradation index $p$ and porosity $\alpha$ are accepted as zero, and thickness ratio is considered $\text{h}=a/10$, and thickness is $\text{a}=10\text{ nm}$. According to results obtained in Fig. 10, for ${e}_{0}a=0$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.046$ while at ΔT = 0 K, it decreases by 2.73% has a value ${\lambda }_{\left(\text{1,1}\right)}=14.635$ at ΔT = 200 K, and decreases by 5.63% reaching ${\lambda }_{\left(\text{1,1}\right)}=14.199$ at $\Delta T=400 K$. For ${e}_{0}a=0.1$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=13.261$ while at ΔT = 0 K, it decreases by 4.28% has a value ${\lambda }_{\left(\text{1,1}\right)}=12.693$ at ΔT = 200 K, and decreases by 8.95% reaching ${\lambda }_{\left(\text{1,1}\right)}=12.074$ at $\Delta T=400 K$. ${e}_{0}a=0.142$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=12.273$ while at ΔT = 0 K, it decreases by 5.04% has a value ${\lambda }_{\left(\text{1,1}\right)}=11.655$ at ΔT = 200 K, and decreases by 10.62% reaching ${\lambda }_{\left(\text{1,1}\right)}=10.970$ at $\Delta T=400 K$. ${e}_{0}a=0.2$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=10.847$ while at ΔT = 0 K, it decreases by 6.54% has a value ${\lambda }_{\left(\text{1,1}\right)}=10.138$ at ΔT = 200 K, and decreases by 13.99% reaching ${\lambda }_{\left(\text{1,1}\right)}=9.330$ at $\Delta T=400 K$. As seen in Fig. 10, the dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ has the highest degree when the nonlocal parameter is zero, while the dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ value decreases as the nonlocal parameter value increases. It is also seen that this value decreases with increasing temperature. Nonlocal parameters and temperature have a softening effect on the material, reducing the dimensionless fundamental frequencies.

Fig. 10

Comparison of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on temperature rise $\Delta T$ and nonlocal parameters ${e}_{0}a=0, 0.1, 0.142, 0.2 nm$, for $\Delta C=0$, thickness ratio $\text{h}=a/10$, material gradation index $p=0$, porosity index $\alpha =0$

Figure 11 shows the change of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on thickness ratio and nonlocal parameter. Where, temperature $\Delta T$, humidity $\Delta C$, material gradation index $p$ and porosity $\alpha$ are accepted as zero, and thickness is $\text{a}=10\text{ nm}$. According to results obtained in Fig. 10, for ${e}_{0}a=0$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.935$ while at $h/a=1/150$, it decreases by 5.58% has a value ${\lambda }_{\left(\text{1,1}\right)}=15.046$ at $\text{h}/\text{a}=1/10$, and decreases by 39.81% reaching ${\lambda }_{\left(\text{1,1}\right)}=9.591$ at $\text{h}/\text{a}=1/5$. For ${e}_{0}a=0.1$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=14.562$ while at $h/a=1/150$, it decreases by 5.58% has a value ${\lambda }_{\left(\text{1,1}\right)}=13.750$ at $\text{h}/\text{a}=1/10$, and decreases by 39.81% reaching ${\lambda }_{\left(\text{1,1}\right)}=8.765$ at $\text{h}/\text{a}=1/5$. For ${e}_{0}a=0.142$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=13.480$ while at $h/a=1/150$, it decreases by 5.59% has a value ${\lambda }_{\left(\text{1,1}\right)}=12.726$ at $\text{h}/\text{a}=1/10$, and decreases by 39.83% reaching ${\lambda }_{\left(\text{1,1}\right)}=8.111$ at $\text{h}/\text{a}=1/5$. For ${e}_{0}a=0.2$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=11.914$ while at $h/a=1/150$, it decreases by 5.60% has a value ${\lambda }_{\left(\text{1,1}\right)}=11.247$ at $\text{h}/\text{a}=1/10$, and decreases by 39.83% reaching ${\lambda }_{\left(\text{1,1}\right)}=7.169$ at $\text{h}/\text{a}=1/5$. As seen in Fig. 11, it is seen that both the thickness ratio change and the nonlocal parameter change affect the dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$. As a result of the calculations, it is seen that the thickness ratio change has the same effect proportionally for different nonlocal parameter values. It is seen that as both the nonlocal parameter value and the plate thickness increase, the fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ value decreases.

Fig. 11

Comparison of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on thickness ratio $\text{h}/\text{a}$, and nonlocal parameters ${e}_{0}a=0, 0.1, 0.142, 0.2 nm$, for temperature rise $\Delta T=0 K$, $\Delta C=0$, material gradation index $\text{p}=0$, porosity index $\alpha =0$

Figure 12 demonstrates the change of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on material gradation index and nonlocal parameter. Where, temperature $\Delta T$, humidity $\Delta C$, and porosity $\alpha$ are accepted as zero, and thickness ratio is considered $h=a/10$, and thickness is $a=10\text{ nm}$. According to results obtained in Fig. 12, for ${e}_{0}a=0$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.046$ while at $p=0$, it decreases by 39.03% has a value ${\lambda }_{\left(\text{1,1}\right)}=9.173$ at $p=1$, and decreases by 52.43% reaching ${\lambda }_{\left(\text{1,1}\right)}=7.157$ at $p=6$. For ${e}_{0}a=0.1$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=13.750$ while at $\text{p}=0$, it decreases by 39.03% has a value ${\lambda }_{\left(\text{1,1}\right)}=8.383$ at $p=1$, and decreases by 52.43% reaching ${\lambda }_{\left(\text{1,1}\right)}=6.541$ at $p=6$. For ${e}_{0}a=0.142$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=12.726$ while at $p=0$, it decreases by 39.03% has a value ${\lambda }_{\left(\text{1,1}\right)}=7.758$ at $p=1$, and decreases by 52.43% reaching ${\lambda }_{\left(\text{1,1}\right)}=6.053$ at $p=6$. For ${e}_{0}a=0.2$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=11.248$ while at $p=0$, it decreases by 39.03% has a value ${\lambda }_{\left(\text{1,1}\right)}=6.857$ at $p=1$, and decreases by 52.43% reaching ${\lambda }_{\left(\text{1,1}\right)}=5.350$ at $p=6$. As seen in Fig. 12, it is seen that both the thickness ratio change and the nonlocal parameter change affect the dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$. As a result of the calculations, it is seen that the material gradation index change has the same effect proportionally for different nonlocal parameter values. It is seen that as both the nonlocal parameter value and the material gradation index increase, the dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ value decreases.

Fig. 12

Comparison of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on $p$, and nonlocal parameters ${e}_{0}a=0, 0.1, 0.142, 0.2 nm$, for temperature rise $\Delta T=0 K$, $\Delta C=0$, thickness ratio $\text{h}=\text{a}/10$, porosity index $\alpha =0$

Figure 13 shows the change of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on temperature increase and thickness ratio. Where, humidity $\Delta C$, nonlocal parameter ${e}_{0}a$, and porosity $\alpha$ are accepted as zero, and thickness is $a=10\text{ nm}$. According to results obtained in Fig. 13, for $h=a/5$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=9.591$ while at $\Delta T=0 K$, it decreases by 0.021% has a value ${\lambda }_{\left(\text{1,1}\right)}=9.589$ at $\Delta T=200 K$, and it increases by 0.021% and returns to the initial value reaching ${\lambda }_{\left(\text{1,1}\right)}=9.591$ at $\Delta T=400 K$. In this case, at $h=a/5$, the temperature change does not have much of an effect on the dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ values of $\Delta \text{T}$. For $h=a/10$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=14.511$ while at $\Delta T=0 K$, it decreases by 3.46% has a value ${\lambda }_{\left(\text{1,1}\right)}=14.009$ at ΔT = 200 K, and decreases by 7.37% reaching ${\lambda }_{\left(\text{1,1}\right)}=13.442$ at ΔT = 400 K. For $h=a/15$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.022$ while at $\Delta T=0 K$, it decreases by 8.85% has a value ${\lambda }_{\left(\text{1,1}\right)}=13.693$ at ΔT = 200 K, and decreases by 19.36% reaching ${\lambda }_{\left(\text{1,1}\right)}=12.113$ at ΔT = 400 K. For $h=a/20$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.177$ while at $\Delta T=0 K$, it decreases by 16.72% has a value ${\lambda }_{\left(\text{1,1}\right)}=12.639$ at ΔT = 200 K, and decreases by 39.45% reaching ${\lambda }_{\left(\text{1,1}\right)}=9.190$ at ΔT = 400 K. As can be seen from Fig. 13, as the temperature increases, the dimensionless fundamental frequency values of the material decrease. In addition, when temperature values are $\Delta T=0 K$, $h=a/5$ has the lowest and $h=a/20$ has the highest dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ values. Increasing temperature values cause dimensionless fundamental frequency values to fall more quickly when the thickness ratio h value is modest. In general, it is seen that the increase in temperature reduces the bending strength of the material and therefore the dimensionless fundamental frequency values decrease.

Fig. 13

Comparison of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on temperature rise $\Delta T$ and thickness ratio $h=a/5, a/10, a/15, a/20$, for $\Delta C=0$, nonlocal parameters ${e}_{0}a=0 nm$, material gradation index $p=0$, porosity index $\alpha =0$

Figure 14 demonstrates the change of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on nonlocal parameter and thickness ratio. Where, temperature $\Delta T$, humidity $\Delta C$, material gradation index $p$, and porosity $\alpha$ are accepted as zero, and thickness is $a=10\text{ nm}$. According to results obtained in Fig. 14, for $h=a/5$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=9.591$ while at ${e}_{0}a=0$, it decreases by 8.61% has a value ${\lambda }_{\left(\text{1,1}\right)}=8.765$ at ${e}_{0}a=0.1$, and decreases by 24.94% reaching ${\lambda }_{\left(\text{1,1}\right)}=7.169$ at ${e}_{0}a=0.2$. For $h=a/10$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.046$ while at ${e}_{0}a=0$, it decreases by 8.61% has a value ${\lambda }_{\left(\text{1,1}\right)}=13.750$ at ${e}_{0}a=0.1$, and decreases by 25.24% reaching ${\lambda }_{\left(\text{1,1}\right)}=11.248$ at ${e}_{0}a=0.2$. For $h=a/15$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.576$ while at ${e}_{0}a=0$, it decreases by 8.61% has a value ${\lambda }_{\left(\text{1,1}\right)}=14.235$ at ${e}_{0}a=0.1$, and decreases by 25.24% reaching ${\lambda }_{\left(\text{1,1}\right)}=11.644$ at ${e}_{0}a=0.2$. For $h=a/20$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.737$ while at ${e}_{0}a=0$, it decreases by 8.61% has a value ${\lambda }_{\left(\text{1,1}\right)}=14.382$ at ${e}_{0}a=0.1$, and decreases by 25.24% reaching ${\lambda }_{\left(\text{1,1}\right)}=11.764$ at ${e}_{0}a=0.2$. As a result of the calculations, it is seen that the nonlocal parameter change has the same effect proportionally for different thickness ratio values. It is seen that as both the nonlocal parameter value and the plate thickness increase, the dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ value decreases.

Fig. 14

Comparison of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on nonlocal parameters ${e}_{0}a (nm)$, and thickness ratio $\text{h}=a/5, a/10, a/15, a/20$, for temperature rise $\Delta T=0 K$, $\Delta C=0$, material gradation index $p=0$, porosity index $\alpha =0$

Figure 15 shows the change of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on material gradation index and thickness ratio. Where, temperature $\Delta T$, humidity $\Delta C$, nonlocal parameter ${e}_{0}a$ and porosity $\alpha$ are accepted as zero, and thickness is $a=10\text{ nm}$. According to results obtained in Fig. 15, for $h=a/5$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=9.591$ while at $p=0$, it decreases by 39.82% has a value ${\lambda }_{\left(\text{1,1}\right)}=5.772$ at $p=1$, and decreases by 53.32% reaching ${\lambda }_{\left(\text{1,1}\right)}=4.447$ at $p=6$. For $h=a/10$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.046$ while at $p=0$, it decreases by 39.03% has a value ${\lambda }_{\left(\text{1,1}\right)}=9.173$ at $p=1$, and decreases by 52.43% reaching ${\lambda }_{\left(\text{1,1}\right)}=7.157$ at $p=6$. For $h=a/15$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.576$ while at $\text{p}=0$, it decreases by 38.93% has a value ${\lambda }_{\left(\text{1,1}\right)}=9.513$ at $p=1$, and decreases by 52.27% reaching ${\lambda }_{\left(\text{1,1}\right)}=7.434$ at $p=6$. For $\text{h}=a/20$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=15.737$ while at $p=0$, it decreases by 38.91% has a value ${\lambda }_{\left(\text{1,1}\right)}=9.614$ at $p=1$, and decreases by 52.25% reaching ${\lambda }_{\left(\text{1,1}\right)}=7.515$ at $p=6$. As a result of the calculations, it is seen that the material gradation index change has the same effect proportionally for different thickness ratio values. It is seen that as both the material gradation index value and the plate thickness increase, the dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ value decreases.

Fig. 15

Comparison of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on material gradation index $p$, and thickness ratio $\text{h}=a/5, a/10, a/15, a/20$, for temperature rise $\Delta T=0 K$, $\Delta C=0$, nonlocal parameters ${e}_{0}a=0 nm$, porosity index $\alpha =0$

Figure 14 demonstrates the change of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on nonlocal parameter and material gradation index. Where, temperature $\Delta T$, humidity $\Delta C$, and porosity $\alpha$ are accepted as zero, and thickness ratio is considered $\text{h}=a/10$, and thickness is $\text{a}=10\text{ nm}$. According to results obtained in Fig. 16, for $p=0.2$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=12.306$ while at ${e}_{0}a=0$, it decreases by 8.61% has a value ${\lambda }_{\left(\text{1,1}\right)}=11.246$ at ${e}_{0}a=0.1$, and it decreases by 25.25% reaching ${\lambda }_{\left(\text{1,1}\right)}=9.199$ at ${e}_{0}a=0.2.$ For $p=1$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=9.173$ while at ${e}_{0}a=0$, it decreases by 7.15% has a value ${\lambda }_{\left(\text{1,1}\right)}=8.517$ at ${e}_{0}a=0.1$, and it decreases by 25.25% reaching ${\lambda }_{\left(\text{1,1}\right)}=6.857$ at ${e}_{0}a=0.2$. For $p=2$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=8.130$ while at ${e}_{0}a=0$, it decreases by 8.61% has a value ${\lambda }_{\left(\text{1,1}\right)}=7.430$ at ${e}_{0}a=0.1$, and it decreases by 25.24% reaching ${\lambda }_{\left(\text{1,1}\right)}=6.078$ at ${e}_{0}a=0.2$. For $p=5$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=7.269$ while at ${e}_{0}a=0$, it decreases by 8.61% has a value ${\lambda }_{\left(\text{1,1}\right)}=6.643$ at ${e}_{0}a=0.1$, and it decreases by 25.24% reaching ${\lambda }_{\left(\text{1,1}\right)}=5.434$ at ${e}_{0}a=0.2$. As a result of the calculations, it is seen that the nonlocal parameter change has the same effect proportionally for different material gradation index values. It is seen that as both the nonlocal parameter value and the material gradation index increase, the dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ value decreases.

Fig. 16

Comparison of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on nonlocal parameters ${e}_{0}a \left(nm\right)$ and material gradation index $p=0.2, 1, 2, 5$, for temperature rise $\Delta T=0$, $\Delta C=0$, thickness ratio $\text{h}=a/10$, porosity index $\alpha =0$

Figure 17 shows the change of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on porosity and material gradation index. Where, temperature $\Delta T$, humidity $\Delta C$, nonlocal parameter ${e}_{0}a$ are accepted as zero and thickness ratio is considered $h=a/10$ and thickness is $\text{a}=10\text{ nm}$. Results have been obtained for the uniform porosity and symmetric porosity cases in Fig. 17a and b, respectively. According to results obtained for uniform porosity in Fig. 17a, for $p=0.2$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=12.306$ while at $\alpha =0$, it increases by 17.14% has a value ${\lambda }_{\left(\text{1,1}\right)}=14.415$ at $\alpha =0.3$, and increases by 194.24% reaching ${\lambda }_{\left(\text{1,1}\right)}=36.209$ at $\alpha =0.6$. For $\text{p}=1$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=9.173$ while at $\alpha =0$, it decreases by 1.3% has a value ${\lambda }_{\left(\text{1,1}\right)}=9.054$ at $\alpha =0.3$, and decreases by 2.1% reaching ${\lambda }_{\left(\text{1,1}\right)}=8.980$ at $\alpha =0.6$. For $p=2$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=8.130$ while at $\alpha =0$, it decreases by 6.17% has a value ${\lambda }_{\left(\text{1,1}\right)}=7.628$ at $\alpha =0.3$, and decreases by 17.50% reaching ${\lambda }_{\left(\text{1,1}\right)}=6.707$ at $\alpha =0.6$. For $p=5$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=7.269$ while at $\alpha =0$, it decreases by 10.29% has a value ${\lambda }_{\left(\text{1,1}\right)}=6.521$ at $\alpha =0.3$, and decreases by 29.45% reaching ${\lambda }_{\left(\text{1,1}\right)}=5.128$ at $\alpha =0.6$. According to results obtained for symmetric porosity in Fig. 17b, for $p=0.2$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=12.306$ while at $\alpha =0$, it decreases by 1.28% has a value ${\lambda }_{\left(\text{1,1}\right)}=12.148$ at $\alpha =0.3$, and decreases by 2.73% reaching ${\lambda }_{\left(\text{1,1}\right)}=11.970$ at $\alpha =0.6$. For $p=1$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=9.173$ while at $\alpha =0$, it decreases by 0.94% has a value ${\lambda }_{\left(\text{1,1}\right)}=9.086$ at $\alpha =0.3$, and decreases by 1.73% reaching ${\lambda }_{\left(\text{1,1}\right)}=9.014$ at $\alpha =0.6$. For $p=2$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=8.130$ while at $\alpha =0$, it decreases by 0.44% has a value ${\lambda }_{\left(\text{1,1}\right)}=8.094$ at $\alpha =0.3$, and decreases by 0.32% reaching ${\lambda }_{\left(\text{1,1}\right)}=8.104$ at $\alpha =0.6$. For $p=5$ case, dimensionless fundamental frequency has a value of ${\lambda }_{\left(\text{1,1}\right)}=7.269$ while at $\alpha =0$, it decreases by 0.12% has a value ${\lambda }_{\left(\text{1,1}\right)}=7.260$ at $\alpha =0.3$, and increases by 0.59.45% reaching ${\lambda }_{\left(\text{1,1}\right)}=7.312$ at $\alpha =0.6$. As seen in Fig. 17a, as the material gradation index increases for uniform porosity case, the dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ value decreases. Additionally, as the porosity index $(\alpha )$ increases at $p=0.2$, th ${\lambda }_{\left(\text{1,1}\right)}$ value also increases. However, at other values of $\text{p}$, ${\lambda }_{\left(\text{1,1}\right)}$ value decreases as the porosity index $(\alpha )$ increases. As seen in Fig. 17b, as the material gradation index increases for symmetric porosity case, the dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ value decreases also. However, variation the dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ more less compared with uniform porosity case.

Fig. 17

Comparison of dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ depending on porosity index and material gradation index $p=0.2, 1, 2, 5$, for temperature rise $\Delta T=0$, $\Delta C=0$, nonlocal parameters ${e}_{0}a=0 nm$, thickness ratio h $=0$

8 Conclusions

In this study, the hygrothermal vibration behavior of a functionally graded and porous nanoplate consisting of metal and ceramics was modeled and examined using high-order plate theory. The nonlocal effect was modeled using Eringen's differential integral elasticity theory. The following summary results were obtained by examining the material grading index, which determines the ceramic and metal material composition of the nanoplate, the effect of uniform and symmetrically distributed porosity in the nanoplate, the effect of nonlinear temperature rise, the effect of humidity and the effect of the size of the nonlocal parameter.

The effect of the material rating index $p$ significantly determines the vibration behavior of the nanoplate by determining the metal and ceramic ratio in the nanoplate. Since the ceramic ratio in the nanoplate is higher than the metal ratio between 0 and 1 values of $p$, the natural frequencies of the nanoplate are high in this region. With the increase of $p$, the metal ratio in the nanoplate increases and accordingly, the natural frequencies decrease because the elasticity modulus of the metal is lower than the elasticity modulus of the ceramic. The effect of temperature is less at low $\text{p}$ values where ceramics are high, but greater at high p values where metal is high. This is because the thermal expansion coefficient of metal is higher than the thermal expansion coefficient of ceramics. It is also seen that increasing humidity also reduces natural frequencies. As the thickness ratio increases, the plate gets closer to the real conditions and therefore the frequency values decrease.

The value of ${e}_{0}a$ which is a nonlocal parameter, shows the effect of small-scale values on the behavior of the material. When ${e}_{0}a$ value is zero, it shows that there is no small-scale effect in the material and therefore the material is considered as a classical mechanical model. As the ${e}_{0}a$ value increases, it shows that the scale considered in the material increases, the increase in this value decreases the natural frequencies. The reason for this is that as the small-scale effect increases, the material softens and the bending strength of the material decreases. When humidity effect examined with nonlocal parameter, it is seen that humidity has no effect much on natural frequency. Furthermore, increasing the temperature of the plate reduces the natural frequencies. As the $h$ value, which expresses the ratio of plate thickness to plate length, increases, the dimensionless frequency values obtained decrease and approach the real values. The material gradation index change has the same effect proportionally for different nonlocal parameter values. It is seen that as both the nonlocal parameter value and the material gradation index increase, the dimensionless fundamental frequency value decreases. Also, both the nonlocal parameter value and the plate thickness increase, the dimensionless fundamental frequency ${\lambda }_{\left(\text{1,1}\right)}$ value decreases. When the changes in the frequencies of the material depending on the value of $\text{p}$, which is the material rating index, and ${e}_{0}a$, which is the nonlocal parameter, are examined, it is seen that increases in both values ​​decrease the frequency values.

The effect of porosity index $\alpha$ shows whether the material is porous or not. Increasing the porosity rate in the material causes the mass of the material to decrease and the material to become more strength. Therefore, while the natural frequency values are low at low porosity values, as the amount of porosity increases, the natural frequency values also increase. At the same time, temperature increases reduce the natural frequencies as they cause a softening effect on the material. Additionally, increasing the humidity in the material also increases the dimensionless frequency of the material. When the changes in the frequencies of the material depending on the material grading index $p$ and porosity α value are examined, it is seen that the frequency values are higher at low $p$ value because the ceramic ratio in the plate is higher. In addition, since increasing porosity increases the porosity of the material, it causes a decrease in the mass of the plate and, as a result, an increase in the strength and frequency.

This research found that the hygrothermal vibration behavior of the nanoplate exhibited a nonlinear shift when high porosity was used in conjunction with FGM material. The porosity ratio and distribution pattern have the most significant influence on this alteration.