1 Introduction

Escape from a potential well is an extensively researched topic in the field of nonlinear dynamic systems [1,2,3,4,5], finding applications in various domains including chemical reactions [6, 7], physics of Josephson junctions [8], MEMS devices [9,10,11,12,13,14], celestial mechanics, and gravitational collapse. It also plays a crucial role in energy harvesting [15] and is closely related to the dynamics of oscillatory systems [16, 17], as well as specific phenomena, such as the capsize of ships [4, 18]. Despite the significant body of previous research, unresolved issues still require further investigation [19].

Various aspects of the escape phenomenon have been studied. For example, the problem of the sharp minimum of the critical excitation amplitude near the primary resonance has been examined under unlimited potential and homogeneous initial conditions [20]. Another area of research focuses on determining safe basins, which represent non-escaping initial conditions under specific excitations, and investigating integrity measures that quantify the size of the non-escaping set [2, 21,22,23]. However, providing accurate analytic results for nonquadratic potential wells is a challenge. Approximation methods such as Melnikov’s method [2] or the use of adiabatic invariants and action-angle variables [24] offer formulas suitable for small excitation values but lose accuracy away from the 1:1 resonance.

Previous studies have addressed the escape problem of weakly damped particles from truncated quadratic potential wells under harmonic excitation, focusing on the location and size of safe escape basins in the initial conditions plane [25]. The escape problem of two strongly coupled particles in a truncated quadratic potential under biharmonic excitation has also been investigated [26]. When the relative vibrations of the particles are significantly faster than the oscillation of the particle’s center of mass within the potential, the system can be effectively reduced to a one-degree-of-freedom system by introducing an effective potential. The effective force field is derived by cross-correlating the original potential with the probability density function of the fast relative motion [27].

This study aims to expand the scope of previous investigations by focusing on a strongly coupled n-particle chain subjected to polyharmonic excitation, a rather peculiar mechanical system per se, although often resulting as a discretized model of slender, continuous structures. To reduce the dynamics of the particle chain, we provide a more rigorous analytical foundation for the classical probability-density-based reduction method previously employed on a heuristic basis in [26]. Although the investigated system is quite unusual, the theoretical results of this article may be used in a wide variety of “slow-fast” systems, where polyharmonic functions are involved and averaging is applicable. Extending the theoretical results for the composition of general periodic functions with linearly independent time periods over the rational numbers is straightforward.

The structure of this paper is as follows. Section 2 discusses the problem setting and provides the solution for relative vibrations in a chain of n particles. Section 3 delves into the model reduction approach based on averaging. Section 4 illustrates these concepts with an example involving a three-particle chain. Section 5 contains a comprehensive discussion, and, finally, Sect. 6 offers conclusions and highlights the scope for future research.

2 Problem setting

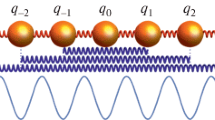
We consider the following problem setting depicted in Fig. 1.

Fig. 1
figure 1

Problem setting of an internally damped, coupled n-particle system in a potential well, where particles have an equilibrium distance of zero, implying the possibility for mutual penetration without physical constraints

Full size image

The movement is one-dimensional and occurs along the x axis. The masses of the n individual particles are denoted by \(m_1\), \(m_2\),..., \(m_n\). The damping coefficient of the \(n-1\) dashpot dampers is represented by \(k_1\), \(k_2\),..., \(k_{n-1}\), while the stiffness of the \(n-1\) linear springs between the particles is denoted by \(c_1\), \(c_2\),..., \(c_{n-1}\). Each particle can be stimulated by a polyharmonic force, which is expressed as \(F_1(t)\), \(F_2(t)\),..., \(F_n(t)\). Initially, the particles are situated in a potential well. For each particle, this is individually given by \(V_1(x_1)\), \(V_2(x_2)\),..., \(V_n(x_n)\), where \(V_i(x_i) = m_i V(x_i)\), with \(V(\cdot )\) defined in more detail below.

Additionally, it is essential to note that, in this system, the particles can penetrate each other, reflecting that the equilibrium distance between the particles is zero.

2.1 Equations of motion

Applying the Euler–Lagrange equations, we can derive the equations of motion of the above system.

$$\begin{aligned} \frac{\text {d}}{\text {d}t}\frac{\partial T}{\partial \dot{q}_i}(t,\dot{\textbf{q}}(t)) = -\frac{\partial U}{\partial q_i}(t,\textbf{q}(t)) -\frac{\partial D}{\partial \dot{q}_i}(t,\dot{\textbf{q}}(t))+Q_i^*(t) \qquad \text {for }i=1,\ldots ,n, \end{aligned}$$
(1)

where the general coordinates are chosen to be \(q_i=x_i\) and

$$\begin{aligned} T&= \sum _{i=1}^{n}\frac{1}{2}m_i \dot{x}_i^2, \end{aligned}$$
(2)
$$\begin{aligned} U&= \sum _{i=1}^{n-1}\frac{1}{2}c_i(x_{i+1}-x_i)^2+V_i(x_i), \end{aligned}$$
(3)
$$\begin{aligned} D&= \sum _{i=1}^{n-1}\frac{1}{2}k_i(\dot{x}_{i+1}-\dot{x}_i)^2, \end{aligned}$$
(4)
$$\begin{aligned} Q_i^*(t)&=F_i(t)=F_{i,0}\sin (\Omega _0 t+\beta _{i,0})+ \sum _{p=1}^PF_{i,p} \sin (\Omega _{i,p} t+\beta _{i,p}), \end{aligned}$$
(5)

where \(P \in \mathbb {N}^+\). We require that the general, continuous potential V(x) is bounded above, i.e., it fulfills

$$\begin{aligned} \lim _{|x |\rightarrow \infty } V(x)&\le C, \text { for some } C \in \mathbb {R}. \end{aligned}$$
(6)

Furthermore, we require that the potential well has a stable equilibrium at \(x=0\), and its linearized angular eigenfrequency around this equilibrium is 1, i.e.:

$$\begin{aligned} V'(x=0)&=0, \end{aligned}$$
(7)
$$\begin{aligned} V''(x=0)&=1. \end{aligned}$$
(8)

In the following, frequency refers to the angular frequency in radians per second.

Furthermore, we assume that V(x) is softening and has a single well, i.e.,

$$\begin{aligned} V''(x)&\le \frac{V'(x)}{x} \le 1. \end{aligned}$$
(9)

In equality (9) is obtained from the definition of a “softening characteristic,” that is, the stiffness of the potential \(c(x):=V'(x)/x\) decreases monotonically as the distance from the bottom of the well \(|x |\) increases. On the other hand, the maximum stiffness at \(x=0\) is given by

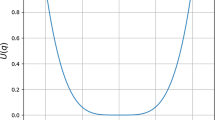
$$\begin{aligned} \lim _{x\rightarrow 0}\frac{V'(x)}{x}=\lim _{x\rightarrow 0}\frac{V'(x)-V'(0)}{x-0}=V''(x)\vert _{x=0}=1. \end{aligned}$$
(10)

Given that V(x) is bounded above, we define the location of the left supremum of V(x) as \( x_l \), where \( x_l \in \mathbb {R}^- \cup \lbrace -\infty \rbrace \), and the location of the right supremum as \( x_r \), where \( x_r \in \mathbb {R}^+ \cup \lbrace \infty \rbrace \). We refer to the interval \( (x_l, x_r) \) as the interior of the well. The term escape is used when the chain leaves this region. For a detailed definition of escape, see Sect. 2.3. Figure 2 shows a graphical representation of a feasible potential.

Fig. 2
figure 2

Example of a feasible potential. The interior of the potential stretches from \(x_l\) to \(x_r\)

Full size image
Fig. 3
figure 3

Amplification and phase depicted against the excitation frequency with \(n=4\) particles for \(m=1\), \(k=0.8\), \(c=1000\). The second particle of the chain is excited. The analytic peak frequencies given by Eq. (54) are depicted with dashed black lines

Full size image

We assume that the masses \(m_i\) are of magnitude \(\mathcal {O}(1)\) and that the forces of the coupling springs are much greater than those of the potential, that is, \(c_i \gg 1 \ge \max _{x \in (x_l,x_r)}V_i''(x)\), or equivalently \(c_i \in \mathcal {O}(\varepsilon ^{-1})\). Additionally, we assume the existence of non-small damping, denoted by \(k_i \in \mathcal {O}(1)\). With the above assumptions on \(c_i\) and \(k_i\), the chain’s internal modes are underdamped (cf. Sect. 2.5). Thus, the corresponding receptance frequency response function has \(n-1\) local maxima (cf. Fig. 3). We refer to the location of the local maxima as resonant frequencies. We postulate that the lowest resonant frequency of relative movements in the particle chain significantly exceeds the linearized eigenfrequency of any singular particle in the potential well.

Each particle is excited by up to \(P+1\) harmonic forces. We assume low-frequency excitation for each particle with possibly different amplitudes \(F_{i,0}\) and initial phases \(\beta _{i,0}\), but with identical frequency \(\Omega _0 \in \mathcal {O}(1)\).

The rest of the excitation frequencies are considered significantly higher than the base frequency, i.e., \(\Omega _{i,p} \gg \Omega _{0}\), and are not necessarily identical for all particles, i.e., \(\Omega _{i,p}\) is independent of \(\Omega _{j,p}\).

Such excitation patterns are relevant in models of cantilever beams used as sensors in Micro-Electro-Mechanical Systems (MEMS). An important application of this can be found in Atomic Force Microscopy (AFM), where a transcendental equation determines the eigenfrequencies of the cantilever beam, which are linearly independent over the rational numbers (cf. Definition 1). This example reflects a realistic physical situation in which the proposed model can be helpful.

Insertion of Eqs. (2–5) in Eq. (1) yields the nonlinear differential equation system

$$\begin{aligned} \textbf{M}\ddot{\textbf{x}} +\textbf{K}\dot{\textbf{x}} +\textbf{C}\textbf{x}+\mathbf {v'(x)}=\textbf{f}(t), \end{aligned}$$
(11)

where the matrices and vectors are

$$\begin{aligned} \textbf{M}&=\textrm{diag}\left( m_1,m_2,\dots ,m_n\right) \in \textbf{R}^{n\times n}, \end{aligned}$$
(12)
$$\begin{aligned} \textbf{K}&=\textrm{diag}\left( k_1,k_1+k_2,\dots ,k_{n-2}+k_{n-1},k_{n-1}\right) -\textrm{subdiag}\left( k_1,k_2,\dots ,k_{n-1}\right) \nonumber \\&\quad -\textrm{superdiag}\left( k_1,k_2,\dots ,k_{n-1}\right) \in \textbf{R}^{n\times n}, \end{aligned}$$
(13)
$$\begin{aligned} \textbf{C}&=\textrm{diag}\left( c_1,c_1+c_2,\dots ,c_{n-2}+c_{n-1},c_{n-1}\right) -\textrm{subdiag}\left( c_1,c_2,\dots ,c_{n-1}\right) \nonumber \\&\quad -\textrm{superdiag}\left( c_1,c_2,\dots ,c_{n-1}\right) \in \textbf{R}^{n\times n}, \end{aligned}$$
(14)
$$\begin{aligned} \textbf{x}&= \begin{bmatrix} x_1, x_2, \dots , x_{n} \end{bmatrix}^\top \in \textbf{R}^{n},\end{aligned}$$
(15)
$$\begin{aligned} \mathbf {v'(x)}&= \begin{bmatrix} V_1'(x_1), V_2'(x_2), \dots , V_n'(x_n) \end{bmatrix}^\top \in \textbf{R}^{n},\end{aligned}$$
(16)
$$\begin{aligned} \textbf{f}(t)&= \begin{bmatrix} F_1(t), F_2(t), \dots , F_n(t) \end{bmatrix}^\top \in \textbf{R}^{n}, \end{aligned}$$
(17)

where diag(\(\cdot \)), subdiag(\(\cdot \)) and superdiag(\(\cdot \)) denote diagonal, subdiagonal, and superdiagonal matrices. Furthermore, bold lowercase symbols denote vectors in the time domain, while bold uppercase symbols indicate matrices. Consistent with the standard literature, vectors containing the Laplace transforms of vector values are also represented using bold uppercase letters. The reader should be mindful of this notation to avoid confusion.

2.2 Decoupling coordinate transformation

The differential equation is strongly coupled in each coordinate nonlinearly in the present form. Furthermore, the springs’ large stiffness but the potential’s moderate restoring force result in a slow-fast system. By applying an appropriate coordinate transform, we can obtain a system that is only weakly coupled by nonlinear terms, and strong coupling is only present in linear terms. Then, ignoring the weak nonlinear coupling in the corresponding equations, we can easily handle the remaining “fast” linear system of ODEs analytically, which allows us to obtain an analytic solution for the “fast” variables and to focus solely on the remaining “slow” variable. We proceed as follows.

We introduce new coordinates, \(\eta \) and \(y_i\) for \(i \in \lbrace 2,\dots ,n \rbrace \).

$$\begin{aligned} \eta =\frac{\sum _{i=1}^n m_i x_i}{\sum _{i=1}^n m_i} \quad \text {and} \quad y_i=x_i-x_{i-1}, \quad \text {for } i \ge 2. \end{aligned}$$
(18)

Thus, the first coordinate represents the center of mass of the chain, and the rest of the coordinates are the relative distances between two consecutive particles. By defining \(M=\sum _{i=1}^n m_i\), we can write the transformation as

$$\begin{aligned} \textbf{y}= \begin{bmatrix} \eta \\ y_2\\ y_3\\ \vdots \\ y_n \end{bmatrix} = \underbrace{\begin{bmatrix} \frac{m_1}{M} &{}\quad \frac{m_2}{M} &{}\quad \frac{m_3}{M} &{}\quad \dots &{}\quad \frac{m_n}{M}\\ -1 &{}\quad 1 &{}\quad 0 &{}\quad \dots &{}\quad 0 \\ 0&{}\quad -1 &{}\quad 1 &{}\quad \ddots &{}\quad \vdots \\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad 0\\ 0&{}\quad \dots &{}\quad 0 &{}\quad -1 &{}\quad 1 \end{bmatrix}}_{=:\textbf{S}^{-1}} \begin{bmatrix} x_1\\ x_2\\ x_3\\ \vdots \\ x_n \end{bmatrix}. \end{aligned}$$
(19)

For the calculation of \(\textbf{S}\), see Eq. (127) in the Appendix.

Inserting \(\textbf{x}=\textbf{Sy}\) into Eq. (11), we can write the equations of motion in the new coordinates as

$$\begin{aligned} \textbf{M} \textbf{S}\ddot{\textbf{y}} +\textbf{K}\textbf{S}\dot{\textbf{y}} +\textbf{C}\textbf{Sy}+\mathbf {v'}(\textbf{Sy})&=\textbf{f}(t),\end{aligned}$$
(20)
$$\begin{aligned} \ddot{\textbf{y}}+ \underbrace{\textbf{S}^{-1}\textbf{M}^{-1}\textbf{K}\textbf{S}}_{=:\tilde{\textbf{K}}}\dot{\textbf{y}} +\underbrace{\textbf{S}^{-1}\textbf{M}^{-1}\textbf{C}\textbf{S}}_{=:\tilde{\textbf{C}}} \textbf{y}+\underbrace{\textbf{S}^{-1}\textbf{M}^{-1}\mathbf {v'}(\textbf{Sy})}_{=:\tilde{\textbf{v}}'}&=\underbrace{\textbf{S}^{-1}\textbf{M}^{-1}\textbf{f}(t)}_{=:\tilde{\textbf{f}}(t)}. \end{aligned}$$
(21)

The matrices \(\tilde{\textbf{K}}\) and \(\tilde{\textbf{C}}\) are given in the Appendix by Eqs. (128–129), respectively. Further, we calculate

$$\begin{aligned} \tilde{\textbf{v}}'&= \textbf{S}^{-1}\textbf{M}^{-1} \begin{bmatrix} m_1V'(\textbf{s}_1 \textbf{y})\\ m_2V'(\textbf{s}_2 \textbf{y})\\ \vdots \\ m_nV'(\textbf{s}_n \textbf{y}) \end{bmatrix} = \begin{bmatrix} \frac{\sum _{i=1}^{n}m_i V'(\textbf{s}_i \textbf{y})}{M}\\ V'(\textbf{s}_2 \textbf{y})-V'(\textbf{s}_1 \textbf{y})\\ \vdots \\ V'(\textbf{s}_n \textbf{y})-V'(\textbf{s}_{n-1} \textbf{y})\\ \end{bmatrix}, \end{aligned}$$
(22)

using the notation \(\textbf{S}=(\textbf{s}_1,\textbf{s}_1,\dots ,\textbf{s}_n)^\text {T}\) with \(\textbf{s}_i \in \mathbb {R}^n\).

Based on [28] and [29], the particular solutions of \(y_2\ldots y_n\) are only negligibly influenced by their coupling to \(\eta \), which is due to the strong damping between the particles and the fact that the coupling to the “outer” potential field is weak since \(c_i/m_i \in \mathcal {O}(\varepsilon ^{-1})\), while the maximal stiffness of the potential \(\max _{x \in (x_l,x_r)} V'(x)/x\) is of magnitude \( \mathcal {O}(1)\).

Considering small relative displacements, i.e., \(|y_i |< 1\) for \(i=2\ldots n\), and assuming that the particles are primarily inside of the potential well, i.e., \(x_i \in (x_l,x_r)\), the force of the potential can be linearized around \(x_{i-1}\) as

$$\begin{aligned} V'(x)\approx V'(x_{i-1})+V''(x_{i-1})(x-x_{i-1}), \end{aligned}$$
(23)

and by \(\textbf{s}_i\textbf{y}_i=x_i\) we find

$$\begin{aligned} V'(\textbf{s}_i \textbf{y})-V' (\textbf{s}_{i-1} \textbf{y})&\approx V'(x_{i-1})+V''(x_{i-1})(x_i-x_{i-1})-V'(x_{i-1}) \end{aligned}$$
(24)
$$\begin{aligned}&\approx V''(x_{i-1}) y_i, \end{aligned}$$
(25)

which we can neglect since \( V''(x) \le 1 \ll c_i\) by our assumptions. Thus, the vector can be rewritten as

$$\begin{aligned} \tilde{\textbf{v}}'&\approx \begin{bmatrix} \frac{\sum _{i=1}^{n}m_i V'(\textbf{s}_i \textbf{y})}{M}, 0, \dots , 0 \end{bmatrix}^\top . \end{aligned}$$
(26)

Similarly, we find

$$\begin{aligned} \tilde{\textbf{f}}(t)&= \begin{bmatrix} \frac{\sum _{i=1}^{n}F_i(t)}{M}, \frac{F_2(t)}{m_2}-\frac{F_1(t)}{m_1}, \dots , \frac{F_n(t)}{m_n}-\frac{F_{n-1}(t)}{m_{n-1}} \end{bmatrix}^\top . \end{aligned}$$
(27)

It is worth noting that only the “fast” system can be approximated well by a linear one by neglecting the nonlinear terms. The modal decoupling of the “slow” part is not possible in this way since neglecting nonlinearities in the equation of \(\eta \) significantly alters the dynamics of the system (cf. Eq. 28). The reason is that the linear springs and dampers mainly affect the “fast” dynamics. However, their effects cancel each other out in the “slow” system, leaving only the potential’s force as the main contributor to the center of mass dynamics.

2.3 Escape definition

The definition of escape is, in general, problem-specific, depending on V(x). The following is suitable for a particle chain in a single-welled potential (i.e., the potential has only one local minimum). The chain escapes if “\(\exists i \in \lbrace 1,\dots ,n \rbrace \) such that \(\lim _{t \rightarrow \infty } |y_i(t) |=\infty \)”. This definition allows for an escape of the whole chain in one direction \(\lim _{t \rightarrow \infty } |\eta (t) |=\infty \), or for the splitting of the chain for \( i \in \lbrace 2,\dots ,n \rbrace \). Due to the strong coupling between the particles, this second scenario is possible for certain potentials, but only with unrealistically large excitation values; therefore, we do not consider it in the following.

The definition of escape can differ for particles or particle chains in a multi-welled potential since the previous definition must not or cannot hold. For example, in the case of a ship capsize, the dynamics is described in angle coordinates, and escape means going from the upright well into a lateral well, but not into infinity.

2.4 The steady-state solutions of the fast subsystem

In general, an analytic expression for the eigenmodes and eigenfrequencies, and so for the particular solutions of \(y_2(t)\ldots y_n(t)\), cannot be given with a closed formula. Therefore, we limit the investigation to a special case where the masses, dampers, and springs are all equal, that is, \(m_i=m\) for all \(i \in {1,\dots ,n}\) and \(k_i=k\) and \(c_i=c \) for all \(i \in {1,\dots ,n-1}\). The equation of motion of the center of mass becomes

$$\begin{aligned} \ddot{\eta }+\frac{\sum _{i=1}^{n} V'(\textbf{s}_i \textbf{y})}{n}=\frac{\sum _{i=1}^{n}F_i(t)}{nm}. \end{aligned}$$
(28)

To address Eq. (28), it is essential to obtain solutions for \( y_2, \ldots , y_n\) first, which requires focusing on the submatrix formed by excluding the first row and column of our current matrices, leading to the following simplified expressions.

$$\begin{aligned} \bar{\textbf{y}}&=[y_2 \quad y_3 \quad \dots \quad y_n]^\top{} & {} \in \mathbb {R}^{n-1}, \end{aligned}$$
(29)
$$\begin{aligned} \bar{\textbf{K}}&=\tilde{\textbf{K}}_{2:n,2:n}{} & {} \in \mathbb {R}^{(n-1)\times (n-1)}, \end{aligned}$$
(30)
$$\begin{aligned} \bar{\textbf{C}}&=\tilde{\textbf{C}}_{2:n,2:n}{} & {} \in \mathbb {R}^{(n-1)\times (n-1)}, \end{aligned}$$
(31)
$$\begin{aligned} \bar{\textbf{f}}&=\tilde{\textbf{f}}_{2:n}{} & {} \in \mathbb {R}^{n-1}, \end{aligned}$$
(32)

where p : q in the vector index denotes the vector obtained by taking the entries from the \(p^\text {th}\) row to the \(q^\text {th}\) row. Similarly, p : q, r : s in the matrix index denotes the matrix block obtained by taking the entries between the rows p and q and between the columns r and s. The equations of motion of the reduced system can be written as

$$\begin{aligned} \ddot{\bar{\textbf{y}}}+ \bar{\textbf{K}} \dot{\bar{\textbf{y}}}+ \bar{\textbf{C}} \bar{\textbf{y}} = \bar{\textbf{f}}(t), \end{aligned}$$
(33)

where \(\bar{\textbf{K}}\) and \(\bar{\textbf{C}}\) are tridiagonal Toeplitz matrices.

As the chosen damping value is non-small and the damping is pervasive (present in all vibration modes, cf. Eq. (36) and observe that \(K<n\)), the homogeneous equation will decay rapidly. Hence, we are only interested in the particular solution given to the polyharmonic excitation. Using the linearity of the simplified problem, we can obtain the solution by applying the Laplace transform. Assuming zero initial conditions, the Laplace transform of Eq. (33) becomes

$$\begin{aligned} s^2\bar{\textbf{Y}}(s)+s\bar{\textbf{K}}\bar{Y}(s)+ \bar{\textbf{C}}\bar{Y}(s)=\bar{\textbf{F}}(s), \end{aligned}$$
(34)

where \(\bar{\textbf{Y}}(s)=\mathcal {L}\lbrace \bar{\textbf{y}}(t) \rbrace \) and \(\bar{\textbf{F}}(s)=\mathcal {L}\lbrace \bar{\textbf{f}}(t) \rbrace \), which is equivalent to

$$\begin{aligned} \underbrace{ \begin{bmatrix} s^2+2\frac{k}{m}s+2\frac{c}{m} &{}\quad -\frac{k}{m}s-\frac{c}{m} &{}\quad 0 &{}\quad \dots &{}\quad 0 \\ -\frac{k}{m}s-\frac{c}{m} &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad 0\\ \vdots &{}\quad \ddots &{}\quad \ddots &{}\quad \ddots &{}\quad -\frac{k}{m}s-\frac{c}{m}\\ 0&{}\quad \dots &{}\quad 0 &{}\quad -\frac{k}{m}s-\frac{c}{m} &{}\quad s^2+2\frac{k}{m}s+2\frac{c}{m} \end{bmatrix}}_{\mathbf {=:A}(s)} \begin{bmatrix} Y_2\\ Y_3\\ \vdots \\ Y_{n-1}\\ Y_n \end{bmatrix} = \begin{bmatrix} \bar{F}_2\\ \bar{F}_3\\ \vdots \\ \bar{F}_{n-1}\\ \bar{F}_n \end{bmatrix}. \end{aligned}$$
(35)

Based on [30] the eigenvalues \(s_{K,1/2}\), \(K=1\ldots n-1\) of the matrix are given as

$$\begin{aligned} s_{K,1/2}=-\frac{k}{m}\left( 1+\cos \frac{K\pi }{n}\right) \pm \sqrt{\frac{k^2}{m^2}\left( 1+\cos \frac{K\pi }{n}\right) ^2-\frac{2c}{m}\left( 1+\cos \frac{K\pi }{n} \right) }, \end{aligned}$$
(36)

and the eigenvectors (mode shapes) are

$$\begin{aligned} \textbf{v}^K=\left[ \sin \left( \frac{\pi K}{n}\right) , \dots , \sin \left( \frac{(n-1)\pi K}{n}\right) \right] ^\top , \text { for } K \in \lbrace 1,\dots ,n-1\rbrace . \end{aligned}$$
(37)

The eigenvectors do not have unit lengths in this representation, so the next step is normalizing them. The \(K^\text {th}\) eigenvector has length

$$\begin{aligned} \left|\textbf{v}^K \right|=\sqrt{\sum _{l=1}^{n-1}\sin ^2\left( \frac{l \pi K}{n}\right) }=\sqrt{\frac{n-1}{2}-\frac{1}{2} \underbrace{\sum _{l=1}^{n-1} \cos \left( \frac{2 \pi l K }{n} \right) }_{\text {=-1}}}=\sqrt{\frac{n}{2}}, \end{aligned}$$
(38)

which follows from the trigonometrical identity \(\sin ^2x=\frac{1-\cos 2x}{2}\) and the fact that the roots of unity add up to zero. We can observe that, independently of the value of K, all eigenvectors have the same magnitude \(\sqrt{n/2}\). We normalize them by this factor and obtain the matrix

$$\begin{aligned} \textbf{Q}= \sqrt{\frac{2}{n}} \begin{bmatrix} \textbf{v}^1,&\textbf{v}^2,&\dots ,&\textbf{v}^{n-1} \end{bmatrix}, \end{aligned}$$
(39)

which is orthogonal and symmetric, i.e., \(\textbf{Q}=\textbf{Q}^{-1}=\textbf{Q}^\top \). The matrix \({\textbf{A} \in \mathbb {C}^{(n-1)\times (n-1)}}\) can be written as

$$\begin{aligned} \textbf{A}=\textbf{Q}\varvec{\Lambda } \textbf{Q}^\top =\textbf{Q}\varvec{\Lambda } \textbf{Q}, \end{aligned}$$
(40)

and so due to the above-mentioned properties the inverse of \(\textbf{A}\) can be written as

$$\begin{aligned} \textbf{A}^{-1}=\textbf{Q}\varvec{\Lambda }^{-1} \textbf{Q}. \end{aligned}$$
(41)

We can give the entries of \(\textbf{A}^{-1}\) as follows.

$$\begin{aligned} A_{ij}^{-1}(s)=\frac{2}{n}\sum _{K=1}^{n-1}\frac{\sin \left( \frac{i \pi K}{n}\right) \sin \left( \frac{j \pi K}{n}\right) }{s^2+2\frac{k}{m}s+2\frac{c}{m}-2 \left( \frac{k}{m}s+ \frac{c}{m}\right) \cos \left( \frac{\pi K}{n} \right) }. \end{aligned}$$
(42)

The system’s linearity can be used to find the particular solution for polyharmonic excitation. First, we calculate the effect of a harmonic excitation. Then, we take the superposition of all harmonics that act on the particle chain.

To start with, we investigate the response to the harmonic \(F_i \sin (\omega _i t +\beta _i)\), acting at the ith \( \in \lbrace 1,\dots ,n-1 \rbrace \) reduced coordinate, not to be confused with the \(i^\text {th}\) particle. We find

$$\begin{aligned} \bar{\textbf{Y}}(s=\jmath \omega _i)=\textbf{A}^{-1}(\jmath \omega _i) \begin{bmatrix} 0, \dots , F_{i}e^{\jmath \beta _i}, \dots , 0 \end{bmatrix}^\top = F_{i}e^{\jmath \beta _i} \textbf{a}_i^{-1}(\jmath \omega _i), \end{aligned}$$
(43)

where \(\textbf{a}_i^{-1}\) denotes the ith column of the matrix \(\textbf{A}^{-1}\) and \(\jmath \) is the imaginary unit. Then the Kth row of vector \(\bar{\textbf{y}}(t)\) has the form

$$\begin{aligned} \bar{y}_K(t)=\left|\bar{Y}_K(\omega _i) \right|\sin (\omega _i t+ \bar{\Psi }_K(\omega _i)), \end{aligned}$$
(44)

where \(\bar{\Psi }_K(\omega _i)=\angle \bar{Y}_K(\omega _i) \) is the phase angle.

If we excite the ith particle according to Eq. (5) in the y coordinates, this excitation manifests twice, as indicated by Eq. (27), except at the end of the chain where it occurs only once. Consequently, we have \(2(P+1)(n-1)\) distinct harmonic terms superimposed.

Let us define \(\bar{\textbf{Y}}_{i,p,+}\) and \(\bar{\textbf{Y}}_{i,p,-}\) as the complex amplitudes of the simple harmonic excitation caused by the pth harmonic excitation, \(p \in \lbrace 0,\dots , P \rbrace \), of the ith particle, \(i \in \lbrace 1,2, \dots , n\rbrace \) when having a plus or minus sign as in Eq. (27):

$$\begin{aligned} \bar{\textbf{Y}}_{i-1,p,+}(\jmath \Omega _{i,p})&= F_{i,p}e^{\jmath \beta _{i,p}} \textbf{a}_i^{-1}(\jmath \Omega _{i,p}),{} & {} i\in \lbrace 2,\dots ,n \rbrace , \quad p\in \lbrace 0,1,\dots ,P\rbrace , \end{aligned}$$
(45)
$$\begin{aligned} \bar{\textbf{Y}}_{i,p,-}(\jmath \Omega _{i,p})&= -F_{i,p}e^{\jmath \beta _{i,p}} \textbf{a}_i^{-1} (\jmath \Omega _{i,p}), \quad{} & {} i\in \lbrace 1,2, \dots ,n-1 \rbrace , \quad p\in \lbrace 0,1,\dots ,P\rbrace . \end{aligned}$$
(46)

The particular solution of the relative distances become

$$\begin{aligned} y_{K+1}(t)=\sum _{i=1}^{n-1} \sum _{p=0}^P \sum _{q \in \lbrace -,+\rbrace } \left|\bar{Y}_{i,p,q,K}(\jmath \Omega _{i,p}) \right|\sin (\Omega _{i,p} t+ \bar{\Psi }_{i,p,q,K}&(\jmath \Omega _{i,p})), \end{aligned}$$
(47)

with \(K\in \lbrace 1,\dots ,n-1\rbrace \), and \(\bar{Y}_{i,p,q,K}\) denoting the Kth row of the vector \(\bar{\textbf{Y}}_{i,p,q}\). Thus, we obtain accurate estimates for \(y_2(t),\dots ,y_n(t)\).

2.5 Resonant frequencies

We are generally interested in the system’s behavior near its resonant frequencies. Therefore, we derive the frequencies of the resonance peaks and the relative amplifications at these points. In order to do that, it is enough to examine the system with a single harmonic excitation, as given in Eq. (43), which acts on the ith reduced coordinate (not on the ith particle). Writing the explicit expression for the Kth row of the vector, we have

$$\begin{aligned} \bar{Y}_K(\jmath \omega _i)&= \frac{2}{n}\sum _{l=1}^{n-1}\frac{\sin \left( \frac{i \pi l}{n}\right) \sin \left( \frac{K \pi l}{n}\right) }{s^2+2\frac{k}{m}s+2\frac{c}{m}-2 \left( \frac{k}{m}s+ \frac{c}{m}\right) \cos \left( \frac{\pi l}{n} \right) } \bigg |_{s=\jmath \omega _i} F_ie^{\beta _i} \end{aligned}$$
(48)
$$\begin{aligned}&=\frac{2}{n}\sum _{l=1}^{n-1}\frac{\sin \left( \frac{i \pi l}{n}\right) \sin \left( \frac{K \pi l}{n}\right) }{\left[ 2 \frac{c}{m} \left( 1-\cos \left( \frac{\pi l}{n}\right) \right) -\omega _i^2\right] -\jmath \left[ 2 \omega _i \frac{k}{m} \left( 1-\cos (\frac{\pi l}{n}\right) \right] } F_ie^{\beta _i}. \end{aligned}$$
(49)

Large vibrations can occur when \(|Y_i |\) is large, which might occur when at least one of the denominators in the sum approaches (although, due to the pervasive damping, never reaches) zero in its absolute value. The absolute value of the denominator is

$$\begin{aligned}&\bigg |\left[ \frac{2c}{m} \left( 1-\cos \left( \frac{\pi l}{n}\right) \right) -\omega _i^2 \right] -\jmath \left[ 2 \omega _i \frac{k}{m} \left( 1-\cos \left( \frac{\pi l}{n}\right) \right) \right] \bigg |\end{aligned}$$
(50)
$$\begin{aligned}&\quad =\sqrt{\left[ \frac{2c}{m} \left( 1-\cos \left( \frac{\pi l}{n}\right) \right) -\omega _i^2 \right] ^2 +4 \omega _i^2 \frac{k^2}{m^2} \left( 1-\cos \left( \frac{\pi l}{n}\right) \right) ^2} \end{aligned}$$
(51)
$$\begin{aligned}&\quad =\sqrt{\omega _i^4+4 \left( 1-\cos \left( \frac{l \pi }{n}\right) \right) \left[ \frac{k^2}{m^2} \left( 1-\cos \left( \frac{l \pi }{n}\right) \right) -\frac{c}{m}\right] \omega _i^2+ \left( \frac{2c}{m}\left( 1-\cos \frac{\pi l}{n}\right) \right) ^2}. \end{aligned}$$
(52)

Since \(k>0\), the absolute value of the denominator is a continuously differentiable function for any \(\omega _i \in \mathbb {R}\), and we can find its minimum value by setting its derivative equal to zero.

Moreover, since the square root function is monotonic, the expression attains its minimum value where the fourth-order polynomial inside the root reaches its minimum. Given that this polynomial is symmetric and \(\omega _i^4\) has a positive coefficient, two scenarios can be anticipated. In the first scenario, the polynomial reaches its local maximum at \(\omega _i = 0\), and its two local minima occur symmetrically around this point. In the second scenario, there is a single local minimum at \(\omega _i = 0\). As we move away from zero, the function values increase monotonically. The latter case corresponds to a strongly overdamped aperiodic system, which is not within the focus of our study (cf. Eq. 58). We obtain the following result by differentiating the expression within the square root.

$$\begin{aligned} 4 \omega _i^3+8 \left( 1-\cos \left( \frac{l \pi }{n}\right) \right) \left( \frac{k^2}{m^2} \left( 1-\cos \left( \frac{l \pi }{n}\right) \right) -\frac{c}{m} \right) \omega _i&=0, \end{aligned}$$
(53)

which is solved by

$$\begin{aligned} \omega _{i,12}&=\pm \sqrt{2 \left( 1-\cos \left( \frac{l \pi }{n}\right) \right) \left( \frac{c}{m}- \frac{k^2}{m^2}\left( 1-\cos \left( \frac{l \pi }{n}\right) \right) \right) }, \end{aligned}$$
(54)
$$\begin{aligned} \omega _{i,3}&=0. \end{aligned}$$
(55)

Substituting values for \(l=1\ldots n-1\), we obtain reasonable analytic estimates for the resonant frequencies of the particle chain. A graphical example with \(n=4\) particles is shown in Fig. 3.

The frequencies given by Eq. (54) are the set of frequencies at which a resonant system response might occur. When exciting at a given node, however, not each frequency will cause resonant motion, since for that it is also required that in Eq. (49) the numerator \(\sin \left( \frac{i \pi l}{n}\right) \sin \left( \frac{K \pi l}{n}\right) \) does not vanish. A graphical example with \(n=4\) and \(l=2\) is given in Fig. 3, where \(\bar{y}_2\equiv y_3\) (thus, \(K=2\)) cannot be excited by the second resonant frequency \(i=2\), since the numerator there becomes 0.

Based on Eq. (54), we can also give an estimate of the maximal value of the damping coefficient \(k_\text {crit}\), for which all internal modes of the chain are oscillatory. All resonant peaks exist if the expression under the square root for all \(l \in \lbrace 1,\dots ,n-1 \rbrace \) is real. Which is the case for

$$\begin{aligned} \frac{c}{m}&> \frac{k^2}{m^2}\left( 1-\cos \left( \frac{l \pi }{n}\right) \right) , \quad \forall l \in \lbrace 1,\dots ,n-1\rbrace , \end{aligned}$$
(56)
$$\begin{aligned} cm&> k^2\left( 1-\cos \left( \frac{(n-1) \pi }{n}\right) \right) = k^2\left( 1+\cos \left( \frac{\pi }{n}\right) \right) , \end{aligned}$$
(57)
$$\begin{aligned} \sqrt{\frac{cm}{2}}&>\sqrt{\frac{cm}{1+\cos \frac{\pi }{n}}} =:k_\text {crit}>k. \end{aligned}$$
(58)

Possible values of n range from 2 to \(\infty \), thus the critical damping coefficient has the range

$$\begin{aligned} k_\text {crit}\in \Bigg (\sqrt{\frac{cm}{2}}, \sqrt{cm} \Bigg ]. \end{aligned}$$
(59)

Lehr’s damping ratio for each mode can be expressed from the modes’ characteristic polynomials given as

$$\begin{aligned} s^2+\underbrace{2 \left( 1+\cos \frac{\pi K}{n}\right) \frac{k}{m}}_{=:2D\omega _0}s+\underbrace{2\left( 1+\cos \frac{\pi K}{n}\right) \frac{c}{m}}_{=:\omega _0^2}=0, \end{aligned}$$
(60)

from which we have

$$\begin{aligned} D=\frac{k}{\sqrt{2cm}} \sqrt{ 1+\cos \frac{\pi K}{n} }, \end{aligned}$$
(61)

taking the largest values for the highest frequencies (K small).

2.6 Special case: harmonic excitation

In the equations of relative motion, the potential force is of the order \(\mathcal {O}(1)\). It is considered negligible compared to the forces of linear springs of the order \(\mathcal {O}(\varepsilon ^{-1})\). Consequently, the equations are linearized. Owing to the validity of the superposition principle for this simplified linear system, our primary interest is directed toward the behavior of the \(i^{\text {th}}\) body when it undergoes simple harmonic excitation.

In order to examine the motion relative to the common center of mass of the particles, it is necessary to find the analytic solutions for \(y_2(t), \ldots , y_n(t)\) under excitation solely by the high-frequency force \(F_{i,p} \sin (\Omega _{i,p} t+ \beta _{i,p})\), where \(p \in \{1, \ldots , P\}\). The equation governing \(\eta \) is an undamped second-order nonlinear differential equation. The absence of damping implies that the motion never settles into a steady state. In contrast, the system of equations that describe the evolution of \(y_2(t), \ldots , y_n(t)\) can be well approximated by a damped linear second-order differential equation system. Due to the significant damping, the motion rapidly converges to the steady-state solution as given by Eq. (47). In the case of single harmonic excitation, steady-state solutions \(y_2(t), \ldots , y_n(t)\) are all pure harmonics. The following gives the oscillations around the center of mass \(\eta (t)\).

$$\begin{aligned} {\textbf {z}}(t):={\textbf {x}}(t)-\eta (t){\textbf {e}}&={\textbf {Sy}}(t)-\eta (t){\textbf {e}},\nonumber \\&= \frac{1}{n} \underbrace{ \begin{bmatrix} -(n-1) &{}\quad -(n-2) &{}\quad \dots &{}\quad -1\\ 1 &{}\quad -(n-2) &{}\quad \dots &{}\quad -1\\ 1 &{}\quad 2 &{}\quad \dots &{}\quad -1\\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 1 &{}\quad 2 &{}\quad \dots &{}\quad n-1 \end{bmatrix}}_{\in \mathbb {R}^{n \times (n-1)} } \begin{bmatrix} y_2\\ y_3\\ \vdots \\ y_n \end{bmatrix}, \end{aligned}$$
(62)

with \({\textbf {e}}=[1\quad 1 \quad \ldots \quad 1]^\top \). Due to Eq. (62), the entries of \(\textbf{z}\) are all linear combinations of \(y_2,\dots ,y_{n}\). The sum consists of \(n-1\) sine functions with different amplitudes and phases but with identical frequency \(\Omega _{i,p}\). The following trigonometric identity is helpful for such an addition of sine functions.

$$\begin{aligned} \sum _{i=1}^n A_i \sin (\omega t+\varphi _i)&=A \sin (\omega t+\varphi ), \end{aligned}$$
(63)

with

$$\begin{aligned} A&=\sqrt{\left( \sum _{i=1}^n A_i \cos \varphi _i \right) ^2 +\left( \sum _{i=1}^n A_i \sin \varphi _i \right) ^2 }, \end{aligned}$$
(64)
$$\begin{aligned} \varphi&= \text {atan2} \left( \sum _{i=1}^n A_i \sin \varphi _i,\sum _{i=1}^n A_i \cos \varphi _i \right) , \end{aligned}$$
(65)

where \(\text {atan2}(y,x)\) denotes the two-argument arctangent, a more precise version of \(\arctan (y/x)\), by providing phase information on \((-\pi ,\pi )\), rather than only on \(\left( -\pi /2, \pi /2\right) \). To determine the amplitude and phase of the harmonic oscillation of the \(j^{\text {th}}\) body, the use of complex numbers is advantageous, using the solution obtained in Eq. (43) for \(\bar{{\textbf {Y}}}(\jmath \Omega _{j2})\):

$$\begin{aligned} {\textbf {Z}}(\jmath \Omega _{j2})&=\bar{{\textbf {S}}} \bar{{\textbf {Y}}}(\jmath \Omega _{j2}), \end{aligned}$$
(66)
$$\begin{aligned} A_K&= |Z_K(\jmath \Omega _{j2}) |,\end{aligned}$$
(67)
$$\begin{aligned} \Psi _K&=\angle Z_K(\jmath \Omega _{j2}),\end{aligned}$$
(68)
$$\begin{aligned} z_K(t)&=A_K \sin (\Omega _{j2}t+\Psi _K). \end{aligned}$$
(69)

These equations indicate that the relative motions of the particles around the center of mass can be expressed as sinusoidal functions. Although these functions share the same frequency, their amplitude and phase values differ.

When subjected to multiple harmonics simultaneously, the linearity of Eq. (33) allows the development of complex relative motions \( \textbf{z}(t) \) within the particle chain around its center of mass. These motions result from the superposition of sinusoidal functions of varying frequencies. The number of frequencies in the excitation force directly equals the number of sinusoidal functions involved.

In addition, given our strong coupling assumption between the particles, it is apparent that the frequencies that excite the center of mass of the particle chain within the potential well are significantly lower than those that excite internal vibrations. Consequently, we can effectively neglect the low-frequency excitation terms when calculating \( \textbf{z} \). See Fig. 5 for a graphical illustration in Sect. 4.

Considering this, we can now revisit Eq. (28). To simplify the equation, we will employ a method proposed by Genda et al. [26], which models the high-frequency oscillations based on the classical probability density of the position of the particles. This approach offers a straightforward means of capturing the system’s dynamics.

3 Averaging-based model reduction

In the previous section, we have derived analytic expressions for the motion of particles around their common center of mass. These can be substituted into Eq. (28). Making use of Eq. (62), we obtain

$$\begin{aligned} \ddot{\eta }+\frac{\sum _{i=1}^{n} V'(\eta +z_i(t))}{n}=\frac{\sum _{i=1}^{n}F_i(t)}{nm}. \end{aligned}$$
(70)

Considering that \(z_i(t)\) and \(F_{i,p} \sin (\Omega _{i,p} t+\beta _{i,p})\) are “fast,” we can average the equation and keep only the “slow” dynamics of the system. To denote the averaged position of the center of mass, we introduce \(\xi :=\left\langle \eta \right\rangle \). The fast harmonic forces all vanish, and we obtain the following result.

$$\begin{aligned} \ddot{\xi }+\left\langle \frac{\sum _{i=1}^{n} V'(\xi +z_i(t))}{n}\right\rangle =\frac{\sum _{i=1}^{n} F_{i,0}\sin (\Omega _0 t+\beta _{i,0})}{nm}. \end{aligned}$$
(71)

Using Eq. (63) we can reduce Eq. (71) further as

$$\begin{aligned} \ddot{\xi }+\left\langle \frac{\sum _{i=1}^{n} V'(\xi +z_i(t))}{n}\right\rangle = F_0 \sin (\Omega _0 t+\beta _{0}), \end{aligned}$$
(72)

with

$$\begin{aligned} F_0:&=\frac{\sqrt{\left( \sum _{i=1}^n F_{i,0} \cos \beta _{i,0} \right) ^2+\left( \sum _{i=1}^n F_{i,0} \sin \beta _{i,0} \right) ^2 }}{nm}, \end{aligned}$$
(73)
$$\begin{aligned} \beta _0 :&= \text {atan2} \left( \sum _{i=1}^n F_{i,0} \sin \beta _{i,0},\sum _{i=1}^n F_{i,0} \cos \beta _{i,0} \right) . \end{aligned}$$
(74)

The averaging of the left-hand side of Eq. (71) takes more effort. [27] showed that the time average of the function \(f(x+g(t))\), where g(t) represents the “fast” variable, can be obtained not only by a time integral but also by a cross-correlation integral of f(x) and the classical probability density (CPD) \(\rho (x)\) of g(t), that is,

$$\begin{aligned} \left\langle f(x+g(t))\right\rangle =\frac{1}{T}\int _{0}^{T} f(x+g(t)) \text {d}t=\int _{-\infty }^\infty f(y)\rho (y-x) \text {d}y. \end{aligned}$$
(75)

Furthermore [27], demonstrated that the averaged function can be expressed using the moments of the classical probability density \(\rho (x)\) for analytic functions. The expression is given by:

$$\begin{aligned} \left\langle f(x+g(t))\right\rangle = \int _{-\infty }^\infty f(y)\rho (y-x) \text {d}y = \sum _{K=0}^\infty m_K \frac{f^{(K)}(x)}{K!}. \end{aligned}$$
(76)

Here, \(m_K\) represents the Kth moment of \(\rho (x)\). The result is valid if the support of \(\rho (x)\) lies within the convergence domain of the Taylor series expansion of f(x).

Hence, once the moments of the “fast” variables \(z_i(t)\) are known, the averaging of Eq. (72) is straightforward, especially if f(x) is some polynomial of order p, in which case only the first p moments must be calculated.

3.1 Derivation of the CPD and moments of the fast motion

For a precise definition of the CPD and the CPDs of various functions derived in the literature, refer to [27] and [31].

The 0th moment for any CPD is invariably 1. In our specific case, \(z_i(t)\) approximates a polyharmonic function, which is the superposition of multiple harmonic components. Given certain conditions, moments of this polyharmonic sum can also be ascertained. It is well established that the probability density function (PDF) for a sum of independent variables can be derived through the convolution of their individual PDFs [32]. CPDs exhibit mathematical characteristics identical to PDFs; they are nonnegative and integrate to 1. However, the variables they represent differ fundamentally. Unlike random variables, which their PDFs fully characterize, CPDs are formed by disregarding the precise timing of particle positions. They retain information on spatial distribution by accounting solely for the duration for which a particle resides at a specific location. Theorem 1 offers an analytical method for determining the CPD of polyharmonic functions.

Definition 1

(Linear independence over \(\mathbb {Q}\)) The numbers \(\omega _1,\dots ,\omega _P\in \mathbb {R}\) are said to be linearly independent over \(\mathbb {Q}\) if

$$\begin{aligned} \sum _{i=1}^{P} r_i\omega _i \ne 0, \end{aligned}$$
(77)

for any \(r_i \in \mathbb {Q}\), except \(r_1=\ldots =r_P=0\).

Weyl showed that the P-dimensional flow on a torus \(\mathbb {T}^P=\mathbb {R}^P/\mathbb {Z}^P\) is equidistributed [33], i.e., a particle starting at \(\varvec{x_0}=[x_{0,1},\dots ,x_{0,P}]^\top \in \mathbb {T}^P\) and moving with uniform velocity in the direction \(\varvec{\omega }=[\omega _{1},\dots ,\omega _{P}]^\top \in \mathbb {R}^P\) on \(\mathbb {T}^P\), i.e.,

$$\begin{aligned} \textbf{x}(t)= (\textbf{x}_0+\varvec{\omega } t) \text { mod }1= \begin{pmatrix} \lbrace x_{0,1}+\omega _1 t \rbrace , \lbrace x_{0,2}+\omega _2 t \rbrace , \dots , \lbrace x_{0,P}+\omega _P t \rbrace \end{pmatrix}^\top , \end{aligned}$$
(78)

has a relative dwell time in any volume element V as indicated by the hypervolume of the volume element \(|V |\), if and only if the numbers \(\omega _1,\dots ,\omega _P\) are linearly independent over \(\mathbb {Q}\).

Here, \(\{\cdot \} \) signifies the fractional part function. By relative dwell time, we refer to the limit \( \lim _{{t \rightarrow \infty }} t_V/t \), where \( t_V \) represents the time spent within the volume element V over the entire observation period t. This concept is congruent with the idea that flow on a P-dimensional torus is ergodic with respect to the Haar measure on \( \mathbb {T}^P\) [34].

Consequently, if we sample particle positions in uniformly distributed random time instances within the interval [0, T] , as \( T \rightarrow \infty \), the positions sampled during these instances will adhere to a uniform multivariate distribution in \( \mathbb {T}^P \). We can interpret these positions as the realizations of a P-dimensional random variable \( \textbf{X} = [X_1, \ldots , X_P]^\top \), where the scalar components are uniformly distributed in [0, 1] and are mutually independent. This understanding enables us to compute the CPD for a polyharmonic excitation.

Theorem 1

Assume that the frequencies \(\omega _1,\dots ,\omega _P\) are linearly independent over \(\mathbb {Q}\). Then, the CPD of

$$\begin{aligned} z(t)=\sum _{i=1}^{P} A_i \sin (\omega _i t+\beta _i) \end{aligned}$$
(79)

can be obtained by

$$\begin{aligned} \rho (x)=(\rho _1 * \rho _2*\cdots * \rho _P)(x), \end{aligned}$$
(80)

where \(\rho _1*\rho _2*\cdots *\rho _P\) denotes the convolution of the functions \(\rho _1, \rho _2,\dots ,\rho _P\), which are given by the arcsine distribution

$$\begin{aligned} \rho _i(x)=\frac{1}{\pi \sqrt{A_i^2-x^2}}. \end{aligned}$$
(81)

Proof

As previously demonstrated, the line on \( \mathbb {T}^P \) parameterized by the arguments of the sines is ergodic, which is synonymous with the flow of these arguments on \( \mathbb {T}^P \) being uniform. In other words, sampling coordinates of this flow at uniformly randomly selected times produces statistics equivalent to those of a P-dimensional uniform distribution on the torus, which suggests that the sum in Eq. (79) yields the same probability distribution as the sum of P uniformly distributed, random variables on \( [0, 2\pi ] \), after applying the transformation \( A_i \sin (\Omega _i X_i+\beta _i)\), respectively.

By [27], the CPD of a simple harmonic term \(A_i\sin (\Omega _it+\beta _i)\) is readily given by Eq. (81). CPDs and PDFs share the same statistical properties.

Furthermore, it is well known [35] that the PDF of the sum of independent random variables is given by the convolution of the individual PDFs (cf. Eq. 80), which finishes the proof of the theorem. \(\square \)

Remark 1

Since the convolution is commutative, it does not matter in which order the operations are performed.

Remark 2

The moments of the centered arcsine distribution with half-width A are given by [27]

$$\begin{aligned} m_K= {\left\{ \begin{array}{ll} A^K \frac{1}{2^K} \left( {\begin{array}{c}K\\ K/2\end{array}}\right) &{} \text {for } K \text { even},\\ 0 &{} \text {for } K \text { odd}, \end{array}\right. } \quad \text {for }K \ge 0. \end{aligned}$$
(82)

Theorem 2

Let \(m_{j,j_i}\) be the \(j_i^\text {th}\) moment of the jth term’s CPD in Eq. (79) with \(j_i \in \mathbb {N}^+\) for all \(j=\lbrace 1,\dots ,P\rbrace \). The \(K^\text {th}\) moment of \(\rho (x)\) in Eq. (80) is given by

$$\begin{aligned} m_K= \left( \sum _{\left( \sum _{j=1}^P j_i \right) =K} \prod _{j=1}^P \frac{m_{j,j_i}}{j_i!}\right) K! \end{aligned}$$
(83)

Proof

The moment-generating function of a random variable X has the form

$$\begin{aligned} M_X(t)=\sum _{K=0}^\infty \frac{m_K}{K!}t^K. \end{aligned}$$
(84)

It is well known that the product of the moment-generating functions of independent random variables \(X_1,X_2,\dots ,X_P\) yields the moment-generating function of the random variable that is obtained by the sum of \(X_1,X_2,\dots ,X_P\) [36]. In other words, the moment-generating function of \(X=\sum _{i=1}^PX_i\) is given by

$$\begin{aligned} M_X(t)=M_{X_1}(t) M_{X_2}(t) \ldots M_{X_P}(t). \end{aligned}$$
(85)

Since the moment-generating functions are power series, the Cauchy product rule can be applied, resulting in Eq. (83). \(\square \)

By combining Eq. (76) with Theorem 2, the effective restoring force in Eq. (72) can be obtained. In the general case, solving Eq. (76) may still be difficult or only numerically possible. However, if V(x) is a polynomial potential, the results are straightforward and can be obtained analytically.

Thus, the reduction of the originally n degree-of-freedom system to a 1 DoF system is complete, given that the distinct “fast” excitation frequencies \(\Omega _{i,p}\) are linearly independent over \(\mathbb {Q}\). A graphical example showing the differences in the CPDs for commensurable and incommensurable \(\omega _1\) and \(\omega _2\) is shown in Fig. 4.

Fig. 4
figure 4

Comparison of commensurability effects on the CPD of motion. Figures re-used from [27]

Full size image

In what follows, we present examples illustrating the utility of the analytic results discussed earlier. After reducing the system to 1 DoF, numerous methods have been documented in the existing literature to analyze the escape behavior of the system further [19, 20, 24, 26, 37]. Thus, the focus will be primarily on the reduction process rather than on subsequent analytic approaches specific to 1 DoF escape problems.

4 Example

4.1 Analytical treatment

In the following, we consider an example with \(n=3\) and

$$\begin{aligned} V(x)=\frac{x^2}{2}-\frac{x^4}{4}. \end{aligned}$$
(86)

Without loss of generality, we consider \(m=1\). The equations of motion are given by

$$\begin{aligned} \begin{bmatrix} \ddot{x}_1\\ \ddot{x}_2\\ \ddot{x}_3 \end{bmatrix} + \begin{bmatrix} k &{}\quad -k &{}\quad 0 \\ -k &{}\quad 2k &{}\quad -k \\ 0 &{}\quad -k &{}\quad k \end{bmatrix} \begin{bmatrix} \dot{x}_1\\ \dot{x}_2\\ \dot{x}_3 \end{bmatrix} + \begin{bmatrix} c &{}\quad -c &{}\quad 0 \\ -c &{}\quad 2c &{}\quad -c \\ 0 &{}\quad -c &{}\quad c \end{bmatrix} \begin{bmatrix} {x}_1\\ {x}_2\\ {x}_3 \end{bmatrix} +\begin{bmatrix} V'(x_1)\\ V'(x_2)\\ V'(x_3) \end{bmatrix} = \underbrace{ \begin{bmatrix} F_{1,0}\sin \left( \Omega _0t+\beta _{0}\right) \\ F_{2,1}\sin \left( \Omega _{2}t+\beta _{2}\right) \\ F_{3,1}\sin \left( \Omega _{3}t+\beta _{3}\right) \end{bmatrix}}_{ =: \begin{bmatrix} F_1(t)\\ F_2(t)\\ F_3(t) \end{bmatrix}}. \end{aligned}$$
(87)

Where \(\Omega _0 \approx 1\) is a low frequency and \(\Omega _{2}\) and \(\Omega _{3}\) are high frequencies, exciting the inner vibrations modes of the chain. The new coordinates, i.e., the center of mass and relative displacements, are defined as follows

$$\begin{aligned} \begin{bmatrix} \eta \\ y_2\\ y_3 \end{bmatrix} = \begin{bmatrix} \frac{1}{3} &{}\quad \frac{1}{3} &{}\quad \frac{1}{3} \\ -1 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad -1 &{}\quad 1 \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}. \end{aligned}$$
(88)

Thus, the differential equations in the new coordinates become

$$\begin{aligned} \ddot{\eta }+\frac{V'(\eta -\frac{2}{3} y_2-\frac{1}{3}y_3)+V'(\eta +\frac{1}{3} y_2-\frac{1}{3}y_3)+V'(\eta +\frac{1}{3} y_2+\frac{2}{3}y_3)}{3}= \frac{\sum _{i=1}^3F_i(t)}{3}, \end{aligned}$$
(89)

or more compactly

$$\begin{aligned} \ddot{\eta }+\frac{\sum _{i=1}^{3}V'(\eta +z_i(t))}{3} =\frac{\sum _{i=1}^3F_i(t)}{3}, \end{aligned}$$
(90)

with \(z_i:=x_i-\eta \). The equations describing the relative motions are given by

$$\begin{aligned} \begin{bmatrix} \ddot{y}_2\\ \ddot{y}_3 \end{bmatrix} + \begin{bmatrix} 2k &{}\quad -k \\ -k &{}\quad 2k \end{bmatrix} \begin{bmatrix} \dot{y}_2\\ \dot{y}_3 \end{bmatrix} + \begin{bmatrix} 2c &{}\quad -c \\ -c &{}\quad 2c \end{bmatrix} \begin{bmatrix} {y}_2\\ {y}_3 \end{bmatrix} + \underbrace{ \begin{bmatrix} V'(x_2)-V'(x_1)\\ V'(x_3)-V'(x_2) \end{bmatrix}}_{\text {negligible}} = \begin{bmatrix} F_2(t)\underbrace{-F_1(t)}_{\text {negligible}}\\ F_3(t)-F_2(t) \end{bmatrix}, \end{aligned}$$
(91)

where in Eq. (91), the force of the potential and the low-frequency excitation can be neglected, being much smaller than the force of the springs. The remaining equation system is linear, and its Laplace transform is given by

$$\begin{aligned} \underbrace{ \begin{bmatrix} s^2+2ks+2c &{}\quad -ks-c\\ -ks-c &{}\quad s^2+2ks+2c \end{bmatrix}}_{=:\textbf{A}(s)} \begin{bmatrix} Y_2(s)\\ Y_3(s) \end{bmatrix} =\textbf{F}(s), \end{aligned}$$
(92)

where \(\mathbf {F(s)}\) is the Fourier transform of the excitation. The inverse of the system matrix \(\textbf{A}(s)\) is given by

$$\begin{aligned} \textbf{A}^{-1}(s)&= \frac{1}{\left( s^2 + ks + c\right) \left( s^2 + 3ks + 3c\right) } \begin{bmatrix} s^2 + 2ks + 2c &{}\quad ks + c \\ ks + c &{}\quad s^2 + 2ks + 2c \end{bmatrix}. \end{aligned}$$
(93)

To facilitate the calculations, let us define the functions

$$\begin{aligned} G_l(s)&:=s^2+lks+lc \qquad \text {for } l\in \lbrace 1,2,3 \rbrace , \end{aligned}$$
(94)
$$\begin{aligned} G_0(s)&:=ks+c. \end{aligned}$$
(95)

The transfer function is obtained by inserting \(s=\jmath \omega \). Then, we can rewrite Eqs. (94–95) which we can also write as

$$\begin{aligned} G_l(\jmath \omega )&=lc-\omega ^2+\jmath \omega l k=\sqrt{(lc-\omega ^2)^2+l^2k^2\omega ^2}\exp \left( \jmath \arctan \frac{lk\omega }{lc-\omega ^2}\right) , \end{aligned}$$
(96)
$$\begin{aligned} G_0(\jmath \omega )&=c-\jmath \omega k=\sqrt{c^2+k^2\omega ^2}\exp \left( \jmath \arctan \frac{k\omega }{c} \right) , \end{aligned}$$
(97)

thus, we can write Eq. (93) as

$$\begin{aligned} \textbf{G}(\jmath \omega )=\frac{1}{G_1(\jmath \omega ) G_3(\jmath \omega )} \begin{bmatrix} G_2(\jmath \omega ) &{}\quad G_0(\jmath \omega )\\ G_0(\jmath \omega ) &{}\quad G_2(\jmath \omega ) \end{bmatrix}. \end{aligned}$$
(98)

Based on Eq. (54), resonant frequencies are to be found around the values

$$\begin{aligned} \omega _{1,\text {peak}}=\sqrt{c-\frac{k^2}{2}} \quad \text {and} \quad \omega _{2,\text {peak}}=\sqrt{3 \left( c-\frac{3k^2}{2}\right) }. \end{aligned}$$
(99)

We now define the values of the high-frequency excitations as follows.

$$\begin{aligned} \Omega _{2}&=\omega _{2,\text {Peak}}, \end{aligned}$$
(100)
$$\begin{aligned} \Omega _{3}&=\omega _{1,\text {Peak}}. \end{aligned}$$
(101)

We can obtain the amplitude and phase of the stationary solutions corresponding to \(F_2(t)\) by

$$\begin{aligned} \begin{bmatrix} Y_{2,2}\\ Y_{3,2} \end{bmatrix} = \frac{1}{G_1(\jmath \Omega _2)G_3(\jmath \Omega _2)} \begin{bmatrix} G_2(\jmath \Omega _2) &{}\quad G_0(\jmath \Omega _2)\\ G_0(\jmath \Omega _2) &{}\quad G_2(\jmath \Omega _2) \end{bmatrix} \begin{bmatrix} F_2 e^{\jmath \beta _2}\\ -F_2 e^{\jmath \beta _2} \end{bmatrix}. \end{aligned}$$
(102)

Using the identity \(G_2(\jmath \omega )-G_0(\jmath \omega )=G_1(\jmath \omega )\) we can simplify Eq. (102) as follows.

$$\begin{aligned}&\begin{bmatrix} Y_{2,2}\\ Y_{3,2} \end{bmatrix} = \frac{1}{G_3(\jmath \Omega _2)} \begin{bmatrix} 1\\ -1 \end{bmatrix} F_2 e^{\jmath \beta _2}, \end{aligned}$$
(103)
$$\begin{aligned}&\begin{bmatrix} Y_{2,2}\\ Y_{3,2} \end{bmatrix} = \frac{2 \sqrt{3}F_2}{9 k \sqrt{4 c-3 k^{2}}}e^{\jmath \left( \beta _2-\arctan \! \left( \frac{\sqrt{12 c-18 k^{2}}}{3 k}\right) \right) } \begin{bmatrix} 1\\ -1 \end{bmatrix}, \end{aligned}$$
(104)

where Eq. (104) is obtained by inserting Eq. (100) in Eq. (103).

Similarly, we can derive the stationary solution corresponding to \(F_3(t)\). The results are as follows.

$$\begin{aligned} \begin{bmatrix} Y_{2,3}\\ Y_{3,3} \end{bmatrix} = \frac{1}{G_1(\jmath \Omega _{3})G_3(\jmath \Omega _3)} \begin{bmatrix} G_0(\jmath \Omega _3)\\ G_2(\jmath \Omega _3) \end{bmatrix} F_3 e^{\jmath \beta _3}. \end{aligned}$$
(105)

Inserting Eq. (101) in Eq. (105) yields

$$\begin{aligned} \begin{bmatrix} Y_{2,3}\\ Y_{3,3} \end{bmatrix} = \frac{2 F_{2} e^{\jmath \left( \beta _3-\gamma _1-\gamma _3\right) }}{k \sqrt{4 c-k^{2}} \sqrt{16 c^{2}+44 c k^{2}-17 k^{4}}} \begin{bmatrix} \sqrt{4 c^{2}+4 ck^{2}-2 k^{4}} e^{\jmath \gamma _0}\\ \sqrt{4 c^{2}+20 ck^{2}-7 k^{4}} e^{\jmath \gamma _2} \end{bmatrix}, \end{aligned}$$
(106)

with

$$\begin{aligned} \gamma _0&:=\arctan \angle G_0(\jmath \omega _{1,\text {Peak}})=\arctan \left( \frac{k \sqrt{4 c-2 k^{2}}}{2 c}\right) , \end{aligned}$$
(107)
$$\begin{aligned} \gamma _l&:=\arctan \angle G_l(\jmath \omega _{1,\text {Peak}})=\arctan \left( \frac{l k \sqrt{4 c-2 k^{2}}}{\left( 2 l -2\right) c +k^{2}}\right) \quad \text {for } l\in \lbrace 1,2,3\rbrace . \end{aligned}$$
(108)

With the complex amplitudes \(Y_{2,2}\dots Y_{3,3}\) we can write the steady-state solutions as

$$\begin{aligned} y_2(t)&=|Y_{2,2} |\sin \left( \omega _{2,\text {Peak}}t+\angle Y_{2,2}\right) +|Y_{2,3} |\sin \left( \omega _{1,\text {Peak}}t+\angle Y_{2,3}\right) ,\end{aligned}$$
(109)
$$\begin{aligned} y_3(t)&=|Y_{3,2} |\sin \left( \omega _{2,\text {Peak}}t+\angle Y_{3,2}\right) +|Y_{3,3} |\sin \left( \omega _{1,\text {Peak}}t+\angle Y_{3,3}\right) . \end{aligned}$$
(110)

The particles’ oscillations around their center of mass are given by

$$\begin{aligned} z_1(t)&=-\frac{2}{3}y_2(t)-\frac{1}{3}y_3(t)=Z_{1,1}\sin (\omega _{1,\text {Peak}}t+\zeta _{1,1})+Z_{1,2}\sin (\omega _{2,\text {Peak}}t+\zeta _{1,2}), \end{aligned}$$
(111)
$$\begin{aligned} z_2(t)&=\frac{1}{3}y_2(t)-\frac{1}{3}y_3(t)=Z_{2,1}\sin (\omega _{1,\text {Peak}}t+\zeta _{2,1})+Z_{2,2}\sin (\omega _{2,\text {Peak}}t+\zeta _{2,2}), \end{aligned}$$
(112)
$$\begin{aligned} z_3(t)&=\frac{1}{3}y_2(t)+\frac{2}{3}y_3(t)=Z_{3,1}\sin (\omega _{1,\text {Peak}}t+\zeta _{3,1})+Z_{3,2}\sin (\omega _{2,\text {Peak}}t+\zeta _{3,2}), \end{aligned}$$
(113)

where \(Z_{1,1}\dots Z_{3,2}\) and \(\zeta _{1,1}\dots \zeta _{3,2}\) are determined with the help of Eqs. (63–65). Thus, the particle’s vibrations around their center of mass are given by biharmonic functions, respectively. Since \(\omega _{1,\text {Peak}}\) and \(\omega _{2,\text {Peak}}\) are incommensurable, i.e., linearly independent over \(\mathbb {Q}\), Theorem 1 can be applied to obtain the moments of the fast variable’s CPD.

Fig. 5
figure 5

Comparison of the numerical solution of \(z_1(t)\) with the analytic one for \(n=3\), \(m=1\), \( k = 3 \), \( c = 10,000 \), \(F_0=0.33\), \( F_2 = 200 \), \( F_3 = 100 \), \(\Omega _0\)=1\(, \Omega _2 = \sqrt{3(c - \frac{3k^2}{2})} \), \( \Omega _3 = \sqrt{c - \frac{k^2}{2}} \), \( \beta _0 = \beta _2 = \beta _3 = \frac{\pi }{2}\)

Full size image

\(z_l\) with \(l \in \lbrace 1,2,3\rbrace \) is a biharmonic motion (see Fig. 5). In [27], for a function of the form \(f(t)=A_1 \sin (\omega _1 t+\beta _1)+A_2 \sin (\omega _2 t+\beta _2)\) with \(\omega _1\) and \(\omega _2\) incommensurable and \(A_1 \ge A_2\) (without loss of generality) the CPD was derived analytically. However, here, only the first few moments are necessary. By Theorem 2 with \(P=2\), we have

$$\begin{aligned} m_K= \left( \sum _{\left( \sum _{j=1}^2 j_i \right) =K} \prod _{j=1}^2 \frac{m_{j,j_i}}{j_i!}\right) K!, \end{aligned}$$
(114)

where \(m_{j,1}\) and \(m_{j,2}\) are given by Eq. (82), respectively. The first few moments are

$$\begin{aligned} m_0&=1, \end{aligned}$$
(115)
$$\begin{aligned} m_1&=m_3=m_5=0, \end{aligned}$$
(116)
$$\begin{aligned} m_2&=\frac{A_1^2+A_2^2}{2}, \end{aligned}$$
(117)
$$\begin{aligned} m_4&=\frac{3}{8}A_1^4+\frac{3}{2}A_1^2A_2^2+\frac{3}{8}A_2^4. \end{aligned}$$
(118)

Therefore, the corresponding moments of \(z_l\) are obtained by substituting \(A_1\) and \(A_2\) with \(Z_{l,1}\) and \(Z_{l,2}\), respectively.

Let us denote the averaged center of mass by \(\xi =\left\langle \eta \right\rangle .\) In Eq. (90), the only terms that are challenging to average are \(V'(\eta +z_l(t))\) for \(l\in \lbrace 1,2,3\rbrace \). As shown in Eq. (76), for analytic functions f(x), such as Eq. (86), averaging can be performed based on a series expansion. Using Eq. (76), the averages are calculated by

$$\begin{aligned} \left\langle V'(\eta +z_l(t)\right\rangle&=m_0 V'(\eta )+\underbrace{m_1}_{=0} V''(\eta )+\frac{m_2 V'''(\eta )}{2}+\underbrace{\dots }_{=0} \end{aligned}$$
(119)
$$\begin{aligned}&=(1-3m_2)\eta -\eta ^3=\left( 1-3 \frac{Z_{1,l}^2+Z_{2,l}^2}{2}\right) \eta -\eta ^3, \end{aligned}$$
(120)

where all the terms above \(m_4\) disappear due to \(V^{(k)}(x)=0\) for \(k\ge 4\). Inserting this result into Eq. (90), we find

$$\begin{aligned} \ddot{\xi }+\left( 1-\underbrace{\frac{\sum _{l=1}^3 Z_{1,l}^2+ Z_{2,l}^2}{2}}_{=:d}\right) \xi -\xi ^3=\frac{F_{1,0}\sin \left( \Omega _0t+\beta _{0}\right) }{3}, \end{aligned}$$
(121)
$$\begin{aligned} \ddot{\xi }+\omega _d^2\xi -\xi ^3=\frac{F_{1,0}\sin \left( \Omega _0t+\beta _{0}\right) }{3}. \end{aligned}$$
(122)

Here, d represents a detuning parameter influenced by all the underlying factors that contribute to steady-state vibrations around the center of mass, denoted as \(z_1(t),z_2(t)\), and \(z_3(t)\). This equation mirrors the motion of a single particle under harmonic excitation. However, the linear eigenfrequency of the system is detuned to \(\omega _d=\sqrt{1-d}\). Introducing appropriate dimensionless time and space coordinates

$$\begin{aligned} \tau :=\omega _d t, \qquad \chi :=\frac{\xi }{\omega _d}, \end{aligned}$$
(123)

we obtain

$$\begin{aligned} \chi ''+\chi -\chi ^3=F \sin (\Omega \tau +\beta _0), \end{aligned}$$
(124)

with

$$\begin{aligned} F:=\frac{F_{1,0}}{3\omega _d^3}, \qquad \Omega :=\frac{\Omega _0}{\omega _d}, \end{aligned}$$
(125)

where \(\square '\) denotes differentiation with respect to \(\tau \).

Equation (124) has been extensively investigated in the literature using various methods, including transformation to action-angle coordinates and subsequent averaging or multiple-scale analysis, [19, 24, 37,38,39]. Therefore, it will not be discussed further in this article. However, in the next section, numerical simulations will be performed to compare the slow dynamics of the direct solution of Eq. (87) to the reduced system dynamics given by Eq. (124).

4.2 Numerical validation

In the following sections, we perform a comparative numerical simulation between the original 3 DoF model and the reduced 1 DoF model. The analysis calculates the escape time for a parameter region specified for \( \Omega _{0} \) and \( F_{1,0} \). The nondimensional parameter values used for the simulations are as follows: \(n=3\), \(m=1\), \( k = 3 \), c = 10,000 , \( F_2 = 1000 \), \( F_3 = 400 \), \( \Omega _2 = \sqrt{3(c - \frac{3k^2}{2})} \), \( {\Omega _3 = \sqrt{c - \frac{k^2}{2}} }\), \( \beta _0 = \beta _2 = \beta _3 = \frac{\pi }{2} \).

With these values, the reduced system results in

$$\begin{aligned} \ddot{\xi }_1+0.6471 \,\xi -\xi ^3&=\frac{F_0}{3}. \end{aligned}$$
(126)

Eq. (126) followed after a lengthy calculation to consider the impact of the internal vibrations of the chain on the center of mass of the chain. One might approach the problem naively simply by neglecting the effect of internal vibrations. However, this primitive approach leads to incorrect results, which shall be demonstrated in Fig. 6 showing the time evolutions of the original 3 DoF (cf. Eq. 87), the CPD-based reduced (with \(\omega _d=0.6471\)) and the naive 1 DoF models (by inserting \(\omega _d=1\) into Eq. (122)) for two different \(F_0\) and \(\Omega _0\) values and homogeneous initial conditions.

Although the CPD-based reduced model does not perfectly match the original one, it undoubtedly agrees better with it than the naive model: a detuning parameter of this magnitude renders the predictive power of the naive model useless.

In Fig. 7, the sensitivity for initial conditions is shown when the parameters are chosen from the chaotic domain. Indeed, we can observe that even a small perturbation in the initial velocity (\(\Delta u_0=0.01\)) results in a larger change in the solution than what substitution of the original model by the reduced one causes.

Fig. 6
figure 6

Time evolution comparison between the center of mass of the original 3 DoF (cf. Eq. 87), the CPD-based, reduced (\(d=0.5813\)) and naive (\(d=0\)) 1 DoF models with homogeneous initial conditions. The remaining parameters are set as indicated in the main text. The discrepancies between the two models are salient. Although the CPD-based reduced model does not align perfectly with the original system, the agreement is much better than with the model reduced naively

Full size image
Fig. 7
figure 7

The figure shows the sensitivity of a model to initial conditions. The red curve represents time series data for homogeneous initial conditions, while the black curve represents data for a small perturbation of the initial velocity \((x_0,u_0)=(0,0.01)\). The green curve shows time series data for a perturbed reduced model. The plots demonstrate that the system is more sensitive to small changes in initial conditions than to being replaced by a 1 DoF model, given the parameter and excitation values. \(F_0=0.13\), \(\Omega _0=0.7\) and the remaining parameters are as defined in the main text

Full size image

Using Melnikov analysis, it has been shown that escape from a quadratic-cubic potential may be preceded by chaotic motion [2, 5]. There is no compelling reason to believe that this would also not hold for a quadratic-quartic potential. Such a scenario, however, suggests the existence of a fractal boundary separating the escaping and non-escaping regimes. In this chaotic context, the system is susceptible to minor alterations in initial conditions or model errors. Consequently, the precise prediction of the escape time using a reduced model becomes infeasible within the chaotic region. However, the reduced model may yield accurate results in areas adjacent to this chaotic region. To test this hypothesis, we conducted a parameter study. The range for \( \Omega _0 \) is set between 0 and 1.2, and for \( F_0 \), it is set between 0 and 1. Parallel to that, we also show how the averaging-based method performs compared to the naive method that neglects the internal vibrations of the chain. In Fig. 8, the escape times of the original model (cf. Fig. 8a), together with the escape times of the averaging-based reduction method (cf. Fig. 8b) and the naive reduction method (cf. Fig. 8c) are presented, respectively. Naive reduction results in a noticeable shift and scaling of the V-shaped escape boundary along the force and frequency axes, indicating that neglecting internal vibrations leads to an inaccurate reduced model, in agreement with Eq. (125) where scaling by \(1/\omega _d^3\) and \(1/\omega _d\) is described, respectively.

Fig. 8
figure 8

Model validation: panel a represents the escape times of the original system, varying the parameters \(F_0\) and \(\Omega _0\) with homogeneous initial conditions applied. Panel b shows the escape times of the reduced system with a detuning parameter of \(d=0.5813\). Panel c shows the naive model reduction approach that neglects the impact of internal vibrations corresponding to \(d=0\). The naive approach shows a notable shift in the frequency and force amplitude of the V-shaped escape boundary (cf. Eq. 125), while the reduced model based on averaging agrees well with the original. Parameters not specified here adhere to those delineated in the main text

Full size image

Comparing escape times to evaluate the models’ goodness is an arbitrary choice. However, comparing trajectories using a single scalar number is challenging. There are probably better measures for model validation. However, the escape time chosen as the measure is adequate to gain insight into the escape dynamics of an n-particle chain, which is one of the authors’ primary interests.

The reduced model we derived is no longer stiff, which markedly improved computational efficiency and significantly decreased simulation time in our executed example. Specifically, the computational cost was reduced by \( 99.75\% \), which corroborates the effectiveness of the model reduction technique.

5 Discussion

This paper presented a model reduction approach for an externally excited, strongly coupled n-particle chain in a potential well. The reduction method leverages the different frequency scales between the chain’s quick internal vibrations and the slow movements of its center of mass within the potential well. The choice of excitation is notably flexible; a polyharmonic excitation affecting all particles is acceptable as long as it includes only one low frequency. This feature ensures that the remaining frequencies primarily trigger high-frequency internal vibrations of the chain.

In addition to the strong coupling between the particles, it is also assumed that non-small damping forces exist among them. This results in the rapid decay of high-frequency transient motions. Such a setting permits a straightforward analytical calculation of steady-state fast vibrations, assuming that the forces from the potential are negligible compared to the linear spring forces. Consequently, the fast relative motions become known time-dependent functions in the nonlinear differential equation governing the motion of the chain’s center of mass. The net effect of these fast oscillations on the differential equation of the center of mass can be accurately approximated by averaging.

A theorem is introduced that extends the cross-correlation-based averaging technique [27] to scenarios where polyharmonic fast motions are present, provided the frequencies are linearly independent over \(\mathbb {Q}\). A second theorem outlines how to calculate the moments of the CPD for such composite motions, which is especially useful for averaging a polynomial function. Building on these findings, we derive the effective potential, resulting in a reduced system with one degree of freedom.

As an illustrative example, a chain of three particles in a quadratic-quartic potential well, excited by a triharmonic force, is presented. The model reduction is carried out analytically, and the numerical validation is performed by computing the escape time for both models across various excitation force and frequency values. In the case of the chosen quadratic-quartic potential, the impact of high-frequency excitation manifests solely as a detuning of the potential’s linearized natural frequency, which allows for the use of several analytical methods already available in the literature.

In order to apply the reduction method, some assumptions had to be made.

  • The particle chain is stiff compared to the outer potential: if the particle chain represents the discretization of a continuous, slender structure, such as a beam or a strut, the applied n-particle chain model is typical. An external field, such as a magnetic one, will have much less stiffness than the stiffness elements that model the material’s elasticity.

  • Nonnegligible damping acts within the particles: In practical cases, this is always true; material damping is omnipresent. Equation (61) allows for determining the Lehr damping ratio. The values of the modal damping used in the example in Sect. 4 correspond to \(D = 0.015\) and \(D \approx 0.026\), which are realistic values for metals and construction materials.

  • The excitation frequencies are linearly independent over \(\mathbb {Q}\), i.e., they are not internally resonant: If the different components of the excitation are generated independently from each other, it is highly unlikely that any of them will be an exact rational combination of the remaining ones. It is well known that there are “infinitely many” irrational numbers as rational ones; therefore, randomly choosing real numbers will almost always result in linearly independent ones over \(\mathbb {Q}\). Furthermore, if the excitation frequencies happen to be linearly dependent but the corresponding \(r_i\) values in Def. 1 are such that their numerators and denominators are large relative primes, the change in the resulting CPD is negligible compared to the convoluted CPD of periodic functions that are linearly independent over \(\mathbb {Q}\).

We must address the issue of the accuracy of the reduced model. According to [27], cross-correlation-based averaging is equivalent to the “common” averaging method, which involves evaluating the averaging integral in time. On the other hand [40], demonstrated that the averaging method with a right-hand side of order \(\varepsilon \) produces a solution that is close to the original system’s solution on a timescale of \(\mathcal {O}(1/\varepsilon )\).

However, comparing the solutions of the original and reduced systems is not always feasible. In many cases, other system properties, such as determining amplification functions or finding periodic, stationary solutions, are more important than matching the exact solution shapes, including transients. For these specific objectives, a rudimentary 1-DoF model serves as an invaluable tool.

6 Conclusions and scope for future research

Model reduction offers two main advantages. First, it enables us to grasp the fundamental slow dynamics of the system and identify the underlying slow force field. Second, the computational cost is significantly reduced. The simple example involving three particles achieved a simulation time reduction of \(99.75\%\). Importantly, as the number of particles increases and their interactions become stronger, making the differential equation system stiffer, the benefits of model reduction become increasingly pronounced.

Future research could extend in several directions. First, the model reduction techniques could be applied to more complex potential wells beyond polynomial forms to test the range of applicability of the current methods. Second, other types of excitation, such as stochastic or time-dependent forces, could be incorporated to see how they affect both slow dynamics and computational efficiency.

It would be interesting to compare the reduced model with the original model using criteria other than the escape time. Not all dynamical systems can escape, for which the reduction method still works. A more general criterion could be used to address this, such as comparing the acceleration of the original system’s center of mass (after appropriate low-pass filtering) to the acceleration predicted by the model, which could be a more general and quantifiable measure.

Also worth exploring is how the model scales with more particles and complex interaction mechanisms. Quantifying the computational advantages would be informative in stiff systems. In line with the observed \(99.75\%\) time reduction in the three-particle example, a scaling law could be developed to save computational time in larger systems.

Extending the model reduction to 2- and 3-dimensional potentials could also be a valuable line of inquiry, providing insights into more physically realistic systems.

A separate area of focus could be investigating cases where there is no damping between the particles. This aspect is fascinating because it would influence the model’s effectiveness and accuracy since no advantage can be gained from the decay of fast transients.

A further extension could involve examining particle chains with nonlinear couplings, a plausible generalization, to ascertain how such complexities influence the system’s slow and fast dynamics.