1 Introduction

We can frequently encounter the use of nano- and micro-scale elements in the applications of nano-electro and micro-electro mechanical systems. Nano-/micro-sensors [1, 2] and nano-/micro-switches [3, 4] are among the most common of these applications. With the developing technology, it is seen that the usage areas of these small-scale applications are gradually expanding. Nanomaterials have excellent mechanical properties due to the volume, surface and quantum effects of nanoparticles. Small changes in these particles cause noticeable effects in the properties of the nanomaterial. For this reason, it is possible to come across various studies [5,6,7] investigating the properties of nanomaterials. Predicting the behavior of these applications that exhibit more sensitive features is also an important issue. It has been understood that the analyses carried out with approaches based on local theory (LT), classical continuum model, cannot reveal the necessary sensitivity in the mentioned small-scale applications. So much so that, as the dimensions get smaller, quantum effects begin to show themselves and even small manipulations in the structure of the element or material cause changes in its behavior. Higher-order continuum models [8,9,10,11,12,13] have been developed to replace classical continuum models that cannot capture these changes. Higher-order continuum models can capture and study the phenomenon called the size effect, thanks to the small-scale parameters included in their constitutive equations. Nonlocal theory (NLT), modified couple stress theory (MCST), simple strain gradient theory (SGT) and doublet mechanics theory include one small-scale parameter in their formulations. Various experimental studies are realized to calculate the values of the scale parameters. It has been determined that the values of these scale parameters differ based on the material. Khorshidi [14] demonstrated that the material length scale parameter used in couple stress theories depends on both the material type and various geometrical dimensions such as thickness and diameter of the material. Also, Wang and Wang [15] proved that the value of nonlocal parameter should be less than 2 nm for single-walled carbon nanotubes.

Lazopoulos and Lazopoulos [16], Xu et al. [17], Papargyri-Beskou et al. [18] examined the size effect for beams with simple SGT. Hassannejad et al. [19] and Alizadeh Hamidi et al. [20] studied the torsional vibration of micro-rods and wires with non-circular cross-sections via MCST for rigid boundary conditions. Uzun and Yaylı [21] presented a solution that can examine the effect of general end conditions on the torsional vibration of non-circular nano-/microwires based on the MCST. In the studies of Hassannejad et al. [19], Alizadeh Hamidi et al. [20], Uzun and Yaylı [21], warping functions were also considered in the problems. Zarezadeh et al. [22] presented the torsional vibration of functionally graded (FG) nanorods under the influence of a magnetic field with the theory of nonlocal elasticity. Islam et al. [23] presented torsional wave propagation and vibration of nano-sized structures based on NLT. Khosravi et al. [24, 25] demonstrated the torsional vibration of triangular nanowire and elliptical nanorods based on the warping effect with the NLT. Taima et al. [26] showed the longitudinal dynamic of stepped nanorods with nonlocal and elastic media effects. Ghorbanpour Arani et al. [27, 28] studied the size effects on the nanoplates and nanobeam systems. Also, we can find many studies [29,30,31,32,33,34,35,36,37,38,39] based on different higher-order approaches in the literature.

SGT has been presented by Lam et al. [11], and it includes more than one size (small-scale) parameter in their formulations. Karamanlı and Vo [40], Lei et al. [41], Zanoosi [42], Akgöz and Civalek [43], Ghorbanpour-Arani et al. [44] presented the mechanical responses of nano- and micro-beams/tubes with strain gradient theory. Studies carried out with nonlocal strain gradient theory (NLSGT) have been encountered frequently in recent times. Merzouki et al. [45], Esen et al. [46], Jena et al. [47] presented the analyses of nanobeams and nanotubes with NLSGT. The use of NLSGT is also frequently encountered in the analysis of rod models. Li et al. [48], Gul and Aydogdu [49] presented the axial vibration of nanorods with NLSGT. While Li et al. [48] examined the simple rod theory, Gul and Aydogdu [49] examined the Bishop rod model. Alizadeh Hamidi et al. [50] presented the torsional vibration of rectangular cross-section nanorods based on nonlocal strain gradient theory. Gu and He [51] investigated the thin nanobeams via NLSGT including G-N theory. Babaei [52] studied the forced vibration of NLSG rods. NLSGT is a combined model that combines the effects of both NLT [10] and SGT [8], and it is possible to see that it has been discussed in various studies [53,54,55,56,57,58,59,60,61,62] based on panels, beams, plates recently. Ghorbanpour-Arani et al. [63] discussed the effects of different nonlocal surface piezoelasticity theories on the wave propagation of coupled double-walled boron nitride nanotubes. Miandoab et al. [64] compared the MCST and NLT on the polysilicon nanobeams.

It is possible to say that composite forms of nano-/micro-scale structures, which are within the scope of various application and study areas, have also become popular recently. Comprising two or more distinct materials, composites are made. Composites can be made in various forms [65,66,67,68]. In this study, the composite material forming the nanoshaft is in functionally graded form. FG composites are formed by providing a smooth transition between the materials that form them. Functionally graded materials (FGMs) with pores are specially designed to meet the uses of various sectors and are an example of widespread development in the industry [69, 70]. The effectiveness of FGMs with pores is closely related to their incredibly high surface area/volume ratio. FGMs designed as thermal insulation coatings in the late twentieth century now appear in forms reinforced with pore factor. The main areas of usage of FGMs are considered as materials and devices that must operate in extreme conditions such as large temperature changes and mechanical stress. FG small-size structures are a class of sophisticated micro- and nanoscale members whose material properties vary throughout the material's spatial direction or directions. FG nano-/micro-scaled structures are interesting offers to enhance the general performance of various nano-/micro-electromechanical systems because of their tunable mechanical properties. We mostly encounter functionally graded composites with/without pores in nanobeam and nanoshell models [71,72,73,74,75]. Functionally graded composites can be in rod forms with circular or tube sections. Nazemnezhad et al. [76] examined the torsional vibration of FG tube rods with size effect and nonlinearity. Shen et al. [77] presented the torsional frequencies of FG solid circular rods with NLSGT. Civalek et al. [78] studied the longitudinal dynamic of FG hollow circular rods with doublet mechanics. Uzun and Yaylı [79] presented the torsional vibration of functionally graded and porous nanotubes with MCST and examined various effects like material gradation parameter, torsional spring stiffnesses and porosity parameter.

In this work, the dynamic of functionally graded tube-shaped torsion nanoshafts with pores in their cross-section is investigated with nonlocal strain gradient, elastic media and deformable boundary effects for the first time. The aim of this work is to demonstrate a solution that can calculate the torsional vibration frequencies of FG porous nanoshafts in an elastic media for general (both deformable and rigid) support conditions. For this purpose, FG porous nanoshafts are modeled with torsional springs restricting rotation at both ends. These elastic springs satisfy the free end condition when set at a sufficiently small stiffness, and the clamped boundary condition when set at a sufficiently large stiffness. The eigenvalue problem obtained in this study, in which Fourier sine series and Stokes’ transform are used together, offers the most general solution since it includes the material properties of FG porous nanoshafts, the stiffness of the springs at both ends, the elastic media parameter and other geometric properties. The eigenvalue problem it presents and the analyses carried out with this eigenvalue problem are the novelty of this study.

2 Equations of motion with nonlocal strain gradient theory

NLSGT [12] is an elasticity theory based on the size effect. This theory of elasticity defines a total stress tensor denoted by \({\sigma }_{ij}^{T}\), and \({\sigma }_{ij}^{T}\) incorporates both the NL stress tensor \({\sigma }_{ij}\) and the higher-order NL stress tensor \({\sigma }_{ijm}^{(1)}\) into its formulations [80]. A stress tensor based on both nonlocal and strain gradient stress tensors is formed in order to combine nonlocal and strain gradient theories into a combined theory. Strain tensors of the referenced point and all other points in the domain function to produce the nonlocal stress tensor at a representative point. Strain gradient bases on the atoms' deformation's higher-order mechanism. This indicates that strain energy density in small-scale systems takes into account higher-order stress–strain energy terms as well as Cauchy stress–strain energy terms [52]. The total stress tensor is introduced as follows [12]:

$${\sigma }_{ij}^{T}={\sigma }_{ij}-{\nabla \sigma }_{ijm}^{(1)}$$
(1)

\({\sigma }_{ij}\) and \({\sigma }_{ijm}^{(1)}\) are written as follows [12, 48]:

$${\sigma }_{xx}=\underset{0}{\overset{L}{\int }}{E\alpha }_{0}\left(x,x{\prime},{e}_{0}a\right){\varepsilon }_{xx}^{\prime}\left(x{\prime}\right)dx{\prime}$$
(2)
$${\sigma }_{xx}^{(1)}={l}_{\rm s}^{2}\underset{0}{\overset{L}{\int }}{E\alpha }_{1}\left(x,x{\prime},{e}_{1}a\right){\varepsilon }_{xx,x}^{\prime}\left(x{\prime}\right)dx{\prime}$$
(3)

Here, \({l}_{\rm s}\) is the material length scale parameter based on the SGT, \(E\) is the elastic (Young’s) modulus. The nonlocality impact is described by \({\alpha }_{0}\), while \({\alpha }_{1}\) is added to characterize the nonlocal impact of the first-order strain gradient field. \({e}_{0}a\) and \({e}_{1}a\) are nonlocal parameters, \(L\) is the length, \({\varepsilon }_{xx}^{\prime}\) is the strain and \({\varepsilon }_{xx,x}^{\prime}\) is the gradient of the strain. It should be said that the SGT mentioned here is the theory proposed by Aifantis [8]. Because the solution of the integral constitutive relations given above is difficult, Eringen [10] proposed an equivalent differential model [80]. Based on this, assuming \({e}_{0}a={ e}_{1}a=\mu\), Eqs. (2) and (3) can be simplified as follows [80]:

$$\left(1-{\mu }^{2}{\nabla }^{2}\right){\sigma }_{xx}=E{\varepsilon }_{xx}$$
(4)
$$\left(1-{\mu }^{2}{\nabla }^{2}\right){\sigma }_{xx}^{(1)}={l}_{\rm s}^{2}E\nabla {\varepsilon }_{xx}$$
(5)

Based on Eqs. (4), (5) and (1), the constitutive equation of the NLSGT is obtained as follows:

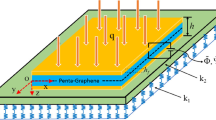
$$\left(1-{\mu }^{2}{\partial }_{xx}\right){\sigma }_{ij}^{T}=E\left(1-{l}_{\rm s}^{2}{\partial }_{xx}\right){\varepsilon }_{xx}$$
(6)

In Eq. (6), \({\partial }_{xx}=\frac{{\partial }^{2}}{\partial {x}^{2}}\). In this study, the NLSGT will be used to study the torsional vibration of composite tube shaft made of porous FGM. The tube shaft made of porous FGM is in an elastic media as in Fig. 1.

Fig. 1
figure 1

Restrained FG porous/non-porous nanoshaft embedded in elastic media

Full size image

3 Properties of composite tube shaft made of porous FGM

Cross-sectional views of the shafts for which torsional vibration analysis will be performed in this study are given in Fig. 2. Figure 2a shows the views of the FG tube shaft with no pores in its cross-section (NPTS), Fig. 2b shows the views of the FG tube shaft with unevenly distributed pores in its cross-section (UEPTS), and Fig. 2c shows the views of the functionally graded tube shaft with evenly distributed pores in its cross-section (EPTS). There are at least two components that make up a composite material. These components have their own characteristic properties and the volume they occupy within the material. Many researchers [74, 81, 82] have adopted the rule of mixture to calculate any property of the composite material (such as shear modulus, Young's modulus, mass density, Poisson's ratio, etc.). In the rule of mixture, the volume ratio of each component is multiplied by the property of the component and the effective material property of the composite is calculated. In terms of the rule of mixture, the mathematical expressions giving the distribution in the material properties of these shafts, whose inner radius dimensions are \(a\), outer radius dimensions \(b\) and radius direction \(r\), are written as follows for NPTS, UEPTS and EPTS, respectively [74, 82]:

Fig. 2
figure 2

Cross-sections of functionally graded nanoshafts

Full size image
$$\Omega \left(r\right)=\left({\Omega }_{b}-{\Omega }_{a}\right){\left(\frac{r-a}{b-a}\right)}^{n}+{\Omega }_{a}$$
(7)
$$\Omega \left(r\right)=\left({\Omega }_{b}-{\Omega }_{a}\right){\left(\frac{r-a}{b-a}\right)}^{n}+{\Omega }_{a}-0.5\kappa \left({\Omega }_{b}+{\Omega }_{a}\right)\left(1-\frac{r-a}{b-a}\right)$$
(8)
$$\Omega \left(r\right)=\left({\Omega }_{b}-{\Omega }_{a}\right){\left(\frac{r-a}{b-a}\right)}^{n}+{\Omega }_{a}-0.5\kappa \left({\Omega }_{b}+{\Omega }_{a}\right)$$
(9)

Here, \(\Omega \left(r\right)\) is any material property of the functionally graded shaft, such as shear modulus G(r) and mass density ρ(r). \({\Omega }_{b}\) and \({\Omega }_{a}\) represent the outer radius and inner radius properties, respectively, while \(n\) is the functionally grading index. Finally, κ is the porosity coefficient, and when this coefficient is taken to zero, the expression that gives the properties of the shaft independent of porosity is obtained. Additionally, an important limitation regarding the porosity coefficient should be mentioned. Although this coefficient is defined with \(0\le \kappa <1\), it should be kept at values closer to zero most of the time. Because, as can be expected, it is not meaningful that a large portion of a material consists of voids (pores). However, depending on the properties of the materials forming the composite and the value of n, increasing this coefficient after a certain point reduces the material parameters to zero and below. In this context, the value of the porosity coefficient is important.

4 Torsional vibration equation based on nonlocal strain gradient theory

This section shows the derivation of the problem giving torsional vibration of FG porous and non-porous shafts surrounded by an elastic media in the context of the NLSGT. The kinetic energy (K) of the composite shaft is defined via:

$$K=\frac{1}{2}\underset{\Pi }{\overset{}{\int }}\rho \left(r\right)\left[{\left({\partial }_{t}{u}_{x}\right)}^{2}+{\left({\partial }_{t}{u}_{y}\right)}^{2}+{\left({\partial }_{t}{u}_{z}\right)}^{2}\right]d\Pi$$
(10)

In the expression of kinetic energy, \(\Pi\) represents the volume occupied by the material and \({\partial }_{t}=\frac{\partial }{\partial t}\). Additionally, here \({u}_{x}\), \({u}_{y}\) and \({u}_{z}\) indicate the displacements of the composite shaft in the x, y and z directions, respectively. In this study, simple rod theory independent of shear deformations is discussed. In this context, components of displacement field for shaft based on the linearized elasticity theories can be written as follows [77, 83]:

$${u}_{x}\left(x,t\right)=0$$
(11)
$${u}_{y}\left(x,t\right)=-z\lambda \left(x,t\right)$$
(12)
$${u}_{z}\left(x,t\right)=y\lambda \left(x,t\right)$$
(13)

In Eqs. (12) and (13), \(\lambda \left(x,t\right)\) represents the torsion angle (angular displacement) of the composite shaft. With the help of the defined displacement expressions, the kinetic energy expression given in Eq. (10) is derived for the composite shaft as follows [80]:

$$K=\frac{1}{2}\underset{0}{\overset{L}{\int }}{J}_{\rho }{\left({\partial }_{t}\lambda \left(x,t\right)\right)}^{2}dx$$
(14)

here, \({J}_{\rho }\) is the mass polar moment of inertia and written for NPTS, UEPTS and EPTS as follows:

$${J}_{\rho }=2\pi \underset{a}{\overset{b}{\int }}\left(\left({\rho }_{b}-{\rho }_{a}\right){\left(\frac{r-a}{b-a}\right)}^{n}+{\rho }_{a}\right){r}^{3}\text{d}r$$
(15)
$${J}_{\rho }=2\pi \underset{a}{\overset{b}{\int }}\left(\left({\rho }_{b}-{\rho }_{a}\right){\left(\frac{r-a}{b-a}\right)}^{n}+{\rho }_{a}-0.5\kappa \left({\rho }_{b}+{\rho }_{a}\right)\left(1-\frac{r-a}{b-a}\right)\right){r}^{3}\text{d}r$$
(16)
$${J}_{\rho }=2\pi \underset{a}{\overset{b}{\int }}\left(\left({\rho }_{b}-{\rho }_{a}\right){\left(\frac{r-a}{b-a}\right)}^{n}+{\rho }_{a}-0.5\kappa \left({\rho }_{b}+{\rho }_{a}\right)\right){r}^{3}\text{d}r$$
(17)

The shaft to be analyzed is surrounded by an elastic media and the work done by the external loads of this system (\(W\)) is expressed as follows [80]:

$$W=-\underset{0}{\overset{L}{\int }}{k}_{\rm{em}}{\lambda \left(x,t\right)}^{2}dx$$
(18)

Here, \({k}_{\rm{em}}\) is the rigidity of the elastic media surrounding the composite shaft. Finally, the strain energy (\(S\)) is written as follows, based on the NLSGT [80]:

$$S=\underset{\Pi }{\overset{}{\int }}\left({\sigma }_{xx}{\varepsilon }_{xx}+{\sigma }_{xx}^{(1)}{\varepsilon }_{xx,x}\right)\text{d}\Pi$$
(19)

In this study, Hamilton's principle is utilized to derive the equation that gives the torsional vibration of the composite shaft in the time interval \({[t}_{1},{t}_{2}]\) [22]:

$$\underset{{t}_{1}}{\overset{{t}_{2}}{\int }}\left(\delta K-\delta S+\delta W\right)=0$$
(20)

in which \({t}_{1}\) and \({t}_{2}\) denote the initial and final times of the motion. If the first variations of kinetic energy, work done by external loads and the strain energy based on the NLSGT are written in Hamilton's principle relation, the equation of motion is derived by [80]:

$$-{J}_{\rho }{\partial }_{xx}\lambda (x,t)-{k}_{\rm{em}}\lambda \left(x,t\right)+{\partial }_{x}M=0$$
(21)

here, \(M\) denotes the torsional moment. Additionally, the following two equations can be written from Eqs. (4) and (5) [80]:

$${M}^{(0)}-{\mu }^{2}{\partial }_{xx}{M}^{(0)}={J}_{G}{\partial }_{x}\lambda (x,t)$$
(22)
$${M}^{(1)}-{\mu }^{2}{\partial }_{xx}{M}^{(1)}={l}_{\rm s}^{2}{J}_{G}{\partial }_{xx}\lambda (x,t)$$
(23)

Here, \({M}^{(0)}\) and \({M}^{(1)}\) are the nonlocal torsional moment and the higher-order nonlocal torsional moment, respectively. It is worth noting here that the above expressions are degenerated and adapted versions for functionally graded porous nanoshafts of El-Borgi et al.'s [80] study. In the study of El-Borgi et al. [80], in addition to nonlocal strain gradient theory, viscoelastic and velocity gradient effects have been also examined. Since the effects mentioned are not examined in this study, the relevant parameters are ignored and the expressions are handled. \({J}_{G}\) is the shear stiffness and is derived for NPTS, UEPTS and EPTS, respectively, as follows:

$${J}_{G}=2\pi \underset{a}{\overset{b}{\int }}\left(\left({G}_{b}-{G}_{a}\right){\left(\frac{r-a}{b-a}\right)}^{n}+{G}_{a}\right){r}^{3}\text{d}r$$
(24)
$${J}_{G}=2\pi \underset{a}{\overset{b}{\int }}\left(\left({G}_{b}-{G}_{a}\right){\left(\frac{r-a}{b-a}\right)}^{n}+{G}_{a}-\frac{\kappa }{2}\left({G}_{b}+{G}_{a}\right)\left(1-\frac{r-a}{b-a}\right)\right){r}^{3}\text{d}r$$
(25)
$${J}_{G}=2\pi \underset{a}{\overset{b}{\int }}\left(\left({G}_{b}-{G}_{a}\right){\left(\frac{r-a}{b-a}\right)}^{n}+{G}_{a}-\frac{\kappa }{2}\left({G}_{b}+{G}_{a}\right)\right){r}^{3}\text{d}r$$
(26)

Here, \({G}_{b}\) and \({G}_{a}\) are the shear moduli at \(r=b\) and \(r=a\) surfaces of the nanoshaft, respectively. Additionally, the following moment relation can be easily written from Eq. (1):

$${{M}=M}^{(0)}-{\partial }_{x}{M}^{(1)}$$
(27)

If Eqs. (22) and (23) are substituted in Eq. (27):

$$M={\mu }^{2}{\partial }_{xx}M+\left(1-{l}_{\rm s}^{2}{\partial }_{xx}\right){J}_{G}{\partial }_{x}$$
(28)

obtained. By taking the derivative of Eq. (21) once with respect to x and inserting it above, \(M\) is calculated as follows [80]:

$$M={J}_{G}{\partial }_{x}\lambda (x,t)-{J}_{G}{l}_{\rm s}^{2}{\partial }_{xxx}\lambda (x,t)+{\mu }^{2}\left({J}_{\rho }{\partial }_{xtt}\lambda (x,t)+{k}_{\rm{em}}{\partial }_{x}\lambda (x,t)\right)$$
(29)

By substituting the resulting M expression into the equation of motion, the equation giving the torsional vibration problem based on the NLSGT is derived as follows [80]:

$${J}_{G}{\partial }_{xx}\lambda (x,t)-{J}_{G}{l}_{\rm s}^{2}{\partial }_{xxxx}\lambda (x,t)+{\mu }^{2}\left({J}_{\rho }{\partial }_{xxtt}\lambda (x,t)+{k}_{\rm{em}}{\partial }_{xx}\lambda (x,t)\right)-{k}_{\rm{em}}\lambda \left(x,t\right)-{J}_{\rho }{\partial }_{tt}\lambda (x,t)=0$$
(30)

The above equation combines the effects of both the Eringen’s NLT and the SGT proposed by Aifantis [8] and can also examine the effects of elastic media.

5 Solution of the torsional vibration equation

In nonlocal strain gradient elasticity, Fourier series expansion together with Stokes’ transformation will be considered to represent the torsional vibration response of functionally graded porous tube nanoshafts. This method offers more flexibility to examine different boundary conditions. Considering harmonic vibrations, \(\lambda \left(x,t\right)\) can be represented as:

$$\lambda \left(x,t\right)=\chi \left(x\right)\text{e}^{i\omega t}$$
(31)

Here, \(\chi \left(x\right)\) is the modal angle function and \(\omega\) is circular frequency. With the help of the above relation, partial differential equation can be discretized to the ordinary differential equation as follows:

$${J}_{G}{d}_{xx}\chi \left(x\right)-{J}_{G}{l}_{\rm s}^{2}{d}_{xxxx}\chi \left(x\right)+{\mu }^{2}\left(-{\omega }^{2}{J}_{\rho }{d}_{xx}\chi \left(x\right)+{k}_{\rm{em}}{d}_{xx}\chi \left(x\right)\right)-{k}_{\rm{e}}\chi \left(x\right)+{\omega }^{2}{J}_{\rho }\chi \left(x\right)=0$$
(32)

The above vibration equation includes both the SGT presented by Aifantis [8] and the NLT presented by Eringen [10]. If we neglect the nonlocal parameter in the equation, the torsional vibration equation of the composite nanoshaft based on the SGT proposed by Aifantis [8] is obtained as follows:

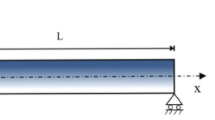
$${J}_{G}{d}_{xx}\chi \left(x\right)-{J}_{G}{l}_{\rm s}^{2}{d}_{xxxx}\chi \left(x\right)-{k}_{\rm{em}}\chi \left(x\right)+{\omega }^{2}{J}_{\rho }\chi \left(x\right)=0$$
(33)

In this study, a solution method in the context of Fourier trigonometric series and Stokes' transform for torsional vibration of composite shafts based on the NLSGT will be used. In the adopted approach, the torsion angle function \(\chi \left(x\right)\) is considered as a sine series in the region \(0<x<L\), and the end points of the shaft are considered as a constant at \(x=0\) and \(x=L\), as follows [21, 79]:

$$\chi \left(x\right)=\left[\begin{array}{c}{\chi }_{0} x=0\\ {\chi }_{L} x=L\\ \sum_{j=1}^{\infty }{F}_{j} \sin\left(\frac{j\pi }{L}x\right) 0<x<L\end{array}\right]$$
(34)

Here, \({F}_{j}\) is the Fourier coefficient. In analytical approaches frequently used in the literature, different trigonometric functions are used to ensure the desired boundary condition. That is, changing the boundary condition requires resolving the governing equation. In this study, by applying the Stokes' transformation, the solution will be forced to meet the desired boundary condition and a general eigenvalue problem that can calculate the frequencies of both rigid and deformable boundary conditions will be obtained. It is useful to point out a situation regarding the selected function here. The authors chose the sine function in this study, but it should be noted that the cosine function could have been chosen instead. In the adopted approach, it is essential to apply the Stokes' transformation and enforce the ends to the desired conditions. In this context, just as the sine function could be used, the cosine function could also be used. However, this time, in order to obtain a satisfactory result, there would be a change in the number of terms of the solution. It is known from the previous studies of the authors that the selected sine function is effective in the vibration of torsional elements with clamped at both ends, even at very low term numbers. Choosing the cosine function instead of sine function will increase the number of terms required for the solution. An increase in the number of terms will require both longer time and more computer capacity. This solution method has been used in the analysis of various elements and detailed mathematical steps can be accessed from studies presented by refs. [21, 79]. Following the mathematical steps, the first four derivatives of the function \(\chi \left(x\right)\) are demonstrated as follows [21, 79]:

$${d}_{x}\chi \left(x\right)=\frac{{\chi }_{L}-{\chi }_{0}}{L}+\sum_{j=1}^{\infty }{\lambda }_{1} \cos\left(\frac{j\pi x}{L}\right)$$
(35)
$${d}_{xx}\chi \left(x\right)=-\sum_{j=1}^{\infty }\frac{j\pi }{L}{\lambda }_{1}\sin\left(\frac{j\pi x}{L}\right)$$
(36)
$${d}_{xxx}\chi \left(x\right)=\frac{{\chi }_{L}^{{\prime}{\prime}}-{\chi }_{0}^{{\prime}{\prime}}}{L}+\sum_{j=1}^{\infty }\left({\lambda }_{2} -\frac{{j}^{2}{\pi }^{2}}{{L}^{2}}{\lambda }_{1}\right) \cos\left(\frac{j\pi x}{L}\right)$$
(37)
$${d}_{xxxx}\chi \left(x\right)=-\sum_{j=1}^{\infty }\frac{j\pi }{L}\left({\lambda }_{2} -\frac{{j}^{2}{\pi }^{2}}{{L}^{2}}{\lambda }_{1}\right) \sin\left(\frac{j\pi x}{L}\right)$$
(38)

In the above derivatives, \({\lambda }_{1}\) and \({\lambda }_{2}\) are expressed as follows:

$${\lambda }_{1}=\frac{2{\left(-1\right)}^{j}{\chi }_{L}}{L}-\frac{2{\chi }_{0}}{L}+\frac{j\pi }{L}{F}_{j}$$
(39a)
$${\lambda }_{2}=\frac{2{\left(-1\right)}^{j}{\chi }_{L}^{{\prime}{\prime}}}{L}-\frac{2{\chi }_{0}^{{\prime}{\prime}}}{L}$$
(39b)

If we substitute \(\chi \left(x\right)\) and its second and fourth derivatives into Eq. (32), the following equation is established:

$$\begin{aligned} & \sum_{j=1}^{\infty }\left[\left(-{J}_{G}{l}_{\rm s}^{2}\right)\left(-\frac{j\pi }{L}\left({\lambda }_{2}-\frac{{j}^{2}{\pi }^{2}}{{L}^{2}}{\lambda }_{1}\right)\right)-\left({J}_{G}-{{\mu }^{2}\omega }^{2}{J}_{\rho }+{\mu }^{2}{k}_{\rm{em}}\right)\left(-\frac{j\pi }{L}{\lambda }_{1}\right)+\left({\omega }^{2}{J}_{\rho }-{k}_{\rm{em}}\right){F}_{j}\right] \\ &\quad \sin\left(\frac{j\pi x}{L}\right)=0 \end{aligned}$$
(40)

By solving this equation, the Fourier coefficient \({F}_{j}\) is calculated for torsional vibration considered with the NLSGT as follows:

$${F}_{j}=\frac{2j\pi ({L}^{2}({J}_{G}+{\mu }^{2}({k}_{\rm{em}}-{\omega }^{2}{J}_{\rho }))+{J}_{G}{j}^{2}{\pi }^{2}{l}_{\rm s}^{2})({\chi }_{0}-{(-1)}^{n}{\chi }_{L})}{{L}^{2}({J}_{G}{j}^{2}{\pi }^{2}+({L}^{2}+{j}^{2}{\pi }^{2}{\mu }^{2})({k}_{\rm{em}}-{\omega }^{2}{J}_{\rho }))+{J}_{G}{{j}^{4}\pi }^{4}{l}_{\rm s}^{2}}$$
(41)

After calculating \({F}_{j}\), the equation calculating the torsion angle based on the NLSGT is obtained as follows:

$$\begin{aligned}\chi \left(x\right)& =\sum_{j=1}^{\infty }\Bigg(\frac{2j\pi ({L}^{2}({J}_{G}+{\mu }^{2}({k}_{\rm{em}}-{\omega }^{2}{J}_{\rho }))+{J}_{G}{j}^{2}{\pi }^{2}{l}_{\rm s}^{2}){\chi }_{0}}{{L}^{2}({J}_{G}{j}^{2}{\pi }^{2}+({L}^{2}+{j}^{2}{\pi }^{2}{\mu }^{2})({k}_{\rm{em}}-{\omega }^{2}{J}_{\rho }))+{J}_{G}{{j}^{4}\pi }^{4}{l}_{\rm s}^{2}} \\ &\quad-\frac{2{(-1)}^{n}j\pi ({L}^{2}({J}_{G}+{\mu }^{2}({k}_{\rm{em}}-{\omega }^{2}{J}_{\rho }))+{J}_{G}{j}^{2}{\pi }^{2}{l}_{\rm s}^{2}){\chi }_{L}}{{L}^{2}({J}_{G}{j}^{2}{\pi }^{2}+({L}^{2}+{j}^{2}{\pi }^{2}{\mu }^{2})({k}_{\rm{em}}-{\omega }^{2}{J}_{\rho }))+{J}_{G}{{j}^{4}\pi }^{4}{l}_{\rm s}^{2}}\Bigg) \sin\left(\frac{j\pi }{L}x\right)\end{aligned}$$
(42)

The eigenvalue problem based on the NLSGT for the torsional vibration of composite nanoshafts will be obtained. With the torque expression based on the NLSGT, the following force boundary conditions are written for the \(x=0\) and \(x=L\) points of the composite nanoshaft:

$${J}_{G}{\partial }_{x}\lambda (x,t)-{J}_{G}{l}_{\rm s}^{2}{\partial }_{xxx}\lambda (x,t)+{\mu }^{2}\left({J}_{\rho }{\partial }_{xtt}\lambda (x,t)+{k}_{\rm{em}}{\partial }_{x}\lambda (x,t)\right){|}_{x=0}={\psi }_{0}{\chi }_{0}$$
(43)
$${J}_{G}{\partial }_{x}\lambda (x,t)-{J}_{G}{l}_{\rm s}^{2}{\partial }_{xxx}\lambda (x,t)+{\mu }^{2}\left({J}_{\rho }{\partial }_{xtt}\lambda (x,t)+{k}_{\rm{em}}{\partial }_{x}\lambda (x,t)\right){|}_{x=L}={-\psi }_{L}{\chi }_{L}$$
(44)

\({\psi }_{0}\) in Eq. (43) denotes the rigidity of the torsional spring at the x = 0 point of the nanoshaft, and \({\psi }_{L}\) in Eq. (44) specifies the rigidity of the torsional spring at the x = L point of the nanoshaft. By solving Eqs. (43) and (44), the following two sets of equations are derived:

$$\begin{aligned} & \left(-{\psi }_{0}+{\mu }^{2}\left(\frac{{J}_{\rho }{\omega }^{2}}{L}-\frac{{k}_{\rm{em}}}{L}\right)-\frac{{J}_{G}}{L}-\sum_{j=1}^{\infty }\frac{2L({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})({L}^{2}{\mu }^{2}({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})+{J}_{G}{\Xi }_{1})}{\left({k}_{\rm{em}}{L}^{2}-{L}^{2}{J}_{\rho }{\omega }^{2}\right){\Xi }_{2}+{J}_{G}{j}^{2}{\pi }^{2}{\Xi }_{1}}\right){\chi }_{0} \\ &\quad+\left(-{\mu }^{2}\left(\frac{{J}_{\rho }{\omega }^{2}}{L}-\frac{{k}_{\rm{em}}}{L}\right)+\frac{{J}_{G}}{L}+\sum_{j=1}^{\infty }\frac{2{(-1)}^{j}L({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})({L}^{2}{\mu }^{2}({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})+{J}_{G}{\Xi }_{1})}{\left({k}_{\rm{em}}{L}^{2}-{L}^{2}{J}_{\rho }{\omega }^{2}\right){\Xi }_{2}+{J}_{G}{j}^{2}{\pi }^{2}{\Xi }_{1}}\right){\chi }_{L}=0 \end{aligned}$$
(45)
$$\begin{aligned} & \left(-{\mu }^{2}\left(\frac{{J}_{\rho }{\omega }^{2}}{L}-\frac{{k}_{\rm{em}}}{L}\right)+\frac{{J}_{G}}{L}+\sum_{j=1}^{\infty }\frac{2{(-1)}^{j}L({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})({L}^{2}{\mu }^{2}({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})+{J}_{G}{\Xi }_{1})}{\left({k}_{\rm{em}}{L}^{2}-{L}^{2}{J}_{\rho }{\omega }^{2}\right){\Xi }_{2}+{J}_{G}{j}^{2}{\pi }^{2}{\Xi }_{1}}\right){\chi }_{0} \\ &\quad+\left(-{\psi }_{L}+{\mu }^{2}\left(\frac{{J}_{\rho }{\omega }^{2}}{L}-\frac{{k}_{\rm{em}}}{L}\right)-\frac{{J}_{G}}{L}-\sum_{j=1}^{\infty }\frac{2L({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})({L}^{2}{\mu }^{2}({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})+{J}_{G}{\Xi }_{1})}{\left({k}_{\rm{em}}{L}^{2}-{L}^{2}{J}_{\rho }{\omega }^{2}\right){\Xi }_{2}+{J}_{G}{j}^{2}{\pi }^{2}{\Xi }_{1}}\right){\chi }_{L}=0 \end{aligned}$$
(46)

in which \({\Xi }_{1}\) and \({\Xi }_{2}\) are defined by:

$${\Xi }_{1}={L}^{2}+{j}^{2}{\pi }^{2}{l}_{\rm s}^{2}$$
(47)
$${{\Xi }_{2}=L}^{2}+{j}^{2}{\pi }^{2}{\mu }^{2}$$
(48)

An eigenvalue problem is set up with the equation systems given in Eqs. (45) and (46):

$$\left[\begin{array}{cc}{H}_{11}& {H}_{12}\\ {H}_{21}& {H}_{22}\end{array}\right]\left[\begin{array}{c}{\chi }_{0}\\ {\chi }_{L}\end{array}\right]=0$$
(49)

The elements of the coefficients matrix \({H}_{11}\), \({H}_{12}\), \({H}_{21}\) and \({H}_{22}\) are written as follows:

$${H}_{11}=-{\psi }_{0}+{\mu }^{2}\left(\frac{{J}_{\rho }{\omega }^{2}}{L}-\frac{{k}_{\rm{em}}}{L}\right)-\frac{{J}_{G}}{L}-\sum_{j=1}^{\infty }\frac{2L({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})({L}^{2}{\mu }^{2}({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})+{J}_{G}{\Xi }_{1})}{\left({k}_{\rm{em}}{L}^{2}-{L}^{2}{J}_{\rho }{\omega }^{2}\right){\Xi }_{2}+{J}_{G}{j}^{2}{\pi }^{2}{\Xi }_{1}}$$
(50)
$${H}_{12}=-{\mu }^{2}\left(\frac{{J}_{\rho }{\omega }^{2}}{L}-\frac{{k}_{\rm{em}}}{L}\right)+\frac{{J}_{G}}{L}+\sum_{j=1}^{\infty }\frac{2{(-1)}^{j}L({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})({L}^{2}{\mu }^{2}({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})+{J}_{G}{\Xi }_{1})}{\left({k}_{\rm{em}}{L}^{2}-{L}^{2}{J}_{\rho }{\omega }^{2}\right){\Xi }_{2}+{J}_{G}{j}^{2}{\pi }^{2}{\Xi }_{1}}$$
(51)
$${H}_{21}=-{\mu }^{2}\left(\frac{{J}_{\rho }{\omega }^{2}}{L}-\frac{{k}_{\rm{em}}}{L}\right)+\frac{{J}_{G}}{L}+\sum_{j=1}^{\infty }\frac{2{(-1)}^{j}L({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})({L}^{2}{\mu }^{2}({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})+{J}_{G}{\Xi }_{1})}{\left({k}_{\rm{em}}{L}^{2}-{L}^{2}{J}_{\rho }{\omega }^{2}\right){\Xi }_{2}+{J}_{G}{j}^{2}{\pi }^{2}{\Xi }_{1}}$$
(52)
$${H}_{22}=-{\psi }_{L}+{\mu }^{2}\left(\frac{{J}_{\rho }{\omega }^{2}}{L}-\frac{{k}_{\rm{em}}}{L}\right)-\frac{{J}_{G}}{L}-\sum_{j=1}^{\infty }\frac{2L({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})({L}^{2}{\mu }^{2}({k}_{\rm{em}}-{J}_{\rho }{\omega }^{2})+{J}_{G}{\Xi }_{1})}{\left({k}_{\rm{em}}{L}^{2}-{L}^{2}{J}_{\rho }{\omega }^{2}\right){\Xi }_{2}+{J}_{G}{j}^{2}{\pi }^{2}{\Xi }_{1}}$$
(53)

To find the torsional vibration frequencies of the composite nanoshaft based on the NLSGT, we need to set the determinant of the coefficients matrix equal to zero (Eq. 54) and obtain the eigenvalues.

$$\left|\begin{array}{cc}{H}_{11}& {H}_{12}\\ {H}_{21}& {H}_{22}\end{array}\right|=0$$
(54)

The eigenvalues obtained with the help of Eq. (54) give us the torsional vibration frequencies of the composite nanoshaft. When looking at the literature, it is understood that the boundary conditions of torsion elements are collected in several cases. Scientists working on this subject have mostly examined the vibration frequencies of macro- or micro-/nanoscale elements, which they consider as torsion bars/rods, under the following boundary conditions: clamped at two ends, clamped at one end and free at the other end, and rarely, free at both ends. However, it is possible to come across models made with deformable springs at one or both ends of the torsion elements, albeit in limited numbers. However, it can be noticed that there is no study presenting the size-dependent torsional vibration of tube shafts constructed from functionally graded porous materials surrounded by an elastic media under deformable boundary conditions, based on nonlocal strain gradient theory. This study targets this gap in the literature. For this purpose, an effective solution method based on the Stokes’ transformation is adopted. A single eigenvalue problem that enables to obtain the torsional vibration of functionally graded porous nanoshafts modeled with deformable torsional springs at both ends is obtained by including the mentioned springs. Thus, a solution is presented that does not require resolving the problem in line with changing boundary conditions. Because just adjusting the stiffness of the torsion springs already allows changing the boundary conditions.

6 Validation and investigation studies

Applications of the method described are accomplished for tube nanoshafts in this section of the study. Tube-shaped cross-sectional views of the investigated nanoshafts composed of FG porous material are presented in Fig. 2a–c. Various examinations for the FG tube shafts made of metal and ceramic components are demonstrated.  The shift of material characteristics of tube shafts is in the radius direction. In this study, the outer radius (r = b) is made of ceramic, whereas the inner radius (r = a) is made of metal. The components in the inner and outer radiuses have the following shear moduli and mass densities: Ga = 26.92 GPa, Gb = 58.07 GPa, ρa = 2707 kg/m3, ρb = 3000 kg/m3. The components in the inner and outer radiuses have equivalent Poisson's ratios, which equal 0.3. For the examined nanoshafts, a = 1 nm, while b = 2a = 2 nm. The slenderness ratio, that is, the length/outer radius ratio, is chosen as 10 for the nanoshafts. In this study, torsional frequencies are discussed via non-dimensional form. Non-dimensional torsional frequencies are calculated via Eq. (55).

$$\overline{{\omega }_{m}}={\omega }_{m}L\sqrt{\frac{{\rho }_{b}}{{G}_{b}}}$$
(55)

here, \(\overline{{\omega }_{m}}\) is the non-dimensional torsional frequency and \(m\) is the mode number. Also, some inputs are also considered with dimensionless forms. Dimensionless elastic media parameter (\({K}_{\text{e}}\)), dimensionless spring parameters for the x = 0 and x = L points of the nanoshafts (\(\overline{{\psi }_{0}}\) and \(\overline{{\psi }_{L}}\)) are formulated as follows, respectively:

$${K}_{\rm{e}}=\frac{{k}_{\rm{em}}{L}^{2}}{{G}_{a}J}$$
(56)
$$\overline{{\psi }_{0}}=\frac{{\psi }_{0}L}{{G}_{b}J}$$
(57)
$$\overline{{\psi }_{L}}=\frac{{\psi }_{L}L}{{G}_{b}J}$$
(58)

Validation studies will be given to demonstrate the usability of the solution method. For the validation study demonstrated with Table 1 including the elastic media effect, the results presented by Numanoğlu and Civalek [84] are taken into account. Numanoğlu and Civalek [84] presented the torsional vibration of homogeneous nanorods in elastic media with the NLT and both analytical and finite element solutions. For this comparison, which does not include the effect of strain gradient and functionally graded material, \({l}_{\rm s}=\kappa=n=0\). Since the clamped–clamped boundary condition is compared, \(\overline{{\psi }_{0}}=\overline{{\psi }_{L}}={10}^{10}\) is considered. In the solution performed with Eq. (54) with 20 terms (j = 20), the dimensionless elastic media parameter is calculated as follows to ensure harmony between the parameters:

Table 1 Comparison of \(\overline{{\omega }_{m}}\) for embedded homogeneous nonlocal rod (\({K}_{\rm{e}}=1)\)
Full size table
$${K}_{\rm{e}}=\frac{{k}_{\rm{em}}{L}^{2}}{{G}_{b}J}$$
(59)

It is understood from the comparison study that the dimensionless nonlocal parameters (μ/L) are considered as 0.05 and 0.1, and the dimensionless elastic media parameter is considered as \({K}_{\rm{e}}=1\), and the method presented in this study is valid.

The second comparison study is on the non-dimensional torsional frequencies of cantilever (clamped-free) nonlocal nanorods. In this comparison, which is also made for homogeneous nanorods, the first mode and varying μ/L values are considered. In this comparison study shown in Fig. 3, calculations are made with term numbers ranging from 10 to 100. As can be understood from the frequencies presented by Islam et al. [23] with the exact solution, although the clamped–clamped boundary condition is met with a low term, a higher number of terms are required for the clamped-free boundary condition. It is clear that the results converge with each other as the number of terms increases. Since 100 terms are deemed sufficient, the comparison is stopped here.

Fig. 3
figure 3

Convergence of frequencies for different \({\varvec{j}}\) and \({\varvec{\mu}}/{\varvec{L}}\) values

Full size image

The third comparison is carried out with nonlocal strain gradient theory, which does not include the elastic media effect. For this comparison, the following formula presented by Shen et al. [77] is used to represent the clamped–clamped boundary condition:

$${\omega }_{m}=\frac{m\pi }{L}\sqrt{\frac{{J}_{G}({L}^{2}+{l}_{\rm s}^{2}{m}^{2}{\pi }^{2})}{{J}_{\rho }({L}^{2}+{\mu }^{2}{m}^{2}{\pi }^{2})}}$$
(60)

Table 2 is both a comparison study and an analysis result for various theories. It is obvious that the results are in perfect harmony with the formula presented by Shen et al. [77]. It should be noted here that the angular frequencies calculated with the help of Eqs. (60) and (54) are nondimensionalized by applying Eq. (55).

Table 2 Non-dimensional frequencies for NPTS (clamped–clamped, \(n=1\))
Full size table

Frequency values for NLSGT, NLT and LT are compared for the first five modes without elastic media effect via Fig. 4. It should also be noted that for this figure and for other analyses performed, the following parameters are valid unless stated otherwise: \(\kappa =0.1\), \(n=1\), \(j=20\), \(\overline{{\psi }_{0}}=\overline{{\psi }_{L}}={10}^{10}\), \(m=1\) (the first mode). For this example, while the size parameter is taken as 1 nm (\(\mu =1\,\text{nm}\)) for NLT, different size parameters’ combinations are considered for NLSGT. \({l}_{\rm s}\) and \(\mu\) are considered as 1 nm and 0.2 nm, respectively, for NLSGT (\({l}_{\rm s}>\upmu\)), while \({l}_{\rm s}\) and \(\mu\) are considered as 0.2 nm and 1 nm, respectively, for NLSGT (\({l}_{\rm s}<\mu\)). Finally, for NLSGT (\({l}_{\rm s}\)= \(\mu\)), \({l}_{\rm s}=\mu =1\,\text{nm}\) is taken. In the first modes of vibration, the frequencies are almost the same for all theories. As the mode number increases, the differences between all frequencies increase in this example. It can also be observed here that size effects are more effective for higher modes. Here, the frequencies of LT and NLSGT (\({l}_{\rm s}\)=μ) are remarkable. Regardless of the mode number, the frequencies of these two analyses are exactly the same. Taking both size parameters equal in the NLSGT brings the results to the same situation as the local theory.

Fig. 4
figure 4

Comparison of frequencies for various theories (NPTS)

Full size image

While Figs. 5, 6 and 7 examine the effect of two different size parameters contained in the NLSGT for the first vibration mode, Figs. 8, 9 and 10 examine it for the second vibration mode. In this study, the effects of two different small-scale parameter on the torsional vibration frequencies of functionally graded porous nanoshafts are studied comparatively. In order to understand the comparison better, the same intervals for values of nonlocal parameter and material length scale parameter are used. Thus, it is observed to what extent both small-scale parameters affect the frequencies of functionally graded porous nanoshafts behaviors. While calculating the frequencies in these figures, the value of the size parameter, which is kept constant, is taken as 1 nm. From the figures given, it is clear that for all three nanoshafts, µ reduces the frequencies, while \({l}_{\rm s}\) increases the frequencies. Here, it is aimed to examine the effects of small-scale parameters as well as the effects of these parameters on the modes. When the frequency values of nanoshafts are examined, it is understood that the change of \({l}_{\rm s}\) and µ causes a more significant change in the frequencies of the second mode. It should be noted that \(\kappa =0.1\) is considered for EPTS and UEPTS throughout the study. In addition, with the help of these figures, it is possible to compare the dimensionless frequencies of NPTS, EPTS and UEPTS. For both vibration modes, we can easily see that the highest frequencies belong to EPTS and the lowest frequencies belong to NPTS. We can say that both pore distributions examined increase the frequencies of functionally graded nanoshafts.

Fig. 5
figure 5

Effect of \({{\varvec{l}}}_{{\varvec{s}}}\) and µ for NPTS (mode 1)

Full size image
Fig. 6
figure 6

Effect of \({{\varvec{l}}}_{{\varvec{s}}}\) and µ for EPTS (mode 1)

Full size image
Fig. 7
figure 7

Effect of \({{\varvec{l}}}_{{\varvec{s}}}\) and µ for UEPTS (mode 1)

Full size image
Fig. 8
figure 8

Effect of \({{\varvec{l}}}_{{\varvec{s}}}\) and µ for NPTS (mode 2)

Full size image
Fig. 9
figure 9

Effect of \({{\varvec{l}}}_{{\varvec{s}}}\) and µ for EPTS (mode 2)

Full size image
Fig. 10
figure 10

Effect of \({{\varvec{l}}}_{{\varvec{s}}}\) and µ for UEPTS (mode 2)

Full size image

Figures 11 and 12 examine the dimensionless elastic media parameter \({K}_{\text{e}}\) effect for the first and second modes of NPTS, respectively. In these graphs drawn for three different nonlocal parameter values, it is clearly seen that the frequencies of NPTS increase with the increase of the dimensionless elastic media parameter. Here, the frequency-reducing effect of µ can be emphasized once again. However, the noteworthy point is that while the increase in the dimensionless elastic media parameter significantly increases the frequencies of the first mode, the effect of this parameter decreases considerably in the second mode.

Fig. 11
figure 11

Effect of elastic media parameter for NPTS (mode 1)

Full size image
Fig. 12
figure 12

Effect of elastic media parameter for NPTS (mode 2)

Full size image

Figures 13 and 14 investigate the dimensionless elastic media parameter effect for the first two modes of EPTS, respectively. In these graphs plotted for three different \({l}_{\rm s}\) values, it is clearly seen that the frequencies of EPTS increase with the increase of the dimensionless elastic media parameter. Here, the frequency-enhancing effect of \({l}_{\rm s}\) can be highlighted once again. We can say again that while the increase in the dimensionless elastic media parameter prominently increases the first mode frequencies, the impact of elastic media decreases considerably in the second mode.

Fig. 13
figure 13

Effect of elastic media parameter for EPTS (mode 1)

Full size image
Fig. 14
figure 14

Effect of elastic media parameter for EPTS (mode 2)

Full size image

The effect of functionally grading index is examined in Figs. 15 and 16. For this purpose, ls = 2 nm, μ = 1 nm and Ke = 0 and Ke = 20 are considered. Functionally grading index effect is measured with the frequency parameter calculated by Eq. (61). As can be seen from both graphs, the value of the frequency parameter decreases as n increases. This decrease is due to decreasing frequency values as n increases. The increase in the metallic properties of composite nanoshafts results in a decrease in frequencies. This reduction is valid for both porous and non-porous nanoshafts. There are three notable situations in these analyses: The first of these is that the increase in low functionally grading index values is more effective on the frequencies. So that, as n increases, the curve showing the change of the frequency parameter tends to become horizontal. The second striking situation is the values of the frequency parameters of NPTS, EPTS and UEPTS. As can be noticed, the highest frequency parameter values are obtained for NPTS, while the lowest frequency parameter values are obtained for EPTS. This reveals that EPTS is most affected by the increase in functionally grading index and NPTS is least affected. The third situation is the difference between the frequency parameters obtained at Ke = 0 and Ke = 20 values. In the case of Ke = 0, that is, when the elastic media effect is neglected, the calculated frequency parameters are lower. This reveals that nanoshafts are more affected by the change of functionally grading index when there is no elastic media effect.

Fig. 15
figure 15

Effect of functionally grading index for \({{\varvec{K}}}_{{\varvec{e}}}=0\)

Full size image
Fig. 16
figure 16

Effect of functionally grading index for \({{\varvec{K}}}_{{\varvec{e}}}=20\)

Full size image
$$\text{frequency\, parameter}=\frac{\overline{\omega } \, \text{for}\, n\ge 0}{\overline{\omega }\, \text{for}\, n=0}$$
(61)

In Figs. 17 and 18, the effects of symmetrical springs (\(\overline{{\psi }_{0}}\) = \(\overline{{\psi }_{L}}\)) are examined for the first and second vibrational modes of NPTS, UEPTS and EPTS, respectively. In these graphs drawn for five different symmetrical spring parameter values, it can be easily seen that the frequencies of the nanoshafts increase with the enhancement of the spring parameters. However, the noteworthy point is that the increase of the spring parameters causes a higher increase in higher modes. It should be noted here that the number of terms used for the solution in the analyses where different spring stiffnesses are considered, that is, in Figs. 17, 18, 19, 20, 21 and 22, is 100 (\(j=100\)).

Fig. 17
figure 17

Effect of symmetric spring parameters for mode 1

Full size image
Fig. 18
figure 18

Effect of symmetric spring parameters for mode 2

Full size image
Fig. 19
figure 19

Effect of anti-symmetric spring parameters for EPTS

Full size image
Fig. 20
figure 20

Effect of anti-symmetric spring parameters for NPTS

Full size image
Fig. 21
figure 21

Effect of anti-symmetric spring parameters for UEPTS

Full size image
Fig. 22
figure 22

Effect of anti-symmetric spring parameters for different \({{\varvec{l}}}_{{\varvec{s}}}\) values

Full size image

In Figs. 19, 20, 21, the changes in the dimensionless vibration frequencies of EPTS, NPTS and UEPTS are plotted for anti-symmetric spring parameters and changing nonlocal parameter values, respectively. In these graphs drawn for the first vibration mode, \({K}_{\rm{e}}=10\), \({l}_{\rm s}=2\,\text{nm}\), \(\overline{{\psi }_{L}}={10}^{10}\) are considered. One of the effectiveness of the solution presented in the study is the option of not taking both spring stiffnesses equal. It is understood from these figures given to show this that increasing the spring stiffness on one side also increases the stiffness of the tube shafts, causing the frequencies to increase. Here also, the effect of the nonlocal parameter can be seen once again. Although the decrease in frequencies with the increase of the nonlocal parameter is easily observed, it should be said here that as the stiffness of \(\overline{{\psi }_{0}}\) increases, the change in the nonlocal parameter affects the frequencies more. That is, the nonlocal parameter is more effective in the vibration of nanoshafts with high spring stiffness. However, the change in the stiffness of \(\overline{{\psi }_{0}}\) affects the frequencies of NPTS the most and the frequencies of EPTS the least.

Figure 22 presents the effect of the anti-symmetric spring state of NPTS, EPTS and UEPTS at ls = 0.5 nm and ls = 15 nm. For this example, μ = 2 nm and Ke = 10 are chosen. The increases in frequencies with the increase in spring stiffness and the increase in the material length scale parameter are observed again here. It is also understood here that the change in spring stiffness affects the frequencies more when the material length scale parameter is high.

7 Conclusions

In this work, based on the torsional vibration of nanoshaft developed using the nonlocal strain gradient elasticity theory and the concept of fractional derivative, the small-size-dependent free torsional vibration response of functionally graded porous nanoshafts is investigated. The solutions of free torsional vibration frequencies and rotations for rigid and restrained functionally graded porous nanoshafts are presented via an exact semi-analytical method. Fourier sine series and Stokes’ transformations are applied to discretize the partial differential equations corresponding to force boundary conditions to consider restrained boundary conditions by the means of elastic springs. The accuracy and validity of the presented model are investigated by comparing rigid and free boundary conditions by giving proper values to elastic spring parameters. Then, the torsional vibration frequencies of functionally graded porous nanoshafts are investigated in a comprehensive study. The key insights obtained from the research can be summarized as follows: The elastic media surrounding the composite nanoshafts strengthens the nanoshafts, resulting in an increase in dimensionless vibration frequencies. This increase is especially striking for the first vibration mode. The increase of the functionally grading index, which represents material change, decreases the frequencies of all nanoshafts examined. This decrease occurs most for EPTS and when the elastic media effect is neglected. With the solution presented in this study, the effect of deformable springs can be examined with both symmetric and anti-symmetric stiffnesses. The results show that as the stiffness of the deformable springs increases, the frequencies also increase. In addition, the effects of two different small-scale parameters are examined. The nonlocal parameter causes the frequencies to decrease, while the material length scale parameter causes the frequencies to increase.