1 Introduction

Micro electro-mechanical and nano-electromechanical systems with features such as lightweight, small size, high sensitivity, fast response, low energy dissipation, and increasing durability have been discovered to have a wide range of applications in recent years. Because of their exceptional electrical, thermal, and mechanical qualities, nanostructures have allowed their application in many engineering domains [1, 2]. Micro/nano-beams serve as integral components in small-scale structures, and understanding their behavior under various static or dynamic loads is crucial. It's noteworthy that, given their classification as thin beams in real-world applications like atomic force microscopes, sensors, and actuators, the utilization of a higher-order beam theory to accurately model the bending of thicker beams is unnecessary. In essence, the Euler–Bernoulli beam theory proves sufficient for modeling and analyzing these slender structures, such as thin nanobeams [3]. In the semiconductor industry, nano-beams play a pivotal role in the design and characterization of nano-electronic devices, including transistors and integrated circuits [4]. Similarly, in biomedical engineering, particularly in the development of lab-on-a-chip devices and biosensors [5], nano-beams find application. This information holds relevance for the design and analysis of innovative nanostructures, encompassing nanobridges and nanocomposites. In nano-electromechanical systems, nanostructures with temperature-dependent characteristics have been used. Thus, developing an accurate mathematical model of nanobeams with temperature-dependent characteristics is a critical problem for nano-electromechanical system design. This discovery is critical in industry, particularly in the design of precise equipment and machines. Nanostructures have the potential to make a substantial difference in people's lives, and research on nanobeams, a crucial component of nanostructures, is required. Because of the increasing use of this matchless category of materials at the micro and nano dimensions in recent years, many experiments have been carried out and many research papers have been published on this issue in order to obtain the best compatible theory to analyze their behavior [6,7,8,9,10]. The quality factor is a fundamental concept in the field of vibration analysis and engineering. It's a measure of how well a mechanical or structural system can store and sustain energy over repeated cycles of vibration. The quality factor is defined as the ratio of the energy stored in the system to the energy dissipated by the system in one complete cycle of vibration. A high-quality factor indicates that the system is efficient at storing and releasing energy, resulting in lower energy losses due to damping. In practical terms, this means that a system with a high quality factor will vibrate for a longer time after being excited, with less energy being lost as heat or other forms of dissipation. This is particularly important in applications where maintaining vibration for a long duration is desirable, such as in musical instruments, electronics, mechanical resonators, and more [11].

To address these challenges, researches have turned to nonlocal elasticity theory, which takes into account the inherit length scales associated with nanoscale phenomena. Nonlocal elasticity theory, unlike classical elasticity, considers the influence of remote interactions on the deformation behavior of materials at small scales, incorporating nonlocal effects arising from the atomic lattice structure. This theory has proven to be a powerful tool in accurately modeling and analyzing the mechanical behavior of nanostructure [12,13,14]. The nonlocal elasticity theory has shown promising results in capturing the size effects and has been widely used in similar studies. It gives a more accurate representation of nanobeam mechanical response compared to other size-dependent theories. Ebrahimi et al. [15] size-dependent Eringen’s nonlocal elasticity theory, that was first introduced by Eringen in 1983, is useful in dealing with phenomena whose origins lie in organizations smaller than the classical continuum models. Such nonlocal continuum mechanics have been widely accepted and have been applied to many problems. Peddison et al. [16] applied the nonlocal elasticity to model a small beam and showed that the nonlocal theory can potentially play a useful role in micro-/nanotechnology applications. Lu et al. [17] numerous studies have been performed to study the static and dynamic behaviors of nanobeams and is widely used to capture the size effect.

Moreover, the interaction between nanoscale structures and their surrounding environment plays a pivotal role in their overall performance. Many practical applications involve nanobeams resting on complex foundations, which introduce additional complexities such as nonlinearities and viscoelastic effects. Nanobeams often rest on foundations that introduce significant mechanical complexities, particularly when considering nonlinear elastic behavior. The incorporation of nonlinear foundation models allows for the consideration of intricate load–displacement relationships that more accurately capture the behavior of real-world support systems.

Furthermore, considering the growing demand for high-performance nanosystems, it becomes imperative to analyze the behavior of nanobeams under diverse environmental conditions. Thermal effects can significantly influence the mechanical properties and response of nanostructures. Changes in temperature can induce thermal stresses and alter the material properties, which, in turn, affect the vibration characteristics of nanobeams. Therefore, a comprehensive study of nanobeam vibrations in a thermal environment is essential for a more accurate understanding of their behavior and performance.

Zhang et al. [18] examined the influence of temperature change on the transverse vibrations of double walled carbon nanotubes. Wang et al. [19] investigated how temperature changes (thermal effect) influence both the vibration behavior and the instability of carbon nanotubes (CNTs) that are used to convey fluid. Benzair et al. [20] investigated the impact of temperature changes, referred to as the thermal effect, on the vibration behavior of single-walled carbon nanotubes (SWCNTs) using the framework of nonlocal Timoshenko beam theory. Murmu and Pradhan [21] investigated how the combined effects of temperature changes and mechanical influences impact the thermo-mechanical vibration behavior of SWCNTs embedded within an elastic medium, using nonlocal elasticity theory. Murmu and Pradhan [22] examined the how the thermal effects influence the stability of embedded CNTs. Chang [23] investigated the combined effects of thermal and mechanical influences impact the vibration and instability behavior of a fluid conveying SWCNTs embedded within an elastic medium, using the nonlocal elasticity theory. Amirian et al. [24] focused on exploring how the thermal vibration behavior of CNTs embedded within a two-parameter elastic foundation is influenced by temperature changes, using the nonlocal Timoshenko's beam theory as a theoretical framework. Tylikowski [25] investigated the instability that may arise from thermally induced vibrations in CNTs using the framework of nonlocal elasticity theory. Pradhan and Mandal [26] focused on conducting a finite element analysis of carbon nanotubes (CNTs) using a combination of nonlocal elasticity theory and the Timoshenko beam theory, considering the influence of thermal effects on the mechanical behavior of CNTs. Sobamowo [27] examined the nonlinear thermal and flow-induced vibration behavior of a fluid conveying CNTs that is supported by both Winkler and Pasternak foundation. Hamza-Cherif et.al [28] investigated the vibration analysis of SWCNTs embedded in an elastic medium under thermal effect based on nonlocal Euler–Bernoulli beam model using differential Transform Method. Ebrahimi and Salari [29] investigated combination effects of temperature changes and mechanical factors impact the thermo-mechanical vibration behavior of SWCNTs embedded within an elastic medium, using higher order shear deformation theory. Ebrahimi and Mahmoodi [30] focused on conducting a vibration analysis of CNTs that contain multiple cracks while being exposed to a thermal environment. Ghayesh [31] examined the nonlinear size-dependent behavior of SWCNTs based on the von-Karman nonlinearity and the nonlocal elasticity theory. Equation of motion and associated boundary conditions are derived based on Hamilton’s principle in the framework of the nonlocal Euler–Bernoulli beam theory. Then, with the aid of a high-dimensional Galerkin scheme, the SWCNT's nonlinear partial differential equation of motion is recast into a reduced-order model. Ghayesh [32] investigated the nonlinear forced dynamics of a three-layered microplate taking into account all the in-plane and out-of-plane motions. Kirchhoff's plate theory, along with von Kármán nonlinear strains, is employed to derive the nonlinear size-dependent transverse and in-plane equations of motion in the modified couple stress theory (MCST) framework, based on Hamilton's energy principle. Uzun et al. [33] presented an efficient solution method based on the Stokes' transformation which can investigate the impacts of deformable boundary conditions and axial point load on the transverse vibration of a nanobeam restrained with lateral springs. Akgöz and Civalek [34] analyzed the buckling problem of nonhomogeneous microbeams with a variable cross-section. The Bernoulli–Euler beam theory in conjunction with modified strain gradient theory is employed to model the structure by considering the size effect. The Rayleigh–Ritz numerical solution method is used to solve the eigenvalue problem for various conditions. Demir et al. [35] developed the finite element method for static analysis of nano-beams under the Winkler foundation and the uniform load. The small scale effect along with Eringen's nonlocal elasticity theory is taken into account. The governing equations are derived based on the minimum potential energy principle. Galerkin weighted residual method is used to obtain the finite element equations. Civalek et al. [36] presented the size-dependent stability analysis of restrained nanobeam with functionally graded material via nonlocal Euler–Bernoulli beam theory using the Fourier series. The nonlocal elasticity theory introduced by Eringen is utilized to show the size effect on the buckling response of restrained functionally graded nanobeam.

The provided list of research works outlines a series of studies conducted by various researchers on the vibration and thermal behavior of functionally graded (FG) nanobeams, particularly considering the effects of nonlocal behavior and temperature changes. Ebrahimi and Salari [37] investigated the influence of temperature on buckling and free vibration of FG size-dependent Timoshenko nanobeams. Ebrahimi and Salari [38] examined the thermal effect on free vibration characteristics of FG size-dependent nanobeams subjected to an in-plane thermal loading based on nonlocal elasticity theory of Eringen. Ebrahimi and Salari [39] investigated how different thermal loadings influence the buckling and vibration behavior of FG nanobeams, considering the effects of nonlocal behavior and temperature dependency. Ebrahimi and Barati [40] focused on investigating the vibration behavior of nonlocal FG nanobeams when exposed to a thermal environment. Hosseini and Rahmani [41] analyzed the thermomechanical vibration behavior of a curved FG nanobeam using the framework of nonlocal elasticity theory. Mirjavadi et al. [42] analyzed how the free vibration and thermal buckling behavior of axially FG nanobeams influenced by size dependent effects and thermal conditions. Azimi et al. [43] investigated the vibration behavior of rotating FG Timoshenko nanobeams with a nonlinear thermal distribution. Shafiei et al. [44] focused on analyzing the flapwise bending vibration behavior of a rotary tapered FG nanobeam within a thermal environment. Shafiei et al. [45] investigated the vibration behavior of a rotary tapered axially FG Timoshenko nanobeam when exposed to a thermal environment. Fang et al. [46] focused on conducting a comprehensive analysis of the vibration and thermal buckling behavior of rotating nonlocal FG nanobeams within a thermal environment. Lal and Dangi [47] investigated the thermal vibration behavior of a temperature-dependent FG non-uniform Timoshenko nanobeam using the framework of nonlocal elasticity theory. Hosseini et al. [48] investigated the influence of temperature changes (thermal effect) on the forced vibration behavior of FG nanobeam subjected to moving load. Bendalda et al. [49] investigated the dynamic properties of nonlocal temperature dependent FG nanobeams under various thermal environment. Gholipour and Ghayesh [50] investigated the forced coupled nonlinear mechanics of FG nanobeams subject to dynamic loads via developing a high-dimensional model. A geometric nonlinear Euler–Bernoulli theory is used to define the displacement distribution. To incorporate small-size influences a nonlocal strain gradient theory scheme, possessing two independent length scale characteristics, is employed. Eroğlu et al. [51] examined free vibration analysis and temperature-dependent buckling behavior of porous FG magneto-electro-thermo-elastic material consisting of cobalt ferrite and barium titanate. A high-order sinusoidal shear deformation theory was used to accurately model the anisotropic material behavior. Anh et al. [52] presented the nonlinear random vibration of FG nanobeams resting on a viscoelastic foundation using the nonlocal strain gradient theory and the regulated equivalent linearization method. The governing equation of motion for the FG nanobeam is derived by using Hamilton’s principle and then converted into an ordinary nonlinear differential equation by the Galerkin method.

The provided list of research works highlights a series of investigations conducted by various researchers on the vibration behavior of nanobeams, particularly considering the effects of nonlocality, temperature changes, magnetic fields, and other factors. Karlićić et al. [53] focused on exploring how the vibration behavior of a cracked nanobeam embedded in an elastic medium influenced by both thermal and magnetic effects. Mohammadi et al. [54] investigated the hygro-mechanical vibration behavior of a rotating viscoelastic nanobeam embedded in a visco-Pasternak elastic medium, while considering the nonlinear thermal effects. Sari [55] focused on examining the superharmonic resonance behavior of a nonlocal nanobeam exposed to axial thermal and magnetic forces while being supported by a nonlinear elastic foundation. Togun and Bağdatlı [56] employed non-local Euler–Bernoulli beam theory on the nonlinear free and forced vibration analysis of a nanobeam resting on an elastic foundation of the Pasternak type. Togun [57] focused on the development and application of a nonlocal beam theory to analyze the nonlinear vibrations of a nanobeam that is supported by an elastic foundation. Ghadiri et al. [58] examined the vibration behavior of a rotating nanocantilever beam while taking into consideration of thermal effects. Gahidiri et al. [59] investigated how both thermal effects and surface effects impact the vibration behavior of a rotating Timoshenko nanobeam within the framework of nonlocal elasticity theory. Ghadiri et al. [60] investigated the non-linear forced vibration behavior of nanobeams subjected to a moving concentrated load while resting on a viscoelastic foundation by considering the combined influences of thermal and surface effects. Shafiei et al. [61] analyzed the nonlinear vibration behavior of a rotating nanobeam under thermal stress by employing Eringen's nonlocal elasticity theory in combination with the differential quadrature method. Demir and Civalek [62] analyzed the thermal vibration behavior of nanobeams embedded within an elastic matrix using a combination of nonlocal finite element method and specialized Hermitian cubic shape functions. Abdullah et al. [63] investigated nonlinear vibration of nanobeams embedded in the linear and nonlinear elastic materials under magnetic and temperature effect. Yapanmış et al. [64] investigated the impact of a magnetic field on the nonlinear vibrations of a nonlocal nanobeam that is embedded in a nonlinear elastic foundation. Numanoğlu et al. [65] introduced a novel approach for solving the eigenvalue problem associated with thermo-mechanical vibration of Timoshenko nanobeams. Rahmani et al. [66] applied Eringen's nonlocal elasticity theory and the modified couple stress theory to analyze the vibration behavior of rotating nanobeams with the consideration of temperature effects. Rahmani et al. [67] investigated the wave propagation characteristics of rotating viscoelastic nanobeams in the presence of temperature effects. The analysis is conducted using a modified couple stress-based nonlocal Eringen's theory. Ahmad et al.[68] investigated vibration analysis of nanobeams subjected to gradient type heating due to a static magnetic field via nonlocal elasticity theory. Shakhlavi et al. [69] focused on exploring how the size-dependent nonlinear axial vibrations of nanorods influenced by magnetic fields, a nonlinear elastic medium, and thermal stress effects. Karmakar and Chakraverty [70] investigated the thermal vibration behavior of a non-homogenous Euler nanobeam that is resting on a Winkler foundation. Sobamowo [71] focused on exploring the size-dependent nonlinear vibration behavior of a nanobeam embedded in a multi-layer elastic medium and subjected to electromechanical and thermomagnetic loadings. Khaniki et al. [72] presented the current stage of the research on electrically actuated NEMS/MEMS by analyzing the latest models and studies in this field in the framework of electro-mechanical coupling and small-size effects.

While numerous articles have explored the impacts of various external factors on the nonlocal mechanical analysis of micro/nanostructures, the influence of thermal environmental factors on small-scale beams remains unexplored within the context of nonlocal elasticity and multiple scale method for Euler–Bernoulli beam theory. Abdullah et al. [63] applied He’s variational principle to investigate the nonlinear vibration of nanobeams embedded in both linear and nonlinear elastic materials, considering magnetic and temperature effects, as well as other factors such as the nonlocal parameter and different types of elastic media. The variations in research objectives and methodologies between these studies are different, and they collectively contribute to the understanding of nanobeam vibration phenomena from different perspectives, affirming the validity and reliability of the proposed approach in the present study. In light of this motivation, the study's methodology, which employs a perturbation method, enables the examination of nonlocal nanobeams nonlinear vibration under the influence of temperature, nonlinear foundation parameters, and boundary conditions. In summary, this study contributes novel insights into the vibration behavior of nanobeams in a thermal environment, considering multiple influential parameters and employing advanced analytical techniques, thereby enhancing our understanding of the dynamic characteristics of these structures. In this context, this research aims to investigate the vibration analysis of a nanobeam resting on a nonlinear elastic foundation in a thermal environment using nonlocal elasticity theory. By considering both the nonlocal effects inherent to nanoscale phenomena and the intricate foundation interactions, this study seeks to provide a deeper insight into the dynamic behavior of nanobeams. The outcomes of this investigation hold the potential to enhance the design and optimization of nanoscale devices, ultimately contributing to the advancement of cutting-edge technologies.

Section 2 provides a comprehensive review of relevant literature, highlighting the key advancements and gaps in the current understanding of nanobeam behavior in thermal environments.The remainder of this article is structured as follows: Sect. 2 presents the mathematical formulation of the problem, introducing the nonlocal elasticity theory, the nonlinear foundation model and the thermal effects. Section 3 details the perturbation method to analyze the nanobeam vibrations. The results and discussions are presented in Sect. 4, followed by conclusions and potential avenues for future research in Sect. 5.

2 Nonlocal elasticity theory

2.1 Description

The stress state at a place inside a body is treated as a function of strains at all points in the neighboring areas, according to the Eringen nonlocal elasticity model [13, 14]. The nonlocal stress-tensor components ij at each position x in a homogeneous elastic solid can be expressed as

$${{\varvec{\upsigma}}}_{\mathbf{i}\mathbf{j}}\left(\mathbf{x}\right)={\int }_{{\varvec{\Omega}}}{\varvec{\upalpha}}\left(\mathbf{x},{\mathbf{x}}^{\mathbf{^{\prime}}}\right){{\varvec{\uptau}}}_{\mathbf{i}\mathbf{j}}{\mathbf{x}}^{\mathbf{^{\prime}}}\mathbf{d}\mathbf{v}$$
(1)

where \({{\varvec{\uptau}}}_{\mathbf{i}\mathbf{j}}(\mathbf{x})\) the component of the local stress tensor available at position x that is connected with the strain tensor components \({{\varvec{\upvarepsilon}}}_{\mathbf{i}\mathbf{j}}\) as:

$${{\varvec{\upvarepsilon}}}_{\mathbf{i}\mathbf{j}}=\frac{1}{2}\left({\mathbf{u}}_{\mathbf{i},\mathbf{j}}+{\mathbf{u}}_{\mathbf{j},\mathbf{i}}\right)$$
(2)

where \({{\varvec{\upsigma}}}_{\mathbf{i}\mathbf{j}}\) and \({{\varvec{\upvarepsilon}}}_{\mathbf{i}\mathbf{j}}\) are the nonlocal stress and strain tensors, respectively; \({{\varvec{\uptau}}}_{\mathbf{i}\mathbf{j}}\) is the classical stress tensor, \(\left(\mathbf{x},{\mathbf{x}}^{\mathbf{^{\prime}}}\right)\) is the kernel function representing the effect of strains at different locations x′ on the stress at a given position x, and V is the total body considered. We can see from the above equation that not only does the strain state at x have an effect on the stress, but the strain state at x′ can also have an effect on the stress state at x [13, 14]. Because it is difficult to apply constitutive relations with integral forms, partial differential expressions are applied, which is expressed as follows

$$\left[1-{{(\mathbf{e}}_{\mathbf{o}}\mathbf{a})}^{2}{\nabla }^{2}\right]{\varvec{\upsigma}}={\mathbf{C}}_{\mathbf{O}}:{\varvec{\upvarepsilon}}$$
(3)

where \({\mathbf{e}}_{\mathbf{o}}\) is the constant and \(\mathbf{a}\) is the internal characteristic length, \({\nabla }^{2}\) is the Laplacian operator, \({\varvec{\upvarepsilon}}\) is the strain vector, and \({\mathbf{C}}_{\mathbf{O}}\) is the elastic stiffness matrix of classical elasticity. It should be noted that \({\mathbf{e}}_{\mathbf{o}}\mathbf{a}\) is a scale coefficient that represents the effect of tiny scale on nanostructure mechanical characteristics [13, 14].

The Hook’s law for the nonlocal continuum theory can be described as the following one-dimensional form where E indicates elasticity modulus

$${{{{\varvec{\upsigma}}}_{\mathbf{x}}-(\mathbf{e}}_{\mathbf{o}}\mathbf{a})}^{2}\frac{{\partial }^{2}{{\varvec{\upsigma}}}_{\mathbf{x}}}{{\partial \mathbf{x}}^{2}}=\mathbf{E}{{\varvec{\upvarepsilon}}}_{\mathbf{x}}$$
(4)

2.2 Equation of motion and boundary conditions

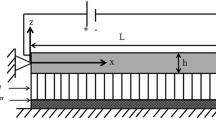
The presented study involves a nanobeam resting on a nonlinear elastic foundation in thermal environment with different boundary conditions. The nanobeam is schematically shown in Fig. 1 with two different boundary conditions: simply supported and clamped–clamped. The nanobeam has a length denoted as “L”. Its cross-section has dimensions”b” (width) and “h” (height). The nanobeam rests on a nonlinear elastic foundation. The elastic foundation comprises three layers: Winkler elastic layer, Pasternak elastic layer and nonlinear elastic layer.

$${\mathbf{u}}_{\left(\mathbf{x}\right)}\left(\mathbf{x},\mathbf{z},\mathbf{t}\right)=\mathbf{u}\left(\mathbf{x},\mathbf{t}\right)-\mathbf{z}\frac{\partial \mathbf{w}}{\partial \mathbf{x}}, \, {\mathbf{u}}_{\left(\mathbf{y}\right)}=0, \, {\mathbf{u}}_{\left(\mathbf{z}\right)}\left(\mathbf{x},\mathbf{z},\mathbf{t}\right)=\mathbf{w}\left(\mathbf{x},\mathbf{t}\right)$$
(5)

where t denotes time and u and w denote the axial and transverse displacements along the x and z axes, respectively. In the context of large amplitude nonlinear vibration and considering the von Kármán nonlinear strain, the strain–displacement relationship is typically given by a higher-order expression that takes into account the nonlinear terms. The von Kármán strain is a geometrically nonlinear strain–displacement relationship commonly used in the theory of shells and plates. If the longitudinal displacement is considered very small compared with the transverse displacement, the strain expression will take the following form. It considers the large deformations and rotations that occur in thin structures.

$${{\varvec{\upvarepsilon}}}_{\mathbf{x}\mathbf{x}}=\frac{\partial \mathbf{u}}{\partial \mathbf{x}}+\frac{1}{2}{\left(\frac{\partial \mathbf{w}}{\partial \mathbf{x}}\right)}^{2}, \, {{\varvec{\upvarepsilon}}}_{\mathbf{b}}=-\mathbf{z}{\varvec{\upkappa}}, \, {\varvec{\upkappa}}=\frac{{\partial }^{2}\mathbf{w}}{\partial {\mathbf{x}}^{2}}$$
(6)

where, \({{\varvec{\upvarepsilon}}}_{\mathbf{x}\mathbf{x}}\) represents the nonlinear extensional strain and \({\varvec{\upkappa}}\) represents the bending strain. The strain–displacement relationship for von Kármán nonlinear strain (i.e. \({{\varvec{\upvarepsilon}}}_{\mathbf{non-Strain}})\) can be expressed as follows:

Fig. 1
figure 1

Boundary conditions of Euler–Bernoulli nonlocal nanobeam subjected to thermal environment a Simply supported b Clamped–Clamped

Full size image
$${{{\varvec{\upvarepsilon}}}_{\mathbf{non-Strain}}={{\varvec{\upvarepsilon}}}_{\mathbf{x}\mathbf{x}}+{{\varvec{\upvarepsilon}}}_{\mathbf{b}}=\left(\frac{\partial \mathbf{u}}{\partial \mathbf{x}}\right)+\frac{1}{2}\left(\frac{\partial \mathbf{w}}{\partial \mathbf{x}}\right)}^{2}+\frac{{\partial }^{2}\mathbf{w}}{{\partial \mathbf{x}}^{2}}$$
(7)

The axial force and resultant bending moment of the beam model given as follows:

$$\mathbf{N}={\int }_{\mathbf{A}}{{\varvec{\upsigma}}}_{\mathbf{x}}\mathbf{d}\mathbf{A}, \, \mathbf{M}={\int }_{\mathbf{A}}\mathbf{z}{{\varvec{\upsigma}}}_{\mathbf{x}}\mathbf{d}\mathbf{A}$$
(8)

The force-strain and moment-strain relation of the non-local beam theory is obtained from Eqs. (4)–(8) as follows:

$$\mathbf{N}-{{(\mathbf{e}}_{\mathbf{o}}\mathbf{a})}^{2}\frac{{\partial }^{2}\mathbf{N}}{\partial {\mathbf{x}}^{2}}=\mathbf{E}\mathbf{A}\left[{\frac{\partial \mathbf{u}}{\partial \mathbf{x}}+\frac{1}{2}\left(\frac{\partial \mathbf{w}}{\partial \mathbf{x}}\right)}^{2}\right]$$
(9)
$$\mathbf{M}-{{(\mathbf{e}}_{\mathbf{o}}\mathbf{a})}^{2}\frac{{\partial }^{2}\mathbf{M}}{\partial {\mathbf{x}}^{2}}=-\mathbf{E}\mathbf{I}\frac{{\partial }^{2}\mathbf{w}}{{\partial \mathbf{x}}^{2}}$$
(10)

where, u is the axial displacement of the beam and w is the transverse displacement of the beam section between supports, \(\mathbf{E}\mathbf{A}\) is longitudinal rigidity and \(\mathbf{E}\mathbf{I}\) is flexural rigidity. Hamilton's principle can be written from following formula:

$${\varvec{\updelta}}{\int }_{\mathbf{t}1}^{\mathbf{t}2}[\mathbf{T}-(\mathbf{U}-\mathbf{W})\mathbf{d}\mathbf{t}=0$$
(11)

where U, T and W are strain energy, kinetic energy and work done by external loads, respectively, and they are expressed as follows:

$$\mathbf{U}=\frac{1}{2}{\int }_{0}^{\mathbf{L}}\left\{\mathbf{N}\left[{\frac{\partial \mathbf{u}}{\partial \mathbf{x}}+\frac{1}{2}\left(\frac{\partial \mathbf{w}}{\partial \mathbf{x}}\right)}^{2}\right]-\mathbf{M}\frac{{\partial }^{2}\mathbf{w}}{{\partial \mathbf{x}}^{2}}\right\}\mathbf{d}\mathbf{x}$$
(12)
$$\mathbf{T}=\frac{1}{2}{\varvec{\uprho}}\mathbf{A}{\int }_{0}^{\mathbf{L}}\left[{{\left(\frac{\partial \mathbf{u}}{\partial \mathbf{t}}\right)}^{2}+\left(\frac{\partial \mathbf{w}}{\partial \mathbf{t}}\right)}^{2}\right]\mathbf{d}\mathbf{x}$$
(13)
$$\mathbf{W}=\int\limits_{0}^{\mathbf{L}}\mathbf{fwdx}+\frac{1}{2}\int\limits_{0}^{\mathbf{L}}{\mathbf{N}}_{\mathbf{temp}}{\left(\frac{\partial \mathbf{w}}{\partial \mathbf{x}}\right)}^{2}\mathbf{dx}$$
(14)

where \({\varvec{\uprho}}\mathbf{A}\) is the mass per unit length, L is the length of the beam, t is the time, f is the external load from the nonlinear elastic foundation and Ntemp is the applied thermal load originating from temperature change and written as follows:

$$\mathbf{f}=-\left[{\mathbf{k}}_{\mathbf{w}}\mathbf{w}-{\mathbf{k}}_{\mathbf{p}}\frac{{\partial }^{2}\mathbf{w}}{\partial {\mathbf{x}}^{2}}+{\mathbf{k}}_{\mathbf{n}\mathbf{l}}{\mathbf{w}}^{3}\right]$$
(15)
$${\mathbf{N}}_{\mathbf{temp}}=\frac{\mathbf{E}\mathbf{A}{\varvec{\upalpha}}{\varvec{\Delta}}\mathbf{T}{\mathbf{L}}^{2}}{\mathbf{E}\mathbf{I}\left(1-2\mathbf{v}\right)}$$
(16)

where ΔT, α and υ are the temperature change, the coefficient of thermal expansion in the direction of the x-axis and the Poisson’s ratio, respectively. Substituting Eqs. (12)–(16) into Eq. (11) and integrating by parts, and collecting the coefficients of \({\varvec{\updelta}}\mathbf{u}\) and \({\varvec{\updelta}}\mathbf{w}\), the following equation of motion are obtained

$$\frac{\partial \mathbf{N}}{\partial \mathbf{x}}={\varvec{\uprho}}\mathbf{A}\frac{{\partial }^{2}\mathbf{u}}{\partial {\mathbf{t}}^{2}}$$
(17)
$$\frac{{\partial }^{2}\mathbf{M}}{\partial {\mathbf{x}}^{2}}+\mathbf{N}\frac{{\partial }^{2}\mathbf{w}}{\partial {\mathbf{x}}^{2}}+{\mathbf{k}}_{\mathbf{w}}\mathbf{w}-{\mathbf{k}}_{\mathbf{p}}\frac{{\partial }^{2}\mathbf{w}}{\partial {\mathbf{x}}^{2}}+{\mathbf{k}}_{\mathbf{n}\mathbf{l}}{\mathbf{w}}^{3}+{\mathbf{N}}_{\mathbf{t}\mathbf{e}\mathbf{m}\mathbf{p}}\frac{{\partial }^{2}\mathbf{w}}{\partial {\mathbf{x}}^{2}}={\varvec{\uprho}}\mathbf{A}\frac{{\partial }^{2}\mathbf{w}}{\partial {\mathbf{t}}^{2}}$$
(18)

Substituting Eq. (18) into Eq. (10), one obtains the expressions of the nonlocal force N and nonlocal moment M as follows:

$$\mathbf{N}=\mathbf{E}\mathbf{A}\left[{\frac{\partial \mathbf{u}}{\partial \mathbf{x}}+\frac{1}{2}\left(\frac{\partial \mathbf{w}}{\partial \mathbf{x}}\right)}^{2}\right]+{{(\mathbf{e}}_{\mathbf{o}}\mathbf{a})}^{2}\frac{{\partial }^{3}\mathbf{u}}{{\partial \mathbf{x}\partial \mathbf{t}}^{2}}$$
(19)
$$\mathbf{M}=-\mathbf{E}\mathbf{I}\frac{{\partial }^{2}\mathbf{w}}{{\partial \mathbf{x}}^{2}}+{{(\mathbf{e}}_{\mathbf{o}}\mathbf{a})}^{2}\left[{\varvec{\uprho}}\mathbf{A}\frac{{\partial }^{2}\mathbf{w}}{{\partial \mathbf{x}}^{2}}-\mathbf{N}\frac{{\partial }^{2}\mathbf{w}}{{\partial \mathbf{x}}^{2}}-{\mathbf{k}}_{\mathbf{w}}\mathbf{w}+{\mathbf{k}}_{\mathbf{p}}\frac{{\partial }^{2}\mathbf{w}}{{\partial \mathbf{x}}^{2}}-{\mathbf{k}}_{\mathbf{n}\mathbf{l}}{\mathbf{w}}^{3}-{\mathbf{N}}_{\mathbf{temp}}\frac{{\partial }^{2}\mathbf{w}}{{\partial \mathbf{x}}^{2}}\right]$$
(20)

It is observed from the Eq. (19) that the equations of motion of the nanobeam involves the displacements of u and w. In order to obtain a single equation in terms of w under the mentioned assumptions of neglecting in-plane inertia [73, 74]. Based on these assumptions, by applying the boundary conditions related to axial motion u(0, t) = u(L, t) = 0.The longitudinal inertia \(\frac{{\partial }^{2}\mathbf{u}}{\partial {\mathbf{t}}^{2}}\) can be neglected based on the discussion about the nonlinear vibration of continuous systems [75, 76], then the axial normal force N can be represented as:

$$\mathbf{N}=\frac{\mathbf{E}\mathbf{A}}{2\mathbf{L}}{\int }_{0}^{\mathbf{L}}{\left(\frac{\partial \mathbf{w}}{\partial \mathbf{x}}\right)}^{2}\mathbf{d}\mathbf{x}$$
(21)

The governing equations of motion and boundary conditions of the Euler–Bernoulli nanobeam model are derived by substituting Eqs. (19)–(21) into Eqs. (17) and (18) as follows:

$$ \begin{aligned} & {\text{EI}}\frac{{\partial ^{4} {\text{w}}}}{{\partial {\text{x}}^{4} }} + \rho {\text{A}}\frac{{\partial ^{2} }}{{\partial {\text{t}}^{2} }}\left( {{\text{w}} - \left( {{\text{e}}_{0} {\text{a}}} \right)^{2} \frac{{\partial ^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }}} \right) + \frac{{{\text{EA}}\alpha \Delta {\text{T}}}}{{1 - 2\varepsilon }}\frac{{\partial ^{2} }}{{\partial {\text{x}}^{2} }}\left( {{\text{w}} - \left( {{\text{e}}_{0} {\text{a}}} \right)^{2} \frac{{\partial ^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }}} \right) + {\text{k}}_{{\text{w}}} \left( {{\text{w}} - \left( {{\text{e}}_{0} {\text{a}}} \right)^{2} \frac{{\partial ^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }}} \right) \\ & \qquad - {\text{k}}_{{\text{p}}} \frac{{\partial ^{2} }}{{\partial {\text{x}}^{2} }}\left( {{\text{w}} - \left( {{\text{e}}_{0} {\text{a}}} \right)^{2} \frac{{\partial ^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }}} \right) + {\text{k}}_{{{\text{nl}}}} \left( {{\text{w}}^{3} - 3\left( {{\text{e}}_{0} {\text{a}}} \right)^{2} \left( {2{\text{w}}\left( {\frac{{\partial {\text{w}}}}{{\partial {\text{x}}}}} \right)^{2} + {\text{w}}^{2} \frac{{\partial ^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }}} \right)} \right) \\ & \quad= \frac{{{\text{EA}}}}{{2{\text{L}}}}\left[ {\mathop {\mathop \smallint \limits^{{\text{L}}} }\limits_{0} \left( {\frac{{\partial {\text{w}}}}{{\partial {\text{x}}}}} \right)^{2} {\text{dx}}} \right]\frac{{\partial ^{2} }}{{\partial {\text{x}}^{2} }}\left( {{\text{w}} - \left( {{\text{e}}_{0} {\text{a}}} \right)^{2} \frac{{\partial ^{2} {\text{w}}}}{{\partial {\text{x}}^{2} }}} \right) \\ \end{aligned} $$
(22)

Equation (22) represents the dimensional equations. The following non-dimensional quantities aims to study problem under general form are considered:

$$\overline{\mathbf{x} }=\frac{\mathbf{x}}{\mathbf{L}}, \, \overline{\mathbf{w} }=\frac{\mathbf{w}}{\mathbf{L}}, \, {\varvec{\upgamma}}=\frac{{\mathbf{e}}_{0}\mathbf{a}}{\mathbf{L}}, \, \overline{\mathbf{t} }=\frac{\mathbf{t}}{{\mathbf{L}}^{2}}\sqrt{\frac{\mathbf{E}\mathbf{I}}{{\varvec{\uprho}}\mathbf{A}}}, \, {\mathbf{K}}_{\mathbf{P}}=\frac{{{\mathbf{k}}_{\mathbf{p}}}^{\mathbf{*}}{\mathbf{L}}^{2}}{\mathbf{E}\mathbf{I}},$$
$${\mathbf{K}}_{\mathbf{w}}=\frac{{{\mathbf{k}}_{\mathbf{w}}}^{\mathbf{*}}{\mathbf{L}}^{4}}{\mathbf{E}\mathbf{I}}{, \, {\mathbf{K}}_{\mathbf{N}\mathbf{L}}=\frac{{{\mathbf{k}}_{\mathbf{n}\mathbf{l}}}^{\mathbf{*}}{\mathbf{L}}^{4}{\mathbf{r}}^{2}}{\mathbf{E}\mathbf{I}}, \, \mathbf{N}}_{\mathbf{t}}=\frac{{\varvec{\upalpha}}\mathbf{A}\left({\varvec{\Delta}}\mathbf{T}\right){\mathbf{L}}^{2}}{\mathbf{I}}, \, \mathbf{A}=\mathbf{b}\mathbf{h}, \, \mathbf{I}=\frac{1}{12}\mathbf{b}{\mathbf{h}}^{3}$$
(23)

where \(\mathbf{r}=\sqrt{\frac{\mathbf{I}}{\mathbf{A}}}\) is the radius of gyration of the cross-section.

Substituting dimensionless parameters into Eq. (22), then the dimensionless form of the equation becomes as follows:

$$\begin{aligned}\frac{{\partial }^{4}\overline{\mathbf{w}} }{\partial {\overline{\mathbf{x}} }^{4}}&+\frac{{\partial }^{2}}{\partial {\overline{\mathbf{t}} }^{2}}\left(\overline{\mathbf{w} }-{{\varvec{\upgamma}}}^{2}\frac{{\partial }^{2}\overline{\mathbf{w}} }{\partial {\overline{\mathbf{x}} }^{2}}\right)+{\mathbf{N}}_{\mathbf{t}}\frac{{\partial }^{2}}{\partial {\overline{\mathbf{x}} }^{2}}\left(\overline{\mathbf{w} }-{{\varvec{\upgamma}}}^{2}\frac{{\partial }^{2}\overline{\mathbf{w}} }{\partial {\overline{\mathbf{x}} }^{2}}\right)+{\mathbf{K}}_{\mathbf{w}}\left(\overline{\mathbf{w} }-{{\varvec{\upgamma}}}^{2}\frac{{\partial }^{2}\overline{\mathbf{w}} }{\partial {\overline{\mathbf{x}} }^{2}}\right)-{\mathbf{K}}_{\mathbf{p}}\frac{{\partial }^{2}}{\partial {\overline{\mathbf{x}} }^{2}}\left(\overline{\mathbf{w} }-{{\varvec{\upgamma}}}^{2}\frac{{\partial }^{2}\overline{\mathbf{w}} }{\partial {\overline{\mathbf{x}} }^{2}}\right)\\ &+{\mathbf{K}}_{\mathbf{N}\mathbf{L}}\left({\overline{\mathbf{w}} }^{3}-3{{\varvec{\upgamma}}}^{2}\left(2\overline{\mathbf{w} }{\left(\frac{\partial \overline{\mathbf{w}} }{\partial \overline{\mathbf{x}} }\right)}^{2}+{\overline{\mathbf{w}} }^{2}\frac{{\partial }^{2}\overline{\mathbf{w}} }{\partial {\overline{\mathbf{x}} }^{2}}\right)\right)=\frac{1}{2}\left[\int\limits_{0}^{1}{\left(\frac{\partial \overline{\mathbf{w}} }{\partial \overline{\mathbf{x}} }\right)}^{2}\mathbf{d}\overline{\mathbf{x} }\right]\frac{{\partial }^{2}}{\partial {\overline{\mathbf{x}} }^{2}}\left(\overline{\mathbf{w} }-{{\varvec{\upgamma}}}^{2}\frac{{\partial }^{2}\overline{\mathbf{w}} }{\partial {\overline{\mathbf{x}} }^{2}}\right)\end{aligned}$$
(24)

The non-dimensional form of boundary conditions can be expressed

$$ \begin{array}{*{20}l} {{\text{S}} - {\text{S case}}} \hfill & {\quad {\text{C}} - {\text{C case}}} \hfill \\ {\bar{\text{w}}\left( 0 \right) = 0\quad \quad \bar{\text{w}}\left( 1 \right) = 0} \hfill & {\quad \bar{\text{w}}\left( 0 \right) = 0\quad \quad \bar{\text{w}}\left( 1 \right) = 0} \hfill \\ {\bar{\text{w}}^{{''}} \left( 0 \right) = 0\quad \quad \bar{\text{w}}^{{''}} \left( 1 \right) = 0} \hfill & {\quad \bar{\text{w}}^{'} \left( 0 \right) = 0\quad \quad \bar{\text{w}}^{'} \left( 1 \right) = 0} \hfill \\ \end{array} $$
(25)

3 Perturbation analysis

The direct application of multiscale methods will be used to compute the approximate solution of the mathematical model, rather than employing perturbation methods [75, 76]. Applying multiscale methods directly to integro-differential equations is more advantageous compared to the application of discretization perturbation methods [77,78,79]. The multiple scale method is being discussed as an approach to solving partial differential equations with associated boundary conditions. Specifically, the focus is on applying multiple scale method to the problem outlined in Ref. [75, 76]. Additionally, the introduction of forcing and damping terms in Eq. (24) is mentioned as a means to derive a nonlinear exact solution.

$$\begin{aligned}\frac{{\partial }^{4}\overline{\mathbf{w}} }{\partial {\overline{\mathbf{x}} }^{4}}&+\frac{{\partial }^{2}}{\partial {\overline{\mathbf{t}} }^{2}}\left(\overline{\mathbf{w} }-{{\varvec{\upgamma}}}^{2}\frac{{\partial }^{2}\overline{\mathbf{w}} }{\partial {\overline{\mathbf{x}} }^{2}}\right)+{\mathbf{N}}_{\mathbf{t}}\frac{{\partial }^{2}}{\partial {\overline{\mathbf{x}} }^{2}}\left(\overline{\mathbf{w} }-{{\varvec{\upgamma}}}^{2}\frac{{\partial }^{2}\overline{\mathbf{w}} }{\partial {\overline{\mathbf{x}} }^{2}}\right)+{\mathbf{K}}_{\mathbf{w}}\left(\overline{\mathbf{w} }-{{\varvec{\upgamma}}}^{2}\frac{{\partial }^{2}\overline{\mathbf{w}} }{\partial {\overline{\mathbf{x}} }^{2}}\right)-{\mathbf{K}}_{\mathbf{p}}\frac{{\partial }^{2}}{\partial {\overline{\mathbf{x}} }^{2}}\left(\overline{\mathbf{w} }-{{\varvec{\upgamma}}}^{2}\frac{{\partial }^{2}\overline{\mathbf{w}} }{\partial {\overline{\mathbf{x}} }^{2}}\right)\\ & \quad+{\mathbf{K}}_{\mathbf{N}\mathbf{L}}\left({\overline{\mathbf{w}} }^{3}-3{{\varvec{\upgamma}}}^{2}\left(2\overline{\mathbf{w} }{\left(\frac{\partial \overline{\mathbf{w}} }{\partial \overline{\mathbf{x}} }\right)}^{2}+{\overline{\mathbf{w}} }^{2}\frac{{\partial }^{2}\overline{\mathbf{w}} }{\partial {\overline{\mathbf{x}} }^{2}}\right)\right)=\frac{1}{2}\left[\int\limits_{0}^{1}{\left(\frac{\partial \overline{\mathbf{w}} }{\partial \overline{\mathbf{x}} }\right)}^{2}\mathbf{d}\overline{\mathbf{x} }\right]\frac{{\partial }^{2}}{\partial {\overline{\mathbf{x}} }^{2}}\left(\overline{\mathbf{w} }-{{\varvec{\upgamma}}}^{2}\frac{{\partial }^{2}\overline{\mathbf{w}} }{\partial {\overline{\mathbf{x}} }^{2}}\right)\\&\quad+\overline{\mathbf{F}}\mathbf{c}\mathbf{o}\mathbf{s}{\varvec{\Omega} }\overline{\mathbf{t} }-2\overline{{\varvec{\upmu}} }\frac{\partial \overline{\mathbf{w}} }{\partial \overline{\mathbf{t}} }\end{aligned}$$
(26)

A transformation process is applied to incorporate stretching and damping effects into a weak nonlinear system, represented by the deflection w, at a certain order represented by ε, \(\overline{\mathbf{w} }=\sqrt{{\varvec{\upvarepsilon}}}\mathbf{y}\). The transformation aims to account for the interactions between stretching, damping, and nonlinearity in a multiscale context. This transformation is carried out following the principles of the multiple scale method.

$$\overline{\mathbf{F} }={\varvec{\upvarepsilon}}\sqrt{{\varvec{\upvarepsilon}}}\mathbf{F}, \, \overline{{\varvec{\upmu}} }={\varvec{\upvarepsilon}}{\varvec{\upmu}}$$
(27)

A straightforward asymptotic expansion has led to the absence of quadratic non-linearities in the problem being studied. This simplification can make the analysis more manageable and facilitate a clearer understanding of the system's behavior.

$$\mathbf{y}\left(\overline{\mathbf{x} },\overline{\mathbf{t} };{\varvec{\upvarepsilon}}\right)={{\varvec{\upvarepsilon}}}^{0}{\mathbf{y}}_{0}\left(\overline{\mathbf{x} },{\mathbf{T}}_{0};{\mathbf{T}}_{1}\right)+{\varvec{\upvarepsilon}}{\mathbf{y}}_{1}\left(\overline{\mathbf{x} },{\mathbf{T}}_{0};{\mathbf{T}}_{1}\right)$$
(28)

where ε is a small parameter representing deflections, indicating that the system’s behavior is being studied at a small scale. This allows for the investigation of a weakly non-linear system using the introduced approach. The method involves the introduction of new independent variables and consideration of fast and slow time scales given as follows:

$${\mathbf{T}}_{0}={{\varvec{\upvarepsilon}}}^{0}\overline{\mathbf{t} }=\overline{\mathbf{t} }{, \, \mathbf{T}}_{1}={{\varvec{\upvarepsilon}}}^{1}\overline{\mathbf{t} }$$

Thus, instead of determining w as a function of t, we determine w as a function of \({\mathbf{T}}_{0}\), \({\mathbf{T}}_{1}\), \({\mathbf{T}}_{2}\),…

$$\frac{\mathbf{d}}{\mathbf{d}\mathbf{t}}=\frac{\mathbf{d}{\mathbf{T}}_{0}}{\mathbf{d}\mathbf{t}}\frac{\partial }{\partial {\mathbf{T}}_{0}}+\frac{\mathbf{d}{\mathbf{T}}_{1}}{\mathbf{d}\mathbf{t}}\frac{\partial }{\partial {\mathbf{T}}_{1}}+\frac{{\mathbf{d}\mathbf{T}}_{2}}{\mathbf{d}\mathbf{t}}\frac{\partial }{\partial {\mathbf{T}}_{2}}+\dots $$
(29)
$$\frac{\mathbf{d}}{\mathbf{d}\mathbf{t}}={{\varvec{\upvarepsilon}}}^{0}{\mathbf{D}}_{0}+{{\varvec{\upvarepsilon}}}^{1}{\mathbf{D}}_{1}+\dots $$
(30)
$$\frac{{\mathbf{d}}^{2}}{{\mathbf{d}\mathbf{t}}^{2}}={{\varvec{\upvarepsilon}}}^{0}{{\mathbf{D}}_{0}}^{2}+2{\varvec{\upvarepsilon}}{\mathbf{D}}_{0}{\mathbf{D}}_{1}+{{\varvec{\upvarepsilon}}}^{2}{{\mathbf{D}}_{1}}^{2}\dots $$
(31)

which ε is a small dimensionless parameter and \({\mathbf{D}}_{\mathbf{n}}\) is the new differential operator, which is defined as

$${\mathbf{D}}_{\mathbf{n}}=\frac{\partial }{{\partial \mathbf{T}}_{\mathbf{n}}},\mathbf{n}=\mathrm{0,1},\mathrm{2,3},\dots $$
(32)

Inserting Eqs. (28)–(31) into Eq. (26), we can get the following relation for the equation of motion and boundary conditions at different orders,

Order (1):

$${{\mathbf{y}}_{0}}^{\mathbf{i}\mathbf{v}}+{{\mathbf{D}}_{0}}^{2}{\mathbf{y}}_{0}-{{\varvec{\upgamma}}}^{2}{{\mathbf{D}}_{0}}^{2}{{\mathbf{y}}_{0}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}+{\mathbf{N}}_{\mathbf{t}}\left({{\mathbf{y}}_{0}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}-{{\varvec{\upgamma}}}^{2}{{\mathbf{y}}_{0}}^{\mathbf{i}\mathbf{v}}\right)-{\mathbf{K}}_{\mathbf{p}}\left({{\mathbf{y}}_{0}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}-{{\varvec{\upgamma}}}^{2}{{\mathbf{y}}_{0}}^{\mathbf{i}\mathbf{v}}\right)+{\mathbf{K}}_{\mathbf{w}}\left({\mathbf{y}}_{0}-{{\varvec{\upgamma}}}^{2}{{\mathbf{y}}_{0}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}\right)=0$$
(33)

Order (ε):

$$\begin{aligned}{{\mathbf{y}}_{1}}^{\mathbf{i}\mathbf{v}}&+{{\mathbf{D}}_{0}}^{2}{\mathbf{y}}_{1}-{{\varvec{\upgamma}}}^{2}{{\mathbf{D}}_{0}}^{2}{{\mathbf{y}}_{1}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}+{\mathbf{N}}_{\mathbf{t}}\left({{\mathbf{y}}_{1}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}-{{\varvec{\upgamma}}}^{2}{{\mathbf{y}}_{1}}^{\mathbf{i}\mathbf{v}}\right)-{\mathbf{K}}_{\mathbf{p}}\left({{\mathbf{y}}_{1}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}-{{\varvec{\upgamma}}}^{2}{{\mathbf{y}}_{1}}^{\mathbf{i}\mathbf{v}}\right)+{\mathbf{K}}_{\mathbf{w}}\left({\mathbf{y}}_{1}-{{\varvec{\upgamma}}}^{2}{{\mathbf{y}}_{1}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}\right)=-2{\mathbf{D}}_{0}{\mathbf{D}}_{1}{\mathbf{y}}_{0}\\&+2{{\varvec{\upgamma}}}^{2}{\mathbf{D}}_{0}{\mathbf{D}}_{1}{{\mathbf{y}}_{0}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}+\frac{1}{2}{\int }_{0}^{1}\left[{{{\mathbf{y}}_{0}}^{\mathbf{^{\prime}}}}^{2}\mathbf{d}\mathbf{x}\right]\left[{{\mathbf{y}}_{0}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}-{{\varvec{\upgamma}}}^{2}{{\mathbf{y}}_{0}}^{\mathbf{i}\mathbf{v}}\right]-{\mathbf{K}}_{\mathbf{N}\mathbf{L}}({{\mathbf{y}}_{0}}^{3}-3{{\varvec{\upgamma}}}^{2}\left(2{\mathbf{y}}_{0}{{{\mathbf{y}}_{0}}^{\mathbf{^{\prime}}}}^{2}+{{\mathbf{y}}_{0}}^{2}{{\mathbf{y}}_{0}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}\right)\\&\quad+\mathbf{F}\mathbf{c}\mathbf{o}\mathbf{s}{\varvec{\Omega}}\mathbf{t}-2{\varvec{\upmu}}{\mathbf{D}}_{0}{\mathbf{y}}_{0}\end{aligned}$$
(34)

3.1 The linear problem

As seen above the first order of perturbation is linear given in Eq. (33). This section solves first-order equations to derive fundamental linear frequencies and mode shapes. The linear solution of the first order of perturbation is represented by

$${\mathbf{y}}_{0}\left(\overline{\mathbf{x} },{\mathbf{T}}_{0}{,\mathbf{T}}_{1}\right)=\left[\mathbf{A}{(\mathbf{T}}_{1}\right){\mathbf{e}}^{\mathbf{i}{\varvec{\upomega}}{\mathbf{T}}_{0}}+\mathbf{c}\mathbf{c}]\mathbf{Y}\left(\overline{\mathbf{x} }\right)$$
(35)

where cc, ω, A(\({\mathbf{T}}_{1}\)) represent to the complex conjugate, natural frequency, complex amplitude, respectively. Inserting Eq. (35) into Eq. (33), the following equation obtained as;

$$\left(1-{\mathbf{N}}_{\mathbf{t}}{{\varvec{\upgamma}}}^{2}+{\mathbf{K}}_{\mathbf{p}}{{\varvec{\upgamma}}}^{2}\right){\mathbf{Y}}^{\mathbf{i}\mathbf{v}}+({{\varvec{\upgamma}}}^{2}{{\varvec{\upomega}}}^{2}+{\mathbf{N}}_{\mathbf{t}}-{\mathbf{K}}_{\mathbf{p}}{-\mathbf{K}}_{\mathbf{w}}{{\varvec{\upgamma}}}^{2}{)\mathbf{Y}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}+({\mathbf{K}}_{\mathbf{w}}-{{\varvec{\upomega}}}^{2})\mathbf{Y}=0$$
(36)

Shape functions are mathematical functions that are used to describe the displacement or deformation of a structure, such as a beam, in terms of its coordinates or other relevant variables. These functions are essential for various numerical methods. For the solution of equation, the following shape function is written as

$$\mathbf{Y}\left(\mathbf{x}\right)={\mathbf{C}}_{1}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{1}\mathbf{x}}+{\mathbf{C}}_{2}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{2}\mathbf{x}}+{\mathbf{C}}_{3}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{3}\mathbf{x}}+{\mathbf{C}}_{4}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{4}\mathbf{x}}$$
(37)

The dispersion relation becomes

$$\left(1-{\mathbf{N}}_{\mathbf{t}}{{\varvec{\upgamma}}}^{2}+{\mathbf{K}}_{\mathbf{p}}{{\varvec{\upgamma}}}^{2}\right){(\mathbf{C}}_{1}{{{\varvec{\upbeta}}}_{1}}^{4}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{1}\mathbf{x}}+{\mathbf{C}}_{2}{{{\varvec{\upbeta}}}_{2}}^{4}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{2}\mathbf{x}}+{\mathbf{C}}_{3}{{{\varvec{\upbeta}}}_{3}}^{4}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{3}\mathbf{x}}+{\mathbf{C}}_{4}{{{\varvec{\upbeta}}}_{4}}^{4}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{4}\mathbf{x}})+\left({{\varvec{\upgamma}}}^{2}{{\varvec{\upomega}}}^{2}+{\mathbf{N}}_{\mathbf{t}}-{\mathbf{K}}_{\mathbf{p}}{-\mathbf{K}}_{\mathbf{w}}{{\varvec{\upgamma}}}^{2}\right)\left(-{\mathbf{C}}_{1}{{{\varvec{\upbeta}}}_{1}}^{2}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{1}\mathbf{x}}-{\mathbf{C}}_{2}{{{\varvec{\upbeta}}}_{2}}^{2}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{2}\mathbf{x}}-{\mathbf{C}}_{3}{{{\varvec{\upbeta}}}_{3}}^{2}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{3}\mathbf{x}}-{\mathbf{C}}_{4}{{{\varvec{\upbeta}}}_{4}}^{2}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{4}\mathbf{x}}\right)+\left({\mathbf{K}}_{\mathbf{w}}-{{\varvec{\upomega}}}^{2}\right)\left({\mathbf{C}}_{1}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{1}\mathbf{x}}+{\mathbf{C}}_{2}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{2}\mathbf{x}}+{\mathbf{C}}_{3}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{3}\mathbf{x}}+{\mathbf{C}}_{4}{\mathbf{e}}^{\mathbf{i}{{\varvec{\upbeta}}}_{4}\mathbf{x}}\right)=0$$
(38)
$$\left(1-{\mathbf{N}}_{\mathbf{t}}{{\varvec{\upgamma}}}^{2}+{\mathbf{K}}_{\mathbf{p}}{{\varvec{\upgamma}}}^{2}\right){{{\varvec{\upbeta}}}_{\mathbf{n}}}^{4}-\left({{\varvec{\upgamma}}}^{2}{{\varvec{\upomega}}}^{2}+{\mathbf{N}}_{\mathbf{t}}-{\mathbf{K}}_{\mathbf{p}}{-\mathbf{K}}_{\mathbf{w}}{{\varvec{\upgamma}}}^{2}\right){{{\varvec{\upbeta}}}_{\mathbf{n}}}^{2}+\left({\mathbf{K}}_{\mathbf{w}}-{{\varvec{\upomega}}}^{2}\right)=0$$
(39)

3.2 The non-linear problem

The secular and non-secular terms assuming a solution of the form are separated to find the solvability condition.

$${\mathbf{y}}_{1}\left(\mathbf{x},{\mathbf{T}}_{0}{,\mathbf{T}}_{1}\right)={\varvec{\upphi}}\left(\mathbf{x},{\mathbf{T}}_{1}\right){\mathbf{e}}^{\mathbf{i}{\varvec{\upomega}}{\mathbf{T}}_{0}}+\mathbf{c}\mathbf{c}+\mathbf{W}\left(\mathbf{x},{\mathbf{T}}_{0}{,\mathbf{T}}_{1}\right)$$
(40)

where cc is a complex conjugate. We know that for solvability condition we will use the order(ε) expansion which is given as

$$[\left(1-{\mathbf{N}}_{\mathbf{t}}{{\varvec{\upgamma}}}^{2}+{\mathbf{K}}_{\mathbf{p}}{{\varvec{\upgamma}}}^{2}\right){{\varvec{\upphi}}}^{\mathbf{i}\mathbf{v}}\left(\mathbf{x}\right)+{({\varvec{\upgamma}}}^{2}{{\varvec{\upomega}}}^{2}+{\mathbf{N}}_{\mathbf{t}}-{\mathbf{K}}_{\mathbf{p}}-{\mathbf{K}}_{\mathbf{w}}{{\varvec{\upgamma}}}^{2}){{\varvec{\upphi}}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}(\mathbf{x})+({\mathbf{K}}_{\mathbf{w}}-{{\varvec{\upomega}}}^{2}){\varvec{\upphi}}]=-2{\mathbf{i}{\varvec{\upomega}}\mathbf{Y}\left(\mathbf{x}\right)\mathbf{D}}_{1}\mathbf{A}+2{{\varvec{\upgamma}}}^{2}\mathbf{i}{\varvec{\upomega}}{\mathbf{Y}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}(\mathbf{x}){\mathbf{D}}_{1}\mathbf{A}+\frac{3{\mathbf{A}}^{2}\overline{\mathbf{A}}}{2}{\int }_{0}^{1}\left[{{\mathbf{Y}\left(\mathbf{x}\right)}^{\mathbf{^{\prime}}}}^{2}\mathbf{d}\mathbf{x}\right]\left[{\mathbf{Y}\left(\mathbf{x}\right)}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}-{{\varvec{\upgamma}}}^{2}{\mathbf{Y}\left(\mathbf{x}\right)}^{\mathbf{i}\mathbf{v}}\right]-{\mathbf{K}}_{\mathbf{N}\mathbf{L}}\left(3{\mathbf{A}}^{2}\overline{\mathbf{A}}{\mathbf{Y }\left(\mathbf{x}\right)}^{3}-3{{\varvec{\upgamma}}}^{2}\left(6{\mathbf{A}}^{2}\overline{\mathbf{A}}\mathbf{Y }\left(\mathbf{x}\right){{\mathbf{Y}}^{\mathbf{^{\prime}}}\left(\mathbf{x}\right)}^{2}+{\left(3{\mathbf{A}}^{2}\overline{\mathbf{A} }\right)\mathbf{Y}\left(\mathbf{x}\right)}^{2}{\mathbf{Y}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}\left(\mathbf{x}\right)\right)\right)+\frac{\mathbf{F}}{2}({\mathbf{e}}^{\mathbf{i}{\varvec{\Omega}}\mathbf{t}})-2{\varvec{\upmu}}\mathbf{i}{\varvec{\upomega}}\mathbf{A}\mathbf{Y}(\mathbf{x})+\mathbf{c}\mathbf{c}+\mathbf{N}\mathbf{S}\mathbf{T}$$
(41)

where \({\mathbf{D}}_{1}\mathbf{A}\) represents the derivative of a quantity A with respect to the variable \({\mathbf{T}}_{1}\). The term cc denotes the complex conjugate of prior terms. NST refers to non-secular terms. The analysis is focused on a primary resonance scenario. Primary resonance occurs when an external excitation frequency \({\varvec{\Omega}}\) is close to the natural frequency \({\varvec{\upomega}}\) of the system. In the case of a primary resonance, the detuning parameter is introduced. It is described in a specific mathematical form that relates the detuning parameter to the excitation frequency \({\varvec{\Omega}}\) and \({\varvec{\upomega}}\).

$${\varvec{\Omega}}={\varvec{\upomega}}+\upvarepsilon {\varvec{\upsigma}}$$
(42)

where \({\varvec{\upsigma}}\) is a detuning parameter, the solvability condition for Eqs. (41) and (42) is obtained as follows

$$2{\mathbf{i}{\varvec{\upomega}}(\mathbf{D}}_{1}\mathbf{A}+{\varvec{\upmu}}\mathbf{A})+2{{\varvec{\upgamma}}}^{2}\mathbf{i}{\varvec{\upomega}}{\mathbf{D}}_{1}\mathbf{A}{\mathbf{z}}_{1}+\frac{3{\mathbf{A}}^{2}\overline{\mathbf{A}}}{2 }\left({{\mathbf{z}}_{1}}^{2}+{{\varvec{\upgamma}}}^{2}{\mathbf{z}}_{1}{\mathbf{z}}_{2}\right)+{\mathbf{K}}_{\mathbf{N}\mathbf{L}}\left(3{\mathbf{A}}^{2}\overline{\mathbf{A} }\right){\mathbf{z}}_{3}-\frac{\mathbf{F}}{2}\left({\mathbf{e}}^{\mathbf{i}{\varvec{\Omega}}\mathbf{t}}\right)=0$$
(43)

where

$${\int }_{0}^{1}{\mathbf{Y}(\mathbf{x})}^{2}\mathbf{d}\mathbf{x}=1 \, {\int }_{0}^{1}{\mathbf{Y}}^{{\mathbf{^{\prime}}}^{2}}\mathbf{d}\mathbf{x}={\mathbf{z}}_{1} \, {\int }_{0}^{1}{\mathbf{Y}}^{{\mathbf{^{\prime}}\mathbf{^{\prime}}}^{2}}\mathbf{d}\mathbf{x}={\mathbf{z}}_{2} \, {\int }_{0}^{1}\mathbf{F}\mathbf{Y}\mathbf{d}\mathbf{x}=\mathbf{f}$$
(44)
$${\int }_{0}^{1}\mathbf{Y}{(\mathbf{x})}^{4}\mathbf{d}\mathbf{x}-3{{\varvec{\upgamma}}}^{2}\left(2{\int }_{0}^{1}{\mathbf{Y}}^{2}\left(\mathbf{x}\right){{\mathbf{Y}}^{\mathbf{^{\prime}}}\left(\mathbf{x}\right)}^{2}\mathbf{d}\mathbf{x}+{\int }_{0}^{1}{{\mathbf{Y}\left(\mathbf{x}\right)}^{3}\mathbf{Y}}^{\mathbf{^{\prime}}\mathbf{^{\prime}}}\left(\mathbf{x}\right)\mathbf{d}\mathbf{x}\right)={\mathbf{z}}_{3}$$
(45)

Here's the general form of a complex amplitude A can be expressed in terms of a real amplitude ɑ and phase θ:

$$\mathbf{A}=\frac{1}{2}\mathbf{a}\left({\mathbf{T}}_{1}\right){\mathbf{e}}^{\mathbf{i}{\varvec{\uptheta}}{\mathbf{T}}_{1}}$$
(46)

where \({\varvec{a}}\boldsymbol{ }\;\mathbf{a}\mathbf{n}\mathbf{d}\;{\varvec{\uptheta}}\) are defined as real-valued functions of \({\mathbf{T}}_{1}\), which represent the amplitude and the phase of the system’s response, respectively.

$${\varvec{\upomega}}\mathbf{a}{{\varvec{\uppsi}}}^{\mathbf{^{\prime}}}={\varvec{\upomega}}\mathbf{a}{\varvec{\upsigma}}+{{\varvec{\upomega}}\mathbf{a}{\varvec{\upgamma}}}^{2}{\varvec{\upsigma}}{\mathbf{z}}_{1}-{{\varvec{\upomega}}\mathbf{a}{\varvec{\upgamma}}}^{2}{{\varvec{\uppsi}}}^{\mathbf{^{\prime}}}{\mathbf{z}}_{1}-\frac{3}{16}{\mathbf{a}}^{3}\left({\mathbf{z}}_{1}^{2}+{{\varvec{\upgamma}}}^{2}{\mathbf{z}}_{1}{\mathbf{z}}_{2}\right)+\frac{3}{8}{\mathbf{a}}^{3}{\mathbf{K}}_{\mathbf{N}\mathbf{L}}{\mathbf{z}}_{3}+\frac{1}{2}\mathbf{f}\mathbf{c}\mathbf{o}\mathbf{s}{\varvec{\uppsi}}$$
$${\varvec{\upomega}}{\mathbf{a}}^{\mathbf{^{\prime}}}\left(1+{{\varvec{\upgamma}}}^{2}{\mathbf{z}}_{1}\right)+{\varvec{\upomega}}{\varvec{\upmu}}\mathbf{a}=\frac{1}{2}\mathbf{f}\mathbf{s}\mathbf{i}\mathbf{n}{\varvec{\uppsi}}$$
(47)

The equation involves a phase angle θ which is given by \({\varvec{\uptheta}}={\varvec{\upsigma}}{\mathbf{T}}_{1}-{\varvec{\uppsi}},\) where σ is a detuning parameter, T1 is a time period, and ψ likely represents another angle or phase. By analyzing the behavior of the system in steady-state conditions and explore the how the nonlinear amplitude changes or evolves over time.

For free and undamped vibrations values of \(\mathbf{f},{\varvec{\upmu}}\; {\mathbf{and}}\; {\varvec{\upsigma}}=0\)

$${{\varvec{\uptheta}}}^{\mathbf{^{\prime}}}=\frac{3{{\mathbf{a}}_{0}}^{2}\left({{\mathbf{z}}_{1}}^{2}+{{\varvec{\upgamma}}}^{2}{\mathbf{z}}_{1}{\mathbf{z}}_{2}\right)}{16{\varvec{\upomega}}\left(1+{{\varvec{\upgamma}}}^{2}{\mathbf{z}}_{1}\right)}+\frac{3{{\mathbf{a}}_{0}}^{2}{\mathbf{K}}_{\mathbf{N}\mathbf{L}}\left({\mathbf{z}}_{3}\right)}{8{\varvec{\upomega}}\left(1+{{\varvec{\upgamma}}}^{2}{\mathbf{z}}_{1}\right)}$$
(48)
$${{\varvec{\upomega}}}_{\mathbf{N}\mathbf{L}}={\varvec{\upomega}}+{{\varvec{\uptheta}}}^{\mathbf{^{\prime}}}$$
(49)
$${{\varvec{\upomega}}}_{\mathbf{N}\mathbf{L}}={\varvec{\upomega}}+\frac{3{{\mathbf{a}}_{0}}^{2}\left({{\mathbf{z}}_{1}}^{2}+{{\varvec{\upgamma}}}^{2}{\mathbf{z}}_{1}{\mathbf{z}}_{2}\right)}{16{\varvec{\upomega}}\left(1+{{\varvec{\upgamma}}}^{2}{\mathbf{z}}_{1}\right)}+\frac{3{{\mathbf{a}}_{0}}^{2}{\mathbf{K}}_{\mathbf{N}\mathbf{L}}\left({\mathbf{z}}_{3}\right)}{8{\varvec{\upomega}}\left(1+{{\varvec{\upgamma}}}^{2}{\mathbf{z}}_{1}\right)}$$
(50)
$${{\varvec{\upomega}}}_{\mathbf{N}\mathbf{L}}={\varvec{\upomega}}+{{\mathbf{a}}_{0}}^{2}{\varvec{\uplambda}}$$
(51)

where \({\varvec{\uplambda}}=\frac{3}{16{\varvec{\upomega}}\left(1+{{\varvec{\upgamma}}}^{2}{\mathbf{z}}_{1}\right)}\left[\left({{\mathbf{z}}_{1}}^{2}+{{\varvec{\upgamma}}}^{2}{\mathbf{z}}_{1}{\mathbf{z}}_{2}\right)+2{\mathbf{K}}_{\mathbf{N}\mathbf{L}}\left({\mathbf{z}}_{3}\right)\right]\)

For forced and damped vibration \({\mathbf{a}}^{\mathbf{^{\prime}}}={{\varvec{\uppsi}}}^{\mathbf{^{\prime}}}=0\)

$${\varvec{\upomega}}\mathbf{a}{\varvec{\upsigma}}\left(1+{{\varvec{\upgamma}}}^{2}{\mathbf{z}}_{1}\right)-\frac{3}{8}{\mathbf{a}}^{3}{\mathbf{K}}_{\mathbf{N}\mathbf{L}}{\mathbf{z}}_{3}-\frac{3{\mathbf{a}}^{3}}{16}\left({{\mathbf{z}}_{1}}^{2}+{{\varvec{\upgamma}}}^{2}{\mathbf{z}}_{1}{\mathbf{z}}_{2}\right)=\sqrt{\frac{{\mathbf{f}}^{2}}{4}-{{\varvec{\upmu}}}^{2}{{\varvec{\upomega}}}^{2}{\mathbf{a}}^{2}}$$
(52)

The solution then becomes

$${\varvec{\upsigma}}={\mathbf{a}}^{2}{\varvec{\uplambda}}\pm \frac{1}{\left(1+{{\varvec{\upgamma}}}^{2}{\mathbf{z}}_{1}\right)}\sqrt{\frac{{\mathbf{f}}^{2}}{{(4{\varvec{\upomega}}}^{2}{\mathbf{a}}^{2})}-{{\varvec{\upmu}}}^{2}}$$
(53)

4 Results and discussion

In this section, numerical results are provided in tabular form and are depicted graphically for simply supported and clamped–clamped boundary conditions. Linear natural frequencies are presented for these end conditions. After obtaining linear natural frequencies, nonlinear frequencies are calculated for the free and un-damped situation.

4.1 Simply supported nanobeam

The influence of nonlinear elastic foundation, temperature and nonlocal parameter are studied on the frequencies of simply supported nanobeam is presented in Table 1. The Winkler and Pasternak Parameters (Kw and Kp) and temperature(Nt) are crucial for calculating linear natural frequency values. In addition to these terms, it is seen that nonlinear elastic foundation parameter(KNL) is needed for the correction term. Damping (µ) 0.1 is selected for the simply supported nanobeam.

Table 1 The first three natural frequencies of a simply supported (S–S) nanobeam under various conditions which include different temperature, Winkler parameter, Pasternak parameter, nonlinear foundation and nonlocal parameter
Full size table

Table 1 presents linear natural frequencies for the first three modes of the nanobeam under different parameter variations, including nonlocal parameter (γ = eoa/L = 0, 0.1, 0.2, 0.3, 0.4 and 0.5), Winkler Parameter (kw = 10,100 and 200), Pasternak Parameter (kp = 5,50 and 100), low temperature (0 K,100 K and 200 K) and high temperature (200 K, 400 K and 600 K) values. Also, the material and geometric properties are selected as follows: the nanobeam has a rectangular cross-section with height and thickness both equal to h = t = 1 nm and width b = 2 h. The length of the nanobeam is L = 20 nm. Modulus of elasticity, Poisson’s ratio, mass of unit volume and thermal expansion coefficient are E = 30 GPa, υ = 0.3, ρ = 1 kg/m3 and \({\alpha }_{T}= -1.6\times 1{0}^{-6} \, {{\text{K}}}^{-1}\) for room and low temperatures and \({\alpha }_{T}= 1.1\times 1{0}^{-6} \, {{\text{K}}}^{-1}\) for high temperatures, respectively [65]. It is observed that linear natural frequency drops as the nonlocal parameter increase. Additionally, it is observed that linear natural frequencies rise with increase of Winkler and Pasternak Parameter due to the stiffness of the nanobeam. An increase in Kw and Kp influence on the natural frequency greatly causing the frequency to rise as shown in Table 1. The effect of temperature is also observed clearly. For low temperatures the frequency rises as temperature increases, whereas for high temperature the frequency drops as temperature increases.

In Table 2, nonlinear correction term for the first mode at different temperature and nonlocal parameter is obtained. The table shows the effect of nonlinear foundation(KNL) on the nonlinear correction term. Correction term decrease as temperatures increases for low temperature values. In contrary, correction term increases as temperature increases for high temperature values. Correction term rises as nonlocal parameter, Winkler parameter, Pasternak parameter and nonlinear foundation parameters increase for both high and low temperature values.

Table 2 The nonlinear correction term of the first mode S–S nanobeam with different ℽ, T, Kp and Kw values when Knl = 10,100 and 200
Full size table

Figures 2, 3, 4, 5, 6, 7 and 8 shows frequency response curves and nonlinear natural frequency change versus amplitude graphs. Figure 2 presents the changing of the nonlinear frequency with the amplitude for low temperature effect (0 K,100 K and 200 K) for the first mode. Figure 2 shows that with rising the amplitude, the nonlinear frequency increases. The rising of amplitude indicates an increase in axial stress as a result of large deflection resulting in a stiffer structure and greater nonlinear frequency. Moreover, as the temperature increases the nonlinear frequencies changes also increases. It also presents the frequency response curves for the first mode at different temperature values. It shows that as temperature values increase, the steady-state amplitude of the nanobeam for the first mode decreases.

Fig. 2
figure 2

a Frequency response curves of S–S nanobeams for different low temperature values T = 0 K,100 K and 200 K, the first mode (ℽ = 0.1, Knl = 10, Kp = 5 and Kw = 10) b Amplitude and nonlinear natural frequency change of S–S nanobeam for different low temperature values when h/l = 1, Knl = 10, Kp = 5 and Kw = 10

Full size image
Fig. 3
figure 3

a Frequency response curves of S–S nanobeams for different high temperature values T = 200 K,400 K and 600 K, the first mode (ℽ = 0.1, KNL = 10, Kp = 5 and Kw = 10) b Amplitude and nonlinear natural frequency change of S–S nanobeam for different high temperature values when ℽ = 0.1, KNL = 10, Kp = 5 and Kw = 10

Full size image
Fig. 4
figure 4

a Frequency response curves of S–S nanobeams for different Winkler parameter Kw = 10,100 and 200, the first mode (ℽ = 0.1, Knl = 10, Kp = 5 and T = 0 K) b Amplitude and nonlinear natural frequency change of S–S nanobeam for different Winkler parameter when ℽ = 0.1, KNL = 10, Kp = 5 and T = 0 K

Full size image
Fig. 5
figure 5

a Frequency response curves of S–S nanobeams for different Pasternak parameter Kp = 5,50 and 100, the first mode (ℽ = 0.1, Knl = 10, Kw = 10 and T = 0 K) b Amplitude and nonlinear natural frequency change of S–S nanobeam for different Pasternak parameter when ℽ = 0.1, Knl = 10, Kw = 10 and T = 0 K

Full size image
Fig. 6
figure 6

a Frequency response curves of S–S nanobeams for different nonlinear foundation parameter Knl = 10, 100 and 200, the first mode (ℽ = 0.1, Kp = 5, Kw = 10 and T = 0 K) b Amplitude and nonlinear natural frequency change of S–S nanobeam for different nonlinear foundation parameter, the first mode and ℽ = 0.1, Kp = 5, Kw = 10 and T = 0 K

Full size image
Fig. 7
figure 7

a Frequency response curves of S–S nanobeams for different nonlocal parameter ℽ = 0, 0.2 and 0.4, the first mode (Knl = 10, Kp = 5, Kw = 10 and T = 0 K) b Amplitude and nonlinear natural frequency change of S–S nanobeam for different nonlocal parameter, the first mode and Knl = 10, Kp = 5, Kw = 10 and T = 0 K

Full size image
Fig. 8
figure 8

a 1st mode (\({\omega }_{1}\)), 2nd mode (\({\omega }_{2}\)) and 3rd mode \(({\omega }_{3)}\) frequency–response curves of S–S nanobeams for (ℽ = 0.1, \({K}_{nl}\)= 10, \({K}_{p}=5, { \, K}_{w}=10 \, {\text{and}} \, T=0 \, {\text{K}})\) b Amplitude and nonlinear natural frequency change of S–S nanobeam for different modes (Knl = 10, Kp = 5, Kw = 10 and T = 0 K)

Full size image

On the contrary, the results of high temperature graphs differ from those of low temperature graphs. Figure 3 shows that as the amplitude grows, so does the nonlinear frequency. Furthermore, when the temperature rises, the nonlinear frequency variations decrease. The frequency response curves for the first mode at various temperature settings are also shown. It demonstrates that as temperature values increase, so does the steady-state amplitude of the nanobeam for the first mode.

Figure 4 shows the effect of Winkler parameter on the amplitude and nonlinear natural frequency changes. As the Winkler parameter (Kw) increases the nonlinear natural frequency changes also rise. So, Winkler parameter is directly proportional to the nonlinear natural frequency where this also applies to the Pasternak parameter. The frequency response curves show that amplitude is at its peak when Kw is small and gradually decrease as the Winkler parameter rises. Figure 5 shows that the amplitude and nonlinear natural frequency change rises as the Pasternak parameter (Kp) rises. From the frequency response curves, it is observed the curves tend to have higher amplitude as the Pasternak parameter drops.

In Fig. 6, the fundamental frequency is the same at the beginning of different nonlinear foundation parameter and step by step the difference will be seen clearly. Nonlinear natural frequencies are affected greatly by nonlinear foundation parameter. Nonlinear natural frequencies change more at high nonlinear foundation parameter. Figure 7 illustrates nonlinear natural frequency changes based on different nonlocal parameter(ℽ). It has also been shown that the steady-state amplitude of the nanobeam ascends when ℽ increases. Figure 8 illustrates the first three nonlinear natural frequency values. It shows that amplitude and nonlinear natural frequency changes increase as the modes increase. Frequency response curves of the first three modes is presented. At higher modes steady-state amplitude of the nanobeam is higher.

4.2 Clamped–clamped nanobeam

The linear natural frequency and correction term are presented in Tables 3 and 4 for the clamped–clamped (C–C) nanobeam. Damping (µ) 0.1 is selected for the C–C nanobeam. The result obtained for clamped nanobeam show a similar trend to simply supported nanobeam. Clamped nanobeams have higher natural frequencies compared to simply supported nanobeams because stiffness of clamped nanobeams are higher than simply supported nanobeams.

Table 3 The first three natural frequencies of a clamped–clamped (C–C) nanobeam under various conditions which include different temperature, Winkler parameter, Pasternak parameter, nonlinear foundation and nonlocal parameter
Full size table
Table 4 The nonlinear correction term of the first mode C–C nanobeam with different eoa/L, ΔT, Kp and Kw values when Knl = 10,100 and 200
Full size table

Table 3 shows that as parameters like Winkler, Pasternak, nonlinear foundation and temperature increases the linear natural frequencies also increase. In contrary, the linear frequencies drop as nonlocal parameter increases. This means that the increment of nonlocal parameter reduces the stiffness of the nanobeam. In Table 4, the effect of the nonlinear foundation parameter is shown in addition to other variable parameters. It is seen that correction terms are inversely proportional to low temperature values and directly proportional to high temperature values. Correction terms are also directly proportional to Winkler, Pasternak and nonlinear foundation parameters. Which means they increase as these parameters increase.

Figure 9 shows nonlinear natural frequency changes versus amplitude curves for clamped–clamped nanobeam as well as the frequency response curves. The graph shows the effect of low temperatures on the first mode of the C–C nanobeams. It is seen nonlinear natural frequencies changes are lower for low temperatures and rises as temperature increase. On other hand, Fig. 10 shows the frequency response curves and the nonlinear natural frequency changes at high temperature values. The nonlinear natural frequencies drop as temperature increases at high temperature values.

Fig. 9
figure 9

a Frequency response curves of C–C nanobeams for different low temperature values T = 0 K,100 K and 200 K, the first mode (ℽ = 0.1, Knl = 10, Kp = 5 and Kw = 10) b Amplitude and nonlinear natural frequency change of C–C nanobeam for different low temperature values when ℽ = 0.1, Knl = 10, Kp = 5 and Kw = 10

Full size image
Fig. 10
figure 10

a Frequency response curves of C–C nanobeams for different high temperature values T = 200 K,400 K and 600 K, the first mode (ℽ = 0.1, Knl = 10, Kp = 5 and Kw = 10) b Amplitude and nonlinear natural frequency change of C–C nanobeam for different high temperature values when ℽ = 0.1, Knl = 10, Kp = 5 and Kw = 10

Full size image

Winkler parameter, Pasternak Parameter and Nonlinear foundation parameter effects are illustrated on Figs. 11, 12 and 13, respectively. It shows that the amplitude and nonlinear natural frequency change increases as the Winkler parameter (Kw) as well as Pasternak parameter (Kp) increases. From the frequency response curves, it is observed the curves tend to have higher amplitude as these parameters drops. Figure 13 shows that as nonlinear foundation parameter effect. The fundamental frequency is the same at the beginning of different nonlinear foundation parameter and gradually the difference will be seen clearly. Nonlinear natural frequencies change more at high nonlinear foundation parameter. When the nonlinear elastic foundation value gets high, hardening behavior shifts to the right. The effect of nonlocal parameter on the first mode of the C–C nanobeam is presented in Fig. 14. It is observed that the effects of amplitudes on nonlinear natural frequency are higher at high nonlocal parameter.

Fig. 11
figure 11

a Frequency response curves of C–C nan-obeams for different Winkler parameter Kw = 10,100 and 200, the first mode (ℽ = 0.1, Knl = 10, Kp = 5 and T = 0 K) b Amplitude and nonlinear natural frequency change of C–C nanobeam for different Winkler parameter when ℽ = 0.1, Knl = 10, Kp = 5 and T = 0 K

Full size image
Fig. 12
figure 12

a Frequency response curves of C–C nanobeams for different Pasternak parameter Kp = 5,50 and 100, the first mode (ℽ = 0.1, Knl = 10, Kw = 10 and T = 0 K) b Amplitude and nonlinear natural frequency change of C–C nanobeam for different Pasternak parameter when ℽ = 0.1, Knl = 10, Kw = 10 and T = 0 K

Full size image
Fig. 13
figure 13

a Frequency response curves of C–C nanobeams for different nonlinear foundation parameter Knl = 10, 100 and 200, the first mode (ℽ = 0.1, Kp = 5, Kw = 10 and T = 0 K) b Amplitude and nonlinear natural frequency change of C–C nanobeam for different nonlinear Foundation parameter, the first mode and ℽ = 1, Kp = 5, Kw = 10 and T = 0 K

Full size image
Fig. 14
figure 14

a Frequency response curves of C–C nanobeams for different nonlocal parameter ℽ = 0, 0.2 and 0.4, the first mode (Knl = 10, Kp = 5, Kw = 10 and T = 0 K) b Amplitude and nonlinear natural frequency change of C–C nanobeam for different nonlocal parameter, the first mode and Knl = 10, Kp = 5, Kw = 10 and T = 0 K

Full size image

The effect of the first three modes on the nonlinear natural frequency of C–C nanobeam is presented in Fig. 15. From the figure, as the modes of the nanobeam increase, the nonlinear frequencies rise. Figures 8, 9, 10, 11, 12, 13, 14 and 15 display the frequency response curves on top of the nonlinear natural frequency changes. The maximum amplitudes are obtained at values where the detuning parameter is greater than zero. This phenomenon is called hardening behavior.

Fig. 15
figure 15

a 1st mode (\({\omega }_{1}\)), 2nd mode (\({\omega }_{2}\)) and 3rd mode \(({\omega }_{3)}\) frequency–response curves of C–C nanobeams for (ℽ = 0.1, \({K}_{nl}\)= 10, \({K}_{p}=5, \, {K}_{w}=10 \, {\text{and}} \, T=0 \, K)\) b Amplitude and nonlinear natural frequency change of C–C nanobeam for different modes (ℽ = 0.1, Knl = 10, Kp = 5, Kw = 10 and T = 0 K)

Full size image

4.3 Validation study

In this section, comparisons have been made with previous studies to check the validity and accuracy of the presented study. However, due to the limited availability of direct comparative results in the literature for nonlocal thermal vibration of a nanobeam resting on a nonlinear elastic foundation. So, initially small-scale parameter effect and thermal coefficient effect is neglected. In Table 5, the non-dimensional first five natural frequencies of simply-supported nanobeams are presented for various Winkler and Pasternak foundation parameter. These frequencies are then compared with the corresponding results from three previously published studies of Demir and Civalek [62], Togun and Bağdatlı [56], Mustafa and Zhang [80] and Yokoyama [81]. It is clear from Table 5 that there is a satisfactory agreement between the results obtained in the present study and those from the reference studies. This suggests that the proposed approach in the current study is valid and capable of producing reliable results.

Table 5 Comparison of non-dimensional frequencies with simply supported boundary conditions
Full size table

In Table 6, a comparative analysis is presented to explore the effects of nonlocal parameters on the first five non-dimensional natural frequencies of simply supported nanobeams under the influence of thermal effects. The purpose of this comparison is to understand how varying nonlocal parameters impact the vibrational behavior of the nanobeams when subjected to temperature changes. It demonstrates that an increase in temperature change leads to a decrease in non-dimensional natural frequencies, particularly affecting the lower vibration modes more prominently.

Table 6 Comparison of first five nondimensional frequencies of simply supported nanobeams under thermal effects for different nonlocal parameters
Full size table

5 Conclusion

In conclusion, this study investigated the vibration analysis of nonlocal nanobeams embedded in a nonlinear elastic medium under thermal effects, considering different boundary conditions. By employing Hamilton's principle and nonlocal elasticity theory, the governing equation and boundary conditions were derived. An approximate analytical expression for the nonlinear frequency of the nanobeam is derived through the application of the multiple scale method. The effect of nonlocal parameter, Winkler parameter, Pasternak parameter, nonlinear foundation parameter and thermal effect on the nanobeam is investigated. Results are depicted graphically and is given in tabular form separately for each end conditions. The analysis demonstrated that clamped nanobeams exhibited higher natural frequencies due to the contribution of the end condition to stiffness, and parameters such as the Winkler and Pasternak values influenced the natural frequency values by affecting system stiffness. The nonlocal parameter had an impact on the amplitude and resulted in distinct frequency response curves. The graphs show that as nonlocal parameters increases, the amplitude shows increment at the same time having a different frequency response curves each time. It’s seen that, as the temperature increases, the nanobeam and its foundation expands, which can change the stiffness of the system and affect the natural frequencies of the beam. This can cause the mode shapes of the nanobeam to change, leading to a shift in its resonance. The damping characteristics of the beam can also be affected by temperature variations, leading to changes in the amount of energy dissipated during vibration. The dimensional amplitude versus nonlinear frequency ratio changes drop as temperature increases for both boundary condition. The reliability of the current research methodology has been evaluated by meticulously comparing the obtained results with those documented in the literature. Disregarding the consideration of the nonlocal effect during the analysis of a nanobeam results in an underestimated estimation of the natural frequencies. Future research in this field could explore the dynamic behavior of nonlocal nanobeams under more complex thermal conditions, investigate the effect of additional factors such as material heterogeneity or geometric imperfections, and explore potential applications in nanoscale devices and systems. By addressing these aspects, a deeper understanding of the behavior and performance of nonlocal nanobeams in thermal environments can be gained, leading to advancements in various engineering and nanotechnology applications.