Dynamic analysis of double cracked bi-directional functionally graded nanobeam using the differential quadrature method

Abstract

This study investigates the free vibration behavior of a double cracked nanobeam composed of bi-directional functionally graded material. The analysis incorporates Eringen’s nonlocal elasticity theory and the Euler–Bernoulli theory. The material properties are considered to vary in both the thickness and length directions. The cracked nanobeam is modeled as a series of interconnected sub-beams, with rotational springs placed at the cracked sections. This modeling approach accounts for the discontinuities in rotational displacement resulting from bending, which is directly related to the bending moment transmitted by the cracked section. The problem is solved using the differential quadrature method, which approximates the derivatives of the field quantities by employing a weighted linear sum of the nodal values. By doing so, the problem is transformed into a linear algebraic system. Various supporting cases are examined, and a parametric study is conducted to analyze the impact of the axial and transverse gradient indices, nonlocal parameter, and crack severity on the obtained results.

1 Introduction

Nanotechnology is a science that studies extremely small elements. In recent years, a lot of researchers discuss nanostructures to study their properties. Nanostructures are commonly used in engineering and medical devices because of their large yield strength and conductivity properties. Nanobeams, nanorods, nanotubes, nanowires, and nanoplates are examples of nanostructures. The applications of nanobeams require investigation of their vibrational behavior [25, 28].

Eringen’s Nonlocal elasticity theory may be used to study nanostructures because of their small scale. In the nonlocal theory of elasticity, stress at a point is a function of strains at all points within the influence domain, while the theory of elasticity assumes that the stress at a point is a function of strain at the same point [15,16,17,18, 37].

Structures are typically assumed to be intact, but the presence of defects, such as cracks, can have a profound impact on their mechanical behavior. Cracks increase structural flexibility and decrease natural frequencies. Therefore, it is crucial to detect and assess the size and location of cracks in structures. Structure health monitoring is used to determine the location of cracks by analysis of the vibration modes. So, the mechanical behaviors of cracked elements are analyzed using several theoretical investigations. There are several types of cracks like shear cracks, torsional cracks, sliding cracks, flexure cracks, corrosion cracks, shrinkage cracks, and tension cracks. There are some reasons that lead to creating cracks in the elements like thermal expansion through heating [4, 23], Loghmani and Hairi Yazdi [31, 41]. Cracked nanobeams with intentional cracks or fractures, can be utilized in micro/nano-electro-mechanical systems (MEMs/NEMs) such as electrically actuated micro/nano-electro-mechanical systems.

Several publications studied non cracked homogenous nanobeam problems. Eltaher et al. [13] studied the vibration analysis of Euler–Bernoulli nanobeams using the finite element method (FEM). Reddy [40] studied analytically vibration of nanobeams. Numanoğlu et al. [35] analyzed the vibration of nanobeam based on Timoshenko beam theory and the nonlocal elasticity theory. They used the separation of variables method and finite element formulation in solving the eigenvalue problem. Zhang et al. [60] studied the free vibration of Euler–Bernoulli beam subjected to a uniform thermal environment using DQM. Eltaher et al. [12] studied analytically the free vibration analysis of viscoelastic perforated nanobeams based on Euler–Bernoulli and Timoshenko beam theories.

Also, several publications studied cracked homogenous nanobeam problems, [32, 36] studied free vibration of cracked Euler–Bernoulli nanobeam using nonlocal elasticity theory. Sourki and Hoseini [51] studied the vibration of cracked nanobeam based on the modified couple stress theory. Bahrami [3] analyzed vibration of multi-cracked Euler–Bernoulli nanobeams using wave propagation methods. Eghbali et al. [11] studied the free lateral vibration of cracked Euler–Bernoulli nanobeam based on the theory of nonlocal strain gradient using piezoelectric effects. They modeled the cracked nanobeam by splitting it into two sub-beams connected to a rotating spring. Darban et al. [8] studied the size-dependent free vibration of cracked Euler–Bernoulli nanobeam based on nonlocal theory of elasticity. They modeled the crack by introducing discontinuities in the transverse displacement and slope and at the location of the crack. Darban et al. [9] studied the size-dependent buckling analysis of cracked Euler–Bernoulli nano-cantilever which is used as sensor and actuator. The crack was modeled by assuming that the two sections at the crack are connected by a rotational spring. Scorza et al. [43] studied the behavior of cracked nanobeam using the stress driven nonlocal model. The cracked nanobeam was modeled to be divided into two segments connected together through a rotational spring at the location of the crack. Eghbali et al. [10] studied the free lateral vibration of cracked Euler–Bernoulli nanobeam based on nonlocal strain gradient theory. The cracked nanobeam was modeled to be divided into two segments attached to a torsion spring.

Functionally graded (FG) materials are composite materials characterized by a gradual variation in properties from one surface to another. These materials find widespread use in engineering and scientific applications due to their advantageous characteristics, including design flexibility, enhanced fracture toughness, reduced weight, and lower stress intensity factor. The unique properties of FG materials have made them highly desirable for structural components across various engineering fields such as nuclear, aerospace, automotive, marine, biomedical, and optical engineering. As a result, their adoption has been rapid and extensive, [2, 45, 55]. Zhao et al. [61] used the strain gradient theory to develop a size-dependent porous axially functional gradient flexoelectric Euler–Bernoulli nanobeam model. A modified power-law formula incorporating porosity volume fraction was presented to describe material properties of porous axially FG nanobeam, and two typical porosity distributions patterns were considered. The DQM was employed to discretize governing equations into a series of linear algebraic equations. Sınır et al. [50] studied the nonlinear free and forced vibrations of axially functionally graded (AFG) Euler–Bernoulli beams with non-uniform cross section. Nonlinearities occur in the system due to this stretching. Damping and forcing terms were included after non-dimensionalization. The equations were solved using perturbation method and mode shapes by DQM. Singh and Sharma [49] used the harmonic DQM to study vibration characteristics of tapered beams made of AFG. They used the power-law function to simulate the variation of material parameters along the length direction. They solve the problem using Timoshenko beam theory for clamped–clamped (C-C) boundary condition. Guler [22] investigated free vibration of cracked beams made of AFG material. They used the power-law distribution to model the variation of material properties. Hossain and Lellep [24] investigated numerically the dynamic behavior of AFG multi-cracked Euler–Bernoulli nanobeam subjected to thermal load due to temperature variation based on nonlocal theory of elasticity using the power series solution technique. The material properties were assumed to be varied exponentially from one end to another one. They modeled the crack as a rotational spring.

Eltaher et al. [14] studied the free vibration analysis of FG nanobeams based on Euler–Bernoulli beam using FEM. Wattanasakulpong and Ungbhakorn [58] used the differential transformation method to investigate the free vibration of FG beams. Esen et al. [19] studied vibration analysis of FG cracked Euler–Bernoulli nanobeam rested on an elastic foundation and exposed to magnetic and thermal fields. They modeled the crack as a rotational spring at the crack’s position. Shabani and Cunedioglu [44] presented the free vibration of a cracked non-uniform symmetric FG beam based on Timoshenko beam theory using FEM. The material properties vary along the thickness direction according to exponential and power laws. Tran et al. [54] studied the free vibration analysis of FG Timoshenko nanobeam on a Winkler elastic foundation based on the nonlocal theory of elasticity.

Nejad and Hadi [34] investigated the free vibration of Euler–Bernoulli nanobeams made of BDFG material. They used the nonlocal elasticity theory to investigate size effects on free vibration analysis of BDFG Euler–Bernoulli nanobeams using DQM. Chen et al. [6] studied size-dependent free vibration, buckling, and dynamic stability of BDFG nanobeam embedded in an elastic medium. Wu et al. [59] studied nonlinear forced vibration of BDFG beams based on the first-order shear deformation theory and von Karman’s geometric nonlinearity. They found that the periodic motion of the beam can undergo cyclic fold bifurcation. Gholami et al. [21] analyzed nonlinear free vibration of BDFG nanobeam. They used modified couple stress theory to investigate small scale using DQM. Sharma and Khinchi [46] investigated the vibration analysis of BDFG beam using harmonic DQM. Sharma and Khinchi [47] investigated BDFG Euler–Bernoulli beam under the hygrothermal effect using FEM. The material properties were modeled to be varied according to the power law. They concluded that the natural frequency increases with the increasing of material gradient parameters in thickness direction and decreases with the increasing of material gradient parameters in the x-direction under C-C and clamped-free (C-F) end conditions. Rajasekaran and Khaniki [39] studied the dynamic behavior of BDFG single and multi-cracked beams. They presented the material variation using different material gradation laws such as power-law, sigmoidal, and exponential varying functions in both thickness and longitudinal directions to model the beam with single or multiple cracks. Kar and Srinivas [26] studied the dynamic analysis of cracked BDFG nanobeam resting on nonlinear elastic foundations in the presence of thermal loads. Alsubaie Abdulmajeed [1] investigated the vibration behavior of porous FG nanobeam resting on viscoelastic foundation based on a simplified high order shear deformation theory. Faghidian & Tounsi [20] conducted an analytical study to investigate the dynamic response of nanobeams. Their analysis was based on the theory of mixture unified gradient. The free vibration of nanoshells/nanoplates made of FG materials and based on the theory of nonlocal first order shear deformation and nonlocal theory of elasticity is investigated by Van Vinh and Tounsi [56], Van Vinh and Tounsi [57], [27]. Based on the Reissner–Mindlin plate theory and the Von-Kármán nonlinearity, [7] analyzed the nonlinear bending of porous sigmoid FG nanoplate via isogeometric finite element formulation. Liu et al. [30] studied the dynamic response of FG nanoplate embedded in a viscoelastic foundation and subjected to moving load using the state-space method. Based on the four-unknown refined integral plate theory on aggregate with the nonlocal elasticity theory, [5] studied the dynamic behavior of FG nanoplate embedded into an elastic medium Rouabhia et al. [42] investigated the buckling of a single layered graphene sheet based on the nonlocal integral first shear deformation theory. They studied the influence of visco-Pasternak foundations on the result.

Based on the above-mentioned review, it is observed that the dynamic performance of cracked BDFG nanobeams is still limited. The main objective of the present study is to develop a new model for predicting the nonlocal vibration response of double cracked BDFG nanobeams based on Euler–Bernoulli beam theory. The rotational spring model is employed to simulate the crack existence. Toward this end, the analysis incorporates Eringen’s nonlocal elasticity theory to capture the contributions of the nonlocal effect. The power-law function is adopted to express the gradation in transverse direction while the exponential longitudinal directions for all the material properties of the bulk. Differential quadrature method, a powerful numerical methodology that can obtain accurate results using a small number of nodal points, is applied to obtain the dynamical response of the cracked BDFG nanobeam. For verification purposes, the predicted results are compared with the previous studies. Numerical studies proved the significant influence of the gradation indices, nonlocal parameter, and crack severity on the fundamental frequency of double cracked BDFG nanobeams for different supporting cases.

2 Formulation of the problem

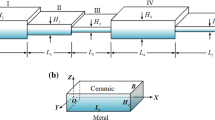
Consider a nanobeam of length $L$, width $b$, and thickness $h$ containing double cracks located at a distance ${x}_{l}$ ($l$ =1, 2) from the left end, as shown in Fig. 1. The beam is divided into 3 sub-beams. These cracks are modeled as a rotational spring at the crack locations.

Fig. 1

Model of double cracked BDFG nanobeam

The modulus of elasticity $E$ and mass density $\rho$ are assumed to be functions in both thickness and axial directions as follows [34]

$$E\left(x, z\right)= {e}^{ \frac{\beta }{L} x}. {g}_{1}(z)$$

(1)

$$\rho \left(x, z\right)= {e}^{ \frac{\beta }{L} x}. {g}_{2}(z)$$

(2)

Based on a power-law distribution, ${g}_{1}\left(z\right)$ and ${g}_{2}\left(z\right)$ can be expressed as follows [34, 58]

$${g}_{1}\left(z\right)={({E}_{\mathrm{c}}-{E}_{\mathrm{m}})\left( \frac{z}{h}+\frac{1}{2}\right)}^{n}+{E}_{\mathrm{m}}$$

(3)

$${g}_{2}\left(z\right)={({\rho }_{\mathrm{c}}-{\rho }_{\mathrm{m}})\left( \frac{z}{h}+\frac{1}{2}\right)}^{n}+{\rho }_{\mathrm{m}}$$

(4)

where $n$ is the transverse gradient index, $\beta$ is the axial gradient index, ${E}_{\mathrm{m}}$ and ${E}_{\mathrm{c}}$ are modulus of elasticity of metal and ceramic material, respectively. Also, ${\rho }_{\mathrm{m}}$ and ${\rho }_{c}$ are the mass density of metal and ceramic materials, respectively.

The axial and transverse displacement can be expressed based on Euler–Bernoulli theory as follows

$$u={u}_{0}\left(x\right)-z\frac{\partial w}{\partial x}$$

(5)

$$w=w\left(x,t\right)$$

(6)

Also, the strain can be expressed as

$${\varepsilon }_{\rm {xx}}=\frac{\partial {u}_{0}}{\partial x}-z\frac{{\partial }^{2}w}{\partial {x}^{2}}$$

(7)

The governing equation of BDFG beam can be written as follows [34]

$${\int }_{{t}_{1}}^{{t}_{2}}\delta U-\delta \overline{K}\mathrm{d }t=0$$

(8)

where ${u}_{0}$ is the axial displacement at the mid plane, and $\delta U,\delta \overline{K }$ represent the variation in strain and kinetic energy, respectively.

$${\int }_{{t}_{1}}^{{t}_{2}}\delta U{{\mathrm{d}}}t={\int }_{{t}_{1}}^{{t}_{2}}{\int }_{V}{\sigma }_{\rm {xx}} \delta {\varepsilon }_{\rm {xx}}dV{\mathrm{d}}t={\int }_{{t}_{1}}^{{t}_{2}}{\int }_{0}^{{L}}\left(\frac{\partial {N}_{\rm {xx}}}{\partial x}\delta {u}_{0}-\frac{{\partial }^{2}{M}_{\rm {xx}}}{\partial {x}^{2}}\delta w\right){\mathrm{d}}x{\mathrm{d}}t$$

(9)

$${N}_{\rm {xx}}={\int }_{A}{\sigma }_{\rm {xx}} {\mathrm{d}}A$$

(10)

$${M}_{\rm {xx}}={\int }_{A}z {\sigma }_{\rm {xx}} {\mathrm{d}}A$$

(11)

$$\begin{aligned} \mathop \int \limits_{{t_{1} }}^{{t_{2} }} \delta \bar{K}{\text{d}}t = \, & \delta \frac{1}{2}\mathop \int \limits_{{t_{1} }}^{{t_{2} }} \mathop \int \limits_{V} \rho \left( {\frac{{\partial u}}{{\partial t}}^{2} + \frac{{\partial W}}{{\partial t}}^{2} } \right){\text{d}}V{\text{d}}t \\ = & \;\,\,\mathop \int \limits_{{t_{1} }}^{{t_{2} }} \mathop \int \limits_{0}^{L} \left( {m_{2} f^{\prime}\frac{{\partial ^{3} w}}{{\partial x\partial t^{2} }} + m_{2} f\frac{{\partial ^{4} w}}{{\partial x^{2} \partial t^{2} }} - m_{0} f\frac{{\partial ^{2} w}}{{\partial t^{2} }}~} \right)\delta w{\text{d}}x{\text{d}}t \\ \end{aligned}$$

(12)

So, the governing equations may be written as

$$\frac{\partial {N}_{\rm {xx}}}{\partial x}=0$$

(13)

$$\frac{{\partial }^{2}{M}_{\rm {xx}}}{\partial {x}^{2}}={m}_{0}f\frac{{\partial }^{2}w}{\partial {t}^{2}}-{m}_{2}{f}{\prime}\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}-{m}_{2}f\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {t}^{2}}$$

(14)

The relation between local and nonlocal stress in nonlocal Euler–Bernoulli beam is expressed as follows [34]

$${\sigma }_{\rm {xx}}-{\left({e}_{0}a\right)}^{2 }\frac{{{\partial }^{2}\sigma }_{\rm {xx}}}{\partial {x}^{2}}=E{\varepsilon }_{\rm {xx}}$$

(15)

in which ${\left({e}_{0}a\right)}^{2}$ is the scale coefficient that represents the effect of small scale.

By integrating Eq. (15), we can get the following equation

$${N}_{\rm {xx}}-{\left({\mathrm{e}}_{0}\mathrm{a}\right)}^{2 }\frac{{{\partial }^{2}N}_{\rm {xx}}}{\partial {x}^{2}}={\int }_{A}E \left(\frac{\partial {u}_{0}}{\partial x}-z\frac{{\partial }^{2}w}{\partial {x}^{2}}\right) dA={I}_{0}f\frac{\partial {u}_{0}}{\partial x}-{I}_{1}f\frac{{\partial }^{2}w}{\partial {x}^{2}}$$

(16)

From Eqs. (13) and (16), we can get the following equation

$$\frac{\partial {u}_{0}}{\partial x}=\frac{{I}_{1}}{{I}_{0}} \frac{{\partial }^{2}w}{\partial {x}^{2}}$$

(17)

By multiplying Eq. (15) by $z$ then integrating the obtained equation, one can get the following equation

$${M}_{\rm {xx}}-{\left({e}_{0}a\right)}^{2 }\frac{{{\partial }^{2}M}_{\rm {xx}}}{\partial {x}^{2}}={\int }_{A}Ez \left(\frac{\partial {u}_{0}}{\partial x}-z\frac{{\partial }^{2}w}{\partial {x}^{2}}\right) dA={I}_{1}f\frac{\partial {u}_{0}}{\partial x}-{I}_{2}f\frac{{\partial }^{2}w}{\partial {x}^{2}}$$

(18)

By substituting Eq. (17) in Eq. (18), then we have

$${M}_{\rm {xx}}-{\left({e}_{0}a\right)}^{2 }\frac{{{\partial }^{2}M}_{\rm {xx}}}{\partial {x}^{2}}={I}_{1}f \frac{{I}_{1}}{{I}_{0}} \frac{{\partial }^{2}w}{\partial {x}^{2}}-{I}_{2}f\frac{{\partial }^{2}w}{\partial {x}^{2}}= \left(\frac{{{I}_{1}}^{2}}{{I}_{0}} -{I}_{2}\right)f\frac{{\partial }^{2}w}{\partial {x}^{2}}=k f\frac{{\partial }^{2}w}{\partial {x}^{2}}$$

(19)

By taking the second derivative of Eq. (19), the equation may be written as

$$\frac{{{\partial }^{2}M}_{\rm {xx}}}{\partial {x}^{2}}-{\left({e}_{0}a\right)}^{2 }\frac{{{\partial }^{4}M}_{\rm {xx}}}{\partial {x}^{4}}=k\left( f\frac{{\partial }^{4}w}{\partial {x}^{4}}+2{f}{\prime}\frac{{\partial }^{3}w}{\partial {x}^{3}}+{f}^{{\prime}{\prime}}\frac{{\partial }^{2}w}{\partial {x}^{2}}\right)$$

(20)

where $f= {e}^{ \frac{\beta }{L} x}$

From the Eq. (14) and Eq. (20), we have

$$k \frac{{\partial }^{4}w}{\partial {x}^{4}}+2k \left(\frac{\beta }{L}\right)\frac{{\partial }^{3}w}{\partial {x}^{3}}+k{\left(\frac{\beta }{L}\right)}^{2}\frac{{\partial }^{2}w}{\partial {x}^{2}}={s}_{1}\frac{{\partial }^{2}w}{\partial {t}^{2}}+{s}_{2}\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}+{s}_{3}\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {t}^{2}}+{s}_{4}\frac{{\partial }^{5}w}{\partial {x}^{3}\partial {t}^{2}}+{s}_{5}\frac{{\partial }^{6}w}{\partial {x}^{4}\partial {t}^{2}}$$

(21)

where ${s}_{1}, {s}_{2}, {s}_{3}, {s}_{4} , {s}_{5}$, and $k$ can be written as [34]

$$\left\{\begin{array}{c}{s}_{1}\\ {s}_{2}\\ {s}_{3}\\ {s}_{4}\\ {s}_{5}\\ k\end{array}\right\}=\left\{\begin{array}{c}{m}_{0}\left[1-{\left({e}_{0}a\right)}^{2 }{\left(\frac{\beta }{L}\right)}^{2}\right]\\ {m}_{2}{\left({e}_{0}a\right)}^{2 }{\left(\frac{\beta }{L}\right)}^{3}-2{m}_{0}{\left({e}_{0}a\right)}^{2 }\left(\frac{\beta }{L}\right)-{m}_{2}\left(\frac{\beta }{L}\right)\\ 3{m}_{2}{\left({e}_{0}a\right)}^{2 }{\left(\frac{\beta }{L}\right)}^{2}-{m}_{0}{\left({e}_{0}a\right)}^{2 }-{m}_{2}\\ 3{m}_{2}{\left({e}_{0}a\right)}^{2 }\left(\frac{\beta }{L}\right)\\ {m}_{2}{\left({e}_{0}a\right)}^{2 }\\ \frac{{{I}_{1}}^{2}}{{I}_{0}}-{I}_{2}\end{array}\right\}$$

(22)

If we assume harmonic behavior of the nonlocal beam in free vibration, the field quantity can be expressed as

$$w\left(x,t\right)=W\left(x\right) {e}^{i\omega t}$$

(23)

where $W\left(x\right)$ is the deflection of the nanobeam, $x$ is the longitudinal coordinate measured from the left end of the beam, $t$ is time, and $\omega$ is the natural frequency.

So, the governing equation based on nonlocal Euler–Bernoulli theory for each sub-beam made of BDFG can be written as follows, [34]

$$k \frac{{\partial }^{4}W}{\partial {x}^{4}}+2k \left(\frac{\beta }{L}\right)\frac{{\partial }^{3}W}{\partial {x}^{3}}+k{\left(\frac{\beta }{L}\right)}^{2}\frac{{\partial }^{2}W}{\partial {x}^{2}}=-{\upomega }^{2}\left({s}_{1}W+{s}_{2}\frac{\partial W}{\partial x}+{s}_{3}\frac{{\partial }^{2}W}{\partial {x}^{2}}+{s}_{4}\frac{{\partial }^{3}W}{\partial {x}^{3}}+{s}_{5}\frac{{\partial }^{4}W}{\partial {x}^{4}}\right)$$

(24)

The coefficients $\left\{{I}_{0}, {I}_{1}, {I}_{2}\right\}$ can be expressed as follows

$$\left\{\begin{array}{ccc}{I}_{0}& {I}_{1}& {I}_{2}\end{array}\right\}={\int }_{A}{g}_{1}\left(z\right)\left\{\begin{array}{ccc}1& z& {z}^{2}\end{array}\right\} dA$$

(25)

where $\mathrm{A is}$ the cross sectional area of the nanobeam.

while $\left\{{m}_{0}, {m}_{1}, {m}_{2}\right\}$ can be expressed as

$$\left\{\begin{array}{ccc}{m}_{0}& {m}_{1}& {m}_{2}\end{array}\right\}={\int }_{A}{g}_{2}\left(z\right)\left\{\begin{array}{ccc}1& z& {z}^{2}\end{array}\right\} dA$$

(26)

For simplicity, the boundary conditions of the nanobeam at external boundaries ($x=0$ and $x=L$) are assumed to be the classical (essential) ones, that can be written as follows.

Simply supported end:

$$W=0 \mathrm{\,\,and\,\, }M=0$$

(27)

Clamped end:

$$W=0 \mathrm{\,\,and\,\, }\frac{dW}{dx}=0$$

(28)

Free end:

$$Q=0 \mathrm{\,\,and\,\,}M=0$$

(29)

At the cracked locations, the boundary conditions can be expressed as [19, 52, 53]

$${W}^{ l}= {W}^{ l+1}$$

(30)

$${M}^{l}= {M}^{l+1}$$

(31)

$${\mathrm{Q}}^{l}= {\mathrm{Q}}^{l+1}$$

(32)

$$\frac{d{W}^{ l+1}}{dx}-\frac{d{W }^{l}}{dx}={K}_{l} \frac{{d}^{2}{W }^{l}}{d{x}^{2}}$$

(33)

where ${M}^{l}$ is the bending moment of sub-beam $l$, ${\mathrm{Q}}^{l}$ is the shear force of sub-beam $l$, ${\mathrm{K}}_{l}$ is crack severity of ${l}^{th}$ crack.

3 Method of solution

The method of differential quadrature is used to reduce the problem to that of linear algebraic system. The distribution of the nodes ${x}_{i}$ is calculated according to Chebyshev–Gauss–Lobatto discretization as [33, 38, 48]

$${x}_{i}={x}_{1}+\frac{{x}_{N}-{x}_{1}}{2}\left(1-\mathrm{cos}\left( \frac{i-1}{N-1} \pi \right) \right),\quad i=\mathrm{1,2},..,N$$

(34)

The derivatives are approximated as [33, 48]:

$${\left.\frac{{\partial }^{m}f(x)}{\partial {x}^{m}}\right|}_{x={x}_{i} }= \sum_{j=1}^{N}{C}_{\rm {ij}}^{m} f\left({x}_{j}\right) ,\quad (i=1 , N ) , (m=1,M)$$

(35)

where $N$ is the number of the nodes for each sub-beam, $M$ is the order of the highest derivative appearing in the problem, $f\left({x}_{i}\right)$ is the nodal values of the function at the points${x}_{i}$, $\left(i = 1, N\right), N > M$ and${ C}_{\rm {ij}}^{m}$, $(i , j = 1, N),$ are the weighting coefficients relating to the mth derivative to the functional values at${x}_{i}$.

For the ${m}^{th}$ order derivative, the weighting coefficients can be expressed as [33, 48]:

$${C}_{\rm {ij}}^{(m)}=\left\{\begin{array}{l} m\left({C}_{\rm {ij}}^{(1)} {C}_{\rm {ii}}^{(m-1)}- \frac{{C}_{\rm {ij}}^{(m-1)}}{{x}_{i}-{x}_{j}}\right) ,\quad i,j=\mathrm{1,2},..,N,\quad i\ne j \quad 2\le m\le N-1 \\ - \sum_{j=1 , j\ne i}^{N}{C}_{\rm {ij}}^{(m)} ,\quad i,j=\mathrm{1,2},..,N,\quad i=j \quad 2\le m\le N-1\end{array}\right.$$

(36)

For first order derivative, the weighting coefficients can be expressed as [33, 48]

$${C}_{\rm {ij}}^{1}=\left\{\begin{array}{c} \frac{1}{{x}_{i}-{x}_{j}}\left(\frac{{P}_{i}}{{P}_{j}}\right),\quad i\ne j\\ - \sum_{j=1 , j\ne i}^{N}{C}_{\rm {ij}}^{1} ,\quad i=j\end{array}\right.$$

(37)

where ${P}_{i}$ is defined as

$${P}_{i}= \prod_{j=1 , j\ne i}^{N}\left({x}_{i}-{x}_{j}\right) ,\quad i,j=\mathrm{1,2},..,N$$

(38)

For the second order derivative, the weighting coefficients can be expressed as [33, 48]

$$C_{\rm {ij}}^{2} = \left\{ {\begin{array}{*{20}l} { 2C_{\rm {ij}}^{1} \left( {C_{\rm {ii}}^{1} - \frac{1}{{x_{i} - x_{j} }}} \right) ,\quad i,j = 1,2,..,N, i \ne j } \\ { - \mathop \sum \limits_{j = 1 , j \ne i}^{N} C_{\rm {ij}}^{2} ,\quad i = 1,2,..,N, i = j } \\ \end{array} } \right.$$

(39)

Applying the DQM to Eq. (24), one can reduce the problem to the following Eigen value problem:

$$\begin{gathered} k \left[ {\mathop \sum \limits_{j = 1}^{N} C_{\rm {ij}}^{4} W_{j} + 2 \left( {\frac{\beta }{L}} \right)\mathop \sum \limits_{j = 1}^{N} C_{\rm {ij}}^{3} W_{j} + \left( {\frac{\beta }{L}} \right)^{2} \mathop \sum \limits_{j = 1}^{N} C_{\rm {ij}}^{2} W_{j} } \right] \hfill \\ \quad\quad= - \omega^{2} \left[ {s_{1} W_{i} + s_{2} \mathop \sum \limits_{j = 1}^{N} C_{\rm {ij}}^{1} W_{j} + s_{3} \mathop \sum \limits_{j = 1}^{N} C_{\rm {ij}}^{2} W_{j} + s_{4} \mathop \sum \limits_{j = 1}^{N} C_{\rm {ij}}^{3} W_{j} + s_{5} \mathop \sum \limits_{j = 1}^{N} C_{\rm {ij}}^{4} W_{j} } \right]\,\,\,\,\,\,\,\,\,(i,j = 1,2,..,N) \hfill \\ \end{gathered}$$

(40)

By applying Eq. (40) on all points of the beam, one can put the governing equation in the following linear algebraic system

$$\left[ {\mathbb{L}} \right]\left[ W \right] = \omega^{2} \left[ {\mathbb{R}} \right]\left[ W \right]$$

(41)

where

$$\left[ {\mathbb{L}} \right] = k \left[ {\left[ {\mathcal{D}} \right] + 2 \left( {\frac{\beta }{L}} \right)\left[ {\mathcal{C}} \right] + \left( {\frac{\beta }{L}} \right)^{2} \left[ {\mathcal{B}} \right]} \right]$$

(42)

$$\left[ {\mathbb{R}} \right] = \left[ {s_{1} \left[ {\mathbb{I}} \right] + s_{2} \left[ {\mathcal{A}} \right] + s_{3} \left[ {\mathcal{B}} \right] + s_{4} \left[ {\mathcal{C}} \right] + s_{5} \left[ {\mathcal{D}} \right]} \right]$$

(43)

in which

$$\left[ {\mathcal{A}} \right]^{l} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & \ldots & {C_{1N} } \\ {C_{21} } & {C_{22} } & \ldots & {C_{2N} } \\ \vdots & \vdots & \ldots & \vdots \\ {C_{N1} } & {C_{N1} } & \ldots & {C_{NN} } \\ \end{array} } \right],\left[ {\mathcal{B}} \right] = \left[ {\mathcal{A}} \right]\left[ {\mathcal{A}} \right], \left[ {\mathcal{C}} \right] = \left[ {\mathcal{A}} \right]\left[ {\mathcal{B}} \right], \left[ {\mathcal{D}} \right] = \left[ {\mathcal{B}} \right]\left[ {\mathcal{B}} \right]$$

(44)

and $\left[{\mathbb{I}}\right] \text{is the identity matrix.}$

4 Model validation

Consider a numerical example of a double cracked nanobeam. The modulus of elasticity $E$ and the mass density $\rho$ can be assumed as shown in Table 1.

Table 1 Material properties of the constituents of FG beam

For practical purposes, the natural frequency may be normalized such as

$$\lambda = \omega L^{2} \sqrt {\frac{{m_{0} }}{{I_{2} }}} ,\,\,\alpha = \frac{{(e_{0} a)}}{L}$$

(45)

where $L$ is the length of the whole beam and $\lambda$ is the dimensionless frequency parameter.

A quadrature numerical scheme is designed to solve this problem. The grid points, $N$, is to be varied from 7 up to 40 point. In Table 2, a convergence study is conducted to determining the suitable $N$ leading to accurate results. It is noted that $N=10$ gives good accurate results. Tables 3 and 4 show the obtained frequencies of a double cracked homogenous Euler–Bernoulli nanobeam compared with [3] for simply supported (S-S), clamped–clamped (C-C), and clamped simply (C-S) and clamped-free (C-F) boundary conditions. Table 5 compares the obtained results for uncracked Euler–Bernoulli beam with different AFG indexes with the exact solution introduced by [29]. From the comparison studies presented in Tables 1, 2, 3, 4 and 5, the newly developed model and solution methodology can accurately predict the natural frequency of the nonlocal double cracked BDFG nanobeams for different types of boundary conditions.

Table 2 Effect of $N$ (number of nodal points) on the obtained frequencies, for uncracked homogenous Euler–Bernoulli nanobeam $\left(\alpha =0, n= 0, \beta =0, K=0\right)$

Table 3 Comparison of the obtained frequencies ${\sqrt{\lambda}}$, for a double cracked Euler–Bernoulli nanobeam with crack locations at $x{\text{ = 0}}{\text{.3}}$ and $x{\text{ = 0}}{\text{.7L}}$ $\left(\alpha =0, n=0, \beta =0\right)$

Table 4 Comparison of the obtained frequencies ${\sqrt{\lambda}}$, for double cracked Euler–Bernoulli nanobeam with crack locations at $x{\text{ = 0}}{\text{.3}}$ and$x{\text{ = 0}}{\text{.7L}}$, $\left(\alpha =0.2, n=0, \beta =0.\right)$

Table 5 Comparison of the obtained frequencies $\lambda$ for uncracked Euler–Bernoulli nanobeam with crack severity $K= 0$, $\left(n=0, \alpha =0\right)$

5 Numerical results and discussion

A parametric study is introduced to investigate the influence of axial gradient index $\beta$, transverse gradient index $n$, nonlocal parameter $\alpha$, crack severity $K$, and cracks position on the obtained natural frequency ${\sqrt{\lambda}}$ of the nonlocal double cracked BDFG Euler–Bernoulli nanobeam.

5.1 Effect of nonlocal parameter $\boldsymbol{\alpha }$

Table 6 introduces the frequencies of double cracked BDFG Euler–Bernoulli nanobeams ${\sqrt{\lambda}}$ for S-S, C-C, C-S, and C-F cases. The first crack position is taken at ${\text{0}}{\text{.3}}$ and the second crack position at ${\text{0}}{\text{.7L}}$. The transverse gradient index $n=1$ and the axial gradient index $\beta$=1 with different values of crack severity $K$ and nonlocal parameter $\alpha$. One can notice that the frequency parameter is reduced with the increase in both crack severity $K$ and nonlocal parameter $\alpha$.

Table 6 First five dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG nanobeam at different values of the nonlocal parameter and the crack severity ($n=1, \beta =1,$ and crack positions of $0.3$ and ${\text{0}}{\text{.7L}}$)

Figures 2, 3 and 4 show the effect of the nonlocal parameter $\alpha$ on the first, second, and third dimensionless frequency parameter ${\sqrt{\lambda}}$ of double cracked BDFG Euler–Bernoulli nanobeam for different supported cases. The power-law gradient index $n$ and the axial gradient index $\beta$ are assumed to be $n=1$ and $\beta =1$. The positions of the cracks are chosen to be at ${\text{0}}{\text{.3}}$ and ${\text{0}}{\text{.7L}}$. Crack severity $K$ is assumed to equal 0, 0.1, and 0.35. These figures show that the value of the frequency parameter decreases with the increase in the nonlocal parameter $\mathrm{\alpha }$ for S-S, C-C, and C-S beams. Furthermore, one can notice that the frequency parameter decreases with the increase in crack severity $K$. Specifically, the frequency parameter for C-C is higher than that of C-S, and the frequency parameter for C-S is higher than that of S-S.

Fig. 2

First dimensionless frequency parameter $\sqrt{{\lambda }_{1}}$ of BDFG nanobeam with double cracks at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the nonlocal parameter ${\upalpha }$, $n = 1, \beta = 1$ for a S-S, b C-C, and c C–S

Fig. 3

Second dimensionless frequency parameter $\sqrt {{\lambda }_{2} }$ of BDFG nanobeam with double cracks at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the nonlocal parameter ${\upalpha }$, $n = 1, \beta = 1$ for a S-S, b C-C, and c C-S

Fig. 4

Third dimensionless frequency parameter $\sqrt {{\lambda }_{3} }$ of BDFG nanobeam with double cracks at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the nonlocal parameter ${\upalpha }$,$n = 1, \beta = 1$ for a S-S, b C-C, and c C-S

5.2 Effect of axial gradient index ${\varvec{\upbeta}}$

Tables 7 and 8 introduce the frequencies of double cracked BDFG Euler–Bernoulli nanobeams for different types of boundary conditions. The crack positions are taken at $0.3, 0.7$, and the transverse gradient index $n=1$ with different values of the crack severity $K$ and axial gradient index $\beta$. Table 7 shows the results at $\alpha$ = 0, while the results at $\alpha$ =0.4 are recorded in Table 8. One can notice that the frequency parameter is decreased with the increases of crack severity $K$. In case of positive axial gradient index $\beta$, the value of the fundamental frequency parameter decreases by increasing the axial gradient index $\beta$ for S-S, C-S, and C-F beams. The opposite effect is noticed for C-C beam. For axial gradient index $\beta$ with negative values, increasing $\beta$ leads to a decrease in the fundamental frequency for S-S beam.

Table 7 First five local dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG nanobeam at different values of the axial gradient index $\beta$ and the crack severity $K$( $=1,$ crack positions of $0.3$ and ${\text{0}}{\text{.7L}}$, and nonlocal parameter $\alpha = 0$)

Table 8 First five local dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG nanobeam at different values of the axial gradient index $\beta$ and the crack severity $K$($=1,$ crack positions of $0.3$ and ${\text{0}}{\text{.7L}}$, and nonlocal parameter $\alpha = 0.4$)

Figures 5, 6 and 7 show the effect of the axial gradient parameter $\beta$ on the first three dimensionless frequency parameter ${\sqrt{\lambda}}$ of double cracked BDFG Euler–Bernoulli nanobeam for different boundary conditions and at three cases of crack severity $= 0, 0.1, 0.35$. The power-law thickness gradient index $n$ is assumed to be$1$. The positions of the cracks are assumed to be at $0.3$ and ${\text{0}}{\text{.7L}}$. It is obvious from Figs. 6 and 7 that the second and third fundamental frequency parameters decrease with increasing negative values of $\beta$, reaching a minimum critical value when $\beta =0$, and then start to increase with positive values of $\beta$. This is attributed to the change in the nanobeam stiffness caused by $\beta$. For positive values of axial graded index $\beta$ and due to the exponentially graded in the $x-$ direction, this makes the ceramic material dominant and increases the beam stiffness. As a result, the predicted frequencies increase. It can be easily seen that the frequency parameter curves for S-S and C-C nanobeams in Figs. 6 and 7 are symmetric. This symmetry is understood since the boundary conditions at both ends are the same for these two cases. In addition, the frequency parameter decreases with the increase in crack severity $K$. Overall, the axial gradient parameter $\beta$ significantly impacts the dimensionless frequency parameters through its effect on the nanobeam stiffness resulting from the axial exponential index gradient profile. Both negative and positive $\beta$ values influence the fundamental frequencies differently.

Fig. 5

First dimensionless frequency parameter $\sqrt {{\lambda }_{1} }$ of BDFG nanobeam with a double crack at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the axial gradient index β $\left( {\alpha = 0, n = 1} \right)$ a S-S, b C-C, and c C-S

Fig. 6

Second dimensionless frequency parameter $\sqrt {{\lambda }_{2} }$ of BDFG nanobeam with a double crack at locations of $0.3$ and $0.7{\text{L}}$ for various boundary conditions versus the transverse gradient index β $\left( {\alpha = 0, n = 1} \right)$ a S-S, b C-C, c C–S

Fig. 7

Third dimensionless frequency parameter $\sqrt {{\lambda }_{3} }$ of BDFG nanobeam with a double crack at locations of $0.3$ and $0.7{\text{L}}$ for various boundary conditions versus the transverse gradient index β $\left( {\alpha = 0, n = 1} \right)$ a S-S, b C-C, and c C-S

In Figs. 8, 9 and 10, the nonlocal effect is considered with $\alpha = 0.4$. In the case of positive axial gradient index $\beta$, the value of the frequency parameter decreases with the increase in the axial gradient index $\beta$ in S-S, and C-S supporting cases, while it increases with the increase in the axial gradient index $\beta$ in the C-C beam. In the case of negative axial gradient index $\beta$, one can notice that the value of the frequency parameter decreases with the increase in the axial gradient index $\beta$ in simply supported beam, while it increases with the increase in the axial gradient index $\beta$ in C-C and C-S beam. One can notice that the frequency parameter decreases with the increase in crack severity $K$ and nonlocal parameter $\alpha$. The value of the frequency parameter in the case of C-C is greater than that of C-S, and this of C-S also is greater than that of S-S.

Fig. 8

First dimensionless frequency parameter $\sqrt {{\lambda }_{1} }$ of BDFG nanobeam with a double crack at locations of ${\text{0}}{\text{.3}}$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the axial gradient index β $\left( {\alpha = 0.4, n = 1} \right)$ a S-S, b C-C, and c C-S

Fig. 9

Second dimensionless frequency parameter $\sqrt {{\lambda }_{2} }$ of BDFG nanobeam with a double crack at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the transverse gradient index β $\left( {\alpha = 0.4, n = 1} \right)$ a S-S, b C-C, and c C-S

Fig. 10

Third dimensionless frequency parameter $\sqrt {{\lambda }_{3} }$ of BDFG nanobeam with a double crack at locations of ${\text{0}}{\text{.3}}$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the transverse gradient index β $\left( {\alpha = 0.4, n = 1} \right)$ a S-S, b C-C, and c C-S

5.3 Effect of transverse gradient index ${\varvec{n}}$

Tables 9 and 10 introduce the frequencies of double cracked BDFG Euler–Bernoulli nanobeams for different types of boundary conditions. The crack positions at $0.3, {\text{0}}{\text{.7L}} ,$ and axial gradient index $\beta =1$ with different values of crack severity $K$ and transverse gradient index $n$. Tables 9 and 10 provide the fundamental frequency values for two different nonlocal parameter values, $\alpha =0$ and $\alpha = 0.4$, respectively. One may notice that the frequency parameter is reduced with the increase in crack severity $K$, besides it is reduced with increasing the transverse gradient $n$ to reach a minimum at almost $n =2$ then the frequency parameter increases with the increasing of $n$.

Table 9 First five local dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG nanobeam at different values of the transverse gradient index $n$ and the crack severity ($\beta =1$, and crack positions of $0.3$ and ${\text{0}}{\text{.7L}} , \alpha = 0$)

Table 10 First five local dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG nanobeam at different values of the transverse gradient index $n$ and the crack severity ($\beta =1$, and crack positions of $0.3$ and ${\text{0}}{\text{.7L}} , \alpha = 0.4$)

For various supported cases, Figs. 11, 12, 13, 14, 15 and 16 depict how the power-law thickness gradient index $n$ affects the dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG Euler–Bernoulli nanobeams. These figures illustrate the influence of $n$ on the first, second, and third dimensionless frequency parameters. The axial gradient index $\beta$ is considered to have a value of 1. The positions of the cracks are assumed to be at $0.3$ and ${\text{0}}{\text{.7L}}$. Crack severity $K$ is assumed to equal 0, 0.1, and 0.35. In Figs. 11, 12 and 13, the nonlocal parameter α is set to zero, while in Figs. 14, 15 and 16, it is assumed to have a value of 0.4. These figures provide evidence that the frequency parameter decreases as the transverse gradient index $n$ increases until reaching a minimum value. Afterward, the frequency parameter increases with further increases in $n$ for S-S, C-C, and C-S beam configurations. Additionally, it can be observed that the frequency parameter decreases as the severity of cracks $K$ and the nonlocal parameter $\alpha$ increase. Moreover, the frequency parameter for the C-C configuration is greater than that of C-S, and that of C-S is also greater than that of S-S.

Fig. 11

First dimensionless frequency parameter $\sqrt {{\lambda }_{1} }$ of BDFG nanobeam with a double crack at locations of $0.3$ and $0.7{\text{L}}$ for various boundary conditions versus the transverse gradient index $n$ $\left( {\alpha = 0,~~\beta = 1} \right)$ a S-S, b C-C, and c C-S

Fig. 12

Second dimensionless frequency parameter $\sqrt{{\lambda }_{2}}$ of BDFG nanobeam with a double crack at locations of $0.3$ and $0.7\mathrm{L}$ for various boundary conditions versus the transverse gradient index $n$ $\left( {\alpha = 0,~~\beta = 1} \right)$ a S-S, b C-C, and c C-S

Fig. 13

Third dimensionless frequency parameter $\sqrt{{\lambda }_{3}}$ of BDFG nanobeam with a double crack at locations of $0.3$ and $0.7\mathrm{L}$ for various boundary conditions versus the transverse gradient index $n$ $\left( {\alpha = 0,~~\beta = 1} \right)$ a S-S, b C-C, and c C-S

Fig. 14

First dimensionless frequency parameter $\sqrt{{\lambda }_{1}}$ of BDFG nanobeam with a double crack at locations of $0.3\mathrm{L}$ and $0.7\mathrm{L}$ for various boundary conditions versus the transverse gradient index $n$ $\left( {\alpha = 0.4,~~\beta = 1} \right)$ a S-S, b C-C, and c C-S

Fig. 15

Second dimensionless frequency parameter $\sqrt{{\lambda }_{2}}$ of BDFG nanobeam with a double crack at locations of $0.3$ and $0.7\mathrm{L}$ for various boundary conditions versus the transverse gradient index $n$ $\left( {\alpha = 0.4,~~\beta = 1} \right)$ a S-S, b C-C, and c C-S

Fig. 16

Third dimensionless frequency parameter $\sqrt{{\lambda }_{3}}$ of BDFG nanobeam with a double crack at locations of $0.3$ and $0.7\mathrm{L}$ for various boundary conditions versus the transverse gradient index $n$ $\left( {\alpha = 0.4,\beta = 1} \right)$ a S-S, b C-C, and c C-S

5.4 Effect of crack severity ${\varvec{K}}$

Tables 11 and 12 introduce the effect of crack severity K, axial and transverse gradient indexes on the frequencies of double cracked BDFG Euler–Bernoulli nanobeam for different supported cases. The crack positions are at 0.3 and 0.7L. Crack severity K is taken to be from 0 to 4 and (n, β) is taken to be (0, 0), (0, 1), (1, 0) and (1, 1). α = 0 in Table 11 and α = 0.4 in Table 12.

Table 11 First five local dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG nanobeam at different values of the crack severity $K$ (crack positions at $0.3$ and ${\text{0}}{\text{.7L}}$, α = 0.4)

Table 12 First five local dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG nanobeam at different values of the crack severity K (crack positions at $0.3$ and ${\text{0}}{\text{.7L}}$, α = 0.4)

Figures 17, 18 and 19 show the effect of the crack severity K on the first, second, and third dimensionless frequency parameter ${\sqrt{\lambda}}$ of double cracked BDFG Euler–Bernoulli nanobeams for different supported cases. The power-law thickness gradient index and the axial gradient index $(n,\beta )$ are taken to be (0, 0), (0, 1), (1, 0) and (0.5, 0.5). The positions of the cracks are taken to be at ${\text{0}}{\text{.3}}$ and ${\text{0}}{\text{.7L}}$. These figures show that the value of the frequency parameter decreases with the increase in the crack severity K in S-S, C-C, and C-S beams. Also, one can notice that the value of the frequency parameter in the case of C-C is greater than that of C-S, and this of C-S also is greater than that of S-S.

Fig. 17

First dimensionless frequency parameter $\sqrt{{\lambda }_{1}}$ of BDFG nanobeam with a double crack at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the crack severity $K (\alpha =0)$ a S-S, b C-C, and c C-S

Fig. 18

Second dimensionless frequency parameter $\sqrt{{\lambda }_{2}}$ of BDFG nanobeam with a double crack at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the crack severity $K (\alpha =0)$ a S-S, b C-C, and c C-S

Fig. 19

Third dimensionless frequency parameter $\sqrt{{\lambda }_{3}}$ of BDFG nanobeam with a double crack at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the crack severity $K (\alpha =0)$ a S-S, b C-C, and c C-S

5.5 Effect of cracks position

Tables 13, 14, 15 and 16 introduce the effect of the position of the first crack ${x}_{1}$ on the frequencies of double cracked BDFG Euler–Bernoulli nanobeams for different supported ends. The second crack position is at ${\text{0}}{\text{.7L}}$. Crack severity $K$ is taken as 0.1 in Tables 13 and 14, and 0.35 in Tables 15 and 16. The BDFG gradient indices $(n, \beta )$ are chosen to be (0, 0), (0.5, 0.5), (1, 1), and (2, 2). The nonlocal parameter is neglected, $\alpha =0$, in Tables 13 and 15 and is considered with $\alpha = 0.4$ in Tables 14 and 16. One may notice that the value of the fundamental frequency parameter reaches the minimum at ${x}_{1}= {\text{0}}{\text{.5L}}$ in S-S and ${x}_{1}=0.05L$ in C-F, but it reaches the maximum at ${x}_{1}= {\text{0}}{\text{.2L}}$ in C-C and ${x}_{1}= {\text{0}}{\text{.4L}}$ in C-S.

Table 13 First five local dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG nanobeams at different values of the first crack position ${x}_{1}$(${x}_{2}= {\text{0}}{\text{.7L}} , K =0.1, \alpha =0)$

Table 14 First five local dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG nanobeams at different values of the first crack position ${x}_{1}$(${x}_{2}= {\text{0}}{\text{.7L}} , K =0.1, \alpha =0.4)$

Table 15 First five local dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG nanobeams at different values of the first crack position ${x}_{1}$(${x}_{2}= {\text{0}}{\text{.7L}} , K =0.35, \alpha =0)$

Table 16 First five local dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG nanobeams at different values of the first crack position ${x}_{1}$(${x}_{2}= {\text{0}}{\text{.7L}} , K =0.35, \alpha =0.4)$

Tables 17, 18, 19 and 20 introduce the effect of second crack position ${x}_{2}$ on the frequencies of double cracked BDFG Euler–Bernoulli nanobeams for different supported cases. The first crack position is assumed to be $0.3\mathrm{L}$. Crack severity $K$ is taken as 0.1 in Tables 17 and 18, and 0.35 in Tables 19 and 20. The BDFG gradient indices $(n, \beta )$ are chosen to be (0, 0), (0.5, 0.5), (1, 1), and (2, 2). The nonlocal parameter is neglected, $\alpha =0$, in Tables 17, 18 and 19 and is considered with $\alpha = 0.4$ in Tables 18 and 20. One may notice that the value of the fundamental frequency parameter reaches the minimum at ${x}_{2}= {\text{0}}{\text{.5L}}$ in S-S and ${x}_{2}= {\text{0}}{\text{.95L}}$ in C-F, but it reaches the maximum at ${x}_{2}=0.8\mathrm{L}$ in C-C and ${x}_{2}= {\text{0}}{\text{.95L}}$ in C-S.

Table 17 First five local dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG nanobeams at different values of the first crack position ${x}_{2}$(${x}_{1}= {\text{0}}{\text{.3}} , K =0.1, \alpha =0)$

Table 18 First five local dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG nanobeams at different values of the first crack position ${x}_{2}$(${x}_{1}= {\text{0}}{\text{.3}} , K =0.1, \alpha =0.4)$

Table 19 First five local dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG nanobeams at different values of the first crack position ${x}_{2}$(${x}_{1}= {\text{0}}{\text{.3}} , K =0.35, \alpha =0)$

Table 20 First five local dimensionless frequency parameters ${\sqrt{\lambda}}$ of double cracked BDFG nanobeams at different values of the first crack position ${x}_{2}$(${x}_{1}= {\text{0}}{\text{.3}} , K =0.35, \alpha =0.4)$

Figures 20, 21, 22, 23, 24, 25, 26, 27 and 28 show the effect of the crack positions on the first, second, and third dimensionless frequency parameter ${\sqrt{\lambda}}$ of double cracked BDFG Euler–Bernoulli nanobeams for different supported cases. The effect of the first crack position on the obtained results can appear in Figs. 20, 24 and 25, while Figs. 26, 27 and 28 show the effect of the second crack position. One can notice that in a simply supported beam, the value of the fundamental frequency increases when the crack position is to be near the support, while the second frequency parameter reaches the maximum when the crack position is at the middle of the span and reaches the minimum when the crack position is at 0.25 or 0.75 of the spans. The third frequency parameter reaches the maximum when the crack position is at 0.35 or 0.65 of the spans. In C-C beam, the value of fundamental frequency decreases when the crack position is near the middle of the beam or the end of the beam. The second frequency parameter reaches the minimum when the crack position is at 0.33 or 0.65 of the spans. The third frequency parameter reaches the maximum when the crack position is at 0.35 or 0.65 of the spans. In C-S beam, the value of fundamental frequency decreases when the crack position is near to the clamped end but it increases when the crack position is near to the simple end.

Fig. 20

First dimensionless frequency parameter $\sqrt{{\lambda }_{1}}$ of BDFG nanobeam with a double crack at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the Position of the first crack ${x}_{1}$ $(\mathrm{\alpha }=0, K=0.35)$ a S-S, b C-C, and c C-S

Fig. 21

Second dimensionless frequency parameter $\sqrt{{\lambda }_{2}}$ of BDFG nanobeam with a double crack at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the Position of the first crack ${x}_{1}$ $(\mathrm{\alpha }=0, K=0.35)$ a S-S, b C-C, and c C-S

Fig. 22

Third dimensionless frequency parameter $\sqrt{{\lambda }_{3}}$ of BDFG nanobeam with a double crack at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the Position of the first crack ${x}_{1}$ $(\mathrm{\alpha }=0, K=0.35)$ a S-S, b C-C, and c C-S

Fig. 23

First dimensionless frequency parameter $\sqrt{{\lambda }_{1}}$ of BDFG nanobeam with a double crack at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the Position of the first crack ${x}_{1}$ $(\mathrm{\alpha }=0, K=0.1)$ a S-S, b C-C, and c C-S

Fig. 24

Second dimensionless frequency parameter $\sqrt{{\lambda }_{2}}$ of BDFG nanobeam with a double crack at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the Position of the first crack ${x}_{1}$ $(\mathrm{\alpha }=0, K=0.1)$ a S-S, b C-C, and c C-S

Fig. 25

Third dimensionless frequency parameter $\sqrt{{\lambda }_{3}}$ of BDFG nanobeam with a double crack at locations of ${\text{0}}{\text{.3}}$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the Position of the first crack ${x}_{1}$ $(\mathrm{\alpha }=0, K=0.1)$ a S-S, b C-C, and c C-S

Fig. 26

First dimensionless frequency parameter $\sqrt{{\lambda }_{1}}$ of BDFG nanobeam with a double crack at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the Position of the first crack ${x}_{2}$ $(\mathrm{\alpha }=0, K=0.35)$ a S-S, b C-C, and c C-S

Fig. 27

Second dimensionless frequency parameter $\sqrt{{\lambda }_{2}}$ of BDFG nanobeam with a double crack at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the Position of the first crack ${x}_{2}$ $(\mathrm{\alpha }=0, K=0.35)$ a S-S, b C-C, and c C-S

Fig. 28

Third dimensionless frequency parameter $\sqrt{{\lambda }_{3}}$ of BDFG nanobeam with a double crack at locations of $0.3$ and ${\text{0}}{\text{.7L}}$ for various boundary conditions versus the Position of the first crack ${x}_{2}$ $(\mathrm{\alpha }=0, K=0.35)$ a S-S, b C-C, and c C-S

6 Conclusion

A numerical scheme based on DQM is successfully examined to analyze the free vibration of a double cracked BDFG Euler–Bernoulli nanobeam with different boundary conditions. Further, a parametric study is employed to investigate the effect of axial gradient index $\beta$, transverse gradient index $n$, scaling effect parameter $\alpha$, and crack severity $K$ on the obtained fundamental frequency.

• (1) The frequency parameter of the double cracked BDFG Euler–Bernoulli nanobeam decreases with increasing the nonlocal parameter $\alpha$.

• (2) the axial gradient parameter β significantly impacts the dimensionless frequency parameters through its effect on the nanobeam stiffness resulting from the axial exponential index gradient profile. Both negative and positive $\beta$ values influence the fundamental frequencies differently.

• (3) The position of the cracks significantly affects the fundamental frequencies, with different optimal positions observed for different supported cases.

• (4) Increasing crack severity $K$ leads to decreased frequency parameters, and the C-C case exhibits higher frequency values compared to the C-S and S-S cases.

• (5) The fundamental frequency increases when the crack position is near the simple support, but decreases when the crack position is near the middle of the span of the C-C beam.

The obtained results have implications for structural health monitoring, enabling improved damage detection and contributing to the safety and longevity of various structures. These findings provide valuable insights that can be applied in the field of structural health monitoring and contribute to advancements in structural safety and durability.