1 Introduction

Cantilever beams with micro- and nanoscale dimensions, known as micro- and nanocantilevers, have vast applications in the micro- and nanoelectromechanical systems (MEMS and NEMS) as sensors and actuators. The mechanical sensors based on the micro- and nanocantilevers are compact and cost-effective and offer high sensitive and real-time detections. They are being used for sensing biological and chemical entities such as DNA, protein, viruses, and volatile organic compounds [1, 2]. The micro- and nanocantilever sensors have generally higher sensitivity to a mass change if they are thinner, and this makes them more prone to instability issues such as buckling. In addition, the presence of an undetected defect such as an edge crack may significantly affect the response of the micro- and nanocantilever sensors. This paper is aimed at studying the size-dependent buckling problem of the micro- and nanocantilevers with an edge crack.

It is well known that the structural elements exhibit size-dependent mechanical response at the micro- and nanoscales. Many discrete and continuum mechanics-based models are available in the literature to capture the size-dependent mechanical response of structures, e.g., [3,4,5,6,7,8]. On the one hand, the atomistic models [9], which are accurate to capture the size dependency, are computationally expensive. On the other hand, Eringen’s theory [10,11,12,13,14,15,16] based on the nonlocal continuum mechanics may be mathematically ill-posed once applied to micro- and nanocantilevers [17,18,19,20]. A computationally affordable and yet accurate enough tool for studying the size-dependent mechanical response of the micro- and nanocantilevers is offered by the stress-driven nonlocal theory of elasticity formulated in [21]. The main idea of the stress-driven theory is to use a nonlocal constitutive equation which defines the strain at each point of the body by a convolution integral in terms of the local elastic stresses at all points and a kernel function to weight the contributions of the long-range interactions. The kernel function depends on a material characteristic length parameter and can be calibrated by static and dynamic experiments [22]. Assuming an exponential form for the kernel function, the integral form of the nonlocal constitutive equation is converted to a differential equation subjected to two constitutive boundary conditions. Within the framework of the stress-driven theory, the Bernoulli–Euler governing equations are six-order differential equations in terms of the transverse displacement (i.e., the deflection of the nanobeam), which are two orders higher than those of the local Bernoulli–Euler beam model. The well-posedness of the problem is assured by the two additional constitutive boundary conditions. The applications of the stress-driven theory to different nanostructural problems can be found, for example, in [23,24,25,26,27,28,29,30,31,32,33,34].

One important extension of the stress-driven theory is presented in [23, 24], where a set of mathematically consistent continuity conditions associated with the integral form of the constitutive equation is derived. Using this formulation, it is possible to apply the stress-driven theory to problems whose solutions require discretization of the domain, such as cracked nanostructures [35, 36]. The stress-driven theory is recently used in [37] to study free transverse vibrations of cracked nanobeams.

The presence of cracks and defects can significantly change the macroscopic response and properties of materials and structures [38,39,40]. In a beam, an edge crack causes a local flexibility and results in discontinuities of displacements and slopes at the cracked cross sections. In the beam theories, the effect of the crack is usually modeled by introducing rotational and translational springs which relate the slope and the transverse displacement at the cracked cross section to the bending moment and the shear force transmitted through it [41,42,43]. The compliances of the springs can be related to the crack length using the method of the energy consideration and the theory of fracture mechanics [44, 45]. It is shown in [37] that the translational spring associated with the shear force has an important effect on the higher modes of the free transverse vibration of the nanobeams with long cracks. However, in the buckling problem of the slender Bernoulli–Euler cantilever beam under the compressive load, the effect of the translational spring is negligible [46] and, therefore, has been usually disregarded (see, for example, [47,48,49]). Note that this is true for the beams with the clamped-free boundary condition, and the effect of the translational spring might be important when dealing with the buckling of cracked beams with other types of the boundary conditions.

In this work, the model presented in [23, 24] is used to study the size-dependent buckling problem of cracked micro- and nanocantilevers. To solve the problem, the domain is divided into two sections connected to each other by a rotational spring at the cracked cross section. The slope discontinuity at the cracked cross section is assumed to be proportional to the bending moment transmitted through it. The buckling equations associated with the Bernoulli–Euler beam and the stress-driven theories are solved separately at each section. The variationally consistent and constitutive boundary and continuity conditions are imposed to determine the buckling loads and the mode shapes. Novel insightful results are presented about the effect of the crack and the nonlocality on the buckling response of the micro- and nanocantilevers. In this paper, only the conservative forces are considered; the extension of the present work to the instability of the cracked nanobeams subjected to the nonconservative forces should be presented elsewhere as the previous investigations on the flutter instability of the large-scale beams resulted in important understandings [50,51,52,53,54]. The problem definition and formulation are presented in Sect. 2. In Sect. 3, results are presented and discussed for different cases by varying the effective parameters. Conclusions of the work are given in Sect. 4.

2 Problem definition and formulation

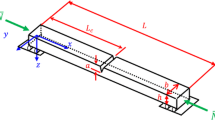
The size-dependent buckling problem of an isotropic Bernoulli–Euler nanocantilever subjected to the compressive load P, as shown in Fig. 1, is considered. The nanocantilever has a rectangular cross section and deforms under the plane stress conditions. The length, in-plane thickness, and out-of-plane width of the nanocantilever are, respectively, L, h, and b. A Cartesian coordinate system \(x - y\) is placed at the mid-thickness with origin at the left end of the nanocantilever. The nanocantilever has a crack at \(x_{{{\text{crack}}}}\) with the length of a, which divides the domain into the left and right sections. The crack is assumed to remain open during the deformation. Throughout the formulation, the notation \(f\left( x \right)^{(i)}\) denotes the ith derivative of the function \(f\left( x \right)\) with respect to x.

Fig. 1
figure 1

Cracked nanocantilever with a rectangular cross section under the compressive load P. The length, in-plane thickness, and out-of-plane width of the nanocantilever are, respectively, L, h, and b

Full size image

In order to account for the effect of the crack on the deformation of the nanocantilever, a rotational spring is placed at the cracked cross section, which causes a discontinuity in the slope proportional to the bending moment, while satisfies the transverse displacement continuity. The spring model has been widely used in the literature to account for the presence of the crack in structural problems, e.g., [37, 44, 45, 55,56,57,58,59,60,61]. Therefore, the compatibility conditions at the cracked cross section \(x_{{{\text{crack}}}}\) are:

$$\begin{aligned} & {}^{{{\text{Right}}}}v^{(1)} \left( {x_{{{\text{crack}}}} } \right) - {}^{{{\text{Left}}}}v^{(1)} \left( {x_{{{\text{crack}}}} } \right) = c_{{{\text{crack}}}} M\left( {x_{{{\text{crack}}}} } \right), \\ & {}^{{{\text{Left}}}}v\left( {x_{{{\text{crack}}}} } \right) = {}^{{{\text{Right}}}}v\left( {x_{{{\text{crack}}}} } \right) \\ \end{aligned}$$
(1)

where \({}^{{{\text{Right}}}}v\) and \({}^{{{\text{Left}}}}v\) are the transverse displacements of the right and left sections. The slopes of the right and left sections are \({}^{{{\text{Right}}}}v^{(1)}\) and \({}^{{{\text{Left}}}}v^{(1)}\), and \(M\left( {x_{{{\text{crack}}}} } \right)\) is the bending moment at the cracked cross section. The parameter \(c_{{{\text{crack}}}}\) is the crack compliance which can be related to the mode I stress intensity factor due to the bending moment. Using the method of energy consideration and the theory of fracture mechanics, the crack compliance can be derived in terms of the stress intensity factor [44, 45], which takes the following form for a rectangular beam with an edge crack under plane stress conditions [45]:

$$\begin{gathered} c_{{{\text{crack}}}} = 12Ch\int_{0}^{\zeta } {F_{M}^{2} } \left( \zeta \right){\text{d}}\zeta \quad {\text{for}}\;{ 0} \le \zeta \le 0.6, \hfill \\ F_{M} \left( \zeta \right) = \sqrt {\tan \frac{\pi \zeta }{2}} \frac{{0.923 + 0.199\left[ {1 - \sin \frac{\pi \zeta }{2}} \right]^{4} }}{{\cos \frac{\pi \zeta }{2}}}, \hfill \\ c_{{{\text{crack}}}} = 2.65335Ch\int_{0}^{\zeta } {\frac{1}{{\left( {1 - \zeta } \right)^{3} }}} {\text{d}}\zeta \quad {\text{for}}\;{ 0}{\text{.6}} < \zeta < 1 \hfill \\ \end{gathered}$$
(2)

where \(\zeta = a/h\) is the relative length of the crack with respect to the nanocantilever thickness. The parameter \(C\) is the local elastic compliance of the nanocantilever associated with the Bernoulli–Euler beam theory, and is given as \(C = 1/(EI)\) with E being Young’s modulus and \(I = bh^{3} /12\). The intact cross section can be modeled by assuming \(a = 0\) which results in \(c_{{{\text{crack}}}} = 0\) and therefore the continuity of the slopes of the right and left sections \({}^{{{\text{Right}}}}v^{(1)} = {}^{{{\text{Left}}}}v^{(1)}\).

The compatibility conditions in Eqs. (1) and (2) are applicable only to the open cracks subjected to the bending moment. However, at the nanoscale level the van der Waals forces between the atoms located at the surfaces of the crack tend to close it, and this might affect the kinematic compatibility conditions (1) and (2). In addition, these compatibility conditions might be further affected by the presence of the compressive load which tends to close the crack. These two effects might become less pronounced in longer nanobeams where the effect of the bending moment is predominant. Nevertheless, the compliance of the cracked cross section in the nanocantilever is expected to be different from that predicted by Eq. (2). Studying the effects of the above-mentioned phenomena on the kinematic compatibility conditions at the cracked cross sections in the nanobeams requires a throughout investigation. Here, in order to simplify the presentation of the results and shed light on the effect of the crack on the buckling loads of the nanobeams, the kinematic compatibility conditions at the cracked cross sections are determined based on Eqs. (1) and (2).

2.1 Governing equations

The constitutive equation based on the stress-driven nonlocal elasticity theory [21] is:

$$\chi \left( x \right) = \int_{0}^{L} {\phi_{{L_{C} }} \left( {x - \xi } \right)CM\left( \xi \right){\text{d}}\xi }$$
(3)

where \(\chi\) is the curvature. The kernel function \(\phi_{{L_{C} }} \left( x \right)\) is usually assumed as [23, 24, 35, 37]:

$$\phi_{{L_{C} }} \left( x \right) = \frac{1}{{2L_{C} }}{\text{e}}^{{\left( { - \frac{\left| x \right|}{{L_{C} }}} \right)}}$$
(4)

with \(L_{C}\) being a material length scale related to the microstructural properties. This form of the kernel function allows to replace the integral form of the constitutive Eq. (3), which is over the entire nanobeam length, with the following differential equations within the right and left sections [23, 24, 35, 37]:

$$\begin{array}{*{20}l} {{}^{{{\text{Left}}}}\chi - L_{C}^{2} {}^{{{\text{Left}}}}\chi^{(2)} = C{}^{{{\text{Left}}}}M} \hfill & {\quad {\text{for}}\;{ 0} \le x \le x_{{{\text{crack}}}} }, \hfill \\ {{}^{{{\text{Right}}}}\chi - L_{C}^{2} {}^{{{\text{Right}}}}\chi^{(2)} = C{}^{{{\text{Right}}}}M} \hfill & {\quad {\text{for}}\;x_{{{\text{crack}}}} \le x \le L} \hfill \\ \end{array}$$
(5)

subjected to the constitutive continuity conditions at the cracked cross section:

$$\begin{gathered} {}^{{{\text{Left}}}}\chi^{(1)} \left( {x_{{{\text{crack}}}} } \right) = - \frac{1}{{L_{C} }}\left[ {{}^{{{\text{Left}}}}\chi \left( {x_{{{\text{crack}}}} } \right) - \int_{{x_{{{\text{crack}}}} }}^{L} {\left( {\frac{1}{{L_{C} }}{\text{e}}^{{\frac{{x_{{{\text{crack}}}} - \xi }}{{L_{C} }}}} C{}^{{{\text{Right}}}}M\left( \xi \right)} \right){\text{d}}\xi } } \right], \hfill \\ {}^{{{\text{Right}}}}\chi^{(1)} \left( {x_{{{\text{crack}}}} } \right) = \frac{1}{{L_{C} }}\left[ {{}^{{{\text{Right}}}}\chi \left( {x_{{{\text{crack}}}} } \right) - \int_{0}^{{x_{{{\text{crack}}}} }} {\left( {\frac{1}{{L_{C} }}{\text{e}}^{{\frac{{\xi - x_{{{\text{crack}}}} }}{{L_{C} }}}} C{}^{{{\text{Left}}}}M\left( \xi \right)} \right){\text{d}}\xi } } \right], \hfill \\ \end{gathered}$$
(6)

and the constitutive boundary conditions [21]:

$$\begin{gathered} {}^{{{\text{Left}}}}\chi^{(1)} \left( 0 \right) = \frac{1}{{L_{C} }}{}^{{{\text{Left}}}}\chi \left( 0 \right), \hfill \\ {}^{{{\text{Right}}}}\chi^{(1)} \left( L \right) = - \frac{1}{{L_{C} }}{}^{{{\text{Right}}}}\chi \left( L \right). \hfill \\ \end{gathered}$$
(7)

The derivation of Eqs. (5)–(7) can be found in [23, 24, 35, 37].

Accounting for the curvature–deflection relation of the Bernoulli–Euler beam, \(\chi = v^{(2)}\), Eqs. (5)–(7) are written in terms of the transverse displacements:

$$\begin{gathered} \begin{array}{*{20}l} {{}^{{{\text{Left}}}}v^{(2)} - L_{C}^{2} {}^{{{\text{Left}}}}v^{(4)} = C{}^{{{\text{Left}}}}M} \hfill & {\quad {\text{for}}\;{ 0} \le x \le x_{{{\text{crack}}}} }, \hfill \\ {{}^{{{\text{Right}}}}v^{(2)} - L_{C}^{2} {}^{{{\text{Right}}}}v^{(4)} = C{}^{{{\text{Right}}}}M} \hfill & {\quad {\text{for}}\;x_{{{\text{crack}}}} \le x \le L}, \hfill \\ \end{array} \hfill \\ \hfill \\ \end{gathered}$$
(8)
$$\begin{gathered} {}^{{{\text{Left}}}}v^{(3)} \left( {x_{{{\text{crack}}}} } \right) = - \frac{1}{{L_{C} }}\left[ {{}^{{{\text{Left}}}}v^{(2)} \left( {x_{{{\text{crack}}}} } \right) - \int_{{x_{{{\text{crack}}}} }}^{L} {\left( {\frac{1}{{L_{C} }}{\text{e}}^{{\frac{{x_{{{\text{crack}}}} - \xi }}{{L_{C} }}}} \left[ {{}^{{{\text{Right}}}}v^{(2)} \left( \xi \right) - L_{C}^{2} {}^{{{\text{Right}}}}v^{(4)} \left( \xi \right)} \right]} \right){\text{d}}\xi } } \right], \hfill \\ {}^{{{\text{Right}}}}v^{(3)} \left( {x_{{{\text{crack}}}} } \right) = \frac{1}{{L_{C} }}\left[ {{}^{{{\text{Right}}}}v^{(2)} \left( {x_{{{\text{crack}}}} } \right) - \int_{0}^{{x_{{{\text{crack}}}} }} {\left( {\frac{1}{{L_{C} }}{\text{e}}^{{\frac{{\xi - x_{{{\text{crack}}}} }}{{L_{C} }}}} \left[ {{}^{{{\text{Left}}}}v^{(2)} \left( \xi \right) - L_{C}^{2} {}^{{{\text{Left}}}}v^{(4)} \left( \xi \right)} \right]} \right){\text{d}}\xi } } \right], \hfill \\ \end{gathered}$$
(9)
$$\begin{gathered} {}^{{{\text{Left}}}}v^{(3)} \left( 0 \right) = \frac{1}{{L_{C} }}{}^{{{\text{Left}}}}v^{(2)} \left( 0 \right), \hfill \\ {}^{{{\text{Right}}}}v^{(3)} \left( L \right) = - \frac{1}{{L_{C} }}{}^{{{\text{Right}}}}v^{(2)} \left( L \right). \hfill \\ \end{gathered}$$
(10)

The Euler–Bernoulli buckling equation of the deformed configuration, \(M^{(2)} + Pv^{(2)} = 0\), can be written in terms of the transverse displacement for the left and right sections using the constitutive Eq. (8):

$$\begin{array}{*{20}l} {L_{C}^{2} {\kern 1pt} {}^{{{\text{Left}}}}v^{(6)} - {}^{{{\text{Left}}}}v^{(4)} - CP{\kern 1pt} {}^{{{\text{Left}}}}v^{(2)} = 0} \hfill & {\quad {\text{for}}\;\;{ 0} \le x \le x_{{{\text{crack}}}} }, \hfill \\ {L_{C}^{2} {\kern 1pt} {}^{{{\text{Right}}}}v^{(6)} - {}^{{{\text{Right}}}}v^{(4)} - CP{\kern 1pt} {}^{{{\text{Right}}}}v^{(2)} = 0} \hfill & {\quad {\text{for}}\;\; \, x_{{{\text{crack}}}} \le x \le L}. \hfill \\ \end{array}$$
(11)

The governing differential Eqs. (11) are sixth-order ordinary differential equations, which differ from the classical fourth-order equation of the Bernoulli–Euler beam theory. The higher-order differential equations justify the necessity of the higher-order constitutive boundary and continuity conditions given in Eqs. (9) and (10). The solutions of Eq. (11) are in terms of twelve unknown constants, which must satisfy four constitutive boundary and continuity conditions in Eqs. (9) and (10), as well as the following four variationally consistent continuity conditions at the cracked cross sections:

$$\begin{aligned} & {}^{{{\text{Right}}}}v^{(1)} \left( {x_{{{\text{crack}}}} } \right) - {}^{{{\text{Left}}}}v^{(1)} \left( {x_{{{\text{crack}}}} } \right) = c_{{{\text{crack}}}} \frac{{\left( {{}^{{{\text{Right}}}}v^{(2)} \left( {x_{{{\text{crack}}}} } \right) - L_{C}^{2} \,{}^{{{\text{Right}}}}v^{(4)} \left( {x_{{{\text{crack}}}} } \right)} \right)}}{C}, \\ & {}^{{{\text{Left}}}}v\left( {x_{{{\text{crack}}}} } \right) = {}^{{{\text{Right}}}}v\left( {x_{crack} } \right), \\ & {}^{{{\text{Left}}}}v^{(2)} \left( {x_{{{\text{crack}}}} } \right) - L_{C}^{2} {}^{{{\text{Leftt}}}}v^{(4)} \left( {x_{crack} } \right) = {}^{{{\text{Right}}}}v^{(2)} \left( {x_{{{\text{crack}}}} } \right) - L_{C}^{2} \,{}^{{{\text{Right}}}}v^{(4)} \left( {x_{{{\text{crack}}}} } \right), \\ & \frac{1}{C}\left[ {{}^{{{\text{Left}}}}v^{(3)} \left( {x_{{{\text{crack}}}} } \right) - L_{C}^{2} {}^{{{\text{Leftt}}}}v^{(5)} \left( {x_{{{\text{crack}}}} } \right)} \right] + P\,{}^{{{\text{Left}}}}v^{(1)} \left( {x_{{{\text{crack}}}} } \right) \\ & \quad =\frac{1}{C}\left[ {{}^{{{\text{Right}}}}v^{(3)} \left( {x_{{{\text{crack}}}} } \right) - L_{C}^{2} {}^{{{\text{Right}}}}v^{(5)} \left( {x_{{{\text{crack}}}} } \right)} \right] + P{}^{{{\text{Right}}}}\,v^{(1)} \left( {x_{{{\text{crack}}}} } \right). \\ \end{aligned}$$
(12)

The first and second equations account for the compatibility conditions at the cracked cross section as given in Eq. (1). The third and fourth equations, respectively, satisfy the continuity of the bending moment and the shear force at the cracked cross section.

The remaining four clamped-free boundary conditions are:

$$\begin{aligned} & {}^{{{\text{Left}}}}v^{(1)} \left( 0 \right) = 0, \\ & {}^{{{\text{Left}}}}v\left( 0 \right) = 0, \\ & {}^{{{\text{Right}}}}v^{(2)} \left( L \right) - L_{C}^{2} {}^{{{\text{Right}}}}v^{(4)} \left( L \right) = 0, \\ & \frac{1}{C}\left[ {{}^{{{\text{Right}}}}v^{(3)} \left( L \right) - L_{C}^{2} {}^{{{\text{Right}}}}v^{(5)} \left( L \right)} \right] + P{}^{{{\text{Right}}}}v^{(1)} \left( L \right) = 0. \\ \end{aligned}$$
(13)

The formulation presented in this Section is also applicable to the micro- and nanobeams with other types of constraints by replacing the clamped-free boundary conditions given in Eq. (13) with appropriate edge conditions.

2.2 Dimensionless equations

Introducing the following dimensionless parameters:

$$\begin{gathered} \lambda = \frac{{L_{C} }}{L}; \,\eta = \frac{v}{L}; \,\overline{x} = \frac{x}{L}; \,\overline{h} = \frac{h}{L}, \hfill \\ \overline{P} = \frac{{PL^{2} C}}{{\pi^{2} }};\, \overline{c}_{{{\text{crack}}}} = \frac{{c_{{{\text{crack}}}} }}{CL} \hfill \\ \end{gathered}$$
(14)

the governing Eqs. (11) in terms of the dimensionless parameters are:

$$\begin{array}{*{20}l} {\lambda^{2} {}^{{{\text{Left}}}}\eta^{(6)} - {}^{{{\text{Left}}}}\eta^{(4)} - \overline{P}\pi^{2} {}^{{{\text{Left}}}}\eta^{(2)} = 0} \hfill & {\quad {\text{for }}\quad {0} \le \overline{x} \le \overline{x}_{{{\text{crack}}}} }, \hfill \\ {L_{C}^{2} {}^{{{\text{Right}}}}\eta^{(6)} - {}^{{{\text{Right}}}}\eta^{(4)} - \overline{P}\pi^{2} {}^{{{\text{Right}}}}\eta^{(2)} = 0} \hfill & {\quad {\text{ for }}\quad \overline{x}_{{{\text{crack}}}} \le \overline{x} \le 1}. \hfill \\ \end{array}$$
(15)

Similarly, the constitutive boundary and continuity conditions in Eqs. (9) and (10) in terms of the dimensionless parameters are:

$$\begin{aligned} {}^{{{\text{Left}}}}\eta^{(3)} \left( {\overline{x}_{{{\text{crack}}}} } \right) & = - \frac{1}{\lambda }\left[ {{}^{{{\text{Left}}}}\eta^{(2)} \left( {\overline{x}_{{{\text{crack}}}} } \right) - \int_{{\overline{x}_{{{\text{crack}}}} }}^{1} {\left( {\frac{1}{\lambda }e^{{\frac{{\overline{x}_{{{\text{crack}}}} - \xi }}{\lambda }}} \left[ {{}^{{{\text{Right}}}}\eta^{(2)} \left( \xi \right) - \lambda^{2} \;{}^{{{\text{Right}}}}\eta^{(4)} \left( \xi \right)} \right]} \right){\text{d}}\xi } } \right], \\ {}^{{{\text{Right}}}}\eta^{(3)} \left( {\overline{x}_{{{\text{crack}}}} } \right) & = \frac{1}{\lambda }\left[ {{}^{{{\text{Right}}}}\eta^{(2)} \left( {\overline{x}_{{{\text{crack}}}} } \right) - \int_{0}^{{\overline{x}_{{{\text{crack}}}} }} {\left( {\frac{1}{\lambda }e^{{\frac{{\xi - \overline{x}_{{{\text{crack}}}} }}{\lambda}}} \left[ {{}^{{{\text{Left}}}}\eta^{(2)} \left( \xi \right) - \lambda^{2} \;{}^{{{\text{Left}}}}\eta^{(4)} \left( \xi \right)} \right]} \right){\text{d}}\xi } } \right] \\ \end{aligned}$$
(16)

and

$$\begin{gathered} {}^{{{\text{Left}}}}\eta^{(3)} \left( 0 \right) = \frac{1}{\lambda }{}^{{{\text{Left}}}}\eta^{(2)} \left( 0 \right), \hfill \\ {}^{{{\text{Right}}}}\eta^{(3)} \left( 1 \right) = - \frac{1}{\lambda }{}^{{{\text{Right}}}}\eta^{(2)} \left( 1 \right). \hfill \\ \end{gathered}$$
(17)

Also, the variationally consistent continuity and boundary conditions (12) and (13) in terms of the dimensionless parameters are:

$$\begin{aligned} & {}^{{{\text{Right}}}}\eta^{(1)} \left( {\overline{x}_{{{\text{crack}}}} } \right) - {}^{{{\text{Left}}}}\eta^{(1)} \left( {\overline{x}_{{{\text{crack}}}} } \right) = \overline{c}_{{{\text{crack}}}} \left[ {{}^{{{\text{Right}}}}\eta^{(2)} \left( {\overline{x}_{{{\text{crack}}}} } \right) - \lambda^{2} \;{}^{{{\text{Right}}}}\eta^{(4)} \left( {\overline{x}_{{{\text{crack}}}} } \right)} \right], \\ & {}^{{{\text{Left}}}}\eta \left( {\overline{x}_{{{\text{crack}}}} } \right) = {}^{{{\text{Right}}}}\eta \left( {\overline{x}_{{{\text{crack}}}} } \right), \\ & {}^{{{\text{Left}}}}\eta^{(2)} \left( {\overline{x}_{{{\text{crack}}}} } \right) - \lambda^{2} \;{}^{{{\text{Left}}}}\eta^{(4)} \left( {\overline{x}_{{{\text{crack}}}} } \right) = {}^{{{\text{Right}}}}\eta^{(2)} \left( {\overline{x}_{{{\text{crack}}}} } \right) - \lambda^{2} \;{}^{{{\text{Right}}}}\eta^{(4)} \left( {\overline{x}_{{{\text{crack}}}} } \right), \\ & \left[ {{}^{{{\text{Left}}}}\eta^{(3)} \left( {\overline{x}_{{{\text{crack}}}} } \right) - \lambda^{2} \;{}^{{{\text{Left}}}}\eta^{(5)} \left( {\overline{x}_{{{\text{crack}}}} } \right)} \right] + \overline{P}\pi^{2} \;{}^{{{\text{Left}}}}\eta^{(1)} \left( {\overline{x}_{{{\text{crack}}}} } \right) \\ & = \left[ {{}^{{{\text{Right}}}}\eta^{(3)} \left( {\overline{x}_{{{\text{crack}}}} } \right) - \lambda^{2} \;{}^{{{\text{Right}}}}\eta^{(5)} \left( {\overline{x}_{{{\text{crack}}}} } \right)} \right] + \overline{P}\pi^{2} \;{}^{{{\text{Right}}}}\eta^{(1)} \left( {\overline{x}_{{{\text{crack}}}} } \right), \\ \end{aligned}$$
(18)

and

$$\begin{aligned} & {}^{{{\text{Left}}}}\eta^{(1)} \left( 0 \right) = 0, \\ & {}^{{{\text{Left}}}}\eta \left( 0 \right) = 0, \\ & {}^{{{\text{Right}}}}\eta^{(2)} \left( 1 \right) - \lambda^{2} {}^{{{\text{ Right}}}}\eta^{(4)} \left( 1 \right) = 0, \\ & \left[ {{}^{{{\text{Right}}}}\eta^{(3)} \left( 1 \right) - \lambda^{2} {}^{\text{ Right}}\eta^{(5)} \left( 1 \right)} \right] + \overline{P}\pi^{2} {}^{{{\text{Right}}}}\eta^{(1)} \left( 1 \right) = 0. \\ \end{aligned}$$
(19)

The dimensionless equations governing the buckling of the left and the right sections of the nanobeam and given in Eq. (15) are linear homogeneous sixth-order ordinary differential equations with constant coefficients. These equations are solved in closed form using the solution technique developed in [26] and briefly outlined in the following. The solution of these equations has the general exponential form of \(A{\text{e}}^{{\beta \overline{x}}}\) with A and \(\beta\) being unknown constants. Substituting the general forms of the solutions into the equations, sixth-order algebraic characteristic equations associated with the differential Eqs. (15) are derived. The characteristic equations are then solved in closed form by expressing them in terms of the third-order algebraic equations using the change of variable technique. Having the roots of the characteristic equations, the closed-form solutions of Eq. (15) are obtained in terms of twelve unknown constants. The closed-form solutions are then used to impose the twelve boundary and continuity conditions (16)–(19). This results in a homogeneous system of algebraic equations whose nontrivial solution exists only if the determinant of the coefficient matrix vanishes. This leads to the calculation of the buckling loads of the cracked nanocantilevers.

3 Results and discussion

The presented formulation in Sect. 2 is applied here to determine the buckling loads and associated mode shapes of cracked nanocantilevers. First, the validity of the model is tested against the available results in the literature for the intact and cracked local and nonlocal cantilever beams. Then, the effects of the crack length and location, as well as the nonlocal parameter, \(\lambda\), on the buckling loads and mode shapes are studied, also for higher modes of buckling.

3.1 Verification

The ratios between the buckling loads of a nonlocal cantilever beam with a crack at the mid-span and those of a local cantilever beam presented in [61] are shown in Fig. 2a on varying the nonlocal parameter. The crack has the length of \({a \mathord{\left/ {\vphantom {a {h = 0.31}}} \right. \kern-\nulldelimiterspace} {h = 0.31}}\), and the thickness-to-length ratio is \({h \mathord{\left/ {\vphantom {h {L = 0.05}}} \right. \kern-\nulldelimiterspace} {L = 0.05}}\). The predictions of the present model converge to those given in [61] based on the local Bernoulli–Euler beam theory for \(\lambda \to 0\).

Fig. 2
figure 2

a Ratios between the buckling loads of the nonlocal and local nanocantilevers with a crack at the mid-span on varying the nonlocal parameter. The dimensionless crack length and the thickness-to-length ratio are \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 0.31\) and \({h \mathord{\left/ {\vphantom {h L}} \right. \kern-\nulldelimiterspace} L} = 0.05\). Results tend to those given in [61] for the local cracked beam. b Ratios between the buckling loads of the cracked and intact nanocantilevers on varying the crack length. The crack is located at the mid-span and \({h \mathord{\left/ {\vphantom {h L}} \right. \kern-\nulldelimiterspace} L} = 0.05\). Results are presented for the nonlocal parameter \(\lambda\) equal to 0 (local model) and 0.5, and tend to those given in [26] for the intact nanobeams

Full size image

The ratios between the buckling loads of the cracked nanocantilevers and those of the intact nanocantilevers given in [26] based on the stress-driven nonlocal theory and the Bernoulli–Euler beam model are presented in Fig. 2b on varying the mid-span crack length. The thickness-to-length ratio is \({h \mathord{\left/ {\vphantom {h {L = 0.05}}} \right. \kern-\nulldelimiterspace} {L = 0.05}}\). Results are presented for the nonlocal parameter \(\lambda\) equal to 0 (local model) and 0.5. As shown in the Figure, the results of the present model tend to those of the model in [26] for shorter crack lengths.

3.2 Effects of crack and nonlocality

The ratios between the buckling loads of the cracked and intact nanocantilevers with \({h \mathord{\left/ {\vphantom {h {L = 0.05}}} \right. \kern-\nulldelimiterspace} {L = 0.05}}\) are shown in Fig. 3a on varying the crack length. The crack is located at the mid-span. Results are presented for the nonlocal parameter \(\lambda\) equal to 0 (local model), 0.25, and 0.5. The buckling loads of the nanocantilevers decrease for longer crack lengths due to the additional compliance brought to the system by the crack. The reduction in the buckling loads of the cracked nanocantilevers is higher for higher values of the nonlocal parameter. This shows that the buckling loads of the nanocantilevers are more sensitive to the presence of edge cracks than the large-scale cantilever beams. For example, the presence of a crack with the length of \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 0.5\) at the mid-span of a local nanocantilever (i.e., \(\lambda = 0\)) reduces the buckling load by 15%. This percentage reduction for the nanocantilevers with the nonlocal parameter equal to 0.25 and 0.5 is, respectively, 20 and 27%.

Fig. 3
figure 3

a Ratios between the buckling loads of the cracked and intact nanocantilevers on varying the crack length. The crack is located at the mid-span and \({h \mathord{\left/ {\vphantom {h L}} \right. \kern-\nulldelimiterspace} L} = 0.05\). Results are presented for the nonlocal parameter \(\lambda\) equal to 0 (local model), 0.25, and 0.5. b Ratios between the buckling loads of the nonlocal and local nanocantilevers on varying the nonlocal parameter. The nanocantilevers have one crack at \(\overline{x}_{{{\text{crack}}}} = 0.2\), and the thickness-to-length ratio is \({h \mathord{\left/ {\vphantom {h L}} \right. \kern-\nulldelimiterspace} L} = 0.05\). Results are presented for the crack length \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h}\) equal to 0 (intact nanocantilever), 0.3, and 0.6

Full size image

Similar to the observation in [26] for the intact nanobeams, the nonlocality increases the buckling loads of the cracked nanocantilevers due to the additional stiffness brought to the system by the nonlocality associated with the stress-driven formulation. This is illustrated in Fig. 3b, where the ratios between the buckling loads of the nonlocal and local nanocantilevers with \({h \mathord{\left/ {\vphantom {h {L = 0.05}}} \right. \kern-\nulldelimiterspace} {L = 0.05}}\) are presented on varying the nonlocal parameter. The crack is located at \(\overline{x}_{{{\text{crack}}}} = 0.2\). Results are given for the crack length \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h}\) equal to 0 (intact nanocantilever), 0.3, and 0.6. For all the cases, the buckling load increases by increasing the nonlocal parameter, i.e., nanocantilevers made of materials with the characteristic lengths comparable with the nanocantilever dimensions. However, the effect of the nonlocal parameter on the buckling loads decreases for nanocantilevers with longer cracks. For instance, changing the nonlocal parameter from 0 to 0.5 increases the buckling load by 97, 84, and 45% for the cases with the crack length \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h}\) equal to, respectively, 0 (intact nanocantilever), 0.3, and 0.6.

The crack location is also an important parameter which may significantly affect the buckling loads. This is shown in Fig. 4, where the ratios between the buckling loads of the cracked and intact nanocantilevers are presented on varying the dimensionless crack location for the nonlocal parameter \(\lambda\) equal to 0 (local model), 0.25, and 0.5. Results are presented for \({h \mathord{\left/ {\vphantom {h {L = 0.05}}} \right. \kern-\nulldelimiterspace} {L = 0.05}}\) and the crack length \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h}\) equal to 0.1, 0.3, and 0.5. For all the cases, the effect of the crack is higher when it is located closer to the clamped end. This is because the bending moment associated with the first mode of the buckling is higher at the cross sections closer to the fixed end, and based on Eq. (1), the discontinuity of the slope at the cracked cross section is higher.

Fig. 4
figure 4

Ratios between the buckling loads of the cracked and intact nanocantilevers on varying the dimensionless crack location for the nonlocal parameter \(\lambda\) equal to a 0 (local model), b 0.25, and c 0.5. Results are presented for \({h \mathord{\left/ {\vphantom {h L}} \right. \kern-\nulldelimiterspace} L} = 0.05\) and the crack length \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h}\) equal to 0.1, 0.3, and 0.5

Full size image

The buckling loads are more sensitive to the crack location for the nanocantilevers with higher nonlocal parameters and longer cracks. For example, changing the crack location \(\overline{x}_{{{\text{crack}}}}\) in the nanocantilever with \(\lambda = 0.25\) from 0.5 to 0.1 reduces the buckling load by 1, 5, and 15%, for the cases with \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h}\) equal to, respectively, 0.1, 0.3, and 0.5. This percentage reduction in the nanocantilever with \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 0.5\) is 12, 15, and 18%, is for the cases with \(\lambda\) equal to, respectively, 0, 0.25, and 0.5.

3.3 Higher modes of buckling

The formulated model can be readily applied to calculate the buckling loads of the higher modes. The critical loads of the first three modes of buckling are presented in Table 1 for nanocantilevers with \({h \mathord{\left/ {\vphantom {h {L = 0.05}}} \right. \kern-\nulldelimiterspace} {L = 0.05}}\) and one crack at the mid-span. Results are presented for the crack length \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h}\) equal to 0 (intact nanocantilever), 0.2, and 0.4, and for the nonlocal parameter \(\lambda\) equal to 0 (local model), 0.25, and 0.5.

Table 1 Dimensionless buckling loads of a nanocantilever with \({h \mathord{\left/ {\vphantom {h L}} \right. \kern-\nulldelimiterspace} L} = 0.05\) and one crack at the mid-span having the length-to-thickness ratio \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h}\) equal to 0 (intact nanocantilever), 0.2, and 0.4
Full size table

It can be understood from the results in the Table that the effect of the nonlocal parameter is higher for the higher modes of buckling. The first, second, and third buckling loads of the nanocantilever with \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 0.4\) increase, respectively, 35, 132, and 178%, due to the change of the nonlocal parameter from 0 to 0.25. Also for the higher modes of buckling the critical load reduces by increasing the crack length. However, the reduction depends on the bending moment at the cracked cross section and is not necessarily higher for higher modes of buckling. For example, the presence of the mid-span crack with \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 0.4\) in the nanocantilever with \(\lambda = 0.25\) reduces the buckling loads of the first and second modes by 12 and 11%, respectively, compared to those of the intact nanocantilever.

The mode shapes associated with the first three modes of buckling of intact and cracked nanocantilevers are presented in Fig. 5. The crack has the length of \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 0.4\) and is located at \(\overline{x}_{{{\text{crack}}}} = 0.7\). The mode shapes are shown for the nonlocal parameter \(\lambda\) equal to 0 (local model) and 0.5. The presence of the crack significantly changes the higher mode shapes, but has a negligible effect on that of the first mode. When the characteristic length scale is comparable with the geometrical dimensions, i.e., the nonlocal nanocantilever, the mode shapes are different from those of the local nanocantilever. For instance, the effect of the crack on the second and third modes of buckling is more noticeable in the nonlocal nanocantilever.

Fig. 5
figure 5

First three buckling mode shapes of local and nonlocal (\(\lambda = 0.5\)), intact and cracked nanocantilevers with \({h \mathord{\left/ {\vphantom {h L}} \right. \kern-\nulldelimiterspace} L} = 0.05\). The crack has the length of \({a \mathord{\left/ {\vphantom {a h}} \right. \kern-\nulldelimiterspace} h} = 0.4\) and is located at \(\overline{x}_{{{\text{crack}}}} = 0.7\)

Full size image

4 Conclusions

The mechanical sensors based on the micro- and nanocantilevers are being used for sensing biological and chemical entities. The size-dependent buckling problem of cracked micro- and nanocantilevers has been studied in this paper. The influence of the crack has been modeled by introducing a rotational spring, which relates the slope discontinuity and the bending moment at the cracked cross section. The crack compliance has been related to its length using the available equations in the literature based on the method of energy consideration and the theory of fracture mechanics. The buckling equations of the portions of the nanocantilever at the left and right of the cracked cross section have been derived and solved separately, based on the stress-driven nonlocal theory and the Bernoulli–Euler beam model. The variationally consistent and constitutive boundary and continuity conditions have been imposed to define the buckling loads and the mode shapes. It has been shown that the results of the present model converge to those of the intact nanocantilevers available in the literature for vanishing crack lengths. Moreover, the results tend to the available results in the literature for local cracked cantilever beams when the nonlocal parameter goes to zero. It has been observed that the buckling loads of the micro- and nanocantilevers reduce for longer cracks. The effect of the crack on the buckling loads is more highlighted when it is located closer to the fixed end. The nonlocality increases the buckling loads. However, the effect of the nonlocality on the buckling loads is weaker when the micro- or nanocantilever has an edge crack. It has been shown that the effect of the crack on the mode shapes is more noticeable for higher modes of buckling. The formulation presented in this paper is also applicable to the micro- and nanobeams with other types of constraints by adopting appropriate boundary conditions.