Analytical study of the annular flow of a generalised Phan-Thien–Tanner fluid

Abstract

The annular flow of complex viscoelastic fluids, described by the generalised Phan-Thien–Tanner model, is studied. This model considers the Mittag-Leffler function instead of the usual linear or exponential functions of the trace of the stress tensor, and includes two new parameters that provide additional fitting flexibility. We derive a semi-analytical solution that provides a better understanding of the behaviour of this type of fluid in annular flows and also helps to improve the modelling of complex materials.

1 Introduction

Viscoelastic materials, such as polymer melts, polymer solutions, and biofluids (e.g. blood, saliva, proteins) have complex behaviour. To better model and understand their rheological behaviour, several constitutive equations have been proposed in the literature. In this study, we consider the study of annular fluid flows that are commonly encountered in industrial processes such as drilling, cable coating, and food processing. In these processes, the fluids are mixtures of various substances, such as water, particles, oils, and other long-chain molecules, that impart the fluid with various non-Newtonian properties.

The literature has many analytical and numerical solutions for annular flows using different constitutive rheological models or different boundary conditions [1,2,3,4,5,6,7,8,9,10,11]. Among them, all the different variants of the Phan-Thien–Tanner (PTT) model have already been studied (linear, quadratic, exponential), except for the more recent PTT model, which uses the Mittag-Leffler function and is called the generalized Phan-Thien–Tanner (gPTT) model [12]. The gPTT model considers the Mittag-Leffler function instead of the classical linear and exponential functions of the trace of the stress tensor (linear PTT and exponential PTT, respectively) to ensure a much wider rheology coverage range and uses two new fitting constants to provide such additional fitting flexibility to the description of the rheological properties of viscoelastic fluids.

Using this constitutive equation, in this work we propose a new approach by deriving a new semi-analytical solution for the annular flow domain. Note that this model was previously studied for Couette and pressure-driven flows, and also in combined electro-osmotic/pressure-driven flows (see [13,14,15]). The obtained solutions allow the characterization of the velocity profile in annuli and can be used to validate the numerical methods and results.

The remainder of this paper is organized as follows: the next section presents the governing equations, followed by the new analytical solution in Sect. 3, the discussion of the results in Sect. 4 and the closure of the paper in Sect. 5.

2 Formulation and governing equations

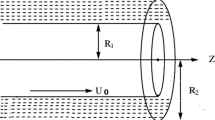
We consider the pressure-driven annular flow of a viscoelastic gPTT fluid, as shown in Fig. 1, where R is the radius of the outer cylinder and aR is the radius of the inner cylinder.

Fig. 1

Schematic of the flow in an annular region

The equations governing the flow of an isothermal incompressible fluid are the continuity equation

$$\begin{aligned} \nabla \cdot \textbf{u}=0, \end{aligned}$$

(1)

and the linear momentum equation

$$\begin{aligned} \rho \frac{\textrm{D} \textbf{u}}{\textrm{D}t}=-\nabla p + \nabla \cdot {\varvec{\sigma }}, \end{aligned}$$

(2)

where $\textbf{u}$ is the velocity vector, $\frac{\textrm{D}}{\textrm{D}t}$ is the material derivative, p is the pressure, t is the time, $\rho$ is the fluid density and ${\varvec{\sigma }}$ is the extra-stress tensor.

2.1 Constitutive equation

In order to achieve a closed system of equations, a constitutive equation for the extra-stress tensor, ${\varvec{\sigma }}$, must be defined. Recently, Ferrás et al. [12] proposed a new differential rheological model based on the Phan-Thien–Tanner constitutive equation (PTT model [16, 17]), derived from the Lodge–Yamamoto type of network theory for polymeric fluids. This new model considers a more general function for the rate of destruction of junctions, the Mittag-Leffler function, where two fitting constants are included, in order to achieve additional fitting flexibility [12]. More details about this model are discussed in [12].

The Mittag-Leffler function is defined by

$$\begin{aligned} E_{\alpha ,\beta }\left( z\right) =\sum _{j=0}^{\infty }\frac{z^j}{\Gamma \left( \alpha j+\beta \right) }, \end{aligned}$$

(3)

where $\alpha$, $\beta$ are real and positive values and $\Gamma$ is the Gamma function. When $\alpha =\beta =1$, the Mittag-Leffler function reduces to the exponential function, and when $\beta =1$ the original one-parameter Mittag-Leffler function, $E_\alpha$, is obtained [18].

The constitutive equation of the gPTT model is given by

$$\begin{aligned} K(\sigma _{kk}){\varvec{\sigma }} +\lambda \overset{\square }{{{\varvec{\sigma }}}}= 2\eta _p\textbf{D}, \end{aligned}$$

(4)

where $\sigma _{kk}$ is the trace of the extra stress tensor, $\lambda$ is the relaxation time and $\eta _p$ is the polymeric viscosity coefficient. $\textbf{D}$ is the rate of deformation tensor and function $K(\sigma _{kk})$ is given by

$$\begin{aligned} K(\sigma _{kk})=\Gamma \left( \beta \right) E_{\alpha ,\beta }\left( \frac{\varepsilon \lambda }{\eta _p}\sigma _{kk}\right) , \end{aligned}$$

(5)

where the normalization $\Gamma \left( \beta \right)$ is used to ensure that $K(0)=1$ for all choices of $\beta$, and $\varepsilon$ represents the extensibility parameter. $\overset{\square }{{{\varvec{\sigma }}}}$ represents the Gordon-Schowalter derivative, defined as

$$\begin{aligned} \overset{\square }{{{\varvec{\sigma }}}}=\frac{\partial {\varvec{\sigma }}}{\partial t} + {\textbf {u}}\cdot \nabla {\varvec{\sigma }}-\left( \nabla {\textbf {u}}\right) ^T\cdot {\varvec{\sigma }}-{\varvec{\sigma }} \cdot \left( \nabla {\textbf {u}}\right) +\xi \left( {\varvec{\sigma }} \cdot {\textbf {D}} + {\textbf {D}} \cdot {\varvec{\sigma }} \right) , \end{aligned}$$

(6)

where $\nabla \textbf{u}$ is the velocity gradient and the constant parameter $\xi$ accounts for the slip between the molecular network and the continuum.

3 Semi-analytical solution for the gPTT model in annuli

We derive the analytical solution for the gPTT model considering a steady fully-developed pressure-driven annular flow (cf. Fig. 1). We consider a unidirectional flow in cylindrical coordinates, where the outer radius is R and the inner radius is aR, with $0<a<1$. Therefore, the momentum equation, Eq. (2), simplifies to

$$\begin{aligned} \frac{1}{r}\frac{\textrm{d}\left( r\sigma _{rz}\right) }{\textrm{d}r}=P_z, \end{aligned}$$

(7)

where $P_z \equiv \frac{\textrm{d}p}{\textrm{d}z}$ is the constant streamwise pressure gradient and $\sigma _{rz}$ is the shear stress.

In order to obtain closed form analytical solutions the slip parameter in the Gordon-Schowalter derivative, Eq. (6), was set to $\xi =0$. So, the constitutive equation for the gPTT model in this flow (Sect. 2.1) can be further simplified, leading to:

$$\begin{aligned}{} & {} K(\sigma _{kk})\sigma _{zz}=2\lambda \dot{\gamma }\sigma _{rz}, \end{aligned}$$

(8)

$$\begin{aligned}{} & {} K(\sigma _{kk})\sigma _{rr}=0, \end{aligned}$$

(9)

$$\begin{aligned}{} & {} K(\sigma _{kk})\sigma _{rz}=\eta _p\dot{\gamma }, \end{aligned}$$

(10)

where the velocity gradient $\dot{\gamma }$ is a function of r ($\dot{\gamma }(r)\equiv \frac{\textrm{d}u}{\textrm{d}r}$) and $\sigma _{kk}=\sigma _{\theta \theta }+\sigma _{zz}+\sigma _{rr}$ is the trace of the extra stress tensor. Under fully-developed flow conditions, $\sigma _{\theta \theta }=0$ and $\sigma _{rr}=0$, the trace of the extra stress tensor becomes $\sigma _{kk}=\sigma _{zz}$.

Integration of the momentum equation results in

$$\begin{aligned} \sigma _{rz}=\frac{P_z}{2}r+\frac{c}{r}, \end{aligned}$$

(11)

where c is a constant of integration. Assuming that $\sigma _{rz}=0$ at $r=bR$ (the location of the maximum velocity, see Fig. 1), with $a<b<1$, we calculate the integration constant $(c=-(P_z/2)b^2R^2)$, resulting in the following shear stress distribution,

$$\begin{aligned} \sigma _{rz}=\frac{-P_zbR}{2}\left( \frac{bR}{r}-\frac{r}{bR}\right) . \end{aligned}$$

(12)

Dividing Eq. (8) by Eq. (10) results in the following relationship between normal and shear stresses,

$$\begin{aligned} \sigma _{zz}=\frac{2\lambda }{\eta _p}\sigma _{rz}^2. \end{aligned}$$

(13)

Solving Eq. (8) for $\dot{\gamma }$, and using Eqs. (12) and (13) results in the following velocity gradient distribution:

$$\begin{aligned} \frac{\text {d}u}{\text {d}r}=-\frac{\Gamma (\beta )}{\eta _p}\frac{P_zbR}{2}\left( \frac{bR}{r}-\frac{r}{bR}\right) E_{\alpha ,\beta }\left( \frac{2\varepsilon \lambda ^2}{\eta _p^2}\left( \frac{P_zbR}{2}\left( \frac{bR}{r}-\frac{r}{bR}\right) \right) ^2\right) . \end{aligned}$$

(14)

The velocity gradient can be written in dimensionless form, using the Weissenberg number, $Wi = \lambda U_c/\delta$, where $U_c=-P_z\delta ^2/\eta _p$ is a characteristic velocity of the flow and $\delta$ is the gap between the two cylinders in the annulus. We also define $\overline{u}=u/U_c$ as the dimensionless velocity and $\overline{r}=r/\delta$ as the normalized radius/distance between the inner and outer cylinders ($\overline{R}=R/\delta$). This gives the following dimensionless velocity gradient:

$$\begin{aligned} \frac{\textrm{d}\overline{u}}{\textrm{d}\overline{r}}=\frac{\Gamma (\beta )}{2} \left( \frac{b^2 \overline{R}^2}{\overline{r}}-\overline{r}\right) E_{\alpha ,\beta }\left( \frac{\varepsilon {Wi}^2}{2} \left( \frac{b^2 \overline{R}^2}{\overline{r}}-\overline{r}\right) ^2\right) . \end{aligned}$$

(15)

Now, we can obtain the velocity profile numerically by solving the following nonlinear problem:

Problem 1

Given $\varepsilon {Wi}^2$ and a, find the value of b that satisfies,

$$\begin{aligned} \int _{a\overline{R}}^{\overline{R}} \frac{\textrm{d}\overline{u}}{\textrm{d}\overline{r}}~d\overline{r}=0. \end{aligned}$$

(16)

Using the value of b, compute the velocity profile:

$$\begin{aligned} \overline{u}(\overline{r})=\int _{a\overline{R}}^{\overline{r}} \frac{\Gamma (\beta )}{2} \left( \frac{b^2 \overline{R}^2}{\overline{r}}-\overline{r}\right) E_{\alpha ,\beta }\left( \frac{\varepsilon {Wi}^2}{2} \left( \frac{b^2 \overline{R}^2}{\overline{r}}-\overline{r}\right) ^2\right) ~d\overline{r}, \end{aligned}$$

(17)

where $0<a<1$ is defined by the user. Equation (17) results from the no-slip boundary condition, $\overline{u}(\overline{R})=0$. The velocity profile in Eq. (17) can be easily approximated numerically by a simple quadrature rule. The solution of Eq. (16) can be obtained by defining $F(b)=\displaystyle \int _{a\overline{R}}^{\overline{R}} \frac{\text {d}\overline{u}}{\text {d}\overline{r}}~d\overline{r}$. So, there exists $0<a<b<1$ such that $F(b)=0$.

Equation (15) can be further expanded using the definition of the Mittag-Leffler function, resulting in

$$\begin{aligned} \frac{\textrm{d}\overline{u}}{\textrm{d}\overline{r}}&= \frac{\Gamma (\beta )}{2} \left( \frac{b^2 \overline{R}^2}{\overline{r}}-\overline{r}\right) \sum _{j=0}^{\infty }\frac{1}{\Gamma \left( \alpha j+\beta \right) }\left( \frac{\varepsilon {Wi}^2}{2} \left( \frac{b^2 \overline{R}^2}{\overline{r}}-\overline{r}\right) ^2\right) ^j \end{aligned}$$

(18)

$$\begin{aligned}&= \frac{\Gamma (\beta )}{2} \sum _{j=0}^{\infty }\frac{1}{\Gamma \left( \alpha j+\beta \right) }\left( \frac{\varepsilon {Wi}^2}{2} \right) ^j\left( \frac{b^2 \overline{R}^2}{\overline{r}}-\overline{r}\right) ^{2j+1} \end{aligned}$$

(19)

and the velocity profile can be obtained from the integration of each term in this sum, leading to the following expression:

$$\begin{aligned} \overline{u}(\overline{r})= \frac{\Gamma (\beta )}{2} \sum _{j=0}^{\infty }\frac{1}{\Gamma \left( \alpha j+\beta \right) }\left( \frac{\varepsilon {Wi}^2}{2} \right) ^j \int _{a\overline{R}}^{\overline{r}}\left( \frac{b^2 \overline{R}^2}{\overline{r}}-\overline{r}\right) ^{2j+1}d\overline{r} \end{aligned}$$

(20)

The integral $\int \left( \frac{A}{\overline{r}}-\overline{r}\right) ^{2j+1}d\overline{r}$, with $A=b^2 \overline{R}^2$, can be easily computed, using the Newton’s binomial. So, the velocity profile, is given by:

$$\begin{aligned} \overline{u}(\overline{r})= \frac{\Gamma (\beta )}{2} \sum _{j=0}^{\infty }\frac{1}{\Gamma \left( \alpha j+\beta \right) }\left( \frac{\varepsilon {Wi}^2}{2} \right) ^j \left[ \sum _{k=0}^{2j+1}{2j+1 \atopwithdelims ()k}\int _{a\overline{R}}^{\overline{r}} \left( \frac{b^2 \overline{R}^2}{\overline{r}}\right) ^{2j+1-k}(-\overline{r})^{k}d\overline{r}\right] \end{aligned}$$

(21)

that can be rewritten as:

$$\begin{aligned} \overline{u}(\overline{r})= \frac{\Gamma (\beta )}{2} \sum _{j=0}^{\infty }\frac{1}{\Gamma \left( \alpha j+\beta \right) }\left( \frac{\varepsilon {Wi}^2}{2} \right) ^j \left[ \sum _{k=0}^{2j+1}{2j+1 \atopwithdelims ()k}(-1)^k\left( b^2 \overline{R}^2\right) ^{2j+1-k} f_{kj} \left( a, \overline{r}\right) \right] \end{aligned}$$

(22)

where:

$$\begin{aligned} f_{kj} \left( a, \overline{r}\right) = {\left\{ \begin{array}{ll} \textrm{ln}\left( \frac{\overline{r}}{a\overline{R}}\right) , \, &{} \text {if}\,k=j.\\ \frac{\overline{r}^{2(k-j)}-(a\overline{R})^{2(k-j)}}{2(k-j)}, &{} \text {if}\,k \ne j. \end{array}\right. } \end{aligned}$$

(23)

Although Eq. (22) is an infinite series, we can obtain an approximated solution with a fair number of correct decimal places by using only $j=3$ or $j=4$ (depending on the problem and the parameters used). This will be explored in detail in the next section.

The second relevant problem from a practical point of view is the corresponding inverse problem of determining the pressure gradient for a given flow rate. In this second case, the following equation must be solved,

$$\begin{aligned} U = \frac{1}{\pi {R}^2(1-a^2)}\int _{a R}^{R} u(r)2\pi {r}~d{r} \end{aligned}$$

(24)

where $\pi {R}^2(1-a^2)$ is the cross section area of the annular region and U is the average velocity in the annular region. Equation (24) in dimensionless form becomes:

$$\begin{aligned} \frac{2}{\overline{R}^2(1-a^2)}\int _{a\overline{R}}^{\overline{R}} \overline{u}(\overline{r})\overline{r}~d\overline{r}-\frac{U}{U_c}=0 \end{aligned}$$

(25)

In this scenario, we can formulate the next problem:

Problem 2

Given $\varepsilon Wi^2_U$ $\left( Wi_U=\lambda U/\delta \right)$ and a, find b and $\varepsilon Wi^2$ such that,

$$\begin{aligned} \overline{u}(\overline{R})=0 ~~~ \wedge ~~~ \frac{2}{\overline{R}^2(1-a^2)}\int _{a\overline{R}}^{\overline{R}} u(\overline{r})\overline{r}~d\overline{r}-\frac{U}{U_c}=0. \end{aligned}$$

(26)

Then use the values of b and $\varepsilon Wi^2$ to compute the velocity profile given by Eq. (22). Note that $U/U_c=Wi_U/Wi$.

4 Results and discussion

4.1 Assessment of the series solution

In this subsection, we compare the numerical solution of the velocity profile given by Eq. (17), with the analytical solution of Eq. (22). These results were obtained using the Mathematica software and we first consider a high-precision numerical solution, where we obtain the value of b using the secant method and then we numerically integrate Eq. (15). This highly accurate numerical solution of the velocity profile was then used as a reference to perform an investigation of the influence of the number of terms in the series on the error of the solution. The new truncated solution is obtained from Eq. (22), truncating the sum with $j+1$ terms. We considered 200 equidistant mesh points along the cylinder gap and measured the maximum relative error obtained at these points (boundaries excluded). The error is calculated by $\frac{\left| \overline{u}(\overline{r})_{num} - \overline{u}(\overline{r})_{t} \right| }{\overline{u}(\overline{r})_{num}}$, where $\overline{u}(\overline{r})_{num}$ is the approximate value of the velocity and $\overline{u}(\overline{r})_{t}$ is the velocity value from the truncated series. Three different values of $\varepsilon Wi^2$ were considered: 0.05, 3.2 and 5. We set $\beta =1$ and tested two different values of $\alpha$, 0.5 and 1.5. We only changed the values of $\alpha$, because this parameter induces more changes in the series. The value of a used was 0.5 in all cases.

In Table 1, we show the maximum relative errors, in percentage. For $\varepsilon Wi^2=0.05$, the error was low, even when considering a single term in the series [Eq. (22)]. For $\alpha =1.5$ we see that the error is much smaller, with the decrease in error becoming less pronounced as the number of terms in the series increases. This is due to the number of significant digits considered.

Table 1 Maximum relative errors (in percentage) for $\varepsilon Wi^2=0.05$

Tables 2 and 3 show the maximum relative errors in percentage for $\varepsilon Wi^2=3.2$ and 5, respectively. As we increase $\varepsilon Wi^2$, the series solution shows convergence problems, and as we increase $\alpha$ (see Table 3), the error decreases faster as the number of terms in the series increases (note also that in this case we even consider a higher $\varepsilon Wi^2$ value). The corresponding velocity profiles are shown in Fig. 2, where $u/U_c$ is the velocity profile normalised by the characteristic velocity, using the highly accurate numerical solution. These particular results indicate that the velocity profile converges to the correct profile as the number of terms in the series increases, and that this convergence is slower for low values of $\alpha$.

Table 2 Maximum relative errors (in percentage) for $\varepsilon Wi^2=3.2$

Table 3 Maximum relative errors (in percentage) for $\varepsilon Wi^2=5$

Fig. 2

Velocity profiles for $\beta =1$, $\alpha =0.5,~1.5$ and two different values of $\varepsilon Wi^2$, 3.2 and 5. a $\alpha =0.5$; b $\alpha =1.5$

Based on these observations, we will consider $j=15$ for the results presented next.

4.2 Problem 1

Figure 3 shows the velocity profiles for $\beta =1$, $\alpha =0.5,~1,~3$ at three different values of the $\varepsilon Wi^2$ of 0.05, 1 and 3.2.

For $\varepsilon Wi^2=0.05$ (Fig. 3a) the velocity profiles for different values of $\alpha$ almost overlap. However, when we increase $\varepsilon Wi^2$ to 1, that no longer happens, in fact we obtain the highest velocity and flow rate for $\alpha =0.5$, the case in which we have the highest rate of destruction of junctions. This behaviour is more pronounced when we increase elasticity (see Fig. 3b). For $\varepsilon Wi^2=3.2$, the differences in the flow rates are obvious, except for $\alpha =3$, where the velocity profile almost overlaps with the case $\varepsilon Wi^2=1$. It is interesting to see that for $\alpha =\beta =1$ we still have a parabolic velocity profile typical of Newtonian fluids, while decreasing $\alpha$ we observe a very pronounced plug-like profile, which is more typical of shear-thinning fluids.

Fig. 3

Velocity profiles for $\beta =1$, $\alpha =0.5,~1\text { and }3$. a $\varepsilon Wi^2=0.05\text { and }1$; b $\varepsilon Wi^2=1\text { and }3.2$

Fig. 4

Normalized shear rate profiles for $\varepsilon Wi^2=3.2$ and $\alpha =0.5,~1\text { and }3$

To understand the slope variation of the velocity profile across the cylinder gap (for different $\alpha$ values), we also plotted the corresponding normalized shear rate, in Fig. 4. This way we have an idea of how much higher shear rates near the wall are for low values of $\alpha$.

Figures 5a, b show the normalized shear and normal stress profiles, for $\beta =1$, $\alpha =0.5,~1\text { and }3$ for $\varepsilon Wi^2= 3.2$. For the three cases, the dimensionless normal stress is always positive and the dimensionless shear stress shows a quasi-linear profile, being positive near the inner cylinder and negative in the vicinity of the outer cylinder. The shear stress is smaller for low values of $\alpha$ since the values of b decrease with decreasing $\alpha$ (see also Eq. (15)).

Fig. 5

Normalized shear and normal stress profiles, for $\beta =1$, $\alpha =0.5,~1\text { and }3$ and $\varepsilon Wi^2= 3.2$. a Normalized shear stress; b normalized normal stress

Figures 6a, b and c show the influence of $\beta$ on the velocity profile. The results are similar to those for the variation of $\alpha$. For a small value of $\varepsilon Wi^2$ (Fig. 6a), the velocity profiles almost overlap for all values of $\beta$, but as $\varepsilon Wi^2$ is increased (Fig. 6b, c), the velocity and the flow rate increase as we decrease $\beta$. That effect is more pronounced for small values of $\beta$.

Fig. 6

Velocity profiles for $\alpha =1$, $\beta =0.5,~1\text { and }3$; a $\varepsilon Wi^2= 0.05\text { and }1$; b $\varepsilon Wi^2= 1\text { and }3.2$; c $\varepsilon Wi^2= 3.2\text { and }5$

The role of $\beta$ is more complex than that of $\alpha$. $\beta$ is used as an argument of the Mittag-Leffler function and to normalize $K(\sigma _{zz})$. This mixed effect of $\beta$ on the rate of destruction of junctions results in smoother variations of velocity due to the variation of $\beta$.

We also study the variations of b with $\varepsilon Wi^2$ (see Fig. 7). We considered three different values of $\alpha$, $0.5,~1 \text {and}~3$ and calculated b for different $\varepsilon Wi^2$. We see that the value of b decreases with the increase of $\varepsilon Wi^2$, and that for $\alpha =3$, the variation is almost linear. Notice that, when $\alpha =0.5$, the reduction is more pronounced. Figure 7 shows that b decreases with the increase of the fluid elasticity, a trend also observed on the velocities profiles of Fig. 6, since the b represents the radial position of the maximum value for the velocity profile. Therefore, the point of maximum velocity approaches the inner cylinder wall as the elasticity of the fluid increases, because of the direct relationship between elasticity and shear-thinning of the shear viscosity.

Fig. 7

Variation of b with the variation $\varepsilon Wi^2$, for $\alpha =0.5,~1\text { and }3$. The closed circle corresponds to value of b obtained for a Newtonian fluid [1, 19]

4.3 Problem 2

This problem is harder to solve because for a given value of the flow rate, U, we have to find b and $\varepsilon Wi^2$ ($\varepsilon Wi^2=\varepsilon \left( \lambda U_c/\delta \right) ^2 = \varepsilon \left( -\lambda \delta P_z/\eta _p\right) ^2$) from a system of two strongly nonlinear equations. The first equation come from the outer wall boundary condition,

$$\begin{aligned} \frac{\Gamma (\beta )}{2} \sum _{j=0}^{\infty }\frac{1}{\Gamma \left( \alpha j+\beta \right) }\left( \frac{\varepsilon {Wi}^2}{2} \right) ^j \left[ \sum _{k=0}^{2j+1}{2j+1 \atopwithdelims ()k}(-1)^k\left( b^2 \overline{R}^2\right) ^{2j+1-k}\left[ f_{kj}(a,\overline{R})\right] \right] =0; \end{aligned}$$

(27)

and the second from the imposed non-dimensionless flow rate

$$\begin{aligned} \frac{\Gamma (\beta )}{\overline{R}^2(1-a^2)} \sum _{j=0}^{\infty }\frac{1}{\Gamma \left( \alpha j+\beta \right) }\left( \frac{\varepsilon {Wi}^2}{2} \right) ^j \left[ \sum _{k=0}^{2j+1}{2j+1 \atopwithdelims ()k}(-1)^k\left( b^2 \overline{R}^2\right) ^{2j+1-k}\left[ h_{kj}(a,\overline{R})\right] \right] -\frac{Wi_U}{Wi}=0\nonumber , \\ \end{aligned}$$

(28)

where $h_{kj}(a,\overline{R})=\overline{R}-a\overline{R}$ if $k=j$ and $h_{kj}(a,\overline{R})=\frac{\overline{R}^{2(k-j)+1}-(a\overline{R})^{2(k-j)+1}}{2(k-j)+1}$ if $k\ne j$. Note that $U/U_c=Wi_U/Wi$, as in Eq. (26).

Since one of the goals of this work is to provide a tool for validating future numerical implementations of this constitutive model in general numerical codes, the Mathematica codes used to obtain the solution are provided as supplementary material.

Fig. 8

Normalized velocity profiles for $\beta =1$ and $\alpha =0.75,~1\text { and }1.25$. a $\varepsilon Wi^2_U=0.05$; b $\varepsilon Wi^2_U=0.2\text { and }0.25$

Figure 8 shows the normalized velocity profiles for $\beta =1$, $\alpha =0.75,~1\text { and }1.25$, $a=0.5$, and, for three different values of $\varepsilon Wi^2_U$: 0.05, 0.2 and 0.25.

For the lowest $\varepsilon Wi^2_U$ (Fig. 8a), the velocity profiles are similar, with higher velocities for lower values of $\alpha$, and, the plug-like profile typical of non-Newtonian fluids is less pronounced due to the low elasticity. Again, this confirms the idea that the lower values of $\alpha$ lead to more plug-like profiles due to the intense shear-thinning.

This effect is more pronounced in Fig. 8b, where we compare the results for two moderate values of elasticity. The combination of a higher $\varepsilon Wi^2_U$ and a lower value of $\alpha$ leads to a less parabolic velocity profile.

The combined effect of elasticity and parameters $\alpha$ and $\beta$ leads to a complex relationship. Physically, we have that a higher rate of destruction of junctions in the network (lower $\alpha$) allows for a faster creation of a new network. For Problem 1, this resulted in a higher flow rate, giving the idea that, this high destruction rate results in less resistance of the flow. When the flow rate is imposed, we observe that the information from the boundary conditions travels at a slower velocity, allowing for a more plug-like profile to be possible.

5 Conclusions

We derived an analytical solution for the velocity profile in series form for the annular flow of a gPTT fluid. A semi-analytic solution is derived for the case where the flow rate is imposed.

We show the influence of the model parameters on the velocity and stress profiles. As expected, the flow velocity increases with the decrease of $\alpha$ and $\beta$ for the same $\varepsilon Wi^2$, resulting in a more pronounced plug-like profile. The influence of $\beta$ is less pronounced due to its double influence on the proposed rate of destruction of junctions (it is a parameter of the Mittag-Leffler function and is also used as a normalization factor).

The analytical and semi-analytical solutions presented in this work are useful for the validation of CFD codes and also provide a better understanding of the model behaviour in simple shear flows.