Skip to main content
SpringerLink
Log in

Vibrational analysis of transversely isotropic hollow cylinder based on fractional generalized thermoelastic diffusion models with nonlocal effects

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

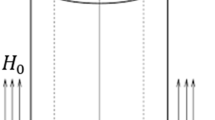
Due to numerous applications of micro-/nano-sized structures in medical, electrical, mechanical, and aeronautical engineering, etc., mathematical modelling of thermoelastic diffusive responses of these structures has become a hot topic of investigation. The inclusion of fractional-order derivatives in these models brings out more productive results. Thus considering fractional generalized thermoelastic diffusion model with nonlocal elastic effects, transient responses of a transversely isotropic hollow cylinder are analysed. The medium is held at undisturbed state initially and periodically varying thermal and continuous concentration loadings applied at the outer boundary of the cylinder. Assuming the plane strain and axisymmetry in the cylinder, the problem is reduced to one dimension which is solved using Laplace transformation along with inversion technique. The objective of this work is to theoretically investigate the impact of nonlocal and fractional-order parameters on thermophysical quantities of a transversely isotropic hollow cylinder and consideration of diffusion phenomenon along with the said effects augments the novelty of this work. Thus, the graphical representation of the results reveals that displacement is less perturbed with the introduction of the nonlocal elastic parameter. The fractional-order parameter has an increasing impact on thermal and diffusion profiles. Time has varying degrees of influence on all the physical quantities.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Abbreviations

b :

Measure of diffusive effect

c :

Measure of thermodiffusive effect

C :

Mass concentration

P :

Chemical potential per unit mass

S :

Entropy per unit mass

T :

Temperature (above the reference temperature \(T_0\))

\(\alpha \) :

Fractional parameter

\(\rho \) :

Mass density

\(\xi \) :

Nonlocal elastic parameter

\(a_{ij}\) :

Thermal modulus tensor

\(b_{ij}\) :

Diffusion modulus tensor

\(c_E\) :

Specific heat at constant strain

\(c_{ijkl}\) :

Elastic parameters

\(d_{ij}\) :

Diffusivity coefficient tensor

\(e_{ij}\) :

Strain tensor

\(K_{ij}\) :

Thermal conductivity tensor

\(u_i\) :

Components of displacement vector

\(q_i\) :

Components of heat flux vector

\(\delta _{ij}\) :

Kronecker’s delta

\(\eta _i\) :

Components of mass flux vector

\(\sigma _{ij}\) :

Stress tensor

\(\tau _0,\tau _1\) :

Thermal relaxation times

\(\tau ^0,\tau ^1\) :

Diffusion relaxation times

\(\nabla \) :

Gradient operator

References

  1. Biot, M.A.: Thermoelasticity and irreversible thermodynamics. J. Appl. Phys. 27, 240–253 (1956). https://doi.org/10.1063/1.1722351

    Article  MathSciNet  Google Scholar 

  2. Lord, H.W., Shulman, Y.: A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 15, 299–309 (1967). https://doi.org/10.1016/0022-5096(67)90024-5

    Article  Google Scholar 

  3. Green, A.E., Lindsay, K.A.: Thermoelasticity. J. Elast. 2, 1–7 (1972). https://doi.org/10.1007/BF00045689

    Article  Google Scholar 

  4. Green, A.E., Naghdi, P.: A re-examination of the basic postulates of thermomechanics. Proc. R. Soc. Lond. A Math. Phys. Sci. 432, 171–194 (1991). https://doi.org/10.1098/rspa.1991.0012

    Article  MathSciNet  Google Scholar 

  5. Green, A.E., Naghdi, P.: On undamped heat waves in an elastic solid. J. Therm. Stress. 15, 253–264 (1992). https://doi.org/10.1080/01495739208946136

    Article  MathSciNet  Google Scholar 

  6. Green, A.E., Naghdi, P.: Thermoelasticity without energy dissipation. J. Elast. 31, 189–208 (1993). https://doi.org/10.1007/BF00044969

    Article  MathSciNet  Google Scholar 

  7. Tzou, D.Y.: A unified field approach for heat conduction from macro-to micro-scales. J. Heat Transf. 117, 8–16 (1995). https://doi.org/10.1115/1.2822329

    Article  Google Scholar 

  8. Chandrasekharaiah, D.S.: Hyperbolic thermoelasticity: a review of recent literature. Appl. Mech. Rev. 51, 705–729 (1998). https://doi.org/10.1115/1.3098984

    Article  Google Scholar 

  9. El-Karamany, A.S., Ezzat, M.A.: On the dual-phase-lag thermoelasticity theory. Meccanica 49, 79–89 (2014). https://doi.org/10.1007/s11012-013-9774-z

    Article  MathSciNet  Google Scholar 

  10. Roy Choudhuri, S.K.: On a thermoelastic three-phase-lag model. J. Therm. Stress. 30, 231–238 (2007). https://doi.org/10.1080/01495730601130919

    Article  Google Scholar 

  11. Ezzat, M.A.: Fundamental solution in thermoelasticity with two relaxation times for cylindrical regions. Int. J. Eng. Sci. 33, 2011–2020 (1995). https://doi.org/10.1016/0020-7225(95)00050-8

    Article  Google Scholar 

  12. Sherief, H.H., Ezzat, M.A.: A problem in generalized magneto-thermoelasticity for an infinitely long annular cylinder. J. Eng. Math. 34, 387–402 (1998). https://doi.org/10.1023/A:1004376014083

    Article  MathSciNet  Google Scholar 

  13. Ezzat, M.A., Bary, A.A.: State space approach of two-temperature magneto-thermoelasticity with thermal relaxation in a medium of perfect conductivity. Int. J. Eng. Sci. 47, 618–630 (2009). https://doi.org/10.1016/j.ijengsci.2008.12.012

    Article  MathSciNet  Google Scholar 

  14. Quintanilla, R.: Moore–Gibson–Thompson thermoelasticity. Math. Mech. Solids 24, 4020–4031 (2019). https://doi.org/10.1177/1081286519862007

    Article  MathSciNet  Google Scholar 

  15. Megahid, S.F., Abouelregal, A.E., Ahmad, H., Fahmy, M.A., Abu-Zinadah, H.: A generalized More–Gibson–Thompson heat transfer model for the study of thermomagnetic responses in a solid half-space. Results Phys. 51, 106619 (2023). https://doi.org/10.1016/j.rinp.2023.106619

    Article  Google Scholar 

  16. Megahid, S.F., Abouelregal, A.E., Askar, S.S., Marin, M.: Study of thermoelectric responses of a conductive semi-solid surface to variable thermal shock in the context of the Moore–Gibson–Thompson thermoelasticity. Axioms 12, 659 (2023). https://doi.org/10.3390/axioms12070659

    Article  Google Scholar 

  17. Abouelregal, A.E., Tiwari, R., Nofal, T.A.: Modeling heat conduction in an infinite media using the thermoelastic MGT equations and the magneto-Seebeck effect under the influence of a constant stationary source. Arch. Appl. Mech. 93, 2113–2128 (2023). https://doi.org/10.1007/s00419-023-02375-7

    Article  Google Scholar 

  18. Abouelregal, A.E., Moaaz, O., Khalil, K.M., Abouhawwash, M., Nasr, M.E.: A phase delay thermoelastic model with higher derivatives and two temperatures for the hall current effect on a micropolar rotating material. J. Vib. Eng. Technol. 1–19 (2023). https://doi.org/10.1007/s42417-023-00922-8

  19. Askar, S.S., Abouelregal, A.E., Foul, A., Sedighi, H.M.: Pulsed excitation heating of semiconductor material and its thermomagnetic response on the basis of fourth-order MGT photothermal model. Acta Mech. 1–19 (2023). https://doi.org/10.1007/s00707-023-03639-7

  20. Nowacki, W.: Dynamic problems of thermodiffusion in elastic solids. Proc. Vib. Probl. 15, 105–128 (1974)

    MathSciNet  Google Scholar 

  21. Sherief, H.H., Hamza, F.A., Saleh, H.A.: The theory of generalized thermoelastic diffusion. Int. J. Eng. Sci. 42, 591–608 (2004). https://doi.org/10.1016/j.ijengsci.2003.05.001

    Article  MathSciNet  Google Scholar 

  22. Sharma, K.: Analysis of deformation due to inclined load in generalized thermodiffusive elastic medium. Int. J. Eng. Sci. Technol. 3, 117–129 (2011). https://doi.org/10.4314/ijest.v3i2.68139

    Article  Google Scholar 

  23. Eringen, A.C.: Theory of nonlocal thermoelasticity. Int. J. Eng. Sci. 12, 1063–1077 (1974). https://doi.org/10.1016/0020-7225(74)90033-0

    Article  Google Scholar 

  24. Balta, F., Suhubi, E.S.: Theory of nonlocal generalised thermoelasticity. Int. J. Eng. Sci. 15, 579–588 (1977). https://doi.org/10.1016/0020-7225(77)90054-4

    Article  Google Scholar 

  25. Dhaliwal, J.W.R.S.: Uniqueness in generalized nonlocal thermoelasticity. J. Therm. Stress. 16, 71–77 (1993). https://doi.org/10.1080/01495739308946217

    Article  MathSciNet  Google Scholar 

  26. Ezzat, M.A., El-Karamany, A.S., El-Bary, A.A.: Generalized thermo-viscoelasticity with memory-dependent derivatives. Int. J. Mech. Sci. 89, 470–475 (2014). https://doi.org/10.1016/j.ijmecsci.2014.10.006

    Article  Google Scholar 

  27. Ezzat, M.A., El-Bary, A.A.: Magneto-thermoelectric viscoelastic materials with memory-dependent derivative involving two-temperature. Int. J. Appl. Electromagn. Mech. 50, 549–567 (2016). https://doi.org/10.3233/JAE-150131

    Article  Google Scholar 

  28. Ezzat, M.A., El-Karamany, A.S., El-Bary, A.A.: On dual-phase-lag thermoelasticity theory with memory-dependent derivative. Mech. Adv. Mater. Struct. 24, 908–916 (2017). https://doi.org/10.1080/15376494.2016.1196793

    Article  Google Scholar 

  29. Gilhotra, G. Sharma, P.K.: A spherical cavity problem with nonlocal elastic effect considering memory-dependent thermoelastic diffusion and laser pulse heat source. Waves Random Complex Med. 1–19 (2021). https://doi.org/10.1080/17455030.2021.1976436

  30. Ezzat, M.A., Ezzat, S.M., Alduraibi, N.S.: On size-dependent thermo-viscoelasticity theory for piezoelectric materials. Waves Random Complex Med. 1–23 (2022). https://doi.org/10.1080/17455030.2022.2043569

  31. Ezzat, M.A., Ezzat, S.M., Alkharraz, M.Y.: State-space approach to nonlocal thermo-viscoelastic piezoelectric materials with fractional dual-phase lag heat transfer. Int. J. Numer. Method. Heat Fluid Flow 32, 3726–3750 (2022). https://doi.org/10.1108/HFF-02-2022-0097

    Article  Google Scholar 

  32. Ezzat, M.A., Al-Muhiameed, Z.I.: Thermo-mechanical response of size-dependent piezoelectric materials in thermo-viscoelasticity theory. Steel Compos. Struct. 45, 535–546 (2022). https://doi.org/10.12989/scs.2022.45.4.535

  33. Abouelregal, A.E., Nasr, M.E., Moaaz, O., Sedighi, H.M.: Thermo-magnetic interaction in a viscoelastic micropolar medium by considering a higher-order two-phase-delay thermoelastic model. Acta Mech. 234, 2519–2541 (2023). https://doi.org/10.1007/s00707-023-03513-6

    Article  MathSciNet  Google Scholar 

  34. Abel, N.H.: Solution de quelques problémes à l’aide d’intégrales définies. Oeuvres 1, 11–27 (1881)

    Google Scholar 

  35. Martínez-Salgado, B.F., Rosas-Sampayo, R., Torres-Hernández, A., Fuentes, C.: Application of fractional calculus to oil industry. Fract. Anal. Appl. Phys. Eng. Technol. 21–42 (2017). https://doi.org/10.5772/intechopen.68571

  36. Ezzat, M.A., Fayik, M.A.: Fractional order theory of thermoelastic diffusion. J. Therm. Stress. 34, 851–872 (2011). https://doi.org/10.1080/01495739.2011.586274

    Article  Google Scholar 

  37. Ezzat, M.A.: Magneto-thermoelasticity with thermoelectric properties and fractional derivative heat transfer. Phys. B: Condens. Matter. 406, 30–35 (2011). https://doi.org/10.1016/j.physb.2010.10.005

    Article  Google Scholar 

  38. Ezzat, M.A., El-Bary, A.A.: MHD free convection flow with fractional heat conduction law. Magnetohydrodynamics 48, 587–606 (2012). https://doi.org/10.22364/mhd.48.4.1

    Article  Google Scholar 

  39. Ezzat, M.A., El-Bary, A.A., Fayik, M.A.: Fractional Fourier law with three-phase lag of thermoelasticity. Mech. Adv. Mater. Struct. 20, 593–602 (2013). https://doi.org/10.1080/15376494.2011.643280

    Article  Google Scholar 

  40. Ezzat, M.A., El-Bary, A.A.: Effects of variable thermal conductivity and fractional order of heat transfer on a perfect conducting infinitely long hollow cylinder. Int. J. Therm. Sci. 108, 62–69 (2016). https://doi.org/10.1016/j.ijthermalsci.2016.04.020

    Article  Google Scholar 

  41. Ezzat, M.A., El-Karamany, A.S., El-Bary, A.A.: Two-temperature theory in Green–Naghdi thermoelasticity with fractional phase-lag heat transfer. Microsyst. Tech. 24, 951–961 (2018). https://doi.org/10.1007/s00542-017-3425-6

    Article  Google Scholar 

  42. Gilhotra, G., Sharma, P.K.: Visco-thermodiffusive elastic interactions in plate within the framework of two-temperature fractional thermoelastic models. Ind. J. Phys. 96, 3867–3879 (2022). https://doi.org/10.1007/s12648-022-02313-3

    Article  Google Scholar 

  43. Geetanjali, G., Bajpai, A., Sharma, P.K.: Impact of variable thermal conductivity and diffusivity on two temperature fractional thermodiffusive elastic half space with dual phase lags. Waves Random Complex Med. 1–23 (2022). https://doi.org/10.1080/17455030.2022.2063987

  44. Deswal, S., Punia, B.S., Kalkal, K.K.: Propagation of waves at an interface between a transversely isotropic rotating thermoelastic solid half space and a fiber-reinforced magneto-thermoelastic rotating solid half space. Acta Mech. 230, 2669–2686 (2019). https://doi.org/10.1007/s00707-019-02418-7

    Article  MathSciNet  Google Scholar 

  45. Hayati, Y., Havaei, G., Eslami, A.: Complete general solution for Lord–Shulman generalized thermoelastodynamics by using potential functions for transversely isotropic solids. Acta Mech. 230, 2751–2769 (2019). https://doi.org/10.1007/s00707-019-02423-w

    Article  MathSciNet  Google Scholar 

  46. Singh, B., Singla, H.: The effect of rotation on the propagation of waves in an incompressible transversely isotropic thermoelastic solid. Acta Mech. 231, 2485–2495 (2020). https://doi.org/10.1007/s00707-020-02662-2

    Article  MathSciNet  Google Scholar 

  47. Sheoran, S.S., Chaudhary, S., Deswal, S.: Thermo-mechanical interactions in a nonlocal transversely isotropic material with rotation under Lord-Shulman model. Waves Random Complex Med. 1–25 (2021). https://doi.org/10.1080/17455030.2021.1986648

  48. Sharma, S.R., Mehalwal, J.C., Sarkar, N., Sharma, D.K.: Vibration analysis of electro-magneto transversely isotropic nonlocal thermoelastic cylinder with voids material. Eur. J. Mech. A/Solids. 92, 104455 (2022). https://doi.org/10.1016/j.euromechsol.2021.104455

    Article  Google Scholar 

  49. Sokolnikoff, I.S.: Mathematical Theory of Elasticity. McGraw-Hill Book Company, Inc., New York/London (1956)

    Google Scholar 

  50. Hamza, F., Abdou, M., Abd El-Latief, A.M.: Generalized fractional thermoelasticity associated with two relaxation times. J. Therm. Stress. 37, 1080–1098 (2014). https://doi.org/10.1080/01495739.2014.936196

    Article  Google Scholar 

  51. Bajpai, A., Sharma, P.K., Kumar, R.: Modeling of thermoelastic diffusion plate under two temperature, fractional-order, and temperature-dependent material properties. J. Appl. Math. Mech. 101, e202000321 (2021). https://doi.org/10.1002/zamm.202000321

    Article  MathSciNet  Google Scholar 

  52. Ghavanloo, E., Rafii-Tabar, H., Fazelzadeh, S.A.: Computational Continuum Mechanics of Nanoscopic Structures. Springer International Publishing, Berlin (2019)

    Book  Google Scholar 

  53. Abouelregal, A.E.: Fractional order generalized thermo-piezoelectric semi-infinite medium with temperature-dependent properties subjected to a ramp-type heating. J. Therm. Stress. 34, 1139–1155 (2011)

    Article  Google Scholar 

  54. Ezzat, M.A., El-Karamany, A.S.: Theory of fractional order in electro-thermoelasticity. Eur. J. Mech. A/Solids. 30, 491–500 (2011). https://doi.org/10.1016/j.euromechsol.2011.02.004

    Article  Google Scholar 

  55. Abouelregal, A.E., Elhagary, M.A., Soleiman, A., Khalil, K.M.: Generalized thermoelastic-diffusion model with higher-order fractional time-derivatives and four-phase-lags. Mech. Based Des. Struct. Mach. 50, 897–914 (2022). https://doi.org/10.1080/15397734.2020.1730189

    Article  Google Scholar 

  56. Strunin, D.V.: On characteristic times in generalized thermoelasticity. J. Appl. Mech. 68, 816–817 (2001). https://doi.org/10.1115/1.1386696

    Article  Google Scholar 

  57. Tiwari, R., Abouelregal, A.E.: Thermo-viscoelastic transversely isotropic rotating hollow cylinder based on three-phase lag thermoelastic model and fractional Kelvin–Voigt type. Acta Mech. 233, 2453–2470 (2022). https://doi.org/10.1007/s00707-022-03234-2

    Article  MathSciNet  Google Scholar 

  58. Sharma, J.N., Kumari, N., Sharma, K.K.: Disturbance due to thermal and mass loads in generalized elasto-thermodiffusive solids. Int. J. Thermophys. 30, 1697–1723 (2009). https://doi.org/10.1007/s10765-009-0638-7

    Article  Google Scholar 

  59. Adomian, G.: A review of the decomposition method in applied mathematics. J. Math. Anal. Appl. 135, 501–544 (1988). https://doi.org/10.1016/0022-247X(88)90170-9

    Article  MathSciNet  Google Scholar 

  60. He, J.H.: Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 178, 257–262 (1999). https://doi.org/10.1016/S0045-7825(99)00018-3

    Article  MathSciNet  Google Scholar 

  61. He, J.H.: Variational iteration method-a kind of non-linear analytical technique: some examples. Int. J. Non Linear. Mech. 34, 699–708 (1999). https://doi.org/10.1016/S0020-7462(98)00048-1

    Article  Google Scholar 

  62. LeVeque, R.J.: Finite Difference Methods for Ordinary and Partial Differential Equations: Steady-State and Time-Dependent Problems. Society for Industrial and Applied Mathematics, Philadelphia (2007)

    Book  Google Scholar 

  63. Reddy, J.N.: An Introduction to Nonlinear Finite Element Analysis Second Edition: with Applications to Heat Transfer, Fluid Mechanics, and Solid Mechanics. OUP, Oxford (2014)

    Book  Google Scholar 

  64. Peng, W., Ma, Y., Li, C., He, T.: Dynamic analysis to the fractional order thermoelastic diffusion problem of an infinite body with a spherical cavity and variable material properties. J. Therm. Stress. 43, 38–54 (2020). https://doi.org/10.1080/01495739.2019.1676681

    Article  Google Scholar 

  65. Atta, D., Abouelregal, A.E., Sedighi, H.M., Alharb, R.A.: Thermodiffusion interactions in a homogeneous spherical shell based on the modified Moore–Gibson–Thompson theory with two time delays. Mech. Time-Depend. 1–22 (2023). https://doi.org/10.1007/s11043-023-09598-9

  66. Honig, G., Hirdes, U.: A method for the numerical inversion of Laplace transforms. J. Comput. Appl. Math. 10, 113–132 (1984). https://doi.org/10.1016/0377-0427(84)90075-X

    Article  MathSciNet  Google Scholar 

  67. Abbas, I.A., Kumar, R., Chawla, V.: Response of thermal source in a transversely isotropic thermoelastic half-space with mass diffusion by using a finite element method. Chin. Phys. B. 21, 084601 (2012). https://doi.org/10.1088/1674-1056/21/8/084601

    Article  Google Scholar 

  68. Ma, Y., Wang, L., Huang, F.: Nonlocal response of multi-field coupling elastic medium based on fractional order strain. J. Appl. Math. Mech. 101, e201900284 (2021). https://doi.org/10.1002/zamm.201900284

    Article  MathSciNet  Google Scholar 

  69. Elhagary, M.A.: Fractional thermoelastic diffusion problem for an infinitely long hollow cylinder using the Caputo–Fabrizio definition. J. Therm. Stress. 44, 281–294 (2021). https://doi.org/10.1080/01495739.2021.1873712

    Article  Google Scholar 

Download references

Acknowledgements

The authors are highly thankful to the reviewers for their valuable suggestions and comments that helped to improve the quality of this work.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Author information

Authors and Affiliations

  1. Department of Mathematics and Scientific Computing, National Institute of Technology, Hamirpur, Himachal Pradesh, India

    Geetanjali Geetanjali & P. K. Sharma

Authors
  1. Geetanjali Geetanjali
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. P. K. Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Geetanjali Geetanjali.

Ethics declarations

Conflict of interest

No potential conflict of interest was reported by the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Geetanjali, G., Sharma, P.K. Vibrational analysis of transversely isotropic hollow cylinder based on fractional generalized thermoelastic diffusion models with nonlocal effects. Acta Mech 235, 147–166 (2024). https://doi.org/10.1007/s00707-023-03738-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-023-03738-5

Search

Navigation