1 Introduction

The dynamic identification of a system, i.e. the estimation of its natural frequencies, damping ratios and modal shapes, is of crucial importance in many branches of engineering. It is usually performed with experimental modal analysis (EMA) methods or by using operational modal analysis (OMA) methods [1]. The first ones allow to identify the linear or nonlinear behaviour of a structural system but they require the knowledge of both the structural excitation and the structural response and thus the set-up of the in-situ tests is very difficult and expensive [1]. As far as the OMA methods are concerning, they are very attractive since they do not require the knowledge of the structural excitation and thus the set-up of the in-situ tests is very simple and cheap [2]. Moreover, since the structural input is due to the ambient vibrations (usually modelled as a white noise process [3,4,5]), OMA methods allow to identify the structural system when it is under operative conditions. This kind of methods have been used to identify structural systems [6,7,8], to perform structural health monitoring (SHM) [9,10,11,12,13], to calibrate finite elements models [14] and to detect structural damages [15, 16]. OMA methods has been applied on historical buildings [7, 17, 18], tall buildings [19, 20], bridges [21,22,23], masonry structures [24], dams [25], offshore platforms [26, 27] and other structural systems [28,29,30,31]. Since the structural input is assumed as a white noise, OMA methods have a stochastic framework. For this reason, the dynamic parameters are usually estimated starting from the power spectral density (PSD) of the structural output process, in case of frequency domain methods, or starting from the correlation function of the structural output process in case of time domain methods. The most popular frequency domain methods are the Peak Picking method (PP) [32], usually linked with the Half Power bandwidth method (HP) [32], and the frequency domain decomposition (FDD) [33, 34]. PP and HP have been initially used as EMA methods and they have a deterministic framework since they are usually applied on the frequency response function (FRF) of the system; however, if applied on the PSD, they can be considered as OMA methods. FDD [33, 34] is based on the singular value decomposition (SVD) [4] of the PSDs matrix and it allows to identify the natural frequencies and the modal shapes of a structural system. A most recent version allows to estimate also the damping ratios but the exact computation of the latters is still an open issue [1]. Several OMA methods developed in time domain are present in literature. Among these, it is worth mentioning: Natural Excitation Technique (NExT) [35], Auto Regressive Moving Average (ARMA) [36], Time Domain Decomposition (TDD) [37], and Stochastic Subspace Identification (SSI) [38,39,40,41]. NExT [35] exploits the auto and cross-correlation functions of the response process that can be considered as a summation of decaying sinusoids similarly to the impulse response functions (IRFs). It was initially used for EMA and then extended to OMA and thus NExT has a deterministic framework. ARMA methods [36] are based on the prediction of the current value of a time series taking into account the past values and the prediction error [1]. If there are multiple excitations, ARMA-Vectors (ARMAV) models [42] can be used. In ARMA model there are two parts: the auto-regressive part and the moving average part. The latter part causes nonlinearity in the model and thus ARMA identification is a highly nonlinear process iteratively implemented. For this reason, it is computationally intensive and difficult to apply especially for large dimension structures [1]. TDD [37] is based on a Single Degree of Freedom (SDoF) approach and, in the cases of Multi-Degree of Freedom (MDoF) systems, the filtering of the acquired signals around the natural frequencies is required. It allows to estimate the modal shapes and if linked with PP and HP it is possible to estimate also the natural frequencies and the damping ratios. Recently, Time Domain - Analytical Signal Method (TD - ASM) [8] has been introduced by the authors. It is the time domain version of Analytical Signal Method (ASM) [7] and it allows to identify the natural frequencies, the damping ratios and the modal shapes of a structural system in the cases in which the mass matrix can be expressed as the product between a constant and the identity matrix. In the other cases only the dominant modal shape can be obtained. A most recent version of TD-ASM, called TAGA [43], links TD-ASM with genetic algorithm in order to overcome the limits of TD-ASM. However, TAGA requires a very high computational burden especially in the case of large structures. SSI can be developed in two different ways, i.e. SSI covariance driven (SSI-COV) and SSI data driven (SSI-DATA). SSI-COV [40] decomposes two times the so-called Toeplitz matrix: firstly, it is decomposed into the product of observability matrix and controllability matrix and then a SVD is performed. By solving simultaneously the equations obtained from the aforementioned decompositions, it is possible to estimate the state transition matrix that characterizes the dynamic of the system under study. Finally, by performing an eigenvalue decomposition of the state transition matrix it is possible to estimate the modal parameters of the system. SSI-DATA [41] uses a QR decomposition of the data Hankel matrix and, successively, a SVD of the projection matrix can be performed. Both SSI-COV and SSI-DATA are faster than ARMAV. However, SSI in general is very difficult to be implemented [1]. Since OMA methods have a stochastic framework, they are difficult to be used by people that have not knowledge in signal analysis and stochastic dynamics. For this reason, in this paper an innovative semi-automated OMA procedure is proposed. It allows to identify the natural frequencies, the damping ratios and the modal shapes of a structural system in few steps. The proposed method is based on the filtering of the output process and, since the analytical signal can be used to identify the natural frequencies with high precision [44,45,46], it is used in the proposed method to perform the identification. In order to prove the validity of the proposed method, numerical simulations and experimental tests have been performed on a 3-storey frame also considering comparisons with the most popular OMA methods.

2 Proposed method

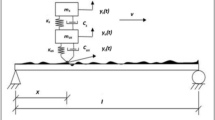
In this section, the proposed method is described in detail to estimate the modal parameters of a structural system excited by ambient vibrations and it is very fast and simple to use since only few interactions with the users are requested. In order to describe the proposed method, the MDoF system depicted in Fig. 1 has been considered.

Fig. 1
figure 1

MDoF frame

Full size image

The differential equation governing the motion of a MDoF system excited by a ground acceleration modelled as a zero-mean white noise W(t) is

$$\begin{aligned} {\left\{ \begin{array}{ll} {\varvec{M}}\varvec{{\ddot{X}}}_{({\text {rel}})}(t)+{\varvec{C}}\varvec{\dot{X}}_{({\text {rel}})}(t)+{\varvec{K}}{\varvec{X}}_{({\text {rel}})}(t)=-{\varvec{M}}{\varvec{r}}W(t)\\ {\varvec{X}}(0)={\varvec{0}} \;\;\; w.p.1\\ \varvec{\dot{X}}(0)={\varvec{0}} \;\;\; w.p.1 \end{array}\right. }\, \end{aligned}$$
(1)

in which \({\varvec{M}}\) is the mass matrix, \({\varvec{C}}\) is the dissipation matrix and \({\varvec{K}}\) is the stiffness matrix. \(\varvec{\ddot{X}}_{({\text {rel}})}(t)\), \(\varvec{\dot{X}}_{({\text {rel}})}(t)\) and \({\varvec{X}}_{({\text {rel}})}(t)\) represent the structural output process expressed, respectively, in terms of acceleration, velocity and displacement relative to the ground while \({\varvec{r}}\) is the forcing location vector that, in case of ground acceleration, contains only unitary values.

Initially, the structural output process has to be acquired. In the proposed method, the latter is expressed in terms of absolute acceleration \(\varvec{\ddot{X}}(t)=\varvec{\ddot{X}}_{({\text {rel}})}(t)+{\varvec{r}}W(t)\). Once that the structural output process has been acquired, its correlation functions matrix, labeled as \({\varvec{R}}_{\varvec{\ddot{X}}}(\tau )\), can be easily calculated considering that the components of \({\varvec{R}}_{\varvec{\ddot{X}}}(\tau )\) are expressed as [4]

$$\begin{aligned} R_{\ddot{X}_i\ddot{X}_j}(\tau )=E\big [\ddot{X}_i(t)\ddot{X}_j(t+\tau )\big ]-\mu _{\ddot{X}_i}\mu _{\ddot{X}_j} \end{aligned}$$
(2)

in which \(i=1,2,\ldots ,n\), \(j=1,2,\ldots ,n\), n is the number of components of \(\varvec{\ddot{X}}(t)\), \(E[\cdot ]\) represents the stochastic mean operator, \(\ddot{X}_i(t)\) and \(\ddot{X}_j(t)\) represent, respectively, the i-th and the j-th component of the structural output process \(\varvec{\ddot{X}}(t)\), while \(\mu _{\ddot{X}_i}\) and \(\mu _{\ddot{X}_j}\) represent the mean of \(\ddot{X}_i(t)\) and the mean of \(\ddot{X}_j(t)\).

The components of the output process’ PSDs matrix can be calculated taking into account the Wiener-Khinchine relationships, i.e. by performing the Fourier transform of the correlation functions matrix’s components and dividing them by \(2\pi \), as reported in the following equation [4]

$$\begin{aligned} S_{\ddot{X}_i\ddot{X}_j}(\omega )= \frac{1}{2\pi } \int \nolimits _{-\infty }^{\infty } e^{-i\omega \tau } R_{\ddot{X}_i\ddot{X}_j}(\tau ) \,{\text {d}}\tau . \end{aligned}$$
(3)

From the peaks of the PSDs matrix it is possible to perform a first estimation of the structural frequencies by extracting the abscissa of each peak. This step represents one of the interactions with the users and it can be easily performed by anyone.

In order to estimate the modal shapes, the contribution of the response process near each estimated frequency has to be extracted. To do this, the response process can be filtered around each peak of the PSDs by using band-pass filters having very little bandwidth. In this way, the i-th component of the process filtered around the j-th frequency, labeled as \(\ddot{X}_i^{(j)}(t)\), can be obtained. and the correlation functions’ matrix \({\varvec{R}}^{filt}(\tau )\) can be calculated considering that its component \(R_{\ddot{X}_i^{(j)}\ddot{X}_1^{(j)}}(\tau )\) are expressed as

$$\begin{aligned} R_{\ddot{X}_i^{(j)}\ddot{X}_1^{(j)}}(\tau )=E\big [\ddot{X}_i^{(j)}(t)\ddot{X}_1^{(j)}(t+\tau )\big ]-\mu _{\ddot{X}_i^{(j)}}\mu _{\ddot{X}_1^{(j)}}. \end{aligned}$$
(4)

Since the i-th component of the response process in terms of absolute acceleration is \(\ddot{X}_i(t)=W(t)+\sum _{k=1}^{n} \phi _{ik}\ddot{Q}_k(t)\), then the same component filtered around the j-th frequency can be expressed as \(\ddot{X}_i^{(j)}(t)=W^{(j)}(t)+\sum _{k=1}^{n} \phi _{ik}\ddot{Q}_k^{(j)}(t)\), being \(\ddot{Q}_k(t)\) the k-th modal acceleration. In case of well separated frequencies, only the component \(\phi _{ij}\ddot{Q}_j^{(j)}(t)\) gives a significant contribution to \(\ddot{X}_i^{(j)}(t)\) and thus the latter can be approximated as \(\ddot{X}_i^{(j)}(t) \approx \phi _{ij}\ddot{Q}_j^{(j)}(t)\). Considering this approximation, the j-th modal shape can be estimated from the components of \({\varvec{R}}^{filt}(\tau )\) calculated in \(\tau =0\) as

$$\begin{aligned} \frac{R_{\ddot{X}_i^{(j)}\ddot{X}_1^{(j)}}(0)}{R_{\ddot{X}_1^{(j)}\ddot{X}_1^{(j)}}(0)}=\frac{\sigma _{\ddot{X}_i^{(j)}\ddot{X}_1^{(j)}}}{\sigma _{\ddot{X}_1^{(j)}}^2} \approx \frac{\phi _{ij}\phi _{1j}R_{\ddot{Q}_j^{(j)}\ddot{Q}_j^{(j)}}(0)}{\phi _{1j}^2R_{\ddot{Q}_j^{(j)}\ddot{Q}_j^{(j)}}(0)}=\frac{\phi _{ij}\sigma _{\ddot{Q}_j^{(j)}}^2}{\phi _{1j}\sigma _{\ddot{Q}_j^{(j)}}^2}= \frac{\phi _{ij}}{\phi _{1j}} \end{aligned}$$
(5)

in which \(\sigma _{\ddot{X}_i^{(j)}\ddot{X}_1^{(j)}}\) is the covariance between \(\ddot{X}_i^{(j)}(t)\) and \(\ddot{X}_1^{(j)}(t)\), \(\sigma _{\ddot{X}_1^{(j)}}^2\) is the variance of the process \(\ddot{X}_1^{(j)}(t)\), while \(R_{\ddot{Q}_j^{(j)}\ddot{Q}_j^{(j)}}(0)\) represents the autocorrelation of the process \(\ddot{Q}_j^{(j)}(t)\) calculated in \(\tau =0\), i.e. the variance \(\sigma _{\ddot{Q}_j^{(j)}}^2\).

Once the modal shapes are estimated, the correlation functions’ matrix \({\varvec{R}}_{\varvec{\ddot{X}}}(\tau )\), whose components have been defined in Eq. (2), can be decomposed as

$$\begin{aligned} {\varvec{R}}_{\varvec{\ddot{Y}}}(\tau )=\varvec{\tilde{\Phi }}^{-1}{\varvec{R}}_{\varvec{\ddot{X}}}(\tau )\varvec{\tilde{\Phi }}^{-T} \end{aligned}$$
(6)

being \(\varvec{\tilde{\Phi }}\) the matrix containing all the estimated modal shapes. Equation (6) is very similar to the modal decomposition of the correlation functions’ matrix, i.e. \({\varvec{R}}_{\varvec{\ddot{Q}}}(\tau )=\varvec{\Phi }^{-1}{\varvec{R}}_{\varvec{\ddot{X}}}(\tau )\varvec{\Phi }^{-T}\). However, \(\varvec{\Phi }\) is normalised with respect to the mass matrix, while \(\varvec{\tilde{\Phi }}\) is normalised with respect to the identity matrix. \({\varvec{R}}_{\varvec{\ddot{Y}}}(\tau )\) is therefore different from the correlation functions’ matrix in modal space \({\varvec{R}}_{\varvec{\ddot{Q}}}(\tau )\) but the j-th component on its diagonal, labeled as \(R_{\ddot{Y}_j}(\tau )\), is proportional to the correspondent component \(R_{\ddot{Q}_j}(\tau )\). \(R_{\ddot{Y}_j}(\tau )\), as well as \(R_{\ddot{Q}_j}(\tau )\), can be considered as the correlation function of the SDoF oscillator’s response excited by a white noise process. For this reason and in order to distinguish \(R_{\ddot{Q}_j}(\tau )\) from \(R_{\ddot{Y}_j}(\tau )\) the latter is called mono-component correlation function.

Since the correlation function \(R_{\ddot{Y}_j}(\tau )\) is mono-component, then it exhibits a good behavior towards the Hilbert transform. The analytical signal of the j-th component on the principal diagonal of \({\varvec{R}}_{\varvec{\ddot{Y}}}(\tau )\) can be calculated in the form [7, 8]

$$\begin{aligned} Z_j(\tau )=R_{\ddot{Y}_j}(\tau )+i\widehat{R}_{\ddot{Y}_j}(\tau ) \end{aligned}$$
(7)

in which \(\widehat{R}_{\ddot{Y}_j}(\tau )\) is the Hilbert transform of \(R_{\ddot{Y}_j}(\tau )\) that is calculated as [7, 8]

$$\begin{aligned} \widehat{R}_{\ddot{Y}_j}(\tau )=\frac{1}{\pi }{\mathscr {P}}\int \nolimits _{-\infty }^{\infty } \frac{R_{\ddot{Y}_j}({\bar{\tau }})}{\tau -{\bar{\tau }}} \,{\text {d}}{\bar{\tau }} \end{aligned}$$
(8)

being \({\mathscr {P}}\) the principal value. \(Z_j(\tau )\) can be expressed in polar form in terms of envelope \(A_j(\tau )\) and phase \(\theta _j(\tau )\) as [7, 8]

$$\begin{aligned} Z_j(\tau )=A_j(\tau )e^{i\theta _j(\tau )}. \end{aligned}$$
(9)

Envelope and phase can be calculated in the form [7, 8]

$$\begin{aligned} A_j(\tau )=\sqrt{R_{\ddot{Y}_j}^2(\tau )+\widehat{R}_{\ddot{Y}_j}^2(\tau )} \approx \sigma _{\ddot{Y}_j}^2e^{-2\pi f_j \zeta _j \tau } \end{aligned}$$
(10)
$$\begin{aligned} \theta _j(\tau )=\arctan \left( \frac{\widehat{R}_{\ddot{Y}_j}(\tau )}{R_{\ddot{Y}_j}(\tau )}\right) \approx 2\pi f_j \sqrt{1-\zeta _j^2}\tau \end{aligned}$$
(11)

being \(\sigma _{\ddot{Y}_j}^2\) the variance of the process \(\ddot{Y}_j(t)\). The j-th instantaneous damped frequency \({\bar{f}}_j(\tau )\) can be calculated by performing

$$\begin{aligned} {\bar{f}}_j(\tau )=\frac{1}{2\pi } \frac{{\text {d}}}{d\tau }(\theta _j(\tau )). \end{aligned}$$
(12)

Moreover, evaluating the mean of Eq. (12), the j-th damped frequency \(f_j\sqrt{1-\zeta _j^2}\) can be easily estimated.

The natural logarithm of Eq. (10) returns the linear form [7, 8]

$$\begin{aligned} \ln (A_j(\tau )) \approx \ln (\sigma _{\ddot{Y}_j}^2)-2\pi f_j \zeta _j \tau =a_{j}+b_{j}\tau , \end{aligned}$$
(13)

consequently, the j-th damping ratio is

$$\begin{aligned} \zeta _j=- \frac{b_{j}}{2\pi f_j}=\sqrt{\frac{{\bar{b}}_{j}^2}{1+{\bar{b}}_{j}^2}} \end{aligned}$$
(14)

being \({\bar{b}}_{j}=b_{j}/(2\pi f_j \sqrt{1-\zeta _j^2})\). Once the damped frequencies and the damping ratios have been estimated, the j-th natural frequency can be trivially calculated as the ratio between the j-th damped frequency and \(\sqrt{1-\zeta _j^2}\).

The flow chart of the proposed method is depicted in Fig. 2.

Fig. 2
figure 2

Flow chart of the proposed method

Full size image

3 Validation of the proposed method

In order to validate the proposed method, experimental tests have been performed considering a three-storey frame excited by a ground acceleration modelled as a broadband noise. Frequencies, damping ratios and modal shapes of the structural system have been estimated by using the proposed method, FDD and SSI and the results obtained have been compared with those related to impulsive tests. Particularly, the discrepancies between the modal parameters estimated from the broadband noise tests and those identified from the impulsive tests are calculated as

$$\begin{aligned} \epsilon =100\frac{p^{{\text {EXP}}}-p^{{\text {EST}}}}{p^{{\text {EXP}}}} \end{aligned}$$
(15)

in which \(p^{{\text {EST}}}\) is the value of the modal parameters estimated from the broadband noise tests while \(p^{{\text {EXP}}}\) are the correspondent modal parameters identified from the impulsive tests. Further, numerical simulations have been performed in order to check the accuracy of the proposed method. In particular, the systems obtained by the modal parameters estimated from the broadband noise tests have been used in the numerical simulations and they were excited by the same base acceleration acquired during the experimental tests. The structural response obtained from the numerical simulations has been compared with the response acquired during the broadband noise tests and the discrepancy between the latters has been calculated as

$$\begin{aligned} \chi =100\frac{\int _{t_{{\text {in}}}}^{t_{{\text {fin}}}} {\ddot{X}}^{({\text {EXP}})}_{({\text {rel}})}(t)-{\ddot{X}}^{({\text {NUM}})}_{({\text {rel}})}(t) \,{\text {d}}t}{\int _{t_{{\text {in}}}}^{t_{{\text {fin}}}} {\ddot{X}}^{({\text {EXP}})}_{({\text {rel}})}(t) \,{\text {d}}t} \end{aligned}$$
(16)

in which \({\ddot{X}}^{({\text {EXP}})}_{({\text {rel}})}(t)\) represents the acquired response, \({\ddot{X}}^{({\text {NUM}})}_{({\text {rel}})}(t)\) is the response obtained from the numerical simulations while \(t_{{\text {in}}}\) and \(t_{{\text {fin}}}\) are the extremes of the time interval considered.

3.1 Experimental set-up

The experimental model tested is depicted in Fig. 3. It is made up of three different storeys and a base beam that allows to fix the frame to the shake table by bolting. The three storeys, the base beam and the columns are made of aluminum alloy elements and the distance between one storey and the next storey is equal to 33.33 cm. Each column, oriented in such a way that the axis of minor inertia is perpendicular to the motion imparted to the base, has a thickness of 2.10 mm and a width of 15.15 mm. The orientation of the columns was chosen in such a way as to minimize any out-of-plane displacements. The masses of the structural system, lumped at the floors, are: \(m_1=0.6193\) kg, \(m_2=0.5974\) kg and \(m_3=0.5647\) kg.

Fig. 3
figure 3

3-storey frame tested

Full size image

In total, 10 broadband noise tests were performed, each of which has a duration of 60 sec and a constant time sampling step \(\Delta t=0.001\) sec. The structural system, represented in Fig. 3, was excited at the base with a broadband noise having variance equal to 0.0910 m\(^2\)/sec\(^4\) through the use of the Quanser Shake Table II: an electro-mechanical shake table present inside the structural dynamics laboratory of the University of Palermo. This platform, driven by a motor which allows to obtain maximum accelerations equal to 2.5 g, is connected to a Universal Power Module (UPM): a device equipped with a power amplifier which amplifies the input current and drives the motor of the shake table in order to obtain the desired base input. The UPM is connected to a control unit which contains the commercial WinCon software. This software allows to specify the details of the desired base input and to calculate the power required to give the previously specified input to the shake table. The WinCon software communicates this last data to the UPM device through the analog output channel of the data acquisition card. During each broadband test performed, the input to the base and the structural response were acquired through the use of piezoelectric accelerometers. In particular, the structural response in terms of absolute acceleration was acquired through the use of Brüel & Kjær 4507-002 Miniature DeltaTron accelerometers while the structural input was acquired through the use of a Seismic Miniature ICP PCB 393B04 accelerometer. The piezoelectric sensors used were connected to an NI PXIe 1082 type acquisition unit, equipped with a 16-channel NI PXIe 4497 type acquisition card, by using BNC cables. The entire test set-up is schematized in Fig. 4.

Fig. 4
figure 4

Set-up of the broadband noise tests

Full size image

As far as the impulsive tests are concerning, 15 tests of 60 sec discretised with a time sampling step of 0.001 sec, were performed. Specifically, 5 tests with impulse to the first floor, 5 tests with impulse to the second floor and 5 tests with impulse to the third floor were performed. The impulse input was generated by using a Brüel & Kjær 8202 impact hammer equipped with a Brüel & Kjær 8200 force transducer. The impact hammer has been connected to a Brüel & Kjær Nexus 2692 signal amplifier which was connected to the NI PXIe 1082 acquisition unit in order to acquire the structural input. The structural response was acquired through the use of Brüel & Kjær 4507-002 Miniature DeltaTron piezoelectric accelerometers connected to the same acquisition unit. The set-up of the impulsive tests is depicted in Fig. 5.

Fig. 5
figure 5

Set-up of the impulsive tests

Full size image

3.2 Experimental and numerical analyses

To check the reliability of the proposed method, first of all, the dynamic parameters of the structural system have been identified by performing impulsive tests. Specifically, after the acquisition of the input–output process, the FRFs matrix of the structural system has been calculated taking into account the deterministic input–output relation in frequency domain, according to which the Fourier transform of the structural output is equal to the product between the FRFs matrix and the Fourier transform of the structural input. The natural frequencies, the damping ratios and the modal shapes have been identified from the FRFs matrix by using the PP linked to the HP. These dynamic parameters have been used as a reference in order to perform a successive comparison between the proposed method, FDD and SSI. The proposed method has been applied to the structural output process obtained from the broadband noise tests and the PSDs matrix of the latter, calculated as in Eq. (3), is depicted in Fig. 6.

Fig. 6
figure 6

PSDs matrix of the structural output process

Full size image

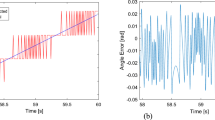
From the peaks of the PSDs in Fig. 6, the natural frequencies have been initially estimated and the structural output process has been filtered by using Butterworth band-pass filters of 8th order having bandwidth [13.1947–13.6138] rad/sec, [38.8508–39.2699] rad/sec and [56.4965–56.9150] rad/sec respectively for the first, the second and the third mode. The modal shapes of the structural system have been estimated as in Eq. (5), and the mono-component correlation functions, obtained by performing the decomposition reported in Eq. (6), have been used to calculate their analytical signals. The latter, calculated as in Eq. (8), are reported in Fig. 7, while the instantaneous frequencies and the envelopes are depicted, respectively, in Figs. 8 and  9.

Fig. 7
figure 7

Analytical signals of the mono-component correlation functions

Full size image
Fig. 8
figure 8

Instantaneous frequencies

Full size image
Fig. 9
figure 9

Envelopes

Full size image

The instantaneous frequencies in Fig. 8 and the envelopes in Fig. 9 have been used to estimate, respectively, the natural frequencies and the damping ratios. The results obtained in terms of frequencies identification and damping ratios identification are reported in Tables 1, 2 while, the results obtained in terms of modal shapes identification are reported in Table 3 and Fig. 10. These results obtained by using the proposed method, FDD and SSI have been compared with those obtained by performing the impulsive tests.

Table 1 Experimental frequencies, identified frequencies and discrepancy: experimental (EXP), proposed method (PM), frequency domain decomposition (FDD), stochastic subspace identification (SSI)
Full size table
Table 2 Experimental damping ratios, identified damping ratios and discrepancy: experimental (EXP), proposed method (PM), frequency domain decomposition (FDD), stochastic subspace identification (SSI)
Full size table
Table 3 Experimental modal shapes, identified modal shapes and discrepancy: experimental (EXP), proposed method (PM), frequency domain decomposition (FDD), stochastic subspace identification (SSI)
Full size table
Fig. 10
figure 10

Modal shapes

Full size image

From the results reported in Table 1 it is clear that all the used OMA methods lead to optimal results in terms of frequency identification; from the results reported in Table 2 it is possible to see that the used methods lead to good results. As far as the modal shapes identification are concerned, in Table 3 and in Fig. 10 it can be observed that all the used methods lead to very good results and that the first mode, that gives the major contribution to the total motion, is best identified when the proposed method is used. Numerical analyses have been performed through MATLAB software having considered as input for each analysis the acquired excitation from experimental tests, then the results obtained in terms of relative acceleration have been compared with the response experimental recorded. This comparison is reported, for one of the samples of the response process, in Figs. 11, 12 and 13.

Fig. 11
figure 11

Relative acceleration of the first floor

Full size image
Fig. 12
figure 12

Relative acceleration of the second floor

Full size image
Fig. 13
figure 13

Relative acceleration of the third floor

Full size image

From the results reported in Figs. 11, 12 and 13 it is clear that all the methods used are able to properly predict the structural response in the time domain. The discrepancy between the response obtained from the numerical simulations and the response experimentally acquired has been calculated as in Eq. (16) for each storey and for each sample of the response process. The mean of the results obtained in terms of discrepancies is reported, for each storey, in Table 4. From the results reported in Table 4, it is clear that all the used methods leads to results that are very similar each other.

Table 4 discrepancy between the response obtained from the numerical simulations and the response experimentally acquired: proposed method (PM), frequency domain decomposition (FDD), stochastic subspace identification (SSI)
Full size table

4 Conclusions

In this paper an innovative operational modal analysis method that allows to identify the natural frequencies, the damping ratios and the modal shapes of a structural system under ambient vibrations is proposed. It is a fast only output procedure based on the signal filtering, on the correlation function of the output process and on its Hilbert transform. It is very simple to implement and it can be easily used by any type of user since few interactions with the latter are required. To assess the accuracy of the proposed method, different experimental tests and numerical simulations have been performed on a 3-storey frame and the results obtained have been compared with those related to other OMA methods. Moreover, a numerical/experimental comparison has been performed showing that the proposed method can identify the global behaviour of the structural system with a precision similar to FDD and SSI. The simplicity of use of the proposed method with the same results obtained therefore makes this method preferable to the other OMA methods for a quick, cheap and simple monitoring.