A novel identification procedure from ambient vibration data

Abstract

Ambient vibration modal identification, also known as Operational Modal Analysis, aims to identify the modal properties of a structure based on vibration data collected when the structure is under its operating conditions, i.e., no initial excitation or known artificial excitation. This procedure for testing and/or monitoring historic buildings, is particularly attractive for civil engineers concerned with the safety of complex historic structures. However, since the external force is not recorded, the identification methods have to be more sophisticated and based on stochastic mechanics. In this context, this contribution will introduce an innovative ambient identification method based on applying the Hilbert Transform, to obtain the analytical representation of the system response in terms of the correlation function. In particular, it is worth stressing that the analytical signal is a complex representation of a time domain signal: the real part is the time domain signal itself, while the imaginary part is its Hilbert transform. A 3DOF numerical example will be presented to show the accuracy of the proposed procedure, and comparisons with data from other methods assess the reliability of the approach. Finally, the identification method will be extended to the real case study of the Chiaramonte Palace, a historic building located in Palermo and known as “Steri”.

1 Introduction

Most of the literature concerning dynamic identification deals with the estimation of the modal parameters (frequencies, damping coefficients and mode shapes) of a structure starting from the measurement of both the dynamic input and structural response signals.

In the past, the dynamic identification of the modal characteristics of buildings was generally based on force vibration tests involving impact tests or other complex setups, applying several types of input exciters directly in-situ. In this context, it is customary to refer to the modal analysis based on artificial forced excitations as Experimental Modal Analysis (EMA) which presupposes the use of both known input and structural response measurements to estimate modal parameters [1, 2].

Based on the number of reference points used to measure data, numerous modal identification algorithms have been developed such as Single-Input/Single-Output (SISO), Single-Input/ Multi-Output (SIMO) and Multi-Input/ Multi-Output (MIMO) techniques [3].

In traditional EMA, the artificial excitation is normally conducted in one or more structural points in order to effectively measure Frequency Response Functions (FRFs) in the frequency domain, or Impulse Response Functions (IRFs) in the time domain. However, the use of multiple inputs and the measurement of these functions would be difficult in the field test and for large structures.

As a consequence, EMA is usually conducted in the lab environment since tests normally interfere with the operating condition of structures and thus, they may not be conducted routinely and economically. Therefore, in recent decades, dynamic tests based on ambient vibrations methods, have rapidly gained ground, especially in the structural health monitoring field, leading to the development of Operational Modal Analysis (OMA) techniques.

As a matter of fact, the modal identification associated with OMA techniques requires the recording of response signals (output only) of the structure, subjected to ambient noise vibrations (wind, traffic, water waves, man-made excitations and so on), without the need to measure the dynamic forces exciting structures. Hence, tests can be also carried out under structural operating conditions making them cheaper and faster than EMA.

As far as both EMA and OMA are concerned, several studies have demonstrated how both frequency and time domain approaches can be appropriate to estimate the structural modal parameters of a large variety of structures [4]. However, since the external forces are not recorded in OMA identification methods, the application of concepts from stochastic mechanics is required [5, 6].

Classical OMA frequency domain techniques generally extract the modal parameters from the biased frequency response functions (FRFs) or from the auto power spectral density functions (PSDs) and cross power spectral density functions (CPSDs) of the outputs. Among OMA procedures, Peak-picking (PP) combined with the Half power (PP+HP) [7] and Frequency Domain Decomposition (FDD) [8, 9] procedures are often utilized. These methods are generally based on the input-output PSD relationship [7]. However, as previously stated, since in this case the input signal is not recorded, OMA refers to a key assumption. The basic idea of OMA hypothesises that the excitation source, due to natural or operative loadings, yields an input force which can be modeled as a white Gaussian noise [5, 8].

In this case, modes can be estimated from the amplitude of their peaks at the correspondent main frequencies of the system [10].

As it is well known, since frequency domain-based methods depend strongly on the frequency resolution of the PSDs, the identified modal parameters, and especially the damping estimation, might not be very accurate when the damping is very high or the modes are very close to each other [7].

Generally, however, classical FDD-based procedures might be suitable only for weakly-damped structures [2, 11]. These kinds of drawbacks led researchers to start looking at time domain system-identification OMA techniques as a promising alternative. Different time domain methods have been developed such as the Least-square curve fitting technique, the Auto-Regressive model with a Moving Average of white noise (ARMA) [12], the Stochastic Subspace Identification techniques (SSI) [13], the Natural Excitation Technique (NExt) [14, 15] and so on [16]. Further, correlation functions can also be employed for the modal identification for OMA just like IRFs for EMA [14]. In particular, auto correlation functions (CORs) and cross correlation functions (CCORs) of the output data can be expressed as a summation of decaying functions, each one characterized by a damped natural frequency, a damping ratio and mode shape. Since the covariance function (COV) is equal to the correlation function for zero mean random processes, many methods have been developed to decompose the covariance matrix into single-mode dependent functions. In this way, the obtained functions are dominated by a specific structural mode and the extraction of the modal parameters can be achieved [4]. However, the main disadvantage of some of these methods seems to be the tendency to yield non-conservative damping estimates with noisy data [3] and to encounter problems in distinguishing structural modes from spurious or noise modes.

On this base, the present study proposes an identification technique combining a proper mode decomposition algorithm with the application of the Hilbert Transform (HT) [17,18,19,20] to the output response data. Specifically, HT properties are exploited to obtain the so-called analytical signal (AS) in terms of correlation functions. The AS is defined as a complex representation of a time domain signal. The contribution of the imaginary part makes the AS highly sensitive to variations of some signal quantities, such as phase and instantaneous frequency, so that it seems to be an appealing tool to detect the modal parameters of a structure with high precision [20]. Notably, since no equipment is requested to excite the structure, and considering the accuracy of the proposed procedure, this technique can be easily applicable also to historic buildings.

In particular, this paper is organized as follows: Sect. 2 contains the description of the identification algorithm and numerical analyses carried out on a single degree of freedom (SDOF) system. In Sect. 3 the algorithm is presented for the more general case of a multi degree of freedom (MDOF) structure and additional analyses are performed on a 3DOF system to prove the efficiency of the proposed method also on multi-story structures. Furthermore, in order to take into account real structures, in Sect. 4 the identification method is extended to the case study of an existing historic building. The presented case study concerns the Chiaramonte Palace, a rare and precious example of Sicilian fourteenth-century architecture.

2 Identification algorithm for SDOF systems

In this paper, an innovative ambient vibration identification method to estimate the frequencies and the damping ratios of a structure from the AS of the output vibration data is proposed. In particular, the estimation of the modal parameters is achieved by considering the properties of the AS defined in terms of correlation functions.

Specifically, once the output signals of a system, subjected to environmental noise, have been acquired in terms of accelerometer data, PSDs and CPSDs response functions are determined in the frequency domain. Thus, by using the Wiener–Khinchine theorem [7], CORs and CCORs of the output data can also be obtained in the time domain.

Finally, by means of the HT, it is possible to define the AS in terms of correlation fucntions. The AS is a complex signal which allows the dynamic characteristics (frequencies, damping coefficients) to be easily extracted from its properties, namely the envelope and phase.

The present identification technique, denoted as Analytical Signal-based method (ASM), can be summarized in the following steps:

• (1) Acquisition of the structural response signals;

• (2) Estimation of the PSDs and CPSDs from output data (Welch’s Method);

• (3) Estimation of the CORs and CCORs from the PSDs and CPSDs, by means of the inverse fast Fourier transform (IFFT);

• (4) Estimation of the AS (by means of the HT) and its properties (Envelope, phase);

• (5) Identification of the modal parameters (e.g. instantaneous frequencies and damping ratios).

The meaning of each step will be explained in detail in the following resorting to a linear SDOF structural system with mass ${M_1}$, stiffness ${K_1}$ and damping ${C_1}$, characterized by a damping ratio ${\zeta _1} = {C_1} / 2\sqrt{{K_1}{M_1}}$ and a natural frequency ${f _1} = \sqrt{{K_1}/{M_1}}/(2\pi )$. These two parameters represent the modal properties to be identified with the proposed procedure.

When the signal of the input force is not acquired and the excitation source is due to ambient vibrations, the key hypothesis of OMA is that the structure can be considered as excited by a white noise process W(t), defined as in [7, 21]. This assumption ensures that all the vibration modes are excited at the same amplitude since the power spectrum of the input is flat.

Let ${x_1(t)}$ denote the displacement response of the SDOF system relative to the ground. The dynamic behavior of the SDOF system is governed by the following equation of motion:

$$\begin{aligned} {{\ddot{x}}_1}(t) +2{\omega _1}{\zeta _1}{\dot{x}_1}(t) + {\omega _1}^2{x_1}(t) = {W(t)} \end{aligned}$$

(1)

where ${\omega _1}=2\pi {f_1}$ represents the circular frequency.

Once the structural response is obtained from Eq. (1), the Welch’s Method is applied to the structural acceleration ${{\ddot{x}}_1}(t)$ in order to estimate the output in terms of PSD [22]. Specifically, the application of the Welch’s Method requires some parameters such as the window function (Hanning, Hamming, etc...), the sub-segments length and the percentage of overlap, to be set [23]. As a matter of fact, the original signal ${{\ddot{x}}_1}(t)$ is divided into ${\bar{N}}$ sub-segments, overlapped in time. To each one a window function is applied in the time domain so that the sub-signal tends to zero at the edges. Then, by means of the Fast Fourier Transform (FFT), computed for each r-th sub-signal with (r = 1,2,...,${\bar{N}}$), the two-sided PSD of the structural acceleration ${{\ddot{x}}_1}(t)$, denoted as $S_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(f)$ can be obtained by:

$$\begin{aligned} S_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(f)={\frac{1}{2\pi }\lim _{T\rightarrow \infty }{\frac{1}{2T}}}E[|X_{1,r}(f)|^2] \end{aligned}$$

(2)

with (r = 1,2,...,${\bar{N}}$) and where $X_{1,r}(f)$ is the Fourier transform of each sub-signal contained in ${{\ddot{x}}_1}(t)$.

According to the Wiener–Khinchine theorem, the IFFT of the $S_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(f)$ yields the corresponding correlation function $R_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau )$:

$$\begin{aligned} R_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau )=\int _{-{\infty }}^{+{\infty }} S_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(f)e^{i2{\pi }f{\tau }}df \end{aligned}$$

(3)

where i is the imaginary unit. At this point, the Hilbert transform (HT) operator can be straightforwardly applied to the correlation function. Its HT is defined as:

$$\begin{aligned} {\hat{R}}_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(t)={\frac{1}{\pi }}P\int _{-{\infty }}^{+{\infty }} {\frac{R_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau )}{t-\tau }}d{\tau } \end{aligned}$$

(4)

where P stands for the principal value. The complex analytical signal $z_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau )$, in terms of the correlation function, is defined as:

$$\begin{aligned} z_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau )=R_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau )+{i}{\hat{R}}_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau ) \end{aligned}$$

(5)

The AS is a complex representation of a time domain signal. Specifically, in this case, the real part is the correlation function itself $R_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau )$, while the imaginary part is its Hilbert transform ${\hat{R}}_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau )$. The two main properties characterizing the AS are the amplitude (or envelope) $A_1(\tau )$ and the phase angle $\theta _1(\tau )$, respectively defined as:

$$\begin{aligned} A_1(\tau ) &= \sqrt{R_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau )^2+{\hat{R}}_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau )^2} \end{aligned}$$

(6)

$$\begin{aligned} \theta _1(\tau ) &= arctan\left[{\frac{{\hat{R}}_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau )}{{R_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau )}}}\right] \end{aligned}$$

(7)

These two functions allow the damping ratio and the main frequency of the system to be derived. In particular, from the phase angle $\theta _1(\tau )$ is possible to estimate the structural frequency while the damping ratio can be determined from the amplitude. According to [24] and considering the Bedrosian theorem [25, 26], the correlation function and its Hilbert transform can be expressed in the form:

$$\begin{aligned} R_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau ) &= {E_1}e^{-i2{\pi }{f_1}{\zeta _1}{\tau }}{sin(2{\pi }{{\bar{f}}_1}{\tau }+{\phi _1})} \end{aligned}$$

(8)

$$\begin{aligned} {\hat{R}}_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau ) &= -{E_1}e^{-i2{\pi }{f_1}{\zeta _1}{\tau }}{cos(2{\pi }{{\bar{f}}_1}{\tau }+{\phi _1})} \end{aligned}$$

(9)

where ${E_1}$ is a constant, ${{\bar{f}}_1}={f_1}{\sqrt{1-\zeta _1^2}}$ the natural damped frequency of the system and ${\phi _1}$ the phase. Thus, the amplitude $A_1(\tau )$ and the phase angle $\theta _1(\tau )$ of the analytical signal assume the following expressions:

$$\begin{aligned} A_1(\tau ) &= {E_1}e^{-i2{\pi }{f_1}{\zeta _1}{\tau }} \end{aligned}$$

(10)

$$\begin{aligned} \theta _1(\tau ) &= 2{\pi }{{\bar{f}}_1}{\tau }+{\phi _1} \end{aligned}$$

(11)

Although the frequency is known from the PSD analysis and it could be identified by the use of the PP method, it is worth noting that the first derivative of the phase angle $\theta _1(\tau )$ (considered as an unwrapped function as discussed in [19]) yields a time dependent function, termed instantaneous frequency:

$$\begin{aligned} {\bar{f}}_{1,ist}(\tau )=\frac{{\dot{\theta }}{_1}(\tau )}{2{\pi }} \end{aligned}$$

(12)

The ${\bar{f}}_{1,ist}(\tau )$ is an almost constant function, so the natural damped frequency of the system ${\bar{f}}_{1}(\tau )$ can be identified as its mean value:

$$\begin{aligned} {\bar{f}}_{1}(\tau )=E[{\bar{f}}_{1,ist}(\tau )] \end{aligned}$$

(13)

with $E[{\cdot }]$ denoting the expectation operator. Further, from the logarithmic representation of the amplitude, the damping ratio can be derived. Note that the natural logarithm of the amplitude, defined in Eq. (10), can be represented by a straight line of coefficients $c_1$ and $c_2$ as follows:

$$\begin{aligned} ln(A_{1}(\tau ))=ln(E_1)-2{\pi }{f_1}{\zeta _1}{\tau }=c_1{\tau }+c_2 \end{aligned}$$

(14)

Consequently, the damping ratio ${\zeta _1}$, associated with the instantaneous frequency ${f_1}$, is given by the relationship between the tangent to the logarithmic representation of $A_1(\tau )$ and the frequency:

$$\begin{aligned} {\zeta _1}=\frac{tan[ln(A_{1}(\tau ))]}{2{\pi }{f_1}} \end{aligned}$$

(15)

2.1 A numerical example: SDOF system

In this section, a numerical example as an application of the identification algorithm to a linear SDOF structural model, shown in Fig. 1, is given in order to demonstrate the validity of the theoretical background of the procedure.

Fig. 1

SDOF structural model

Fig. 2

a PSD function of the structural acceleration response; b COR function of the structural acceleration response

The SDOF structural properties are set so that the value of the damping ratio ${\zeta _1}$ is 0.0500 and the natural damped frequency ${{\bar{f}}_1}= 29.9625 \text {Hz}$. These two parameters represent the reference exact values to be identified with the proposed procedure. Taking into account these parameters, the response acceleration ${{\ddot{x}}_1}(t)$ is obtained by numerical integration of Eq. (1). In this manner, the PSD can be obtained employing the Welch method. Specifically, $S_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(f)$, has been computed according to Eq.(2) using a Hamming window, an overlap of 50% between adjacent segments and a sample rate of 1000 Hz. Next, by transforming frequency-domain data to the time domain, $R_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau )$ has been obtained as in Eq. (3) (Fig. 2b).

The tridimensional representation of $z_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(\tau )$ in Fig. 3, with its projected real and imaginary parts, shows the complex nature of the AS.

Fig. 3

Analytical signal: complex representation of a time domain signal (AS-black thick line; real part-black line; imaginary part-dashed dotted black line; phase diagram-dotted black line)

While, the AS properties, instantaneous frequency and amplitude are depicted in Fig. 4a, b, respecitvely. As it can be seen in Fig. 4a, the function ${\bar{f}}_{1,ist}(\tau )$ shows steady values over the time with its mean value yielding the natural damped frequency of the system. For this example, the identified natural damped frequency ${\bar{f}}_{1}(\tau )$ is equal to 29.9278 Hz with a discrepancy of 0.1156% with respect to the exact value. From Fig. 4b it emerges that the logarithmic representation of the amplitude can be clearly approximated by a straight line so that the damping ratio can be identified as in Eq. (15).

Fig. 4

a Instantaneous frequency function; b Logarithmic representation of the amplitude of the AS

Results obtained from the application of the proposed identification algorithm on this SDOF system are summarized in Table 1. In particular, Table 1 shows the natural damped frequency and the damping ratio estimated by the ASM proposed method and the classical PP+HP, as well as the discrepancies computed with respect to the exact values (${{\bar{f}}_1}= 29.9625 \text {Hz}$, ${\zeta _1}=0.0500$) (Case 1). As it can be seen, both methods lead to similar results, although the ASM yields slightly more accurate estimates compared to PP+HP.

Importantly, the small differences occurring between exact and identified values, computed for both the modal parameters, prove the reliability of the proposed approach as an output data-based tool for the estimation of modal parameters. Furhter, an additional analysis has been carried out increasing the damping ratio of the system. Specifically, it has been proved that methods based on the knowledge of auto and cross-spectra of the output (such as PP+HP) are more accurate for damping ratio lower that 0.05 [7]. Therefore, in order to investigate the capability of the ASM to overcome limits involved in frequency domain-methods, the damping ratio of the system has been increased to ${\zeta _1}=0.0100$. The obtained values and discrepancies on the identification of frequency and damping ratio are reported in Table 1 under the ”Case 2”label.

As shown in Table 1, using both PP+HP and the ASM methods, the natural damped frequency is still well estimated, whereas the ASM can achieve a better estimation for higher damping ratios.

Table 1 Estimated natural frequency and damping ratio for the exact values of ${\zeta _1}=0.0500$ (Case 1) and ${\zeta _1}=0.0100$ (Case 2)

Fig. 5

Discrepancy ${\varepsilon }$ between the natural damped frequencies estimated by the PP + HP and the ASM method with respect to the theoretical values

Notably, for the Case 2, it clearly emerges that lower errors are obtained from the ASM method with a discrepancy equal to 0.62% compared to the 2.64% achieved by the PP + HP.

In order to assess the reliability of the proposed method, further additional analyses have been performed by taking into account a wider range of variation of the damping value. Specifically, Fig. 5 shows the percentage discrepancy ${\varepsilon }$ between the natural damped frequencies estimated by the PP+HP (line with squares) and the ASM method (line with circles) with respect to the theoretical values of ${\zeta _1}$ variable in the interval [0.05–0.10]. As can be seen in Fig. 5, for ${\zeta _1}=0.0500$ the two methods yield almost the same values of frequencies. However, as the damping ratio of the structure increases, significant discrepancies are achieved from the PP+HP method, while the ASM method always leads to a steady trend with smaller errors on the identified values of damping ratios. This result suggests that the ASM, overcoming the limitations involved in frequency domain-based methods, can be adopted as a reliable identification method even when dealing with structures characterized by damping ratios greater than 5%.

3 Identification algorithm for MDOF systems

This section presents the identification algortihm extended to the more general case of MDOF systems. To deal with a MDOF system, the proposed procedure has to take into account that the initial PSD matrix of the response data contains multicomponent PSDs and CPSDs characterized by the contribution of all the modes for each degree of freedom.

In this case, the modal parameters cannot be extracted directly from the derived analytical signals in the time domain. Consequently, the use of AS is combined with a proper mode decomposition algorithm. By assuming a stationary white noise input signal, the initial output PSD matrix is decomposed in a summation of monocomponent functions. Specifically, after the second step, described in Sec.2, concerning the PSD estimation by the Welch’s Method, a decomposition of the PSD matrix into ”filtered” PSDs and CPSDs (FPSDs and FCPSDs), by means of proper filters, is applied in order to estimate the corresponding filtered FCORs and FCCORs.

In this regard, consider the dynamic behavior of a MDOF system with n degrees of freedom, subjected to an input force modeled as a white noise process W(t), that can be expressed in compact form as:

$$\begin{aligned} {{\mathbf{M}{\ddot{\mathbf{x}}}}}(t)+ {{\mathbf{C}{\dot{\mathbf{x}}}}}(t) +\mathbf{{K x}}(t) =-\mathbf{{Mr}} W(t) \end{aligned}$$

(16)

where $\mathbf {M}$, $\mathbf {C}$, $\mathbf {K}$ denote the mass, damping, and stiffness $n \times n$ matrices respectively and $\mathbf {r}$ is the $n \times 1$ influence vector. The structural displacements relative to the ground ${x_j}(t)$ (with ${j} =1, 2,\ldots ,n$) are collected in the vector $\mathbf{{x}}(t)=[{x_1}(t), {x_2}(t),\ldots , {x_n}(t)]^T$ (with T denoting matrix transposition).

As well known, from modal analysis, the response of a MDOF linear system is the sum of the modal responses:

$$\begin{aligned} {x_j}(t)=\sum _{p=1}^{n}{\phi _{jp}}{q_p}(t)=\sum _{j=1}^{n}{x_{jp}}(t) \end{aligned}$$

(17)

(with j =1,2,..n and p mode)

where ${\phi _{jp}}$ is the (jp) element of the system modal matrix and ${q_p}(t)$ the displacement in the modal space. From the superposition formula it emerges that the response ${x_j}(t)$ of each degree of freedom j is influenced by all the structural modes ${\phi _{jp}}$. As a consequence, moving to the frequency domain, also the response PSDs and CPSDs will contain the contribution of all the modes.

Firstly, aiming at the detection of the main frequencies, a frequency domain representation of the response data is obtained. To this end, the Welch’s Method is applied to the response accelerations ${\ddot{x}_j}(t)$. Similar to the SDOF case, dividing each response into ${\bar{N}}$ sub-signal components (r =1,...,${\bar{N}}$) and considering the mean of all the contributes in the frequency domain, the final two-sided auto and cross power spectral density functions $S_{{{\ddot{x}}_j}{{\ddot{x}}_k}}(f)$ (with j, k =1, 2,...,n) of the MDOF system can be obtained as follows:

$$\begin{aligned} S_{{{\ddot{x}}_j}{{\ddot{x}}_k}}(f)={\frac{1}{2\pi }\lim _{T\rightarrow \infty }{\frac{1}{2T}}}E[X_{j,r}(f)X_{k,r}(f)^*] \end{aligned}$$

(18)

where * denotes the conjugate transpose and $X_{j,r}(f)$ is the Fourier transform of the r-th subsignal ${{\ddot{x}}_j}(t)$. Specifically, when k=j the PSDs $S_{{{\ddot{x}}_j}{{\ddot{x}}_j}}(f)$ are obtained, while if k$\ne$j, $S_{{{\ddot{x}}_j}{{\ddot{x}}_k}}(f)$ represent the CPSDs of the system.

Thus, the two-sided PSD matrix ${{\mathbf{S}_{{{\ddot{\mathbf{x}}}}{{\ddot{\mathbf{x}}}}}}}(f)$, containing the auto PSDs $S_{{{\ddot{x}}_j}{{\ddot{x}}_j},r}(f)$ and the cross ones $S_{{{\ddot{x}}_j}{{\ddot{x}}_k},r}(f)$ as diagonal and off-diagonal terms respectively, can be written as:

$$\begin{aligned} {{\mathbf{S}_{{{\ddot{\mathbf{x}}}}{{\ddot{\mathbf{x}}}}}}}(f) = \left| \begin{array}{cccc} S_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(f) & S_{{{\ddot{x}}_1}{{\ddot{x}}_2}}(f) & \ldots & S_{{{\ddot{x}}_1}{{\ddot{x}}_n}}(f)\\ S_{{{\ddot{x}}_2}{{\ddot{x}}_1}}(f) & S_{{{\ddot{x}}_2}{{\ddot{x}}_2}}(f) & \ldots & S_{{{\ddot{x}}_2}{{\ddot{x}}_n}}(f) \\ \ldots & \ldots & \ldots & \ldots \\ S_{{{\ddot{x}}_n}{{\ddot{x}}_1}}(f) & S_{{{\ddot{x}}_n}{{\ddot{x}}_2}}(f) & \ldots & S_{{{\ddot{x}}_n}{{\ddot{x}}_n}}(f) \end{array} \right| \end{aligned}$$

It is worth stressing that each term of ${{\mathbf{S}_{{{\ddot{\mathbf{x}}}}{{\ddot{\mathbf{x}}}}}}}(f)$, obtained by the use of the Welch’s Method, is a multicomponent function.

At this stage, the ASM requires operating on monocomponent signals and to derive the damping from the analytical signals in the time domain. In this regard, to decompose multicomponent signals many kinds of filters exist in literature: Butterworth, Elliptic or Chebyshev and so on, with different specifications [27]. In order to isolate the contribution of each mode, the use of filters requires the definition of a frequency range centered on the frequency of the analyzed mode. However, frequencies can be easily obtained by means of the Fourier transform of the structural response.

Once the filter has been applied to each multicomponent PSDs and CPSDs of the original PSD matrix, as many ”filtered” PSDs and CPSDs (FPSDs and FCPSDs) as the number of DOFs are obtained for each mode, each one containing characteristics of only one individual mode.

From this point, the identification procedure for each signal is the same as that described for the SDOF case. Clearly, for a SDOF structure, the procedure leads to a unique set of identified modal parameters, while for a MDOF system, the mean of the values obtained for each degree of freedom should be considered.

Then, by means of the IFFT, from the previous FPSDs and FCPSDs, the estimation of the FCORs and FCCORs ${_F}R_{{{\ddot{x}}_j}{{\ddot{x}}_k}}(f)$ is achieved.

Finally, by applying the HT to the FCORs and FCCORs, the filtered analytical signals are derived too, and the same procedure shown for the SDOF case can be carried out.

3.1 A numerical example: 3DOF system

In order to assess the reliability of the proposed procedure, the identification of the modal parameters of a linear 3DOF structural model (Fig. 6a), is considered and results are compared with those achieved by applying the PP+HP.

Fig. 6

a 3DOF structural model; b auto PSD functions of the structural acceleration responses

The mass of each storey is assumed to be the same and equal to ${M_j}$=794 kg for j = 1,2,3. The natural damped frequencies of the structure are ${{\bar{f}}_j}$ (Hz) =[6.23, 17.45, 25.22] and the system is assumed to be a classically damped structure with damping ratio of each mode ${\zeta _j}$=0.08.

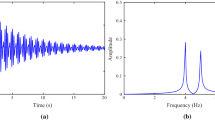
The two-sided multicomponent PSDs, $S_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(f)$, $S_{{{\ddot{x}}_2}{{\ddot{x}}_2}}(f)$ and $S_{{{\ddot{x}}_3}{{\ddot{x}}_3}}(f)$ are shown in Fig. 6b. In order to isolate the contribution of each mode, in this case a Butterworth band-pass filter of order 8 has been has been applied to each multicomponent PSDs and CPSDs of the original $6 \times 6$ PSD matrix, so that corresponding FPSDs and FCPSDs have been obtained for each mode.

Thus, applying the filter to the original multicomponent PSD $S_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(f)$ for instance, in the frequency range centered on the first frequency of the system (5.46–7.03 Hz), a filtered PSD, denoted as ${_F}S_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(f)$, characterized by the contribution of the first mode only, is obtained. Repeating the same procedure for each original auto PSD $S_{{{\ddot{x}}_j}{{\ddot{x}}_j}}(f)$, three auto FPSDs ${_F}S_{{{\ddot{x}}_j}{{\ddot{x}}_j}}(f)$ are obtained in total for the first mode (Fig. 7a). They represent the PSDs of three single oscillators dominated by the modal parameters of the first mode only. In the same way, filtering the original CPSDs $S_{{{\ddot{x}}_j}{{\ddot{x}}_k}}(f)$, six FCPSDs ${_F}S_{{{\ddot{x}}_j}{{\ddot{x}}_k}}(f)$ are obtained for the first mode.

Adjusting the frequency range of the filter to the second (15.03–19.34 Hz) and to the third mode (22.38–28.78 Hz), the FPSDs, depicted in Fig. 7b, c, and the FCPSDs are obtained. By considering these FPSDs and FCPSDs in Eq. (3), the FCORs and FCCORs can be computed. In Fig. 8a–c the FCORs ${_F}R_{{{\ddot{x}}_j}{{\ddot{x}}_j}}(f)$ are depicted for the first, the second and the third mode.

Proceeding with the application of the HT to the FCORs and FCCORs, the modal parameters are then identified as the average of the values obtained by all the filtered analytical signals.

Fig. 7

Auto FPSD functions of the structural acceleration responses: a in correspondence of the first mode; b in correspondence of the second mode; c in correspondence of the third mode

The obtained values and discrepancies on the identification of frequencies and damping ratios derived from the application of the ASM are listed in Table 2 along with those identified by the PP+HP method.

Fig. 8

Auto FCOR functions of the structural acceleration responses: a in correspondence of the first mode; b in correspondence of the second mode; c in correspondence of the third mode

In particular, the present case, characterized by a theoretical value of ${\zeta _j}$=0.08 is listed under the label ”Case 2”. Supplemental analyses have been performed on the same benchmark structure aiming at investigating the robustness of the ASM method by considering a variation of the damping ratio. Specifically, in Table 2, the results are presented also for the exact values of ${\zeta _j}=0.0500$ (Case 1) and ${\zeta _j}=0.0100$ (Case 3), for $\textit{j} = 1,2,3$. As it can be observed in Table 2, the ASM provides good estimates for both the natural damped frequencies and damping ratios for all the modes. Moreover, more accurate results are obtained by the ASM than using the PP+HP method. In particular, the ASM mehtod presents stable and lower discrepancies in the entire range of interest of ${\zeta _j}$ for all three structural modes.

Table 2 Estimated natural frequency and damping ratio for the exact values of ${\zeta _j}=0.0500$ (Case 1), ${\zeta _j}=0.0800$ (Case 2) and ${\zeta _j}=0.0100$ (Case 3), for $\textit{j} = 1,2,3$

4 A case study: Chiaramonte Palace in Palermo

In this section a practical implementation of the proposed procedure, applied to a real case study, is presented and results have been compared with those achieved by applying the PP+HP.

The building considered in this paper is the Chiaramonte Palace, located in Palermo (Italy). This imposing fortress-palace, also known as ”Lo Steri” (from ”hosterium”, meaning a fortified place), is in the city area called ”Marina”, a hinge between the harbour and part of the ancient Arabic quarter named Kalsa (Fig. 9a). The palace is a three-floor masonry structure built in the 1307 by the will of Giovanni Chiaramonte the ”Old”, member of the most powerful and influent family of that time [28].

It represents a rare and precious example of XIV-century Sicilian architectural style showing Arabics and Normans influences. Its role as a symbol of the royal power in Sicily justifies its dimensions and peculiarities: its squared floor plans, gravitating on a porticoed courtyard, hold broad delegation rooms for public assemblies. The palace went through many changes and restorations and it was used for different scopes since the fifteenth century. Many spaces were converted into and offices, exhibition areas and museums [29] and currently it houses the rectorate of the University of Palermo. The palace square plan, with a side of about 40 meters, consists of four wings surrounding the magnificent courtyard with its portico on the ground floor and the upper loggia, anticipating the Renaissance model of a mansion.

Fig. 9

a Prospective view of Chiaramonte Palace in Palermo; b The inner courtyard

The courtyard (Fig. 9b) is the main architectural element of the building and it is the object of the present study. The magnificent dual arcade, surmounted by a terrace, presents essential shapes with ogival arches resting on columns with capitals of different appearance and provenance. It extends over an area of about 420 $\hbox {m}^{2}$, with a 20.25 x 20.40 m squared plan and an overall height of 19.50 m, on three floors. Field tests have been performed to identify its dynamic characteristics with the purpose of the calibration of a numerical model for future evaluation of the structural health in order to preserve the historical and architectural uniqueness of the building in a relevant seismic area as Palermo [30].

As far as the first step of the procedure is concerned, the acceleration measurements have been acquired using eight high-sensitivity piezoelectric mono-axial accelerometers, whose characteristics are listed in Table 3.

Table 3 Accelerometers features

Four couples of the overall eight accelerometers have been located at four measuring points to record bi-axial accelerations, along the ${u_1}$ and ${u_2}$ directions, respectively. Accelerometers n. 1–4 have been oriented along the ${u_1}$ axis while n. 5–8 along the ${u_2}$ axis. The couple $\{$n.1, n.5$\}$ has been placed at the ground floor, the another one, $\{$n.2, n.6$\}$, at the first floor and the two couples $\{$n.3, n.7$\}$ and $\{$n.4, n.8$\}$ at the second floor of the courtyard (Fig. 10). Six tests have been performed considering an observation window of ten minutes and acceleration data have been recorded by sensors using a sampling frequency of 100 Hz. Further details of the experimental setup are reported in references [30]. Data in the following refer to one of the six tests since no significant variations have been found.

The structural recorded accelerations ${x_j}(t)$ (with j =1, 2,..., N ), being N=8 the number of recording channels, are assumed to be stationary and ergodic random processes, outputs of a linear system excited by white noise input.

Clearly, the considered case study taken into account, represents a MDOF system so, similarly to the 3DOF system previously analysed, the identification of modal parameters starts from the evaluation of the initial PSD matrix of the response data containing multicomponent PSD and CPSD functions associated to the acquired data and characterized by the contribution of all the modes for each channel. The PSD matrix is obtained using Welch’s Method which subdivides each of the eight acceleration responses ${x_j}(t)$ into N sub-signals and computes a modified periodogram for each segment.

In this study a length of the sub-segments of 40.95 sec (4096 sampling points) has been assumed. Each segment has been multiplied by a Hamming function for windowing and a 50% overlap between adjacent segments have been set to avoid information loss at the beginning and end of each segment.

The multicomponent PSDs $S_{{{\ddot{x}}_j}{{\ddot{x}}_j}}(f)$ and the cross ones $S_{{{\ddot{x}}_j}{{\ddot{x}}_k}}(f)$ (with j,k =1, 2,..., N) which fill the two-sided PSD matrix ${{\mathbf{S}_{{{\ddot{\mathbf{x}}}}{{\ddot{\mathbf{x}}}}}}}(f)$, as diagonal and off-diagonal terms respectively, are obtained according to Eq. (18). Figure 11a, b show auto PSDs functions $S_{{{\ddot{x}}_j}{{\ddot{x}}_j}}(f)$ obtained from the acquired accelerations for channels 1–4 (${u_1}$-axis) and 5–8 (${u_2}$-axis), respectively. It can be clearly pointed out the presence of structural modes in the frequency range 0–6 Hz. Furthermore, it should be also noticed that, in the frequency range between 3.0 and 4.2 Hz, PSDs exhibit a series of local maxima representing possible multiple modes closely spaced.

Fig. 10

Location of measuring points and sensor labelling

Fig. 11

PSDs of acquired signals: a channels 1–4 ${u_1}$-axis; b channels 5–8 ${u_1}$-axis

Table 4 lists the first four identified natural frequencies and the corresponding damping ratios, estimated directly from the peaks of the PSDs using the PP+HP method. Frequencies can be considered accurate enough since the deviation from different data sets was very small, while damping ratios appear to be lower than expected for masonry buildings; however, the structure has been investigated in operational conditions and this is consistent with the fact that the energy dissipation associated to micro-tremors is usually much smaller than during strong excitation as earthquakes.

Table 4 Estimated natural frequencies and damping ratios with the PP + HP method

In order to extract the filtered signals (FPSDs and FCPSDs) a Butterworth band-pass filter of order 8 is applied to each multicomponent PSD (auto and cross) of the original PSD matrix.

Thus, by choosing the filter centered, for instance, in the frequency range on the first frequency of the system (2.62–2.89 Hz), from the original multicomponent $S_{{{\ddot{x}}_1}{{\ddot{x}}_1}}(f)$, the filtered function is obtained.

The procedure is repeated for each original PSD $S_{{{\ddot{x}}_j}{{\ddot{x}}_j}}(f)$, so that eight FPSDs ${_F}S_{{{\ddot{x}}_j}{{\ddot{x}}_j}}(f)$ are obtained in total for the first mode: four along the ${u_1}$ axis and four along the ${u_2}$ axis.

In Fig. 12a the four filtered functions ${_F}S_{{{\ddot{x}}_j}{{\ddot{x}}_j}}(f)$ in terms of accelerations recorded along the ${u_1}$ axis, are depicted. They represent the PSDs of four single oscillators dominated by the modal parameters of the first mode only.

Fig. 12

FPSDs of the structural acceleration responses (recorded along the ${u_1}$ axis): a in correspondence of the first mode; b in correspondence of the second mode

In the same way, filtering the original CPSDs ${_F}S_{{{\ddot{x}}_j}{{\ddot{x}}_k}}(f)$, corresponding FCPSDs ${_F}S_{{{\ddot{x}}_j}{{\ddot{x}}_k}}(f)$ are obtained for the first mode.

Changing the frequency range of the filter to the next modes, FPSDs and FCPSDs are obtained for the other modes too. In Fig. 12b the four functions ${_F}S_{{{\ddot{x}}_j}{{\ddot{x}}_j}}(f)$ of acceleration responses only recorded along the ${u_1}$ axis are depicted considering this time the filtering in the frequency range of the second mode (3.38–3.74 Hz). As it can be seen, the contribution of the first mode, highlighted in Fig. 12b by the peak in the range 2.62–2.89 Hz, disappeared as well as all the other modes except from the second one.

In this manner, henceforward the modal analysis for each signal is retrieved to the simple case of a SDOF system and at the end, the modal parameters of the original MDOF system will be computed as the mean of the frequency and damping ratio values obtained for each channel. Next, the IFFT is applied to estimate the FCORs adn FCCORs.

In Fig. 13a, b the FCORs, denoted as ${_F}R_{{{\ddot{x}}_j}{{\ddot{x}}_j}}(f)$ of the signals recorded along the ${u_1}$ axis are shown. Figure 13a shows the four functions ${_F}R_{{{\ddot{x}}_j}{{\ddot{x}}_j}}(f)$ filtered in correspondence of the first mode while Fig. 13b in correspondence of the second one. Finally, by applying the HT to the FCORs and FCCORs, filtered analytical signals are obtained and from their properties the modal properties are determined as shown previously for the SDOF system. Table 5 shows results derived from the application of the ASM for the first four modes. Discrepancies have been computed assuming the PP+HP method as reference. As shown, by using the proposed approach, the identified frequencies are almost identical to those estimated by the PP+HP (Table 4).

Clearly, dealing with an existing historic building, any exact theoretical values are not available.

Nevertheless, the good agreement between the proposed procedure and the traditional PP+HP method, suggests the reliability of the proposed technique in terms of frequencies identification.

Larger differences are achieved in the definition of damping coefficients. However, since the analytical signal is more sensitive to changes in structural characteristics over time, the extraction of modal parameters from instantaneous frequency and amplitude of monocomponent correlation functions may be particularly efficient in the field of structural monitoring.

Fig. 13

FCORs of the structural acceleration responses (recorded along the ${u_1}$ axis) : a in correspondence of the first mode; b in correspondence of the second mode

Table 5 Estimated natural frequencies and damping ratios with the ASM

5 Conclusion

In this paper, a novel identification procedure based on ambient vibration data, denoted as Analytical Signal-based method (ASM) has been developed. The method aims at the estimation of the modal parameters of a structure from the output data only, and it is based on the use of the Analytical Signal and the Hilbert Transform, applied to properly decomposed response data. Indeed, when a MDOF system is considered, the structural responses are characterized by all the structural modes and modal parameters cannot be extracted directly. The decomposition of the output signal, by means of the Butterworth filter, leads to a set of monocomponent signals corresponding to several SDOF systems, each one containing information about a specific structural mode.

As shown, natural frequencies and damping ratios can be obtained from the analytical signal of the estimated filtered correlation functions, which, in turn, have been achieved from the filtered power spectral density functions of the output signal.

In order to investigate the reliability of this approach, the ASM has been applied to a SDOF and a 3DOF building model. In particular, the present method aims at overcoming the limit imposed by traditional OMA approaches in frequency domain which are generally more accurate for systems with a damping ratio lower than 0.05. Therefore, in this study a structural system characterized by several values of the damping ratio greater than the 5% has been considered. Results indicate that the present technique can achieve a better estimation of frequencies and damping ratios compared to the classical PP+HP approach, even for highly damped systems.

Finally, the proposed approach has been used to estimate dynamic characteristics of structures of the cultural heritage. Specifically, ambient vibration tests have been performed on the Chiamonte-Steri Palace, a historical building located in Palermo. The ASM has been applied to recorded signals of eight accelerometers appropriately located in the inner courtyard of the structure.

Results derived by the use of ASM, compared to the classical PP+HP, suggest that the proposed approach can be considered as a reliable output-only technique for frequencies and damping ratios determination from the analytical signal.

On the basis of the encouraging results, future research will aim at investigating the reliability of the ASM to estimate the mode shapes so that the overall dynamic behavior of the system can be detected.