Dynamic characterization of an aeroelastic typical section under nonlinear energy sink passive control by using multiple scales and harmonic balance methods

Abstract

Aeroelastic systems can be subjected to a self-excited behavior and experience the so-called phenomenon of flutter. Under this condition, airfoils can exhibit self-sustained oscillations. Due to structural nonlinearities, the system’s response is characterized by limit cycle oscillations (LCOs). The high vibration levels can lead to fatigue and catastrophic failure, thereby justifying flutter suppression schemes. This work proposes an investigation about the bifurcation behavior induced by vibration absorbers known as Nonlinear Energy Sinks (NES) aiming to alleviate aeroelastic LCOs in pitch, plunge, and control surface typical section. Unsteady aerodynamic loads are modeled according to generalized Theodorsen and Wagner theories, represented in state space. Pitching hardening nonlinearity is included in the model. A conventional NES approach is considered, in which a pure cubic stiffness spring is adopted. A combined methodology based on multiple scales and harmonic balance perturbation methods is used to build analytical solutions to characterize the dynamics of the aeroelastic system under the influence of NES. After a numerical validation of the analytical approach, the different response regimes and respective boundaries induced by NES are characterized based on the bifurcations of the aeroelastic system. A thorough analysis of the Target Energy Transfer (TET) phenomenon is also performed, and its relationship with response types induced by NES is discovered. Lastly, a characterization of the Slow Invariant Manifold in terms of the aeroelastic critical mode and NES motion is presented, and its significant features are discussed. Parametric studies are carried out based on both bifurcation and TET analyses to access the effect of NES parameters on the aeroelastic system dynamics aiming for a future investigation by employing an optimization process in the NES design.

Appendices

The aeroelastic typical section with an NES: equations of motion

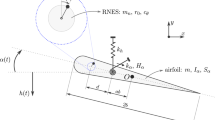
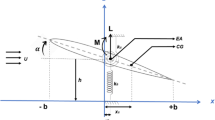
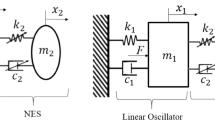
Admitting the system as illustrated in Fig. 1, the kinetic energy of the system can be expressed by:

$$\begin{aligned} {\mathcal {T}} = {\mathcal {T}}_s + {\mathcal {T}}_n , \end{aligned}$$

(31)

where ${\mathcal {T}}_s$ and ${\mathcal {T}}_n$ are the kinetic energies of the airfoil with control surface and the NES, respectively, given by:

$$\begin{aligned} {\mathcal {T}}_s= & {} \frac{1}{2} m {\dot{h}}^2 + S_\alpha {\dot{\alpha }} {\dot{h}} + S_\beta {\dot{\beta }} {\dot{h}} + \frac{1}{2} I_\alpha {\dot{\alpha }}^2 + \frac{1}{2} I_\beta {\dot{\beta }}^2 + (I_\beta + S_\beta (c- a)b) {\dot{\alpha }} {\dot{\beta }} ,\end{aligned}$$

(32)

$$\begin{aligned} {\mathcal {T}}_n= & {} \frac{1}{2} m_n {\dot{z}}^2_n . \end{aligned}$$

(33)

Similarly, the potential energy can be given by:

$$\begin{aligned} {\mathcal {V}} = {\mathcal {V}}_s + {\mathcal {V}}_n , \end{aligned}$$

(34)

where ${\mathcal {V}}_s$ and ${\mathcal {V}}_n$ are the potential energies of the airfoil with control surface and the NES, respectively, given by:

$$\begin{aligned} {\mathcal {V}}_s= & {} \frac{1}{2} k_h h^2 + \frac{1}{2} k_\alpha \alpha ^2 + \frac{1}{4} k_\alpha H_\alpha \alpha ^4 + \frac{1}{2} k_\beta \beta ^2 , \end{aligned}$$

(35)

$$\begin{aligned} {\mathcal {V}}_n= & {} \frac{1}{4} k_n (h - d \alpha - z_n)^4 . \end{aligned}$$

(36)

Admitting no structural damping from the typical section, the work done by the damping forces corresponds only to the NES, i.e., ${\mathcal {B}} = {\mathcal {B}}_n$. From the Rayleigh function:

$$\begin{aligned} {\mathcal {B}}_n = \frac{1}{2} c_n ({\dot{h}} - d {\dot{\alpha }} - {\dot{z}}_n)^2 . \end{aligned}$$

(37)

The Lagrange equations can be applied to the problem, resulting in:

$$\begin{aligned}{} & {} \frac{\textrm{d}}{\textrm{d}t}\left( \frac{\partial {\mathcal {T}}}{\partial {\dot{\alpha }}}\right) - \frac{\partial {\mathcal {T}}}{\partial \alpha } + \frac{\partial {\mathcal {B}}}{\partial {\dot{\alpha }}} + \frac{\partial {\mathcal {V}}}{\partial \alpha } = M_\alpha , \end{aligned}$$

(38.1)

$$\begin{aligned}{} & {} \frac{\textrm{d}}{\textrm{d}t}\left( \frac{\partial {\mathcal {T}}}{\partial {\dot{\beta }}}\right) - \frac{\partial {\mathcal {T}}}{\partial \beta } + \frac{\partial {\mathcal {B}}}{\partial {\dot{\beta }}} + \frac{\partial {\mathcal {V}}}{\partial \beta } = M_\beta , \end{aligned}$$

(38.2)

$$\begin{aligned}{} & {} \frac{\textrm{d}}{\textrm{d}t}\left( \frac{\partial {\mathcal {T}}}{\partial {\dot{h}}}\right) - \frac{\partial {\mathcal {T}}}{\partial h} + \frac{\partial {\mathcal {B}}}{\partial {\dot{h}}} + \frac{\partial {\mathcal {V}}}{\partial h} = - L, \end{aligned}$$

(38.3)

$$\begin{aligned}{} & {} \frac{\textrm{d}}{\textrm{d}t}\left( \frac{\partial {\mathcal {T}}}{\partial {\dot{z}}_n}\right) - \frac{\partial {\mathcal {T}}}{\partial z_n} + \frac{\partial {\mathcal {B}}}{\partial {\dot{z}}_n} + \frac{\partial {\mathcal {V}}}{\partial z_n} = 0 , \end{aligned}$$

(38.4)

where L, $M_\alpha$, and $M_\beta$ are the aerodynamic loading terms.

Introducing Eqs. (31)–(37) into Eqs. (38.1)–(38.4), the typical aeroelastic section with an NES equations of motion is:

$$\begin{aligned} \left\{ \begin{array}{l} I_{\alpha } \ddot{\alpha } + \left[ I_{\beta } + b(c - a) S_\beta \right] \ddot{\beta } + S_{\alpha } \ddot{h} + k_{\alpha } \left( \alpha + H_\alpha \alpha ^3 \right) \\ \quad - d c_n ({\dot{h}} - d {\dot{\alpha }} - {\dot{z}}_n) - d k_n (h - d \alpha - z_n)^3 = M_{\alpha } \\ I_{\beta } \ddot{\beta } + \left[ I_{\beta } + b (c - a) S_{\beta } \right] \ \ddot{\alpha } + S_{\beta } \ddot{h} + k_{\beta } \beta = M_{\beta } \\ m \ddot{h} + S_{\alpha } \ddot{\alpha } + S_{\beta } \ddot{\beta } + k_{h} h + c_n ({\dot{h}} - d {\dot{\alpha }} - {\dot{z}}_n) + k_n (h - d \alpha - z_n)^3 = -L \\ m_n \ddot{z}_n - c_n ({\dot{h}} - d {\dot{\alpha }} - {\dot{z}}_n) - k_n (h - d \alpha - z_n)^3 = 0 \end{array} \right. . \end{aligned}$$

(39)

Equations and formulae

1.1 Matrices from Eq. (7)

The total inertia, damping and stiffness matrices can be detailed as:

$$\begin{aligned} {\textbf{M}}_t = \left[ \begin{array}{ll} {\textbf{M}}_s - {\textbf{M}}_a &{} {\textbf{0}}_{3 \times 1} \\ {\textbf{0}}_{1 \times 3} &{} 1 \end{array}\right] \ , \ {\textbf{B}}_t = \left[ \begin{array}{ll} -{\textbf{B}}_a &{} \quad - {\textbf{A}}_{1} \\ - {\textbf{A}}_{2} &{} \quad (c_2 + c_4)(U/b) \end{array} \right] \ , \ {\textbf{K}}_t = \left[ \begin{array}{ll} {\textbf{K}}_s - {\textbf{K}}_a &{} \quad - {\textbf{A}}_{3} \\ - {\textbf{A}}_{4} &{} \quad c_2 c_4 (U/b)^2 \end{array}\right] , \end{aligned}$$

(40)

where the subscripts s and a are referred to structural and aerodynamic terms.

The structural matrices are:

$$\begin{aligned} {\textbf{M}}_{s}= & {} \begin{bmatrix} r_{\alpha }^{2} &{} \quad r_{\beta }^{2} + (c - a) x_{\beta } &{} \quad x_{\alpha } \\ r_{\beta }^{2} + (c - a) x_{\beta } &{} \quad r_{\beta }^{2} &{} \quad x_{\beta } \\ x_{\alpha } &{} \quad x_{\beta } &{} \quad 1 \end{bmatrix} \ , \end{aligned}$$

(41)

$$\begin{aligned} {\textbf{K}}_{s}= & {} \begin{bmatrix} r_{\alpha }^{2} \omega _{\alpha }^{2} &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad r_{\beta }^{2} \omega _{\beta }^{2} &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad \omega _{h}^{2} \end{bmatrix} \ . \end{aligned}$$

(42)

The aerodynamic inertia matrix comprises the effects due to the non-circulatory flow around the airfoil and can be given as:

$$\begin{aligned} {\textbf{M}}_{a} = - \dfrac{\rho b^2}{m}\begin{bmatrix} \pi \left( \frac{1}{8} + a^2 \right) &{} \quad - T_7 + (c - a) T_1 &{} \quad -\pi a \\ 2 T_{13} &{} \quad - \frac{T_3}{\pi } &{} \quad - T_1 \\ - \pi a &{} \quad - T_1 &{} \quad \pi \end{bmatrix} \ . \end{aligned}$$

(43)

The aerodynamic damping and stiffness matrices regarding circulatory (c) and non-circulatory (nc) flow dynamics (${\textbf{B}}_a = {\textbf{B}}_{nc} + {\textbf{B}}_{c}$ and ${\textbf{K}}_a = {\textbf{K}}_{nc} + {\textbf{K}}_{c}$) are:

$$\begin{aligned} {\textbf{B}}_{nc}= & {} - \dfrac{\rho b^2}{m}\begin{bmatrix} \pi \left( \frac{1}{8} + a^2 \right) &{} \quad - T_7 + (c - a) T_1 &{} \quad -\pi a \\ 2 T_{13} &{} \quad - \frac{T_3}{\pi } &{} \quad - T_1 \\ - \pi a &{} \quad - T_1 &{} \quad \pi \end{bmatrix} \ ,\end{aligned}$$

(44)

$$\begin{aligned} {\textbf{B}}_{c}= & {} - \dfrac{\rho b^2}{m}\begin{bmatrix} \pi \left( \frac{1}{8} + a^2 \right) &{} \quad - T_7 + (c - a) T_1 &{} \quad -\pi a \\ 2 T_{13} &{} \quad - \frac{T_3}{\pi } &{} \quad - T_1 \\ - \pi a &{} \quad - T_1 &{} \quad \pi \end{bmatrix} \ . \end{aligned}$$

(45)

1.2 Theodorsen’s constants

The Theodorsen constants are [21]:

$$\begin{aligned} \begin{aligned} T_1&= - \dfrac{2 + c^2}{3} \sqrt{1 - c^2} + c \cos ^{-1}(c) \ , \\ T_3&= - \dfrac{1 - c^2}{8} \left( 5 c^2 + 4 \right) + \dfrac{1}{4} c \left( 7 + 2 c^2\right) \sqrt{1 - c^2} \cos ^{-1}(c) - \left( \dfrac{1}{8} + c^2\right) \left( \cos ^{-1}(c)\right) ^2 \ , \\ T_4&= c \sqrt{1 - c^2} - \cos ^{-1}(c) \ , \\ T_5&= - \left( 1 - c^2 \right) - \left( \cos ^{-1}(c)\right) ^2 + 2 c \sqrt{1 - c^2} \cos ^{-1}(c) \ , \\ T_7&= c \left( \dfrac{7 + 2 c^2}{8}\right) \sqrt{1 - c^2} - \left( \dfrac{1}{8} + c^2\right) \cos ^{-1}(c) \ , \\ T_8&= - \dfrac{1}{3} \left( 1 + 2 c^2 \right) \sqrt{1 - c^2} + c \cos ^{-1}(c) \ , \\ T_9&= \dfrac{1}{2}\left[ \dfrac{\sqrt{1 - c^2} \left( 1 - c^2\right) }{3} + a T_4 \right] \ , \\ T_{10}&= \sqrt{1 - c^2} + \cos ^{-1}(c) \ , \\ T_{11}&= \left( 2 - c \right) \sqrt{1 - c^2} - \left( 1 - 2 c\right) \cos ^{-1}(c) \ , \\ T_{12}&= \left( 2 + c \right) \sqrt{1 - c^2} - \left( 1 + 2 c\right) \cos ^{-1}(c) \ , \\ T_{13}&= - \dfrac{1}{2}\left[ T_7 + \left( c-a\right) T_1 \right] \ . \end{aligned} \end{aligned}$$

(46)

1.3 Matrices from Eq. (10)

The matrices from Eq. (10) are defined by:

$$\begin{aligned} {\textbf{B}}_{t_0} = \begin{bmatrix} \delta _{11} U_c &{} \quad \delta _{12} U_c &{} \quad \delta _{13} U_c &{} \quad \delta _{14} U_c^2\\ \delta _{21} U_c &{} \quad \delta _{22} U_c &{} \quad \delta _{23} U_c &{} \quad \delta _{24} U_c^2\\ \delta _{31} U_c &{} \quad \delta _{32} U_c &{} \quad \delta _{33} U_c &{} \quad \delta _{34} U_c^2\\ \delta _{41} &{} \quad \delta _{42} &{} \quad \delta _{43} &{} \quad \delta _{44} U_c \end{bmatrix}, \quad {\textbf{B}}_{t_1} = \begin{bmatrix} \delta _{11} &{} \quad \delta _{12} &{} \quad \delta _{13} &{} \quad 2 \delta _{14} U_c \\ \delta _{21} &{} \quad \delta _{22} &{} \quad \delta _{23} &{} \quad 2 \delta _{24} U_c \\ \delta _{31} &{} \quad \delta _{32} &{} \quad \delta _{33} &{} \quad 2 \delta _{34} U_c \\ 0 &{} \quad 0 &{} \quad 0 &{} \quad \delta _{44} \end{bmatrix}, \end{aligned}$$

(47)

where

$$\begin{aligned} \begin{aligned} \delta _{11}&= (a^2 - a + 1/4) \rho \pi b/m, \\ \delta _{12}&= (T_1 + (a - c) T_4 - T_8 + T_{11}(1/2 - a \pi ^2/2 - \pi ^2/4)) \rho b/m, \\ \delta _{13}&= - (a + 1/2) b \pi \rho /m, \\ \delta _{14}&= -2 (a + 1/2)(c_3 c_4 + c_1 c_2) \pi \rho /m, \\ \delta _{21}&= T_{12} (1/2 - a) b \rho /(2 m) + (T_4 (a - 1/2) - 2 T_9 - T_1) b \rho /m, \\ \delta _{22}&= T_{11} T_{12} b \pi \rho /(4 m) - T_{11} T_4 b \rho /(2 m \pi ), \\ \delta _{23}&= T_{12} b \rho /(2 m), \\ \delta _{24}&= T_{12} (c_3 c_4 + c_1 c_2) \rho /m, \\ \delta _{31}&= (1/2 - a) b \pi \rho /m + b \pi \rho /m, \\ \delta _{32}&= T_{11} b \pi ^2 \rho /(2 m) - T_4 b \rho /m, \\ \delta _{33}&= b \pi \rho /m, \\ \delta _{34}&= 2 (c_3 c_4 + c_1 c_2) \pi \rho /m, \\ \delta _{41}&= a - 1/2, \\ \delta _{42}&= - T_{11}/(2 \pi ), \\ \delta _{43}&= -1, \\ \delta _{44}&= (c_4 + c_2)/b, \end{aligned} \end{aligned}$$

(48)

and

$$\begin{aligned} {\textbf{K}}_{t_0} = \begin{bmatrix} r_\alpha ^2 \omega _\alpha ^2 - \eta _{11} U_c^2 &{} \quad \eta _{12} U_c^2 &{} \quad \eta _{13} &{} \quad \eta _{14} U_c^3\\ \eta _{21} U_c^2 &{} \quad r_\beta ^2 \omega _\beta ^2 + \eta _{22} U_c^2 &{} \quad \eta _{23} &{} \quad \eta _{24} U_c^3\\ \eta _{31} U_c^2 &{} \quad \eta _{32} U_c^2 &{} \quad \eta _{33} &{} \quad \eta _{34} U_c^3\\ \eta _{41} U_c &{} \quad \eta _{42} U_c &{} \quad \eta _{43} &{} \quad \eta _{44} U_c^2 \end{bmatrix}, \end{aligned}$$

(49)

and

$$\begin{aligned} {\textbf{K}}_{t_1} = \begin{bmatrix} -2 \eta _{11} U_c &{} \quad 2 \eta _{12} U_c &{} \quad 0 &{} \quad 3 \eta _{14} U_c^2 \\ 2 \eta _{21} U_c &{} \quad 2 \eta _{22} U_c &{} \quad 0 &{} \quad 3 \eta _{24} U_c^2 \\ 2 \eta _{31} U_c &{} \quad 2 \eta _{32} U_c &{} \quad 0 &{} \quad 3 \eta _{34} U_c^2 \\ \eta _{41} &{} \quad \eta _{42} &{} \quad 0 &{} \quad 2 \eta _{44} U_c \end{bmatrix}, \end{aligned}$$

(50)

where

$$\begin{aligned} \begin{aligned} \eta _{11}&= (a + 1/2) \pi \rho /m, \\ \eta _{12}&= (T_4 + T_{10}) \rho /m - T_{10}(a+1/2)\rho /m, \\ \eta _{13}&= 0, \\ \eta _{14}&= - 2 (a + 1/2) c_2 (c_3 + c_1) c_4 \pi \rho /(b m), \\ \eta _{21}&= T_{12} \rho /(2 m), \\ \eta _{22}&= (T_5 - T_{10} T_4) \rho /(m \pi ) + (T_{10} T_{12} \rho )/(2 m \pi ), \\ \eta _{23}&= 0, \\ \eta _{24}&= T_{12} c_2 (c_3 + c_1) c_4 \rho /(b m) , \\ \eta _{31}&= \pi \rho /m, \\ \eta _{32}&= (T_{10} \rho )/m, \\ \eta _{33}&= \omega _h^2, \\ \eta _{34}&= 2 c_2 (c_3 + c_1) c_4 \pi \rho /(b m), \\ \eta _{41}&= -1/b, \\ \eta _{42}&= - T_{10}/(b \pi ), \\ \eta _{43}&= 0, \\ \eta _{44}&= c_2 c_4/b^2. \end{aligned} \end{aligned}$$

(51)

1.4 Polynomial functions of Eq. (21)

The polynomial functions ${\mathcal {F}}_1(b)$ and ${\mathcal {F}}_2(b)$ of Eq. (21) are given by:

$$\begin{aligned} {\mathcal {F}}_1(b)= & {} \theta _1 b + 2 \theta _2 b^3 + 3 \theta _3 b^5, \end{aligned}$$

(52)

$$\begin{aligned} {\mathcal {F}}_2(b)= & {} \varTheta _1 b^2 + \theta _2 b^4 + \varTheta _3 b^6 + \varTheta _4 b^8 + \varTheta _5 b^{10} + \varTheta _6 b^{12} \end{aligned}$$

(53)

where

$$\begin{aligned} \begin{aligned} \varTheta _1&= \theta _1 \sigma {\mathcal {R}}e\left\{ \varUpsilon _1\right\} + {\mathcal {R}}e\left\{ \varUpsilon _3\right\} {\mathcal {R}}e\left\{ \varphi _1\right\} + {\mathcal {I}}m\left\{ \varUpsilon _3\right\} {\mathcal {I}}m\left\{ \varphi _1\right\} , \\ \varTheta _2&= \theta _2 \sigma {\mathcal {R}}e\left\{ \varUpsilon _1\right\} + \theta _1^2 {\mathcal {R}}e\left\{ \varUpsilon _2\right\} + {\mathcal {R}}e\left\{ \varUpsilon _3\right\} {\mathcal {R}}e\left\{ \varphi _2\right\} + {\mathcal {I}}m\left\{ \varUpsilon _3\right\} {\mathcal {I}}m\left\{ \varphi _2\right\} + \\&\quad + {\mathcal {R}}e\left\{ \varUpsilon _4\right\} {\mathcal {R}}e\left\{ \psi _1\right\} + {\mathcal {I}}m\left\{ \varUpsilon _4\right\} {\mathcal {I}}m\left\{ \varphi _1\right\} , \\ \varTheta _3&= \theta _3 \sigma {\mathcal {R}}e\left\{ \varUpsilon _1\right\} + 2 \theta _1 \theta _2 {\mathcal {R}}e\left\{ \varUpsilon _2\right\} + {\mathcal {R}}e\left\{ \varUpsilon _4\right\} {\mathcal {R}}e\left\{ \varphi _2\right\} + {\mathcal {I}}m\left\{ \varUpsilon _4\right\} {\mathcal {I}}m\left\{ \varphi _2\right\} , \\ \varTheta _4&= (\theta _2^2 + 2 \theta _1 \theta _3) {\mathcal {R}}e\left\{ \varUpsilon _2\right\} ,\\ \varTheta _5&= 2 \theta _2 \theta _3 {\mathcal {R}}e\left\{ \varUpsilon _2\right\} ,\\ \varTheta _6&= {\mathcal {R}}e\left\{ \varUpsilon _2\right\} \theta _3^2. \end{aligned} \end{aligned}$$

(54)