A method of coating analysis based on cylindrical indenter loading on coated structure

Abstract

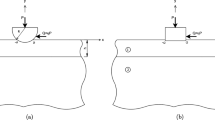
The most common coated structure contact problems include spherical, conical and cylindrical contact. The evaluation of mechanical performance for coating structures has always been a very important issue in the field of mechanics and materials; due to the too small proportion between the thickness of the coating and the substrate, the deviation of traditional evaluation methods becomes unacceptable. Indentation technology is the basis for analysis, measurement, and the standardized application of coating structures. The research object of this paper is cylindrical contact, which is one part of building the theoretical framework of contact mechanics of coating structures. In the paper, an accurate and efficient general theory of the frictional cylindrical contact problem for the coated structure is presented. The general solutions are expressed in the form of harmonic functions. 3D exact solutions of a transversely isotropic elasticity coated structure under frictional cylindrical punch contact are derived, based on the general solution and the boundary conditions. The theory is proposed in two cases, including the frictionless contact and the frictional contact. By contrast with existing theories (obtained in this paper by degradation), the numerical calculations show the good convergence, high accuracy, efficiency, and stability. The difference of stress singularity analysis between Finite Element Method (FEM) and the presented theory is explained, which shows the theory’s validity and applicability. This analytical theory plays an important role in boundary stress singularity analysis. The finite element comparison shows that the analytical theory plays an important role in boundary stress singularity analysis and further, proves the validity and applicability of this theory. In the numerical analysis, the influence of coating thickness on interface stress is shown, the distribution forms of stress and displacement are given, and the influence of material parameters and coating thickness on interface failure is investigated. The analytical expressions are presented with the elementary functions. In the era of highly developed computer intelligence, the presented theory will be the basis of the interface failure problem analysis and material parameters’ determination, also for future use deep learning to solve the problem of contact mechanics provides the basis of large precise sample.

Appendix

In Appendixes A and B, general solutions for both frictionless and frictional situations are listed for the application of this contact theory.

1.1 Appendix A: The functions for the frictionless contact

$$ \begin{aligned} U & = u + iv = e^{i\varphi } (u_{r} + iu_{\varphi } ),\sigma_{1} = \sigma_{x} + \sigma_{y} = \sigma_{r} + \sigma_{\varphi } , \\ \sigma_{2} & = \sigma_{x} - \sigma_{y} + 2i\tau_{xy} = e^{2i\varphi } (\sigma_{r} - \sigma_{\varphi } + 2i\tau_{r\varphi } ),\tau_{z} = \tau_{xz} + i\tau_{yz} = e^{i\varphi } (\tau_{rz} + i\tau_{\varphi z} ). \\ \end{aligned} $$

(A1)

where

$$ \begin{aligned} U & = \sum\limits_{n = 1}^{\infty } {\left( {\overline{U}_{n} + U_{n} } \right)} ,w = \sum\limits_{n = 1}^{\infty } {\left( {\overline{w}_{n} + w_{n} } \right)} ,\sigma_{1} = \sum\limits_{n = 1}^{\infty } {\left( {\overline{\sigma }_{1n} + \sigma_{1n} } \right)} , \\ & \quad {\text{for}} \,\, {\text{coating}}\;0 \le z \le h, \\ \sigma_{2} & = \sum\limits_{n = 1}^{\infty } {\left( {\overline{\sigma }_{2n} + \sigma_{2n} } \right)} ,\sigma_{z} = \sum\limits_{n = 1}^{\infty } {\left( {\overline{\sigma }_{zn} + \sigma_{zn} } \right)} ,\tau_{z} = \sum\limits_{n = 1}^{\infty } {\left( {\overline{\tau }_{zn} + \tau_{zn} } \right)} , \\ \end{aligned} $$

(A2.1)

$$ \begin{aligned} U^{\prime} & = \sum\limits_{n = 1}^{\infty } {U^{\prime}_{n} } ,w^{\prime} = \sum\limits_{n = 1}^{\infty } {w^{\prime}_{n} } ,\sigma^{\prime}_{1} = \sum\limits_{n = 1}^{\infty } {\sigma^{\prime}_{1n} } , \\ & \quad {\text{for}}\, \, {\text{coating}}\;z \le 0, \\ \sigma^{\prime}_{2} & = \sum\limits_{n = 1}^{\infty } {\sigma^{\prime}_{2n} } ,\sigma^{\prime}_{z} = \sum\limits_{n = 1}^{\infty } {\sigma^{\prime}_{zn} } ,\tau^{\prime}_{z} = \sum\limits_{n = 1}^{\infty } {\tau^{\prime}_{zn} } , \\ \end{aligned} $$

(A2.2)

the functions in Eq. (A2.1) are presented in Eq. (A3.1), and the functions in Eq. (A2.2) are presented Eq. (A3.2):

$$ \begin{aligned} U_{n} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{{e^{i\varphi } }}{r}P_{z} A_{njk} \left( {1 - \frac{{\sqrt {a^{2} - l_{1njk}^{2} } }}{a}} \right)} } , \\ \overline{U}_{n} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{{e^{i\varphi } }}{r}P_{z} \overline{A}_{njk} \left( {1 - \frac{{\sqrt {a^{2} - \overline{l}_{1njk}^{2} } }}{a}} \right)} } , \\ w_{n} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{1}{a}s_{j} k_{j} P_{z} A_{njk} \sin^{ - 1} \left( {\frac{{l_{1njk} }}{r}} \right)} } , \\ \overline{w}_{n} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{1}{a}s_{j} k_{j} P_{z} \overline{A}_{njk} \sin^{ - 1} \left( {\frac{{\overline{l}_{1njk} }}{r}} \right)} } , \\ \sigma_{1n} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{2}{a}\left( {m_{j} - c_{66} } \right)P_{z} A_{njk} \frac{{\sqrt {a^{2} - l_{1njk}^{2} } }}{{l_{2njk}^{2} - l_{1njk}^{2} }}} } , \\ \overline{\sigma }_{1n} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{2}{a}\left( {m_{j} - c_{66} } \right)P_{z} \overline{A}_{njk} \frac{{\sqrt {a^{2} - \overline{l}_{1njk}^{2} } }}{{\overline{l}_{2njk}^{2} - \overline{l}_{1njk}^{2} }}} } , \\ \end{aligned} $$

$$ \begin{aligned} \sigma_{2n} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{{2c_{66} }}{a}e^{i2\varphi } P_{z} A_{njk} } } \left[ {\frac{{\sqrt {a^{2} - l_{1njk}^{2} } }}{{l_{2njk}^{2} - l_{1njk}^{2} }} - \frac{2a}{{r^{2} }}\left( {1 - \frac{{\sqrt {a^{2} - l_{1njk}^{2} } }}{a}} \right)} \right], \\ \overline{\sigma }_{2n} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{{2c_{66} }}{a}e^{i2\varphi } P_{z} \overline{A}_{njk} } } \left[ {\frac{{\sqrt {a^{2} - \overline{l}_{1njk}^{2} } }}{{\overline{l}_{2njk}^{2} - \overline{l}_{1njk}^{2} }} - \frac{2a}{{r^{2} }}\left( {1 - \frac{{\sqrt {a^{2} - \overline{l}_{1njk}^{2} } }}{a}} \right)} \right], \\ \sigma_{zn} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{1}{a}\omega_{j} P_{z} A_{njk} \frac{{\sqrt {a^{2} - l_{1njk}^{2} } }}{{l_{2njk}^{2} - l_{1njk}^{2} }}} } , \\ \overline{\sigma }_{zn} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{1}{a}\omega_{j} P_{z} \overline{A}_{njk} \frac{{\sqrt {a^{2} - \overline{l}_{1njk}^{2} } }}{{\overline{l}_{2njk}^{2} - \overline{l}_{1njk}^{2} }}} } , \\ \tau_{zn} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{1}{a}e^{i\varphi } s_{j} \omega_{j} P_{z} A_{njk} \frac{{l_{1njk} \sqrt {l_{2njk}^{2} - a^{2} } }}{{l_{2njk} \left( {l_{2njk}^{2} - l_{1njk}^{2} } \right)}}} } , \\ \overline{\tau }_{zn} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{1}{a}e^{i\varphi } s_{j} \omega_{j} P_{z} \overline{A}_{njk} \frac{{\overline{l}_{1njk} \sqrt {\overline{l}_{2njk}^{2} - a^{2} } }}{{\overline{l}_{2njk} \left( {\overline{l}_{2njk}^{2} - \overline{l}_{1njk}^{2} } \right)}}} } , \\ \end{aligned} $$

(A3.1)

$$ \begin{aligned} U^{\prime}_{n} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{{e^{i\varphi } }}{r}P_{z} A^{\prime}_{njk} \left( {1 - \frac{{\sqrt {a^{2} - l_{1njk}^{\prime 2} } }}{a}} \right)} } , \\ w^{\prime}_{n} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{1}{a}s^{\prime}_{j} k^{\prime}_{j} P_{z} A^{\prime}_{njk} \sin^{ - 1} \left( {\frac{{l^{\prime}_{1njk} }}{r}} \right)} } , \\ \sigma^{\prime}_{1n} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{2}{a}\left( {m^{\prime}_{j} - c^{\prime}_{66} } \right)P_{z} A^{\prime}_{njk} \frac{{\sqrt {a^{2} - l_{1njk}^{\prime 2} } }}{{l_{2njk}^{\prime 2} - l_{1njk}^{\prime 2} }}} } , \\ \sigma^{\prime}_{2n} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{{2c^{\prime}_{66} }}{a}e^{i2\varphi } P_{z} A^{\prime}_{njk} } } \left[ {\frac{{\sqrt {a^{2} - l_{1njk}^{\prime 2} } }}{{l_{2njk}^{\prime 2} - l_{1njk}^{\prime 2} }} - \frac{2a}{{r^{2} }}\left( {1 - \frac{{\sqrt {a^{2} - l_{1njk}^{\prime 2} } }}{a}} \right)} \right], \\ \sigma^{\prime}_{zn} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{1}{a}\omega^{\prime}_{j} P_{z} A^{\prime}_{njk} \frac{{\sqrt {a^{2} - l_{1njk}^{\prime 2} } }}{{l_{2njk}^{\prime 2} - l_{1njk}^{\prime 2} }}} } , \\ \tau^{\prime}_{zn} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{1}{a}e^{i\varphi } s^{\prime}_{j} \omega^{\prime}_{j} P_{z} A^{\prime}_{njk} \frac{{l^{\prime}_{1njk} \sqrt {l_{2njk}^{\prime 2} - a^{2} } }}{{l^{\prime}_{2njk} \left( {l_{2njk}^{\prime 2} - l_{1njk}^{\prime 2} } \right)}}} } . \\ \end{aligned} $$

(A3.2)

The undetermined coefficients $A_{njk}$, $A^{\prime}_{njk}$ and $\overline{A}_{njk}$ are determined by the following recursive formulas (A4.1)–(A4.3):

$$ \overline{A}_{112} = \overline{A}_{121} = 0,\,\sum\limits_{j = 1}^{2} {s_{j} \omega_{j} \overline{A}_{1jj} } = 0,\,\sum\limits_{j = 1}^{2} {\omega_{j} \overline{A}_{1jj} } = \frac{1}{2\pi }, $$

(A4.1)

$$ \begin{aligned} & \overline{A}_{{\left( {n + 1} \right)21}} = \overline{A}_{{\left( {n + 1} \right)1\left( {2n + 2} \right)}} = 0, \\ & \omega_{1} \overline{A}_{{\left( {n + 1} \right)11}} + \omega_{2} \overline{A}_{{\left( {n + 1} \right)22}} = - \omega_{1} A_{n11} , \\ & \omega_{1} \overline{A}_{{\left( {n + 1} \right)1\left( {2n + 1} \right)}} + \omega_{2} \overline{A}_{{\left( {n + 1} \right)2\left( {2n + 2} \right)}} = - \omega_{2} A_{{n2\left( {2n} \right)}} , \\ & \omega_{1} \overline{A}_{{\left( {n + 1} \right)1\left( {m + 1} \right)}} + \omega_{2} \overline{A}_{{\left( {n + 1} \right)2\left( {m + 2} \right)}} = - \omega_{1} A_{{n1\left( {m + 1} \right)}} - \omega_{2} A_{n2m} , \\ & s_{1} \omega_{1} \overline{A}_{{\left( {n + 1} \right)11}} + s_{2} \omega_{2} \overline{A}_{{\left( {n + 1} \right)22}} = s_{1} \omega_{1} A_{n11} , \\ & s_{1} \omega_{1} \overline{A}_{{\left( {n + 1} \right)1\left( {2n + 1} \right)}} + s_{2} \omega_{2} \overline{A}_{{\left( {n + 1} \right)2\left( {2n + 2} \right)}} = s_{2} \omega_{2} A_{{n2\left( {2n} \right)}} , \\ & s_{1} \omega_{1} \overline{A}_{{\left( {n + 1} \right)1\left( {m + 1} \right)}} + s_{2} \omega_{2} \overline{A}_{{\left( {n + 1} \right)2\left( {m + 2} \right)}} = s_{1} \omega_{1} A_{{n1\left( {m + 1} \right)}} + s_{2} \omega_{2} A_{n2m} , \\ & \quad (n = 1,2, \ldots ,\infty ;m = 1,2, \ldots ,2n - 1), \\ \end{aligned} $$

(A4.2)

$$ \begin{aligned} & \sum\limits_{j = 1}^{2} {\left( {A_{njk} - A^{\prime}_{njk} } \right) = - \sum\limits_{j = 1}^{2} {\overline{A}_{njk} } } , \\ & \sum\limits_{j = 1}^{2} {\left( {s_{j} k_{j} A_{njk} + s^{\prime}_{j} k^{\prime}_{j} A^{\prime}_{njk} } \right) = \sum\limits_{j = 1}^{2} {s_{j} k_{j} \overline{A}_{njk} } } , \\ & \sum\limits_{j = 1}^{2} {\left( { - \omega_{j} A_{njk} + \omega^{\prime}_{j} A^{\prime}_{njk} } \right) = \sum\limits_{j = 1}^{2} {\omega_{j} \overline{A}_{njk} } } , \\ & \sum\limits_{j = 1}^{2} {\left( {s_{j} \omega_{j} A_{njk} + s^{\prime}_{j} \omega^{\prime}_{j} A^{\prime}_{njk} } \right) = \sum\limits_{j = 1}^{2} {s_{j} \omega_{j} \overline{A}_{njk} } } , \\ & \quad ( n = 1,2, \ldots ,\infty ;j = 1,2;k = 1,2, \ldots ,2n). \\ \end{aligned} $$

(A4.3)

1.2 Appendix B: The functions for the frictional contact

$$ \begin{aligned} U & = u + iv = e^{i\varphi } (u_{r} + iu_{\varphi } ),\,\sigma_{1} = \sigma_{x} + \sigma_{y} = \sigma_{r} + \sigma_{\varphi } , \\ \sigma_{2} & = \sigma_{x} - \sigma_{y} + 2i\tau_{xy} = e^{2i\varphi } (\sigma_{r} - \sigma_{\varphi } + 2i\tau_{r\varphi } ),\,\tau_{z} = \tau_{xz} + i\tau_{yz} = e^{i\varphi } (\tau_{rz} + i\tau_{\varphi z} ), \\ \end{aligned} $$

(B1)

where

$$ \begin{aligned} U & = \sum\limits_{n = 1}^{\infty } {\left( {\overline{U}_{n} + U_{n} } \right)} ,w = \sum\limits_{n = 1}^{\infty } {\left( {\overline{w}_{n} + w_{n} } \right)} ,\sigma_{1} = \sum\limits_{n = 1}^{\infty } {\left( {\overline{\sigma }_{1n} + \sigma_{1n} } \right)} , \\ & \quad {\text{for}}\, {\text{coating}}\;0 \le z \le h. \\ \sigma_{2} & = \sum\limits_{n = 1}^{\infty } {\left( {\overline{\sigma }_{2n} + \sigma_{2n} } \right)} ,\sigma_{z} = \sum\limits_{n = 1}^{\infty } {\left( {\overline{\sigma }_{zn} + \sigma_{zn} } \right)} ,\tau_{z} = \sum\limits_{n = 1}^{\infty } {\left( {\overline{\tau }_{zn} + \tau_{zn} } \right)} , \\ \end{aligned} $$

(B2.1)

$$ \begin{aligned} U^{\prime} & = \sum\limits_{n = 1}^{\infty } {U^{\prime}_{n} } ,w^{\prime} = \sum\limits_{n = 1}^{\infty } {w^{\prime}_{n} } ,\sigma^{\prime}_{1} = \sum\limits_{n = 1}^{\infty } {\sigma^{\prime}_{1n} } , \\ & \quad {\text{for}} \,{\text{coating}}\;z \le 0, \\ \sigma^{\prime}_{2} & = \sum\limits_{n = 1}^{\infty } {\sigma^{\prime}_{2n} } ,\sigma^{\prime}_{z} = \sum\limits_{n = 1}^{\infty } {\sigma^{\prime}_{zn} } ,\tau^{\prime}_{z} = \sum\limits_{n = 1}^{\infty } {\tau^{\prime}_{zn} } , \\ \end{aligned} $$

(B2.2)

the functions in Eq. (B2.1) are presented in Eq. (B3.1), and the functions in Eq. (B2.2) are presented Eq. (B3.2):

$$ \begin{aligned} U_{n} &= \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{{P_{z} }}{2a}B_{njk} \left[ { - f\sin^{ - 1} \left( {\frac{{l_{1njk} }}{r}} \right) + \overline{f}e^{i2\varphi } \left( {\frac{{2z_{njk} }}{{r^{2} }}\sqrt {a^{2} - l_{1njk}^{2} } - \frac{{2az_{njk} }}{{r^{2} }} + \frac{{l_{1njk} }}{{r^{2} }}\sqrt {r^{2} - l_{1njk}^{2} } } \right)} \right]} } \\ & \quad - \frac{{P_{z} }}{2a}B_{n0} \left[ {f\sin^{ - 1} \left( {\frac{{l_{1n0} }}{r}} \right) + \overline{f}e^{i2\varphi } \left( {\frac{{2z_{n0} }}{{r^{2} }}\sqrt {a^{2} - l_{1n0}^{2} } - \frac{{2az_{n0} }}{{r^{2} }} + \frac{{l_{1n0} }}{{r^{2} }}\sqrt {r^{2} - l_{1n0}^{2} } } \right)} \right], \\ \end{aligned} $$

$$ \begin{aligned} \overline{U}_{n} &= \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{{P_{z} }}{2a}\overline{B}_{njk} \left[ { - f\sin^{ - 1} \left( {\frac{{\overline{l}_{1njk} }}{r}} \right) + \overline{f}e^{i2\varphi } \left( { - \frac{{2\overline{z}_{njk} }}{{r^{2} }}\sqrt {a^{2} - \overline{l}_{1njk}^{2} } + \frac{{2a\overline{z}_{njk} }}{{r^{2} }} + \frac{{\overline{l}_{1njk} }}{{r^{2} }}\sqrt {r^{2} - \overline{l}_{1njk}^{2} } } \right)} \right]} } \\ & \quad - \frac{{P_{z} }}{2a}\overline{B}_{n0} \left[ {f\sin^{ - 1} \left( {\frac{{\overline{l}_{1n0} }}{r}} \right) + \overline{f}e^{i2\varphi } \left( { - \frac{{2\overline{z}_{n0} }}{{r^{2} }}\sqrt {a^{2} - \overline{l}_{1n0}^{2} } + \frac{{2a\overline{z}_{n0} }}{{r^{2} }} + \frac{{\overline{l}_{1n0} }}{{r^{2} }}\sqrt {r^{2} - \overline{l}_{1n0}^{2} } } \right)} \right], \\ \end{aligned} $$

$$ \begin{aligned} w_{n} &= \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{{P_{z} }}{2a}\left( {\overline{f}e^{i\varphi } + fe^{ - i\varphi } } \right)s_{j} k_{j} B_{njk} } } \left( {\frac{a}{r} - \frac{{\sqrt {a^{2} - l_{1njk}^{2} } }}{r}} \right), \\ \overline{w}_{n} &= \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{{P_{z} }}{2a}\left( {\overline{f}e^{i\varphi } + fe^{ - i\varphi } } \right)s_{j} k_{j} \overline{B}_{njk} } } \left( {\frac{a}{r} - \frac{{\sqrt {a^{2} - \overline{l}_{1njk}^{2} } }}{r}} \right), \\ \sigma_{1n} &= \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{{P_{z} }}{a}\left( {\overline{f}e^{i\varphi } + fe^{ - i\varphi } } \right)\left( {m_{j} - c_{66} } \right)B_{njk} \frac{{l_{1njk} \sqrt {r^{2} - l_{1njk}^{2} } }}{{r\left( {l_{2njk}^{2} - l_{1njk}^{2} } \right)}}} } , \\ \overline{\sigma }_{1n} &= \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{{P_{z} }}{a}\left( {\overline{f}e^{i\varphi } + fe^{ - i\varphi } } \right)\left( {m_{j} - c_{66} } \right)\overline{B}_{njk} \frac{{\overline{l}_{1njk} \sqrt {r^{2} - \overline{l}_{1njk}^{2} } }}{{r\left( {\overline{l}_{2njk}^{2} - \overline{l}_{1njk}^{2} } \right)}}} } , \\ \end{aligned} $$

$$ \begin{aligned} \sigma_{2n} &= \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{{c_{66} P_{z} }}{a}B_{njk} \left[ {fe^{i\varphi } \frac{{l_{1njk} \sqrt {r^{2} - l_{1njk}^{2} } }}{{r\left( {l_{2njk}^{2} - l_{1njk}^{2} } \right)}} + \overline{f}e^{i3\varphi } \left\{ {\frac{{8az_{njk} }}{{r^{3} }}} \right.} \right.} } \\ & \quad - \left. {\left. {\frac{{\sqrt {r^{2} - l_{1njk}^{2} } }}{{r^{3} l_{1njk} \left( {l_{2njk}^{2} - l_{1njk}^{2} } \right)}}\left[ {8a^{2} l_{2njk}^{2} - 8a^{2} r^{2} + \left( {3r^{2} - 4a^{2} + 4z_{njk}^{2} } \right)l_{1njk}^{2} } \right]} \right\}} \right] \\ & \quad + \frac{{c_{66} P_{z} }}{a}B_{n0} \left[ {fe^{i\varphi } \frac{{l_{1n0} \sqrt {r^{2} - l_{1n0}^{2} } }}{{r\left( {l_{2n0}^{2} - l_{1n0}^{2} } \right)}} - \overline{f}e^{i3\varphi } \left\{ {\frac{{8az_{n0} }}{{r^{3} }}} \right.} \right. \\ & \quad - \left. {\left. {\frac{{\sqrt {r^{2} - l_{1n0}^{2} } }}{{r^{3} l_{1n0} \left( {l_{2n0}^{2} - l_{1n0}^{2} } \right)}}\left[ {8a^{2} l_{2n0}^{2} - 8a^{2} r^{2} + \left( {3r^{2} - 4a^{2} + 4z_{n0}^{2} } \right)l_{1n0}^{2} } \right]} \right\}} \right], \\ \end{aligned} $$

$$ \begin{aligned} \overline{\sigma }_{2n} &= \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{{c_{66} P_{z} }}{a}\overline{B}_{njk} \left[ {fe^{i\varphi } \frac{{\overline{l}_{1njk} \sqrt {r^{2} - \overline{l}_{1njk}^{2} } }}{{r\left( {\overline{l}_{2njk}^{2} - \overline{l}_{1njk}^{2} } \right)}} + \overline{f}e^{i3\varphi } \left\{ { - \frac{{8a\overline{z}_{njk} }}{{r^{3} }}} \right.} \right.} } \\ & \quad - \left. {\left. {\frac{{\sqrt {r^{2} - \overline{l}_{1njk}^{2} } }}{{r^{3} \overline{l}_{1njk} \left( {\overline{l}_{2njk}^{2} - \overline{l}_{1njk}^{2} } \right)}}\left[ {8a^{2} \overline{l}_{2njk}^{2} - 8a^{2} r^{2} + \left( {3r^{2} - 4a^{2} + 4\overline{z}_{njk}^{2} } \right)\overline{l}_{1njk}^{2} } \right]} \right\}} \right] \\ & \quad + \frac{{c_{66} P_{z} }}{a}\overline{B}_{n0} \left[ {fe^{i\varphi } \frac{{\overline{l}_{1n0} \sqrt {r^{2} - \overline{l}_{1n0}^{2} } }}{{r\left( {\overline{l}_{2n0}^{2} - \overline{l}_{1n0}^{2} } \right)}} - \overline{f}e^{i3\varphi } \left\{ { - \frac{{8a\overline{z}_{n0} }}{{r^{3} }}} \right.} \right. \\ & \quad - \left. {\left. {\frac{{\sqrt {r^{2} - \overline{l}_{1n0}^{2} } }}{{r^{3} \overline{l}_{1n0} \left( {\overline{l}_{2n0}^{2} - \overline{l}_{1n0}^{2} } \right)}}\left[ {8a^{2} \overline{l}_{2n0}^{2} - 8a^{2} r^{2} + \left( {3r^{2} - 4a^{2} + 4\overline{z}_{n0}^{2} } \right)\overline{l}_{1n0}^{2} } \right]} \right\}} \right], \\ \end{aligned} $$

$$ \begin{aligned} \sigma_{zn} &= \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{{P_{z} }}{2a}\left( {\overline{f}e^{i\varphi } + fe^{ - i\varphi } } \right)\omega_{j} B_{njk} \frac{{l_{1njk} \sqrt {r^{2} - l_{1njk}^{2} } }}{{r\left( {l_{2njk}^{2} - l_{1njk}^{2} } \right)}}} }, \\ \overline{\sigma }_{zn} &= \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{{P_{z} }}{2a}\left( {\overline{f}e^{i\varphi } + fe^{ - i\varphi } } \right)\omega_{j} \overline{B}_{njk} \frac{{\overline{l}_{1njk} \sqrt {r^{2} - \overline{l}_{1njk}^{2} } }}{{r\left( {\overline{l}_{2njk}^{2} - \overline{l}_{1njk}^{2} } \right)}}} }, \\ \end{aligned} $$

$$ \begin{aligned} \tau_{zn} & = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{{P_{z} }}{2a}s_{j} \omega_{j} B_{njk} \left[ {f\frac{{\sqrt {a^{2} - l_{1njk}^{2} } }}{{l_{2njk}^{2} - l_{1njk}^{2} }} + \overline{f}e^{i2\varphi } \left( {\frac{{\sqrt {a^{2} - l_{1njk}^{2} } }}{{l_{2njk}^{2} - l_{1njk}^{2} }} - \frac{2a}{{r^{2} }} + \frac{2}{{r^{2} }}\sqrt {a^{2} - l_{1njk}^{2} } } \right)} \right]} } \\ & \quad + \frac{{s_{0} c_{44} P_{z} }}{2a}B_{n0} \left[ {f\frac{{\sqrt {a^{2} - l_{1n0}^{2} } }}{{l_{2n0}^{2} - l_{1n0}^{2} }} - \overline{f}e^{i2\varphi } \left( {\frac{{\sqrt {a^{2} - l_{1n0}^{2} } }}{{l_{2n0}^{2} - l_{1n0}^{2} }} - \frac{2a}{{r^{2} }} + \frac{2}{{r^{2} }}\sqrt {a^{2} - l_{1n0}^{2} } } \right)} \right], \\ \overline{\tau }_{zn} &= \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{{P_{z} }}{2a}s_{j} \omega_{j} \overline{B}_{njk} \left[ {f\frac{{\sqrt {a^{2} - \overline{l}_{1njk}^{2} } }}{{\overline{l}_{2njk}^{2} - \overline{l}_{1njk}^{2} }} + \overline{f}e^{i2\varphi } \left( {\frac{{\sqrt {a^{2} - \overline{l}_{1njk}^{2} } }}{{\overline{l}_{2njk}^{2} - \overline{l}_{1njk}^{2} }} - \frac{2a}{{r^{2} }} + \frac{2}{{r^{2} }}\sqrt {a^{2} - \overline{l}_{1njk}^{2} } } \right)} \right]} } \\ & \quad - \frac{{s_{0} c_{44} P_{z} }}{2a}\overline{B}_{n0} \left[ {f\frac{{\sqrt {a^{2} - \overline{l}_{1n0}^{2} } }}{{\overline{l}_{2n0}^{2} - \overline{l}_{1n0}^{2} }} - \overline{f}e^{i2\varphi } \left( {\frac{{\sqrt {a^{2} - \overline{l}_{1n0}^{2} } }}{{\overline{l}_{2n0}^{2} - \overline{l}_{1n0}^{2} }} - \frac{2a}{{r^{2} }} + \frac{2}{{r^{2} }}\sqrt {a^{2} - \overline{l}_{1n0}^{2} } } \right)} \right], \\ \end{aligned} $$

(B3.1)

$$ \begin{aligned} U^{\prime}_{n} &= \sum\limits_{{k = 1}}^{{2n}} {\sum\limits_{{j = 1}}^{2} { - \frac{{P_{z} }}{{2a}}B^{\prime}_{{njk}} \left[ { - f\sin ^{{ - 1}} \left( {\frac{{l^{\prime}_{{1njk}} }}{r}} \right) + \bar{f}e^{{i2\varphi }} \left( { - \frac{{2z^{\prime}_{{njk}} }}{{r^{2} }}\sqrt {a^{2} - l_{{1njk}}^{{\prime 2}} } + \frac{{2az^{\prime}_{{njk}} }}{{r^{2} }} + \frac{{l^{\prime}_{{1njk}} }}{{r^{2} }}\sqrt {r^{2} - l_{{1njk}}^{{\prime 2}} } } \right)} \right]} } \\ & \quad - \frac{{P_{z} }}{{2a}}B^{\prime}_{{n0}} \left[ {f\sin ^{{ - 1}} \left( {\frac{{l^{\prime}_{{1n0}} }}{r}} \right) + \bar{f}e^{{i2\varphi }} \left( { - \frac{{2z^{\prime}_{{n0}} }}{{r^{2} }}\sqrt {a^{2} - l_{{1n0}}^{{\prime 2}} } + \frac{{2az^{\prime}_{{n0}} }}{{r^{2} }} + \frac{{l^{\prime}_{{1n0}} }}{{r^{2} }}\sqrt {r^{2} - l _{{1n0}}^{{\prime 2}} } } \right)} \right], \\ \end{aligned} $$

$$ \begin{gathered} w^{\prime}_{n} = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{{P_{z} }}{2a}\left( {\overline{f}e^{i\varphi } + fe^{ - i\varphi } } \right)s^{\prime}_{j} k^{\prime}_{j} B^{\prime}_{njk} } } \left( {\frac{a}{r} - \frac{{\sqrt {a^{2} - l_{1njk}^{\prime 2} } }}{r}} \right), \hfill \\ \sigma^{\prime}_{1n} = \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} {\frac{{P_{z} }}{a}\left( {\overline{f}e^{i\varphi } + fe^{ - i\varphi } } \right)\left( {m^{\prime}_{j} - c^{\prime}_{66} } \right)B^{\prime}_{njk} \frac{{l^{\prime}_{1njk} \sqrt {r^{2} - l_{1njk}^{\prime 2} } }}{{r\left( {l_{2njk}^{\prime 2} - l_{1njk}^{\prime 2} } \right)}}} } , \hfill \\ \end{gathered} $$

$$ \begin{aligned} \sigma^{\prime}_{2n} &= \sum\limits_{k = 1}^{2n} {\sum\limits_{j = 1}^{2} { - \frac{{c^{\prime}_{66} P_{z} }}{a}B^{\prime}_{njk} \left[ {fe^{i\varphi } \frac{{l^{\prime}_{1njk} \sqrt {r^{2} - l_{1njk}^{\prime 2} } }}{{r\left( {l_{2njk}^{\prime 2} - l_{1njk}^{\prime 2} } \right)}} + \overline{f}e^{i3\varphi } \left\{ { - \frac{{8az^{\prime}_{njk} }}{{r^{3} }}} \right.} \right.} } \\ & \quad - \left. {\left. {\frac{{\sqrt {r^{2} - l_{1njk}^{\prime 2} } }}{{r^{3} l^{\prime}_{1njk} \left( {l_{2njk}^{\prime 2} - l_{1njk}^{\prime 2} } \right)}}\left[ {8a^{2} l_{2njk}^{\prime 2} - 8a^{2} r^{2} + \left( {3r^{2} - 4a^{2} + 4z_{njk}^{\prime 2} } \right)l_{1njk}^{\prime 2} } \right]} \right\}} \right] \\ & \quad + \frac{{c^{\prime}_{66} P_{z} }}{a}B^{\prime}_{n0} \left[ {fe^{i\varphi } \frac{{l^{\prime}_{1n0} \sqrt {r^{2} - l_{1n0}^{\prime 2} } }}{{r\left( {l_{2n0}^{2} - l_{1n0}^{2} } \right)}} - \overline{f}e^{i3\varphi } \left\{ { - \frac{{8az^{\prime}_{n0} }}{{r^{3} }}} \right.} \right. \\ & \quad - \left. {\left. {\frac{{\sqrt {r^{2} - l_{1n0}^{\prime 2} } }}{{r^{3} l^{\prime}_{1n0} \left( {l_{2n0}^{\prime 2} - l_{1n0}^{\prime 2} } \right)}}\left[ {8a^{2} l_{2n0}^{\prime 2} - 8a^{2} r^{2} + \left( {3r^{2} - 4a^{2} + 4z_{n0}^{2} } \right)l_{1n0}^{\prime 2} } \right]} \right\}} \right], \\ \end{aligned} $$

$$\begin{aligned} \sigma ^{\prime}_{{zn}} &= \sum\limits_{{k = 1}}^{{2n}} {\sum\limits_{{j = 1}}^{2} {\frac{{P_{z} }}{{2a}}\left( {\bar{f}e^{{i\varphi }} + fe^{{ - i\varphi }} } \right)\omega ^{\prime}_{j} B^{\prime}_{{njk}} \frac{{l^{\prime}_{{1njk}} \sqrt {r^{2} - l_{{1njk}}^{{\prime 2}} } }}{{r\left( {l_{{2njk}}^{{\prime 2}} - l_{{1njk}}^{{\prime 2}} } \right)}}} } , \\ \tau ^{\prime}_{{zn}} &= \sum\limits_{{k = 1}}^{{2n}} {\sum\limits_{{j = 1}}^{2} {\frac{{P_{z} }}{{2a}}s^{\prime}_{j} \omega ^{\prime}_{j} B^{\prime}_{{njk}} \left[ {f\frac{{\sqrt {a^{2} - l_{{1njk}}^{{\prime 2}} } }}{{l_{{2njk}}^{{\prime 2}} - l_{{1njk}}^{{\prime 2}} }}} \right.} } \left. { + \bar{f}e^{{i2\varphi }} \left( {\frac{{\sqrt {a^{2} - l_{{1njk}}^{{\prime 2}} } }}{{l_{{2njk}}^{{\prime 2}} - l_{{1njk}}^{{\prime 2}} }} - \frac{{2a}}{{r^{2} }} + \frac{2}{{r^{2} }}\sqrt {a^{2} - l_{{1njk}}^{{\prime 2}} } } \right)} \right] \\ & \quad - \frac{{s^{\prime}_{0} c^{\prime}_{{44}} P_{z} }}{{2a}}B^{\prime}_{{n0}} \left[ {f\frac{{\sqrt {a^{2} - l_{{1n0}}^{{\prime 2}} } }}{{l_{{2n0}}^{{\prime 2}} - l_{{1n0}}^{{\prime 2}} }}} \right.\left. { - \bar{f}e^{{i2\varphi }} \left( {\frac{{\sqrt {a^{2} - l_{{1n0}}^{{\prime 2}} } }}{{l_{{2n0}}^{{\prime 2}} - l_{{1n0}}^{{\prime 2}} }} - \frac{{2a}}{{r^{2} }} + \frac{2}{{r^{2} }}\sqrt {a^{2} - l_{{1n0}}^{{\prime 2}} } } \right)} \right], \\ \end{aligned}$$

(B3.2)

and the undetermined coefficients $B_{n0}$, $\overline{B}_{n0}$, $B^{\prime}_{n0}$ $B_{njk}$, $\overline{B}_{njk}$ and $B^{\prime}_{njk}$ are determined by the following recursive formulas (B4.1)–(B4.3):

$$ \begin{aligned} & \overline{B}_{112} = \overline{B}_{121} = 0,\,\sum\limits_{j = 1}^{2} {\omega_{1} \overline{B}_{1jj} = 0} , \\ & c_{44} s_{0} \overline{B}_{10} + \sum\limits_{j = 1}^{2} {s_{j} \omega_{j} \overline{B}_{1jj} } = 0, \\ & c_{44} s_{0} \overline{B}_{10} - \sum {s_{j} \omega_{j} \overline{B}_{1jj} = - \frac{1}{\pi },} \\ \end{aligned} $$

(B4.1)

$$ \begin{aligned} & \overline{B}_{{\left( {n + 1} \right)0}} = B_{n0} , \\ & \overline{B}_{{\left( {n + 1} \right)21}} = \overline{B}_{{\left( {n + 1} \right)1\left( {2n + 2} \right)}} = 0, \\ & \omega_{1} \overline{B}_{{\left( {n + 1} \right)11}} + \omega_{2} \overline{B}_{{\left( {n + 1} \right)22}} = - \omega_{1} B_{n11} , \\ & \omega_{1} \overline{B}_{{\left( {n + 1} \right)1\left( {2n + 1} \right)}} + \omega_{2} \overline{B}_{{\left( {n + 1} \right)2\left( {2n + 2} \right)}} = - \omega_{2} B_{{n1\left( {2n} \right)}} , \\ & \omega_{1} \overline{B}_{{\left( {n + 1} \right)1\left( {m + 1} \right)}} + \omega_{2} \overline{B}_{{\left( {n + 1} \right)2\left( {m + 2} \right)}} = - \omega_{1} B_{{n1\left( {m + 1} \right)}} - \omega_{{2B_{n2m} }} , \\ & s_{1} \omega_{1} \overline{B}_{{\left( {n + 1} \right)11}} + s_{2} \omega_{2} \overline{B}_{{\left( {n + 1} \right)22}} = s_{1} \omega_{1} B_{n11} , \\ & s_{1} \omega_{1} \overline{B}_{{\left( {n + 1} \right)1\left( {2n + 1} \right)}} + s_{2} \omega_{2} \overline{B}_{{\left( {n + 1} \right)2\left( {2n + 2} \right)}} = s_{2} \omega_{2} B_{{n2\left( {2n} \right)}} , \\ & s_{1} \omega_{1} \overline{B}_{{\left( {n + 1} \right)1\left( {m + 1} \right)}} + s_{2} \omega_{2} \overline{B}_{{\left( {n + 1} \right)2\left( {m + 2} \right)}} = s_{1} \omega_{1} B_{{n1\left( {m + 1} \right)}} + s_{2} \omega_{2} B_{n2m} , \\ & \quad ( n = 1,2, \ldots ,\infty ;m = 1,2, \ldots ,2n - 1), \\ \end{aligned} $$

(B4.2)

$$ \begin{aligned} & B_{n0} - B^{\prime}_{n0} = - \overline{B}_{n0} , \\ & \sum\limits_{j = 1}^{2} {\left( {B_{njk} - B^{\prime}_{njk} } \right) = - \sum\limits_{j = 1}^{2} {\overline{B}_{njk} } } , \\ & \sum\limits_{j = 1}^{2} {\left( {s_{j} k_{j} B_{njk} + s^{\prime}_{j} k^{\prime}_{j} B^{\prime}_{njk} } \right) = \sum\limits_{j = 1}^{2} {s_{j} k_{j} \overline{B}_{njk} } } , \\ & \sum\limits_{j = 1}^{2} {\left( { - \omega_{j} B_{njk} + \omega^{\prime}_{j} B^{\prime}_{njk} } \right) = \sum\limits_{j = 1}^{2} {\omega_{j} \overline{B}_{njk} } } , \\ & c_{44} s_{0} B_{n0} + c^{\prime}_{44} s^{\prime}_{0} + B^{\prime}_{n0} = c_{44} s_{0} \overline{B}_{n0} , \\ & \sum\limits_{j = 1}^{2} {\left( {s_{j} \omega_{j} B_{njk} + s^{\prime}_{j} \omega^{\prime}_{j} B^{\prime}_{njk} } \right) = \sum\limits_{j = 1}^{2} {s_{j} \omega_{j} \overline{B}_{njk} } } , \\ & \quad ( n = 1,2, \ldots ,\infty ;k = 1,2, \ldots ,2n). \\ \end{aligned} $$

(B4.3)

1.3 Appendix C: General solution

In the Cartesian coordinates $(x,y,z)$, when the plane $xOy$ is parallel to the isotropic plane, the constitutive equations of the three-dimensional transversely isotropic material are in the form of

$$ \begin{aligned} \sigma_{x} & = c_{11} \frac{\partial u}{{\partial x}} + c_{12} \frac{\partial v}{{\partial y}} + c_{13} \frac{\partial w}{{\partial z}},\,\tau_{yz} = c_{44} \left( {\frac{\partial v}{{\partial z}} + \frac{\partial w}{{\partial y}}} \right), \\ \sigma_{y} & = c_{12} \frac{\partial u}{{\partial x}} + c_{11} \frac{\partial v}{{\partial y}} + c_{13} \frac{\partial w}{{\partial z}},\,\tau_{zx} = c_{44} \left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial x}}} \right), \\ \sigma_{z} & = c_{13} \frac{\partial u}{{\partial x}} + c_{13} \frac{\partial v}{{\partial y}} + c_{33} \frac{\partial w}{{\partial z}},\,\tau_{xy} = \frac{1}{2}(c_{11} - c_{12} )\left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right). \\ \end{aligned} $$

(C1)

Disregarding of body forces, the mechanical equilibrium differential equations are

$$ \frac{{\partial \sigma_{x} }}{\partial x} + \frac{{\partial \tau_{xy} }}{\partial y} + \frac{{\partial \tau_{xz} }}{\partial z} = 0 ,\,\frac{{\partial \tau_{xy} }}{\partial x} + \frac{{\partial \sigma_{y} }}{\partial y} + \frac{{\partial \tau_{yz} }}{\partial z} = 0,\,\frac{{\partial \tau_{zx} }}{\partial x} + \frac{{\partial \tau_{yz} }}{\partial y} + \frac{{\partial \sigma_{z} }}{\partial z} = 0. $$

(C2)

In the cylinder coordinates $(r,\phi ,z)$, when the plane $rO\phi$ is parallel to the isotropic plane, the constitutive equations of the three-dimensional transversely isotropic material are in the form of

$$ \begin{aligned} \sigma_{r} & = c_{11} \frac{{\partial u_{r} }}{\partial r} + c_{12} \left( {\frac{{u_{r} }}{r} + \frac{1}{r}\frac{{\partial u_{\varphi } }}{\partial \varphi }} \right) + c_{13} \frac{{\partial u_{z} }}{\partial z},\tau_{r\varphi } = c_{66} \left( {\frac{1}{r}\frac{{\partial u_{r} }}{\partial \varphi } + \frac{{\partial u_{\varphi } }}{\partial r} - \frac{{u_{\varphi } }}{r}} \right), \\ \sigma_{\varphi } & = c_{12} \frac{{\partial u_{r} }}{\partial r} + c_{11} \left( {\frac{{u_{r} }}{r} + \frac{1}{r}\frac{{\partial u_{\varphi } }}{\partial \varphi }} \right) + c_{13} \frac{{\partial u_{z} }}{\partial z},\tau_{\varphi z} = c_{44} \left( {\frac{{\partial u_{\varphi } }}{\partial z} + \frac{1}{r}\frac{{\partial u_{z} }}{\partial \varphi }} \right), \\ \sigma_{z} & = c_{13} \left( {\frac{{\partial u_{r} }}{\partial r} + \frac{{u_{r} }}{r} + \frac{1}{r}\frac{{\partial u_{\varphi } }}{\partial \varphi }} \right) + c_{33} \frac{{\partial u_{z} }}{\partial z},\tau_{zr} = c_{44} \left( {\frac{{\partial u_{z} }}{\partial r} + \frac{{\partial u_{r} }}{\partial z}} \right). \\ \end{aligned} $$

(C3)

Disregarding of body forces, mechanical equilibrium differential equations are

$$ \begin{aligned} & \frac{{\partial \sigma_{r} }}{\partial r} + \frac{1}{r}\frac{{\partial \tau_{r\varphi } }}{\partial \varphi } + \frac{{\partial \tau_{rz} }}{\partial z} + \frac{{\sigma_{r} - \sigma_{\varphi } }}{r} = 0, \\ & \frac{{\partial \tau_{r\varphi } }}{\partial r} + \frac{1}{r}\frac{{\partial \sigma_{\varphi } }}{\partial \varphi } + \frac{{\partial \tau_{\varphi z} }}{\partial z} + \frac{{2\tau_{r\varphi } }}{r} = 0, \\ & \frac{{\partial \tau_{rz} }}{\partial r} + \frac{1}{r}\frac{{\partial \tau_{\varphi z} }}{\partial \varphi } + \frac{{\partial \sigma_{z} }}{\partial z} + \frac{{\tau_{rz} }}{r} = 0, \\ \end{aligned} $$

(C4)

where $u_{m}$ and $\sigma_{m}$$(\tau_{mn} )$ $(m,n = r,\varphi ,z)$ represent components of the mechanical displacement and normal stress, respectively; $c_{ij}$ $(i,j = 1,2, \ldots ,6)$ are the elastic modulus. For transversely isotropic materials, $c_{66} = (c_{11} - c_{12} )/2$.

Substituting Eqs. (C1) and (C3) into Eqs. (C2) and (C4), we have the following combined general solution

$$ \begin{aligned} U & = u + iv = e^{i\varphi } (u_{r} + iu_{\varphi } ),\,\sigma_{1} = \sigma_{x} + \sigma_{y} = \sigma_{r} + \sigma_{\varphi } , \\ \sigma_{2} & = \sigma_{x} - \sigma_{y} + 2i\tau_{xy} = e^{2i\varphi } (\sigma_{r} - \sigma_{\varphi } + 2i\tau_{r\varphi } ),\,\tau_{z} = \tau_{xz} + i\tau_{yz} = e^{i\varphi } (\tau_{rz} + i\tau_{\varphi z} ). \\ \end{aligned} $$

(C5)

Rewrite the general solution in a compact form of

$$ \begin{aligned} U & = \Delta \left( {i\psi_{0} + \sum\limits_{j = 1}^{2} {\psi_{j} } } \right),\,w = \sum\limits_{j = 1}^{2} {s_{j} k_{j} \frac{{\partial \psi_{j} }}{{\partial z_{j} }}} , \\ \sigma_{1} & = 2\sum\limits_{j = 1}^{2} {\left( {m_{j} - c_{66} } \right)\frac{{\partial^{2} \psi_{j} }}{{\partial z_{j}^{2} }}} = - 2\sum\limits_{j = 1}^{2} {\left( {m_{j} - c_{66} } \right)\,\Lambda \psi_{j} } ,\,\sigma_{2} = 2c_{66} \Delta^{2} \left( {i\psi_{0} + \sum\limits_{j = 1}^{2} {\psi_{j} } } \right), \\ \sigma_{z} & = \sum\limits_{j = 1}^{2} {\omega_{j} \frac{{\partial^{2} \psi_{j} }}{{\partial z_{j}^{2} }}} = - \sum\limits_{j = 1}^{2} {\omega_{j} \Lambda \psi_{j} } ,\,\tau_{z} = \Delta \left( {s_{0} c_{44} i\frac{{\partial \psi_{0} }}{{\partial z_{0} }} + \sum\limits_{j = 1}^{2} {s_{j} \omega_{j} \frac{{\partial \psi_{j} }}{{\partial z_{j} }}} } \right), \\ \end{aligned} $$

(C6)

where

$$ \begin{aligned} k_{j} & = \frac{{c_{11} - c_{44} s_{j}^{2} }}{{(c_{13} + c_{44} )s_{j}^{2} }},\,\omega_{j} = c_{33} s_{j}^{2} k_{j} - c_{13} , \\ m_{j} & = 2c_{66} - \omega_{1j} s_{j}^{2} ,\,\Delta = \partial /\partial x + i\partial /\partial y, \\ \Delta^{2} & = \partial^{2} /\partial x^{2} - \partial^{2} /\partial y^{2} + 2i\partial^{2} /\partial x\partial y. \\ \end{aligned} $$

(C7)

For an axisymmetric problem, the general solutions of Eqs. (C4) and (C3) are

$$ \begin{aligned} u_{r} & = \sum\limits_{j = 1}^{2} {\frac{{\partial \psi_{j} }}{\partial r}} ,\,u_{z} = \sum\limits_{j = 1}^{2} {s_{j} k_{j} \frac{{\partial \psi_{j} }}{{\partial z_{j} }}} ,\,u_{\varphi } = 0, \\ \sigma_{r} & = - 2c_{66} \sum\limits_{j = 1}^{2} {\frac{1}{r}\frac{{\partial \psi_{j} }}{\partial r}} - \sum\limits_{j = 1}^{2} {s_{j}^{2} \omega_{j} \frac{{\partial^{2} \psi_{j} }}{{\partial z_{j}^{2} }}} , \\ \sigma_{\phi } & = 2c_{66} \sum\limits_{j = 1}^{2} {\frac{1}{r}\frac{{\partial \psi_{j} }}{\partial r}} - \sum\limits_{j = 1}^{2} {(s_{j}^{2} \omega_{j} - 2c_{66} )\frac{{\partial^{2} \psi_{j} }}{{\partial z_{j}^{2} }}} , \\ \sigma_{z} & = \sum\limits_{j = 1}^{2} {\omega_{j} \frac{{\partial^{2} \psi_{j} }}{{\partial z_{j}^{2} }}} ,\,\tau_{zr} = \sum\limits_{j = 1}^{2} {s_{j} \omega_{j} \frac{{\partial^{2} \psi_{j} }}{{\partial r\partial z_{j} }}} ,\,\tau_{r\phi } = \tau_{\phi z} = 0, \\ \end{aligned} $$

(C8)

when $s_{1} \ne s_{2}$, $\psi_{j}$ satisfies the harmonic equation

$$ \left( {\Lambda + \frac{{\partial^{2} }}{{\partial z_{j}^{2} }}} \right)\psi_{j} = 0\quad \left( {j = 0,1,2} \right), $$

(C9)

and

$$ \begin{aligned} \Lambda & = \partial^{2} /\partial x^{2} + \partial^{2} /\partial y^{2} = \partial^{2} /\partial r^{2} + \partial /(r\partial r) + \partial^{2} /(r^{2} \partial \phi^{2} ), \\ z_{j} & = s_{j} z\quad (j = 0,1,2), \\ s_{0} & = \sqrt {c_{66} /c_{44} } , \\ \end{aligned} $$

(C10)

where the eigenvalues $s_{j} \,\left( {j = 1,2} \right)$ satisfying ${\text{Re}} (s_{j} ) > 0$ should be satisfied with the following equation:

$$ as^{4} - bs^{2} + c = 0, $$

(C11)

with

$$ a = c_{33} c_{44} ,\,b = c_{11} c_{33} + c_{44}^{2} - \left( {c_{13} + c_{44} } \right)^{2} ,\,c = c_{11} c_{44} . $$

(C12)

It should be noted that the general solution in Eq. (C8) is only used when $s_{1} \ne s_{2}$.