1 Introduction

In many engineering applications, it is required to bring a mechanical system from one level of constant displacement to another desired displacement through the application of a suitable force. While this intuitively points to applying a step function type of force, such forces cannot be applied to many structural and mechanical systems because of their inertias. Hence, papers in the literature that deal with step function force inputs are not directly relevant to this study. One thus perceives the need to find practical forces, which are continuous in time, that must be applied so that the system moves from one constant displacement state to another without undershoots or overshoots. Deviations of the displacement from the desired final constant displacement state created by undershoots and overshoots can cause deleterious effect that could damage the structural/mechanical system and/or reduce its functionality. Moreover, if the transit from one constant displacement state to another constant displacement state is required of a subsystem, undershoots and overshoots may prevent the larger system (of which the subsystem is a part) from functioning properly or may delay its functioning until such time as the deviations from the desired constant level are small enough for the larger system to adequately function.

An initial study to handle this problem for a classically damped linear vibrating system was provided in Ref. [1]. This study hinges on the understanding of a single-degree-of-freedom (SDOF) damped linear oscillator whose displacement is required to transit from one constant displacement level to another desired level without any undershoots and overshoots. Control forces required to be applied to the oscillator to accomplish this transit were obtained using successively complex control methodologies: polynomials in time, open-loop control, and closed loop control. It should be pointed out that though the problem of determining such practical control forces has gone largely unnoticed, there is considerable literature on the behavior of linear systems to step inputs (see for example, Refs. [2,3,4,5]), which are not easily realizable in many structural and mechanical systems due to their inertias.

In the literature what is meant by the problem of overshooting is “making sure that y(t) approaches r(t) ‘from below’ " (y(t) is the actual trajectory and r(t) the desired one) [6], i.e. it is addressed during the transition time, while in this paper undershooting and overshooting are meant after the transition, i.e. once the desired final state is reached, although we also pay attention to what happens during the transition, but without introducing apposite constraints to eliminate overshoots and undershoots during this phase. Most of the papers have been developed in the linear realm [2, 7,8,9], and there appear to be few attempts [6, 10,11,12] to handle the nonlinear problem in the current literature. Furthermore, the main stream is that of using feedback (active or closed-loop) control [7,8,9, 13].

This paper deals with explorations and extensions for handling nonlinear oscillating systems as opposed to linear ones, with objectives and methods different from those present in the literature (apart from [1]), since we adopt an open-loop (passive) control. It belongs to the realm of “design" problems (the controller has been properly designed); according to [7], “there have been relatively few design oriented results, especially in the continuous time arena", and this work is aimed at reducing a bit this paucity. We look at an SDOF nonlinear oscillating system and attempt to find the necessary control forces to transit its displacement from a given constant level to another desired constant level with no undershoots and/or overshoots after the control has been switched off. To the best of our knowledge, Ref. [1], which deals only with linear systems, appears to be the closest reported study.

Two approaches to finding the control forces are investigated in this paper. The first considers a generic transit trajectory given by a polynomial function (in time) to obtain the necessary control, while the second employs a transit trajectory that uses knowledge of the undamped, unforced behavior of the nonlinear system to augment a polynomial function of time. The latter approach is useful when such behavior of the nonlinear system can be explicitly obtained, as occurs with some models of nonlinear mechanical systems that are often employed. A commonly occurring nonlinear SDOF system modelled by a Duffing-type oscillator is used in this paper to illustrate the results.

The structure of the paper is as follows. Section 2 states the problem. Section 3 provides the first approach. It gives a generic way for obtaining the control force that permits a nonlinear oscillator to have a polynomial target trajectory so that no overshoots/undershoots occur when transitioning from one given constant displacement state to another desired constant displacement state by using a generic target trajectory. In Sect. 3.1 the approach is applied to the damped Duffing oscillator. Monotonicity properties of the control force are presented in Sect. 3.2. In Sect. 3.3 practical considerations that lead to inaccuracies in the application of the desired forces and that might result in perturbations in the trajectory of the Duffing oscillator are considered. Robustness of the approach to fairly large perturbations in the oscillator’s state is investigated. Section 4 deals with the second approach. It uses a target trajectory that utilizes the solution to the undamped, unforced Duffing equation augmented by a polynomial. Detailed comparisons between the control forces obtained from the two approaches are made.

2 The problem

We want to extend the goal of [1] to the generic nonlinear system

$$\begin{aligned}&\ddot{x}+ \delta \dot{x} + g(x) = f(t), \quad \delta >0. \end{aligned}$$
(1)

Without loss of generality, we assume that \(g(0)=0\), so that \(x=0\) is an equilibrium position without external force (\(f(t)=0\)), and thus also \(\dot{x}=0\). After a possible preliminary application of available modal reduction techniques [14], this equation describes the relevant motion of “any" mechanical system where the dynamics has substantially only one degree-of-freedom (as in all resonant problems without internal resonance, or in the presence of 2D nonlinear invariant manifolds extending the linear modes [15]).

More specifically, the objective is, starting from the given and known initial conditions \(x(0)=x_0\) and \(\dot{x}(0)=\dot{x}_0\), to arrive at \(x(T)=x_f\) and \(\dot{x}(T)=0\) in a given time T. This final condition guarantees that for \(t \ge T\), i.e. after the control is switched off, the solution is the equilibrium point \(x_f\) obtained for

$$\begin{aligned}&f(t)=f(T)=g(x_f)=\text {constant}, \end{aligned}$$
(2)

which clearly has no overshoots or undershoots. T is the duration of time over which the transit from the initial state to the final state is effected. The key point is that the transit must occur without overshoots and undershoots, and so cannot be obtained by a step force.

Commonly the initial conditions vanish, \(x_0=0\) and \(\dot{x}_0=0\), but we consider generic values to be more comprehensive and to accommodate uncertainties and imperfections, as we will see in due course.

3 Generic nonlinear term

We assume that the target transit trajectory is given by

$$\begin{aligned}&x(t)=a_0+a_1 t + a_2 t^2 + a_3 t^3 + a_4 t^4 + a_5 t^5. \end{aligned}$$
(3)

Actually, there are infinitely many trajectories satisfying the goal of not having undershoots and overshoots. We limit to polynomials because they are perhaps the simplest, at least from a mathematical point of view, a property that is welcome from a practical point of view. Within the family of polynomial transit trajectories, the (3) is the minimal one allowing satisfaction of all the requested constraints (see the following), so it is the simplest and, in some rough sense, the “optimal" one. Of course it is possible to select other trajectories, satisfying different optimality criteria (in term or time duration, requested energy, force limits, etc.). This is outside the scope of the present work, and is left for further developments.

A sufficient condition for not having overshoots or undershoots also during the transition (which actually is not our main goal, but just an added value) is that (3) is monotonic, i.e.

$$\begin{aligned}&\dot{x}(t)=a_1 +2 a_2 t +3 a_3 t^2 +4 a_4 t^3 +5 a_5 t^4=0 \end{aligned}$$
(4)

has no real solutions for \(0<t<T\). Addressing this in detail is out of the scope of the present work.

By enforcing the boundary conditions

$$\begin{aligned}&x(0)=x_0, \quad \dot{x}(0)=\dot{x}_0, \nonumber \\&x(T)=x_f, \quad \dot{x}(T)=0, \end{aligned}$$
(5)

and the continuity of the force,

$$\begin{aligned}&f(0)=f_0, \quad f(T)=g(x_f), \end{aligned}$$
(6)

we get

$$\begin{aligned}&a_0=x_0, \quad a_1=\dot{x}_0, \quad a_2=- \frac{1}{2} (\delta \dot{x}_0+g(x_0)-f_0), \nonumber \\&a_3 = \frac{3}{2 \, T} (\delta \dot{x}_0+g(x_0)-f_0) - 6 \frac{ \dot{x}_0}{T^2} + 10 \frac{ (x_f-x_0)}{T^3}, \nonumber \\&a_4 = - \frac{3}{2 \, T^2} (\delta \dot{x}_0+g(x_0)-f_0) + 8 \frac{ \dot{x}_0}{T^3} - 15 \frac{ (x_f-x_0)}{T^4}, \nonumber \\&a_5 = \frac{1}{2 \, T^3} (\delta \dot{x}_0+g(x_0)-f_0) - 3 \frac{ \dot{x}_0}{T^4} + 6 \frac{ (x_f-x_0)}{T^5}. \end{aligned}$$
(7)

The coefficients simplify considerably if the system starts from rest, so that \(x_0=\dot{x}_0=0\). We then have (remember that we have assumed \(g(0)=0\) without loss of generality, so that also \(f(0)=f_0=0\))

$$\begin{aligned}&a_0=a_1=a_2=0, \quad a_3 = 10 \frac{ x_f}{T^3}, \quad a_4 = - 15 \frac{ x_f}{T^4}, \quad a_5 = 6 \frac{ x_f}{T^5}; \end{aligned}$$
(8)

in that case the transit trajectory is

$$\begin{aligned}&x(\tau )=x_f \left( 10 \tau ^3 - 15 \tau ^4 + 6 \tau ^5 \right) , \end{aligned}$$
(9)

where we have defined \(\tau =t/T { \in [0,1]}\).

Inserting Eq. (3) into (1) we obtain the searched forcing:

$$\begin{aligned} f(t)&= (2 a_2 + 6 a_3 t + 12 a_4 t^2 + 20 a_5 t^3) \nonumber \\&\quad + \delta (a_1 + 2 a_2 t + 3 a_3 t^2 + 4 a_4 t^3 + 5 a_5 t^4) \nonumber \\&\quad + g(a_0+a_1 t + a_2 t^2 + a_3 t^3 + a_4 t^4 + a_5 t^5). \end{aligned}$$
(10)

It is worth remarking that it is very general, and applies to any nonlinear system without restrictions; it requires only the knowledge of the nonlinear term g(x), in agreement with the open-loop approach that needs the knowledge of the system.

As seen from (7), the smaller T is, the larger the coefficients become, and the force required, in general, increases as might be expected, because larger forces are required to move the mass when the time duration of the motion reduces.

If we do not require the continuity of the f(t), i.e. \(f(0) \ne f_0\) and \(f(T) \ne g(x_f)\), a cubic expression in (3) is enough. In this case we get

$$\begin{aligned} a_0&=x_0, \quad a_1=\dot{x}_0, \quad a_2=- 2 \frac{ \dot{x}_0}{T} + 3 \frac{x_f-x_0}{T^2}, \nonumber \\ a_3&= \frac{\dot{x}_0}{T^2} -2 \frac{x_f-x_0}{T^3}, \end{aligned}$$
(11)

and

$$\begin{aligned} f(t)&= (2 a_2 + 6 a_3 t) + \delta (a_1 + 2 a_2 t + 3 a_3 t^2) \nonumber \\&\quad + g(a_0+a_1 t + a_2 t^2 + a_3 t^3). \end{aligned}$$
(12)

We have

$$\begin{aligned} f(0)&= - 4 \frac{ \dot{x}_0}{T} + 6 \frac{x_f-x_0}{T^2} + \delta \dot{x}_0 + g(x_0), \nonumber \\ f(T)&= 2 \frac{ \dot{x}_0}{T} - 6 \frac{x_f-x_0}{T^2} + g(x_f). \end{aligned}$$
(13)

We can also think of giving up only one of the two, i.e. \(f(0) \ne 0\) or \(f(T) \ne g(x_f)\), and in this case a quartic expression is needed in (3).

Stability of the proposed approach remains to be studied. If the control force f(t) in (10) leads to instability, an additional controller can be used, or the force can be adjusted continuously by changing \(x_0\) and \(\dot{x}_0\) according to the measured displacement and velocity; this will be discussed in the next example. Also stability in the regime \(t > T\) may not be assured. Actually, defining \(\hat{x}=x-x_f\), the linearized equation of motion around \(x=x_f\) is given by

$$\begin{aligned}&\ddot{\hat{x}} + \delta \dot{\hat{x}} + a \hat{x} = 0, \quad a=\left. \frac{ \partial g}{ \partial x} \right| _{x=x_f}. \end{aligned}$$
(14)

Thus, the final equilibrium state is stable if \(a>0\). We do not discuss this latter aspect further since this work deals only with the transit from one to the other equilibrium states.

3.1 An example

As an illustrative example we consider the case \(g(x)=x+x^3\), that correspond to a Duffing equation, and \(\delta =0.05\). Note that the normalized, undamped, natural frequency of the linearized system is \(\omega =1\), so that the natural period is \(P=2 \pi = 6.283\).

Starting from \(x_0=\dot{x}_0=0\) we have that the target trajectory and the associated forcing are (remember that \(\tau =t/T\)):

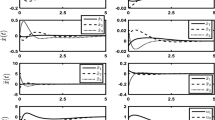
$$\begin{aligned} x(\tau )&= x_f \left( 10 \tau ^3 - 15 \tau ^4 + 6 \tau ^5 \right) , \nonumber \\ f(\tau )&=x_f^3 \left( 10 \tau ^3 - 15 \tau ^4 + 6 \tau ^5 \right) \nonumber \\&\quad +x_f \left( \frac{120\tau ^3-180 \tau ^2+60\tau }{T^2} + \frac{1.5 \tau ^4 -3 \tau ^3+1.5 \tau ^2}{T} + 10 \tau ^3 -15 \tau ^4 + 6 \tau ^5 \right) . \end{aligned}$$
(15)

They are shown in Figs. 1 and 2 for \(x_f=1.4\). Note that \(f(T)=g(x_f)=4.144\).

The dependence of \(f(\tau )\) on the duration T over which the force is applied is worthy of attention. For very small values of T (Fig. 2a) \(f(\tau )\) oscillates, with a large amplitude and therefore would be unsuitable for most engineering applications. For slightly larger values of T (\(T/P=0.2\) in Fig. 2b), it still oscillates but with a lesser amplitude, even though its maximum is larger than f(T) and its minimum smaller than 0. By increasing T (e.g. \(T/P=0.3\) in Fig. 2b), \(f(\tau )\) is still not monotonically increasing, but now \(0 \le f(t) \le f(T)\), which might make it perhaps suitable for some practical applications. Finally, for \(T/P>0.5\) the force-time history monotonically increases. Furthermore, the system reaches its final displacement \(x_f\) relatively fast, i.e. in about one half of the natural period of the linearized system. This monotonically increasing character of the control force, and the relatively short duration of time needed to achieve the desired terminal displacement \(x_f\), can make the use of such a control force very attractive from a practical point of view in many engineered systems.

Fig. 1
figure 1

The solution x(t) for \(\delta =0.05, x_0=0\) and \(\dot{x}_0=0\)

Full size image
Fig. 2
figure 2

The solution f(t) for \(\delta =0.05, x_0=0\), \(\dot{x}_0=0\) and \(x_f=1.4\). a \(T/P=0.078\), b \(T/P=0.2;0.3;0.4;0.5;{\textbf {0.6}};0.7;0.8\) (from the upper to the lower curve at \(t/T=0.2\))

Full size image

3.2 On the monotonicity of f(t)

As illustrated in Fig. 2, there is a (critical) value, \(T_\textrm{cr}\), of T above which the excitation f(t) is monotonic, which is welcome from a practical point of view.

This critical point is an inflection point of f(t), i.e. it is characterized by \(\dot{f}(t)=0\) and \(\ddot{f}(t)=0\). Given all the other parameters, these are two nonlinear algebraic equations in the two unknowns \(\tau =t/T \in [0,1]\) and T, that can be easily solved numerically and that provide the value of \(T_\textrm{cr}\). The solution can be found, for example, by drawing the two functions \(\dot{f}(t)=0\) and \(\ddot{f}(t)=0\) in the parameters plane \((\tau ,T)\), and then looking for their intersection. For the case of Fig. 2 these are reported in Fig. 3, and the solution is given by \(\tau =0.340103\) and \(T_\textrm{cr}=3.218083=0.512 P\), which is in agreement with the findings of Fig. 2.

Fig. 3
figure 3

The solutions of \(\dot{f}(t)=0\) (black) and \(\ddot{f}(t)=0\) (red) in the parameters plane \((\tau ,T)\) (color figure online)

Full size image

3.3 The effect of imperfections

To illustrate how the proposed method works with imperfections, and thus to implicitly study its stability and robustness, we add imperfection to the trajectory. More precisely, we divide the interval [0, T] in N points. At each of these instants \(t_i=i T/N, i=1,\ldots ,N\) points we:

  • add a random perturbation to the position \(x(t_i)\) and velocity \(\dot{x}(t_i)\). The amplitude of the perturbations of position and velocity are denoted by \(\alpha \) and \(\beta \), respectively;

  • determine the new force (10) with the coefficients \(a_i\) recalculated by means of (7), with the updated position \(x_0=x(t_i)+\alpha \, r_1\) and velocity \(\dot{x}_0=\dot{x}(t_i)+\beta \, r_2\) (\(r_{1,2}\) are uncorrelated random numbers uniformly distributed in \([-1,1]\)), \(f_0=f(t_i)\) and time of transit equal to \(T-t_i\). Note that by the previous choice f(t) is continuous;

  • proceed to the next instants.

The results, which are perturbations of the case of Figs. 1 and 2 for \(T/P=0.6\), are illustrated in Fig. 4 for different values of \(\alpha \) and always for \(\beta =\alpha \) (the case with \(\beta \ne \alpha \) does not introduce major qualitative differences in our simulations).

Fig. 4
figure 4

The solution x(t) and f(t) with perturbations. \(\delta =0.05, x_0=0, \dot{x}_0=0, x_f=1.4, T/P=0.6\) and \(N=20\). a \(\alpha =0.025\), b \(\alpha =0.05\), c \(\alpha =0.1\)

Full size image

We note that in general the excitation is very close to that of the unperturbed case, even for “large" perturbations (\(\alpha =0.1\)), apart from the final part. This is due to the fact that we strictly enforce the conditions \(x(T)=x_f\), \(\hat{x}(T)=0\) and \(f(T)=g(x_f)\), i.e. we do not accept perturbations on the final state. This requires extra effort in the last part of the transit interval, which, as expected, increases in magnitude for increasing perturbations.

To better appreciate this phenomenon we have performed a Monte Carlo simulations (with 200 samples) for different values of \(\alpha \). The mean and standard deviation of the maximum (to be compared with the value 4.144 in the absence of perturbations) and minimum (to be compared with the value 0 in the absence of perturbations) of f(t) are reported in Table 1. It is worth remarking that, as in Fig. 4, they are attained in the last part of the transit interval, commonly for \(\tau \in [1-(1/N),1]\).

Table 1 The statics (mean; standard deviation) of maximum and minimum values of f(t) for different values of imperfections amplitude \(\alpha \)
Full size table

The behaviour of the maximum and minimum of f(t) is also reported in the boxplots of Fig. 5. For increasing perturbation we observe an almost linear increase of the mean value of \(\max \{f(t)\}\) and a more involved decrement of \(\min \{f(t)\}\), with, as expected, an increase of the standard deviation.

Fig. 5
figure 5

The boxplot of maximum and minimum of f(t) for increasing values of the imperfections amplitude \(\alpha \). The parameters are the same of Fig. 4

Full size image

It is interesting to see how the maximum and minimum of f(t) are influenced by the number of subdivisions of the transit interval. The results for smaller and larger values of N are reported in Fig. 6, where it is clearly seen that, for every value of the imperfection amplitude \(\alpha \), the maximum and minimum of f(t) increase with N. This can be explained by noting that by increasing N the last subinterval of the transit is shorter, while the amplitude of the imperfection remains the same. Thus, it requires more effort to bring the solution to the final state (on which we do not accept perturbations, as previously said), since it has less time at its disposal. Difficulties at time \(t=T\), though of a different nature, are also encountered in terminal optimal control problems [16]. A simple way to overcome this problem is to allow some discrepancies in the final state, i.e. admitting that the transition ends at \(x_f+\varepsilon \), \(\varepsilon \) small, instead of exactly at \(x_f\), and let the stability for \(t>T\) to control the dynamics after the control is switched off.

Fig. 6
figure 6

The boxplot of maximum and minimum of f(t) for increasing values of the imperfections amplitude \(\alpha \). The parameters are the same of Fig. 4, but a \(N=10\) and b \(N=40\). Note that the vertical axes have different scales

Full size image

The conclusion is that the proposed method is robust and stable, but could be improved in the final part by allowing some approximation in the final stage.

4 The Duffing equation

In this section we specifically consider the Duffing equation [17]

$$\begin{aligned}&\ddot{x}+ \delta \dot{x} + x + k_3 x^3 = f(t), \quad \delta >0, \end{aligned}$$
(16)

which is important from a practical, and indeed historical, point of view [18]. It is the prototype equation for 1DOF systems with smooth odd nonlinearity.

In this section, contrary to what has been done previously, we exploit the solution of the undamped unforced nonlinear system. In fact, for \(\delta =0\) and \(f(t)=0\) the solution of (16) is

$$\begin{aligned}&x(t) = c_1 \, sn(a \, t + c_2, b), \end{aligned}$$
(17)

where

$$\begin{aligned}&a^2=1+\frac{c_1^2 k_3}{2}, \quad b^2 = \frac{c_1^2 k_3}{c_1^2 k_3 + 2}, \end{aligned}$$
(18)

and where \(c_1\) and \(c_2\) are constants of integration, to be determined by the boundary conditions. The functions sn, cn and dn (that will be used in the following) are the Jacobian elliptic functions [19]. Note that for \(k_3>0\) both a and b are real, while for \(k_3<0\) the parameter b is imaginary.

We look for a transit trajectory in the form

$$\begin{aligned}&x(t)= c_1 sn(a \, t + c_2, b) + a_0+a_1 t + a_2 t^2 + a_3 t^3, \end{aligned}$$
(19)

so that the forcing is given by

$$\begin{aligned} f(t)&= \delta [ c_1 \, a \, cn(a \, t + c_2, b) dn(a \, t + c_2, b) + a_1 + 2 a_2 t + 3 a_3 t^2] \nonumber \\ {}&\quad +3 \, k_3 \, c_1 [(a_3 \, t^3 + a_2 \, t^2 + a_1 \,t + a_0) \, c_1 \,sn(a \,t+c_2,b)^2 \nonumber \\ {}&\quad + (a_3^2 \, t^6+2 \, a_2 \, a_3 \, t^5+2 \, a_1 \, a_3 \, t^4+a_2^2 \, t^4+2 \, a_0 \, a_3 \, t^3+2 \, a_1 \, a_2 \, t^3 \nonumber \\ {}&\quad +2 \, a_0 \, a_2 \, t^2+a_1^2 \, t^2+2 \, a_0 \, a_1 \, t+a_0^2) \, sn(a \, t+c2, b)] \nonumber \\ {}&\quad +2 \, a_2+6 \, a_3 \, t + a_0 + a_1 \, t + a_2 \, t^2 + a_3 \, t^3 + k_3 (a_3 \, t^3 + a_2 \, t^2 + a_1 \, t+a_0)^3. \end{aligned}$$
(20)

The choice of this transit trajectory was dictated by the willing to exploit as much as possible the free (nonlinear) dynamics of the structures, that is then expected to reduce as much as possible the control efforts. Actually, the free dynamics alone are not able to get the results, and so we needed to “correct" them, and we did it with polynomials, again with the aim of proposing the simplest solution.

From the boundary conditions (5), we obtain

$$\begin{aligned} a_0&=x_0 - c_1 sn( c_2, b), \quad a_1= \dot{x}_0- c_1 \, a \, cn(c_2,b) \, dn(c_2,b), \nonumber \\ a_2&=\frac{c_1 \, a [2 \, cn(c_2,b) \, dn(c_2,b) + cn(a\,T+c_2,b) \, dn(a\,T+c_2,b)]-2 \dot{x}_0}{T} \nonumber \\&\quad + 3 \frac{c_1 [sn(c_2,b)-sn(a\,T+c_2,b)] + x_f-x_0}{T^2} \nonumber \\ a_3&=\frac{- c_1 \, a [cn(c_2,b) \, dn(c_2,b) + cn(a\,T+c_2,b) \, dn(a\,T+c_2,b)] + \dot{x}_0}{T^2} \nonumber \\&\quad - 2 \frac{c_1 [sn(c_2,b)-sn(a\,T+c_2,b)] + x_f-x_0}{T^3}. \end{aligned}$$
(21)

The two remaining constants \(c_1\) and \(c_2\) can be computed by the continuity conditions (6). This leads to two nonlinear algebraic equations, that can be solved numerically.

For illustrative purposes, we consider the following parameters:

$$\begin{aligned}&\delta =0.05, \quad T=0.49, \quad k_3=1, \quad x_0=0, \quad \dot{x}_0=0, \quad x_f=1.4. \end{aligned}$$
(22)

These values are the same as those considered in Sect. 3.1. Note that the final magnitude of the driving force is \(f(T)=x_f+k_3 x_f^3=4.144\), and that \(T=0.49\) corresponds to \(T/P=0.078\), i.e. the same value used in Fig. 2a.

Due to the nonlinear nature of the equations, multiple solutions are possible for the same values of the parameters, and this is an element of novelty with respect to the approach in Sect. 3. Actually, to capture all solutions, a contour plot of the solutions of two Eq. (6) can be drawn: the various points of intersection represent the different solutions of the problem, that in turn give the different transit trajectories. For the parameter values (22), which we consider below, this is shown in Fig. 7.

Fig. 7
figure 7

The solutions of \(f(0)=0\) (red curve) and \(f(T)=g(x_f)\) (black curve) for \(\delta =0.05, T=0.49, k_3=1, x_0=0, \dot{x}_0=0, x_f=1.4\). The dot highlights the case of the first row of Table 2, corresponding to the minimum force (color figure online)

Full size image

The various solutions are shown in Table 2 and illustrated in Fig. 8.

The solutions are monotonic in x(t), and have different maximum and minimum values of f(t), i.e. different amplitudes (Table 2). Since, according to (20) and (21), the amplitude is related to the value of \(c_1\), and because we are interested in having the lowest amplitude, we will consider only the solution with the lowest value of \(c_1\): in the case of Table 2 it is the first one. As seen from Fig. 8a, the general form of the control needed is very similar to that shown in Fig. 2a.

It is interesting to detect what happens to the amplitude of f(t) by varying the transit time T, which is a parameter of major interest in practical applications. Still referring to the values (22), except for T, the maximum and the minimum of f(t) as a function of T are shown in Fig. 9, where two different branches of the solution are shown, in blue and in red.

Table 2 Solutions for \(\delta =0.05, T=0.49, k_3=1, x_0=0, \dot{x}_0=0, x_f=1.4\)
Full size table
Fig. 8
figure 8

Solutions x(t) and f(t) for \(\delta =0.05, T=0.49, k_3=1, x_0=0, \dot{x}_0=0, x_f=1.4\)

Full size image
Fig. 9
figure 9

The functions \(f_{\max }\) (the upper one) and \(f_{\min }\) (the lower one) as a function of T for \(\delta =0.05, k_3=1, x_0=0, \dot{x}_0=0, x_f=1.4\)

Full size image

The main observation is that the amplitude is a decreasing function of the transit time, according to common sense (the slower the easier).

There are some characteristic values of T:

  1. 1.

    For increasing values of the transit time, at \(T\simeq 0.802\) (\(T/P=0.128\)) the initial blue branch of the solution disappears, by a mechanism similar to a saddle-node bifurcation (two solutions collide and disappear). Above this value there is another branch, the red one, that actually exists also for \(T<0.802\).

  2. 2.

    At \(T\simeq 1.75\) (\(T/P=0.274\)) the maximum value of the force \(f_{\max }\) becomes equal to the final value \(f(T)=4.144\), as shown by the dashed line. Above \(T\simeq 1.75\) there is no need to have extra force above the target value. For \(T > 1.75\) we report in Fig. 9—dashdot—the value of the internal local maximum of f(T) (like in Fig. 2).

  3. 3.

    At \(T\simeq 1.97\) (\(T/P=0.313\)) the minimum value of the force \(f_{\min }\) becomes equal to zero. Above \(T\simeq 1.97\) there is no need to have negative forces to transit. For \(T > 1.97\) we report in Fig. 9—dashdot—the value of the internal local minimum of f(T).

  4. 4.

    At \(T\simeq 3.92\) (\(T/P=0.624\)) the function f(t) becomes monotonic (see Fig. 10). This represents the range of major practical interest. It is worth noting the T is 62.4% of the natural period P of the system, so that we are still in a quite “fast" transit regime (see [1] for further details).

Fig. 10
figure 10

Solutions x(t) and f(t) for \(\delta =0.05, T=4.0, k_3=1, x_0=0, \dot{x}_0=0, x_f=1.4\)

Full size image

From a practical point of view, in addition to the maximum required force, it is also important to consider the work done during the transit, which is given by

$$\begin{aligned}&W=\int _0^{x_f} f(x)\textrm{d}x = \int _0^T f(t) \dot{x}(t) \textrm{d}t. \end{aligned}$$
(23)

The work as a function of T is reported in Fig. 11. It is a decreasing function of T, as expected. It is to be noted that in the interval \( 0.75 \simeq T \simeq 0.802\) (see the magnification of Fig. 11b) less work is done by using the red branch of the solution compared to the blue branch, even though the red branch shows a higher maximum force (see Fig. 9), so that here it is not evident which is the most convenient solution from a practical point of view.

Fig. 11
figure 11

The work W as a function of T for \(\delta =0.05, k_3=1, x_0=0, \dot{x}_0=0, x_f=1.4\). The red segment of the plot beyond \(T \simeq 0.8\) is where a single solution emerges for the forcing function (control), and the green segment of the plot shows the region in which the forcing (control) becomes monotonic (color figure online)

Full size image

Another relevant aspect is that W is smaller than the hypothetical work that would be required if both the force and the position would increase linearly from the initial to the final states, that is given by \(\hat{W}=f(T) \times x_f / 2 = 2.9\).

To better understand the effects of the final position, we now consider \(x_f=0.7\) while keeping the other values reported in (22). In this case \(f(T)=1.043\). The same procedure for obtaining the solution in the case \(x_f=1.4\) is used. The maximum and the minimum values of f(t) as a function of T are reported in Fig. 12. The overall qualitative behaviour is the same for \(x_f=1.4\), apart from an initial major complexity due to a second branch disappearing through a saddle-node bifurcation. The thresholds for having \(f(t)<f(T)\), \(\forall t \in (0,T)\), at \(T=2.32\), and \(f(t)>0\), \(\forall t \in (0,T)\), at \(T=2.33\), practically coincide. Above \(T \cong 3.84\), i.e. at 61% of P, the excitation f(t) is monotonically increasing.

The associated work W is reported in Fig. 13. It is less than \(\hat{W}=0.365\) for \(T>0.95\).

Fig. 12
figure 12

The functions \(f_{\max ,\min }\) as a function of T for \(\delta =0.05, k_3=1, x_0=0, \dot{x}_0=0, x_f=0.7\)

Full size image
Fig. 13
figure 13

The work W as a function of T for \(\delta =0.05, k_3=1, x_0=0, \dot{x}_0=0, x_f=0.7\). The brown segment of the plot beyond \(T \simeq 1.2\) is where a single solution emerges for the forcing function (control), and the green segment of the plot shows the region in which the forcing (control) becomes monotonic (color figure online)

Full size image

By increasing \(x_f\), the lowest values of T for which \(0 \le f(t) \le f(T)\) for \(0 \le t \le T\) are reported in Table 3. The lowest value of T for which the force is monotone increasing is also shown. Note that the first threshold is inversely dependent on \(x_f\), while the second one is almost independent of \(x_f\).

5 Conclusions

This paper investigates the problem of controlling a single-degree-of-freedom nonlinear dynamical system so that it transits in time from a given state to one of given constant displacement amplitude at, and after, a pre-specified duration of time T. The aim is to obtain control forces that can be used in practical situations for engineered systems. Two strategies for doing this are explored and they are illustrated by application to the damped Duffing’s equation. The first is based on one of the methods proposed in Ref. [1], the second uses the free dynamics of the nonlinear system.

In the first approach the target trajectory for the nonlinear system is assumed to be a polynomial in time, which then provides in closed form the control force required. The nature of the control force as the duration of time T is changed is investigated for the Duffing’s system and it is shown that for values of T that exceed a threshold, the control force is monotonic and increases to its maximum value at time T. The robustness of the approach is analyzed by looking at discontinuous random perturbations at instants of time during the system’s time-transit and it is shown that for small perturbations, the control appears to be robust.

Table 3 Thresholds on T for different values of \(x_f\)
Full size table

The second approach, which is a novel way of looking at the system, employs the free dynamics of the undamped Duffing’s oscillator. In this approach the target trajectory is taken to be the trajectory of the free undamped Duffing’s oscillator to which is appended a polynomial in time. The nonlinear nature of the system now provides multiple forcing functions that transport the system from a given initial state to a given final constant displacement state at, and beyond, a given duration of time, T. These multiple solutions are explored computationally and it is shown that for a given value of the final displacement their number depends on the duration T. After choosing the control force that has the lowest peak value, the value of T beyond which it is monotonically increasing is determined. The manner in which the multiple solutions affect the total work done they do is also investigated. The work done decreases with increasing T, as expected, and it is shown that smaller peak amplitude control forces do not necessarily imply that they perform less work over the duration T. As the desired final constant value of the displacement increases, in order for the force over the duration T to be less than its value at time T it is shown that the value of T decreases. However, the lowest value of T for the force to be monotone increasing is computationally shown to be far less sensitive to the desired final constant value of the displacement, a somewhat non-intuitive result.

There are many possible further developments. Among them, we believe that the most interesting consists of introducing some quantitative optimality criteria to select the best transit trajectory, in terms of minimal transition time, minimal requested energy, constraints on the force, etc. They will improve the qualitative criterion used in this paper, i.e. the simplicity of the solution. Another possible development consists of applying the proposed technique to different nonlinear systems. Finally, we feel that the comparison with experimental results will be certainly a step that needs to be done in the near future.