Static analysis of functionally graded plate structures resting on variable elastic foundation under various boundary conditions

Abstract

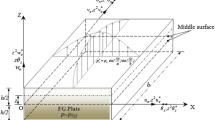
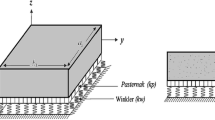
Functionally graded materials are widely utilized in several industrial applications, and their accurate modeling is challenging for researchers, principally for FGM nanostructures. This study develops and presents a quasi-3D analytical plate theory to explore the bending behavior of a new model of FG plate structures (FGPSs), resting on modified four parameters Winkler/Pasternak elastic foundations, under various boundary conditions. For this context, different types of functionally graded nanoplates (FGNPs), including (i) the classical FG nanoplate, (ii) the FG sandwich nanoplate, (iii) the trigonometric FG nanoplate of type A, and (4) the trigonometric FG nanoplate of type B as well as their macro-counterparts are also examined. Cosine functions describe the material gradation and material properties through the thickness of the FGNPs. The modified continuum nonlocal strain gradient theory is utilized to include the material and geometrical nanosize length scales. The kinematic relations of the plate are achieved according to hybrid hyperbolic-parabolic functions to satisfy parabolic variation of shear along the thickness of FGNP and zero shears at the inferior and superior surfaces. The equilibrium equations are obtained using the virtual work principle and solved using the Galerkin method to cover various boundary conditions. The results for the macro-counterparts of FGNPs are obtained by taking the small-scale parameters zero in the special cases. The precision and consistency of the generated analytical model are confirmed by comparing the findings to results from the scientific literature. Moreover, a comprehensive parametric study is also performed to determine the sensitivity of the bending response of FGPSs to boundary conditions, EF parameters, nonlocal length-scale, strain gradient microstructure-scale, and geometry.

Appendix

$$\begin{gathered} K_{{11}} = A_{{11}} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y + A_{{66}} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - \user2{\lambda }\left[ {\left( {A_{{11}} + A_{{66}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { + A_{{11}} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{5} X_{m} }}{{\partial x^{5} }}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y + A_{{66}} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right], \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{12}} = \left( {A_{{12}} + A_{{66}} } \right)\left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { - \user2{\lambda }\left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right]} \right), \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{13}} = - B_{{11}} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y - \left( {B_{{12}} + 2B_{{66}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y \hfill \\\quad\quad\quad - \lambda \left[ { - \left( {B_{{12}} + 2B_{{66}} + B_{{11}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right.\left. { - B_{{11}} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{5} X_{m} }}{{\partial x^{5} }}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right], \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{14}} = B_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y + B_{{66}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - \user2{\lambda }\left[ {\left( {B_{{11}}^{s} + B_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { + B_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{5} X_{m} }}{{\partial x^{5} }}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y + B_{{66}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right], \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{15}} = \left( {B_{{12}}^{s} + B_{{66}}^{s} } \right)\left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { - \user2{\lambda }\left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right]} \right), \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{16}} = G_{{13}}^{s} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { - \user2{\lambda }\left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right]} \right), \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{21}} = \left( {A_{{12}} + A_{{66}} } \right)\left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{1} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { - \user2{\lambda }\left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right]} \right), \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{22}} = A_{{11}} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y + A_{{66}} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - \user2{\lambda }\left[ {\left( {A_{{11}} + A_{{66}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { + A_{{11}} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{5} Y_{n} }}{{\partial y^{5} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y + A_{{66}} \mathop {\mathop \int \limits^{a} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right], \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{23}} = - B_{{11}} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial x}}{\text{d}}x{\text{d}}y - \left( {B_{{12}} + 2B_{{66}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial Y_{n} }}{{\partial x}}X_{m} \frac{{\partial Y_{n} }}{{\partial x}}{\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - \lambda \left( { - \left( {B_{{11}} + B_{{12}} + 2B_{{66}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial x}}{\text{d}}x{\text{d}}y} \right. - \left( {B_{{12}} + 2B_{{66}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial Y_{n} }}{{\partial x}}X_{m} \frac{{\partial Y_{n} }}{{\partial x}}{\text{d}}x{\text{d}}y\left. { - B_{{11}} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{5} Y_{n} }}{{\partial y^{5} }}X_{m} \frac{{\partial Y_{n} }}{{\partial x}}{\text{d}}x{\text{d}}y} \right), \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{24}} = \left( {B_{{12}}^{s} + B_{{66}}^{s} } \right)\left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { - \lambda \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right]} \right), \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{25}} = B_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y + B_{{66}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - \lambda \left[ {\left( {B_{{11}}^{s} + B_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { + B_{{66}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y + B_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{5} Y_{n} }}{{\partial y^{5} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right], \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{26}} = G_{{13}}^{s} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { - \user2{\lambda }\left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right]} \right), \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{13}} = B_{{11}} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{n} }}{{\partial x^{4} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y + \left( {B_{{12}} + 2B_{{66}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - \lambda \left[ {B_{{11}} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{6} X_{n} }}{{\partial x^{6} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right. + \left( {B_{{11}} + B_{{12}} + 2B_{{66}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y \left. { + \left( {B_{{12}} + 2B_{{66}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right], \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{23}} = B_{{11}} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y + \left( {B_{{12}} + 2B_{{66}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - \lambda \left[ {\left( {B_{{11}} + B_{{12}} + 2B_{{66}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { + \left( {B_{{12}} + 2B_{{66}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y + B_{{11}} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{6} Y_{n} }}{{\partial y^{6} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right], \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{33}} = - D_{{11}} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right) \hfill \\ \quad \quad \quad - 2\left( {D_{{12}} + 2D_{{66}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - \lambda \left[ { - D_{{11}} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{6} X_{m} }}{{\partial x^{6} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right)} \right. \hfill \\ \quad \quad \quad - 2\left( {D_{{12}} + 2D_{{66}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - D_{{11}} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{6} Y_{n} }}{{\partial y^{6} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right) \hfill \\ \quad \quad \quad \left. { - 2\left( {D_{{12}} + 2D_{{66}} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right] \hfill \\ \quad \quad \quad - k_{w} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right. \left. { - \mu \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right]} \right) \hfill \\ \quad \quad \quad + k_{{S1}} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right. \left. { - \mu \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right]} \right) \hfill \\ \quad \quad \quad + k_{{S2}} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right. \left. { - \mu \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right]} \right), \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{34}} = D_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y + \left( {D_{{12}}^{s} + 2D_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - \lambda \left[ {D_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{6} X_{m} }}{{\partial x^{6} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right. + \left( {D_{{11}}^{s} + D_{{12}}^{s} + 2D_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y \left. { + \left( {D_{{12}}^{s} + 2D_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right], \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{35}} = D_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y + \left( {D_{{12}}^{s} + 2D_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - \lambda \left[ {\left( {D_{{12}}^{s} + 2D_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad + D_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{6} Y_{n} }}{{\partial y^{6} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad \left. { + \left( {D_{{11}}^{s} + D_{{12}}^{s} + 2D_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right], \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{36}} = H_{{13}}^{s} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}Y_{n} X_{m} Y_{n} dxdy + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} dxdy} \right. \hfill \\ \quad \quad \quad - \lambda \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}Y_{n} X_{m} Y_{n} dxdy + 2\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} dxdy} \right. + \left. {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} dxdy} \right) \hfill \\ \quad \quad \quad - \Phi ^{\prime } \left( z \right)k_{w} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} Y_{n} X_{m} Y_{n} dxdy} \right. \left. { - \mu \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}Y_{n} X_{m} Y_{n} dxdy + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} dxdy} \right]} \right) \hfill \\ \quad \quad \quad - k_{w} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} Y_{n} X_{m} Y_{n} dxdy} \right. \left. { - \mu \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}Y_{n} X_{m} Y_{n} dxdy + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} dxdy} \right]} \right) \hfill \\ \quad \quad \quad - \Phi ^{\prime } \left( z \right)k_{{S1}} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}Y_{n} X_{m} Y_{n} dxdy} \right. - \mu \left. {\left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}Y_{n} X_{m} Y_{n} dxdy + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} dxdy} \right]} \right) \hfill \\ \quad \quad \quad - \Phi ^{\prime } \left( z \right)k_{{S2}} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} dxdy} \right. \left. { - \mu \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} dxdy + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} dxdy} \right]} \right). \hfill \\ \end{gathered}$$

$$\begin{gathered} C_{{41}} = B_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y + B_{{66}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - \lambda \left[ {B_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{5} X_{m} }}{{\partial x^{5} }}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right. + \left( {B_{{11}}^{s} + B_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad \left. { + B_{{66}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right], \hfill \\ \end{gathered}$$

$$\begin{gathered} C_{{42}} = \left( {B_{{12}}^{s} + B_{{66}}^{s} } \right)\left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { - \lambda \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right]} \right), \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{43}} = - D_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y - \left( {D_{{12}}^{s} + 2D_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - \lambda \left[ { - \left( {D_{{11}}^{s} + D_{{12}}^{s} + 2D_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right. - D_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{5} X_{m} }}{{\partial x^{5} }}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad \left. { - \left( {D_{{12}}^{s} + 2D_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right], \hfill \\ \end{gathered}$$

$$\begin{gathered} C_{{44}} = F_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y + F_{{66}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - A_{{44}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y - \lambda \left[ {F_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{5} X_{m} }}{{\partial x^{5} }}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad + \left( {F_{{66}}^{s} + F_{{11}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y - A_{{44}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad \left. { + F_{{66}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y - A_{{44}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right], \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{45}} = \left( {F_{{12}}^{s} + F_{{66}}^{s} } \right)\left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { - \lambda \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right]} \right), \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{46}} = \left( {J_{{13}}^{s} - A_{{44}}^{s} } \right)\left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right. \hfill \\ \left. {\quad \quad \quad - \lambda \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{3} X_{m} }}{{\partial x^{3} }}Y_{n} \frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial X_{m} }}{{\partial x}}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}\frac{{\partial X_{m} }}{{\partial x}}Y_{n} {\text{d}}x{\text{d}}y} \right]} \right), \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{15}} = \left( {B_{{12}}^{s} + B_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - \lambda \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right], \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{52}} = B_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y + B_{{66}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - \lambda \left( {\left( {B_{{11}}^{s} + B_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { + B_{{66}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y + B_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{5} Y_{n} }}{{\partial y^{5} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right), \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{53}} = - D_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y - \left( {D_{{12}}^{s} + 2D_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - \lambda \left[ { - \left( {D_{{12}}^{s} + 2D_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right. - D_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{5} Y_{n} }}{{\partial y^{5} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y \hfill \\ \quad\quad\quad\left. { - \left( {D_{{11}}^{s} + D_{{12}}^{s} + 2D_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right], \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{54}} = \left( {F_{{12}}^{s} + F_{{66}}^{s} } \right)\left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { - \lambda \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right]} \right), \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{55}} = F_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y + F_{{66}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad - A_{{44}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y - \lambda \left( {\left( {F_{{11}}^{s} + F_{{66}}^{s} } \right)\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad + F_{{66}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y - A_{{44}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y \hfill \\ \quad \quad \quad \left. { + F_{{11}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{5} Y_{n} }}{{\partial y^{5} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y - A_{{44}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right), \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{56}} = \left( {J_{{13}}^{s} - A_{{44}}^{s} } \right)\left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad \left. { - \lambda \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial Y_{n} }}{{\partial y}}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{3} Y_{n} }}{{\partial y^{3} }}X_{m} \frac{{\partial Y_{n} }}{{\partial y}}{\text{d}}x{\text{d}}y} \right]} \right), \hfill \\ \end{gathered}$$

$$K_{{61}} = - G_{{13}}^{s} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right.\left. { - \user2{\lambda }\left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right]} \right),$$

$$K_{{62}} = - G_{{13}}^{s} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right)\left. { - \user2{\lambda }\left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right]} \right),$$

$$\begin{gathered} K_{{63}} = \left( {H_{{13}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right. \hfill \\ \quad \quad \quad - \lambda \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y + 2\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right.\left. {\left. { + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right]} \right), \hfill \\ \end{gathered}$$

$$K_{{64}} = \left( {A_{{44}}^{s} - J_{{13}}^{s} } \right)\left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y - \lambda \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{4} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right]} \right),$$

$$\begin{gathered} K_{{65}} = \left( {A_{{44}}^{s} - J_{{13}}^{s} } \right)\left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right. \hfill \\ \left. {\quad \quad \quad - \lambda \left[ {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right]} \right), \hfill \\ \end{gathered}$$

$$\begin{gathered} K_{{66}} = A_{{44}}^{s} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right) \hfill \\ \quad \quad \quad - K_{{33}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y - \lambda \left[ {A_{{44}}^{s} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{4} X_{m} }}{{\partial x^{2} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right)} \right. \hfill \\ \quad \quad \quad - K_{{33}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}Y_{n} X_{m} Y_{n} {\text{d}}x{\text{d}}y + A_{{44}}^{s} \left( {\mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} \frac{{\partial ^{2} X_{m} }}{{\partial x^{2} }}\frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y + \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{4} Y_{n} }}{{\partial y^{4} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right)\left. { - K_{{33}}^{s} \mathop {\mathop \int \limits^{a} }\limits_{0} \mathop {\mathop \int \limits^{b} }\limits_{0} X_{m} \frac{{\partial ^{2} Y_{n} }}{{\partial y^{2} }}X_{m} Y_{n} {\text{d}}x{\text{d}}y} \right]. \hfill \\ \end{gathered}$$